Skip to main content
SpringerLink
Log in

Impact of maker-taker fees on stock exchange competition from an agent-based simulation

  • Research Article
  • Published:
Journal of Computational Social Science Aims and scope Submit manuscript

Abstract

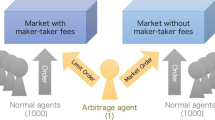
One fee structure offered by stock exchanges is maker-taker fees, in which the exchange pays rebates to traders who place limit orders and collects trading fees from traders who place market orders. A stock market that employs maker-taker fees is thought to outpace its stock market competition in the sense that its relative market volume share will increase due to the expectation of efficient market formation. However, whether this idea is true has not been sufficiently investigated. Therefore, in the present study, we constructed two artificial markets, one with maker-taker fees and the other without them, and investigated how the trading shares of these two markets vary. We also calculated and compared market liquidity, volatility, and efficiency of the two markets. As a result, the market volume share of the market with maker-taker fees was found to increase with the rebate amount when the stock exchange provided sufficient rebates. Otherwise, the market with maker-taker fees lost market volume share to the market without maker-taker fees. In addition, we found that market liquidity increased and volatility decreased in the market that adopted maker-taker fees. In the market that does not adopt maker-taker fees, market liquidity and volatility did not necessarily improve. In contrast, market efficiency was found to improve in both markets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. A limit order is a buy order or sell order that is placed at a specific price.

  2. A market order is a buy order or sell order that is placed without specifying a price.

  3. Bid means buy, and ask means sell. The best bid quote is the highest buy order price and the best ask quote is the lowest sell order price.

  4. In this study, we use logarithmic returns. Therefore, the expected return is the difference between the logarithm of the current price and the logarithm of the expected price, that is, \({r_e}^t_j=\ln {{P_e}^t_j}-\ln {P^{t}}=\ln {({P_e}^t_j/P^{t})}\), which allows us to derive Eq. (3).

  5. The reason why \(t_e=1{,}000{,}000\) was chosen is that this value was sufficient to grasp the trend of the experiment, and no difference in the trend occurred even if the period was extended.

  6. Varying parameters such as the profit expected by the exchange (\(R_{EX}\) in the model) may change the boundary between intervals A and B, but the tendency for the share to change similarly depending on the amount of rebate is not expected to change.

References

  1. Battalio, R., Corwin, S. A., & Jennings, R. (2016). Can brokers have it all? On the relation between make-take fees and limit order execution quality. The Journal of Finance, 71(5), 2193–2238.

    Article  Google Scholar 

  2. Brolley, M., & Malinova, K. (2020). Maker-taker fees and liquidity: The role of commission structures. https://ssrn.com/abstract=3726190. Accessed 23 June 2022.

  3. CFTC-SEC. (2011). Recommendations regarding regulatory responses to the market events of may 6, 2010. Tech. rep., CFTC-SEC Joint Advisory Committee.

  4. Chen, S. H., Chang, C. L., & Du, Y. R. (2012). Agent-based economic models and econometrics. The Knowledge Engineering Review, 27(2), 187–219.

    Article  Google Scholar 

  5. Chiarella, C., Iori, G., & Perelló, J. (2009). The impact of heterogeneous trading rules on the limit order book and order flows. Journal of Economic Dynamics and Control, 33(3), 525–537.

    Article  Google Scholar 

  6. Cont, R. (2001). Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance, 1, 223–236.

    Article  Google Scholar 

  7. Cox, J., Van Ness, B., & Van Ness, R. (2019). Increasing the tick: Examining the impact of the tick size change on maker-taker and taker-maker market models. Financial Review, 54(3), 417–449.

    Article  Google Scholar 

  8. Di Maggio, M., Liu, J., Rizova, S., & Wiley, R. (2020). Exchange fees and overall trading costs. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.3625801

    Article  Google Scholar 

  9. Foucault, T., Kadan, O., & Kandel, E. (2013). Liquidity cycles and make/take fees in electronic markets. The Journal of Finance, 68(1), 299–341.

    Article  Google Scholar 

  10. Garvey, R., Huang, T., & Wu, F. (2017). What influences ‘maker-taker’ decisions in U.S. equity markets? SSRN Electronic Journal. https://doi.org/10.2139/ssrn.3037319.

    Article  Google Scholar 

  11. Kusada, Y., Mizuta, T., Hayakawa, S., & Izumi, K. (2014). Impacts of position-based market makers on markets’ shares of trading volumes-an artificial market approach. In: Social Modeling and Simulations+ Econophysics Colloquium 2014.

  12. Lin, Y., Swan, P., & Harris, F. (2016). Maker-taker fee, liquidity competition, and high frequency trading. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.2826376

    Article  Google Scholar 

  13. Lutat, M. (2010). The effect of maker-taker pricing on market liquidity in electronic trading systems—Empirical evidence from European equity trading. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.1752843

    Article  Google Scholar 

  14. MacKenzie, D., & Pardo-Guerra, J. P. (2014). Insurgent capitalism: Island, bricolage and the re-making of finance. Economy and Society, 43(2), 153–182. https://doi.org/10.1080/03085147.2014.881597.

    Article  Google Scholar 

  15. Mandelbrot, B. (1967). The variation of some other speculative prices. The Journal of Business, 40(4), 393–413. http://www.jstor.org/stable/2351623. Accessed 23 June 2022.

  16. Mizuta, T., Izumi, K., Yagi, I., & Yoshimura, S. (2015). Investigation of price variation limits, short selling regulation, and uptick rules and their optimal design by artificial market simulations. Electronics and Communications in Japan, 98(7), 13–21.

    Article  Google Scholar 

  17. Mizuta, T., Matsumoto, W., Kosugi, S., Izumi, K., Kusumoto, T., & Yoshimura, S. (2014). Do dark pools stabilize markets and reduce market impacts? investigations using multi-agent simulations. In: 2014 IEEE Conference on computational intelligence for financial engineering & economics (CIFEr), pp. 71–76. IEEE.

  18. Mizuta, T., Noritake, Y., Hayakawa, S., & Izumi, K. (2016). Affecting market efficiency by increasing speed of order matching systems on financial exchanges-investigation using agent based model. In: 2016 IEEE Symposium Series on Computational Intelligence (SSCI), pp. 1–8. IEEE.

  19. Muranaga, J. (1999). Dynamics of market liquidity of Japanese stocks: An analysis of tick-by-tick data of the tokyo stock exchange. In: B.F.I. Settlements (ed.) Market liquidity: Research findings and selected policy implications, vol. 11, pp. 1–25. Bank for International Settlements. https://EconPapers.repec.org/RePEc:bis:biscgc:11-13.

  20. Nakajima, Y., Shiozawa, Y. (2004). Usefulness and feasibility of market maker in a thin market. In The International Conference experiments in economic sciences: new approaches to solving real-world problems, pp. 1000–1003. https://www.cc.kyoto-su.ac.jp/project/orc/execo/EES2004/proceedings.html. Accessed 23 June 2022.

  21. Nishizaki, K., Tsuchikawa, A., & Yagi, T. (2013). Indicators related to liquidity in JGB markets. Bank of Japan Review Series 13-E-3, Bank of Japan. https://EconPapers.repec.org/RePEc:boj:bojrev:13-e-3. Accessed 23 June 2022.

  22. Sewell, M. (2011). Characterization of financial time series. http://finance.martinsewell.com/stylized-facts/. Accessed 23 June 2022.

  23. Yagi, I., Hoshino, M., & Mizuta, T. (2020). Analysis of the impact of maker-taker fees on the stock market using agent-based simulation. In Proceedings of the first ACM international conference on AI in finance, ICAIF '20. New York: Association for Computing Machinery. https://doi.org/10.1145/3383455.3422523.

  24. Yagi, I., Masuda, Y., & Mizuta, T. (2019). Detection of factors influencing market liquidity using an agent-based simulation. In A. S. Chakrabarti, L. Pichl, & T. Kaizoji (Eds.), Network theory and agent-based modeling in economics and finance (pp. 111–131). Springer.

    Chapter  Google Scholar 

  25. Yeh, C. H., & Yang, C. Y. (2013). Do price limits hurt the market? Journal of Economic Interaction and Coordination, 8(1), 125–153. https://doi.org/10.1007/s11403-012-0107-4

    Article  Google Scholar 

  26. Zhou, X., & Li, H. (2017). Buying on margin and short selling in an artificial double auction market. https://doi.org/10.1007/s10614-017-9722-4.

Download references

Author information

Authors and Affiliations

  1. Information and Computer Sciences, Graduate School of Kanagawa Institute of Technology, Atsugi, Kanagawa, Japan

    Mahiro Hoshino

  2. SPARX Asset Management Co., Ltd., Minato, Tokyo, Japan

    Takanobu Mizuta

  3. Faculty of Information Technology, Kanagawa Institute of Technology, Atsugi, Kanagawa, Japan

    Yasuhiro Sudo

  4. Department of Information Systems and Applied Mathematics, Faculty of Informatics, Kogakuin University, Shinjuku, Tokyo, Japan

    Isao Yagi

Authors
  1. Mahiro Hoshino
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Takanobu Mizuta
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yasuhiro Sudo
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Isao Yagi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Isao Yagi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix

A Validity of artificial market models

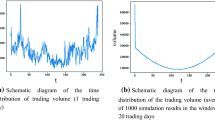
Many empirical studies have pointed out that in real markets, statistical properties such as fat tails and volatility clustering (stylized facts) appear [6, 22]. A fat tail is a condition in which a frequency distribution (histogram) is created from data on the rate of change of prices, and the kurtosis is large and the bottom of the distribution is thicker compared to a normal distribution. When the kurtosis is positive, the distribution has a fat tail. Volatility clustering refers to the tendency for large changes in returns to be followed by large changes for some time, and small changes to be followed by small changes [15]. This is quantitatively indicated by the fact that returns and autocorrelations of squared and absolute values of returns are positive even when there is a lag.

In this model, the parameters were set to reproduce stylized facts and to keep the model as stable as possible. To achieve these goals, we followed the model of Yagi et al. [24]. As an example, Table 2 shows the stylized facts when the basic maker-taker fees are not adopted and \(R_\mathrm{M}\)=– 0.050%. The lag used in 2 indicates the degree of shift in the autocorrelation of the squared returns. Label lag1 indicates the autocorrelation between the t-period and the \(t-1\)-period, and label lag2 indicates the autocorrelation between the t-period and the \(t-2\)-period. As can be seen from this table, both the kurtosis and the autocorrelations are positive.

Table 2 Stylized facts (with \(R_\mathrm{M}\)=-0.050%)
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hoshino, M., Mizuta, T., Sudo, Y. et al. Impact of maker-taker fees on stock exchange competition from an agent-based simulation. J Comput Soc Sc 5, 1323–1342 (2022). https://doi.org/10.1007/s42001-022-00169-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42001-022-00169-5

Keywords

Search

Navigation