Abstract
We provide the first strategic analysis of the interaction between a continuum of potentially green consumers and two firms in regional science. Firm 1 (2) sells new (remanufactured) toner cartridges. Each firm selects its price and a consumer purchases from the firm that offers her the highest utility. Utility is given by a surplus measure, the price, and by the transport cost incurred in traveling to a firm’s location. We first derive the best response functions of the two firms. Second, we stipulate a numerical value for the surplus measure and show that when the two firms select their “monopoly” prices, the Nash equilibrium is unique. Third, we specify a linear transport cost function with a constant coefficient and show that the costlier it is for consumers to get to the locations of the two firms, the higher is the price charged by these two firms. Finally, our analysis shows that there is a need to study models in which the two toner cartridges are dissimilar, the interaction between consumers and firms is repeated, and behavioral factors are taken into account.
Similar content being viewed by others
Notes
Go to https://vsc.gsa.gov/green/files/CPG.pdf for additional details. Accessed on 8 March 2018.
Ferrer and Ayres (2000), Dethloff (2001), Madsen and Jensen-Butler (2004), Aghazadeh (2008) and Hamdouch et al. (2016) mention transport related issues in the context of remanufacturing, resource recovery, and sub-regional economic activity but the reader should note that there is no overlap between the topics covered in these five papers and the specific questions we address in the present paper.
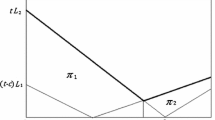
See Tirole (1988, pp. 279–282) and Fudenberg and Tirole (1991, pp. 14–15) for textbook expositions of the Hotelling (1929) model. See Tadelis (2013, pp. 43–126) and Batabyal and Nijkamp (2016) for, respectively, a textbook account and a recent application of static games of complete information. The Hotelling (1929) model is a general model and hence either it or its variants have been used to study a variety of research topics in economics. Specifically, this model has been used to study topics as diverse as strategic outsourcing for supply chain management by Shy and Stenbacka (2003), the influences of store-brand introductions by Groznik and Heese (2010), facility location problems by Gastner (2011), and channel performance by Fu et al. (2013). It is important to understand that these four papers all contain new applications of the Hotelling model. As such, the results emanating from these papers are new from an applications perspective. Similarly, the results we obtain in our paper are also new in the sense that we use the Hotelling model to provide the first strategic analysis in regional science of the ways in which transport costs influence the decision to buy either a new or a remanufactured good.
For concreteness, in the remainder of this paper, we shall think of our remanufactured good as a toner cartridge. The reader should note that the model we analyze and the results we obtain are in no way dependent on the remanufactured good being a toner cartridge. Other real world examples of new and remanufactured goods include new and remanufactured cameras and new and remanufactured cell phones.
The symbol \( s \) denotes the surplus a consumer derives from consuming either the new or the remanufactured good. This surplus measure is gross of the price and the transport cost. It is common to include such a measure in models of the sort that we are analyzing in this paper. See Tirole (1988, p. 279) for additional details on this point.
If the cost of producing either a new or a remanufactured toner cartridge can be modeled with a linear cost function then it would be straightforward to account for this cost in the analysis and the basic structure of our subsequent mathematical results in Sects. 4 through 6 below would be unchanged.
In order to make this paper interesting to as many readers as possible, we have decided to first derive the best response functions and to then use these functions to solve for the Nash equilibrium in Sect. 4. This is standard practice in many game theory textbooks. See Tadelis (2013, pp. 84–95) for some examples. Having said this, we recognize that we could also first state the Nash equilibrium in the form of a Proposition and then proceed to provide a proof of this Proposition.
In Sect. 4 below, we study the changes that arise in the market for new and remanufactured toner cartridges when this assumption is violated.
Note the use of the assumption that our environmentally conscious consumers are uniformly distributed on the interval [0,1].
Note that the right-hand-side (RHS) and the left-hand-side (LHS) of Eq. (2) are greater than zero.
In Sect. 2, we provided a detailed explanation of the reasons for working with a single surplus measure \( s \) and for only considering a horizontally differentiated product space. The reader should note that these two features together also provide the rationale for the symmetry—see Eqs. (7) and (8)—in our mathematical results.
We need \( s \ge 1.5 \) for consumer \( \tilde{z} = 1/2 \) to be indifferent between purchasing and not purchasing when \( p_{1} = p_{2} = 1. \) In this instance, all the other consumers will prefer purchasing a toner cartridge to not purchasing one.
References
Aghazadeh S (2008) The success of reverse logistics in supporting the environment: the case of the computer industry. Int J Env Sustain Dev 7:452–464
Agrawal V, Atasu A, Van Ittersum K (2015) Remanufacturing, third-party competition, and consumers’ perceived value of new products. Manage Sci 61:60–72
Atasu A, Guide VDR, Van Wassenhove LN (2010) So what if remanufacturing cannibalizes my new product sales? Calif Manage Rev 52:56–76
Batabyal AA, Beladi H (2016a) A game model of competition for market share between a new good producer and a remanufacturer. Econ Bull 36:963–969
Batabyal AA, Beladi H (2016b) A game model of new and remanufactured goods, brown and green consumers, and market share dominance. J Quant Econ 14:345–354
Batabyal AA, Beladi H (2018) Advertising and competition for market share between a new good producer and a remanufacturer. Ger Econ Rev 19:113–118
Batabyal AA, Nijkamp P (2016) A game model of international trade, transport costs, invasive species, and protocol compliance. Transp Res Part D 46:267–272
Carlton DW, Perloff JM (1994) Modern Industrial Organization, 2nd edn. Harper Collins College Publishers, New York
Dethloff J (2001) Vehicle routing and reverse logistics: the vehicle routing problem with simultaneous delivery and pick-up. OR Spektrum 23:79–96
Ferrer G, Ayres RU (2000) The impact of remanufacturing in the economy. Ecol Econ 32:413–429
Ferrer G, Swaminathan JM (2006) Managing new and remanufactured products. Manage Sci 52:15–26
Fu Y, Lai KK, Lian L (2013) Bricks or clicks: the impact of manufacturer’s encroachment on both manufacture-owned and traditional retail channels. Asia Pac J Mark Logist 25:695–714
Fudenberg D, Tirole J (1991) Game theory. MIT Press, Cambridge
Gastner MT (2011) Scaling and entropy in p-median facility location along a line. Phys Rev E84:1–7
Groznik A, Heese HS (2010) Supply chain interactions due to store-brand interactions: the impact of retail competition. Eur J Oper Res 203:575–582
Hamdouch Y, Qiang QP, Ghoudi K (2016) A closed-loop supply chain equilibrium model with random and price-sensitive demand and return. Netw Spatial Econ 17:459–503
Hotelling H (1929) Stability in competition. Econ J 39:41–57
Lebreton B, Tuma A (2006) A Quantitative approach to assessing the profitability of car and truck tire remanufacturing. Int J Prod Econ 104:639–652
Lund RT (1984) Remanufacturing. Technol Rev 87(19–23):28–29
Madsen B, Jensen-Butler C (2004) Theoretical and operational issues in sub-regional economic modelling, illustrated through the development and application of the LINE model. Econ Model 21:471–508
Mitra S, Webster S (2008) Competition in remanufacturing and the effects of government subsidies. Int J Prod Econ 111:287–298
Shi L, Sheng Z, Xu F (2015) The dynamics of competition in remanufacturing: a stability analysis. Econ Model 50:245–253
Shy O, Stenbacka R (2003) Strategic outsourcing. J Econ Behav Organ 50:203–224
Tadelis S (2013) Game theory: an introduction. Princeton University Press, Princeton
Tirole J (1988) The Theory of Industrial Organization. MIT Press, Cambridge
Acknowledgements
For their helpful comments on two previous versions of this paper, we thank the Editor-in-Chief Yoshiro Higano, two anonymous reviewers, and audiences at several seminars. In addition, Batabyal acknowledges financial support from the Gosnell endowment at RIT. The usual absolution applies.
Author information
Authors and Affiliations
Corresponding author
About this article
Cite this article
Batabyal, A.A., Beladi, H. How transport costs affect the decision to purchase a new or a remanufactured good. Asia-Pac J Reg Sci 2, 529–542 (2018). https://doi.org/10.1007/s41685-018-0078-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41685-018-0078-0