Abstract
In ion-annihilation electrochemiluminescence (ECL), luminophore ions are generated by oxidation as well as reduction at electrodes surfaces, and subsequently recombine into an electronically excited state, which emits light. The intensity of the emitted light is often limited by the kinetic rate of recombination of the luminophore ion species. Recombination or annihilation rates are high ranging up to approximately 1010 M−1 s−1 and can be difficult to determine using scanning electrochemical microscopy or high-frequency oscillations of an electrode potential. Here, we propose determining annihilation kinetics by measuring the relative change of the emitted light intensity as a function of luminophore concentration. Using finite element simulations of annihilation ECL in a geometry of two closely spaced electrodes biased at constant potentials, we show that, with increasing concentrations, luminescence intensity crosses over from a quadratic dependence on concentration to a linear regime—depending on the rate of annihilation. Our numerical results are applicable to scanning electrochemical microscopy as well as nanofluidic electrochemical devices to determine fast ion-annihilation kinetics.
Similar content being viewed by others
1 Introduction
Electrogenerated chemiluminescence [1] (ECL) is light generation by luminophore molecules which is triggered by electrochemical excitation. Important applications of ECL lie in electroanalytical biosensing [2, 3], in which antibodies or aptamers are labeled with luminophores to enable a large variety of different assays. In addition, ECL has been extensively investigated for imaging [4, 5] as well as light generation [6].
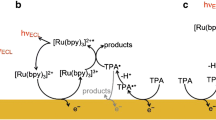
A prototypical ECL reaction scheme for efficient light generation is the annihilation pathway. In this pathway, luminophore molecules are oxidized and reduced with respect to their bulk oxidation state by applying anodic and cathodic potentials at two separate working electrodes, respectively, which are positioned at a close distance. Oxidized and reduced molecules diffuse towards each other, recombine, and subsequently emit light. This annihilation reaction scheme is shown in Fig. 1a. The following reactions occur for an ECL luminophore with the bulk oxidation state A:
A is oxidized at the anode to \({\rm {A}}^{+}\), and reduced at the cathode to \({\text{A}}^{ - }\). The generated ions diffuse into the bulk solution of the electrochemical cell and recombine (i.e., annihilate) to A and the excited state A*, which relaxes to the ground state A by emitting a photon. Subsequently, luminophores A diffuse again to the electrode surfaces to repeat oxidation/reduction, annihilation, and light emission. Annihilation is characterized by the reaction rate \(k_{\text{ann}}\), and the lifetime of the excited state is characterized by the rate \(k_{4}\). The formalism of Eqs. (1)–(4) is simplified as ECL reactants and products are species with distinctly different spin multiplicities, which may lead to additional kinetic complications because of spin conservation rules [7]. Typical luminophores that can undergo such an annihilation pathway are 9,10-diphenylanthracene (DPA), pyrene, tris(bipyridine)ruthenium(II) ([Ru(bpy)3]2+), and 5,6,11,12-tetraphenyltetracene (rubrene) [1, 7].
Schematic of reaction pathways of ECL luminophores in an electrochemical cell defined by two electrodes positioned at a short nano- or microscale distance, biased at constant oxidation and reduction potentials, respectively. a Direct annihilation pathway, b 2-electron redox cycling, c both competing processes
Annihilation rates have been measured directly previously by driving the reaction by high-frequency pulsation of a single electrode between oxidation to reduction overpotentials [8]. When varying the frequency, regions of accumulation of \({\text{A}}^{ - }\) and \({\text{A}}^{ + }\) are generated at different distances from the electrode surface. By observing light intensity as a function of the frequency of potential modulation and comparing with theoretical expectation, \(k_{\text{ann}}\) was determined. Experiments at high frequency can be very demanding experimentally due to additional effects such as parasitic impedances.
Under steady-state conditions, annihilation rates were estimated using a rotating ring-disk electrode setup [9]. By changing the rotation rate, and, thus, generating different concentration profiles, and measuring the ECL intensity as well as the shape of the emitted ECL pattern, it was possible to determine rates up to a limit of 107 M−1 s−1. Rates can also be determined when using constantly biased double-band microelectrodes and mapping the distribution of ECL emission in between both electrodes with a high spatial resolution [10].
In such two-electrode direct current (DC) measurements, generally fast reaction rates or short lifetimes of intermediate reaction products can be investigated well for short distances between both electrodes. Then, the lifetime or time for a reaction can reach the same order of magnitude or can be shorter than the time of diffusion from one electrode to the other: reaction and diffusion rates compete with one another. Very short inter-electrode distances in the nanometer range can be realized experimentally with scanning electrochemical microscopy (SECM) [11,12,13] or by microfabricated thin-layer nanogap devices [14,15,16]. A different way of measuring annihilation rates can then be opened up by a competing reaction pathway. When using highly purified solvent, \(k_{\text{ann}}\) is often very high in the order of 107–1010 M−1 s−1 [8, 17]. For low rates and short inter-electrode distance h, it is possible that an ion generated at an electrode surface diffuses along the entire distance h without encountering and recombining with its complimentary ion. Then, upon reaching the opposite electrode, a 2-electron transfer reaction takes place as shown in Fig. 1b:
Figure 1c depicts an intermediate regime, in which both the annihilation pathways (1)–(4) (i.e., Fig. 1a) and 2-electron processes (5)–(6) (i.e., Fig. 1b) take place and compete with each other.
It is impossible to distinguish both pathways by amperometry, unfortunately, as both modes (1)–(4) and (5)–(6) yield the exact same current (assuming identical diffusion coefficients D for all oxidation states of the luminophore molecule). This compensation of currents was explicitly shown by Amatore and coworkers [18] as well as by Wang and coworkers [19]. In a 2-electron process, a charge of 2\(e^{ - }\) is transferred after a diffusion time t =\(h^{2}/(2D)\), leading to a current of 4\(e^{ - }\)D\(h^{ - 2}\) per luminophore. In the case of annihilation, an ion/molecule generated in the bulk of the electrochemical cell diffuses to an electrode in the shorter time \((0.5h)^{2}/(2D)\) along the distance \(0.5h\), exchanging 1\(e^{ - }\). In contrast to this 2-electron process, in annihilation mode, a molecule has to travel for this diffusion time twice by completing a full round trip of redox cycling towards center in between the electrodes and back for a single electrode reaction, leading to the identical current of \(2e^{ - }D/(2 \cdot (0.5h)^{2})=4e^{ - }Dh^{-2}\) per molecule.Footnote 1
However, the intensity of emitted light depends on the reaction pathway as photons are emitted in the annihilation regime but not for 2-electron redox cycling (5)–(6). This fact has been exploited by the group of Bard to determine \(k_{\text{ann}}\) in rubrene and [Ru(bpy)3]2+ using an SECM [17]. The change in light emission was recorded while reducing the inter-electrode distance h in SECM approach curves. For decreasing h, light emission increases as the diffusion-limited reactions (1)–(4) become more efficient. For very short distances h, however, the intensity decreases as the 2-electron pathway starts to dominate. \(k_{\text{ann}}\) was determined by comparison of experimentally and numerically determined approach curves.
2 Concentration-Dependent Luminescence Intensity
Here, we show that annihilation rates can be determined by measuring ECL light intensity as a function of bulk luminophore concentration. Whether the annihilation or 2-electrode redox cycling scheme occurs predominantly depends on exactly three parameters: on the rate of annihilation \(k_{\text{ann}}\), on the diffusion time t along h across the electrochemical cell, t = h2/(2D), and on the concentration of the bulk species A. Both reaction schemes compete with each other, and a ‘cross-over’ or intermediate regime (Fig. 1c) occurs when this diffusion time t is in the same order of magnitude as the time it takes for two complementary luminophore ions to encounter each other and recombine in the bulk. In other words, in the intermediate regime, characteristic frequencies of both competing processes are of a similar magnitude. Then the frequency of annihilation
is approximately comparable to the frequency of diffusive shuttling across the inter-electrode distance
i.e., the condition
is fulfilled. We employed two-dimensional numerical finite element calculations (COMSOL) to determine the concentration profiles of all involved species, \({\text{A}}, {\text{A}}^{ + } , {\text{A}}^{ - } , {\text{A}}^{ *}\) along the inter-electrode distance (see Supporting Information for simulation details as well as Refs. [16, 20]). We simulated a geometry of two 20-µm-long electrodes forming a nanochannel which is diffusively coupled on both sides to a reservoir of a constant concentration of species \({\text{A}}\).
Concentration profiles are shown in Fig. 2 for an inter-electrode distance h = 100 nm, an exemplary annihilation rate kann = 109 M−1 s−1, a lifetime of the excited state of 1 µs (k4 = 106 s−1, typical for [Ru(bpy)3]2+* [21]), a diffusion coefficient of 10−9 m2 s−1 and three different bulk concentration of \({\text{A}}\). For [A] = 0.1 mM (Fig. 2b, corresponding to Fig. 1b), generated cations and anions are unlikely to encounter each other, 2-electron transfer at the electrodes is dominant, linear concentration profiles typical for redox cycling [22] occur, and light generation/generation of A* is reduced. For a high concentration of [A] = 10 mM on the other hand (see Fig. 2d, corresponding to Fig. 1a) almost all \({\text{A}}^{ + }\) and \({\text{A}}^{ - }\) recombine, and their flux to the electrodes (slopes of blue and green curves a h = 0 nm and 100 nm, respectively) is negligible. At a concentration of [A] = 1 mM (Fig. 2c, corresponding to Fig. 1c), both reaction pathways take place as shown by comparable slopes of A and \({\text{A}}^{ + }\) (and \({\text{A}}^{ - }\)) concentrations at the electrode surfaces, leading to comparable contributions of 1- and 2-electron processes.
Finite element calculation of concentrations according to Eqs. (1)–(6) for an annihilation rate kann of 109 M−1 s−1 and k4 = 106 s−1. a Two-dimensional profile of the excited state A* for [A] = 1 mM. z denotes the direction parallel to the inter-electrode distance, and y denotes the direction parallel to the electrode surfaces. b–d Concentration profiles along z as indicated by the orange line in (a) with the cathode at z = 0 nm and the anode at z = 100 nm. The bulk concentration of A is varied from b 0.1 mM to c 1 mM to d 10 mM, leading to different pathways of a b predominant 2-electron process, c an intermediate regime in which both pathways occur, and d predominant annihilation
The simulation results show that the concentration of the excited state A* is smaller than the concentration A at any position. The smaller concentration of A* is caused by its limited lifetime, and the ratio of [A*] and [A] is determined by the emission rate k4. We did not calculate the intensity of emitted light explicitly; it is directly proportional to [A*].
In the annihilation regime with a high bulk luminophore concentration, the concentration of A*, and, thus, the intensity of ECL light emission, depend linearly on [A]. When crossing over into the 2-electron redox cycling regime, A* generation and light emission still occur. However, emission does not scale linearly with [A], but quadratically instead. The origin for this quadratic behavior is that decreasing [A] reduces directly the concentration of all luminophore ion species. The chance of \({\text{A}}^{ + }\) and \({\text{A}}^{ - }\) encountering each other is additionally reduced as 2-electron transfer reactions at the electrode take over (in contrast to the annihilation regime, where all \({\text{A}}^{ + }\) and \({\text{A}}^{ - }\) recombine). This combination of a decrease in concentration and the competing pathway leads to a quadratic reduction of [A*] and light emission intensity.
This behavior of linear and quadratic relationships is shown in Fig. 3. Finite element calculations of the concentration of excited luminophore states A* integrated over the area/volume in between both electrodes are shown as a function of bulk concentration [A]. [A*] is equivalent to ECL light intensity. Results are depicted for inter-electrode distances of 50 nm, 100 nm, and 200 nm (Fig. 3a–c, respectively), and four different annihilation rates kann = 107–1010 M−1 s−1 are shown in double-logarithmic as well as linear plots (insets). For the linear behavior, [A*] is expected to increase by two orders of magnitude when increasing [A] from 0.1 to 10 mM (e.g., green curve in Fig. 3c); in the quadratic regime dominated by redox cycling, an increase of four orders of magnitude is expected (see any red curve in Fig. 3). The numerical results show that a linear annihilation regime is favored for larger distances between the electrodes, and, importantly, faster annihilation kinetics.
Finite element simulation of the concentration of excited luminophores A* (equivalent to ECL intensity) as a function of the annihilation rate kann and the concentration of bulk luminophores A (k4 = 106 s−1). The inter-electrode distance in the electrochemical cell is a 50 nm, b 100 nm, and c 200 nm. Insets show identical curves using linear scales. In all curves, crossing over from a quadratic to a linear behavior with increasing [A] can be observed, with a linear relationship occurring for larger h, kann, and [A]
To highlight the different regimes more clearly, in Fig. 4 the change in [A*] is shown for an increase of the bulk concentration [A] by a factor of 100 from 0.1 mM to 10 mM (i.e., the ratio of [A*] at 10 mM A divided by [A*] at 0.1 mM A is shown). This ratio is depicted as a function of kann.
Numerically determined ratio of change in concentration of A* (equivalent to light intensity) for increasing the bulk concentration A of luminophores by a factor of 100 from 0.1 to 10 mM. The ratio decreases from 10.000 (quadratic; 2-electron regime) to 100 (linear; annihilation) with increasing annihilation rate and shorter inter-electrode distance, showing an intermediate regime from approximately kann = 108–1010 M−1 s−1
This result shows that, for a fixed electrode geometry h, the increase in excited luminophore concentration [A*] and light emission is expected to depend very strongly on the rate of annihilation up to a 100-fold difference (for an increase of the bulk concentration [A] by two orders of magnitude).
Therefore, we predict that by experimentally measuring light emission as a function of bulk luminophore concentration and comparing to a numerical simulation, a precise measurement of very fast annihilation kinetics is possible.
While it is hardly possible to experimentally measure absolute intensities, differential changes in intensity can be detected reliably. Inter-electrode distances are often known very exactly, in particular for microfabricated nanogap electrode geometries. Bulk luminophore concentrations can also be determined precisely and changed during an experiment, either by titration or by employing microfluidic mixing. A femtoliter volume between two electrode surfaces containing only attomoles of luminophores with a low quantum efficiency does not yield very intense light. Nonetheless, using state-of-the-art detectors such as an electron multiplied CCD camera or a photomultiplier tube as well as long integration times, smallest number of photons can be observed, making light intensity detection at low concentrations feasible.
3 Conclusion
We predict that recombination kinetics of annihilation electrochemiluminescence can be determined by detecting the change in luminescence intensity when increasing the concentration of luminophore molecules in a setup of two closely spaced and constantly biased electrodes. Our numerical results show that this increase in intensity is expected to show a transition from a quadratic to a linear dependence on concentration. Intensity–concentration curves strongly depend on the annihilation rate, and rates above 1010 M−1 s−1 could be measurable for inter-electrode distances of around 100 nm. Thus, scanning electron microscopy as well as microfabricated thin-layer cells should be suitable for experimentation.
Change history
17 July 2019
The article Towards Determining Kinetics of Annihilation Electrogenerated Chemiluminescence by Concentration-Dependent Luminescent Intensity.
Notes
We have recently demonstrated DC annihilation ECL in nanofluidic electrochemical devices [16]. Such devices allow for determining additional molecular information by stochastic amperometry [23]: For example, the current generated per molecule in redox cycling can be determined by analysis of current fluctuations in chronoamperometry. We point out that the inability to distinguish both pathways amperometrically also extends to stochastic chronoamperometry. The methods probe number density fluctuation in the entire detection area between the electrode, averaging over all oxidation states. Thus, 2-electron and annihilation reactions will exhibit identical current ‘noise’, i.e., identical standard deviations of a chronoamperometrically detected current magnitude. On the other hand, the shot noise caused by Brownian motion of analytes traveling from one electrode to the other should differ for a 2-electron vs. 1-electron process. However, a shot noise regime so far has not been accessible experimentally, as it demands low-current measurement at high acquisition frequencies [24].
References
Richter MM. Electrochemiluminescence (ECL). Chem Rev. 2004;104:3003–36. https://doi.org/10.1021/cr020373d.
Kirschbaum SEK, Baeumner AJ. A review of electrochemiluminescence (ECL) in and for microfluidic analytical devices. Anal Bioanal Chem. 2015;407:3911–26. https://doi.org/10.1007/s00216-015-8557-x.
Liu Z, Qi W, Xu G. Recent advances in electrochemiluminescence. Chem Soc Rev. 2015;44:3117–42. https://doi.org/10.1039/C5CS00086F.
Guo W, Liu Y, Cao Z, Su B. Imaging analysis based on electrogenerated chemiluminescence. J Anal Test. 2017;1:14. https://doi.org/10.1007/s41664-017-0013-9.
Voci S, Goudeau B, Valenti G, Lesch A, Jović M, Rapino S, Paolucci F, Arbault S, Sojic N. Surface-confined electrochemiluminescence microscopy of cell membranes. J Am Chem Soc. 2018;140:14753–60. https://doi.org/10.1021/jacs.8b08080.
Méance S, Gamby J, Faure M, Kou Q, Haghiri-Gosnet AM. Electrochemiluminescence on-a-chip: towards a hand-held electrically powered optofluidic source. Talanta. 2014;129:150–4. https://doi.org/10.1016/j.talanta.2014.05.026.
Kapturkiewicz A. Electrochemical generation of excited intramolecular charge-transfer states. ChemElectroChem. 2017;4:1604–38. https://doi.org/10.1002/celc.201600865.
Collinson MM, Wightman RM, Pastore P. Evaluation of ion-annihilation reaction kinetics using high-frequency generation of electrochemiluminescence. J. Phys. 1994;98:11942–7.
Maloy JT, Prater KB, Bard AJ. Electrogenerated chemiluminescence. V. Rotating-ring-disk electrode. Digital simulation and experimental evaluation. J Am Chem Soc. 1971;93:5959–68. https://doi.org/10.1021/ja00752a003.
Amatore C, Pebay C, Servant L, Sojic N, Szunerits S, Thouin L. Mapping electrochemiluminescence as generated at double-band microelectrodes by confocal microscopy under steady state. ChemPhysChem. 2006;7:1322–7. https://doi.org/10.1002/cphc.200500626.
Polcari D, Dauphin-Ducharme P, Mauzeroll J. Scanning electrochemical microscopy: a comprehensive review of experimental parameters from 1989 to 2015. Chem Rev. 2016;116:13234–78. https://doi.org/10.1021/acs.chemrev.6b00067.
Izquierdo J, Knittel P, Kranz C. Scanning electrochemical microscopy: an analytical perspective. Anal Bioanal Chem. 2018;410:307–24. https://doi.org/10.1007/s00216-017-0742-7.
Kai T, Zhou M, Johnson S, Ahn HS, Bard AJ. Direct observation of C2O4·– and CO2·– by oxidation of oxalate within nanogap of scanning electrochemical microscope. J Am Chem Soc. 2018. https://doi.org/10.1021/jacs.8b08900.
White HS, McKelvey K. Redox cycling in nanogap electrochemical cells. Curr Opin Electrochem. 2018;7:48–53. https://doi.org/10.1016/j.coelec.2017.10.021.
Marken F, Mathwig K. Nano- and micro-gap electrochemical transducers: novel benchtop fabrication techniques and electrical migration effects. Curr Opin Electrochem. 2018;7:15–21. https://doi.org/10.1016/j.coelec.2017.10.004.
Al-Kutubi H, Voci S, Rassaei L, Sojic N, Mathwig K. Enhanced annihilation electrochemiluminescence by nanofluidic confinement. Chem Sci. 2018;9:8946–50. https://doi.org/10.1039/C8SC03209B.
Rodríguez-López J, Shen M, Nepomnyashchii AB, Bard AJ. Scanning electrochemical microscopy study of ion annihilation electrogenerated chemiluminescence of rubrene and [Ru(bpy)3]2+. J Am Chem Soc. 2012;134:9240–50. https://doi.org/10.1021/ja301016n.
Amatore C, Bonhomme F, Bruneel JL, Servant L, Thouin L. Mapping dynamic concentration profiles with micrometric resolution near an active microscopic surface by confocal resonance Raman microscopy. Application to diffusion near ultramicroelectrodes: first direct evidence for a conproportionation reaction. J Electroanal Chem. 2000;484:1–17. https://doi.org/10.1016/s0022-0728(00)00057-7.
Wang Q, Rodríguez-López J, Bard AJ. Evaluation of the chemical reactions from two electrogenerated species in picoliter volumes by scanning electrochemical microscopy. ChemPhysChem. 2010;11:2969–78. https://doi.org/10.1002/cphc.201000183.
Valenti G, Scarabino S, Goudeau B, Lesch A, Jović M, Villani E, Sentic M, Rapino S, Arbault S, Paolucci F, Sojic N. Single cell electrochemiluminescence imaging: from the proof-of-concept to disposable device-based analysis. J Am Chem Soc. 2017;139:16830–7. https://doi.org/10.1021/jacs.7b09260.
Caspar JV, Meyer TJ. Photochemistry of Ru(bpy) 2+3 . Solvent effects. J Am Chem Soc. 1983;10:5583–90. https://doi.org/10.1021/ja00355a009.
Mampallil D, Mathwig K, Kang S, Lemay SG. Redox couples with unequal diffusion coefficients: effect on redox cycling. Anal Chem. 2013;85:6053–8. https://doi.org/10.1021/ac400910n.
Singh PS, Lemay SG. Stochastic processes in electrochemistry. Anal Chem. 2016;88:5017–27. https://doi.org/10.1021/acs.analchem.6b00683.
Krause KJ, Mathwig K, Wolfrum B, Lemay SG. Brownian motion in electrochemical nanodevices. Eur Phys J Spec Top. 2014;223:3165–78. https://doi.org/10.1140/epjst/e2014-02325-5.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original version of this article was revised due to a retrospective Open Access order.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Mathwig, K., Sojic, N. Towards Determining Kinetics of Annihilation Electrogenerated Chemiluminescence by Concentration-Dependent Luminescent Intensity. J. Anal. Test. 3, 160–165 (2019). https://doi.org/10.1007/s41664-019-00094-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41664-019-00094-z