Skip to main content
SpringerLink
Log in

Simultaneous Optimization of Non-Isothermal Design of Water Networks with Regeneration and Recycling

  • Original Research Paper
  • Published:
Process Integration and Optimization for Sustainability Aims and scope Submit manuscript

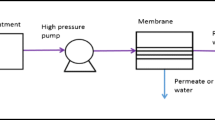
Abstract

Most of the water network design strategies considering regeneration and recycling are using the assumptions that the processes are isothermal and steady state. However, almost all of the available processes have temperature change from the inlets to the outlets of the units. Moreover, to maintain the process units’ temperature under the specified limit, additional heat exchangers are usually required. The traditional approach of designing water network and heat exchanger network are usually made separately. It is reasonable to expect that a simultaneous design procedure of water network and heat exchanger network that considers process temperature change may result in a better design option. In this work, systematic design of non-isothermal water networks with regeneration and recycling is proposed. Superstructure model with non-linear programming (NLP) model is developed accordingly to incorporate all possible networks. Regeneration units and heat exchangers are introduced to achieve the specified contaminant requirements and temperature limits of each process unit. The superstructure model is enhanced with regeneration unit model by considering the removal ratio of contaminants. As opposed to the traditional model, the novel heat exchanger model in this work is constructed separately for the heating side and the cooling side to increase further flexibility to the original model. The overall model is optimized simultaneously to achieve feasible heat exchange network and optimal configuration. The total annual cost (TAC) and global equivalent cost (GEC) are considered as the objective function to represent the economic benefits of the given case study. Several case studies are provided to demonstrate the effectiveness of the proposed design strategy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Abbreviations

\( {\displaystyle \begin{array}{l}{P}_1,{P}_2,{P}_3,\dots \in P\\ {}{P}_1,{P}_2,{P}_3,\dots \in {P}^{\hbox{'}}\\ {}{P}_1,{P}_2,{P}_3,\dots \in {P}^{\hbox{'}\hbox{'}}\end{array}} \) :

P ≠ P'and P' ≠ P'' (Process)

\( {\displaystyle \begin{array}{l}{R}_1,{R}_2,{R}_3,\dots \in R\ \\ {}{R}_1,{R}_2,{R}_3,\dots \in {R}^{\hbox{'}}\\ {}{R}_1,{R}_2,{R}_3,\dots \in {R}^{\hbox{'}\hbox{'}}\end{array}} \) :

R ≠ R'and R' ≠ R'' (Regeneration)

\( {\displaystyle \begin{array}{l}{Eh}_1,{Eh}_2,{Eh}_3,\dots \in Eh\\ {}{Eh}_1,{Eh}_2,{Eh}_3,\dots \in {Eh}^{\hbox{'}}\\ {}{Eh}_1,{Eh}_2,{Eh}_3,\dots \in {Eh}^{\hbox{'}\hbox{'}}\end{array}} \) :

Eh ≠ Eh'and Eh' ≠ Eh'' (Exchanger heating side)

\( {\displaystyle \begin{array}{l}{Ec}_1,{Ec}_2,{Ec}_3,\dots \in Eh\\ {}{Ec}_1,{Ec}_2,{Ec}_3,\dots \in {Eh}^{\hbox{'}}\\ {}{Ec}_1,{Ec}_2,{Ec}_3,\dots \in {Eh}^{\hbox{'}\hbox{'}}\end{array}} \) :

Ec ≠ Ec'and Ec' ≠ Ec'' (Exchanger cooling side)

C1, C2, C 3, … ∈ C :

Component

Un ∈ P, R, Eh, Ec :

Units

Hu 1, Hu 2, Hu 3, … ∈ Hu :

Hot utility

Cu 1, Cu 2, Cu 3, … ∈ Cu :

Cold utility

in:

Input condition

out:

Output condition

f :

Fresh water

w :

Waste water

M C,P :

Amount of contaminant C generated by the process P (g/h)

\( {C}_{\max C,P}^{in} \) :

Limiting inlet concentration C of process P (ppm)

\( {C}_{\max C,P}^{out} \) :

Limiting outlet concentration C of process P (ppm)

PR C,R :

Removal ratio of contaminant C in regeneration R

PHD P :

Heat duty of process P (kW)

RHD R :

Heat duty of regeneration R (kW)

T f :

Temperature of freshwater inlet

\( {T}_{\max P}^{in} \) :

Maximum for limit inlet temperature of process P (°C)

\( {T}_{\min P}^{in} \) :

Minimum for limit inlet temperature of process P (°C)

\( {T}_{\max P}^{out} \) :

Maximum for limit outlet temperature of process P (°C)

\( {T}_{\min P}^{out} \) :

Minimum for limit outlet temperature of process P (°C)

\( {T}_{\max \mathrm{R}}^{in} \) :

Maximum limit for inlet temperature of regeneration R (°C)

\( {T}_{\min \mathrm{R}}^{in} \) :

Minimum limit for inlet temperature of regeneration R (°C)

\( {T}_{\max \mathrm{R}}^{out} \) :

Maximum limit for outlet temperature of regeneration R (°C)

\( {T}_{\min \mathrm{R}}^{out} \) :

Minimum limit for outlet temperature of regeneration R (°C)

\( {C}_{\max C}^w \) :

Maximum limit for concentration of contaminant C in waste flow (ppm)

\( {T}_{\max T}^w \) :

Maximum limit for temperature of waste flow (°C)

C Fw :

Cost of fresh water

C Hu,Un :

Cost of hot utility

C Cu,Un :

Cost of cold utility

\( {T}_{Hu, Un}^{in} \) :

Inlet temperature of hot utility

\( {T}_{Cu, Un}^{in} \) :

Inlet temperature of cold utility

\( {T}_{Hu, Un}^{out} \) :

Outlet temperature of cold utility

Cp :

Heat capacity of water

C fixed :

Fixed charges for heat exchangers and utility units

C area :

Area cost coefficient for heat exchangers and utility units

U Eh,Ec,hu,cu :

Overall heat transfer coefficients for hot stream, cold stream, and heat exchanger

H :

Hours of plant operation

T f :

Inlet temperature of fresh water

\( {T}_{\max T}^w \) :

Maximum limit for temperature of wastewater stream

α:

Regeneration cost factor

β :

Wastewater cost factor

γ :

Minimum temperature difference of the heat exchangers’ inlet and outlet

λ:

Exponent parameter for area cost

NEh,Ec :

Number of heat exchanger

NHu,Un :

Number of hot utility

N Cu,Un :

Number of cold utility

\( {F}_P^f \) :

Flowrate from fresh water to process P (t/h)

\( {F}_R^f \) :

Flowrate from fresh water to regeneration R (t/h)

\( {F}_{Eh}^f \) :

Flowrate from fresh water to exchanger heating side Eh (t/h)

\( {F}_{Ec}^f \) :

Flowrate from fresh water to exchanger cooling side Ec (t/h)

F P→P' :

Flowrate from process P to process P’ (t/h)

F R→R' :

Flowrate from regeneration R to regeneration R’ (t/h)

F Eh→Eh' :

Flowrate from exchanger heating side Eh to exchanger heating side Eh’ (t/h)

F Ec→Ec' :

Flowrate from exchanger cooling side Ec to exchanger cooling side Ec’ (t/h)

F P→R :

Flowrate from process P to regeneration R (t/h)

F P→Eh :

Flowrate from process P to exchanger heating side Eh (t/h)

F P→Ec :

Flowrate from process P to exchanger cooling side Ec (t/h)

F R→P :

Flowrate from regeneration R to process P (t/h)

F R→Eh :

Flowrate from regeneration R to exchanger heating side Eh (t/h)

F R→Ec :

Flowrate from regeneration R to exchanger cooling side Ec (t/h)

F Eh→P :

Flowrate from exchanger heating side Eh to process P (t/h)

F Eh→R :

Flowrate from exchanger heating side Eh to regeneration R (t/h)

F Eh→Ec :

Flowrate from exchanger heating side Eh to exchanger cooling side Ec (t/h)

F Ec→P :

Flowrate from exchanger cooling side Ec to process P (t/h)

F Ec→R :

Flowrate from exchanger cooling side Ec to regeneration R (t/h)

F Ec→Eh :

Flowrate from exchanger cooling side Ec to exchanger heating side Eh (t/h)

\( {F}_P^w \) :

Flowrate from process P to discharge (t/h)

\( {F}_R^w \) :

Flowrate from regeneration R to discharge (t/h)

\( {F}_{Eh}^w \) :

Flowrate from exchanger heating side Eh to discharge (t/h)

\( {F}_{Ec}^w \) :

Flowrate from exchanger cooling side Ec to discharge (t/h)

\( {C}_{C,P}^{in} \) :

Inlet concentration C of process P (ppm)

\( {C}_{C,P}^{out} \) :

Outlet concentration C of process P (ppm)

\( {C}_{C,R}^{in} \) :

Inlet concentration C of regeneration R (ppm)

\( {C}_{C,R}^{out} \) :

Outlet concentration C of regeneration R (ppm)

C C,Eh :

Inlet concentration C of exchanger heating side Eh (ppm)

C C,Ec :

Inlet concentration C of exchanger cooling side Ec (ppm)

\( {C}_C^w \) :

Concentration C of wastewater (ppm)

\( {T}_P^{in} \) :

Inlet temperature of process P (°C)

\( {T}_P^{out} \) :

Outlet temperature of process P (°C)

\( {T}_R^{in} \) :

Inlet temperature of regeneration R (°C)

\( {T}_R^{out} \) :

outlet temperature of regeneration R (°C)

\( {T}_{Eh}^{in} \) :

Inlet temperature of exchanger heating side Eh (°C)

\( {T}_{Eh}^{out} \) :

outlet temperature of exchanger heating side Eh (°C)

\( {T}_{Ec}^{in} \) :

Inlet temperature of exchanger cooling side Ec (°C)

\( {T}_{Ec}^{out} \) :

Outlet temperature of exchanger cooling side Ec (°C)

T w :

Temperature of wastewater (°C)

\( {Q}_P^{in} \) :

Inlet heat duty of process P inlet using hot utility (ton.°C.CP/h)

\( {Q}_R^{in} \) :

Inlet heat duty of regeneration R using hot utility (ton.°C.CP/h)

\( {Q}_{Eh}^{in} \) :

Inlet heat duty of exchanger heating side Eh using hot utility (ton.°C.CP/h)

\( {Q}_{Ec}^{in} \) :

Inlet heat quality of exchanger cooling side Ec using hot utility (ton.°C.CP/h)

\( {T}_{Hu, Un}^j \) :

Temperature for unit before heated by hot utility

\( {T}_{Hu, Un}^k \) :

Temperature for unit after heated by hot utility

\( {T}_{Cu, Un}^j \) :

Temperature for unit before cooled by cold utility

\( {T}_{Cu, Un}^k \) :

Temperature for unit after cooled by cold utility

ΔT Eh,Ec :

Temperature difference of the mixing exchangers’ inlet and outlet

ΔT Hu,Un :

Temperature difference of the hot utility’ inlet and outlet

ΔT Cu,Un :

Temperature difference of the cold utility’ inlet and outlet

Q Eh,En :

The exchanged energy by the heat exchanger

A Eh,Ec :

Heat transfer area of mixing heat exchanger

A Hu,Un :

Heat transfer area of hot utility

A Cu,Un :

Heat transfer area of cold utility

\( {D}_P^{in} \) :

Removal heat duty in process P inlet using cooling utility (ton.°C.CP/h)

\( {D}_R^{in} \) :

Removal heat duty in regeneration R inlet using cooling utility (ton.°C.CP/h)

\( {D}_{Eh}^{in} \) :

Removal heat duty in exchanger heating side Eh inlet using cooling utility (ton.°C.CP/h)

\( {D}_{Ec}^{in} \) :

Removal heat duty in exchanger cooling side Ec inlet using cooling utility (ton.°C.CP/h)

\( {D}_w^{in} \) :

Removal heat in exchanger cooling side Ec inlet using cooling utility (ton.°C.CP/h)

Cannual :

Annual cost (M$)

References

  • Ahmetović E, Kravanja Z (2013) Simultaneous synthesis of process water and heat exchanger networks. Energy 57:236–250

    Article  Google Scholar 

  • Ahmetović E, Ibrića N, Kravanja Z, Grossmann IE (2015) Water and energy integration: a comprehensive literature review of non-isothermal water network synthesis. Comput Chem Eng 82:144–171

    Article  Google Scholar 

  • Bagajewicz M, Rodera H, Savelski M (2002) Energy efficient water utilization systems in process plants. Comput Chem Eng 26:59–79

    Article  Google Scholar 

  • Bogataj M, Bagajewicz MJ (2008) Synthesis of non-isothermal heat integrated water networks in chemical processes. Comput Chem Eng 32:310–3142

    Article  Google Scholar 

  • Boix M, Montastruc L, Pibouleau L, Azzaro-Pantel C, Domenech S (2012) Minimizing water and energy consumptions in water and heat exchange networks. Appl Therm Eng 36:442–455

    Article  Google Scholar 

  • Chen JJJ (1987) Comments on improvements on a replacement for the logarithmic mean. Chem Eng Sci 42:2488–2489

    Article  Google Scholar 

  • De-León Almaraz S, Boix M, Montastruc L, Azzaro-Pantel C, Liao Z, Domenech S (2016) Design of a water allocation and energy network for multi-contaminant problems using multi-objective optimization. Process Saf Environ Prot 103:348–364

    Article  Google Scholar 

  • Dong HG, Lin CY, Chang CT (2008) Simultaneous optimization approach for integrated water-allocation and heat-exchange networks. Chem Eng Sci 63:3664–3678

    Article  Google Scholar 

  • Feng X, Bai J, Wang H, Zheng X (2008) Grass-roots design of regeneration recycling water networks. Comput Chem Eng 32:1892–1907

    Article  Google Scholar 

  • Gunaratnam M, Alva-Argáez A, Kokossis A, Kim JK, Smith R (2005) Automated design of total water systems. Ind Eng Chem Res 44:588–599

    Article  Google Scholar 

  • Hou Y, Wang J, Chen Z, Li X, Zhang J (2014) Simultaneous integration of water and energy on conceptual methodology for both single- and multi-contaminant problems. Chem Eng Sci 117:436–444

    Article  Google Scholar 

  • Ibrić N, Ahmetović E, Kravanja Z (2013) A two-step solution strategy for the synthesis of pinched and threshold heat-integrated process water networks. Chem Eng Trans 35:43–48

    Google Scholar 

  • Leewongtanawit B, Kim JK (2009) Improving energy recovery for water minimisation. Energy 34:880–893

    Article  Google Scholar 

  • Liao Z, Rong G, Wang J, Yang Y (2011) Systematic optimization of heat-integrated water allocation networks. Ind Eng Chem Res 50:6713–6727

    Article  Google Scholar 

  • Linnhoff B, Hindmarsh E (1983) The pinch design method for heat exchanger networks. Chem Eng Sci 38:745–763

    Article  Google Scholar 

  • Liu Y, Luo Y, Yuan X (2015) Simultaneous integration of water and energy in heat-integrated water allocation networks. AICHE J 61:2202–2214

    Article  Google Scholar 

  • Luo Y, Luo X, Yuan X (2012) Thermodynamic analysis of homogeneous non-isothermal mixing influence on the water-using networks’ energy target. Comput Aided Chem Eng 31:420–424

    Article  Google Scholar 

  • Martínez-Patiño J, Picón-Núñez M, Serra LM, Verda V (2012) Systematic approach for the synthesis of water and energy networks. Appl Therm Eng 48:458–464

    Article  Google Scholar 

  • Polley GT, Picón-Núñez M, López-Maciel JDJ (2010) Design of water and heat recovery networks for the simultaneous minimisation of water and energy consumption. Appl Threm Eng 30:2290–2299

    Article  Google Scholar 

  • Savulescu L, Kim JK, Smith R (2005) Studies on simultaneous energy and water minimisation—part II: systems with maximum re-use of water. Chem Eng Sci 60:3291–3308

    Article  Google Scholar 

  • Wang YP, Smith R (1994) Wastewater minimisation. Chem Eng Sci 49:981–1006

    Article  Google Scholar 

  • Yan F, Wu H, Li W, Zhang J (2016) Simultaneous optimization of heat-integrated water networks by a nonlinear program. Chem Eng Sci 140:76–89

    Article  Google Scholar 

  • Yee TF, Grossmann IE (1990) Simultaneous optimization models for heat integration—II. Heat exchanger network synthesis. Comput Chem Eng 14:1165–1184

    Article  Google Scholar 

  • Zhou L, Liao Z, Wang J, Jiang B, Yang Y, Yu H (2015) Simultaneous optimization of heat-integrated water allocation networks using the mathematical model with equilibrium constraints strategy. Ind Eng Chem Res 54:3355–3366

    Article  Google Scholar 

Download references

Acknowledgments

The authors wish to thank the anonymous reviewers for the useful comments that helped improve the readability of this work. The research was partially supported by the Ministry of Science and Technology, Taiwan under contract no. MOST 106-2221-E-005-095-, the 105科技部補助大專校院延攬特殊優秀人才 award, and a grant from National Chung-Hsing University 10617003G 新進教師經費補助.

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, National Chung Hsing University, Taichung, 40227, Taiwan

    Wen-Hao Cheng & Vincentius Surya Kurnia Adi

Authors
  1. Wen-Hao Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vincentius Surya Kurnia Adi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vincentius Surya Kurnia Adi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cheng, WH., Adi, V.S.K. Simultaneous Optimization of Non-Isothermal Design of Water Networks with Regeneration and Recycling. Process Integr Optim Sustain 2, 183–203 (2018). https://doi.org/10.1007/s41660-018-0045-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s41660-018-0045-2

Keywords

Search

Navigation