Q-Targeting in New Keynesian Models

Abstract

We consider optimal monetary policy in a model that integrates credit frictions in the standard New Keynesian model with sticky prices and wages as well as adjustment costs of capital. Different from traditional models with credit frictions, such as those by Carlstrom and Fuerst (Econ Theory 12:583–597, 1998), our model is able to generate an anti-cyclical external finance premium as observed empirically in the U.S. economy. Monetary policy is characterized by a Taylor rule according to which the nominal interest rate is set as a function of the deviation of the inflation rate from its target rate, the output gap, and Tobin’s q. The latter is measured by the relative price of newly installed capital. We show that monetary policy should optimally decrease interest rates with higher capital prices. However, the consideration of Tobin’s q implies only small welfare effects. These results are robust with respect to a more general Epstein and Zin (Econometrica 57:937–969, 1989) welfare specification and to exogenous shifts to both the atemporal marginal rate of substitution between consumption and leisure as well as the households’ discounting behavior.

Appendices

Appendix 1: Analysis of the Model

1.1 Price Setting

Consider the relative price $P_{jt+s}/P_{t+s}$ of an intermediary goods producer j receiving the signal to choose its optimal relative price $p_{At}=P_{At}/P_t$ in period t and that has not been able to reset its price up to period $t+s$:

$$\begin{aligned} \frac{P_{jt+s}}{P_{t+s}}=\frac{\pi _{t+s-1}\cdots \pi _t}{\pi _{t+s}\cdots \pi _{t+1}}p_{At}=\frac{\pi _t}{\pi _{t+s}}p_{At}. \end{aligned}$$

Accordingly, the firm will choose $p_{At}$ in period t to maximize

$$\begin{aligned} \mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _y)^s \frac{\Lambda _{t+s}}{\Lambda _t} \left[ \left( \frac{\pi _t}{\pi _{t+s}}p_{At}\right) ^{-\epsilon _y}Y_{t+s}-g_{t+s}\left( \frac{\pi _t}{\pi _{t+s}}p_{At}\right) ^{1-\epsilon _y}Y_{t+s}\right] . \end{aligned}$$

The first-order condition for this problem is:

$$\begin{aligned} 0=\mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _y)^s\frac{\Lambda _{t+s}}{\Lambda _t} \left[ (1-\epsilon _y)\left( \frac{\pi _t}{\pi _{t+s}}\right) ^{1-\epsilon _y}Y_{t+s}p_{At}^{-\epsilon _y}+ \epsilon _y g_{t+s}\left( \frac{\pi _t}{\pi _{t+s}}\right) ^{-\epsilon _y}Y_{t+s}p_{At}^{-\epsilon _y-1} \right] \end{aligned}$$

and can be written as

$$\begin{aligned} p_{At}&= \frac{\epsilon _y}{\epsilon _y-1}\frac{\Gamma _{1t}}{\pi _t\Gamma _{2t}}, \end{aligned}$$

(7.1a)

$$\begin{aligned} \Gamma _{1t}&= \mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _y)^s \pi _{t+s}^{\epsilon _y}g_{t+s}\Lambda _{t+s}Y_{t+s}= \pi _{t}^{\epsilon _y}g_t \Lambda _t Y_t + (\beta \varphi _y)\mathbb {E}_t\Gamma _{1t+1}, \end{aligned}$$

(7.1b)

$$\begin{aligned} \Gamma _{2t}&= \mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _y)^s \pi _{t+s}^{\epsilon _y-1}\Lambda _{t+s}Y_{t+s}=\pi _{t}^{\epsilon _y-1} \Lambda _t Y_t + (\beta \varphi _y)\mathbb {E}_t\Gamma _{2t+1}. \end{aligned}$$

(7.1c)

The price index (2.3) implies

$$\begin{aligned} P_t^{1-\epsilon _y}=(1-\varphi _y)P_{At}^{1-\epsilon _y}+\varphi _y P_{Nt}^{1-\epsilon _y}=(1-\varphi _y)P_{At}^{1-\epsilon _y}+\varphi _y (\pi _{t-1}P_{t-1})^{1-\epsilon _y}. \end{aligned}$$

The second equality follows from the updating rule (2.7) and the fact that the non-optimizers are a random sample of optimizers and non-optimizers. Dividing by $P_t$ on both sides delivers:

$$\begin{aligned} 1 = (1-\varphi _y)p_{At}^{1-\epsilon _y} + \varphi _y (\pi _{t-1}/\pi _t)^{1-\epsilon _y}. \end{aligned}$$

(7.1d)

Market clearing requires

$$\begin{aligned} {\tilde{Y}}_t = \int _{0}^1 Y_{jt}dj = \int _0^1 \left( \frac{P_{jt}}{P_t}\right) ^{-\epsilon _y}Y_t dj=\underbrace{\left( \frac{{\tilde{P}}_t}{P_t}\right) ^{-\epsilon _y}}_{\equiv s_t^y}Y_t,\quad {\tilde{P}}_t^{-\epsilon _y}\equiv \int _0^1 P_{jt}^{-\epsilon _y}dj, \end{aligned}$$

so that

$$\begin{aligned} s_t^y Y_t&={\tilde{Y}}_t,\quad s_t^y:=\left( \int _0^1 P_{jt}^{-\epsilon _y}dj\right) P_t^{\epsilon _y}. \end{aligned}$$

(7.1e)

Using the same reasoning for ${\tilde{P}}_t$ as for the price index $P_t$ yields:

$$\begin{aligned} s_t^y = (1-\varphi _y)p_{At}^{-\epsilon _y} + \varphi _y (\pi _{t-1}/\pi _t)^{-\epsilon _y}s_{t-1}^y. \end{aligned}$$

(7.1f)

1.2 Wage Setting

Consider the real wage $W_{ht}/P_t$ of a household member who has set his wage optimally in period t to ${\tilde{w}}_t=W_{At}/P_t$ and who has not been able to do so again until period $s=1, 2, \dots$. This is given by

$$\begin{aligned} \frac{W_{Nt+s}}{P_{t+s}}=\frac{\prod _{i=1}^s \pi _{t+i-1}W_{At}}{\prod _{i=1}^s \pi _{t+s}P_t}=\frac{\pi _t}{\pi _{t+s}}{\tilde{w}}_t, \end{aligned}$$

and the demand for his type of labor service equals

$$\begin{aligned} N_{ht+s}=\left( \frac{(\pi _{t}/\pi _{t+s}){\tilde{w}}_t}{w_{t+s}}\right) ^{-\epsilon _n}N_{t+s}, \end{aligned}$$

where $w_{t+s}$ denotes the real wage prevailing in period $t+s$. Accordingly, the Lagrangian for the optimal real wage reads:

$$\begin{aligned} \mathscr {L}= & {} \mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _n)^s\Bigg \{ \frac{{(C_{ht+s}-\chi \bar{C}_{t+s})^{1-\eta }-1}}{1-{\eta }}- \frac{\nu _0}{1+\nu _1}\left[ \left( \frac{(\pi _t/\pi _{t+s}) {\tilde{w}}_{t}}{w_{t+s}}\right) ^{-\epsilon _n}N_{t+s}\right] ^{1+\nu _1}\\&+\Lambda _{ht+s}\left[ \frac{\pi _t}{\pi _{t+s}}{\tilde{w}}_t\left( \frac{(\pi _t/\pi _{t+s}){\tilde{w}}_{t}}{w_{t+s}}\right) ^{-\epsilon _n}N_{t+s} + RMT \right] \Bigg \}. \end{aligned}$$

The first-order condition with respect to ${\tilde{w}}_t$ is

$$\begin{aligned} 0&=\mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _n)^s\Bigg \{\epsilon _n \nu _0 {\tilde{w}}_t^{-\epsilon _n(1+\nu _1)-1}\left( \frac{(\pi _t/\pi _{t+s})}{w_{t+s}}\right) ^{-\epsilon _{n}(1+\nu _1)}N_{t+s}^{1+\nu _1}\\&\quad +(1-\epsilon _n)\Lambda _{ht+s}{\tilde{w}}_t^{-\epsilon _n}w_{t+s}^{\epsilon _n}\left( \frac{\pi _t}{\pi _{t+s}}\right) ^{1-\epsilon _n}N_{t+s}\Bigg \}. \end{aligned}$$

Using $\Lambda _{ht+s}=\Lambda _{t+s}$ this can be arranged to read

$$\begin{aligned} {\tilde{w}}_t&=\frac{\epsilon _n}{\epsilon _n-1}\frac{\Delta _{1t}}{\Delta _{2t}}, \end{aligned}$$

(7.2a)

where

$$\begin{aligned} \Delta _{1t}&=\nu _0 \mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _n)^s \left( \frac{\pi _t {\tilde{w}}_t}{\pi _{t+s}w_{t+s}}\right) ^{-\epsilon _n(1+\nu _1)}N_{t+s}^{1+\nu _1},\nonumber \\&=\nu _0\left( \frac{{\tilde{w}}_t}{w_t}\right) ^{-\epsilon _n(1+\nu _1)}N_t^{1+\nu _1} + (\beta \varphi _n)\mathbb {E}_t\left( \frac{\pi _t{\tilde{w}}_t}{{\tilde{\pi }}_{t+1}w_{t+1}}\right) ^{-\epsilon _n(1+\nu _1)}\Delta _{1t+1}, \end{aligned}$$

(7.2b)

$$\begin{aligned} \Delta _{2t}&=\mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _n)^s \Lambda _{t+s}\left( \frac{{\tilde{w}}_t}{w_{t+s}}\right) ^{-\epsilon _n}\left( \frac{\pi _t}{\pi _{t+s}}\right) ^{1-\epsilon _n}N_{t+s},\nonumber \\&=\Lambda _t \left( \frac{{\tilde{w}}_t}{w_t}\right) ^{-\epsilon _n}N_t + (\beta \varphi _n)\mathbb {E}_t\left( \frac{{\tilde{w}}_t}{{\tilde{w}}_{t+1}}\right) ^{-\epsilon _n}\left( \frac{ \pi _t}{\pi _{t+1}}\right) ^{1-\epsilon _n}\Delta _{2t+1}. \end{aligned}$$

(7.2c)

The wage index (2.25) implies

$$\begin{aligned} W_t^{1-\epsilon _n}=(1-\varphi _n)W_{At}^{1-\epsilon _n}+\varphi _n (\pi _{t-1}W_{t- 1})^{1-\epsilon _n} \end{aligned}$$

so that the real wage equals

$$\begin{aligned} w_t^{1-\epsilon _n}&= (1-\varphi _n){\tilde{w}}_t^{1-\epsilon _n}+\varphi _n\left( \frac{\pi _{t-1}}{\pi _t}w_{t-1}\right) ^{1-\epsilon _n}. \end{aligned}$$

(7.2d)

Finally consider the index

$$\begin{aligned} {\tilde{N}}_t^{1+\nu _1} := \int _0^1 N_{ht}^{1+\nu _1}dh, \end{aligned}$$

in the family’s current-period utility function. Using (2.24), this can be written

$$\begin{aligned} {\tilde{N}}_t^{1+\nu _1}=N_t^{1+\nu _1}\int _0^1 \left( \frac{W_{ht}}{W_t}\right) ^{-\epsilon _n(1+\nu _1)}dh. \end{aligned}$$

Let

$$\begin{aligned} {\tilde{W}}_t^{-\epsilon _n(1+\nu _1)}=\int _0^1 W_{ht}^{-\epsilon _n(1+\nu _1)}dh=(1-\varphi _n)(W_{At})^{-\epsilon _n(1+\nu _1)}+\varphi _n (\pi _{t-1}W_{Nt-1})^{-\epsilon _n(1+\nu _1)} \end{aligned}$$

and

$$\begin{aligned} (s^n_t)^{1+\nu _1}=\left( \frac{{\tilde{W}}_t}{W_t}\right) ^{-\epsilon _n(1+\nu _1)}=\left( \frac{{\tilde{W}}_t/P_t}{W_t/P_t}\right) ^{-\epsilon _n(1+\nu _1)} =\left( \frac{{\tilde{w}}_t}{w_t}\right) ^{-\epsilon _n(1+\nu _1)}. \end{aligned}$$

Using the same line of argument employed to derive (7.1f) yields the dynamic equation for the measure of wage dispersion $s^n_t$:

$$\begin{aligned} (s_t^n)^{1+\nu _1} = (1-\varphi _n)\left( \frac{{\tilde{w}}_{t}}{w_t}\right) ^{-\epsilon _n(1+\nu _1)} + \varphi _n\left( \frac{\pi _{t-1}w_{t-1}}{\pi _t w_t}\right) ^{-\epsilon _n(1+\nu _1)}(s^n_{t-1})^{1+\nu _1} \end{aligned}$$

(7.2e)

so that

$$\begin{aligned} {\tilde{N}}_t&= s^n_t N_t,\quad s_t^n:=\left( \int _0^1 W_{ht}^{-\epsilon _n (1+\nu _1)}dh\right) ^{\frac{1}{1+\nu _1}}W_t^{-\epsilon _n}. \end{aligned}$$

(7.2f)

Note that we must track the variable ${\tilde{N}}_t$ in order to compute our welfare measure.

1.3 Dynamics

The full model consists of Eqs. (7.1), (7.2), (2.5), (2.13), (2.19a), (2.20), (2.22), (2.29), (2.35), (2.36), (2.37), the resource constraint (2.38), the capital accumulation equation (2.34), the Taylor rule (2.32), and the dynamics of the shocks, (2.10) and (2.31), respectively. In order to compute our welfare measure we have to add the recursive definitions of $V^C_t$ and $V^N_t$ implied by (2.39). These are

$$\begin{aligned} V_t^C&= \left[ \frac{(C_t-\chi C_{t-1})^{1-\eta }-1}{1-\eta }\right] + \beta \mathbb {E}_tV_{t+1}^C, \end{aligned}$$

(7.3a)

$$\begin{aligned} V_t^N&= \frac{\nu _0}{1+\nu _1}{\tilde{N}}_t^{1+\nu _1}+\beta \mathbb {E}_tV_{t+1}^N. \end{aligned}$$

(7.3b)

For convenience, we summarize the entire system below:

$$\begin{aligned} \Lambda _t= \,& {} (C_t - \chi C_{t-1})^{-\eta }, \end{aligned}$$

(7.4.1)

$$\begin{aligned} q_t= \,& {} \frac{1}{\Psi '(I_t/K_t)}, \end{aligned}$$

(7.4.2)

$$\begin{aligned} r_{Kt}=\, & {} q_t \Psi (I_t/K_t) - (I_t/K_t), \end{aligned}$$

(7.4.3)

$$\begin{aligned} w_t=\, & {} (1-\alpha )(g_t/v_t){\tilde{Y}}_t/N_t, \end{aligned}$$

(7.4.4)

$$\begin{aligned} r_{Yt}=\, & {} \alpha (g_t/v_t){\tilde{Y}}_t/K_t, \end{aligned}$$

(7.4.5)

$$\begin{aligned} {\tilde{Y}}_t=\, & {} Z_t N_t^{1-\alpha }K_t^\alpha , \end{aligned}$$

(7.4.6)

$$\begin{aligned} 1=\, & {} v_t \left[ \Omega _t - \Phi ({\bar{\omega }}_t)\kappa - \frac{f({\bar{\omega }}_t)\phi ({\bar{\omega }}_t)\kappa }{1-\Phi ({\bar{\omega }}_t)}\right] , \end{aligned}$$

(7.4.7)

$$\begin{aligned} r_{Lt}=\, & {} \frac{{\bar{\omega }}_t}{h({\bar{\omega }}_t)}-1, \end{aligned}$$

(7.4.8)

$$\begin{aligned} g_t {\tilde{Y}}_t= \,& {} \frac{v_t}{1-v_t h({\bar{\omega }}_t)}\left[ q_t(1-\delta )+r_{Yt}+r_{Kt}\right] X_t, \end{aligned}$$

(7.4.9)

$$\begin{aligned} p_{At}=\, & {} \frac{\epsilon _y}{\epsilon _y-1}\frac{\Gamma _{1t}}{\pi _t\Gamma _{2t}}, \end{aligned}$$

(7.4.10)

$$\begin{aligned} 1=\, & {} (1-\varphi _y)p_{At}^{1-\epsilon _y} + \varphi _y (\pi _{t-1}/\pi _t)^{1-\epsilon _y}, \end{aligned}$$

(7.4.11)

$$\begin{aligned} s_t^y=\, & {} (1-\varphi _y)p_{At}^{-\epsilon _y} + \varphi _y (\pi _{t-1}/\pi _t)^{-\epsilon _y}s_{t-1}^y, \end{aligned}$$

(7.4.12)

$$\begin{aligned} s_t^y Y_t=\, & {} {\tilde{Y}}_t, \end{aligned}$$

(7.4.13)

$$\begin{aligned} {\tilde{w}}_t=\, & {} \frac{\epsilon _n}{\epsilon _n-1}\frac{\Delta _{1t}}{\Delta _{2t}}, \end{aligned}$$

(7.4.14)

$$\begin{aligned} w_t^{1-\epsilon _n}=\, & {} (1-\varphi _n){\tilde{w}}_t^{1-\epsilon _n}+\varphi _n\left( \frac{\pi _{t-1}}{\pi _t}w_{t-1}\right) ^{1-\epsilon _n}, \end{aligned}$$

(7.4.15)

$$\begin{aligned} (s_t^n)^{1+\nu _1}=\, & {} (1-\varphi _n)\left( \frac{{\tilde{w}}_{t}}{w_t}\right) ^{-\epsilon _n(1+\nu _1)} + \varphi _n\left( \frac{\pi _{t-1}w_{t-1}}{\pi _t w_t}\right) ^{-\epsilon _n(1+\nu _1)}(s^n_{t-1})^{1+\nu _1}, \end{aligned}$$

(7.4.16)

$$\begin{aligned} \tilde{N}_t=\, & {} s^n_t N_t, \end{aligned}$$

(7.4.17)

$$\begin{aligned} Y_t=\, & {} C_t + I_t + G_t + \Phi ({\bar{\omega }}_t)\kappa g_t {\tilde{Y}}_t, \end{aligned}$$

(7.4.18)

$$\begin{aligned} K_{t+1}=\, & {} \Psi (I_t/K_t)K_t + (1-\delta )K_t, \end{aligned}$$

(7.4.19)

$$\begin{aligned} q_t X_{t+1}=\, & {} f({\bar{\omega }}_t)g_t{\tilde{Y}}_t - D_{t}^P - \Delta _{t}^P, \end{aligned}$$

(7.4.20)

$$\begin{aligned} Q_{t+1}=\, & {} Q_t^{\delta _1}\left( \frac{\pi }{\beta }\right) ^{1-\delta _1}\left( \frac{\pi _t}{\pi }\right) ^{\delta _2}(q_t)^{\delta _3}(Y_t/Y)^{\delta _4}, \end{aligned}$$

(7.4.21)

$$\begin{aligned} q_t=\, & {} \beta \mathbb {E}_t\frac{\Lambda _{t+1}}{\Lambda _t}\left( q_{t+1}(1-\delta )+r_{Yt+1}+r_{Kt+1}\right) , \end{aligned}$$

(7.4.22)

$$\begin{aligned} 1=\, & {} \beta \mathbb {E}_t\frac{\Lambda _{t+1}}{\Lambda _t}\frac{Q_{t+1}}{\pi _{t+1}}, \end{aligned}$$

(7.4.23)

$$\begin{aligned} q_t=\, & {} \gamma \beta \mathbb {E}_t\frac{\Lambda _{t+1}}{\Lambda _t}\left[ q_{t+1}(1-\delta )+r_{Yt+1}+r_{Kt+1}\right] \frac{v_{t+1} f({\bar{\omega }}_{t+1})}{1-v_{t+1}h({\bar{\omega }}_{t+1})}, \end{aligned}$$

(7.4.24)

$$\begin{aligned} \Gamma _{1t}=\, & {} \mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _y)^s \pi _{t+s}^{\epsilon _y}g_{t+s}\Lambda _{t+s}Y_{t+s}= \pi _{t}^{\epsilon _y}g_t \Lambda _t Y_t + (\beta \varphi _y)\mathbb {E}_t\Gamma _{1t+1}, \end{aligned}$$

(7.4.25)

$$\begin{aligned} \Gamma _{2t}=\, & {} \mathbb {E}_t\sum _{s=0}^\infty (\beta \varphi _y)^s \pi _{t+s}^{\epsilon _y-1}\Lambda _{t+s}Y_{t+s}=\pi _{t}^{\epsilon _y-1} \Lambda _t Y_t + (\beta \varphi _y)\mathbb {E}_t\Gamma _{2t+1}, \end{aligned}$$

(7.4.26)

$$\begin{aligned} \Delta _{1t}=\, & {} \nu _0\left( \frac{{\tilde{w}}_t}{w_t}\right) ^{-\epsilon _n(1+\nu _1)}N_t^{1+\nu _1} + (\beta \varphi _n)\mathbb {E}_t\left( \frac{\pi _t{\tilde{w}}_t}{\tilde{\pi }_{t+1}w_{t+1}}\right) ^{-\epsilon _n(1+\nu _1)}\Delta _{1t+1}, \end{aligned}$$

(7.4.27)

$$\begin{aligned} \Delta _{2t}=\, & {} \Lambda _t \left( \frac{{\tilde{w}}_t}{w_t}\right) ^{-\epsilon _n}N_t + (\beta \varphi _n)\mathbb {E}_t\left( \frac{{\tilde{w}}_t}{{\tilde{w}}_{t+1}}\right) ^{-\epsilon _n}\left( \frac{ \pi _t}{\pi _{t+1}}\right) ^{1-\epsilon _n}\Delta _{2t+1}, \end{aligned}$$

(7.4.28)

$$\begin{aligned} V_t^C=\, & {} \left[ \frac{(C_t-\chi C_{t-1})^{1-\eta }-1}{1-\eta }\right] + \beta \mathbb {E}_tV_{t+1}^C, \end{aligned}$$

(7.4.29)

$$\begin{aligned} V_t^N=\,& {} \frac{\nu _0}{1+\nu _1}\tilde{N}_t^{1+\nu _1}+\beta \mathbb {E}_tV_{t+1}^N. \end{aligned}$$

(7.4.30)

1.4 Stationary Solution and Calibration

The model is solved via a second-order approximation of the decision rules at the stationary solution of the deterministic version of the model. This solution follows from the model’s equations if we set the shocks equal to $Z_t=1$, and $G_t=G$ and cancel the time indices.

In the first step we determine v and $\bar{\omega }$. We proceed as Carlstrom and Fuerst (1997, 1998) and employ a log-normal distribution for $\phi$ with parameters $\mu _\omega$ and $\sigma _\omega$. We determine these parameters and the stationary bankruptcy threshold $\bar{\omega }$ from three conditions:

• i. We assume a mean of one: $\mathbb {E}(\omega ) = \Omega =1$,

• ii. a bankruptcy rate of $\Phi (\bar{\omega })=0.00974$ (taken from Carlstrom and Fuerst (1998), p. 590).

• iii. and an external finance premium of $\frac{\bar{\omega }}{h(\bar{\omega })}-1=r_L=1.0187^{0.25}-1$ (also taken from Carlstrom and Fuerst (1998), p. 590)

Given $\bar{\omega }$ we can solve (7.4.7) for v.

In the second step we determine the additional discount parameter $\gamma$. The stationary versions of (7.4.22) and (7.4.24) imply

$$\begin{aligned} \gamma =\frac{1-vg(\bar{\omega })}{vf(\bar{\omega })}. \end{aligned}$$

In the third step we solve the stationary wage and price equations. It is immediate from Eq. (7.4.11) that $p_A=1$ so that Eq. (7.4.12) implies $s^y=1$ and Eq. (7.4.13) $Y={\tilde{Y}}$. Equations (7.4.10), (7.4.25), and (7.4.26) deliver

$$\begin{aligned} g&=\frac{\epsilon _y-1}{\epsilon _y}, \end{aligned}$$

(7.5a)

$$\begin{aligned} \Gamma _1&= \frac{g\Lambda Y\pi ^{\epsilon }}{1-\beta \varphi _y}, \end{aligned}$$

(7.5b)

$$\begin{aligned} \Gamma _2&= \frac{\Lambda Y\pi ^{\epsilon -1}}{1-\beta \varphi _y}. \end{aligned}$$

(7.5c)

Equation (7.4.15) implies ${\tilde{w}} = w$ so that ${\tilde{s}}^n=1$ via (7.4.16) and $N={\tilde{N}}$ from (7.4.17). The stationary values of the auxiliary variables follow from (7.4.27) and (7.4.28) as

$$\begin{aligned} \Delta _1&= \nu _0 \frac{N^{1+\nu _1}}{1-\beta \varphi _n}, \end{aligned}$$

(7.5d)

$$\begin{aligned} \Delta _2&= \frac{\Lambda N}{1-\beta \varphi _n} \end{aligned}$$

(7.5e)

so (7.4.14) implies

$$\begin{aligned} \nu _0 N^{\nu _1}&=\frac{\epsilon _n-1}{\epsilon _n}\Lambda w. \end{aligned}$$

(7.5f)

In the fourth step we solve for Y / K. Our assumption with respect to the function $\Psi$ in (2.34) imply $q=1$ (see (2.5a)) and $r_K=0$ (see (2.5b)) so that Eqs. (7.4.5) and (7.4.22) can be solved for

$$\begin{aligned} \frac{Y}{K}&= \frac{1-\beta (1-\delta )}{\alpha \beta (g/v)}. \end{aligned}$$

(7.5g)

The production function (7.4.6) yields

$$\begin{aligned} \frac{K}{N}&= \left( \frac{Y}{K}\right) ^{\frac{1}{\alpha -1}}. \end{aligned}$$

(7.5h)

Given N this allows us to compute K, Y, $I=\delta K$. The solution for consumption follows from (7.4.18):

$$\begin{aligned} C&= Y(1-g\Phi (\bar{\omega })\kappa )-I-G \end{aligned}$$

(7.5i)

so that $\Lambda$ is determined by (7.4.1):

$$\begin{aligned} \Lambda&=[(1-\chi )C]^{-\eta }. \end{aligned}$$

(7.5j)

Equation (7.4.4) determines the stationary real wage w. We are now able to determine the parameter $\nu _0$ from condition (7.5f) and the auxiliary variables $\Gamma _1$, $\Gamma _2$, $\Delta _1$ and $\Delta _2$ from (7.5b)–(7.5e).

In the last step we can compute the stock of capital owned by firms in the primary sector from (7.4.9)

$$\begin{aligned} X&= \frac{g Y (1-vg(\bar{\omega }))}{v(1-\delta + r_Y)}, \end{aligned}$$

(7.5k)

and dividends distributed from primary production firms to the household from (2.35)

$$\begin{aligned} D^P&= f(\bar{\omega })g{\tilde{Y}} - X - \Delta ^P. \end{aligned}$$

(7.5l)

In our simulations we follow Carlstrom and Fuerst (1998) and set $\Delta ^P=0$.¹⁵ The stationary values of the life-time utility associated with consumption $V^C$ and working hours $V^N$ equal

$$\begin{aligned} V^C&= \frac{1}{1-\beta } \frac{[(1-\chi )C]^{1-\eta }-1}{1-\eta }, \end{aligned}$$

(7.5m)

$$\begin{aligned} V^N&= \frac{1}{1-\beta } \frac{\nu _0}{1+\nu _1}N^{1+\nu _1}. \end{aligned}$$

(7.5n)

Finally, the stationary version of the Euler equation (7.4.23) determines the nominal interest rate

$$\begin{aligned} Q&= \frac{\pi }{\beta }. \end{aligned}$$

(7.5o)

Appendix 2: Approximation of $\lambda$

Note that

$$\begin{aligned} (1-\lambda )^{1-\eta }V^C_t + \frac{(1-\lambda )^{1-\eta }-1}{(1-\eta )(1-\beta )}=\mathbb {E}_t\sum _{s=0}^\infty \beta ^s \frac{(1-\lambda )^{1-\eta }(C_{t+s}-\chi C_{t+s-1})^{1-\eta }-1}{1-\eta } \end{aligned}$$

so that condition (2.41) can be written

$$\begin{aligned} \bar{V}_t = \bar{V}^C_t - \bar{V}^N_t = (1-\lambda )^{1-\eta }V^C_t + \frac{(1-\lambda )^{1-\eta }-1}{(1-\eta )(1-\beta )}- V^N_t. \end{aligned}$$

(8.1)

This equation can be solve for $\lambda$, yielding

$$\begin{aligned} \lambda = 1 - \left[ \frac{1 + (1-\eta )(1-\beta )[\bar{V}^C_t + V^N_t - \bar{V}^N_t]}{1+(1-\eta )(1-\beta )V^C_t}\right] ^\frac{1}{1-\eta }. \end{aligned}$$

Thus, with $\sigma =1$, we get

$$\begin{aligned} \lambda \simeq \lambda (\mathbf {x}) + \lambda _\sigma (\mathbf {x}) + \frac{1}{2}\lambda _{\sigma \sigma } \end{aligned}$$

With identical initial conditions $\lambda ({\mathbf {x}})=0$. As shown by Schmitt-Grohé and Uribe (2004a), the first-order effect of the scaling factor $\sigma$ on the policy functions of the model is nil. As a consequence, $\lambda _{\sigma }(\mathbf {x})=0$. Using this and differentiating (8.1) twice yields the Eq. (2.42) in the body of the paper.

Appendix 3: Zero Lower Bound

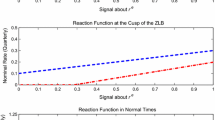
The Taylor rules which we consider must satisfy the non-negativity constraint on the nominal interest rate: $Q_t\ge 1$. Since our solution rests on perturbation methods, we cannot directly take care of this constraint. We, thus, follow Schmitt-Grohé and Uribe (2004a), p.31, who propose to disregard solutions which entail a significant probability to violate this constraint. Assume $Q_t-Q$ is distributed normally with mean zero and variance $\sigma _Q$ so that $\bar{z}\equiv (Q_t-Q)/\sigma _Q$ is a standard normal random variable. For $\bar{z}=-2.05$ the probability of the event $z\le \bar{z}$ is 2 percent. Therefore, we disregard solutions for which $\sigma _Q\ge (Q-1)/2.05$.

To determine whether or not a particular monetary policy violates this condition, we must compute the unconditional variance $\sigma ^2_{Q}$ of the deviation of the interest factor $Q_t$ from its non-stochastic stationary solution Q.

Let

$$\begin{aligned} \mathbf {x}_t=\begin{bmatrix}K_t,&X_t&C_{t-1},&Q_t,&w_{t-1},&s^y_{t-1},&s^n_{t-1},&\pi _{t-1}\end{bmatrix}' \end{aligned}$$

denote the vector of endogenous state variables, $\bar{\mathbf {x}}_t = \mathbf {x}_t-\mathbf {x}$ the deviation of the states from the non-stochastic steady state, and $\mathbf {z}_t = [\ln Z_t, \ln (G_t/G)]'$ the vector of exogenous state variables. The first-order solution of the model is given by

$$\begin{aligned} \bar{\mathbf {x}}_{t+1}&= L^x \bar{\mathbf {x}}_t + L^z \mathbf {z}_t, \end{aligned}$$

(9.1)

$$\begin{aligned} \mathbf {z}_{t+1}&= \Pi \mathbf {z}_{t}+\varvec{\epsilon }_{t+1}, \quad \mathbb {E}(\varvec{\epsilon }_{t+1} \varvec{\epsilon }_{t+1}')=\Sigma ^\epsilon =\Omega \Omega '. \end{aligned}$$

(9.2)

We seek to determine $\Sigma ^x\equiv \mathbb {E}(\bar{\mathbf {x}}_t \bar{\mathbf {x}}_t')$. Since $\mathbf {z}_t$ is a stationary stochastic process and since the eigenvalues of $L^x$ are within the unit circle, $\Sigma ^x$ exists and is independent of the time index t. Multiplying both sides of (9.1) with $\bar{\mathbf {x}}_{t+1}$ yields:

$$\begin{aligned} \begin{aligned} \mathbb {E}(\bar{\mathbf {x}}_{t+1}\bar{\mathbf {x}}_{t+1}')&=\mathbb {E}(L^x \bar{\mathbf {x}}_t+L^z\mathbf {z}_t)(L^x \bar{\mathbf {x}}_t+L^z\mathbf {z}_t)'\\&=\mathbb {E}(L^x \bar{\mathbf {x}}_t\bar{\mathbf {x}}_t'(L^x)')+\mathbb {E}(L^z\mathbf {z}_t \mathbf {z}_t'(L^z)') + \mathbb {E}(L^x \bar{\mathbf {x}}_t\mathbf {z}_t'(L^z)')+ \mathbb {E}(L^z \mathbf {z}_t\bar{\mathbf {x}}_t'(L^x)'),\\ \Sigma ^x&=L^x\Sigma ^x (L^x)'+ L^z \Sigma ^z (L^z)' + L^x\Sigma ^{xz}(L^z)' + L^z (\Sigma ^{xz})'(L^x)'. \end{aligned} \end{aligned}$$

Applying the vec-operator on both sides of the previous equation yields:¹⁶

$$\begin{aligned} {\text {vec}}\,\Sigma ^x&= \left( I_{n(x)^2}-L^x \otimes L^x \right) ^{-1}{\text {vec}}\,\left( L^z \Sigma ^z (L^z)' + L^x\Sigma ^{xz}(L^z)'+ L^z(\Sigma ^{xz})'(L^x)'\right) . \end{aligned}$$

(9.3a)

The matrices $\Sigma ^{xz}$ and $\Sigma ^z$ in this expression follow from the same reasoning. Consider $\Sigma ^{xz}=\mathbb {E}(\bar{\mathbf {x}}_t\mathbf {z}_t')$:

$$\begin{aligned} \begin{aligned} \Sigma ^{xz}&=\mathbb {E}(\bar{\mathbf {x}}_{t+1}\mathbf {z}_{t+1}')=\mathbb {E}(L^x \bar{\mathbf {x}}_t + L^z\mathbf {z}_t)(\Pi \mathbf {z}_t+\varvec{\epsilon }_{t+1})',\\&=\mathbb {E}(L^x \bar{\mathbf {x}}_t \mathbf {z}_t'\Pi ') + \mathbb {E}(L^z \mathbf {z}_{t}\mathbf {z}_t'\Pi ')+\mathbb {E}(L^x\bar{\mathbf {x}}_t\varvec{\epsilon }_{t+1}')+\mathbb {E}(L^z\mathbf {z}_t\varvec{\epsilon }_{t+1}'),\\ \Sigma ^{xz}&=L^x \Sigma ^{xz}\Pi ' + L^z\Sigma ^z\Pi ',\end{aligned} \end{aligned}$$

because the expectation of the terms that involve $\varvec{\epsilon }_{t+1}$ is zero, since $\mathbf {z}_{t}$ and $\bar{\mathbf {x}}_t$ are predetermined when $\varvec{\epsilon }_{t+1}$ is realized. Therefore,

$$\begin{aligned} {\text {vec}}\,\Sigma ^{xz}&=\left( I_{n(x)n(z)}-\Pi \otimes L^x\right) ^{-1}{\text {vec}}\,\left( L^z\Sigma ^z\Pi '\right) . \end{aligned}$$

(9.3b)

Finally:

$$\begin{aligned} \begin{aligned} \Sigma ^z&\equiv \mathbb {E}(\mathbf {z}_{t+1} \mathbf {z}_{t+1}') = \mathbb {E}(\Pi \mathbf {z}_t + \varvec{\epsilon }_{t+1})(\Pi \mathbf {z}_t + \varvec{\epsilon }_{t+1})',\\&=\mathbb {E}(\Pi \mathbf {z}_t\mathbf {z}_t'\Pi ') + \mathbb {E}(\varvec{\epsilon }_{t+1}\varvec{\epsilon }_{t+1}')+\mathbb {E}(\Pi \mathbf {z}_t\varvec{\epsilon }_{t+_1}') + \mathbb {E}(\varvec{\epsilon }_{t+1}\mathbf {z}_t'\Pi '),\\ \Sigma ^z&= \Pi \Sigma ^z \Pi ' + \Sigma ^\epsilon \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} {\text {vec}}\,\Sigma ^z&= \left( I_{n(z)^2} - \Pi \otimes \Pi \right) ^{-1}{\text {vec}}\,\Sigma ^\epsilon . \end{aligned}$$

(9.3c)

Equations (9.3) allow us to compute $\sigma _Q$ as the square root of the third diagonal element of $\Sigma ^x$, given the model’s first order solution $L^x$ and $L^z$.

Appendix 4: Additional Results

1.1 Impulse Response of Price and Wage Dispersion

Figure 4 presents the impulse response of the measures of price and wage dispersion, $s^y_t$ and $s^n_t$, respectively, to a shock to total factor productivity. The scale on the ordinate are percentage points. Both measures have a steady state value of unity, in which case all price setters set the same price and all wage setters demand the same wage. The shock lowers the marginal costs of production so that firms being able to reset their price decrease prices. Equation (7.4.12), thus, implies that the measure of price dispersion will increase. On the contrary, the measure of wage dispersion decreases, since the wage setters demand higher wages (see Eq. (7.4.16)). However, the size of the change of both measures is almost negligible.

Fig. 4

Impulse responses of price and wage dispersion. Notes: Case 1 (2) refers to a model with nominal frictions only and the simple (optimal) Taylor rule. Case 3 (4) refers to the model with all frictions and the simple (optimal) Taylor rule

1.2 Wealth Shock

As an additional exercise to study the sensitivity of our results we add a third shock to our benchmark model. As Mimir (2016), we assume that a financial shock proportionately changes the net wealth of all producers in the primary sector, i.e., we change Eq. (7.4.9) to

$$\begin{aligned} g_t {\tilde{Y}}_t = \frac{v_t}{1-v_t h(\bar{\omega }_t)}\left[ q_t(1-\delta )+r_{Yt}+r_{Kt}\right] X_t e^{\xi _t}, \end{aligned}$$

and assume that $\xi _t$ follows a first-order autoregressive process

$$\begin{aligned} \xi _t=\rho _{\xi } \xi _{t-1}+\epsilon _{\xi t}, \quad \epsilon _{\xi t} \quad \text { iid } \quad N(0,\sigma _{\xi }^2). \end{aligned}$$

We take the values of the parameters $\rho _\xi =0.37$ and $\sigma _\xi =0.05$ from the estimates of Mimir (2016).

A positive wealth shock decreases the external finance premium and lowers the mark-up on factor costs. Therefore, intermediary goods prices decrease and real wages increase triggering a positive response of hours, output, consumption, and investment (see Fig. 5). The latter, in turn, increases Tobin’s q. In the case of small adjustment costs of capital, $\zeta =0.5$, these effects occur immediately, whereas in the case of high adjustment costs, $\zeta =2.5$, labor supply and output drop in the impact period of the shock and increase thereafter. While similar in their effects on consumption, labor supply, and Tobin’s q, the direct impact of a TFP shock has much larger effects than the indirect effect of a wealth shock, even though the latter is much larger in size ($\sigma _Z=0.0064$ versus $\sigma _\xi =0.05$). Since both the TFP and the net wealth shock have similar effects (for the former, see Fig. 2 in the main text) so that the coincidence of a positiv TFP shock and a negative wealth shock dampens the reaction on Tobin’s q, the central bank does not gain from targeting Tobin’s q in addition to inflation and the output gap. Table 5 confirms this intuition.

Fig. 5

Impulse responses to a financial shock. Notes: Case 1 (2) refers to the model with $\zeta =0.5$ and the simple (optimal) Taylor rule. Case 3 (4) refers to the model with $\zeta =2. 5$ and the simple (optimal) Taylor rule

In the case of small adjustment costs of capital, $\zeta =0.5$, the fine tuned Taylor rule aggressively increases the interest rate in response to inflation and the output gap. In the case of high adjustment costs, $\zeta =2.5$, where the effects of a TFP shock on output occur more gradually, the central bank changes its interest rate more cautiously (see also the upper right panel of Fig. 5).

Table 5 Welfare effects in the model with an additional financial shock