Skip to main content
SpringerLink
Log in

Pseudospectral quadrature simulation technique for spatio-temporally parabolic multi-dimensional nonlinear fractional evolution equation

  • Original Research Paper
  • Published:
The Journal of Analysis Aims and scope Submit manuscript

Abstract

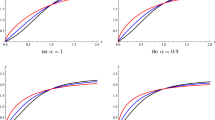
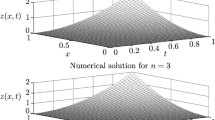
The aim of this paper, the author is to introduce the Jacobi pseudospectral quadrature simulation technique for the multi-dimensional nonlinear fractional evolution equation. We define Lagrange interpolants polynomial as a test function, which satisfies the Kronecker delta property at Jacobi-Gauss-Lobatto points. For this point, Jacobi polynomials are introduced and their functional grids of partial joining an item are determined. Utilizing the Jacobi derivatives matrices the given multi-dimensional nonlinear fractional evolution equations are reduced to a system of nonlinear algebraic equations, which will be solved using Newton’s Raphson method. The proposed strategy is set up in both directions to demonstrate the numerical solutions and to prove the theory of error estimates for the equations. The proficiency, precision, and legitimacy of the introduced strategy are exhibited by its application to three test models and compared with exact solutions and other existing methods. Besides, the proposed numerical method is reported to demonstrate the efficiency of our scheme. A comparison of the numerical and exact solutions is shown in figures and tables.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Data availability

All necessary data has been given.

References

  1. Amin, R., K. Shah, M. Asif, I. Khan, and F. Ullah. 2021. An efficient algorithm for numerical solution of fractional integro-differential equations via Haar wavelet. Journal of Computational and Applied Mathematics 381: 113028.

    Article  MathSciNet  Google Scholar 

  2. Asgari, M., and R. Ezzati. 2017. Using operational matrix of two-dimensional Bernstein polynomials for solving two-dimensional integral equations of fractional order. Applied Mathematics and Computation 307: 290–298.

    Article  MathSciNet  Google Scholar 

  3. Assari, P., H. Adibi, and M. Dehghan. 2013. A meshless method for solving nonlinear two-dimensional integral equations of the second kind on non-rectangular domains using radial basis functions with error analysis. Journal of Computational and Applied Mathematics 239: 72–92.

    Article  MathSciNet  Google Scholar 

  4. Babolian, E., S. Bazm, and P. Lima. 2011. Numerical solution of nonlinear two-dimensional integral equations using rationalized Haar functions. Communications in Nonlinear Science and Numerical Simulation 16 (3): 1164–1175.

    Article  MathSciNet  Google Scholar 

  5. Balyan, L.K., A.K. Mittal, M. Kumar, and M. Choube. 2020. Stability analysis and highly accurate numerical approximation of fisher’s equations using pseudospectral method. Mathematics and Computers in Simulation 177: 86–104.

    Article  MathSciNet  Google Scholar 

  6. Bagley, R., and P. Torvik. 1983. A theoretical basis for the application of fractional calculus to visco-elasticity. Journal of Rheoloy 27: 201–210.

    Article  Google Scholar 

  7. Bedi, P., A. Kumar, T. Abdeljawad, Z.A. Khan, and A. Khan. 2020. Existence and approximate controllability of Hilfer fractional evolution equations with almost sectorial operators. Advances in Difference Equations 2020 (1): 1–15.

    Article  MathSciNet  Google Scholar 

  8. Brunner, H. 1984. Iterated collocation methods and their discretizations for Volterra integral equations. SIAM journal on numerical analysis 21 (6): 1132–1145.

    Article  MathSciNet  Google Scholar 

  9. Chen, H., D. Xu, J. Cao, and J. Zhou. 2018. A backward Euler alternating direction implicit difference scheme for the three-dimensional fractional evolution equation. Numerical Methods for Partial Differential Equations 34 (3): 938–958.

    Article  MathSciNet  Google Scholar 

  10. Chen, H., D. Xu, and Y. Peng. 2017. A second order BDF alternating direction implicit difference scheme for the two-dimensional fractional evolution equation. Applied Mathematical Modelling 41: 54–67.

    Article  MathSciNet  Google Scholar 

  11. Chen, H., D. Xu, and Y. Peng. 2015. An alternating direction implicit fractional trapezoidal rule type difference scheme for the two-dimensional fractional evolution equation. International Journal of Computer Mathematics 92 (10): 2178–2197.

    Article  MathSciNet  Google Scholar 

  12. Chen, H., D. Xu, and J. Zhou. 2019. A second-order accurate numerical method with graded meshes for an evolution equation with a weakly singular kernel. Journal of Computational and Applied Mathematics 356: 152–163.

    Article  MathSciNet  Google Scholar 

  13. Dehghan, M., and M. Abbaszadeh. 2017. Spectral element technique for nonlinear fractional evolution equation, stability and convergence analysis. Applied Numerical Mathematics 119: 51–66.

    Article  MathSciNet  Google Scholar 

  14. El-Borai, M.M., K.E.S. El-Nadi, and E.G. El-Akabawy. 2010. On some fractional evolution equations. Computers and mathematics with applications 59 (3): 1352–1355.

    Article  MathSciNet  Google Scholar 

  15. Ferdous, F., and M.G. Hafez. 2018. Oblique closed form solutions of some important fractional evolution equations via the modified Kudryashov method arising in physical problems. Journal of Ocean Engineering and Science 3 (3): 244–252.

    Article  Google Scholar 

  16. Fujita, Y. 1990. Integro-differential equation which interpolates the heat equation and the wave equation. Osaka J. Math. 27 (1990): 309–321.

    MathSciNet  Google Scholar 

  17. Ghehsareh, H.R., S.H. Bateni, and A. Zaghian. 2015. A meshfree method based on the radial basis functions for solution of two-dimensional fractional evolution equation. Engineering Analysis with Boundary Elements 61: 52–60.

    Article  MathSciNet  Google Scholar 

  18. Gottlieb, S., and C. Wang. 2012. Stability and convergence analysis of fully discrete fourier collocation spectral method for 3-d viscous burgers’ equation. Journal of Scientific Computing 53 (1): 102–128.

    Article  MathSciNet  Google Scholar 

  19. Gu, H., and J.J. Trujillo. 2015. Existence of mild solution for evolution equation with Hilfer fractional derivative. Applied Mathematics and Computation 257: 344–354.

    Article  MathSciNet  Google Scholar 

  20. Hammad, H.A., H. Aydi, and N. Mlaiki. 2021. Contributions of the fixed point technique to solve the 2D Volterra integral equations, Riemann-Liouville fractional integrals, and Atangana-Baleanu integral operators. Advances in Difference Equations 1: 1–20.

    MathSciNet  Google Scholar 

  21. Han, G., and R. Wang, 2001. The extrapolation method for two-dimensional Volterra integral equations based on the asymptotic expansion of iterated Galerkin solutions. The Journal of Integral Equations and Applications, 15-34.

  22. Hashemi, M.S. 2021. A novel approach to find exact solutions of fractional evolution equations with non-singular kernel derivative. Chaos, Solitons and Fractals 152: 111367.

    Article  MathSciNet  Google Scholar 

  23. Hesameddini, E., and M. Shahbazi. 2018. Two-dimensional shifted Legendre polynomials operational matrix method for solving the two-dimensional integral equations of fractional order. Applied Mathematics and Computation 322: 40–54.

    Article  MathSciNet  Google Scholar 

  24. Hesthaven, J.S., S. Gottlieb, and D. Gottlieb. 2007. Spectral methods for time-dependent problems, vol. 21. Cambridge University Press.

    Book  Google Scholar 

  25. Heydari, M.H., M.R. Hooshmandasl, and F. Mohammadi. 2014. Legendre wavelets method for solving fractional partial differential equations with Dirichlet boundary conditions. Applied Mathematics and Computation 234: 267–276.

    Article  MathSciNet  Google Scholar 

  26. Ilyas, A., S.A. Malik, and S. Saif. 2021. Inverse problems for a multi-term time fractional evolution equation with an involution. Inverse Problems in Science and Engineering 29 (13): 3377–3405.

    Article  MathSciNet  Google Scholar 

  27. Jafari, H., H. Tajadodi, and D. Baleanu. 2014. Application of a homogeneous balance method to exact solutions of nonlinear fractional evolution equations. Journal of Computational and Nonlinear Dynamics 9 (2): 021019.

    Article  Google Scholar 

  28. Jani, M., S. Javadi, E. Babolian, and D. Bhatta. 2018. Bernstein dual-Petrov-Galerkin method: application to 2D time fractional diffusion equation. Computational and Applied Mathematics 37 (2): 2335–2353.

    Article  MathSciNet  Google Scholar 

  29. Jin, B., R. Lazarov, and Z. Zhou. 2019. Numerical methods for time-fractional evolution equations with nonsmooth data: a concise overview. Computer Methods in Applied Mechanics and Engineering 346: 332–358.

    Article  MathSciNet  Google Scholar 

  30. Khater, A.H., A.B. Shamardan, D.K. Callebaut, and M.R.A. Sakran. 2007. Numerical solutions of integral and integro-differential equations using Legendre polynomials. Numerical Algorithms 46 (3): 195–218.

    Article  MathSciNet  Google Scholar 

  31. Khebchareon, M., A.K. Pani, and G. Fairweather. 2015. Alternating direction implicit Galerkin methods for an evolution equation with a positive-type memory term. Journal of Scientific Computing 65 (3): 1166–1188.

    Article  MathSciNet  Google Scholar 

  32. Kilbas, A., H. Srivastava, and J. Trujillo. 2006. Theory and applications of fractional differential equations. Boston: Elsevier.

    Google Scholar 

  33. Larsson, S., V. Thomée, and L. Wahlbin. 1998. Numerical solution of parabolic integro-differential equations by the discontinuous Galerkin method. Mathematics of computation 67 (221): 45–71.

    Article  MathSciNet  Google Scholar 

  34. Li, L., and D. Xu. 2013. Alternating direction implicit-Euler method for the two-dimensional fractional evolution equation. Journal of Computational Physics 236: 157–168.

    Article  MathSciNet  Google Scholar 

  35. Li, Y., and N. Sun. 2011. Numerical solution of fractional differential equations using the generalized block pulse operational matrix. Computers and Mathematics with Applications 62 (3): 1046–1054.

    Article  MathSciNet  Google Scholar 

  36. Ma, X., and C. Huang. 2013. Numerical solution of fractional integro-differential equations by a hybrid collocation method. Applied Mathematics and Computation 219 (12): 6750–6760.

    Article  MathSciNet  Google Scholar 

  37. Mahmudov, N.I., and S. Zorlu. 2014. On the approximate controllability of fractional evolution equations with compact analytic semigroup. Journal of Computational and Applied Mathematics 259: 194–204.

    Article  MathSciNet  Google Scholar 

  38. Mandal, M., and G. Nelakanti. 2019. Superconvergence results of Legendre spectral projection methods for weakly singular Fredholm-Hammerstein integral equations. Journal of Computational and Applied Mathematics 349: 114–131.

    Article  MathSciNet  Google Scholar 

  39. Mittal, A.K. 2022. A spectrally accurate time-space pseudospectral method for reaction-diffusion Malaria infection model. Computational and Applied Mathematics 41 (8): 1–21.

    Article  MathSciNet  Google Scholar 

  40. Mittal, A.K. 2022. Error analysis and approximation of Jacobi pseudospectral method for the integer and fractional order integro-differential equation. Applied Numerical Mathematics 171: 249–268.

    Article  MathSciNet  Google Scholar 

  41. Mittal, A.K. 2020. A stable time-space jacobi pseudospectral method for two-dimensional sine-gordon equation.Journal of Applied Mathematics and Computing, pages 1–26.

  42. Mittal, A.K. and L.K. Balyan. 2019. A highly accurate time-space pseudospectral approximation and stability analysis of two dimensional brusselator model for chemical systems. International Journal of Applied and Computational Mathematics, pages 5(5), 140.

  43. Mittal, A.K., and L.K. Balyan. 2020. Chebyshev pseudospectral approximation of two dimensional fractional schrödinger equation on a convex and rectangular domain. AIMS Mathematics, pages 5 (3): 1642–1662.

  44. Pani, A.K., G. Fairweather, and R.I. Fernandes. 2008. Alternating direction implicit orthogonal spline collocation methods for an evolution equation with a positive-type memory term. SIAM journal on numerical analysis 46 (1): 344–364.

    Article  MathSciNet  Google Scholar 

  45. Panda, S.K., E. Karapınar, and A. Atangana. 2020. A numerical schemes and comparisons for fixed point results with applications to the solutions of Volterra integral equations in dislocatedextendedb-metricspace. Alexandria Engineering Journal 59 (2): 815–827.

    Article  Google Scholar 

  46. Panda, S.K., A. Atangana, and T. Abdeljawad. 2022. Existence results and numerical study on novel coronavirus 2019-nCoV/Sars-CoV-2 model using differential operators based on the generalized Mittag-Leffler kernel and fixed points. Fractals 30 (08): 2240214.

    Article  Google Scholar 

  47. Panda, S.K., K.S. Kalla, A.M. Nagy, and L. Priyanka. 2023. Numerical simulations and complex valued fractional order neural networks via \((\varepsilon -\mu ) \)-uniformly contractive mappings. Chaos, Solitons and Fractals 173: 113738.

    Article  MathSciNet  Google Scholar 

  48. Rahman, R.U., M.M.M. Qousini, A. Alshehri, S.M. Eldin, K. El-Rashidy, and M.S. Osman. 2023. Evaluation of the performance of fractional evolution equations based on fractional operators and sensitivity assessment. Results in Physics 49: 106537.

    Article  Google Scholar 

  49. Zhou, Y., and F. Jiao. 2010. Nonlocal Cauchy problem for fractional evolution equations. Nonlinear Analysis: Real World Applications 11 (5): 4465–4475.

    MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors sincerely thank the reviewers for providing constructive comments for improvement of the manuscript. The first author thankfully acknowledges to the Ministry of Human Resource Development, India, for providing financial support for this research.

Author information

Authors and Affiliations

  1. Centre for Advanced Data Science, VIT Chennai, Chennai, Tamil Nadu, 600127, India

    A. K. Mittal

  2. Department of Mathematics, SAS, VIT Chennai, Chennai, Tamil Nadu, 600127, India

    A. K. Mittal

Authors
  1. A. K. Mittal
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All persons who meet authorship criteria are listed as authors, and all authors certify that they have participated sufficiently in the work to take public responsibility for the content, including participation in the concept, design, analysis, writing, or revision of the manuscript. Furthermore, each author certifies that this material or similar material has not been and will not be submitted to or published in any other publication.

Corresponding author

Correspondence to A. K. Mittal.

Ethics declarations

Conflict of interest

The authors declare no Conflict of interest exists.

Additional information

Communicated by Samy Ponnusamy.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mittal, A.K. Pseudospectral quadrature simulation technique for spatio-temporally parabolic multi-dimensional nonlinear fractional evolution equation. J Anal (2024). https://doi.org/10.1007/s41478-024-00750-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s41478-024-00750-3

Keywords

Mathematics Subject Classification

Search

Navigation