Skip to main content
SpringerLink
Log in

A new global smoothness indicator of fifth order weighted non-oscillatory scheme for hyperbolic conservation laws

  • Original Research Paper
  • Published:
The Journal of Analysis Aims and scope Submit manuscript

Abstract

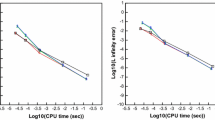
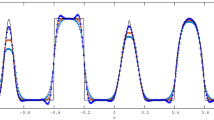
In this work we introduce fifth-order weighted essentially non-oscillatory (WENO) scheme using new global smoothness indicator which demonstrates improved numerical results compared to the solutions obtained using the fifth order WENO-JS schemes. The proposed scheme achieves an optimal level of approximation, even at critical points where both the first and second derivatives vanishes, but not the third derivative. Numerical examples are presented in the subsequent section to check the robustness and accuracy of the proposed scheme for one and two-dimensional systems of hyperbolic equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability

No data is used.

References

  1. Harten, Ami. 1997. High resolution schemes for hyperbolic conservation laws. Journal of Computational Physics 135 (2): 260–278.

    Article  Google Scholar 

  2. Harten, Ami, Stanley Osher, Björn. Engquist, and Sukumar R. Chakravarthy. 1986. Some results on uniformly high-order accurate essentially nonoscillatory schemes. Applied Numerical Mathematics 2 (35): 347–377.

    Article  MathSciNet  Google Scholar 

  3. Harten, Ami, Bjorn Engquist, Stanley Osher, and Chakravarthy., and Sukumar R. 1987. Uniformly high order accurate essentially non-oscillatory schemes III. Journal of Computational Physics 71 (2): 231–303.

    Article  MathSciNet  Google Scholar 

  4. Harten, Ami, Bjorn Engquist, Stanley Osher, and Sukumar R. Chakravarthy. 1997. Uniformly high order accurate essentially non-oscillatory schemes, III, 190–218. Berlin Heidelberg: Springer.

    Google Scholar 

  5. Balsara, Dinshaw S., and Chi-Wang. Shu. 2000. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. Journal of Computational Physics 160 (2): 405–452.

    Article  MathSciNet  Google Scholar 

  6. Jiang, Guang-Shan., and Chi-Wang. Shu. 1996. Efficient implementation of weighted eno schemes. Journal of Computational Physics 126 (1): 202–228.

    Article  MathSciNet  Google Scholar 

  7. LeVeque, Randall J. et al. Finite volume methods for hyperbolic problems, volume 31. Cambridge university press, 2002.

  8. Shu, Chi-Wang. 2009. High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Review 51 (1): 82–126.

    Article  MathSciNet  Google Scholar 

  9. Shu, Chi-Wang. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. Technical report NASA/CR-97-206253, NAS 1.26:206253, ICASE-97-65, Institute for computer applications in science and engineering; Hampton, VA United States, 1997.

  10. Shu, Chi-Wang. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced numerical approximation of nonlinear hyperbolic equations, 325–432. Springer, 1998.

  11. Shu, Chi-Wang., and Stanley Osher. 1988. Efficient implementation of essentially non-oscillatory shock-capturing schemes. Journal of Computational Physics 77 (2): 439–471.

    Article  MathSciNet  Google Scholar 

  12. Shu, Chi-Wang., and Stanley Osher. 1989. Efficient implementation of essentially non-oscillatory shock-capturing schemes, II shock-capturing schemes. Journal of Computational Physics 83 (1): 32–78.

    Article  MathSciNet  Google Scholar 

  13. Liu, Xu-Dong., Stanley Osher, and Tony Chan. 1994. Weighted essentially non-oscillatory schemes. Journal of Computational Physics 115 (1): 200–212.

    Article  MathSciNet  Google Scholar 

  14. Toro, Eleuterio F. Riemann solvers and numerical methods for fluid dynamics: a practical introduction. Springer Science & Business Media, 2013.

  15. Gottlieb, S., and C.-W. Shu. 1998. Total variation diminishing runge-kutta schemes. Mathematics of Computation 67 (221): 73–85. https://doi.org/10.1090/S0025-5718-98-00913-2.

    Article  MathSciNet  Google Scholar 

  16. Sweby, Peter K. 1984. High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM journal on numerical analysis 21 (5): 995–1011.

    Article  MathSciNet  Google Scholar 

  17. Dubey, Ritesh Kumar. 2013. Flux limited schemes: their classification and accuracy based on total variation stability regions. Applied Mathematics and Computation 224: 325–336.

    Article  MathSciNet  Google Scholar 

  18. Lax, P.D. 1954. Weak solutions of nonlinear hyperbolic equations and their numerical computation. Communications on pure and applied mathematics 7 (1): 159–93.

    Article  MathSciNet  Google Scholar 

  19. Woodward, Paul, and Phillip Colella. 1984. The numerical simulation of two-dimensional fluid flow with strong shocks. Journal of computational physics 54 (1): 115–173.

    Article  MathSciNet  Google Scholar 

  20. Schulz-Rinne, Carsten W., James P. Collins, and Harland M. Glaz. 1993. Numerical solution of the Riemann problem for two-dimensional gas dynamics. SIAM Journal on Scientific Computing 14 (6): 1394–1414.

    Article  MathSciNet  Google Scholar 

  21. San, Omer, and Kursat Kara. 2015. Evaluation of Riemann flux solvers for WENO reconstruction schemes Kelvin-Helmholtz instability. Computers Fluids 117: 24–41.

    Article  MathSciNet  Google Scholar 

  22. San, Omer, and Kursat Kara. 1984. High resolution schemes and the entropy condition. SIAM Journal on Numerical Analysis 21 (5): 955–984.

    Article  MathSciNet  Google Scholar 

  23. Harten, Ami A. 1984. new smoothness indicator for improving the weighted essentially non-oscillatory scheme. SIAM Journal on Numerical Analysis 21 (1): 1–23.

    Article  MathSciNet  Google Scholar 

  24. Fan, Ping, Yiqing Shen, Baolin Tian, and Chao Yang. 2014. On a class of high resolution total-variation-stable finite-difference schemes. Journal of Computational Physics 269: 329–354.

    Article  MathSciNet  Google Scholar 

  25. Castro, Marcos, Bruno Costa, and Wai Don. 2014. Sun High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws. Journal of Computational Physics 269: 329–354.

    MathSciNet  Google Scholar 

  26. Fan, Ping. 2014. High order weighted essentially nonoscillatory WENO-\(\eta\) schemes for hyperbolic conservation laws. Journal of Computational Physics 269: 355–385.

    Article  MathSciNet  Google Scholar 

  27. Hu, Fuxing, Rong Wang, and Xueyong Chen. 2016. A modified fifth-order WENOZ method for hyperbolic conservation laws. Journal of Computational and Applied Mathematics 303: 56–68.

    Article  MathSciNet  Google Scholar 

  28. Acker, F., and Borges, RB de R., Costa, Bruno. 2016. An improved WENO-Z scheme.Journal of Computational Physics. 313: 726–753

  29. Borges, Rafael, Monique Carmona, Bruno Costa, and Wai Don. 2008. Sun An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. Journal of computational physics 227 (6): 3191–3211.

    Article  MathSciNet  Google Scholar 

  30. Henrick, Andrew K., Tariq D. Aslam, and Joseph M. Powers. 2005. Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points. Journal of Computational Physics 207 (2): 542–567.

    Article  Google Scholar 

  31. Biswas, Biswarup, and Ritesh Kumar Dubey. 2020. ENO and WENO schemes using arc-length based smoothness measurement critical points. Computers & Mathematics with Applications 80 (12): 2780–2795.

    Article  MathSciNet  Google Scholar 

  32. Pandey, Prashant Kumar, Farzad Ismail, and Ritesh Kumar Dubey. 2022. High-resolution WENO schemes using local variation-based smoothness indicator. Computational and Applied Mathematics 41 (5): 208.

    Article  MathSciNet  Google Scholar 

Download references

Funding

Author Ritesh Kumar Dubey acknowledge the SERB India project fund through file number CRG/2022/002659.

Author information

Authors and Affiliations

  1. Department of Mathematics, SRM institute of science and technology, Kattankulathur, Chengalpattu, 603203, India

    Vikas Kumar Jayswal & Ritesh Kumar Dubey

Authors
  1. Vikas Kumar Jayswal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ritesh Kumar Dubey
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ritesh Kumar Dubey.

Ethics declarations

Conflicts of interest

Authors certify that there is no actual or potential conflict of interest in relation to this article.

Additional information

Communicated by Dhirendra Bahuguna.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jayswal, V.K., Dubey, R.K. A new global smoothness indicator of fifth order weighted non-oscillatory scheme for hyperbolic conservation laws. J Anal (2024). https://doi.org/10.1007/s41478-024-00739-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s41478-024-00739-y

Keywords

Mathematics subject classifications

Search

Navigation