1 Introduction

Spallation reactions, where high-energy, light particles collide with a heavy target, resulting in a lighter remnant nucleus and the ejection of numerous light particles, play an important role in a wide range of applications [1]. Ever since cosmic ray spallation reactions were studied in the 1930s [2], they have attracted much attention from researchers in applied and fundamental fields [3]. This interest only increased with the proposition of an optimum neutron resource, as well as the application of nuclear waste transmutation in an accelerator-driven system. Over the years, there have been extensive developments of applications entailing spallation reactions, including material physics [4], nuclear waste disposal [5,6,7], particle physics and nuclear physics [8], rare isotope production, accelerator radiation protection [9], cancer hadron therapy [11], and cosmic rays in the atmosphere [10].

A nucleon-induced spallation reaction is a two-stage process. First, the hard nucleon–nucleon (NN) collisions take place, dissipating the incident energy and resulting in a nuclei with high excitation energy. In the second stage, de-excitation takes place via evaporation and fission processes [12, 13]. In addition to fission and fusion, spallation is an effective process of releasing neutrons from nuclei; unlike the other two reactions, it is an endothermic process. To sustain a spallation reaction, a beam of high-energy particles, usually protons, must be supplied and focused on a heavy target. Spallation can be an important source of neutrons whose flux can easily be controlled by the drive beam [14]. However, it is hard to obtain the large quantity of reaction data necessary, in consideration of the low feasibility and high costs. Therefore, theoretical studies are imperative to improve our understanding of these reactions. There are many spallation models and codes currently used, including the particle and heavy-ion transport code system (PHITS) [15], the Boltzmann–Uehling–Uhlenbeck (BUU) transport model [16], the quantum molecular dynamics (QMD) model [17,18,19], the cascade model (JAM1.0) [20], the intranuclear cascade model (INCL)4 [21], ISABEL [22, 23], and the Monte Carlo code GEANT4 [24, 25]. These models and codes are used in conjunction with various statistical decay models, such as the generalized evaporation model (GEM) [26, 27], GEMINI [28], and the abrasion–ablation model (ABLA) [29]. More recently, a Bayesian neural network (BNN) method has been proposed for spallation reactions [30]. Nonetheless, the discrepancies between observables in theoretical calculations and experimental data are still relatively large, proving that the theoretical models are not well founded. One of the problems the theoretical models struggle with is being able to reproduce the production cross sections of the light cluster well. Attempts have been made to study the formation mechanism of clusters, such as deuteron, to improve upon the modeling. A surface coalescence mechanism has been used in INCL, Jaeri QMD (JQMD), and improved QMD (ImQMD) models to improve the description of the light complex particles emitted in various nucleon-induced reactions [21, 31, 32]. The pre-equilibrium light complex particle emission has been described reasonably well [18, 19]. An investigation into the formation mechanism of deuteron clusters is conducive to solving the current controversial clustering problem.

In this work, we study neutron-induced reactions by using the isospin-dependent QMD model (IQMD) model. The GEMINI model is applied to simulate the pre-fragment decays. The version of the IQMD model used is IQMD-BNU. The framework of the IQMD \(+\) GEMINI model has been applied to study nuclear reactions in an energy region from 10 MeV to GeV [33,34,35,36,37,38,39,40,41,42]. By using these models, we attempt to study the formation mechanism of deuteron clusters. The reaction channel of \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) is added into the model. In Sect. 2, a brief introduction of the IQMD model and cluster mechanism is made. Section 3 describes and analyzes the subsequent calculation results, with some brief discussion about the results. In Sect. 4, we summarize our findings, provide some concluding remarks, and discuss potential future directions that our work can take.

2 Model

2.1 IQMD-BNU

The IQMD model is based on the same principles as the QMD model [43,44,45]. By considering the evolution of nucleons in mean field potentials and the binary NN collisions, the IQMD model has been widely and successfully used for the analysis of heavy-ion collisions (HICs) at incident energies below 2 GeV/nucleon.

The IQMD-BNU model was introduced and compared with other model versions in a transport-code-comparison project [46, 47]. In a QMD-type model [48], each nucleon is represented by a Gaussian wave packet [49]

$$\begin{aligned} \psi _{i}\left( {\varvec{r}}_{i}\right) =\frac{1}{\left( 2 \pi \sigma _{r}^{2}\right) ^{3 / 4}} \mathrm {e}^{-\frac{\left( r_{i}-r_{i 0}\right) ^{2}}{2 \sigma _{r}^{2}}+\mathrm {i}\left( r_{i}-{\varvec{r}}_{i 0}\right) \cdot {\varvec{p}}_{i 0} / \hbar }, \end{aligned}$$
(1)

where \(\sigma _{r}\) and \({\varvec{r}}_{i 0}\) are the width and centroid of the wave packet, respectively. Usually, \(\sigma _{r}^2\) is set at \(1.0~\hbox { fm}^{2}\). The total N-body wavefunction is considered to be a direct product of these coherent states,

$$\begin{aligned}&\psi \left( {\varvec{r}}_{1}, \ldots , {\varvec{r}}_{N}\right) =\phi _{k_{1}}\left( {\varvec{r}}_{1}\right) \phi _{k_{2}}\left( {\varvec{r}}_{2}\right) \cdots \phi _{k_{N}}\left( {\varvec{r}}_{N}\right) , \end{aligned}$$
(2)
$$\begin{aligned}&\phi _{k_{i}}\left( {\varvec{r}}_{i}\right) = \frac{1}{\left( 2 \pi \sigma _{r}^{2}\right) ^{3 / 4}} \cdot \exp \left[ -\frac{\left( {\varvec{r}}_{i}-{\varvec{r}}_{i 0}\right) ^{2}}{2 \sigma _{r}^{2}}+\frac{\mathrm {i} {\varvec{p}}_{i 0} \cdot \left( {\varvec{r}}_{i}-{\varvec{r}}_{i 0}\right) }{\hbar }\right] , \end{aligned}$$
(3)

where \(\phi _{k_{i}}\) is the wavefunction of the ith particle at a state \(k_{i}\) (\(p_{i}=\hbar k_{i}\)). \(\phi _{k_{i}}\) is chosen as the Gaussian wave packet to avoid the negative values of the phase-space distribution (\(f_N\)). By the Wigner transformation of the N-body wavefunction, the phase-space density is given by

$$\begin{aligned} \begin{aligned}&f_{N}\left( {\varvec{r}}_{1}, \ldots , {\varvec{r}}_{N} ; {\varvec{p}}_{1}, \ldots , {\varvec{p}}_{N}\right) =\prod _{i=1}^{N} f\left( {\varvec{r}}_{i}, {\varvec{p}}_{i}\right) \\&\quad =\prod _{i=1}^{N} \frac{1}{(\pi \hbar )^{3}} \exp \left[ -\frac{\left( {\varvec{r}}_{i}-{\varvec{r}}_{i 0}\right) ^{2}}{2 \sigma _{r}^{2}}-\frac{\left( {\varvec{p}}_{i}-{\varvec{p}}_{i 0}\right) ^{2}}{2 \sigma _{p}^{2}}\right] , \end{aligned} \end{aligned}$$
(4)

where \({\varvec{r}}_{i 0}=\left\langle {\varvec{r}}_{i}\right\rangle \) and \({\varvec{p}}_{i 0}=\left\langle {\varvec{p}}_{i}\right\rangle \) are the centroids of wave packets in coordinate and momentum space, respectively.

The time evolution of the nucleons in the system is considered under self-consistent conditions. The mean field is governed by the Hamiltonian equations of motion,

$$\begin{aligned} \begin{aligned} \dot{\mathbf{r }}_{i}&= \nabla _{\mathbf{p }_{i}} H , \\ \dot{\mathbf{p }}_{i}&= -\nabla _{\mathbf{r }_{i}} H , \end{aligned} \end{aligned}$$
(5)

where the Hamiltonian, H, constitutes a kinetic energy component, T, a Coulombic potential energy term, and a nuclear potential energy term,

$$\begin{aligned} H = T + U_\text {Coul} + \int V_\text {n}(\rho , \delta ) \mathrm {d}\mathbf{r }. \end{aligned}$$
(6)

The density can be calculated by taking the integral of the phase-space density [Eq. (4)] over momentum space. The nuclear potential \(V_\text {n}\) includes a two- and three-body Skyrme interaction term, as well as a symmetry potential term. The nuclear potential energy density of the asymmetric nuclear matter, with density \(\rho \) and asymmetry \(\delta \), is given by

$$\begin{aligned} \begin{aligned} V_\text {n}(\rho , \delta ) =&\frac{\alpha }{2} \frac{\rho ^2}{\rho _0} + \frac{\beta }{\gamma +1} \frac{\rho ^{\gamma +1}}{\rho _0^{\gamma }} + \frac{C_\text {sp}}{2}\left( \frac{\rho }{\rho _{0}}\right) ^{\gamma _{i}} \rho \delta ^{2}, \end{aligned} \end{aligned}$$
(7)

where \(\rho _0 = 0.16\hbox { fm}^{-3}\) is the normal density. The constant parameters are taken to have values of \(\alpha = -356\hbox { MeV}\), \(\beta = 303\hbox { MeV}\), \(\gamma = 7/6, C_\text {sp} = 38.06\hbox { MeV}\), and \(\gamma _{i} = 0.75\). These values provide a compressibility of 200 MeV at saturation density for isospin symmetric nuclear matter.

The binary NN collisions are also included in our model. Specifically, the NN elastic scattering cross section can be expressed by the following formula,

$$\begin{aligned} \left( \frac{\mathrm {d} \sigma }{\mathrm {d} \Omega } \right) _{i} = \sigma _{i} ^\text {free} f_{i}^\text {angl} f _{i}^\text {med}, \end{aligned}$$
(8)

where \(\sigma ^\text {free}\) is the elastic scattering cross section of NN collisions in free space, \(f^\text {angl}\) is the angular distribution correction, and \(f^\text {med}\) is the in-medium correction. The isospin-dependent parameterization of \(\sigma ^\text {free}\) and \(f^\text {angl}\) is taken from Ref. [50]. The in-medium factor for elastic scatterings is written as [51]

$$\begin{aligned} \begin{aligned}&f _\text {el}^\text {med} = \sigma _{0}/\sigma ^\text {free} \tanh (\sigma ^\text {free}/\sigma _{0}),\\&\sigma _{0} = 0.85\rho ^{-2/3}. \end{aligned} \end{aligned}$$
(9)

To compensate for the fermionic features, the phase-space density constraint (PSDC) method, taken from the constraint molecular dynamics (CoMD) model [52], is used. The phase-space occupation probability, \({\overline{f}}_{i}\), is calculated by performing integration on an hypercube of volume \(h^{3}\) in the phase space centered around the ith nucleon at each time step. The effect of Pauli blocking is considered based on the phase-space occupation probability \({\overline{f}}_{i}\); only NN scattering producing final states with \({\overline{f}}_{i}<\) 1 is allowed.

2.2 GEMINI

The statistical code GEMINI, proposed by Charity in the 1980s [53], can be utilized to model the decay of a compound nucleus in fusion reactions and excited fragments in HICs. The GEMINI code is applied to the process of de-excitation of hot fragments [54, 55].

The IQMD code will stop running whenever the excitation energies of the two heaviest pre-fragments are less than a specified value, \(E_\text {stop} = 3\hbox { MeV}/A\). The charge number, mass number, and excitation energy of each pre-fragment are output by the IQMD code. If the excitation energy is greater than zero, the modeling of the sequential decay of the pre-fragment will be performed by the statistical code GEMINI. This statistical code not only allows light-particle evaporation and symmetric fission, but all possible binary decay modes. Subsequently, a Monte Carlo technique is used to track all the decay chains until the resulting products are unable to decay further. Part of the necessary decay width data comes from the Hauser–Feshbach formalism of the evaporation of light particles.

In summary, if the excited energy of the pre-fragments is lower than \(\hbox {3 MeV}/A\), the statistical decay model GEMINI is preferred. We start the simulation of GEMINI after a simulation time of 1000 \(\hbox {fm}/c\) in the IQMD model, also using the PSDC method. We assume that the evolution is stable enough until \(1000\hbox { fm}/c\). For further details on GEMINI, refer to Ref. [53].

Fig. 1
figure 1

Cross section of the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction, in relation to the incident energy, \(E_\text {lab}\). The circles show the experimental data taken from Ref. [56,57,58,59,60,61,62,63,64,65]. The solid curves are a result of the calculations from the empirical formula, as shown in Eq. (12)

Full size image

2.3 IQMD + GEMINI model updates

In the standard version of the IQMD model, only the elastic and inelastic NN collisions are considered. Taking the neutron–proton collision as an example, the scattering is performed if two requirements are satisfied. First, the nucleons must pass the point of closest approach in the next time step. Second, the collision parameter of the neutron–proton collision is less than the value of \(\sqrt{f^\text {med}_\text {np}\sigma ^\text {free}_\text {np}/\pi }\), where \(\sigma ^\text {free}_\text {np}\) and \(f^\text {med}_\text {np}\) are the cross section in free space and the in-medium factor of the neutron–proton scattering, respectively.

In this work, the decay channel \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) is added, with the goal of studying the deuteron formation. The neutron–proton collision is performed according to the total cross section,

$$\begin{aligned} \sigma _\text {t} = f^\text {med}_\text {np}\sigma ^\text {free}_\text {np} +f^\text {med}_\text {d}\sigma _\text {d}. \end{aligned}$$
(10)

where \(\sigma _\text {d}\) is the cross section of the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction, and \(f^\text {med}_\text {d}\) is the in-medium factor. The cross section of the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction has been measured in various experiments, with the incident energy ranging from 0.01 to 100 MeV [56,57,58,59,60,61,62,63,64,65]. The experimental data are depicted as circles in Fig. 1. By fitting the data, an empirical formula of \(\sigma _\text {d}\) as a function of the incident energy is obtained,

$$\begin{aligned} \sigma _\text {d}\left(E\right) =\left\{\begin{array}{ll}-0.14\ln (E)-0.25&\quad E<{0.14}\,\hbox{ MeV}\\0:035&\quad 0.14\leqslant E\leqslant {10}\hbox { MeV}\\-0.011\ln (E)+0.061 & \quad E>{10}\hbox { MeV}, \end{array}\right.\end{aligned}$$
(11)

where the unit of the cross section is mb. The empirical value of the in-medium factor is,

$$\begin{aligned} f^\text {med}_\text {d}=\left\{ { \begin{array}{*{1}{l}}{1}\\ {0}\end{array}} \right. \begin{array}{*{1}{l}} {\rho < 0.2 \rho _{0}}\\ {\rho \geqslant 0.2 \rho _{0}} \end{array}, \end{aligned}$$
(12)

where \(\rho \) is the density in the center of the colliding neutron and proton, and \(\rho _{0}\) is the normal density. This in-medium factor value means that the deuteron can only be produced in the low-density region, i.e., the deuteron is generated when a neutron and a proton are close enough, and the medium density is less than \(0.2\rho _{0}\). When a deuteron evolves to a medium density greater than \(0.2\rho _{0}\), it will break up into a neutron and a proton.

It should be noted that the gamma rays were ignored in the \(\hbox {n+p}\rightarrow \hbox {d}+\gamma \) decay channel in this work, since the beam energy is much larger than the energy. As a weak composite system, the propagation of the deuterons is approximately treated the same as the propagation of a neutron and proton under a nucleonic mean field potential. For the deuteron break-up mechanism, we adopt a phenomenological method that causes the deuteron to decay when its medium density is less than \(0.2\rho _0\). A long-term deuteron production mechanism in the QMD model is still an open question, which requires further study.

Fig. 2
figure 2

The distribution of a the excited energy, \(E^{*}\), and (b) the charge (atomic number, Z) of pre-fragments for n+\(^{28}\)Si at an incident energy of 60 MeV, calculated within the IQMD model. The percentage of pre-fragments in each distribution is represented by p

Full size image

3 Results and discussion

The excited energy and charge distribution of pre-fragments for the \(\hbox {n}+^{28}\hbox {Si}\) reaction at 60 MeV are displayed in Fig. 2. The percentage of pre-fragments is represented by p. The excitation energy of the fragments can be calculated using,

$$\begin{aligned} E^{*}=\frac{\sum _{i} U_{i}+\sum _{i} \frac{\left( {\mathbf {p}}_{i}-{\mathbf {p}}_\text {f}\right) ^{2}}{2 m}-B\left( Z_\text {f}, A_\text {f}\right) }{A_\text {f}}. \end{aligned}$$
(13)

Here, \(U_{i}\) and \({\mathbf {p}}_{i}\) are the single-particle potential and momentum of the ith nucleon in the rest frame of the fragment, while \({\mathbf {p}}_\text {f}\) , \(Z_\text {f}\), and \(A_\text {f}\) are the average momentum per nucleon, charge number, and mass number of the fragment, respectively. The variable \(B\left( Z_\text {f}, A_\text {f}\right) \) is the binding energy of a nucleus with charge number \(Z_\text {f}\) and mass number \(A_\text {f}\). The summation is present to account for all the nucleons belonging to the same fragment. From Fig. 2a, one can see that the excited energy distribution of the pre-fragments has a center peak at around \(1~\hbox { MeV}/A\). We calculate that the excitation energy required to form \(^{29}\hbox {Si}\) is 2.28 MeV; at this point, the energy of the neutron is all transferred to \(^{29}\hbox {Si}\). Only, \(1~\hbox { MeV}/A\) is the approximate value of the center peak of the excited energy distribution; this is a result of peripheral collisions, where neutrons only transfer part of the energy to \(^{28}\hbox {Si}\). The interrupt time in our work is 1000 \(\hbox {fm}/c\). Figure 2b shows the charge distribution of pre-fragments. More than \(95\%\) of pre-fragments have an atomic number of 12, 13, or 14. This means that the predominant reaction mechanisms of light nuclei with neutrons are scattering and nucleon trapping.

Fig. 3
figure 3

The distribution of a formation time, b the relative kinetic energy, c density at the formation position, and d total energy, of a deuteron cluster for \(n+^{28}\)Si at 60 MeV. Here, p represents the percentage of the deuteron clusters in the distribution

Full size image

To study the formation of a deuteron cluster in detail, the formation time, collision energy, density at its position of formation, and excitation energy are shown in Fig. 3. The highest percentage of deuteron clusters are formed in the time frame 0–100 fm/c (Fig. 3a). The deuteron cluster is formed at this time because the incoming neutron captures a proton in the target, in the low-density region. From 100 to 1000 fm/c, the deuteron is formed from the excited nucleus in the low-density area during the reaction. It should be noted that the neutrons that form deuterons are not necessarily incident neutrons. Figure 3b shows the relative kinetic energy of the neutron and proton in the excitation system when the deuteron cluster is formed. As the relative kinetic energy increases from 0 to 10 MeV, the probability of deuteron generation increases gradually. After 10 MeV, this probability gets smaller. At 60 MeV, the probability that a deuteron is formed is lower than one percent. This is because the cross section of deuterons decreased gradually above 10 MeV, as shown in Fig. 1, in turn causing the probability of deuteron production to also decrease gradually. Figure 3c shows the ratio between density and normal density, at the position where the deuteron cluster formed. The deuteron cluster prefers to form in a density ratio of 0.3–0.5. When the ratio is greater than 0.6, even though the deuteron cluster will form, the cluster will soon disappear owing to interactions with other nucleons. When the ratio is below 0.3, the density is too small for a deuteron cluster to form. Figure 3d displays the distribution of the total energy of the deuteron cluster. The reason for negative total energies is a result of the choice to ignore the gamma photons.

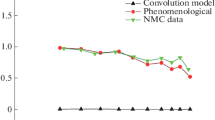
Figure 4 shows the deuteron cluster formation cross section in \(^{28}\)Si(n,d), \(^{16}\)O(n,d), and \(^{12}\text {C}\)(n,d) reactions at beam energies of 20–100 MeV. The dotted line is the result of the deuteron cluster produced by fragmentation without the introduction of \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction channel. The solid line is the result of the deuteron cluster produced by fragmentation and the neutron–proton collision, after the addition of this reaction channel. The hollow circles represent experimental data [66,67,68]. With the introduction of the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction channel into the modeling, the cross-section results are significantly optimized for each set of reactions, bringing the results much closer to the experimental data values. In Fig. 4a, the prediction of the cross section for \(^{28}\)Si(n,d) reactions has the same trend as the experimental data at 20–50 MeV. By calculating the ratio of neutron–proton collisions forming a deuteron cluster, it is found that the contribution rate is greater than 52.6\(\%\). By the same method, the contribution rate of neutron–proton collisions for deuteron cluster formation is 36.5\(\%\) for \(^{16}\text {O}\)(n,d) reactions (Fig. 4b) and is 47.3\(\%\) for \(^{12}\text {C}\)(n,d) reactions (Fig. 4c). Hence, the addition of the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction channel is very significant when modeling the deuteron cluster cross section. It is necessary to place greater focus on neutron–proton collisions when studying the effect on the formation and evolution of deuteron clusters.

Fig. 4
figure 4

(Color online) Measuring the cross section of a \(^{28}\)Si(n,d), b \(^{16}\)O(n,d), and c \(^{12}\)C(n,d) reactions at a beam energy range of 20–100 MeV. The lines are calculated by the IQMD + GEMINI model with and without the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction channel. The hollow circles are data measured from experiments [66,67,68]

Full size image

4 Summary

A combination of the IQMD model and the GEMINI code was applied to study neutron-induced reactions. It was shown that the deuteron production cross sections calculated by the standard version of the IQMD+GEMINI model are much smaller than the data. In an attempt to optimize the modeling of the deuteron production cross sections, the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction channel was added to the IQMD model. The empirical formula of the cross section and its in-medium factor of the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction were used. When the deuteron evolved to a medium density greater than \(0.2\rho _{0}\), it decayed into a neutron and a proton by the reaction d + N \(\rightarrow \) n + p + N, where N is a nucleon. The contribution of neutron–proton collisions forming deuteron clusters was calculated. It was found that the contribution rate was greater than \(52.6\%\) for \(^{28}\)Si(n,d) reactions, \(36.5\%\) for \(^{16}\text {O}\)(n,d) reactions, and \(47.3\%\) for \(^{12}\text {C}\)(n,d) reactions. The deuteron production cross sections in the neutron-induced reactions \(^{12}\)C(n,d), \(^{16}\)O(n,d), and \(^{28}\)Si(n,d) with incident energy 20–100 MeV were calculated and compared to the experimental data. The deuteron production cross sections increased having incorporated the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction channel in the model and bring the values closer to the experimental data. The results indicated that the deuteron cluster is generated in a low-density region via the neutron–proton collision. In future work, the deuteron production mechanism in the QMD still requires further study, but our results hint that the \(\hbox {n}\,+\,\hbox {p}\,\rightarrow \,\hbox {d}\) reaction channel should be considered in the transport model when studying deuteron clusters in HICs.