Oil Extraction, Economic Growth, and Oil Price Dynamics

Abstract

We use economic production function theory and an empirical model of oil prices based only on oil extraction data to analyze the dynamics of the economy and oil prices as we transition into the contraction phase of oil extraction. We explore the implications with respect to several common scenarios. We find that price feedback cycles which lead to increased production during the growth phase of oil extraction go into reverse in the contraction phase of oil extraction speeding decline.

Introduction

This paper is an attempt to understand the economic dynamics of peak oil extraction, or more generally peak resource extraction. We use economic production function theory and empirical data to analyze the price dynamics of oil extraction and their economic effects.

There is considerable variation in estimates of remaining oil reserves (as opposed to resources) without climate mitigation policies in place. On the low side are the Association for the Study of Peak Oil and Gas (ASPO) and Uppsala Global Energy Systems (UGES). Total and the International Energy Agency (IEA) give somewhat higher estimates. Exxon, BP, and the Energy Information Administration (EIA) give high estimates. The International Institute for Applied System Analysis (IIASA) on which the International Panel on Climate Change (IPCC) basis its climate change scenarios gives relatively high estimates. Hotelling’s rule has a very poor record predicting both future extraction rates and future prices Gaudet (2007). Other models used to predict remaining reserves, such as Hubbert linearization, have been criticized (we believe unfairly), because they do not consider prices. In fact, the quantity of oil reserves, by definition, is very much a function of price Erlingsen (2015). Campbell and Laherrère (1998) correctly estimated the peak of the conventional oil reserves at 2005. One can essentially classify the “conventional” as inexpensive reserves. Extraction rates have risen since 2005 by tapping higher cost reserves. The higher the price, the larger the reserves, because high prices permit the use of expensive extraction technologies to recover more oil. In Wang et al. (2016), the authors give three scenarios for China’s Ultimate Recoverable Resource (URR) based on three different price scenarios. Rystad Energy’s UCube database software package computes future extraction rates to 2100 as a function of price. Thus, a robust model predicting future prices would be a valuable asset to those predicting future extraction which is important for economic reasons and for concerns about greenhouse gas emissions. Viewing the previous price estimates of the EIA Staff (2015), one sees that they lack a robust price predicting model as any volatility in prices leads to very poor price estimates.

Many empirical studies  (Fraser and Rimas 2011; Reynolds 2002; Montgomery 2007; Hamilton 2009; Reynolds and Baek 2011; Ayres and Warr 2009; Kümmel 2011; Giraud and Kahraman 0000) show that food and energy are key quantities to consider when evaluating economic production. The “Cost Share Theorem” from neoclassic equilibrium theory Ayres and Warr (2009, Appendix 1) says that cost share is proportional to the elasticity or scaling factors of the variables in the production function equation. Because the cost share of labor is almost 10 times the cost share of energy in the economy, many economists discount the idea that energy is important for economic production. In Appendix 1, we prove the dynamic production function identities, (5.10) and (5.11), which suggest that cost share dynamics indicate the importance of a quantity in an economy. In particular, important items have either slowly increasing or decreasing cost shares in a growing economy and increasing cost shares in a contracting economy. We differ from other works on economic production functions, such as Solow (1956), Ayres and Warr (2009), Kümmel (2011); in that, we make very few assumptions on the structure of the economy or the nature of the economic production function. We assume only some regularity of the production function to obtain our results. Our results are thus much more general and can be applied to a larger set of economies, both past and present. Our conclusions from these computations are summarized in “Economic Production Function Theory” section. In “An Example” section, we give an example to illustrate how this might work.

In “An Empirical Study of Oil Prices” section, We present an empirical model for the price of oil at year t as a function of extraction at year t, year $t-1$, and year $t-2$. In particular, we find that the term with the strongest effect on price is the discreet first derivative of the extraction rate with the discreet second derivative playing a mollifying role. Our model indicates that a decrease in extraction rate raises prices temporarily, but that eventually increased extraction rates increase the price by increasing economic production. We hope that understanding this model will enable better future price prediction aiding those predicting remaining oil reserves.

In “Scenarios” section, we evaluate the probability of various scenarios for future price dynamics found in the literature with our findings. We find the most probable that the price of oil during the contraction phase of oil extraction will be relatively high but decreasing as extraction rates decrease creating negative feedback loops accelerating the contraction because of contraction of economic production. Higher price extraction will be unprofitable reducing extraction rates which will result in lower prices resulting in less extraction, etc. During the expansion phase of oil extraction, high prices increased the extraction rate and low prices increased the market for oil. During the contraction phase, our data suggest that high prices will decrease the market for oil and low prices will decrease the extraction rate.

A word about vocabulary. Technically oil is not “produced” but rather “extracted” from the earth. The oil industry uses the term “production” rather than extraction as does our data. We prefer the term “extraction” but use the terms interchangeably.

Economic Production Function Theory

Economic production functions not only indicate what macro economic quantities one should measure to detect motors of economic growth, but also give indications of the dynamics of the economy when production of these economic motors peaks and goes into decline.

In Appendix 1, we define variables, make our assumptions explicitly, and prove the mathematical results on which we will base our analysis of empirical data. The results are elementary in the sense that they require only algebra and a bit of calculus of several variables. Our assumptions are minimal, and, to our knowledge, are satisfied by all other works on economic production functions. Our point of view is different than that found in Kümmel (2011), Ayres and Warr (2009); in that, we see the economic production function as a measure of economic activity and freely use the implicit function theorem to choose variables with which to express this measure. That is, we choose the variables we think best help us to understand the dynamics of prices. Cost share, defined in Eq. (5.2), provides the link between prices and economic production. Prices can be expressed as the product of cost share and economic production divided by quantity (5.8). Intuitively, one might think of cost share as the preferences side of price and the size of the economy as the size of the possible market side of the price.

We are interested in the dynamics of prices expressed in (5.9). A pervasive implicit assumption which we do not share is that resources are a function of the economy. Evidence of this assumption is the frequently encountered reasoning that the price of oil must rise, because extraction costs are rising and the economy needs oil. Equation (5.8) gives a different story. It says that if important quantities decrease, the economy decreases and then the only way the price can rise is through an increase in cost share which, in general, means that another area of the economy must shrink. The idea that the economy is a function of resources goes back at least to Malthus (1798) and is shared among others by Verhulst (1844), Forrester (1971), and Meadows (1974).

We believe that the role of technology is to increase the scaling factors of resources (see Eq. (5.5)).

The Cost Share Theorem

The “Cost Share Theorem” from neoclassic equilibrium theory Ayres and Warr (2009, appendix 1) says that for an economy in equilibrium, cost share is proportional to the elasticity or scaling factors of the variables in the production function equation. Because the cost share of labor is almost ten times the cost share of energy in the economy, many economists discount the idea that energy is important for economic production. We make the following remarks relative to the cost share theorem and Theorem 5.1:

Remark 2.1

• 1. Equation (5.9) suggests that in a growing or shrinking economy, the dynamics of the cost share is the important consideration, not the size. For important quantities, the derivative of the cost share is small or negative, that is, in a growing economy, the cost share of important quantities decreases or remains constant, while the cost share of unimportant quantities increases. This makes sense. Important quantities, such as oil, permit the growth of less important parts of the economy, such as art or competitive sports.

• 2. Equilibrium theory studies steady states. The economy is dynamic. A dynamical system might converge to a steady state, but one does not expect a dynamical system to be in a steady state, while it is changing. We feel that a dynamical system approach to modeling the economy would be more useful as in Meadows (1974), Meadows (2005); Bardi (2011).

• 3. In the above cited articles, empirical evidence did not support the Cost Share Theorem. Rather than question, the hypotheses on which the theorem is based, the authors attempted to save equilibrium theory by introducing constraints (thus introducing a Lagrange multiplier to explain the importance of energy in the economy). We do not use neoclassic equilibrium theory.

There is a high probability that the hypotheses on which The Cost Share Theorem is based are not verified. From a political point of view, a large cost share frequently translates into political power, so that sectors unimportant for economic production can wield political clout. This dynamic can induce governments to embrace counter productive policies as during the stagflation period (see “Secular Cycles” section), the government might support large sectors of the economy which are unimportant in economic production rather than important areas of the economy with smaller cost shares.

In our view, a small cost share is not a sign of unimportance; in the case of energy production, it is a sign of what might be called ecodiversity.

An Example

We suppose a very limited economy produces three quantities: E, G, and F. We assume that prices are adjusted for inflation for the three quantities and we normalize all prices to one. The size of this economy is $Y(t)=\sum _{i=1}^3 p_iq_i = E + G + F$. Now, suppose that E is a motor of economic growth in the following sense, when E grows 10%, this produces a growth of 5% in both G and F in the next time period. Growth in G has no effect on E or F. However, F is a drag on economic growth, since a 10% growth in F causes a 5% percent contraction in E and G. We can name our quantities to make the example more realistic. We call E energy production, which permits us to produce more of G and F. Let us call G gold extraction and F fun production. Fun decreases growth in E and G, because, in fact, many people do not like producing energy or mining for gold, so as soon as there is something fun, they stop work to enjoy the fun which reduces the production of E and G.

Let us assume that $t=n \in {\mathbb N}$ and that the initial conditions are $E_0=G_0=F_0=1$. Now, assume that population growth would cause growth of 10% in each time period, but the interactions occur in the next time period. Thus $E_1=G_1=F_1 =1.1,$ but $E_2 = 1.21-.05 =1.16$ because of the fun interaction. We have $G_2=1.21 - .05 + .05 = 1.21$ and $F_2 = 1.21 + .05=1.26$. We see that the cost share $C_E$ has dropped from 1/3 to 0.32, $C_G$ is unchanged, and $C_F$ increases from 1/3 to .35, while $I_Y (0,2) = 1.21$. Repeating the experiment with $E_0 = G_0/2 = F_0/2=1/2$, we obtain $E_1 = .55$, $G_1 = 1.1$, $F_1=1.1$, $E_2 = .575$, $G_2 = 1.21$, and $F_2 = 1.26$. With these initial conditions, $C_E$ decreases from .2 to .19, $C_G$ is almost unchanged, and $C_F$ increases from .40 to .41. In this case, $I_Y(0,2)= 1.22,$ so that a smaller initial cost share of the economic motor produces greater overall growth.

Remark 2.2

Not all quantities that drag on economic growth are fun.

Empirical Results

Secular Cycles

Turchin and Nefedov (2009) empirically identified recurring secular or economic cycles in agrarian societies. Similar phenomena apply to oil and resource production, so we recall their findings.

The cycle begins with a period of growth, in population and living standards lasting on the order of a hundred of years, and comes a period of stagflation in which population density approaches the carrying capacity of the land (one says increased population pressure) lasting on the order of half a century. During the stagflation period, peasants leave the countryside for cities, the difference between the elite and the commoners increases, and the price of food rises relative to wages. Population ceases to grow, because food production ceases to grow. Initially, the elite is somewhat better off in the stagflation period, because wages are low and they can employ a larger number of former peasants who have left the countryside. As the stagflation period progresses, the ratio of elite population to working class population rises (the working class has a lower birthrate and a higher mortality rate due to malnutrition and cramped living conditions in cities) creating competition among the elite. Social mobility increases, mostly downward as elites lose their status. The inter-elite competition creates fissures which lead to civil war and the final crisis stage lasting a few decades in which population decreases and the state breaks down. There follows an inter-cycle lasting several decades before a new growth period ensues.

Secular cycles have been linked to unsustainable agricultural production systems schindlerar and schindlerar, Fraser and Rimas (2011).

An Empirical Study of Oil Prices

In this section, we study empirical data to understand what the price dynamics of the contraction phase of oil extraction might be.

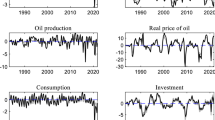
We worked with data from BP’s 2016 Statistical Review. We used prices and extraction data from the BP’s data set:

• Annual crude oil prices in 2015 US dollars per barrel (deflated using the Consumer Price Index for the US) available from 1861 to 2015.

• Annual world oil production expressed as a daily mean in millions barrels per day (MMbbl per day) from 1965 to 2015. These data include crude oil, shale oil, oil sands, and NGLs (natural gas liquids—the liquid content of natural gas where this is recovered separately). However, these data exclude liquid fuels from other sources, such as biomass and derivatives of coal and natural gas.

We used data from Etemad et al. (1998) to obtain annual world crude oil extraction in thousand metric tons from 1937 to 1970. We used the world average conversion factor of 7.6 barrels per ton to convert this data to barrels per year.

Remark 3.1

All data we use are very approximate. Laherrère (2014) has exhaustively documented incoherence in extraction data from all standard sources. Laherrère states (correctly) that since the data are accurate to at most 3%, it is both illogical and misleading to provide the data beyond two decimal points. We repeat the error of BP of including extra decimals, because we did not want to alter the data. We use a single price for the price of oil provided by BP, but there is a large spectrum of prices for oil of different densities, chemistry, and provenance Laherrère (2015). BP groups extraction data for crude oil, condensate, and NGL’s, a large spectrum of products not all used for the same purpose and of course with different prices. The fact that our regression analysis works suggests that there are correlations within the data and averaging going on.

In light of Remark 3.1, our aim is not to get the best fit possible, but to understand factors that influence price.

Let $\left( P_t\right) _{t}$ denote the time series of oil prices (in 2015 dollars adjusted for inflation) from year 1861 to year 2015 and $\left( Q_t\right) _{t}$ the time series of quantities of oil extracted (in million barrels daily) from year 1965 to year 2015 for BP data and from 1937 to 1970 for Etemad and Luciani data from Etemad et al. (1998).

A possible first idea to study the series $\left( P_t\right) _{t=1861 \dots 2015}$ may be to fit a classical time series model to the data. As the series of prices is clearly not stationary, one can apply a preliminary Box–Cox transformation to stabilize the variance. We thus define the log prices:

$$\begin{aligned} p_t=\log P_t. \end{aligned}$$

(3.1)

This transformation is consistent with the assumption of log normality of the prices often encountered in the literature. One can try to eliminate the trend by differentiating. The lag-1 difference operator $\nabla$ is defined for a series $\left( x_t\right) _t$ by the following:

$$\begin{aligned} \nabla x_t \mathop {=}\limits ^{\mathrm{{def}}}x_t-x_{t-1}. \end{aligned}$$

We are then led to study the so-called log return at year t:

$$\begin{aligned} r_t = \nabla p_t=p_t-p_{t-1}=\log P_t-\log P_{t-1}. \end{aligned}$$

(3.2)

It is well known that the log returns data $(\nabla p_t)_t$ may, at first glance, look like a white noise. But, by looking closer, one would observe that the magnitude of the fluctuations still depends on time. In fact, the series $(|r_t|)_t$ and $(r_t^2)_t$ are often strongly autocorrelated. Moreover, the distribution of the log returns may also present heavy tails. To consider these two stylized facts, the log returns are often modeled by non-linear models, such as ARCH/GARCH models or derivative models (Cheong 2009; Hou and Suardy 2012).

Many other techniques to forecast oil prices have been considered by researchers: financial models, structural models, and computational methods using artificial neural networks, see Behmiri and Manso (2013) and references therein. In structural models, oil prices are modeled as a function of explanatory variables, such as oil consumption, oil extraction, and even non-oil variables, such as interest rates. However, the use of such models is limited by the need of future values of the explanatory variables to derive predictions of oil prices. Furthermore, the number of possible explanatory variables may be very large.

Price Explained by Oil Extraction

The approach we consider here is structural. We try to derive information on the price from a single explanatory time series: oil extraction. From Fig. 1, one sees that $Q_t$ cannot explain $P_t,$ because the price P is not uniquely determined by the extracted quantity Q; in other words, several prices correspond to the same produced quantity. For this reason, we attempt to use, in addition to $Q_t$, the lag-1 difference and the lag-2 difference of the series $(Q_t)_t$ at year t:

$$\begin{aligned} \nabla Q_t&\mathop {=}\limits ^{\mathrm{{def}}}&Q_t-Q_{t-1},\end{aligned}$$

(3.3)

$$\begin{aligned} \nabla ^2 Q_t&\mathop {=}\limits ^{\mathrm{{def}}}&\nabla (Q_t-Q_{t-1})=Q_t-2\,Q_{t-1}+Q_{t-2}. \end{aligned}$$

(3.4)

Fig. 1

Oil price as a function of oil production from 1965 to 2015

Note that $Q_t$, $\nabla Q_t,$ and $\nabla ^2 Q_t$ are linearly independent, so their span is the same as that of $Q_t$, $Q_{t-1}$ and $Q_{t-2}$. We prefer the former variables to the latter, because $\nabla Q_t$ and $\nabla ^2 Q_t$ are the discreet first and second derivatives of $Q_t$ with step time $h=1$ making them easier to interpret. From an economic point of view, it is quite natural to postulate that the market for oil a given year is influenced by production in the previous years.

We consider the following model:

$$\begin{aligned} p_t=a+b\,Q_t +c\,\nabla Q_t+d\,\nabla ^2 Q_t +\epsilon _t \end{aligned}$$

(3.5)

where a, b, c, and d are coefficients determined by the linear regression and $(\epsilon _t)_t$ is a centered second-order stationary process. Equation (3.5) is equivalent to

$$\begin{aligned} P_t=\exp (a+b\,Q_t +c\,\nabla Q_t+d\,\nabla ^2 Q_t+\epsilon _t). \end{aligned}$$

(3.6)

The dependency of price $P_t$ on these variables is non-linear. As the logarithm function flattens large values, the model considers the inelasticity of oil prices. That is, small changes in the supply provoke large changes in price.

Data From 1965 to 2015

The R output for the linear regression with the data starting at year 1965 is given in Appendix Fig. 9. First, note that we have lost two years because of the lag-2 differences $(\nabla ^2 Q_t)_t$ that are only available form year 1967 with the data set starting in 1965. Adjusted R-squared being 0.5544 means that the model explain $55.44\%$ of the variance from the mean considering the number of explanatory variables. From the stars in the R output, we obtain four significant coefficients for the model (3.5) that are:

$$\begin{aligned} \begin{array}{lll} a &{} \approx &{} 2.1\\ b &{} \approx &{} 0.029\\ c &{} \approx &{} -0.20\\ d &{} \approx &{} 0.081.\\ \end{array} \end{aligned}$$

Remark 3.2

We considered several other models. The regression with the 3-lag difference $\nabla ^3Q_t$ in addition to the other variables gave a coefficient which was not significant. Using $\tilde{p}_t \mathop {=}\limits ^{\mathrm{{def}}}\log (\log P(t))$ marginally improved the fit of the model (with the same variables). In fact, taking further logs also marginally improved the fit. We use the above model for simplicity and because, as we will see, the model is not robust over different time periods.

Fig. 2

Fitted price from 1967 to 2015

We have plotted the adjusted prices and the real prices in Fig. 2. Moreover, the model allows us to derive a prediction of the price $P_{t+1}$ at year t. Namely, if the residuals are independent, as they are centered, the prediction of $\epsilon _{t+1}$ is zero. Then, from the extracted quantity at year $t+1$, we obtain, at year, t a prediction of the price:

$$\begin{aligned} \hat{P}_{t+1}= & {} \exp \left( a+b\,Q_{t+1}+c\,\nabla Q_{t+1}+d\,\nabla ^2 Q_{t+1}\right) \\= & {} \exp \left( a+b\,Q_{t+1}+c\,\left( Q_{t+1}-Q_t\right) +d\,\left( Q_{t+1}-2\,Q_t+Q_{t-1}\right) \right) . \end{aligned}$$

(3.7)

The conclusions we have made above are, in fact, not justified here, because the residuals of the regression are correlated. One can observe the dependence of the residuals while plotting the autocorrelation function and the partial autocorrelation function with the R commands acf and pacf. One can also perform the Box–Pierce test, the turning point test, and the difference sign test with the R commands Box.test, turning.point.test, and difference.sign.test. All these tests reject the hypothesis of a white noise at the level $\alpha =5\%$. We attempt then to fit an ARMA model to the residuals. As the partial autocorrelation at lag 1 was very high, we have chosen the AR(1) model. In fact, among the models ARMA(p, q) with $p=0,1,2$ and $q=0,1,2$, the one that minimizes the AIC and the BIC criteria is the AR(1) model. Finally, we perform a linear regression with a covariance structure of an AR(1) with the R command gls. The model is fitted by maximizing the log-likelihood. The R output is given in Appendix Fig. 11. The coefficients of the model (3.5) are as follows:

$$\begin{aligned} \begin{array}{lll} a &{} \approx &{} 1.6\\ b &{} \approx &{} 0.032\\ c &{} \approx &{} -0.062\\ d &{} \approx &{} 0.018 \end{array} \end{aligned}$$

(3.8)

with an AR(1)-noise $(\epsilon _t)_t$ such that:

$$\begin{aligned} \epsilon _t-\phi \,\epsilon _{t-1}=\eta _t \end{aligned}$$

with $\phi$ estimated by 0.816 and $(\eta _t)_t$ an actual centered white noise with estimated standard deviation 0.474. The intervals R command allows us to obtain $95\%$ CI for the model coefficients (see Fig. 10). The plot of price and fitted price is given in Fig. 3.

Fig. 3

Fitted price from 1967 to 2015

Fig. 4

Percent increases in quantity from 1971 to 2015

We tested the stability of the coefficients by trying the regression in different sub-intervals and found that the coefficients were not stable. This means that the model cannot be used directly to predict future prices; there is some sort of averaging going on. One must understand why the coefficients differ in different time frames and then analyze how future conditions might effect the coefficients. To this end, we split the data into four periods with different growth rate and price characteristics (see Fig. 4) and computed the coefficients of the classical linear regression for each period (see Figs. 5, 6).

Fig. 5

Adjusted price and linear regression coefficients for the first period

Fig. 6

Adjusted price and linear regression coefficients for the last three periods

Data From 1937 to 1970

From Fig. 7, one sees that, for this period, the price is a function of the extracted quantity. A linear regression of the log price with explanatory variables $Q_t$ and $\nabla Q_t$ shows that the coefficient of $\nabla Q_t$ is not significant in the R output of Appendix Fig. 12. The R output for the sub-model of (3.5 with $c=d=0$ is given in Appendix Fig. 13. Again, the residuals are not i.i.d. Therefore, we use the linear model with covariance structure ARMA(1, 1) chosen among the ARMA(p, q) models with $p=0,1,2$ and $q=0,1,2$ with the Akaike AIC criterion. The R output is given in Appendix Fig. 14. The model coefficients are as follows:

$$\begin{aligned} \begin{array}{lll} a &{} = &{} 2.943\\ b &{} = &{} -0.01\\ \end{array} \end{aligned}$$

with an ARMA(1, 1)-noise $(\epsilon _t)_t$ such that:

$$\begin{aligned} \epsilon _t-\phi \,\epsilon _{t-1}=\eta _t +\theta \,\eta _{t-1} \end{aligned}$$

with $(\phi ,\theta )$ estimated by (0.04, 0.69) and $(\eta _t)_t$ an actual centered white noise with estimated standard deviation 0.08. The intervals R command allows us to obtain $95\%$ confidence intervals for the model coefficients (see Appendix Fig. 15). The plot of price and fitted price is given in Fig. 8.

Fig. 7

Oil price as a function of oil production from 1937 to 1970

Fig. 8

Fitted price from 1937 to 1970

Interpretation of the Results

It is well known that oil prices are correlated with economic growth. Indeed, some use estimates of future Gross World Product (GWP) to obtain estimates of future oil prices. It is not surprising then that the model (3.5) gives a reasonable fit of GWP if one replaces $p_t$ by $y_t \mathop {=}\limits ^{\mathrm{{def}}}\log Y_t$ where $Y_t$ denotes GWP. We will make some conjectures about this relationship presently.

We begin by examining what the predictive model (3.7) for the period 1967–2015 using the coefficients (3.8).

If extraction is constant for 2 years, then $\nabla Q_t=\nabla ^2 Q_t=0$. In that case, the model reduces to

$$\begin{aligned} p_{\mathrm {basic}}(t) = \exp ( 1.591 + 0.032 \times Q_t +\epsilon _t) \end{aligned}$$

(3.9)

with 0 the expected value of $\epsilon _t$. We call this the basic price formula that predicts the price if extraction is constant. Note that the price increases with the quantity, consistent with a positive derivative in (5.11) as $\dfrac{\partial {P_t}}{\partial {Q_t}} /P_t = .032>0$.

Suppose $\nabla Q_t=$ constant $\ne 0$. Then, $\nabla ^2 Q_t=0$ and the model becomes

$$\begin{aligned} p(t) = \exp (1.591 + 0.032 \times Q_t - 0.062 \times \nabla Q_t). \end{aligned}$$

(3.10)

Note that the coefficient of $\nabla Q_t$ is about twice as large as the coefficient of $Q_t$ and of opposite sign. Thus, $\nabla Q_t$ gives a larger price signal than $Q_t$. The signal goes in the opposite direction of the change, but it only lasts for a year. One might understand this as follows: a rise (fall) in extraction causes growth (contraction) in the economy much more next year than this year (as in the example in “An Example” section).

Example 3.1

If extraction is constant at 88 MMbll per day, the basic price is $\hat{P}_{\mathrm basic}(t) \approx \$82/barrel$. If $Q_t= 88,$ $Q_{t-1}=86,$ and $Q_{t-2}=84,$ then $\nabla Q_t=\nabla Q_{t-1}=2$ and $\nabla ^2 Q_t=0$. Then, $\hat{P}_t \approx \$72$/barrel less than the basic price, because extraction is rising. If $Q_{t-1}=90$ and $Q_{t-2}= 92,$ then $\nabla Q_t=\nabla Q_{t-1}=-2$ and $\nabla ^2 Q_t= 0$. Then $\hat{P}(t) \approx \$93$/barrel greater than the basic price because extraction is falling.

The second derivative is negative at local maxima and positive at local minima, so that the second derivative will mollify the price change caused by the first derivative. This explains why peak extraction is frequently associated with low prices. A minimum in extraction will thus be associated with relatively high prices. Economically, this factor can be interpreted as follows: it takes 2 years for the economic growth (contraction) produced by an increase (decrease) in extraction to take hold. The first year it is rather fragile and easily reduced (increased) by a drop (rise) in extraction.

Example 3.2

• 1. If $Q_t = 88$, $Q_{t-1} =86$, and $Q_{t-2} =88,$ then extraction reaches a local minimum at $Q_{t-1}$. We compute $\hat{P}(t) \approx \$78$ rather than $72 as in Example 3.1 with the same increase in extraction from 86 MMbll per day.

• 2. If $Q_t = 88$, $Q_{t-1}=90$, and $Q_{t-2} =88$, then extraction reaches a local maximum at $Q_{t-1}$. We compute $\hat{P}(t) \approx \$86$ rather than $93 as in Example 3.1 with the same decrease in extraction from 90 MMbll per day.

• 3. It is interesting to note that if $Q_t= q_0\rho ^t$ with $\rho = (1+r)$ and the growth rate r in a reasonable range ($0<r<.12$), then $\hat{p}(t)$ is an increasing function of t. For example, if $Q_t = 80 (1.02)^t$, then $\hat{p}(3) \approx$ $58.3 < $60.8 $\approx \hat{p}(4)$, thus increasing extraction at a constant rate produces increasing prices. However, $\hat{p}(4)$ is much lower than the basic price at the same extraction quantity which is $87.6.

We believe that the differences in the different periods we studied stem from the importance of oil in the economy, that is the size of the partial derivative of economic production with respect to oil varied during the different periods. From 1937 to 1970, oil extraction increased regularly and so was never an impediment to economic growth. In the 1970’s, oil shocks created irregular supplies and constraints in oil supplies reduced economic growth. Mathematically, this is expressed by a larger partial derivative of economic production with respect to oil extraction levels. this period, as in the period from 2005 to 2014. This leads us to the following conjectures in accord with (5.10) and our empirical results:

Conjecture 3.1

The principle signal of scarcity of oil production is that $\dfrac{\partial {p}}{\partial {q}}> 0$.

Conjecture 3.2

Volatility in the supply of oil leads to increased price dependence on the discreet first and second derivatives of supply.

The standard scarcity rent view that lower quantities leads to higher prices can be explained by temporary dependence on the first- and second-discreet derivatives of extraction levels. After the short-term spikes, the price stabilizes with economic production adjusting to the new level of extraction. In other words, a shortage of important items in economic production ultimately leads to lower prices, because economic production contracts reducing demand. This can be read from Eq. (5.8).

In Alba et al. (1994), the authors note that $\dfrac{\partial {p}}{\partial {q}}> 0$ is unstable. When extraction levels are increasing, $\dfrac{\partial {p}}{\partial {q}}> 0$ encourages many actors to enter the extraction business which commonly leads to sharp increases in extraction levels and a price collapse. This occurred in the late 1970’s and early 1980’s and again from 2000 to 2013 when capital expenses increased at roughly 11% per year (Kopits 2014; Mushalnik 2016). If extraction levels are decreasing, then $\dfrac{\partial {p}}{\partial {q}}> 0$ leads to bankruptcies of higher priced extractors which leads to sharply decreasing extraction levels.

Scenarios

The success of our analysis using the dynamic production function identities should be judged by its ability to predict the dynamics of future scenarios.

Throughout this section, we make the following hypothesis:

(H4) For most of the contraction phase of oil extraction, $\dfrac{\partial {Y}}{\partial {q_i}}>0$ and is relatively large.

Hypothesis (H4) and (5.10) give us the following bound on price increases:

$$\begin{aligned} I_{\tilde{p}_i}(t_1,t_2) < I_{\tilde{C}_i}(t_1,t_2) / I_{q_i}(t_1,t_2). \end{aligned}$$

(4.1)

Cost Share Dynamics

In the case of a sharp unexpected change in extraction levels, that is in the case of oil shocks or gluts, one can approximate $I_{\tilde{p}_i}(t_1,t_2)$ with $I_{p_i}(t_1,t_2)$. The index $I_{\tilde{C}_i}(t_1,t_2)$ can be estimated using sampling techniques. These measures can then be used with $I_Q(t_1,t_2)$ to estimate the effect of an oil shock or glut on the economy.

Observe that consumers choices influence cost share. For example, in the 1940’s, people routinely heated to 14 °C. Suppose that lower prices and/or technology reduce the amount of money relative to a salary to heat to 14 degrees. The consumer can decide to either use her disposable income to purchase other items, or heat to 16 °C. Likewise, when the price of fuel is high, consumers tend to buy more fuel efficient vehicles than when the price is low. For fundamental quantities, such as oil, we thus expect that in a growing economy $I_{\tilde{C}_i}> I_{\tilde{C}^{\min }_i}$, where $I_{\tilde{C}_i^{\min }}$ is the minimum possible cost share. In a shrinking economy, we expect that $I_{\tilde{C}_i}$ will be very close to $I_{\tilde{C}_i^{\min }}$. Moreover, in a contracting economy, substitutes may be found for oil, so that $I_{C_i} < I_{\tilde{C}_i}$. From (5.8), we have, for any times $t_1$ and $t_2$,

$$\begin{aligned} I_{\tilde{p}_i}(t_1,t_2) = I_{Y_i}(t_1,t_2) I_{\tilde{C}_i}(t_1,t_2)/I_{q_i}(t_1,t_2). \end{aligned}$$

(4.2)

It is clear from (4.2) that during the expansion phase oil extraction, economic growth and consumer choices will support oil prices, while during the contraction phase, economic contraction, and consumer choices will tend to decrease prices. We believe that (4.2) can be used to measure and calibrate Jevons paradox which we believe will decrease prices during the contraction phase.

In the preceding argument, the cost share we speak of is not exactly $C_i$. It is the cost share in consumer budgets. Because a standard effect of stagflation is to reduce wages, consumers with lower wages will be more sensitive to higher prices and change their preferences accordingly. This is a further reason to compute $C_i$ with sampling techniques.

Rising cost share of energy is not benign. It means a loss of diversity in the economy. It means less money for some non-core sectors in the economy which leads to lower wages and fewer opportunities in these areas. This is a principle aspect of stagflation. The cost share of food and energy rises in family budgets and less money can be devoted to other areas of the economy. This leads us to make the following

Conjecture 4.1

When the cost share of essential items, such as food or energy, rises quickly, the necessary adjustment in the economy causes a recession.

Conjecture 4.1 is supported by the fact that recessions have always followed price shocks in oil and by the work of  Hamilton (2009).

These ideas can be illustrated by computing the scaling factors (see (5.5)) of oil extraction in the economic production function for the growth and stagflation phases (see “Current Analysis” section) of oil extraction (using GWP data compiled by the World Watch Institute). The scaling factor for the growth phase in oil extraction is $\alpha _g \approx 2/3 < 1$ ($R_{\mathrm { adj}}^2$= .999). For the stagflation phase, $\alpha _s \approx 2.3> 1$ ($R_{\mathrm { adj}}^2$= .913). Our interpretation is as in “Interpretation of the Results” section, during the expansion phase, oil was readily available. During the stagflation phase, oil production became more problematic and thus was used more efficiently and the scaling factor increased to 2.3, this due, in great part to technological progress. If one sees resources as a function of the economy, this can be viewed as a very positive development as the economy requires fewer resources to grow (the EIA calls this decreased energy intensity of the economy). If, on the other hand, you see the economy as a function of resources, this is ominous. While extraction levels are rising, greater efficiency leads to a positive feedback loop. An increase in oil extraction rates of 10% using $\alpha _g$ produces an increase in economic activity of 6.7%. From (5.6), assuming constant cost share, this leads to a decrease in price of about 3%. An equal increase in extraction rate using $\alpha _s$ results in an increase of economic production of 22% and an increase in price, assuming constant cost share, of almost 13%. A contraction of 10% in supply using $\alpha _g$ results in a contraction of economic production of about 6.7%. Assuming constant cost share, this gives an increase of price of about 3.5%. If instead one uses $\alpha _s$, one obtains a contraction in economic output of 22% and a decrease in price of 15% (assuming constant cost share), so that all increase in price must come from increased cost share forcing other areas of the economy to shrink. This situation can lead to a negative feedback loop leading to collapse in a manner similar to the collapse in complex societies described by Tainter (2010). What we have called increased efficiency and technology, Tainter describes as increased complexity to deal with supply problems. Note that our empirical model (3.7) suggests that the price shifts occur in phases. In the case of a contraction, the first step is an increase in price causing the cost share of oil to rise producing a recession which causes the price to drop. We note that the price of whale oil in the 19th century reached its maximum just after production of whale oil peaked decreased slightly and remained relatively flat afterwards Bardi (2004).

Current Analysis

Using the vocabulary of Turchin and Nefedov, we put the growth phase of oil extraction from 1865 to 1973. Before 1973, there was strong regular growth in extraction volumes. We then enter a period of volatility in extraction volumes characterized by the price shocks of the 1970’s. Although there was a strong political component to the price shocks in the 1970’s (Laurent 1985), the period gives valuable lessons on how prices behave when oil supplies are constrained. We begin to see signs of stagflation with respect to oil extraction in the late 1970’s: stagnant wages and increased difference between the elites and the working class (Piketty 2013). Of course, the modern economy of the 20th and 21st centuries is much more stratified than that of the agrarian societies studied by Turchin and Nefedov with several classes of workers (blue collar, white collar, etc.) and some classes of workers (white collar) at least initially belong to what can be considered an elite class.

If one considers the oil extracting firms to be a class of elites, one sees inter-elite competition intensifying in two distinct periods. We speak of the price wars of the late 1980’s and beginning in late 2014 to the present.

The reasons for decreased pressure on oil prices in the 1990’s should be the subject of future research. Perhaps, economic growth during that period was driven by the high-technology sector less reliant on oil. Perhaps, efficiency gains attained during the period of high prices took pressure off of prices. Perhaps, stagnant wages reduced demand of the working class.

The low price of oil relative to extraction costs for the last 2 years with the extracted volume in 2016 will roughly be that of 2015, we believe that we have entered a period similar the 1990’s in which the model (3.5) may not apply or at least $\dfrac{\partial {p_i}}{\partial {q_i}} < 0$ because oil is not currently a limitation on economic growth (or at least economic growth dependent on oil). Current limitations could be low wages, poor returns on investments, substitution, or choosing less oil intensive lifestyles. This period will end either when other limitations have ended, or when production falls.

Analysis of Common Scenarios

The Magic Market

A common scenario is that the contraction phase of oil extraction will cause shortages of oil which will cause prices to increase and the market will find a solution. This scenario contradicts Conjecture 3.1 and implies great efficiency gains will be needed to keep the economy from contracting.

This scenario does not fit with the empirical evidence presented in Mullainathan and Shafir (2013) in which scarcity of essential items is associated with extremely short-term thinking and poor general performance.

Empirically, we see that current markets are dysfunctional. The current low-price environment is attracting record amounts of capital to produce oil at a loss (Schindler 2015; Berman 2016). Companies are sacrificing future production through cuts in long-erm capital expenses (Staff 2015) and maintaining current production aided by hedges and bankruptcy regulations (McDonald 2016). Furthermore, consumers in the U.S. are purchasing inefficient vehicles unaware that many analysts are expecting oil extraction levels to fall. The (non-OPEC) oil extraction industry has accumulated a large amount of debt (Likvern 2016) in the last 5 years which will make it difficult to invest in new projects even if prices rise significantly.

For these reasons, we find this scenario improbable.

The Undulating Plateau (Prolonged Stagflation)

The IEA in their World Energy Outlook frequently refers to an undulating plateau in oil extraction lasting several decades to about 2050. This scenario implies roughly constant extraction levels and increasing prices, because extraction costs are increasing. Thus, $\dfrac{\partial {q_i}}{\partial {p_i}}$ is close to 0. This means that $|\dfrac{\partial {p_i}}{\partial {q_i}}|$ is large, so that there will be high price volatility. Moreover, the economy will lose diversity, because, in general, $\dfrac{\partial {C_i}}{\partial {p_i}}>0$. We believe that the loss of diversity translates into lower wages and increased efficiency in the use of oil to combat rising cost share. These two forces along with a stagnating economy contribute to downward pressure on prices (see (4.2)). The undulating plateau would thus end when the market price for oil falls below the cost of extraction. Indeed, this description fits the 2005 to 2014 period, and the current low price of oil seems to be the signal that the contraction phase has begun.

The Rule of Hotelling

The rule of Hotelling predicts that the price of oil increases exponentially irrespective of the quantity produced. This implies that, in the contractive stage of oil extraction, $\dfrac{\partial {p_i}}{\partial {q_i}}<<0$. To satisfy (H4), $\dfrac{\partial {C_i}}{\partial {q_i}} <0$. This implies efficiency must grow dramatically. Since efficiency is a bounded quantity, this will not be sustainable.

Probable Scenarios

The oil extraction industry is cyclical with periods of high prices spurring investment followed by periods of low prices in which investment falls. We believe that this is due to hysteresis, or a lag between when investment and increase in production. Offshore projects take between 5 and 10 years to complete. Between 1999 and 2013, capital expenses in the oil industry increased at an average rate of 11% per year. In 2015, capital expenses fell 16% and are expected to fall by a similar amount in 2016. As noted, most of the fall in capital expenses concerns projects that would begin to flow in 2020, so we have only felt the impact of a small portion of this fall in investment, while we continue to feel the effects of the increase in investment sustained through 2014. Much oil extraction is not profitable at current prices (Likvern 2016; Berman 2016).

According to Rystad Energy, oil extraction will decline slightly from 2016 to 2020 (Katakey 2016). We believe that efficiency gains should make this decrease bearable and that prices will not rise significantly. After 2020, we anticipate that non-OPEC oil extraction will fall more rapidly because of the cuts in capital expenses that have taken place in the last 2 years and accumulated debt of the oil extraction industry (Likvern 2016). This will cause tension between the extraction industry and the financial sector as they grapple with ways to pay off debt and maintain extraction levels (inter-elite competition). In any case, whether it is investors or extractors, this will cause increased social mobility, mostly downward which will put downward pressure on oil prices.

Eventually, extraction rates will fall fast enough to raise prices at least temporarily, as suggested by the empirical model (3.6), until companies and citizens go bankrupt and demand decreases. We anticipate improved efficiency in oil use will be used to reduce cost share, there will not be a corresponding price rebound. We expect efficiency to increase, in other words, we expect the scaling coefficient in (5.5) to increase if Y(t) is replaced by the part of the economy dependent on oil. The larger economy might not contract as quickly if substitution of other energy sources is used, but this should not increase the price of oil. Therefore, we expect the average price to fall with falling production.

A Seneca cliff Bardi (2011) can be imagined if, for example, a precipitous drop in non-OPEC (after 2020) extraction coincides with conflict in the Persian Gulf simultaneously reducing OPEC extraction rates. If extraction rates fall precipitously and remain low for 2 years, one can expect a price spike followed by a drop in prices which decimates first industries which use oil followed by the oil extraction industry and a recovery will be highly unlikely.

Note that both theoretical considerations from the dynamic production function identities and the empirical model (3.6) indicate that price dynamics will speed the rate of decline in oil extraction. During the growth phase of oil extraction, low prices increased demand, and high prices increase supply, during the contraction phase, low prices will diminish supply, and high prices will diminish demand.

Conclusion

Our analysis and empirical evidence are consistent with oil being a fundamental quantity in economic production. Our analysis indicates that once the contraction period for oil extraction begins, price dynamics will accelerate the decline in extraction rates: extraction rates decline because of a decrease in profitability of the extraction business.

Our empirical model for prices can be used by those studying future extraction rates whose models currently do not consider price parameters.

We believe that the contraction period in oil extraction has begun and that policy makers should be making contingency plans. Strategies for economies facing energy constraints are reviewed in Schindler and Schindler (0000).

Appendices

Appendix 1: Mathematical Results

Definitions and Hypotheses

Let Y(t) be a measure of economic production expressed in currency where t denotes time. We make no assumptions about the structure of the economy other than the existence of a well-developed monetary system to determine the distribution of wealth. Let $q(t) \in {\mathbb R}^{d}$ be the measurable quantities in the economy (quantities with a price). We will make use of the following assumptions:

(H1)

$$\begin{aligned} \overline{Y}(t)= \overline{Y}(q(t),t) \end{aligned}$$

(5.1)

is a locally $C^1({\mathbb R}^{d} \times {\mathbb R}\mapsto {\mathbb R})$ with $q(t)=(q_1(t), \dots q_{d}(t)) \in {\mathbb R}^{d}$. Prices are locally $C^1({\mathbb R}^d \times {\mathbb R}\mapsto {\mathbb R})$ functions of quantities.

(H2) Over short periods of time, the economic production function depends more on q(t) than on the time variable; therefore, for short periods of time, $\overline{Y}(q(t),t) \approx Y(q(t)),$ $q(t) \in {\mathbb R}^d$.

(H3) For short periods of time, we have $\dfrac{\partial {Y}}{\partial {q_i}} \ne 0$ for $i=1, \dots , d$.

Remark 5.1

• The regularity assumptions are not essential to the theory developed below, their purpose is to simplify notation.

• In the real world, $d =d(t)$. Care must be taken when applying results to new quantities or disappearing quantities.

Assumption (H1) is not a strong assumption, as the very fact that GDP is measurable, means that we measure certain quantities and use prices to evaluate the value added by the domestic economy.

Assumption (H2) essentially says that we assume that it takes time for the economy to change. Certain quantities are fungible, but we assume that it takes a certain amount of time to switch from one item to the other.

Assumption (H3) is not a strong assumption, as we are eliminating only quantities that have a small effect on the economy at any given time.

Because the units of Y(t) are in currency, an equivalent formulation can be to consider Y(p(t)) where $p(t) \in {\mathbb R}^d$ is the vector of prices of q(t). We use this formulation in (5.11).

Let $p_i(t)$ be the cost per unit of $q_i(t)$ and let $C_i(t)$ be the cost share or intensity of $q_i$ in the economy,

$$\begin{aligned} C_i (t) \mathop {=}\limits ^{\mathrm{{def}}}p_i(t) q_i(t) / Y(t). \end{aligned}$$

(5.2)

We will denote by $Y_i(t,u) =Y_i(\overline{q}_i (t),u)$, with $\overline{q}_i(t) \in {\mathbb R}^{d-1}$, consisting of $q_j$, $j \ne i$, the quantity

$$\begin{aligned} Y_i(t,u) \mathop {=}\limits ^{\mathrm{{def}}}\int _{0}^{u} \dfrac{\partial {Y(\overline{q}_i(t),q_i(s))}}{\partial {q_i}} q_i'(s) \mathrm d s \end{aligned}$$

(5.3)

where we make the technical assumption that $Y_i(\overline{q}_i(t),q_i(0)) =0$ for all $i \in 1,d$ and all $t \in {\mathbb R}_+$. We define the functions $\tilde{p}_i(t, u)$ and $\tilde{C}_i(t,u)$ similarly. We define the index

$$\begin{aligned} I_{Y_i}(t_1,t_2)= \;& {} I_{Y_i}(t,t_1,t_2) \\=\; & {} Y_i(t,t_2)/Y_i(t,t_1). \end{aligned}$$

(5.4)

We do not indicate the dependence on t in the index and will always assume that $t \in [t_1,t_2]$. We define the indices $I_{\tilde{C}_i}(t_1,t_2)$ and $I_{\tilde{p}_i}(t_1,t_2)$ similarly.

Elasticity or how quantities scale in the economic production function is very important. Suppose, $d =1$. One can write

$$\begin{aligned} Y(t) = K q^{\alpha (t)}, \end{aligned}$$

(5.5)

where K is a constant. If $\alpha (t) \equiv \alpha,$, a constant, then the production function is homogeneous of degree $\alpha$ and we call $\alpha$ the elasticity or scaling factor. If $\alpha =1,$ Y is linear in q, if $\alpha < 1$, Y is sublinear in q, otherwise, Y is superlinear in q. Substituting (5.5) into (5.2) and solving for p, we find that

$$\begin{aligned} p(t)= KC(t) q^{\alpha -1}. \end{aligned}$$

(5.6)

For constant C(t), we see that if Y is sublinear in q, price is a decreasing function of quantity, if Y is linear in q, the price is independent of q, and if Y is superlinear in q, the price is an increasing function of quantity.

Scaling factors are important in many sciences and mathematics. One looks for constant or average scaling empirically by normalizing quantities at a start date, taking logs and performing linear regression.

Main Results

Theorem 5.1

Assume (H1), then

• 1. If $\alpha _i(t)$ is the scaling factor of $q_i$ in Y, then $\alpha _i(t)-1$ is the scaling factor of $p_i/C_i$.

• 2. Assume that $C_i$ is constant. Then, sublinear scaling of Y in $q_i$ occurs if and only if $p_i(q_i)$ is monotone decreasing, linear scaling implies price is independent of $q_i$, and superlinear scaling occurs if and only if $p_i(q_i)$ is monotone increasing.

• 3. The greater $\dfrac{\partial {Y}}{\partial {q_i}}$, the smaller the scarcity rent in the sense of (5.9) (see discussion below).

• 4. The index of $Y_i(u)$ for any $(t_1,t_2) \in {\mathbb R}^2_+x$ is given by

  $$\begin{aligned} I_{Y_i}(t_1,t_2) = I_{\tilde{p}_i}(t_1,t_2) I_{\tilde{C}_i}(t_2,t_1) I_{q_i}(t_1,t_2). \end{aligned}$$

  (5.7)

Proof

From (5.2), one immediately obtains

$$\begin{aligned} p_i(t) = C_i(t) Y(t)/q_i(t). \end{aligned}$$

(5.8)

Properties (1) and (2) can be read directly from (5.8).

Taking the derivative of (5.8), one obtains the dynamic price identity:

$$\begin{aligned} \dfrac{\partial { p_i}}{\partial { q_i}} = \dfrac{\partial { C_i}}{\partial { q_i}} \frac{Y}{q_i} + C_i \frac{\dfrac{\partial {Y}}{\partial {q_i}} q_i - Y}{q^2}. \end{aligned}$$

(5.9)

The scarcity rent of a quantity varies inversely to its importance in the economic production function in the following sense. The more important a quantity in the economic production function, the greater the partial derivative of Y with respect to that quantity. However, from (5.9), we see that the price is an increasing function of the partial derivative of Y with respect to q, or price decreases as quantity decreases, a negative scarcity . This proves (3). (Of course, for an important quantity, one would expect the derivative of the cost share to be strongly negative and dominate the positive term.)

Solving (5.2) for Y, taking the log and then the derivative with respect to $q_i$, one obtains the first dynamic production function identity:

$$\begin{aligned} \dfrac{\partial {Y}}{\partial {q_i}} = Y\left( \frac{\dfrac{\partial {p_i}}{\partial {q_i}}}{p_i} - \frac{\dfrac{\partial { C_i}}{\partial { q_i}}}{C_i} + \frac{1}{q_i} \right) . \end{aligned}$$

(5.10)

Taking the derivative with respect to prices, we obtain the second dynamic production function identity:

$$\begin{aligned} \dfrac{\partial {Y}}{\partial {p_i}} = Y\left( \frac{\dfrac{\partial {q_i}}{\partial {p_i}}}{q_i} - \frac{\dfrac{\partial { C_i}}{\partial { p_i}}}{C_i} + \frac{1}{p_i} \right) . \end{aligned}$$

(5.11)

The sign of the left-hand side of (5.10) is the same as the sign in parentheses on the right-hand side. To obtain (5.7), we multiply (5.10) by $\frac{\mathrm d q}{\mathrm d t} /Y$ and integrate from $t_1$ to $t_2$ and take the exponential of the resulting equation. $\square$

Remark 5.2

• 1. The reason for deriving equations (5.7), (5.11), and (5.10) is that $Y_i(u)$ is impossible to measure, directly because one cannot vary just one quantity in the economy, during periods of growth or contraction, many quantities vary simultaneously. In some cases, we can draw conclusions on $I_{\tilde{p}_i}$ and $I_{\tilde{C}_i}$ from measurements of $I_{p_i}$ and $I_{C_i}$ where $I_{C_i}$ is not measured using (5.2) but rather by sampling different classes of society, for example, the class that consumes the most oil. See “Cost Share Dynamics” section.

• 2. Equation (5.9) should not be considered a precise model, because different quantities in the equation move at different speeds. Prices move more quickly than does the reaction of the economy to price changes. It makes more sense to use (5.9) with annual data using the average yearly prices than with spot prices.

• 3. Equation (5.9) is not, in general, an accurate way to measure $\dfrac{\partial {Y}}{\partial {q_i}},$ because the term in parentheses can be the difference between two small numbers of similar magnitude and, hence, numerically unstable. Equation (5.7) does provide a method for measuring the contribution of a quantity in $I_{Y}(t_1,t_2)$ in cases where

  $$\begin{aligned} \tilde{C}_i(t)\approx & {} C_i(t) \text{ and } \end{aligned}$$

  (5.12)
  $$\begin{aligned} \tilde{p}_i(t)\approx & {} p_i(t) \end{aligned}$$

  (5.13)

  since $I_{Y}(t_1,t_2) = I_{Y_u}\Pi _{j=1}^d I_{Y_j}(t_1,t_2)$. because of the simultaneous growth of other independent quantities. These equations tell us that in times of economic growth, the cost share of economic motors should either stagnate or decrease and that the cost per unit should increase. In times of economic contraction, the opposite dynamic can be deduced. Economic drags on the economy have the opposite dynamic.

• 4. The variable useful work, $U \mathop {=}\limits ^{\mathrm{{def}}}eE$, where e is efficiency and E is primary energy (or more properly energy) production, was introduced by Ayres and Warr (2006), we can write $Y(U(t),\bar{q}) = Y(e(t)E(t), \bar{q}),$ where $\bar{q} \in {\mathbb R}^{d-1}$ are the remaining quantities. Then, (5.8) becomes $p_E= C_E Y(eE, \bar{q})/q_E$. Assuming Y to be an increasing function of U, one sees that energy efficiency increases the price per unit of energy assuming that $C_E(t)$ remains constant. We thus have a very simple explanation of the empirically observed Jevons paradox or the rebound effect (Jevons 1866; Robert et al. 2009). Efficiency can be used to lower prices if it is used to decrease cost share. See discussion in “Cost Share Dynamics” section.

Representative Variables and the Implicit Function Theorem

One might be interested in using standard techniques to determine the nature of Y(t). If one accepts assumptions (H2) and (H3), one can use the implicit function theorem to reduce the number of variables to a small set of representative variables locally. This is very familiar to investors who use economic indicators to gauge the state of the economy. One can judge the quality of the indicator variables by seeing how closely the empirical scaling factors of the variables compare to the general scaling factors of the prices computed from $p_i/C_i$. By choosing overlapping time periods, empirical results will show whether or not the computed functions can be stitched together for longer periods of time.

Appendix 2: Plots, R commands, and R output

Fig. 9

R output for linear regression (data from 1965 to 2015)

Fig. 10

Confidence intervals for generalized linear model

Fig. 11

R output for generalized linear model

Fig. 12

R output for linear regression with Q and $\nabla Q$

Fig. 13

R output for linear regression with Q

Fig. 14

R output for generalized linear regression with Q from 1937 to 1970

Fig. 15

R output confidence intervals for generalized linear regression with Q from 1937 to 1970