A history of solar activity over millennia

Abstract

Presented here is a review of present knowledge of the long-term behavior of solar activity on a multi-millennial timescale, as reconstructed using the indirect proxy method. The concept of solar activity is discussed along with an overview of the special indices used to quantify different aspects of variable solar activity, with special emphasis upon sunspot number. Over long timescales, quantitative information about past solar activity can only be obtained using a method based upon indirect proxies, such as the cosmogenic isotopes $^{14}$C and $^{10}$Be in natural stratified archives (e.g., tree rings or ice cores). We give an historical overview of the development of the proxy-based method for past solar-activity reconstruction over millennia, as well as a description of the modern state. Special attention is paid to the verification and cross-calibration of reconstructions. It is argued that this method of cosmogenic isotopes makes a solid basis for studies of solar variability in the past on a long timescale (centuries to millennia) during the Holocene. A separate section is devoted to reconstructions of strong solar energetic-particle (SEP) events in the past, that suggest that the present-day average SEP flux is broadly consistent with estimates on longer timescales, and that the occurrence of extra-strong events is unlikely. Finally, the main features of the long-term evolution of solar magnetic activity, including the statistics of grand minima and maxima occurrence, are summarized and their possible implications, especially for solar/stellar dynamo theory, are discussed.

1 Introduction

The concept of the perfectness and constancy of the sun, postulated by Aristotle, was a strong belief for centuries and an official doctrine of Christian and Muslim countries. However, as people had noticed already before the time of Aristotle, some slight transient changes of the sun can be observed even with the naked eye. Although scientists knew about the existence of “imperfect” spots on the sun since the early seventeenth century, it was only in the nineteenth century that the scientific community recognized that solar activity varies in the course of an 11-year solar cycle. Solar variability was later found to have many different manifestations, including the fact that the “solar constant”, or the total solar irradiance, TSI, (the amount of total incoming solar electromagnetic radiation in all wavelengths per unit area at the top of the atmosphere) is not a constant. The sun appears much more complicated and active than a static hot plasma ball, with a great variety of nonstationary active processes going beyond the adiabatic equilibrium foreseen in the basic theory of sun-as-star. Such transient nonstationary (often eruptive) processes can be broadly regarded as solar activity, in contrast to the so-called “quiet” sun. Solar activity includes active transient and long-lived phenomena on the solar surface, such as spectacular solar flares, sunspots, prominences, coronal mass ejections (CMEs), etc.

The very fact of the existence of solar activity poses an enigma for solar physics, leading to the development of sophisticated models of an upper layer known as the convection zone and the solar corona. The sun is the only star, which can be studied in great detail and thus can be considered as a proxy for cool stars. Quite a number of dedicated ground-based and space-borne experiments are being carried out to learn more about solar variability. The use of the sun as a paradigm for cool stars leads to a better understanding of the processes driving the broader population of cool sun-like stars. Therefore, studying and modelling solar activity can increase the level of our understanding of nature.

On the other hand, the study of variable solar activity is not of purely academic interest, as it directly affects the terrestrial environment. Although changes in the sun are barely visible without the aid of precise scientific instruments, these changes have great impact on many aspects of our lives. In particular, the heliosphere (a spatial region of about 200–300 astronomical units across) is mainly controlled by the solar magnetic field. This leads to the modulation of galactic cosmic rays (GCRs) by the solar magnetic activity. Additionally, eruptive and transient phenomena in the sun/corona and in the interplanetary medium can lead to sporadic acceleration of energetic particles with greatly enhanced flux. Such processes can modify the radiation environment on Earth and need to be taken into account for planning and maintaining space missions and even transpolar jet flights. Solar activity can cause, through coupling of solar wind and the Earth’s magnetosphere, strong geomagnetic storms in the magnetosphere and ionosphere, which may disturb radio-wave propagation and navigation-system stability, or induce dangerous spurious currents in long pipes or power lines. Another important aspect is the link between solar-activity variations and the Earth’s climate (see, e.g., reviews by Haigh 2007; Gray et al. 2010; Mironova et al. 2015).

It is important to study solar variability on different timescales. The primary basis for such studies is observational (or reconstructed) data. The sun’s activity is systematically explored in different ways (solar, heliospheric, interplanetary, magnetospheric, terrestrial), including ground-based and space-borne experiments and dedicated missions during the last few decades, thus covering 3–4 solar cycles. However, it should be noted that the modern epoch was characterized, until the earlier 2000s by high solar activity dominated by an 11-year cyclicity, and it is not straightforward to extrapolate present knowledge (especially empirical and semi-empirical relationships and models) to a longer timescale. The current cycle 24 indicates the return to the normal moderate level of solar activity, as manifested, e.g., via the extended and weak solar minimum in 2008–2009 and weak solar and heliospheric parameters, which are unusual for the space era but may be quite typical for the normal activity (see, e.g., Gibson et al. 2011). On the other hand, contrary to some predictions, a Grand minimum of activity has no started. Thus, we may experience, in the near future, the interplanetary conditions quite different with respect to those we got used to during the last decades.

Therefore, the behavior of solar activity in the past, before the era of direct measurements, is of great importance for a variety of reasons. For example, it allows an improved knowledge of the statistical behavior of the solar-dynamo process, which generates the cyclically-varying solar-magnetic field, making it possible to estimate the fractions of time the sun spends in states of very-low activity, what are called grand minima. Such studies require a long time series of solar-activity data. The longest direct series of solar activity is the 400-year-long sunspot-number series, which depicts the dramatic contrast between the (almost spotless) Maunder minimum and the modern period of very high activity. Thanks to the recent development of precise technologies, including accelerator mass spectrometry, solar activity can be reconstructed over multiple millennia from concentrations of cosmogenic isotopes $^{14}$C and $^{10}$Be in terrestrial archives. This allows one to study the temporal evolution of solar magnetic activity, and thus of the solar dynamo, on much longer timescales than are available from direct measurements.

This paper gives an overview of the present status of our knowledge of long-term solar activity, covering the period of Holocene (the last 11 millennia). A description of the concept of solar activity and a discussion of observational methods and indices are presented in Sect. 2. The proxy method of solar-activity reconstruction is described in some detail in Sect. 3. Section 4 gives an overview of what is known about past solar activity. The long-term averaged flux of solar energetic particles is discussed in Sect. 5. Finally, conclusions are summarized in Sect. 6.

2 Solar activity: concept and observations

2.1 The concept of solar activity

The sun is known to be far from a static state, the so-called “quiet” sun described by simple stellar-evolution theories, but instead goes through various nonstationary active processes. Such nonstationary and nonequilibrium (often eruptive) processes can be broadly regarded as solar activity. The presence of magnetic activity, including stellar flares, is considered as a common typical feature of sun-like stars (Maehara et al. 2012). Although a direct projection of the energy and occurrence frequency of superflares on sun-like stars (e.g.,Shibata et al. 2013) does not agree with solar data (Aulanier et al. 2013) and terrestrial proxy (see Sect. 5), the existence of solar/stellar activity is clear. Whereas the concept of solar activity is quite a common term nowadays, it is neither straightforwardly interpreted nor unambiguously defined. For instance, solar-surface magnetic variability, eruption phenomena, coronal activity, radiation of the sun as a star or even interplanetary transients and geomagnetic disturbances can be related to the concept of solar activity. A variety of indices quantifying solar activity have been proposed in order to represent different observables and caused effects. Most of the indices are highly correlated to each other due to the dominant 11-year cycle, but may differ in fine details and/or long-term trends. In addition to the solar indices, indirect proxy data is often used to quantify solar activity via its presumably known effect on the magnetosphere or heliosphere. The indices of solar activity that are often used for long-term studies are reviewed below.

2.2 Indices of solar activity

Solar (as well as other) indices can be divided into physical and synthetic according to the way they are obtained/calculated. Physical indices quantify the directly-measurable values of a real physical observable, such as, e.g., the radioflux, and thus have clear physical meaning as they quantify physical features of different aspects of solar activity and their effects. Synthetic indices (the most common being sunspot number) are calculated (or synthesized) using a special algorithm from observed (often not measurable in physical units) data or phenomena. Additionally, solar activity indices can be either direct (i.e., directly relating to the sun) or indirect (relating to indirect effects caused by solar activity), as discussed in subsequent Sects. 2.2.1 and 2.2.2.

2.2.1 Direct solar indices

The most commonly used index of solar activity is based on sunspot number. Sunspots are dark areas on the solar disc (of size up to tens of thousands of km, lifetime up to half-a-year), characterized by a strong magnetic field, which leads to a lower temperature (about 4000 K compared to 5800 K in the photosphere) and observed as darkening.

Sunspot number is a synthetic, rather than a physical, index, but it has still become quite a useful parameter in quantifying the level of solar activity. This index presents the weighted number of individual sunspots and/or sunspot groups, calculated in a prescribed manner from simple visual solar observations. The use of the sunspot number makes it possible to combine together thousands and thousands of regular and fragmentary solar observations made by earlier professional and amateur astronomers. The technique, initially developed by Rudolf Wolf, yielded the longest series of directly and regularly-observed scientific quantities. Therefore, it is common to quantify solar magnetic activity via sunspot numbers. For details see the review on sunspot numbers and solar cycles (Hathaway and Wilson 2004; Hathaway 2015).

2.2.1.1 Wolf (WSN) and International (ISN) sunspot number series

The concept of the sunspot number was developed by Rudolf Wolf of the Zürich observatory in the middle of the nineteenth century. The sunspot series, initiated by him, is called the Zürich or Wolf sunspot number (WSN) series. The relative sunspot number $R_{z}$ is defined as

$$\begin{aligned} R_z = k\, (10\, G + N) , \end{aligned}$$

(1)

where G is the number of sunspot groups, N is the number of individual sunspots in all groups visible on the solar disc and k denotes the individual correction factor, which compensates for differences in observational techniques and instruments used by different observers, and is used to normalize different observations to each other.

Fig. 1

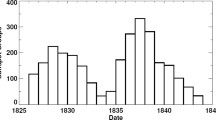
Annual sunspot activity for the last centuries. a International sunspot number series versions 1 and 2 (the latter is scaled with a 0.6 factor, see SILSO, http://sidc.be/silso/datafiles). b Number of sunspot groups: HS98—(Hoyt and Schatten 1998); U16—(Usoskin et al. 2016b); S16—(Svalgaard and Schatten 2016). Standard (Zürich) cycle numbering is shown between the panels. Approximate dates of the Maunder minimum (MM) and Dalton minimum (DM) are shown in the lower panel

The value of $R_{z}$ (see Fig. 1a) is calculated for each day using only one observation made by the “primary” observer (judged as the most reliable observer during a given time) for the day. The primary observers were Staudacher (1749–1787), Flaugergues (1788–1825), Schwabe (1826–1847), Wolf (1848–1893), Wolfer (1893–1928), Brunner (1929–1944), Waldmeier (1945–1980) and Koeckelenbergh (since 1980). If observations by the primary observer are not available for a certain day, the secondary, tertiary, etc. observers are used (see the hierarchy of observers in Waldmeier 1961). The use of only one observer for each day aims to make $R_{z}$ a homogeneous time series. As a drawback, such an approach ignores all other observations available for the day, which constitute a large fraction of the existing information. Moreover, possible errors of the primary observer cannot be caught or estimated. The observational uncertainties in the monthly $R_{z}$ can be up to 25% (e.g., Vitinsky et al. 1986). The WSN series is based on observations performed at the Zürich Observatory during 1849–1981 using almost the same technique. This part of the series is fairly stable and homogeneous although an offset due to the change of the weighting procedure might have been introduced in 1945–1946 (Clette et al. 2014) but the correction for this effect is not clear and leads to uncertainties (Lockwood et al. 2014a; Friedli 2016). However, prior to that there have been many gaps in the data that were interpolated. If no sunspot observations are available for some period, the data gap is filled, without note in the final WSN series, using an interpolation between the available data and by employing some proxy data. In addition, earlier parts of the sunspot series were “corrected” by Wolf using geomagnetic observation (see details in Svalgaard 2012), which makes the series less homogeneous. Therefore, the WSN series is a combination of direct observations and interpolations for the period before 1849, leading to possible errors and inhomogeneities as discussed, e.g, by Vitinsky et al. (1986), Wilson (1998), Letfus (1999), Svalgaard (2012), Clette et al. (2014). The quality of the Wolf series before 1749 is rather poor and hardly reliable (Hoyt et al. 1994; Hoyt and Schatten 1998; Hathaway and Wilson 2004).

The main problem of the WSN was a lack of documentation so that only the final product was available without information of the raw data, that made a full revision of the series hardly possible. Although this information does exist, it was hidden in hand-written notes of Rudolf Wolf and his successors. The situation is being improved now with an effort of the Rudolf Wolf Gesellschaft (http://www.wolfinstitute.ch) to scan and digitize the original Wolf’s notes (Friedli 2016).

Note that the sun has been routinely photographed since 1876 so that full information on daily sunspot activity is available (the Greenwich series) for the last 140 years.

The routine production of the WSN series was terminated in Zürich in 1982. Since then, the sunspot number series is routinely updated as the International sunspot number (ISN) $R_{i}$, provided by the Solar Influences Data Analysis Center in Belgium (Clette et al. 2007). The international sunspot number series is computed using the same definition (Eq. 1) as WSN but it has a significant distinction from the WSN: it is based not on a single primary solar observation for each day but instead uses a weighted average of more than 20 approved observers. The ISN (see SILSO, http://sidc.be/silso/datafiles) has been recently updated to version 2 with corrections to some known inhomogeneities (Clette et al. 2014). A potential user should know that the ISN (v.2) is calibrated to Wolfer, in contrast to earlier WSN and ISN (v.1) calibrated to Wolf. As a result, a constant scaling factor 0.6 should be applied to compare ISN (v.2) to ISN (v.1). The two versions are shown in Fig. 1a. One can see that the ISN v.2 (scaled by the 0.6 factor) is somewhat smaller than v.1 after the 1940s, because of the correction for the Waldmeier discontinuity (see below), but they are nearly identical before that.

In addition to the standard sunspot number $R_{i}$, there is also a series of hemispheric sunspot numbers $R_{\mathrm {N}}$ and $R_{\mathrm {S}}$, which account for spots only in the northern and southern solar hemispheres, respectively (note that $R_i=R_{\mathrm {N}}+R_{\mathrm {S}}$). These series are used to study the N-S asymmetry of solar activity (Temmer et al. 2002).

2.2.1.2 Group sunspot number (GSN) series

Since the WSN series is of lower quality before the 1850s and is hardly reliable before 1750, there was a need to re-evaluate early sunspot data. This tremendous work has been done by Hoyt and Schatten (1996, 1998), who performed an extensive archive search and nearly doubled the amount of original information compared to the Wolf series. They have produced a new series of sunspot activity called the group sunspot numbers (GSN—see Fig. 1b), including all available archival records. The daily group sunspot number $R_{g}$ is defined as follows:

$$\begin{aligned} R_g= \frac{12.08}{n}\sum _i{k'_iG_i} , \end{aligned}$$

(2)

where $G_i$ is the number of sunspot groups recorded by the i-th observer, $k'$ is the observer’s individual correction factor, n is the number of observers for the particular day, and 12.08 is a normalization number scaling $R_{g}$ to $R_{z}$ values for the period of 1874–1976. However, the exact scaling factor 12.08 has recently been questioned due to an inhomogeneity within the RGO data between 1874–1885 (Cliver and Ling 2016; Willis et al. 2016). $R_{g}$ is more robust than $R_{z}$ or $R_i$ since it is based on more easily identified sunspot groups and does not include the number of individual spots. By this the GSN avoids a problem related to the visibility of small sunspots since a group of several small spots would appear as one blurred spot for an observer with a low-quality telescope. Another potential uncertainty may be related to the way of grouping individual spots into sunspot groups that could be done differently in the past and nowadays (Clette et al. 2014). This uncertainty directly affecting the GSN is also important for WSN/ISN series since the number of groups composes 50–90% of the WSN/ISN values.

Another important advantage of the GSN series is that all the raw data are available. The GSN series includes not only one “primary” observation, but all available observations, and covers the period since 1610, being, thus, 140 years longer than the original WSN series. It is particularly interesting that the period of the Maunder minimum (1645–1715) was surprisingly well covered with daily observations (Ribes and Nesme-Ribes 1993; Hoyt and Schatten 1996) allowing for a detailed analysis of sunspot activity during this grand minimum (see also Sect. 4.2). Systematic uncertainties of the $R_{g}$ values are estimated to be about 10% before 1640, less than 5% from 1640–1728 and from 1800–1849, 15–20% from 1728–1799, and about 1% since 1849 (Hoyt and Schatten 1998). The GSN series is more reliable and homogeneous than the WSN series before 1849. The two series are nearly identical after the 1870s (Hoyt and Schatten 1998; Letfus 1999; Hathaway and Wilson 2004). However, the GSN series still contains some lacunas, uncertainties and possible inhomogeneities (see, e.g.,Letfus 2000; Usoskin et al. 2003a; Vaquero et al. 2012; Cliver and Ling 2016).

2.2.1.3 Updates of the series

The search for other lost or missing records of past solar instrumental observations has not ended even since the extensive work by Hoyt and Schatten. Archival searches still give new interesting findings of forgotten sunspot observations, often outside major observatories—see a detailed review book by Vaquero and Vázquez (2009) and original papers by Casas et al. (2006), Vaquero et al. (2005, 2007), Arlt (2008), Arlt (2009). Interestingly, not only sunspot counts but also regular drawings, forgotten for centuries, are being restored nowadays in dusty archives. A very interesting work has been done by Rainer Arlt (Arlt 2008, 2009; Arlt and Abdolvand 2011; Arlt et al. 2013) on recovering, digitizing, and analyzing regular drawings by S.H. Schwabe of 1825–1867 and J.C. Staudacher of 1749–1796. This work led to the extension of the Maunder butterfly diagram for several solar cycles backwards (Arlt 2009; Usoskin et al. 2009c; Arlt and Abdolvand 2011; Arlt et al. 2013)—see a newly built butterfly diagram for solar cycles Nos. 7–10 shown in Fig. 2. A recent finding of the lost data by G. Marcgraf and correcting some earlier uncertain data for the period 1636–1642 by Vaquero et al. (2011) made it possible to revise the pattern of the beginning of the Maunder minimum. Recent corrections to the group number database have been collected (http://haso.unex.es/?q=content/data) by Vaquero et al. (2016) who updated the database of Hoyt and Schatten (1998) by correcting some errors and inexactitudes.

Fig. 2

Maunder butterfly diagram of sunspot occurrence reconstructed by Arlt et al. (2013) for 1825–1867 using recovered drawing of S.H. Schwabe

Several inconsistencies and discontinuities have been found in the existing sunspot series. For instance, Leussu et al. (2013) have shown that the values of WSN before 1848 (when Wolf had started his own observations) were overestimated by ${\approx }20\%$ because of the incorrect k-factor ascribed by Wolf to Schwabe. This error, called the “Wolf discontinuity”, erroneously alters the WSN/ISN series but does not affect the GSN series. Another reported error is the so-called “Waldmeier discontinuity” around 1947 (Clette et al. 2014), related to the fact that Waldmeier had modified the procedure of counting spots, including ‘weighting’ sunspot number, without a proper noticing which led to a greater sunspot number compared to the standard technique. This suggests that the WSN/ISN may be overestimated by 10–20% past 1947 (Clette et al. 2014; Lockwood et al. 2014b), but this does not directly affect the GSN series. As studied by Friedli (2016), this weighting might have been introduced intermittently already in the early twentieth century.

Clette et al. (2014) and Cliver and Ling (2016) proposed, based on the ratio of number of groups reported by Wolfer to that based on the Royal Greenwich Observatory (RGO) data, that there might be a transition in the calibration of GSN around the turn of the nineteenth to twentieth century (or even until 1915) related to inhomogeneous quality of the RGO data used to build the GSN at that period. On the other hand, independent observations of David Hadden from Iowa or Madrid Observatory (Carrasco et al. 2013; Aparicio et al. 2014) reveal that the problem with RGO data is essential only before the 1880s but not after that. Willis et al. (2016) studied RGO data for the years 1874–1885 and found that the database of Hoyt and Schatten (1998) might have slightly underestimated the RGO number of groups during that time. Sarychev and Roshchina (2009) suggested that the RGO data are erroneous for the period 1874–1880 but quite homogeneous after that. Vaquero et al. (2014) reported that ISN values for the period prior to 1850 are discordant with the number of spotless days, and concluded that the problem could be related to the calibration constants by Wolf (as found by Leussu et al. 2013) and to the non-linearity of ISN for low values. Most of these errors affect the WSN/ISN series, while GSN is more robust.

Thus, such inconsistencies should be investigated, and new series, with corrections of the known problems, need to be produced. Several such efforts have been made recently leading to inconsistent solar activity reconstructions. One of the new reconstructions was made by Clette et al. (2014) who introduced a revised version of the ISN (v.2 – see Fig. 1a), correcting the two apparent discontinuities, Wolf and Waldmeier, as described above. In addition, the entire series was rescaled to the reference level of Wolfer, while the ‘classic’ WSN/ISN series was scaled to Wolf. This leads to a constant scaling with the factor $1.667 = 1/6$ of the ISN_v.2 series with respect to other series. Keeping this scaling in mind, the ISN_v2 series is systematically different from the earlier one after the 1940s, and for a few decades in the mid-nineteenth century. This was not a fundamental revision by a scaling correction for a couple of errors.

A full revision of the GSN series was performed by Svalgaard and Schatten (2016) who used the number of sunspot group by Hoyt and Schatten (1998) but applied different method to construct the new GSN series. They also used a daisy-chain linear regression to calibrate different observers but doing it in several steps. A few key observers, called the ‘backbones’, were selected, and other observers were re-normalized to the ‘backbones’ using linear regressions. Then the ‘backbones’ were calibrated to each other, again using the linear scaling. Before 1800, when the daisy-chain calibration cannot be directly applied, two other methods, the ‘high-low’ (observers reporting larger number of groups were favored over those reporting smaller number of groups) and ‘brightest star’ (only the highest daily number of sunspot groups per year was considered) methods. This GSN series, called S16, is shown in Fig. 1b as the blue dotted curve. It suggests a much higher, than usually thought, level of solar activity in the 19th and especially 18th centuries, comparable to that during the mid-twentieth century. As a result of the ‘brightest star’ method, it yields moderate values during the Maunder minimum in contrast to the present paradigm of virtually no sunspots (Eddy 1976; Ribes and Nesme-Ribes 1993; Hoyt and Schatten 1996; Usoskin et al. 2015).

The use of the traditional k-factor method of linear scaling for inter-calibration of solar observers has been found invalid (Dudok et al. 2016; Lockwood et al. 2016c, b; Usoskin et al. 2016b), and a need for a modern non-parametric method has emerged. This is illustrated by Fig. 3 which shows the ratio of the sunspot group number reported by Wolfer, $G_\mathrm{Wolfer}$, to that by Wolf, $G_\mathrm{Wolf}$, for days when both reports are available. This ratio obviously depends on the level of activity, being about two for low-activity days $G_\mathrm{Wolfer}=1$ and only ${\approx } 1.2$ for high-activity days. The ratio is strongly non-linear due to the fact that large sunspot groups dominate during periods of high activity. The horizontal dash-dotted line denotes the constant scaling k-factor of 1.667 used earlier (Clette et al. 2014) between Wolf and Wolfer. One can see that the use of the k-factor leads to a significant, by ${\approx } 40\%$, over-correction of the numbers from Wolf when scaling them to Wolfer.

Several new methods, free of the linear assumption, have been proposed recently. One, called the ADF-method (Usoskin et al. 2016b), is based on a comparison of statistics of the active-day fraction (ADF) in the sunspot (group) records of an observer with that of the reference data-set (the RGO record of sunspot groups for the period 1900–1976). By comparing them, the observational acuity threshold $A_\mathrm{th}$ can be found defined so that the observer is supposed to report all the sunspot groups with area greater than the threshold and to miss smaller groups. This threshold characterizes the quality of the observer and is further used to calibrate his/her records. The values of the defined thresholds for some principal observers of the eighteenth to nineteenth century are given in Table 1. Based on the defined observational acuity thresholds for each observer, a new GSN series was constructed, called U16, is depicted in Fig. 1b as the red curve. It lies lower than GSN S16 around solar maxima but slightly higher than HS98, in the eighteenth–nineteenth centuries.

Fig. 3

Correction c-factor of Wolf to Wolfer. The grey scale represents the probability density function (PDF) of the ratio of the number of groups reported by Wolfer for days, when Wolf reported a given number of groups. The big dots with error bars depict the mean values. The dashed line is a functional exponential fit. The horizontal dot-dashed line represents the constant correction k-factor 1.667 (Clette et al. 2014). Modified after (Usoskin et al. 2016b)

Table 1 Values of the observational acuity threshold for the key observers of the 18–19th centuries (modified after Usoskin et al. 2016b)

Another new method was proposed by Friedli (2016) who revised the WSN series basing on recently digitized Wolf’s original notes and using the relation between numbers of groups and individual spots. This series appears consistent with the GSN Us16 series and close to the classical ISN series but is lower than the GSN S16 series.

Several attempts to test/validate different sunspot reconstructions using indirect proxies yielded indicative results: tests based on cosmogenic radionuclides (Asvestari et al. 2017), including $^{44}$Ti in measured in the fallen meteorites (see Fig. 19) as well as geomagnetic and heliospheric proxies (Lockwood et al. 2016a, b) favor the ‘lower’ reconstructions (Hoyt and Schatten 1998; Usoskin et al. 2016b) against the ‘high’ reconstructions (Svalgaard and Schatten 2016). On the other hand, comparison with the solar open magnetic field models (Owens et al. 2016) cannot distinguish between different series.

The current situation with the sunspot number series is developing quickly and can hardly be resolved now. The old ‘classical’ WSN and GSN series need to be corrected for apparent inhomogeneities. Yet, newly emerging revisions of the sunspot series are mutually inconsistent and require efforts of the solar community on a consensus approach. On the other hand, the scientific community needs a ‘consensus’ series of solar activity, and the work in this direction is under way. Currently, probably the most reliable information of solar activity before the twentieth century can be obtained from cosmogenic isotope data (Sect. 3). This review will be updated as the situation progresses.

2.2.1.4 Other indices

An example of a synthetic index of solar activity is the flare index, representing solar flare activity (e.g., Özgüç et al. 2003; Kleczek 1952). The flare index quantifies daily flare activity in the following manner; it is computed as a product of the flare’s relative importance I in the $\mathrm {H}_{\alpha }$-range and duration t, $Q=It$, thus being a rough measure of the total energy emitted by the flare. The daily flare index is produced by Bogazici University (Özgüç et al. 2003) and is available since 1936.

A traditional physical index of solar activity is related to the radioflux of the sun in the wavelength range of 10.7 cm and is called the F10.7 index (e.g., Tapping and Charrois 1994). This index represents the flux (in solar flux units, $1 \mathrm{sfu} = 10^{-22}\ \mathrm{Wm}^{-2}\ \mathrm{Hz}^{-1}$) of solar radio emission at a centimetric wavelength. There are at least two sources of 10.7 cm flux—free-free emission from hot coronal plasma and gyromagnetic emission from active regions (Tapping 1987). It is a good quantitative measure of the level of solar activity, which is not directly related to sunspots. Close correlation between the F10.7 index and sunspot number indicates that the latter is a good index of general solar activity, including coronal activity. The solar F10.7 cm record has been measured continuously since 1947.

Another physical index is the coronal index (e.g., Rybanský et al. 2005), which is a measure of the irradiance of the sun as a star in the coronal green line. Computation of the coronal index is based on observations of green corona intensities (Fe xiv emission line at 530.3 nm wavelength) from coronal stations all over the world, the data being transformed to the Lomnický Štit photometric scale. This index is considered a basic optical index of solar activity. A synthesized homogeneous database of the Fe xiv 530.3 nm coronal-emission line intensities has existed since 1943 and covers seven solar cycles.

Often sunspot area is considered as a physical index representing solar activity (e.g., Baranyi et al. 2001; Balmaceda et al. 2005). This index gives the total area of visible spots on the solar disc in units of millionths of the sun’s visible hemisphere, corrected for apparent distortion due to the curvature of the solar surface. The area of individual groups may vary between tens of millionths (for small groups) up to several thousands of millionths for huge groups. This index has a physical meaning related to the solar magnetic flux emerging at sunspots. Sunspot areas are available since 1874 in the Greenwich series obtained from daily photographic images of the sun.

Sunspot group areas were routinely produced by the Royal Greenwich Observatory from daily photographic images of the sun for the period between 1874–1976 and after 1976 extended by the SOON network. Note, that the quality of the RGO data before 1880–1890s may be uneven (see discussion in Sect. 2.2.1). Sunspot areas can be reconstructed even before that using drawing of the sun by H. Schwabe for the years 1826–1867 (Arlt et al. 2013; Senthamizh Pavai et al. 2015) and images by Spörer for the period 1861–1894 (Diercke et al. 2015). In addition, some fragmentary solar drawings exist even for earlier periods, including the Maunder minimum in the seventeenth century (Ribes and Nesme-Ribes 1993; Vaquero et al. 2004; Arlt 2008).

An important quantity is solar irradiance, total and spectral (Fröhlich 2012). Irradiance variations are physically related to solar magnetic variability (e.g., Solanki et al. 2000), and are often considered manifestations of solar activity, which is of primary importance for solar-terrestrial relations.

Other physical indices include spectral sun-as-star observations, such as the Ca II-K index (e.g., Donnelly et al. 1994; Foukal 1996), the space-based Mg II core-to-wing ratio as an index of solar UVI (e.g., Donnelly et al. 1994; Viereck and Puga 1999; Snow et al. 2005) and many others.

All the above indices are closely correlated to sunspot numbers on the solar-cycle scale, but may depict quite different behavior on short or long timescales.

2.2.2 Indirect indices

Sometimes quantitative measures of solar-variability effects are also considered as indices of solar activity. These are related not to solar activity per se, but rather to its effect on different environments. Accordingly, such indices are called indirect, and can be roughly divided into terrestrial/geomagnetic and heliospheric/interplanetary.

Geomagnetic indices quantify different effects of geomagnetic activity ultimately caused by solar variability, mostly by variations of solar-wind properties and the interplanetary magnetic field. For example, the aa-index, which provides a global index of magnetic activity relative to a quiet-day curve for a pair of antipodal magnetic observatories (in England and Australia), is available from 1868 (Mayaud 1972). An extension of the geomagnetic series is available from the 1840s using the Helsinki Ak(H) index (Nevanlinna 2004a, b). Although the homogeneity of the geomagnetic series is compromised (e.g., Lukianova et al. 2009; Love 2011), it still remains an important indirect index of solar activity. A review of the geomagnetic effects of solar activity can be found, e.g., in Pulkkinen (2007). It is noteworthy that geomagnetic indices, in particular low-latitude aurorae (Silverman 2006), are associated with coronal/interplanetary activity (high-speed solar-wind streams, interplanetary transients, etc.) that may not be directly related to the sunspot-cycle phase and amplitude, and therefore serve only as an approximate index of solar activity. One of the earliest instrumental geomagnetic indices is related to the daily magnetic declination range, the range of diurnal variation of magnetic needle readings at a fixed location, and is available from the 1780s (Nevanlinna 1995). However, this data exists as several fragmentary sets, which are difficult to combine into a homogeneous data series.

Several geomagnetic activity indices have been proposed recently. One is the IDV (interdiurnal variability) index (Svalgaard and Cliver 2005; Lockwood et al. 2013) based on Bartels’ historical u-index of geomagnetic activity, related to the difference between successive daily values of the horizontal or vertical component of the geomagnetic field. Another index is IHV (inter-hourly variability) calculated from the absolute differences between successive hourly values of the horizontal component of the geomagnetic field during night hours to minimize the effect of the daily curve (Svalgaard et al. 2004; Mursula and Martini 2006). Some details of the derivation and use of these indirect indices for long-term solar-activity studies can be found, e.g., in the Living Review by Lockwood (2013).

Heliospheric indices are related to features of the solar wind or the interplanetary magnetic field measured (or estimated) in the interplanetary space. For example, the time evolution of the total (or open) solar magnetic flux is extensively debated (e.g., Lockwood et al. 1999; Wang et al. 2005; Krivova et al. 2007).

A special case of heliospheric indices is related to the galactic cosmic-ray intensity recorded in natural terrestrial archives. Since this indirect proxy is based on data recorded naturally throughout the ages and revealed now, it makes possible the reconstruction of solar activity changes on long timescales, as discussed in Sect. 3.

2.3 Solar activity observations in the pre-telescopic epoch

Instrumental solar data is based on regular observation (drawings or counting of spots) of the sun using optical instruments, e.g., the telescope used by Galileo in the early seventeenth century. These observations have mostly been made by professional astronomers whose qualifications and scientific thoroughness were doubtless. They form the basis of the group sunspot number series (Hoyt and Schatten 1998), which can be more-or-less reliably extended back to 1610 (see discussion in Sect. 2.2.1). However, some fragmentary records of qualitative solar and geomagnetic observations exist even for earlier times, as discussed below (Sects. 2.3.1–2.3.2).

2.3.1 Instrumental observations: camera obscura

The invention of the telescope revolutionized astronomy. However, another solar astronomical instrument, the camera obscura, also made it possible to provide relatively good solar images and was still in use until the late eighteenth century. Camera obscuras were known from early times, and they have been used in major cathedrals to define the sun’s position (see the review by Vaquero 2007; Vaquero and Vázquez 2009). The earliest known drawing of the solar disc was made by Frisius, who observed the solar eclipse in 1544 using a camera obscura. That observation was performed during the Spörer minimum and no spots were observed on the sun. The first known observation of a sunspot using a camera obscura was done by Kepler in May 1607, who erroneously ascribed the spot on the sun to a transit of Mercury. Although such observations were sparse and related to other phenomena (solar eclipses or transits of planets), there were also regular solar observations by camera obscura. For example, about 300 pages of logs of solar observations made in the cathedral of San Petronio in Bologna from 1655–1736 were published by Eustachio Manfredi in 1736 (see the full story in Vaquero 2007). Therefore, observations and drawings made using camera obscura can be regarded as instrumental observations.

2.3.2 Naked-eye observations

Even before regular professional observations performed with the aid of specially-developed instruments (what we now regard as scientific observations) people were interested in unusual phenomena. Several historical records exist based on naked-eye observations of transient phenomena on the sun or in the sky.

From even before the telescopic era, a large amount of evidence of spots being observed on the solar disc can be traced back as far as to the middle of the fourth century BC (Theophrastus of Athens). The earliest known drawing of sunspots is dated to December 8, 1128 AD as published in “The Chronicle of John of Worcester” (Willis and Stephenson 2001). However, such evidence from Occidental and Moslem sources is scarce and mostly related to observations of transits of inner planets over the sun’s disc, probably because of the dominance of the dogma on the perfectness of the sun’s body, which dates back to Aristotle’s doctrine (Bray and Loughhead 1964). Oriental sources are much richer for naked-eye sunspot records, but that data is also fragmentary and irregular (see, e.g., Clark and Stephenson 1978; Wittmann and Xu 1987; Yau and Stephenson 1988). Spots on the sun are mentioned in official Chinese and Korean chronicles from 165 BC to 1918 AD. While these chronicles are fairly reliable, the data is not straightforward to interpret since it can be influenced by meteorological phenomena, e.g., dust loading in the atmosphere due to dust storms (Willis et al. 1980) or volcanic eruptions (Scuderi 1990) can facilitate sunspots observations. Direct comparison of Oriental naked-eye sunspot observations and European telescopic data shows that naked-eye observations can serve only as a qualitative indicator of sunspot activity, but can hardly be quantitatively interpreted (see, e.g.,Willis et al. 1996, and references therein). Moreover, as a modern experiment of naked-eye observations (Mossman 1989) shows, Oriental chronicles contain only a tiny ($^{1}{/}_{200}\,\textendash \,^{1}{/}_{1000}$) fraction of the number of sunspots potentially visible with the naked eye (Eddy et al. 1989). This indicates that records of sunspot observations in the official chronicles were highly irregular (Eddy 1983) and probably dependent on dominating traditions during specific historical periods (Clark and Stephenson 1978). Although naked-eye observations tend to qualitatively follow the general trend in solar activity according to a posteriori information (e.g., Vaquero et al. 2002), extraction of any independent quantitative information from these records seems impossible.

Visual observations of aurorae borealis at middle latitudes form another proxy for solar activity (e.g., Siscoe 1980; Schove 1983; Křivský 1984; Silverman 1992; Schröder 1992; Lee et al. 2004; Basurah 2004; Vázquez and Vaquero 2010). Fragmentary records of aurorae can be found in both Occidental and Oriental sources since antiquity. The first known dated notation of an aurora is from March 12, 567 BC from Babylon (Stephenson et al. 2004). Aurorae may appear at middle latitudes as a result of enhanced geomagnetic activity due to transient interplanetary phenomena. Although auroral activity reflects coronal and interplanetary features rather than magnetic fields on the solar surface, there is a strong correlation between long-term variations of sunspot numbers and the frequency and latitude extent of aurora occurrences. Because of the phenomenon’s short duration and low brightness, the probability of seeing aurora is severely affected by other factors such as the weather (sky overcast, heat lightnings), the Moon’s phase, season, etc. The fact that these observations were not systematic in early times (before the beginning of the eighteenth century) makes it difficult to produce a homogeneous data set. Moreover, the geomagnetic latitude of the same geographical location may change quite dramatically over centuries, due to the migration of the geomagnetic axis, which also affects the probability of watching aurorae (Siscoe and Verosub 1983; Oguti and Egeland 1995). For example, the geomagnetic latitude of Seoul ($37.5^{\circ }$ N $127^{\circ }$ E), which is currently less than $30^{\circ }$, was about $40^{\circ }$ a millennium ago (Kovaltsov and Usoskin 2007). This dramatic change alone can explain the enhanced frequency of aurorae observations recorded in oriental chronicles.

2.3.3 Mathematical/statistical extrapolations

Due to the lack of reliable information regarding solar activity in the pre-instrumental era, it seems natural to try to extend the sunspot series back in time, before 1610 AD, by means of extrapolating its statistical properties. Indeed, numerous attempts of this kind have been made even recently (e.g., Nagovitsyn 1997; de Meyer 1998; Rigozo et al. 2001; Zharkova et al. 2015). Such models aim to find the main feature of the actually-observed sunspot series, e.g., a modulated carrier frequency or a multi-harmonic representation, which is then extrapolated backwards in time. The main disadvantage of this approach is that it is not a reconstruction based upon measured or observed quantities, but rather a “post-diction” based on extrapolation. This method is often used for short-term predictions, but it can hardly be used for the reliable long-term reconstruction of solar activity. In particular, it assumes that the sunspot time series is stationary, i.e., a limited time realization contains full information on its future and past. Clearly, such models cannot include periods exceeding the time span of observations upon which the extrapolation is based. Hence, the pre- or post-diction becomes increasingly unreliable with growing extrapolation time and its accuracy is hard to estimate.

Sometimes a combination of the above approaches is used, i.e., a fit of the mathematical model to indirect qualitative proxy data. In such models a mathematical extrapolation of the sunspot series is slightly tuned and fitted to some proxy data for earlier times. For example, Schove (1955, 1979) fitted the slightly variable but phase-locked carrier frequency (about 11 years) to fragmentary data from naked-eye sunspot observations and auroral sightings. The phase locking is achieved by assuming exactly nine solar cycles per calendar century. This series, known as Schove series, reflects qualitative long-term variations of the solar activity, including some grand minima, but cannot pretend to be a quantitative representation in solar activity level. The Schove series played an important historical role in the 1960s. In particular, a comparison of the $\varDelta ^{14}$C data with this series succeeded in convincing the scientific community that secular variations of $^{14}$C in tree rings have solar and not climatic origins (Stuiver 1961). This formed a cornerstone of the precise method of solar-activity reconstruction, which uses cosmogenic isotopes from terrestrial archives. However, attempts to reconstruct the phase and amplitude of the 11-year cycle, using this method, were unsuccessful. For example, Schove (1955) made predictions of forthcoming solar cycles up to 2005, which failed. We note that all these works are not able to reproduce, for example, the Maunder minimum (which cannot be represented as a result of the superposition of different harmonic oscillations), yielding too high sunspot activity compared to that observed. From the modern point of view, the Schove series can be regarded as archaic.

2.4 The solar cycle and its variations

2.4.1 Quasi-periodicities

2.4.1.1 11-years Schwabe cycle

The main feature of solar activity is its pronounced quasi-periodicity with a period of about 11 years, known as the Schwabe cycle. However, the cycle varies in both amplitude and duration. The first observation of a possible regular variability in sunspot numbers was made by the Danish astronomer Christian Horrebow in the 1770s on the basis of his sunspot observations from 1761–1769 (see details in Gleissberg 1952; Vitinsky 1965), but the results were forgotten. It took over 70 years before the amateur astronomer Schwabe announced in 1844 that sunspot activity varies cyclically with a period of about 10 years. This cycle, called the 11-year or Schwabe cycle, is the most prominent variability in the sunspot-number series. It is recognized now as a fundamental feature of solar activity originating from the solar-dynamo process. This 11-year cyclicity is prominent in many other parameters including solar, heliospheric, geomagnetic, space weather, climate and others. The background for the 11-year Schwabe cycle is the 22-year Hale magnetic polarity cycle. Hale found that the polarity of sunspot magnetic fields changes in both hemispheres when a new 11-year cycle starts (Hale et al. 1919). This relates to the reversal of the global magnetic field of the sun with the period of 22 years. It is often considered that the 11-year Schwabe cycle is the modulo of the sign-alternating Hale cycle (e.g., Sonett 1983; Bracewell 1986; Kurths and Ruzmaikin 1990; de Meyer 1998; Mininni et al. 2001), but this is only a mathematical representation. A detailed review of solar cyclic variability can be found in (Hathaway 2015).

2.4.1.2 Phase catastrophe?

Sometimes the regular time evolution of solar activity is broken up by periods of greatly depressed activity called grand minima. The last grand minimum (and the only one covered by direct solar observations) was the famous Maunder minimum from 1645–1715 (Eddy 1976, 1983). Other grand minima in the past, known from cosmogenic isotope data, include, e.g., the Spörer minimum around 1450–1550 and the Wolf minimum around the fourteenth century (see the detailed discussion in Sect. 4.2). Sometimes the Dalton minimum (ca. 1790–1820) is also considered to be a grand minimum. However, sunspot activity was not completely suppressed and still showed Schwabe cyclicity during the Dalton minimum. As suggested by Schüssler et al. (1997), this can be a separate, intermediate state of the dynamo between the grand minimum and normal activity, or an unsuccessful attempt of the sun to switch to the grand minimum state (Frick et al. 1997; Sokoloff 2004). This is observed as the phase catastrophe of solar-activity evolution (e.g., Vitinsky et al. 1986; Kremliovsky 1994). A peculiarity in the phase evolution of sunspot activity around 1800 was also noted by Sonett (1983), who ascribed it to a possible error in Wolf sunspot data and by Wilson (1988a), who reported on a possible misplacement of sunspot minima for cycles 4–6 in the WSN series. It has been also suggested that the phase catastrophe can be related to a tiny cycle, which might have been lost at the end of the eighteenth century because of very sparse observations (Usoskin et al. 2001a, 2002b, 2003b; Zolotova and Ponyavin 2007). We note that a new independent evidence proving the existence of the lost cycle has been found recently in the reconstructed sunspot butterfly diagram for that period (Usoskin et al. 2009c).

2.4.1.3 Centennial Gleissberg cycle

The long-term change (trend) in the Schwabe cycle amplitude is known as the secular Gleissberg cycle (Gleissberg 1939) with the mean period of about 90 years. However, the Gleissberg cycle is not a cycle in the strict periodic sense but rather a modulation of the cycle envelope with a varying timescale of 60–120 years (e.g., Gleissberg 1971; Kuklin 1976; Ogurtsov et al. 2002).

Longer (super-secular) cycles cannot be studied using direct solar observations, but only indicatively by means of indirect proxies such as cosmogenic isotopes discussed in Sect. 3. Analysis of the proxy data also yields the Gleissberg secular cycle (Feynman and Gabriel 1990; Peristykh and Damon 2003), but the question of its phase locking and persistency/intermittency still remains open.

2.4.1.4 210-years Suess/de Vries cycle

Several longer cycles have been found in the cosmogenic isotope data. A cycle with a period of 205–210 years, called the de Vries or Suess cycle in different sources, is a prominent feature, observed in various cosmogenic data (e.g., Suess 1980; Sonett and Finney 1990; Zhentao 1990; Usoskin et al. 2004; Steinhilber et al. 2012). It mostly manifests itself as the recurrence period of Grand minima within clusters (Usoskin et al. 2007).

2.4.1.5 Millennial Eddy cycle

Sometimes variations with a characteristic time of 600–700 years or 1000–1200 years are discussed (e.g., Vitinsky et al. 1986; Sonett and Finney 1990; Vasiliev and Dergachev 2002; Steinhilber et al. 2012; Abreu et al. 2012), but they are intermittent and can hardly be regarded as a typical feature of solar activity. Sometimes it is called Eddy cycle (Steinhilber et al. 2012).

2.4.1.6 ${\approx } 2400$-years Hallstatt cycle

A 2000–2400-year cycle is also noticeable in radiocarbon data series (see, e.g., Vitinsky et al. 1986; Damon and Sonett 1991; Vasiliev and Dergachev 2002).

It can be studied only using very long series, covering the whole Holocene. It was traditionally ascribed to climatic or geomagnetic variability (Vasiliev and Dergachev 2002; Vasiliev et al. 2012) but a recent joint study (Usoskin et al. 2016a) of $^{14}$C and $^{10}$Be data-sets has shown that the Hallstatt cycle is of solar origin and is manifested through clustered occurrence of Grand minima and maxima around its lows and highs, respectively.

2.4.2 Randomness versus regularity

The short-term (days–months) variability of sunspot numbers is greater than the observational uncertainties indicating the presence of random fluctuations (noise). As typical for most real signals, this noise is not uniform (white), but rather red or correlated noise (e.g., Ostryakov and Usoskin 1990a; Oliver and Ballester 1996; Frick et al. 1997), namely, its variance depends on the level of the signal. While the existence of regularity and randomness in sunspot series is apparent, their relationship is not clear (e.g., Wilson 1994)—are they mutually independent or intrinsically tied together? Moreover, the question of whether randomness in sunspot data is due to chaotic or stochastic processes is still open.

Earlier it was common to describe sunspot activity as a multi-harmonic process with several basic harmonics (e.g., Vitinsky 1965; Sonett 1983; Vitinsky et al. 1986) with an addition of random noise, which plays no role in the solar-cycle evolution. However, it has been shown (e.g., Rozelot 1994; Weiss and Tobias 2000; Charbonneau 2001; Mininni et al. 2002) that such an oversimplified approach depends on the chosen reference time interval and does not adequately describe the long-term evolution of solar activity. A multi-harmonic representation is based on an assumption of the stationarity of the benchmark series, but this assumption is broadly invalid for solar activity (e.g., Kremliovsky 1994; Sello 2000; Polygiannakis et al. 2003). Moreover, a multi-harmonic representation cannot, for an apparent reason, be extrapolated to a timescale larger than that covered by the benchmark series. The fact that purely mathematical/statistical models cannot give good predictions of solar activity (as will be discussed later) implies that the nature of the solar cycle is not a multi-periodic or other purely deterministic process, but random (chaotic or stochastic) processes play an essential role in sunspot cycle formation (e.g., Moss et al. 2008; Käpylä et al. 2012). An old idea of the possible planetary influence on the dynamo has received a new pulse recently with some unspecified torque effect on the assumed quasi-rigid non-axisymmetric tahocline (Abreu et al. 2012). However, this result was criticized by Poluianov and Usoskin (2014) as being an artifact of an inappropriate analysis (aliasing effect of incorrect smoothing). In addition, Cauquoin et al. (2014) have shown that such periodicities were not observed in $^{10}$Be data 330 kyr ago.

Different numeric tests, such as an analysis of the Lyapunov exponents (Ostryakov and Usoskin 1990b; Mundt et al. 1991; Kremliovsky 1995; Sello 2000), Kolmogorov entropy (Carbonell et al. 1994; Sello 2000) and Hurst exponent (Ruzmaikin et al. 1994; Oliver and Ballester 1998), confirm the chaotic/stochastic nature of the solar-activity time evolution (see, e.g., a review by Panchev and Tsekov 2007).

It was suggested quite a while ago that the variability of the solar cycle may be a temporal realization of a low-dimensional chaotic system (e.g., Ruzmaikin 1981). This concept became popular in the early 1990s, when many authors considered solar activity as an example of low-dimensional deterministic chaos, described by the strange attractor (e.g., Kurths and Ruzmaikin 1990; Ostryakov and Usoskin 1990b; Morfill et al. 1991; Mundt et al. 1991; Rozelot 1995; Salakhutdinova 1999; Serre and Nesme-Ribes 2000; Hanslmeier et al. 2013). Such a process naturally contains randomness, which is an intrinsic feature of the system rather than an independent additive or multiplicative noise. However, although this approach easily produces features seemingly similar to those of solar activity, quantitative parameters of the low-dimensional attractor have varied greatly as obtained by different authors. Later it was realized that the analyzed data set was too short (Carbonell et al. 1993, 1994), and the results were strongly dependent on the choice of filtering methods (Price et al. 1992). Developing this approach, Mininni et al. (2000, 2001) suggest that one considers sunspot activity as an example of a 2D Van der Pol relaxation oscillator with an intrinsic stochastic component.

Such phenomenological or basic principles models, while succeeding in reproducing (to some extent) the observed features of solar-activity variability, do not provide insight into the nature of regular and random components of solar variability. In this sense efforts to understand the nature of randomness in sunspot activity in the framework of dynamo theory are more advanced. Corresponding theoretical dynamo models have been developed (see reviews by Ossendrijver 2003; Charbonneau 2010), which include stochastic processes (e.g., Weiss et al. 1984; Feynman and Gabriel 1990; Schmalz and Stix 1991; Moss et al. 1992; Hoyng 1993; Brooke and Moss 1994; Lawrence et al. 1995; Schmitt et al. 1996; Charbonneau and Dikpati 2000; Brandenburg and Sokoloff 2002). For example, Feynman and Gabriel (1990) suggest that the transition from a regular to a chaotic dynamo passes through bifurcation. Charbonneau and Dikpati (2000) studied stochastic fluctuations in a Babcock–Leighton dynamo model and succeeded in the qualitative reproduction of the anti-correlation between cycle amplitude and length (Waldmeier rule). Their model also predicts a phase-lock of the Schwabe cycle, i.e., that the 11-year cycle is an internal “clock” of the sun. Most often the idea of fluctuations is related to the $\alpha$-effect, which is the result of the electromotive force averaged over turbulent vortices, and thus can contain a fluctuating contribution (e.g., Hoyng 1993; Ossendrijver et al. 1996; Brandenburg and Spiegel 2008; Moss et al. 2008). Note that a significant fluctuating component (with the amplitude more than 100% of the regular component) is essential in all these models.

2.4.3 A note on solar activity predictions

Randomness (see Sect. 2.4.2) in the SN series is directly related to the predictability of solar activity. Forecasting solar activity has been a subject of intense study for many years (e.g., Yule 1927; Newton 1928; Gleissberg 1948; Vitinsky 1965) and has greatly intensified recently with a hundred of journal articles being published to predict the solar cycle No. 24 maximum (see, e.g., reviews by Pesnell 2012, 2016), following the boost of space-technology development and increasing debates on solar-terrestrial relations. In fact, the situation has not been improved since the previous cycle, No. 23. The predictions for the peak sunspot number of solar cycle No. 24 range by a factor of 5, between 40 and 200, reflecting the lack of a reliable consensus method (Tobias et al. 2006). Detailed review of the solar activity prediction methods and results have been recently provided by (Hathaway 2009; Petrovay 2010; Pesnell 2012).

A detailed classification of the prediction methods is given by Pesnell (2012) who separates climatology, precursor, theoretical (dynamo model), spectral, neural network, and stock market prediction methods. All prediction methods can be generically divided into precursor and statistical (including the majority of the above classifications) techniques or their combinations (Hathaway et al. 1999). The fact that the prediction of solar cycle is not improved with adding more data (the new solar cycle) suggests that such methods are not able to give reliable prognoses.

The precursor methods are usually based on phenomenological, but sometimes physical, links between the poloidal solar-magnetic field, estimated, e.g., from geomagnetic activity in the declining phase of the preceding cycle or in the minimum time (e.g.,Hathaway 2009), with the toroidal field responsible for sunspot formation. These methods usually yield better short-term predictions of a forthcoming cycle maximum than the statistical methods, but cannot be applied to timescales longer than one solar cycle.

Statistical methods, including a low-dimensional solar-attractor representation (Kurths and Ruzmaikin 1990), are based solely on the statistical properties of sunspot activity and may give a reasonable result for short-term forecasting, but yield very poor results for long-term predictions (see reviews by, e.g., Conway 1998; Hathaway et al. 1999; Li et al. 2001; Usoskin and Mursula 2003; Kane 2007) because of chaotic/stochastic behavior (see Sect. 2.4.2).

A new method based on sophisticated dynamo numerical simulations emerges (e.g., Dikpati and Gilman 2006; Dikpati et al. 2008; Choudhuri et al. 2007; Jiang et al. 2007), but the results are so far contradictory with each other. Prospectives of this approach are also not clear because of the stochastic component, which drives the dynamo out of the deterministic regime, and uncertainties in the input parameters (Tobias et al. 2006; Bushby and Tobias 2007; Karak and Nandy 2012).

Some models, mostly based on precursor method, succeed in reasonable predictions of a forthcoming solar cycle (i.e., several years ahead), but they do not pretend to extend further in time. On the other hand, many claims of the solar activity forecast for 40–50 years ahead and even beyond that, even millennia ahead (Zharkova et al. 2015), have been made recently, often without sensible argumentation. However, so far there is no evidence of any method giving a reasonable prediction of solar activity beyond the solar-cycle scale (see, e.g., Sect. 2.3.3), probably because of the intrinsic limit of solar-activity predictability due to its stochastic/chaotic nature (Kremliovsky 1995; Tobias et al. 2006). Accordingly, such attempts can be regarded as speculative, unless they are verified by the actual behavior of solar activity. Note that even an exact prediction of the amplitude of one solar cycle can be just a random coincidence and cannot serve as a proof of the method’s veracity. Only a sequence of successful predictions can form a basis for confidence, which requires several decades.

Note that several “predictions” of the general decline of the coming solar activity have been made recently (Solanki et al. 2004; Abreu et al. 2008; Lockwood et al. 2011), however, these are not really true predictions but rather acknowledgements of the fact that the Modern Grand maximum (Usoskin et al. 2003c; Solanki et al. 2004) has ceased. Similar caution can be made about predictions of a Grand minimum (e.g., Lockwood et al. 2011; Miyahara et al. 2010)—a grand minimum should appear soon or later, but presently we are hardly able to predict its occurrence.

2.5 Summary

In this section, the concept of solar activity and quantifying indices is discussed, as well as the main features of solar-activity temporal behavior.

The concept of solar activity is quite broad and covers non-stationary and non-equilibrium (often eruptive) processes, in contrast to the “quiet” sun concept, and their effects upon the terrestrial and heliospheric environment. Many indices are used to quantify different aspects of variable solar activity. Quantitative indices include direct (i.e., related directly to solar variability) and indirect (i.e., related to terrestrial and interplanetary effects caused by solar activity), they can be physical or synthetic. While all indices depict the dominant 11-year cyclic variability, their relationships on other timescales (short scale or long-term trends) may vary to a great extent.

The most common and the longest available index of solar activity is the sunspot number, which is a synthetic index and is useful for the quantitative representation of overall solar activity outside the grand minimum. During the grand Maunder minimum, however, it may give only a clue about solar activity whose level may drop below the sunspot formation threshold. The sunspot number series is available for the period from 1610 AD, after the invention of the telescope, and covers, in particular, the Maunder minimum in the late seventeenth century. However, this series has big uncertainties before 1900 (Sect. 2.2.1). Fragmentary non-instrumental observations of the sun before 1610, while giving a possible hint of relative changes in solar activity, cannot be interpreted in a quantitative manner.

Solar activity in all its manifestations is dominated by the 11-year Schwabe cycle, which has, in fact, a variable length of 9–14 years for individual cycles. The amplitude of the Schwabe cycle varies greatly—from the almost spotless Maunder minimum to the very high cycle 19, possibly in relation to the Gleissberg or secular cycle. Longer super-secular characteristic times can also be found in various proxies of solar activity, as discussed in Sect. 4.

Solar activity contains essential chaotic/stochastic components, that lead to irregular variations and make the prediction of solar activity for a timescale exceeding one solar cycle impossible.

3 The proxy method of past solar-activity reconstruction

In addition to direct solar observations, described in Sect. 2.2.1, there are also indirect solar proxies, which are used to study solar activity in the pre-telescopic era. Unfortunately, we do not have any reliable data that could give a direct index of solar variability before the beginning of the sunspot-number series. Therefore, one must use indirect proxies, i.e., quantitative parameters, which can be measured nowadays but represent different effects of solar magnetic activity in the past. It is common to use, for this purpose, signatures of terrestrial indirect effects induced by variable solar-magnetic activity, that is stored in natural archives. Such traceable signatures can be related to nuclear (used in the cosmogenic-isotope method) or chemical (used, e.g., in the nitrate method) effects caused by cosmic rays (CRs) in the Earth’s atmosphere, lunar rocks or meteorites.

The most common proxy of solar activity is formed by the data on cosmogenic radionuclides (e.g., $^{10}$Be and $^{14}$C), which are produced by cosmic rays in the Earth’s atmosphere (e.g, Stuiver and Quay 1980; Beer et al. 1990; Bard et al. 1997; Beer 2000; Beer et al. 2012).

Other cosmogenic nuclides, which are used in geological and paleomagnetic dating, are less suitable for studies of solar activity (see e.g., Beer 2000; Beer et al. 2012). Cosmic rays are the main source of cosmogenic nuclides in the atmosphere (excluding anthropogenic factors during the last decades) with the maximum production being in the upper troposphere—lower stratosphere. After a complicated transport in the atmosphere, the cosmogenic isotopes are stored in natural archives such as polar ice, trees, marine sediments, etc. This process is also affected by changes in the geomagnetic field and climate. Cosmic rays experience heliospheric modulation due to solar wind and the frozen-in solar magnetic field. The intensity of modulation depends on solar activity and, therefore, cosmic-ray flux and the ensuing cosmogenic isotope intensity depends inversely on solar activity. An important advantage of the cosmogenic data is that primary archiving is done naturally in a similar manner throughout the ages, and these archives are measured nowadays in laboratories using modern techniques. If necessary, all measurements can be repeated and improved, as has been done for some radiocarbon samples. In contrast to fixed historical archival data (such as sunspot or auroral observations) this approach makes it possible to obtain homogeneous data sets of stable quality and to improve the quality of data with the invention of new methods (such as accelerator mass spectrometry). Cosmogenic isotope data is the main regular indicator of solar activity on the very long-term scale but it cannot resolve the details of individual solar cycles. The redistribution of nuclides in terrestrial reservoirs and archiving may be affected by local and global climate/circulation processes, which are, to a large extent, unknown for the past. However, a combined study of different nuclides data, whose responses to terrestrial effects are very different, may allow for disentangling external and terrestrial signals.

Fig. 4

Cyclic variations since 1951. a Time profiles of International sunspot number v.2 (scaled with 0.6-factor) (http://sidc.be/silso/datafiles); b cosmic-ray flux as the count rate of a polar neutron monitor (Oulu NM http://cosmicrays.oulu.fi, Climax NM data used before 1964), 100% NM count rate corresponds to May 1965

3.1 The physical basis of the method

3.1.1 Heliospheric modulation of cosmic rays

The flux of cosmic rays (highly energetic fully ionized nuclei) is considered roughly constant (at least at the time scales relevant for the present study) in the vicinity of the Solar system. However, before reaching the vicinity of Earth, galactic cosmic rays experience complicated transport in the heliosphere that leads to modulation of their flux. Heliospheric transport of GCR is described by Parker’s theory (Parker 1965; Toptygin 1985) and includes four basic processes: the diffusion of particles due to their scattering on magnetic inhomogeneities, the convection of particles by out-blowing solar wind, adiabatic energy losses in expanding solar wind, drifts of particles in the magnetic field, including the gradient-curvature drift in the regular heliospheric magnetic field, and the drift along the heliospheric current sheet, which is a thin magnetic interface between the two heliomagnetic hemispheres (Potgieter 2013). Because of variable solar-magnetic activity, CR flux in the vicinity of Earth is strongly modulated (see Fig. 4). The most prominent feature in CR modulation is the 11-year cycle, which is in inverse relation to solar activity. The 11-year cycle in CR is delayed (from a month up to two years) with respect to the sunspots (Usoskin et al. 1998). The time profile of cosmic-ray flux as measured by a neutron monitor (NM) is shown in Fig. 4 (panel b) together with the sunspot numbers (panel a). Besides the inverse relation between them, some other features can also be noted. A 22-year cyclicity manifests itself in cosmic-ray modulation through the alteration of sharp and flat maxima in cosmic-ray data, originated from the charge-dependent drift mechanism. One may also note short-term fluctuations, which are not directly related to sunspot numbers but are driven by interplanetary transients caused by solar eruptive events, e.g., flares or CMEs. An interesting feature is related to the recent decade. The CR flux in 2009 was the highest ever recorded by NMs (Moraal and Stoker 2010), as caused by the favorable heliospheric conditions (unusually weak heliospheric magnetic field and the flat heliospheric current sheet) (McDonald et al. 2010). On the other hand, the sunspot minimum was comparable to other minima. The level of CR modulation during the cycle 24 was moderate, much more shallow than for the previous cycles, reflecting the weak solar cycle 24. For the previous 50 years of high and roughly-stable solar activity, no trends have been observed in CR data; however, as will be discussed later, the overall level of CR has changed significantly on the centurial-millennial timescales.

Full solution of the CR transport problems is a complicated task and requires sophisticated 3D time-dependent self-consistent modelling. However, the problem can be essentially simplified for applications at a long-timescale. An assumption on the azimuthal symmetry (requires times longer that the solar-rotation period) and quasi-steady changes reduces it to a 2D quasi-steady problem. Further assumption of the spherical symmetry of the heliosphere reduces the problem to a 1D case. This approximation can be used only for rough estimates, since it neglects the drift effect, but it is useful for long-term studies, when the heliospheric parameters cannot be evaluated independently. Further, but still reasonable, assumptions (constant solar-wind speed, roughly power-law CR energy spectrum, slow spatial changes of the CR density) lead to the force-field approximation (Gleeson and Axford 1968; Caballero-Lopez and Moraal 2004), which can be solved analytically. The differential intensity $J_i$ of the cosmic-ray nuclei of type i with kinetic energy T at 1 AU is given in this case as

$$\begin{aligned} J_i(T,\phi )=J_{{\mathrm {LIS},}i}(T+\varPhi _i) \frac{(T)(T+2T_{\mathrm {r}})}{(T+\varPhi _i)(T+\varPhi _i+2T_{\mathrm {r}})} , \end{aligned}$$

(3)

where $\varPhi _i=(Z_i e/A_i)\phi$ for a cosmic nuclei of i-th type (charge and mass numbers are $Z_i$ and $A_i$), T and $\phi$ are expressed in MeV/nucleon and in MV, respectively, $T_{\mathrm {r}}=938\mathrm {\ MeV}$. T is the CR particle’s kinetic energy, and $\phi$ is the modulation potential. The local interstellar spectrum (LIS) $J_{\mathrm {LIS}}$ forms the boundary condition for the heliospheric transport problem. Since LIS is not measured directly, i.e., outside the heliosphere, it is not well known in the energy range affected by CR modulation (below 100 GeV). Recent data from Voyager 1 and 2 spacecraft traveling beyond the termination shock give a clue for the lower-ebergy range of LIS (Webber et al. 2008; Bisschoff and Potgieter 2016), although the residual modulation beyond the heliopause may still affect this (Herbst et al. 2012). Presently-used approximations for LIS (e.g., Garcia-Munoz et al. 1975; Burger et al. 2000; Webber and Higbie 2003, 2009) agree with each other for energies above 20 GeV but may contain uncertainties of up to a factor of 1.5 around 1 GeV. These uncertainties in the boundary conditions make the results of the modulation theory slightly model-dependent (see discussion in Usoskin et al. 2005; Herbst et al. 2010) and require the LIS model to be explicitly cited. This approach gives results, which are at least dimensionally consistent with the full theory and can be used for long-term studies¹ (Usoskin et al. 2002a; Caballero-Lopez and Moraal 2004). Differential CR intensity is described by the only time-variable parameter, called the modulation potential $\phi$, which is mathematically interpreted as the averaged rigidity (i.e., the particle’s momentum per unit of charge) loss of a CR particle in the heliosphere. However, it is only a formal spectral index whose physical interpretation is not straightforward, especially on short timescales and during active periods of the sun (Caballero-Lopez and Moraal 2004). Despite its cloudy physical meaning, this force-field approach provides a very useful and simple single-parametric approximation for the differential spectrum of GCR, since the spectrum of different GCR species directly measured near the Earth can be perfectly fitted by Eq. (3) using only the parameter $\phi$ in a wide range of solar activity levels (Usoskin et al. 2011). Therefore, changes in the whole energy spectrum (in the energy range from 100 MeV/nucleon to 100 GeV/nucleon) of cosmic rays due to the solar modulation can be described by this single number within the framework of the adopted LIS. The concept of modulation potential is a key concept for the method of solar-activity reconstruction by cosmogenic isotope proxy as it makes it possible to parameterize the GCR with one single parameter.

3.1.2 Geomagnetic shielding

Cosmic rays are charged particles and therefore are affected by the Earth’s magnetic field. Thus the geomagnetic field puts an additional shielding on the incoming flux of cosmic rays. It is usually expressed in terms of the cutoff rigidity $P_{\mathrm {c}}$, which is the minimum rigidity a vertically incident CR particle must posses (on average) in order to reach the ground via secondaries of the cascade at a given location and time (Cooke et al. 1991). Neglecting such effects as the East-West asymmetry, which is roughly averaged out for the isotropic particle flux, or nondipole magnetic momenta, which decay rapidly with distance, one can come to a simple approximation, called the Störmer’s equation, that describes the vertical geomagnetic cutoff rigidity $P_{\mathrm {c}}$:

$$\begin{aligned} P_{\mathrm {c}}\approx 1.9\,M\ \left( {R_{\mathrm {o}}/ R}\right) ^2\ \cos ^4 \lambda _G \ \mathrm {[GV]} , \end{aligned}$$

(4)

where M is the geomagnetic dipole moment (in $10^{25}\ \mathrm{G\ cm}^{3}$), $R_{\mathrm {o}}$ is the Earth’s mean radius, R is the distance from the given location to the dipole center, and $\lambda _G$ is the geomagnetic latitude. The cutoff concept works like a Heaviside step-function so that all cosmic rays whose rigidity is below the cutoff are not allowed to enter the atmosphere while all particles with higher rigidity can penetrate. This approximation provides a good compromise between simplicity and reality (Nevalainen et al. 2013), especially when using the eccentric dipole description of the geomagnetic field (Fraser-Smith 1987). The eccentric dipole has the same dipole moment and orientation as the centered dipole, but the dipole’s center and consequently the poles, defined as crossings of the axis with the surface, are shifted with respect to geographical ones.

The shielding effect is the strongest at the geomagnetic equator, where the present-day value of $P_{\mathrm {c}}$ may reach up to 17 GV in the region of India. There is almost no cutoff in the geomagnetic polar regions ($\lambda _G\ge 60^\circ$). However, even in the latter case the atmospheric cutoff becomes important, i.e., particles must have rigidity above 0.5 GV in order to initiate the atmospheric cascade which can reach ground (see Sect. 3.1.3).

The geomagnetic field is seemingly stable on the short-term scale, but it changes essentially on centurial-to-millennial timescales (e.g., Korte and Constable 2006). Such past changes can be evaluated based on measurements of the residual magnetization of independently-dated samples. These can be paleo- (i.e., natural stratified archives such as lake or marine sediments or volcanic lava) or archaeological (e.g., clay bricks that preserve magnetization upon baking) samples. Most paleo-magnetic data preserve not only the magnetic field intensity but also the direction of the local field, while archeo-magnetic samples provide information on the intensity only. Using a large database of such samples, it is possible to reconstruct (under reasonable assumptions) the large-scale magnetic field of the Earth. Data available provides good global coverage for the last three millennia, allowing for a reliable paleomagnetic reconstruction of the true dipole moment (DM) or virtual axial dipole moment² (VADM) and its orientation (Licht et al. 2013). Less precise, but still reliable reconstructions of the DM and its orientation are possible for the last seven millennia (Knudsen et al. 2008; Usoskin et al. 2016a). Directional paleomagnetic reconstruction are less reliable on a longer timescale, because of the spatial sparseness of the paleo/archeo-magnetic samples in the earlier part of the Holocene (Korte et al. 2011). Some paleomagnetic reconstructions are shown in Fig. 5. All paleomagnetic models depict a similar long-term trend—an enhanced intensity during the period between 1500 BC and 500 AD and a significantly lower field before that.

Changes in the dipole moment M inversely modulate the flux of CR at Earth, with strong effects in tropical regions and globally. The migration of the geomagnetic axis, which changes the geomagnetic latitude $\lambda _G$ of a given geographical location is also important; while not affecting the global flux of CR, it can dramatically change the CR effect regionally, especially at middle and high latitude. These changes affect the flux of CR impinging on the Earth’s atmosphere both locally and globally and must be taken into account when reconstructing solar activity from terrestrial proxy data (Usoskin et al. 2008, 2010). Accounting for these effects is quite straightforward provided the geomagnetic changes in the past are known independently, e.g., from archeo and paleo-magnetic studies (Donadini et al. 2010). However, because of progressively increasing uncertainties of paleomagnetic reconstructions back in time, it presently forms the main difficulty for the proxy method on the long-term scale (Snowball and Muscheler 2007), especially in the early part of the Holocene. On the other hand, the geomagnetic field variations are relatively well known for the last few millennia (Genevey et al. 2008; Korte and Constable 2008; Knudsen et al. 2008; Licht et al. 2013).

Fig. 5

Geomagnetic field intensity over millennia: VADM reconstructions over past 9000 years (a), with a zoom for the last 3200 years (b). Notations are: GMAG.9k (Usoskin et al. 2016a) with $1\sigma$ (gray shading) and the full range variability (hatching); AF_M (Licht et al. 2013); G08 (Genevey et al. 2008); pfm9k.1b and pfm9k.1a (Nilsson et al. 2014); Kn08 (Knudsen et al. 2008); and SHA-DIF.14k (Pavón-Carrasco et al. 2014). Modified after (Usoskin et al. 2016a)

3.1.3 Cosmic-ray–induced atmospheric cascade

When an energetic CR particle enters the atmosphere, it first moves straight in the upper layers, suffering mostly from ionization energy losses that lead to the ionization of the ambient rarefied air and gradual deceleration of the particles. However, after traversing some amount of matter (the nuclear interaction mean-free path is on the order of 100 g/cm$^{2}$ for a proton in the air) the CR particle may collide with a nucleus in the atmosphere, producing a number of secondaries. These secondaries have their own fate in the atmosphere, in particular they may suffer further collisions and interactions forming an atmospheric cascade (e.g., Dorman 2004). Because of the thickness of the Earth’s atmosphere (1033 g/cm$^{2}$ at sea level) the number of subsequent interactions can be large, leading to a fully-developed cascade (also called an air shower) consisting of secondary rather than primary particles. A schematic view of the atmospheric cascade is shown in Fig. 6. Three main components can be separated in the cascade:

• The “hadronic” nucleonic component is formed by the products of nuclear collisions of primary cosmic rays and their secondaries with the atmospheric nuclei, and consists mostly of superthermal protons and neutrons.

• The “soft” or electromagnetic component consists of electrons, positrons and photons.

• The “hard” or muon component consists mostly of muons; pions are short lived and decay almost immediately upon production, feeding muons and the “soft” component.

The development of the cascade depends mostly on the amount of matter traversed and is usually linked to residual atmospheric depth, which is very close to the static barometric pressure, rather than to the actual altitude, that may vary depending on the exact atmospheric density profile.

Fig. 6

Schematic view of an atmospheric cascade caused by energetic cosmic rays in the atmosphere. Left-to-right are denoted, respectively, the soft, muon and hadronic components of the cascade. Symbols “N, p, n, $\mu$, $\pi$, e$^{-}$, e$^{+}$, and $\gamma$” denote nuclei, protons, neutrons, muons, pions, electrons, positrons, and photons, respectively. Stars denote nuclear collisions, ovals—decay processes. This sketch does not represent the full development of the cascade and serves solely as an illustration for the processes discussed in the text. Image reproduced by permission from Usoskin (2011), copyright by SAIt

Cosmogenic isotopes are a by-product of the hadronic branch of the cascade (details are given below). Accordingly, in order to evaluate cosmic-ray flux from the cosmogenic isotope data, one needs to know the physics of cascade development. Several models have been developed for this cascade, in particular its hadronic branch with emphasis on the generation of cosmogenic isotope production. The first models were simplified quasi-analytical (e.g., Lingenfelter 1963; O’Brien and Burke 1973) or semi-empirical models (e.g., Castagnoli and Lal 1980). With the fast advance of computing facilities it became possible to exploit the best numerical method suitable for such problems—Monte-Carlo (e.g., Masarik and Beer 1999, 2009; Webber and Higbie 2003; Webber et al. 2007; Usoskin and Kovaltsov 2008b; Kovaltsov and Usoskin 2010; Kovaltsov et al. 2012; Argento et al. 2013). The fact that models, based on different independent Monte-Carlo packages, namely, a general GEANT tool and a specific CORSIKA code, yield similar results provides additional verification of the approach.

3.1.4 Transport and deposition

A scheme for the transport and redistribution of the two most useful cosmogenic isotopes, $^{14}$C and $^{10}$Be, is shown in Fig. 7. After a more-or-less similar production, the two isotopes follow quite different fates, as discussed in detail in Sects. 3.2.3 and 3.3.3. Therefore, expected terrestrial effects are quite different for the isotopes and comparing them with each other can help in disentangling solar and climatic effects (see Sect. 3.7.3). A reader can find great detail also in a book by Beer et al. (2012).

Fig. 7

Schematic representation of $^{14}$C (left) and $^{10}$Be (right) production chains. The flux of cosmic rays impinging on the Earth is affected by both heliospheric modulation and geomagnetic field changes. The climate may affect the redistribution of the isotopes between different reservoirs. Dashed line denotes a possible influence of solar activity on climate

3.2 Radioisotope $^{14}$C

The most commonly used cosmogenic isotope is radiocarbon $^{14}$C. This radionuclide is an unstable isotope of carbon with a half-life $\left( T_{1/2}\right)$ of about 5730 years. Since the radiocarbon method is extensively used in other science disciplines where accurate dating is a key issue (e.g., archeology, paleoclimatology, quaternary geology), it was developed primarily for this task. The solar-activity–reconstruction method, based on radiocarbon data, was initially developed as a by-product of the dating techniques used in archeology and Quaternary geology, in an effort to improve the quality of the dating by means of better information on the $^{14}$C variable source function. The present-day radiocarbon calibration curve, based on a dendrochronological scale, uninterruptedly covers the whole Holocene (and extending to 50 000 BP—Reimer et al. 2013) and provides a solid quantitative basis for studying solar activity variations on the multi-millennial time scale.

3.2.1 Measurements

Radiocarbon is usually measured in tree rings, which allows an absolute dating of the samples by means of dendrochronology. Using a complicated technique, the $^{14}$C activity³ A is measured in an independently dated sample, which is then corrected for age as

$$\begin{aligned} A^* = A\cdot \exp {\left( \frac{0.693\, t}{T_{1/2}}\right) }, \end{aligned}$$

(5)

where t and $T_{1/2}$ are the age of the sample and the half-life of the isotope, respectively. Then the relative deviation from the standard activity $A_o$ of oxalic acid (the National Bureau of Standards) is calculated:

$$\begin{aligned} \delta ^{14}\mathrm {C} = \left( \frac{A^*-A_o}{A_o}\right) \cdot 1000 . \end{aligned}$$

(6)

After correction for the carbon isotope fractionating (account for the $^{13}$C isotope) of the sample, the radiocarbon value of $\varDelta ^{14}$C is calculated (see details in Stuiver and Pollach 1977).

$$\begin{aligned} \varDelta ^{14}\mathrm {C} = \delta ^{14}\mathrm {C} - (2\cdot \delta ^{13}\mathrm {C} +50)\cdot (1+\delta ^{14}\mathrm {C}/1000) , \end{aligned}$$

(7)

where $\delta ^{13}$C is the per mille deviation of the $^{13}$C content in the sample from that in the standard belemnite sample calculated similarly to Eq. (6). The value of $\varDelta ^{14}$C (measured in per mille ‰) is further used as the index of radiocarbon relative activity. The series of $\varDelta ^{14}$C for the Holocene is presented in Fig. 8a as published by the IntCal13 collaboration of 21 dating laboratories as a result of systematic precise measurements of dated samples from around the world (Reimer et al. 2013) http://www.radiocarbon.org/IntCal13.htm. Panel b depicts the production rate $Q_\mathrm{14C}$ reconstructed by Roth and Joos (2013) using the most up-to-date carbon cycle model.

Fig. 8

Radiocarbon series for the Holocene. Upper panel Measured content of $\varDelta ^{14}$C in tree rings by IntCal13 collaboration (Reimer et al. 2013) (http://www.radiocarbon.org/IntCal13.htm). The long-term trend is caused by the geomagnetic field variations and the slow response of the oceans. Lower panel Production rate of $^{14}$C in the atmosphere, reconstructed from the measured $\varDelta ^{14}$C, along with the 95% confidence interval (Roth and Joos 2013)

A potentially interesting approach has been made by Lal et al. (2005), who measured the amount of $^{14}$C directly produced by CR in polar ice. Although this method is free of the carbon-cycle influence, the first results, while being in general agreement with other methods, are not precise.

3.2.2 Production

The main source of radioisotope $^{14}$C (except anthropogenic sources during the last decades) is cosmic rays in the atmosphere. It is produced as a result of the capture of a thermal neutron by atmospheric nitrogen

$$\begin{aligned} ^{14}\mathrm {N} + n \rightarrow \, \, ^{14}\mathrm {C} + p . \end{aligned}$$

(8)

Neutrons are always present in the atmosphere as a product of the cosmic-ray–induced cascade (see Sect. 3.1.3) but their flux varies in time along with the modulation of cosmic-ray flux. This provides continuous source of the isotope in the atmosphere, while the sinks are isotope decay and transport into other reservoirs as described below (the carbon cycle).

The connection between the cosmogenic-isotope–production rate, Q, at a given location (quantified via the geomagnetic latitude $\lambda _{\mathrm {G}}$) and the cosmic-ray flux is given by

$$\begin{aligned} Q = \int ^\infty _{P_{\mathrm {c}}(\lambda _{\mathrm {G}})} S(P,\phi )\ Y(P)\ dP , \end{aligned}$$

(9)

where $P_{\mathrm {c}}$ is the local cosmic-ray–rigidity cutoff (see Sect. 3.1.2), $S(P,\phi )$ is the differential energy spectrum of CR (see Sect. 3.1.1) and Y(P) is the differential yield function of cosmogenic isotope production, calculated using a Monte-Carlo simulation of the cosmic-ray–induced atmospheric cascade (Kovaltsov et al. 2012; Poluianov et al. 2016). Because of the global nature of the carbon cycle and its long attenuation time, the radiocarbon is globally mixed before the final deposition, and Eq. (9) should be integrated over the globe. The yield function Y(P) of the $^{14}$C production is shown in Fig. 9a together with those for $^{10}$Be (see Sect. 3.3.2) and for a ground-based neutron monitor (NM), which is the main instrument for studying cosmic-ray variability during the modern epoch. One can see that the yield function increases with the energy of CR. On the other hand, the energy spectrum of CR decreases with energy. Accordingly, the differential production rate (i.e., the product of the yield function and the spectrum, $F=Y\cdot S$—the integrand of Eq. 9), shown in Fig. 9b, is more informative. The differential production rate reflects the sensitivity to cosmic rays, and the total production rate is simply an integral of F over energy above the geomagnetic threshold.

Fig. 9

Differential production yield functions of cosmogenic isotopes and ground-based neutron monitors as a function of cosmic-ray energy. a Columnar yield functions of $^{10}$Be (Poluianov et al. 2016), $^{14}$C (Poluianov et al. 2016), polar neutron monitor (Mishev et al. 2013) as well as the energy spectrum of galactic cosmic protons for medium modulation ($\phi$ = 550 MV). b The differential production rate for $^{10}$Be and $^{14}$C cosmogenic isotopes, and the differential response function of a polar neutron monitor

Thanks to the development of atmospheric cascade models (Sect. 3.1.3), there are numerical models that allow one to compute the radiocarbon production rate as a function of the modulation potential $\phi$ and the geomagnetic dipole moment M. The overall production of $^{14}$C is shown in Fig. 10.

The production rate of radiocarbon, $Q_{^{14}\mathrm {C}}$, can vary as affected by different factors (see, e.g., Damon and Sonett 1991):

• Variations of the cosmic-ray flux on a geological timescale due to the changing galactic background (e.g., a nearby supernova explosion or crossing the dense galactic arm).

• Secular-to-millennial variations are caused by the slowly-changing geomagnetic field. This is an important component of the variability, which needs to be independently evaluated from paleo and archeo-magnetic studies.

• Modulation of cosmic rays in the heliosphere by solar magnetic activity. This variation is the primary aim of the present method.

• Short-term variability of CR on a daily scale (suppression due to interplanetary transients or enhancement due to solar energetic-particle events) can be hardly resolved in radiocarbon data.

Fig. 10

Globally-averaged production rate of $^{14}$C as a function of the modulation potential $\phi$ and geomagnetic dipole moment M, computed using the yield function by Kovaltsov et al. (2012), LIS by Burger et al. (2000) and cosmic-ray–modulation model by Usoskin et al. (2005). Other models (Masarik and Beer 2009; Poluianov et al. 2016) yield a similar result

Therefore, the production rate of $^{14}$C in the atmosphere can be modelled for a given time (namely, the modulation potential and geomagnetic dipole moment) and location. The global production rate Q is then obtained as a result of global averaging.

Until recently there was a discrepancy between the modeled global-average $^{14}$C production rates of $2.0\,\textendash \,2.3\ \mathrm{atoms}\ \mathrm{cm}^{-2}\ \mathrm{s}^{-1}$ (see, e.g., O’Brien 1979; Masarik and Beer 1999; Goslar 2001; Usoskin et al. 2006b, and references therein) and the steady-state production calculated from the $^{14}$C inventory in the carbon-cycle model (see Sect. 3.2.3) being $1.6{\,\textendash \,}1.8\ \mathrm{atoms}\ \mathrm{cm}^{-2}\ \mathrm{s}^{-1}$ for the pre-industrial period (e.g.,Goslar 2001, and references therein). The situation has been resolved recently with a new numerical model (Kovaltsov et al. 2012; Poluianov et al. 2016). For example, the mean global-averaged $^{14}$C production rate for the period 1750–1900 is estimated from measurements as $1.75 \pm 0.01\ \mathrm{atoms}\ \mathrm{cm}^{-2}\ \mathrm{s}^{-1}$ (Roth and Joos 2013). The production model (Usoskin et al. 2016a; Poluianov et al. 2016) yields for the same period theoretical production rate $1.71{\,\textendash \,}1.76\ \mathrm{atoms}\ \mathrm{cm}^{-2}\ \mathrm{s}^{-1}$, depending on the solar activity and geomagnetic field reconstructions used, being thus in an excellent agreement with the data.

3.2.3 Transport and deposition

Upon production cosmogenic radiocarbon gets quickly oxidized to carbon dioxide $\hbox {CO}_{2}$ and takes part in the regular carbon cycle of interrelated systems: atmosphere-biosphere-ocean (Fig. 7). Because of the long residence time, radiocarbon becomes globally mixed in the atmosphere and involved in an exchange with the ocean. It is common to distinguish between an upper layer of the ocean, which can directly exchange $\hbox {CO}_{2}$ with the air and deeper layers. The measured $\varDelta ^{14}$C comes from the biosphere (trees), which receives radiocarbon from the atmosphere. Therefore, the processes involved in the carbon cycle are quite complicated. The carbon cycle is usually described using a box model (Oeschger et al. 1974; Siegenthaler et al. 1980), where it is represented by fluxes between different carbon reservoirs and mixing within the ocean reservoir(s), as shown in Fig. 11. Production and radioactive decay are also included in box models. Free parameters in a typical box model are the $^{14}$C production rate Q, the air-sea exchange rate (expressed as turnover rate $\kappa$), and the vertical–eddy-diffusion coefficient K, which quantifies ocean ventilation. Starting from the original representation (Oeschger et al. 1974), a variety of box models have been developed, which take into account subdivisions of the ocean reservoir and direct exchange between the deep ocean and the atmosphere at high latitudes. More complex models, including a diffusive approach, are able to simulate more realistic scenarios, but they require knowledge of a large number of model parameters. These parameters can be evaluated for the present time using the bomb test–studying the transport and distribution of the radiocarbon produced during the atmospheric nuclear tests. However, for long-term studies, only the production rate is considered variable, while the gas-exchange rate and ocean mixing are kept constant. Under such assumptions, there is no sense in subdividing reservoirs or processes, and a simple carbon box model is sufficient.

Fig. 11

A 12-box model of the carbon cycle (Broeker and Peng 1986; Siegenthaler et al. 1980). The number on each individual box is the steady-state $\varDelta ^{14}$C of this particular reservoir expressed in per mil. Image reproduced by permission from Bard et al. (1997), copyright by Elsevier

Using the carbon cycle model and assuming that all its parameters are constant in time, one can evaluate the production rate Q from the measured $\varDelta ^{14}$C data. This assumption is well validated for the the Holocene (Damon et al. 1978; Stuiver et al. 1991) as there is no evidence of considerable oceanic change or other natural variability of the carbon cycle (Gerber et al. 2002), and accordingly all variations of $\varDelta ^{14}$C predominantly reflect the production rate. This is supported by the strong similarity of the fluctuations of the $^{10}$Be data in polar ice cores (Sect. 3.3) compared to $^{14}$C, despite their completely different geochemical fate (Bard et al. 1997; Steinhilber et al. 2012). However, the changes in the carbon cycle during the last glaciation and deglaciation were dramatic, especially regarding ocean ventilation; this and the lack of independent information about the carbon cycle parameters, make it hardly possible to qualitatively estimate solar activity from $^{14}$C before the Holocene.

A new-generation carbon cycle model has been developed moving from static box-exchange models to a dynamical model. Roth and Joos (2013) presented a fully featured model of intermediate complexity, named Bern3D-LPJ, which includes in addition to the dynamical atmosphere, a 3D dynamic ocean, ocean sediments, and a vegetation models. So far this is the most sophisticated and complete carbon cycle model. A multi-millennial reconstruction of the $^{14}$C production rate, obtained as a result of application of this model to the IntCal09 radiocarbon data (Reimer et al. 2009) is shown in Fig. 8b.

First attempts to extract information on production-rate variations from measured $\varDelta ^{14}$C were based on simple frequency separations of the signals. All slow changes were ascribed to climatic and geomagnetic variations, while short-term fluctuations were believed to be of solar origin. This was done by removing the long-term trend from the $\varDelta ^{14}$C series and claiming the residual as being a series of solar variability (e.g., Peristykh and Damon 2003). This oversimplified approach was natural at earlier times, before the development of carbon cycle models, but later it was replaced by the inversion of the carbon cycle (i.e., the reconstruction of the production rate from the measured $^{14}$C concentration). Although mathematically this problem can be solved correctly as a system of linear differential equations, the presence of fluctuating noise with large magnitude makes it not straightforward, since the time derivative cannot be reliably identified leading thus to possible amplification of the high-frequency noise in $\varDelta ^{14}$C data. One traditional approach (e.g., Stuiver and Quay 1980) is based on an iterative procedure, first assuming a constant production rate, and then fitting the calculated $\varDelta ^{14}$C variations to the actual measurements using a feedback scheme. A concurrent approach based on the presentation of the carbon cycle as a Fourier filter (Usoskin and Kromer 2005) produces similar results. Roughly speaking, the carbon cycle acts as an attenuating and delaying filter for the $^{14}$C signal (see Fig. 12). The higher the frequency is, the greater the signal is attenuated. In particular, the large 11-year solar cycle expected in the $^{14}$C is attenuated by a factor of hundred in the measured $\varDelta ^{14}$C data, making it hardly detectable. Because of the slow oceanic response, the $^{14}$C data is also delayed with respect to the production signal. The production rate $Q_{^{14}\mathrm {C}}$ for the Holocene is shown in Fig. 8 and depicts both short-term fluctuations as well as slower variations, mostly due to geomagnetic field changes (see Sect. 3.2.5).

Fig. 12

The frequency characteristics of the carbon cycle: attenuation (left-hand panel) and phase shift (right-hand panel) as a function of the frequency of the $^{14}$C production signal. Lines stand for a classical Oeschger–Siegenthaler box model (Siegenthaler et al. 1980), and open circles for a sophisticated PANDORA model (Bard et al. 1997)

3.2.4 The Suess effect and nuclear bomb tests

Unfortunately, cosmogenic $^{14}$C data cannot be easily used for the last century, primarily because of the extensive burning of fossil fuels. Since fossil fuels do not contain $^{14}$C, the produced $\hbox {CO}_{2}$ dilutes the atmospheric $^{14}\hbox {CO}_{2}$ concentration with respect to the pre-industrial epoch. Therefore, the measured $\varDelta ^{14}$C cannot be straightforwardly translated into the production rate Q after the late nineteenth century, and a special correction for fossil fuel burning is needed. This effect, known as the Suess effect (e.g., Suess 1955), can be up to −25‰ in $\varDelta ^{14}$C in 1950 (Tans et al. 1979), which is an order of magnitude larger than the amplitude of the 11-year cycle of a few ‰. Moreover, while the cosmogenic production of $^{14}$C is roughly homogeneous over the globe and time, the use of fossil fuels is highly nonuniform (e.g., de Jong and Mook 1982) both spatially (developed countries, in the northern hemisphere) and temporarily (World Wars, Great Depression, industrialization, etc.). This makes it very difficult to perform an absolute normalization of the radiocarbon production to the direct measurements. Sophisticated numerical models (e.g., Sabine et al. 2004; Mikaloff Fletcher et al. 2006) aim to account for the Suess effect and make good progress. However, the results obtained indicate that the determination of the Suess effect does not yet reach the accuracy required for the precise modelling and reconstruction of the $^{14}$C production for the industrial epoch. Note that the atmospheric concentration of another carbon isotope $^{13}$C is partly affected by land use, which has also been modified during the last century.

Another anthropogenic activity greatly disturbing the natural variability of $^{14}$C is related to the atmospheric nuclear bomb tests actively performed in the 1960s. For example, the radiocarbon concentration nearly doubled in the early 1960s in the northern hemisphere after nuclear tests performed by the USSR and the USA in 1961 (Damon et al. 1978). On one hand, such sources of momentary spot injections of radioactive tracers (including $^{14}$C) provide a good opportunity to verify and calibrate the exchange parameters for different carbon-cycle reservoirs and circulation models (e.g., Bard et al. 1987; Sweeney et al. 2007). Thus, the present-day carbon cycle is more-or-less known. On the other hand, the extensive additional production of isotopes during nuclear tests makes it hardly possible to use the $^{14}$C as a proxy for solar activity after the 1950s (Joos 1994).

These anthropogenic effects do not allow one to make a straightforward link between pre-industrial data and direct experiments performed during more recent decades. Therefore, the question of the absolute normalization of $^{14}$C model is still open (see, e.g., the discussion in Solanki et al. 2004, 2005; Muscheler et al. 2005).

3.2.5 The effect of the geomagnetic field

As discussed in Sect. 3.1.2, knowledge of geomagnetic shielding is an important aspect of the cosmogenic isotope method. Since radiocarbon is globally mixed in the atmosphere before deposition, its production is affected by changes in the geomagnetic dipole moment M, while magnetic-axis migration plays hardly any role in $^{14}$C data.

The crucial role of paleomagnetic reconstructions has long been known (e.g., Elsasser et al. 1956; Kigoshi and Hasegawa 1966). Many earlier corrections for possible geomagnetic-field changes were performed by detrending the measured $\varDelta ^{14}$C abundance or production rate Q (Stuiver and Quay 1980; Voss et al. 1996; Peristykh and Damon 2003), under the assumption that geomagnetic and solar signals can be disentangled from the production in the frequency domain. Accordingly, the temporal series of either measured $\varDelta ^{14}$C or its production rate Q is decomposed into the slow changing trend and faster oscillations. The trend is supposed to be entirely due to geomagnetic changes, while the oscillations are ascribed to solar variability. Such a method, however, obliterates all information on possible long-term variations of solar activity. On the other hand, this also misinterprets the short-term (centennial timescale) variations of the geomagnetic field which are essential (e.g., Licht et al. 2013). Accordingly, the frequency-domain decomposition may lead to erroneous results. A direct correction for the geomagnetic field effect should be used instead.

Simplified empirical correction factors were also often used (e.g., Stuiver and Quay 1980; Stuiver et al. 1991). The modern approach is based on a physics-based model (e.g., Solanki et al. 2004; Vonmoos et al. 2006) and allows the quantitative reconstruction of solar activity, explicitly using independent reconstructions of the geomagnetic field. In this case the major source of errors in solar activity reconstructions is related to uncertainties in the paleomagnetic data (Snowball and Muscheler 2007). These errors are insignificant for the last several millennia (Licht et al. 2013; Usoskin et al. 2016a), but become increasingly important for earlier times.

3.3 Cosmogenic isotope $^{10}$Be

3.3.1 Measurements

The cosmogenic isotope $^{10}$Be is useful for long-term studies of solar activity because of its long half-life of around $1.5 \times 10^{6}$ years. Its concentration is usually measured in stratified ice cores allowing for independent dating. The $^{10}$Be/$^{9}$Be ratio needs to be precisely measured at an accuracy better than $10^{-13}$. This can be done using AMS (Accelerator Mass Spectrometry) technique, which makes the measurements complicated and expensive. Correction for the decay is straightforward and does not include isotope fractionating. From the measured samples, first the $^{10}$Be concentration is defined, usually in units of $10^{4}$ atoms/g. Sometimes, a correction for the snow precipitation amount is considered leading to the observable $^{10}$Be flux, which is the number of atoms, precipitating to the surface per cm$^{2}$ per second.

There exist different $^{10}$Be series suitable for studies of long-term solar activity, coming from ice cores in Greenland and Antarctica. They have been obtained from different cores with different resolutions, and include data from Milcent, Greenland (Beer et al. 1983); Camp Century, Greenland (Beer et al. 1988); Dye 3, Greenland (Beer et al. 1990); Dome Concordia and South Pole, Antarctica (Raisbeck et al. 1990); GRIP, Greenland (Yiou et al. 1997); GISP2, Greenland (Finkel and Nishiizumi 1997); Dome Fuji, Antarctica (Horiuchi et al. 2007, 2008; Miyake et al. 2015); Dronning Maud Land, Antarctica (Ruth et al. 2007); NGRIP (North Greenland Ice Core Project), Greenland (Berggren et al. 2009); NEEM (North Greenland Eemian Ice Drilling), Greenland (Sigl et al. 2015); West Antarctic Ice Sheet Divide Ice Core (WAIS/WDC), Antarctica (Sigl et al. 2015), etc.

We note that data on $^{10}$Be in other archives, e.g., lake sediments, is usually more complicated to interpret because of the potential influence of the climate (Horiuchi et al. 1999; Belmaker et al. 2008).

Details of the $^{10}$Be series and their comparison with each other can be found in Beer (2000), Muscheler et al. (2007), and Beer et al. (2012).

3.3.2 Production

The isotope $^{10}$Be is produced as a result of spallation of atmospheric nitrogen and oxygen (carbon is less abundant in the atmosphere and makes a negligible contribution) by the nucleonic component of the cosmic-ray–induced atmospheric cascade (Sect. 3.1.3).

A small contribution may also exist from photo-nuclear reactions (Bezuglov et al. 2012). The cross section (a few mb) of the spallation reactions is almost independent of the energy of impacting particles and has a threshold of about 15 MeV. Thus, the production of $^{10}$Be is defined mostly by the multiplicity of the nucleonic component, which increases with the energy of primary cosmic rays (see Fig. 9). Maximum production occurs at an altitude of 10–15 km due to a balance between the total energy of the cascade (which increases with altitude) and the number of secondaries (decreasing with altitude). Most of the global $^{10}$Be is produced in the stratosphere (55–70%) and the rest in the troposphere (Lal and Peters 1967; Masarik and Beer 1999, 2009; Usoskin and Kovaltsov 2008b; Kovaltsov and Usoskin 2010).

Computation of $^{10}$Be isotope production is straightforward, provided a model of the atmospheric cascade is available. The first consistent model was developed by D. Lal et al. (Bhandari et al. 1966; Lal and Peters 1967; Lal and Suess 1968), using an empirical approach based on fitting simplified model calculations to measurements of the isotope concentrations and “star” (inelastic nuclear collisions) formations in the atmosphere. Next was an analytical model by O’Brien (1979), who solved the problem of the GCR-induced cascade in the atmosphere using an analytical stationary approximation in the form of the Boltzmann equation. Those models were based on calculating the rate of inelastic collisions or “stars” and then applying the mean spallation yield per “star”. A new step in the modelling of isotope production was made by Masarik and Beer (1999), who performed a full Monte-Carlo simulation of a GCR-initiated cascade in the atmosphere and used cross sections of spallation reactions directly instead of the average “star” efficiency. Modern models (Webber and Higbie 2003; Webber et al. 2007; Usoskin and Kovaltsov 2008b; Kovaltsov and Usoskin 2010; Poluianov et al. 2016) are based on a full Monte-Carlo simulation of the atmospheric cascade, using improved cross sections. The global production rate of $^{10}$Be is about $0.02{\,\textendash \,}0.04\ \mathrm{atoms}\ \mathrm{cm}^{-2}\ \mathrm{s}^{-1}$ (Masarik and Beer 1999; Webber et al. 2007; Kovaltsov and Usoskin 2010; Poluianov et al. 2016), which is lower than that for $^{14}$C (about $2\ \mathrm{atoms}\ \mathrm{cm}^{-2}\ \mathrm{s}^{-1}$; see Sect. 3.2.2) by two orders of magnitude. The yield function of $^{10}$Be production is shown in Fig. 9a and the differential production rate in Fig. 9b. One can see that the peak of $^{10}$Be sensitivity, especially in polar regions, is shifted towards lower energies (below 1 GeV) compared with a neutron monitor. This implies that the $^{10}$Be isotope is relatively more sensitive to less energetic CR and is, therefore, more affected by solar energetic particles (Usoskin et al. 2006b). Comparison of model computations with direct beryllium production experiments (Usoskin and Kovaltsov 2008b; Kovaltsov and Usoskin 2010), and also the results of modelling of the short-living $^{7}$Be isotope (Usoskin et al. 2009a) suggest that some numerical models (Masarik and Beer 1999; Webber and Higbie 2003; Webber et al. 2007) tend to underestimate the production.

Although the production of $^{10}$Be can be more-or-less precisely modelled, a simple normalization “surface”, similar to that shown in Fig. 10 for $^{14}$C, is not easy to produce because of partial mixing in the atmosphere (see Sect. 3.3.3). Simplified models, assuming either only global (e.g., Beer 2000) or polar production (Bard et al. 1997; Usoskin et al. 2004), have been used until recently. However, it has been recognized that a more realistic model of the limited atmospheric mixing should be used. Without detailed knowledge of $^{10}$Be transport in the atmosphere, it is impossible to relate the quantitatively-measured concentration to the production (as done for $^{14}$C using the carbon cycle), and one has to assume that the measured abundance is proportional (with an unknown coefficient) to the production rate in a specific geographical region (see Sect. 3.3.3).

3.3.3 Atmospheric transport

After production, the $^{10}$Be isotope has a seemingly simple (Fig. 7) but difficult-to-account-for fate in the atmosphere. Its atmospheric residence time depends on scavenging, stratosphere-troposphere exchange and inter-tropospheric mixing (e.g., McHargue and Damon 1991). Soon after production, the isotope is thought to become attached to atmospheric aerosols and follows their fate (Beer et al. 2012). In addition, it may be removed from the lower troposphere by wet deposition (rain and snow). The mean residence time of the aerosol-bound radionuclide in the atmosphere is quite different for the troposphere, being a few weeks, and stratosphere, where it is one to two years (Raisbeck et al. 1981). Accordingly, $^{10}$Be produced in the troposphere is deposited mostly locally, i.e., in the polar regions, while stratospheric $^{10}$Be can be partly or totally mixed. In addition, because of the seasonal (usually Spring) intrusion of stratospheric air into the troposphere at mid-latitudes, there is an additional contribution of stratospheric $^{10}$Be. Therefore, the measured $^{10}$Be concentration (or flux) in polar ice is modulated not only by production but also by climate/precipitation effects (e.g., Steig et al. 1996; Bard et al. 1997). This led Lal (1987) to the extreme conclusion that variations of polar $^{10}$Be reflect a meteorological, rather than solar, signal. However, comparison between Greenland and Antarctic $^{10}$Be series and between $^{10}$Be and $^{14}$C data (e.g., Bard et al. 1997; Horiuchi et al. 2008; Beer et al. 2012; Steinhilber et al. 2012) suggests that the beryllium data mostly depicts production variations (i.e., solar signal) on top of which some meteorological effects can be superposed (see also Sect. 3.7.3).

Fig. 13

Wet (a) and dry (b) deposition of $^{10}$Be, computed using the NASA GISS model (Field et al. 2006) for a fixed sea-surface temperature

Since both assumptions of the global and purely-local polar production of $^{10}$Be archived in polar ice are over-simplified, several attempts have been made to overcome this problem. For instance, McCracken (2004) proposed several simple mathematical models of partial atmospheric mixing (without division in the troposphere and stratosphere) and compared them with observed data. From this semi-empirical approach McCracken concluded that M2 (full mixing above $60^{\circ }$ latitude and a limited mixing between $40^{\circ }$ and $60^{\circ }$ latitude) is a reasonable model for Antarctica. Vonmoos et al. (2006) assumed that the production of $^{10}$Be recorded in Greenland is related to the entire hemisphere in the stratosphere (i.e, global stratospheric mixing) but is limited to latitudes above $40^{\circ }$ latitude in the troposphere (partial tropospheric mixing). This approach uses either semi-empirical or indirect arguments in choosing the unknown degree of mixing.

Recent efforts in employing modern atmospheric 3D circulation models for simulations of $^{10}$Be transport and deposition, including realistic air-mass transport and dry-vs-wet deposition (Field et al. 2006; Heikkilä et al. 2008, 2009), look more promising. An example of $^{10}$Be deposition computed on the world grid using the NASA GISS model (Field et al. 2006) is shown in Fig. 13. Precision of the models allows one to distinguish local effects, e.g., for Greenland (Heikkilä et al. 2008). A simulation performed by combining a detailed $^{10}$Be-production model with an air-dynamics model can result in an absolute model relating production and deposition of the radionuclide. The validity and usefulness of this approach has been demonstrated by Usoskin et al. (2009a), who directly modeled production (using the CRAC model—Usoskin and Kovaltsov 2008b) and transport (using the GISS ModelE—Koch et al. 2006) of a short-living beryllium isotope $^{7}$Be and showed that such a combined model is able to correctly reproduce both the absolute level and temporal variations of the $^{7}$Be concentration measured in near ground air around the globe. Keeping in mind the similarity between production and transport of the two beryllium isotopes, $^{7}$Be and $^{10}$Be, this serves as support for the advanced modelling of $^{10}$Be transport. A similar general agreement between measured and modelled seasonal variability has been recently found for $^{10}$Be in an Antarctic ice core (Pedro et al. 2011).

3.3.4 Effect of the geomagnetic field

In order to properly account for geomagnetic changes (Sect. 3.1.2), one needs to know the effective region in which the radionuclide is produced before being stored in the archive analyzed. For instance, if the concentration of $^{10}$Be measured in polar ice reflects mainly the isotope’s production in the polar atmosphere (as, e.g., assumed by Usoskin et al. 2003c), no strong geomagnetic signal is expected to be observed, since the geographical poles are mostly related to high geomagnetic latitudes. On the other hand, assuming global mixing of atmospheric $^{10}$Be before deposition in polar ice (e.g., Masarik and Beer 1999), one expects that only changes in the geomagnetic dipole moment affect will the signal. However, because of partial mixing, which can be different in the stratosphere and troposphere, taking into account migration and displacement of the geomagnetic dipole axis may be essential for a reliable reconstruction of solar variability from $^{10}$Be data (McCracken 2004). Therefore, only a full combination of the transport and production models, the latter explicitly including geomagnetic effects estimated from paleomagnetic reconstructions, can adequately account for geomagnetic changes and separate the solar signal. These forms a new generation of physics-based models for the cosmogenic-isotope proxy method. We note that paleomagnetic data should ideally not only provide the dipole moment (VADM or VDM) but should also provide estimates of the geomagnetic axis attitude and displacement of the dipole center (Korte et al. 2011).

3.4 Other potential proxy

An interesting new potential proxy for solar activity (or cosmic ray) variability on the long-term centennial-to-millennial time scale has been proposed recently by Traversi et al. (2012). This is the nitrate content in a polar ice core Talos Dome in Antarctica, which has a favorite location in the sense of snow accumulation and conservation of such volatile specie as nitrate. Nitrate-related species are partly produced in the stratosphere/troposphere as a result of the ionization of the atmospheric air by cosmic rays and, partly, via terrestrial sources (e.g., lightnings) and are subject to air transport (Rozanov et al. 2012). As shown by Traversi et al. (2012), the nitrate concentration/flux measured in the Talos Dome ice core for the Holocene period agrees well with the cosmogenic data of $^{14}$C in tree rings and $^{10}$Be in both Antarctic and Greenland ice cores, on the time scales from centennia to millennia. Due to the large errors of the ice core dating, 200–300 years (Schüpbach et al. 2011), shorter time scales cannot be considered. The level of the nitrate variability is generally consistent with that predicted by theoretical models assuming its production by GCR in the atmosphere (Semeniuk et al. 2011; Rozanov et al. 2012). The ability of nitrate to catch up long-term cosmic ray variability has been confirmed also by an analysis of nitrate and $^{10}$Be data for the Laschamp event ca. 40 kyears ago (Traversi et al. 2016). Thus, the nitrate in an ice core provides a potential to become a new proxy of long-term solar activity, with independent atmospheric fate, which would strengthen the robustness of the reconstructions. However, an independent confirmation of the result and a more detailed model are needed before it can serve as a new quantitative proxy. Note that the mechanism of the nitrate production and transport is not related to the possible nitrate peaks claimed to be caused by strong solar energetic-particle events (see Sect. 5.3).

3.5 Towards a quantitative physical model

Several methods have been developed historically to convert measured cosmogenic-isotope data into a solar activity index, ranging from very simple regressions to physics-based models. A new step in long-term solar-activity reconstruction has been made recently, which is the development of the proxy method in which physics-based models are used, instead of a phenomenological regression, to link SN with cosmogenic-isotope production (Usoskin et al. 2003c, 2007, 2014, 2016a; Solanki et al. 2004; Vonmoos et al. 2006; Muscheler et al. 2007; Steinhilber et al. 2012). Due to recent theoretical developments, it is now possible to construct a chain of physical models to model the entire relationship between solar activity and cosmogenic data. A multi-proxy approach based on different cosmogenic proxy data combined in a joint reconstruction is progressive (Steinhilber et al. 2012).

The physics-based reconstruction of solar activity (in terms of sunspot numbers) from cosmogenic proxy data includes several steps:

• Computation of the isotope’s production rate in the atmosphere from the measured concentration in the archive (Sects. 3.2.2 and 3.3.2);

• Computation, considering independently-known secular geomagnetic changes (see Sect. 3.2.5) and a model of the CR-induced atmospheric cascade, of the GCR spectrum parameter quantified via the modulation potential $\phi$ (Sect. 3.5.2), some reconstructions being terminated at this point;

• Computation of a heliospheric index, whether of the open solar magnetic flux or of the average HMF intensity at the Earth’s orbit (Sect. 3.5.2)

• Computation of a solar index (sunspot number series), corresponding to the above-derived heliospheric parameter (Sect. 3.5.3).

Presently, all these steps can be completed using appropriate models. Some models stop after computations of the modulation potential as its translation into the solar index may include additional uncertainties. Although the uncertainties of the models may be considerable, the models allow a full basic quantitative reconstruction of solar activity in the past. However, much needs to be done, both theoretically and experimentally, to obtain an improved reconstruction.

3.5.1 Regression models

Mathematical regression is the most apparent and often used (even recently) method of solar-activity reconstruction from proxy data (see, e.g., Stuiver and Quay 1980; Ogurtsov 2004). The reconstruction of solar activity is performed in two consecutive steps. First, a phenomenological regression (either linear or nonlinear) is built between a proxy data set and a direct solar-activity index for the available “training” period (e.g., since 1750 for WSN or since 1610 for GSN). Then this regression is extrapolated backwards to evaluate SN from the proxy data. The main shortcoming of the regression method is that it depends on the time resolution and choice of the “training” period. The former is illustrated by Fig. 14, which shows the scatter plot of the $^{10}$Be concentration versus GSN for the annual and 11-year smoothed data. One can see that the slope of the $^{10}$Be-vs-GSN relation (about –500 g/atom) within individual cycles is significantly different from the slope of the long-term relation (about –100 g/atom), i.e., individual cycles do not lie on the line of the 11-year averaged cycles. Moreover, the slope of the regression for individual 11-year cycles varies essentially depending on the solar activity level. Therefore, a formal regression built using the annual data for 1610–1985 yields a much stronger GSN-vs-$^{10}$Be dependence than for the cycle-averaged data (see Fig. 14b), leading to a potentially-erroneous evaluation of the sunspot number from the $^{10}$Be proxy data.

Fig. 14

Scatter plot of smoothed group sunspot numbers versus (2-year delayed) $^{10}$Be concentration. a Annual (connected small dots) and 11-year averaged (big open dots) values. b Best-fit linear regressions between the annual (dashed line) and 11-year averaged values (solid line). The dots are the same as in panel (a). (After Usoskin and Kovaltsov 2004)

It is equally dangerous to evaluate other solar/heliospheric/terrestrial indices from sunspot numbers by extrapolating an empirical relation obtained for the last few decades back in time. This is because the last decades (after the 1950s), which are well covered by direct observations of solar, terrestrial and heliospheric parameters, corresponded to a very high level of solar activity. After a steep rise in activity level between the late 19th and mid 20th centuries, the activity remained at a roughly constant high level, being totally dominated by the 11-year cycle without a long-term trends. Accordingly, all empirical relations built based on data for this period are focused on the 11-year variability and can overlook possible long-term trends (Mursula et al. 2003). This may affect all regression-based reconstructions, whose results cannot be independently (directly or indirectly) tested. In particular, this may be related to solar irradiance reconstructions, which are often based on regression-like models, built and verified using data for the last three solar cycles, when there was no strong trend in solar activity.

Fig. 15

An unsuccessful attempt of the reconstruction of cosmic-ray intensity in the past using a regression with sunspot numbers. Dots represent the observed cosmic-ray intensity since 1951. Note the absence of a long-term trend. Image reproduced by permission from Belov et al. (2006), copyright by Elsevier

As an example let us consider an attempt (Belov et al. 2006) to reconstruct cosmic-ray intensity since 1610 from sunspot numbers using a (nonlinear) regression. The regression between the count rate of a neutron monitor and sunspot numbers (Fig. 4), established for the last 50 years is highly significant. Based on that, Belov et al. (2006) extrapolated the regression back in time to produce a reconstruction of cosmic-ray intensity (quantified in NM count rate) to 1560 (see Fig. 15). One can see that there is no notable long-term trend in the reconstruction, and the fact that all CR maxima essentially lie at the same level, from the Maunder minimum to modern times, is noteworthy. It would be difficult to dispute such a result if there was no direct test for CR levels in the past. Independent reconstructions based on cosmogenic isotopes or theoretical considerations (e.g., Usoskin et al. 2002a; Scherer et al. 2004; Scherer and Fichtner 2004; McCracken and Beer 2007) provide clear evidence that cosmic-ray intensity was essentially higher during the Maunder minimum than nowadays. This example shows how easy it is to overlook an essential feature in a reconstruction based on a regression extrapolated far beyond the period it is based on. Fortunately, for this particular case we do have independent information that can prevent us from making big errors. In many other cases, however, such information does not exist (e.g., for total or spectral solar irradiance), and those who make such unverifiable reconstructions should be careful about the validity of their models beyond the range of the established relations.

3.5.2 Reconstruction of heliospheric parameters

The modulation potential $\phi$ (see Sect. 3.1.1) is directly related to cosmogenic isotope production in the atmosphere. It is a parameter describing the spectrum of galactic cosmic rays (see the definition and full description of this index in Usoskin et al. 2005) in the force-field approximation and is sometimes used as a stand-alone index of solar (or, actually, heliospheric) activity. We note that, provided the isotope production rate Q is estimated and geomagnetic changes can be properly accounted for, it is straightforward to obtain a time series of the modulation potential, using, e.g., the relation shown in Fig. 10.

Several reconstructions of modulation potential for the last few millenia are shown in Fig. 16. While being quite consistent in the relative changes, they differ in the absolute level and fine details, mostly because of the ambiguity of the exact value of the modulation potential (see discussion in Sect. 3.1.1).

Reconstructions of solar activity often end at this point, representing solar activity by the modulation potential, as some authors (e.g., Beer et al. 2003; Vonmoos et al. 2006; Muscheler et al. 2007) believe that further steps (see Sect. 3.5.3) may introduce additional uncertainties. However, since $\phi$ is a heliospheric, rather than solar, index, the same uncertainties remain when using it as an index of solar activity. Moreover, the modulation potential is a model-dependent quantity (see discussion in Sect. 3.1.1) and therefore does not provide an unambiguous measure of heliospheric activity. In addition, the modulation potential is not a physical index but rather a formal fitting parameter to describe the GCR spectrum near Earth and, thus, is not a universal solar-activity index.

Fig. 16

Two reconstructions of the smoothed modulation potential $\phi$ for the last few decades: 22-year smoothed reconstruction (Steinhilber et al. 2012) based on a composition of $^{14}$C and $^{10}$Be data (blue dotted curve) and a 10-year averaged reconstruction (Usoskin et al. 2014) based on $^{14}$C data (red curve). Error bars (roughly 50–100 MV for each curve) are not shown

Modulation of GCR in the heliosphere (see Sect. 3.1.1) is mostly defined by the turbulent heliospheric magnetic field (HMF), which ultimately originates from the sun and is thus related to solar activity. It has been shown, using a theoretical model of the heliospheric transport of cosmic rays (e.g., Usoskin et al. 2002a), that on the long-term scale (beyond the 11-year solar cycle) the modulation potential $\phi$ is closely related to the open solar magnetic flux $F_{o}$, which is a physical quantity describing the solar magnetic variability (e.g., Solanki et al. 2000; Krivova et al. 2007).

Sometimes, instead of the open magnetic flux, the mean HMF intensity at Earth orbit, B, is used as a heliospheric index (Caballero-Lopez and Moraal 2004; McCracken 2007; Steinhilber et al. 2010). Note that B is linearly related to $F_{o}$ assuming constant solar-wind speed, which is valid on long-term scales. An example of HMF reconstruction for the last 600 years is shown in Fig. 17. In addition, the count rate of a “pseudo” neutron monitor (i.e., a count rate of a neutron monitor if it was operated in the past) is considered as a solar/heliospheric index (e.g., Beer 2000; McCracken and Beer 2007).

Fig. 17

An example of reconstruction of the heliospheric magnetic field at Earth orbit for the last 600 years from $^{10}$Be data. Image reproduced by permission from McCracken (2007), copyright by AGU

3.5.3 A link to sunspot numbers

The open solar magnetic flux $F_{o}$ described above is related to the solar surface magnetic phenomena such as sunspots or faculae. Modern physics-based models allow one to calculate the open solar magnetic flux from data of solar observation, in particular sunspots (Solanki et al. 2000, 2002; Krivova et al. 2007; Owens et al. 2012) or geomagnetic activity indices (Lockwood et al. 2014b). Besides the solar active regions, the model includes ephemeral regions. Although these models are based on physical principals, they contain some unknowns like the decay time of the open flux, which cannot be measured or theoretically calculated and has to be found by means of fitting the model to data. This free parameter has been determined by requiring the model output to reproduce the best available data sets for the last 30 years with the help of a genetic algorithm. Inversion of the model, i.e., the computation of sunspot numbers for given $F_{o}$ values is formally a straightforward solution of a system of linear differential equations, however, the presence of noise in the real data makes it only possible in a numerical-statistical way (see, e.g., Usoskin et al. 2004, 2007). By inverting this model one can compute the sunspot-number series corresponding to the reconstructed open flux, thus forging the final link in a chain quantitatively connecting solar activity to the measured cosmogenic isotope abundance. A sunspot-number series reconstructed for the Holocene using $^{14}$C isotope data is shown in Fig. 18.

Fig. 18

Long-term sunspot-number reconstruction from $^{14}$C data with error bars (after Usoskin et al. 2016a). Group sunspot numbers (Hoyt and Schatten 1998) are shown after 1610

As very important for the climate research, the variations of the total solar irradiance (TSI) are sometimes reconstructed from the solar proxy data (Steinhilber et al. 2009; Vieira et al. 2011). However, the absolute range of the TSI variability on the centennial-millennial time scales still remains unknown (Schmidt et al. 2012).

3.6 Solar activity reconstructions

Detailed computational models of cosmogenic isotope production in the atmosphere (e.g., Masarik and Beer 1999) have opened up a new possibility for long-term solar-activity reconstruction (e.g., Beer 2000). The first quantitative reconstructions of solar activity from cosmogenic proxy appeared in the early 2000s based on $^{10}$Be deposited in polar ice (Beer et al. 2003; Usoskin et al. 2003c).

Beer et al. (2003) reconstructed the modulation potential on a multi-millennial timescale using the model computations by Masarik and Beer (1999) and the $^{10}$Be data from the GISP2 core in Greenland. This result has been extended, even including the $^{14}$C data set, and presently covers the whole Holocene (Vonmoos et al. 2006; Steinhilber et al. 2010, 2012). Usoskin et al. (2003c) presented a reconstruction of sunspot activity over the last millennium, based on $^{10}$Be data from both Greenland and Antarctica, using a physics-based model described in detail in Usoskin et al. (2004). This result reproduces the four known grand minima of solar activity—Maunder, Spörer, Wolf and Oort minima (see Sect. 4.2). Later Solanki et al. (2004) reconstructed 10-year–averaged sunspot numbers from the $^{14}$C content in tree rings throughout the Holocene and estimated its uncertainties. This result was disputed by Muscheler et al. (2005), whose concurrent model, however, rested on an erroneous normalization, as argued in Solanki et al. (2005). A full revision of the benchmark reconstruction (Solanki et al. 2004), using newer paleomagnetic data, an updated open solar flux model Krivova et al. (2007), and a revised radiocarbon production model (Kovaltsov et al. 2012), has made recently (Usoskin et al. 2014, 2016a). The most recent $^{14}$C-based reconstruction of solar activity is shown in Fig. 18.

Reconstruction of the HMF from $^{10}$Be data has been performed by Caballero-Lopez and Moraal (2004), using a model of CR modulation in the heliosphere and a $^{10}$Be production model by Webber and Higbie (2003). It was revised (McCracken 2007) to present a detailed reconstruction of HMF intensity since 1428. A recent reconstruction of the heliospheric modulation potential was done by Steinhilber et al. (2012) using the combined principal component analysis of several data sets.

The obtained results are discussed in Sect. 4.

3.7 Verification of reconstructions

Because of the diversity of the methods and results of solar-activity reconstruction, it is vitally important to verify them. Even though a full verification is not possible, there are different means of indirect or partial verification, as discussed below. Several solar-activity reconstructions on the millennium timescale, which differ from each other to some degree and are based on terrestrial cosmogenic isotope data, have been published by various groups. Also, they may suffer from systematic effects. Therefore, there is a need for an independent method to verify/calibrate these results in order to provide a reliable quantitative estimate of the level of solar activity in the past, prior to the era of direct observations.

3.7.1 Comparison with direct data

The most direct verification of solar-activity reconstruction is a comparison with the actual GSN sunspot data for the last few centuries. However, regression-based models (see Sect. 3.5.1) cannot be tested in this way, since it would require a long set of independent direct data outside the “training” interval. It is usual to include all available data into the “training” period to increase the statistics of the regression, which rules out the possibility of testing the model. On the other hand, such a comparison to the actual GSN since 1610 can be regarded as a direct test for a physics-based model since it does not include phenomenological links over the same time interval. The period of the last four centuries is pretty good for testing purposes since it includes the whole range of solar activity levels from the nearly spotless Maunder minimum to the modern period of a very active sun. However, because of the uncertainties in the sunspot number series (see Sect. 2.2.1), this method shows only an approximate agreement, and direct sunspot numbers cannot serve as the ultimate basis to verify the cosmogenic-based reconstructions. On the contrary, the latter can be used to verify the sunspot number data.

Models focused on the reconstruction of heliospheric parameters (HMF or the modulation potential $\phi$) cannot be verified in this manner since no heliospheric data exists before the middle of the twentieth century. Comparison to direct cosmic-ray data after the 1950s (or, with caveats, after the 1930s—McCracken and Beer 2007) is less conclusive, since the latter are of shorter length and correspond to a period of high solar activity, leading to larger uncertainties during grand minima. Moreover, $^{14}$C data cannot be tested in this way because of the anthropogenic (Suess) effect and nuclear tests (Sect. 3.2.4).

It is important that some (semi)empirical relations forming the basis for the proxy method are established for the recent decades of high solar activity. The end of the Modern grand maximum of activity and the current moderate level of activity, characterized by the highest ever observed cosmic ray flux as recorded by ground-based neutron monitors, the very low level of the HMF and geomagnetic activity, should help to verify the connections between solar activity, cosmic ray fluxes, geomagnetic activity, the heliospheric magnetic field, and open field. Since some of these connections are somewhat controversial, these extreme conditions should help to quantify them better.

3.7.2 Meteorites and lunar rocks: A direct probe of the galactic cosmic-ray flux

Another more-or-less direct test of solar/heliospheric activity in the past comes from cosmogenic isotopes measured in lunar rock or meteorites. Cosmogenic isotopes, produced in meteoritic or lunar rocks during their exposure to CR in interplanetary space, provide a direct measure of cosmic-ray flux. Uncertainties due to imprecisely known terrestrial processes, including the geomagnetic shielding and redistribution process, are naturally avoided in this case, since the nuclides are directly produced by cosmic rays in the body of the rock, where they remain until they are measured, without any transport or redistribution. The activity of a cosmogenic isotope in meteorite/lunar rock corresponds to an integral of the balance between the isotope’s production and decay, thus representing the time-integrated CR flux over a period determined by the mean life of the radioisotope. The results of different analyses of measurements of cosmogenic isotopes in meteoritic and lunar rocks show that the average GCR flux remained roughly constant—within 10% over the last million years and within a factor of 1.5 for longer periods of up to $10^{9}$ years (e.g., Vogt et al. 1990; Grieder 2001).

By means of measuring the abundance of relatively short-lived cosmogenic isotopes in meteorites, which fell through the ages, one can evaluate the variability of the CR flux, since the production of cosmogenic isotopes ceases after the fall of the meteorite. A nearly ideal isotope for studying centurial-scale variability is $^{44}$Ti with a half-life of $59.2 \pm 0.6$ years (a lifetime of about 85 years). The isotope is produced in nuclear interactions of energetic CR with nuclei of iron and nickel in the body of a meteorite (Bonino et al. 1995; Taricco et al. 2006). Because of its mean life, $^{44}$Ti is relatively insensitive to variations in cosmic-ray flux on decadal (11-year Schwabe cycle) or shorter timescales, but is very sensitive to the level of CR flux and its variations on a centurial scale. Using a full model of $^{44}$Ti production in a stony meteorite (Michel and Neumann 1998) and data on the measured activity of cosmogenic isotope $^{44}$Ti in meteorites, which fell during the past 235 years (Taricco et al. 2006), provides a method to test, in a straightforward manner, reconstructions of solar activity after the Maunder minimum. First, the expected $^{44}$Ti activity needs to be calculated from the reconstructed series using the modulation potential, and then compared with the results of actual measurements (see Fig. 19). Since the life-time of the $^{44}$Ti is much longer than the 11-year cycle, this method does not allow for the reconstruction of solar/heliospheric activity, but it serves as a direct way to test existing reconstructions independently. As shown by Usoskin et al. (2006c), the $^{44}$Ti data confirms significant secular variations of the solar magnetic flux during the last century (cf. Lockwood et al. 1999; Solanki et al. 2000; Wang et al. 2005). Moreover, the recent sunspot number reconstructions yielding high solar activity during the 17th and 18th appear inconsistent with the data of $^{44}$Ti in meteorites (Fig. 19).

Fig. 19

Time profile of the $^{44}$Ti activity measured (grey dots with error bars) in the meteorites fallen during the last 250 years (Taricco et al. 2006). The red and blue colored curves with the $1\sigma$ model uncertainties (hatched areas) depict the modelled $^{44}$Ti activity computed for “high” (e.g., Svalgaard and Schatten 2016) and “low” (e.g., Hoyt and Schatten 1998; Usoskin et al. 2016b) reconstructions of solar activity, respectively. Modified after Asvestari et al. (2017)

3.7.3 Comparison between isotopes

As an indirect test of the solar-activity reconstruction, one can compare different isotopes. The idea behind this test is that two isotopes, $^{14}$C and $^{10}$Be, have essentially different terrestrial fates, so that only the production signal, namely, solar modulation of cosmic rays, can be regarded as common in the two series. Processes of transport/deposition are different (moreover, the $^{14}$C series is obtained as an average of the world-wide–distributed samples). The effect of changing geomagnetic fields is also different (although not completely) for the two isotopes, since radiocarbon is globally mixed, while $^{10}$Be is only partly mixed before being stored in an archive. Even comparison between data of the same $^{10}$Be isotope, but measured in far-spaced ice cores (e.g., Greenland and Antarctica), may help in separating climatic and extraterrestrial factors, since meteorology in the two opposite polar areas is quite different.

The first thorough consistent comparison between $^{10}$Be and $^{14}$C records for the last millennium was performed by Bard et al. (1997). They assumed that the measured $^{10}$Be concentration in Antarctica is directly related to CR variations. Accordingly, $^{14}$C production was considered as proportional to $^{10}$Be data. Then, applying a 12-box carbon-cycle model, Bard et al. (1997) computed the expected $\varDelta ^{14}$C synthetic record. Finally, these $^{10}$Be-based $\varDelta ^{14}$C variations were compared with the actual measurements of $\varDelta ^{14}$C in tree rings, which depicted a close agreement in the profile of temporal variation (coefficient of linear correlation $r = 0.81$ with exact phasing). Despite some fine discrepancies, which can indicate periods of climatic influence in either (or both) of the series, that result has clearly proven the dominance of solar modulation of cosmogenic nuclide production variations during the last millennium. This conclusion has been confirmed (e.g., Usoskin et al. 2003c; Muscheler et al. 2007) in the sense that quantitative solar-activity reconstructions, based on $^{10}$Be and $^{14}$C data series for the last millennium, yield very similar results, which differ only in small details. However, a longer comparison over the entire Holocene timescale suggests that, while centennial variations of solar activity reconstructed from the two isotopes are very close to each other, there might be a discrepancy in the very long-term trend (Vonmoos et al. 2006; Inceoglu et al. 2015; Usoskin et al. 2016a), whose nature is not clear (climate changes, geomagnetic effects or model uncertainties).

Recently, Usoskin et al. (2009b) studied the dominance of the solar signal in different cosmogenic isotope data on different time scales. They compared the expected $^{10}$Be variations computed from $^{14}$C-based reconstruction of cosmic ray intensity with the actually measured $^{10}$Be abundance at the sites and found that: (1) There is good agreement between the $^{14}$C and $^{10}$Be data sets, on different timescales and at different locations, confirming the existence of a common solar signal in both isotope data; (2) The $^{10}$Be data are driven by the solar signal on timescales from about centennial to millennial time scales; (3) The synchronization is lost on short (${<}100$ years) timescales, either due to local climate or chronological uncertainties (Delaygue and Bard 2011) but the solar signal becomes important even at short scales during periods of Grand minima of solar activity, (4) There is an indication of a possible systematic uncertainty in the early Holocene (cf. Vonmoos et al. 2006; Inceoglu et al. 2015; Usoskin et al. 2016a), likely due to a not-perfectly-stable thermohaline circulation. Overall, both $^{14}$C- and $^{10}$Be-based records are consistent with each other over a wide range of timescales and time intervals.

Thus, comparison of the results obtained from different sources implies that the variations of cosmogenic nuclides on the long-term scale (centuries to millennia) during the Holocene are primarily defined by the solar modulation of CR.

3.8 Composite reconstruction

Most of the earlier solar activity reconstructions are based on single proxy records, either $^{14}$C or $^{10}$Be. Although they are dominated by the same production signal, viz. solar activity, (see Sect. 3.7.3), they still contain essential fractions of noise.

A promising first step in the direction of extracting the common solar signal from different proxy records was made by Steinhilber et al. (2012) who combined, in a composite reconstruction, different $^{10}$Be ice core records from Greenland and Antarctica with the global $^{14}$C tree ring record. The composite was made in a mathematical way, using the principal component analysis as a numerical tool. This analysis formally finds the common variability in different series, that is assumed to be the solar signal. However, since the used mathematical tool can only work with the relative variability, the reconstruction also yields the relative values rather than absolute values, and it is not available in the terms of sunspot numbers. A particular problem with the composite series is related to the dating uncertainty of $^{10}$Be. While $^{14}$C data are ‘absolutely’ dated via dendrochronology, the uncertainties in the ice core dating make the $^{10}$Be series loose by up to 80 years in the earlier Holocene (Adolphi and Muscheler 2016). Accordingly, the series should be either heavily smoothed, as done by Steinhilber et al. (2012) or corrected for the dating errors, before applying a composite analysis.

A full physics-based multi-proxy composite reconstruction of the solar activity on the millennial time scale is still pending.

3.9 Summary

In this section, a proxy method of past–solar-activity reconstruction is described in detail.

This method is based on the use of indirect proxies of solar activity, i.e., quantitative parameters, which can be measured now, but represent signatures, stored in natural archives, of the different effects of solar magnetic activity in the past. Such traceable signatures can be related to nuclear or chemical effects caused by cosmic rays in the Earth’s atmosphere, lunar rocks or meteorites. This approach allows one to obtain homogeneous data sets with stable quality and to improve the quality of data when new measurement techniques become available. It provides the only possible regular indicator of solar activity on a very long-term scale.

The most common proxy of solar activity is formed by data of the cosmogenic radionuclides, $^{10}$Be and $^{14}$C, produced by cosmic rays in the Earth’s atmosphere. After a complicated transport in the atmosphere, these cosmogenic isotopes are stored in natural archives such as polar ice, trees, marine sediments, from where they can now be measured. This process is also affected by changes in the geomagnetic field and the climate.

Radioisotope $^{14}$C, measured in independently-dated tree rings, forms a very useful proxy for long-term solar-activity variability. It participates in the complicated carbon cycle, which smoothes out spatial and short-term variability of isotope production. For the Holocene period, with its stable climate, it provides a useful tool for studying solar activity in the past. Existing models allow the quantitative conversion between the measured relative abundance of $^{14}$C and the production rate in the atmosphere. The use of radiocarbon for earlier periods, the glacial and deglaciation epochs, is limited by severe climate and ocean ventilation changes. Radiocarbon data cannot be used after the end of the nineteenth century because of the Suess effect and atmospheric nuclear tests.

Another solar activity proxy is the cosmogenic $^{10}$Be isotope measured in stratified polar ice cores. Atmospheric transport of $^{10}$Be is relatively straightforward, but its details are as of yet unresolved, leading to the lack of a reliable quantitative model relating the measured isotope concentration in ice to the atmospheric production. Presently, it is common to assume that the production rate is proportional, with an unknown coefficient, to the measured concentration. However, a newly-developed generation of models, which include 3D atmospheric-circulation models, will hopefully solve this problem soon.

Recently, a new proxy, nitrate concentration measured in an Antarctic ice core, has been proposed for long-term solar activity reconstructions, but it still needs verification and model support.

Modern physics-based models make it possible to build a chain, which quantitatively connects isotope production rate and sunspot activity, including subsequently the GCR flux quantified via the modulation potential, the heliospheric index, quantified via the open solar magnetic flux or the average HMF intensity at the Earth’s orbit, and finally the sunspot-number series. Presently, all these steps can be made using appropriate models allowing for a full basic quantitative reconstruction of solar activity in the past. The main uncertainties in the solar-activity reconstruction arise from paleo-magnetic models and the overall normalization.

An independent verification of the reconstructions, including direct comparison with sunspot numbers, cosmogenic isotopes in meteorites and the comparison of different models with each other, confirms their veracity in both relative variations and absolute level. It also implies that the variations in cosmogenic nuclides on the long-term scale (centuries to millennia) during the Holocene are primarily defined by the solar modulation of CR.

4 Variability of solar activity over millennia

Several reconstructions of solar activity on multi-millennial timescales have been performed recently using physics-based models (see Sect. 3) from measurements of $^{14}$C in tree rings and $^{10}$Be in polar ice. In this section we discuss the temporal variability of thus-reconstructed solar activity on a longer scale.

Here we consider the $^{14}$C-based decade reconstruction (Usoskin et al. 2016a) of sunspot numbers (shown in Fig. 20). It is identical to that shown in Fig. 18, but is split into two panels for better visibility and highlights the identified grand minima and maxima of solar activity. This series forms the basis for the forthcoming analysis, while differences related to the use of other reconstructions are discussed.

Fig. 20

Sunspot activity (decadal data) throughout the Holocene, reconstructed from $^{14}$C by Usoskin et al. (2016a). Blue circles and red stars denote grand minima and maxima, respectively

4.1 Quasi-periodicities and characteristic times

Although the variability of solar activity in Fig. 20 looks random at first look, some weak quasi-periodicities can be suggested, as discussed in Sect. 2.4. A simple periodicity analysis yields several peaks in the range of periods between 80 and 150 years (cf., Peristykh and Damon 2003), corresponding to the frequency band of the Gleissberg cycle (Ogurtsov et al. 2002). The de Vries/Suess cycle, with a period of about 210 years, forms a prominent in the power spectrum, but it is intermittent and tends to become strong with around 2400 clustering time (Usoskin and Kovaltsov 2004). Another variation with a period of around 350 years can be observed after 6000 BC (cf. Steinhilber et al. 2012). Variations with a characteristic time of 600–700 years are intermittent and can be hardly regarded as a typical feature of solar activity. There is also a weak millennial quasi-periodicity with the period of 1000–1200 years called Eddy cycle (Steinhilber et al. 2012). Of special interest is the 2000–2400 year Hallstatt cycle (see, e.g., Vitinsky et al. 1986; Damon and Sonett 1991; Vasiliev and Dergachev 2002), which is relatively stable and mostly manifests itself as a modulation of long-term solar activity, leading to the clustering of grand minima (Usoskin et al. 2016a). Although its possible terrestrial origin (geomagnetic or climate) was discussed earlier (Vasiliev and Dergachev 2002; Vasiliev et al. 2012), it is shown by Usoskin et al. (2016a) to have solar origin. In particular, grand minima and maxima tend to cluster around highs and lows of the Hallstatt cycle.

4.2 Grand minima of solar activity

A very particular type of solar activity is the grand minimum, when solar activity is greatly reduced. The most famous is the Maunder minimum in the late seventeenth century, which is discussed below in some detail (for details see Soon and Yaskell 2003; Usoskin et al. 2015). Grand minima are believed to correspond to a special state of the dynamo (Sokoloff 2004; Miyahara et al. 2006b; Moss et al. 2008; Käpylä et al. 2016), and its very existence poses a challenge for the solar-dynamo theory. It is noteworthy that dynamo models do not agree on how often such episodes occur in the sun’s history and whether their appearance is regular or random. For example, the commonly used mean-field dynamo yields a fairly-regular 11-year cycle (Charbonneau 2010), while dynamo models including a stochastic driver predict the intermittency of solar magnetic activity (Choudhuri 1992; Schüssler et al. 1994; Schmitt et al. 1996; Ossendrijver 2000; Weiss and Tobias 2000; Mininni et al. 2001; Charbonneau 2001). Most of the models predict purely random occurrence of the grand minima, without any intrinsic long-term memory (Moss et al. 2008). Although cosmogenic isotope data suggest the possible existence of such memory (Usoskin et al. 2007), statistics is not sufficient to distinguish between the two cases (Usoskin et al. 2009d).

4.2.1 The Maunder minimum

The Maunder minimum (MM) is a representative of grand minima in solar activity (e.g., Eddy 1976), when sunspots have almost completely vanished from the solar surface, while the solar wind kept blowing, although at a reduced pace (Cliver et al. 1998; Usoskin et al. 2001b). As proposed by Lockwood and Owens (2014), the solar wind was uniform and slow, 250–275 km/s, nearly half of the modern time velocity. There is some uncertainty in the definition of the duration of MM: the “formal” duration is 1645–1715 (Eddy 1976), while its deep phase with the absence of apparent sunspot cyclic activity is often considered as 1645–1700, with the low, but very clear, solar cycle of 1700–1712 being ascribed to a recovery or transition phase (Usoskin et al. 2000). MM was amazingly well covered by direct sunspot observations (Hoyt and Schatten 1996)—more than 95% of days have formal records (however many of them are generic) and 30–50% of days have explicit data (Vaquero et al. 2015). The late part of MM after the 1680s is particularly weel covered with direct data from the French school of astronomy (Ribes and Nesme-Ribes 1993). On the other hand, sunspots appeared rarely (during $\sim$2% of the days) and seemingly sporadically, without an indication of the 11-year cycle.

Some recent studies suggested that the sunspot activity level might have been underestimated during MM: Zolotova and Ponyavin (2015) proposed that the annual number of sunspot groups was as high as 3–8 (the sunspot number 50–100) during MM, Svalgaard and Schatten (2016) proposed much more modest peak annual number of sunspot groups as 2–3 (25 – 40 in sunspot number) but still too high. These claims were based on the fact that original data include many generic statements of the absence of sunspots for long periods of time, and should be dismissed. However, these statements made by professional astronomers in a dedicated monitoring of the sun, should be considered seriously. A thorough analysis of all the available sunspot data made by applying ‘filters’ of different degrees of strictness was made by Vaquero et al. (2015) who concluded that the level of sunspot activity was indeed very low during MM, even if considering only explicit records. The low level of activity during MM was confirmed also by an aggregate study of other indirect data for that period (Usoskin et al. 2015): while there are known auroral observations during MM, they all are limited to high latitudes (close to the auroral oval), where polar lights occur even without strong geomagnetic storms; data of cosmogenic isotopes $^{14}$C measured in tree trunks and $^{44}$Ti in fallen meteorites clearly indicate a very high flux of cosmic rays (low solar activity) during MM.

Such low level of activity makes it almost impossible to apply standard methods of time-series analysis to sunspot data during MM (e.g., Frick et al. 1997). Therefore, special methods such as the distribution of spotless days versus days with sunspots (e.g., Harvey and White 1999; Kovaltsov et al. 2004; Vaquero et al. 2014) or an analysis of sparsely-occurring events (Usoskin et al. 2000) should be applied in this case. Using these methods, Usoskin et al. (2001b) have shown that sunspot occurrence during the Maunder minimum was gathered into two large clusters (1652–1662 and 1672–1689), with the mass centers of these clusters being in 1658 and 1679–1680. Together with the sunspot maxima before (1640) and after (1705) the deep Maunder minimum, this implies a dominant 22-year periodicity in sunspot activity throughout the Maunder minimum (Mursula et al. 2001), with a subdominant 11-year cycle emerging towards the end of the Maunder minimum (Ribes and Nesme-Ribes 1993; Mendoza 1997; Usoskin et al. 2000; Vaquero et al. 2015) and becoming dominant again after 1700. Similar behavior of a dominant 22-year cycle and a weak subdominant Schwabe cycle during the Maunder minimum has been found in other indirect solar proxy data: auroral occurrence (Křivský and Pejml 1988; Schlamminger 1990; Silverman 1992) and $^{14}$C data (Stuiver and Braziunas 1993; Kocharov et al. 1995; Peristykh and Damon 1998; Miyahara et al. 2006b). This is in general agreement with the concept of “immersion” of 11-year cycles during the Maunder minimum (Vitinsky et al. 1986, and references therein). This concept means that full cycles cannot be resolved and sunspot activity only appears as pulses around cycle-maximum times.

An analysis of $^{10}$Be data (Beer et al. 1998) implied that the 11-year cycle was weak but fairly regular during the Maunder minimum, but its phase was inverted (Usoskin et al. 2001b). A recent theoretical study (Owens et al. 2012; Wang and Sheeley 2012) confirms that such a phase change between cosmic rays and solar activity can indeed appear for very weak cycles.

Until recently, it was believed (Vitinsky et al. 1986; Ribes and Nesme-Ribes 1993; Sokoloff and Nesme-Ribes 1994; Usoskin et al. 2000, 2001b; Miyahara et al. 2006b) that transition from the normal high activity to the deep minimum did not have any apparent precursor before MM. However, newly recovered data suggest that the start of the Maunder minimum might had been not very sudden but via a regular cycle of reduced height (Vaquero et al. 2011). A 22-year cycle was dominant in sunspot occurrence during the deep minimum (1645–1700), with the subdominant 11-year cycle, which became visible only in the late phase of the Maunder minimum. There is an indication that the length of solar cycle may slightly extend during and already slightly before a grand minimum (Miyahara et al. 2004; Nagaya et al. 2012), which is in agreement (note that the possible cycle maximum in 1650 discussed there was based on an erroneous data point and should be dismissed) with the results by Vaquero et al. (2015).

The 11-year Schwabe cycle started dominating solar activity after 1700. Recovery of sunspot activity from the deep minimum to normal activity was gradual, passing through a period of nearly-linear amplification of the 11-year cycle.

Although the Maunder minimum is the only one with available direct sunspot observations, its predecessor, the Spörer minimum from 1450–1550, is covered by precise bi-annual measurements of $^{14}$C (Miyahara et al. 2006a). An analysis of this data (Miyahara et al. 2006a, b) reveals a similar pattern with the dominant 22-year cycle and suppressed 11-year cycle, thus supporting the idea that the above general scenario may be typical for a grand minimum. A similar pattern has been recently also for an un-named grand minima in the fourth century BC (Nagaya et al. 2012).

A very important feature of sunspot activity during the Maunder minimum was its strong north-south asymmetry, as sunspots were only observed in the southern solar hemisphere during the end of the Maunder minimum (Ribes and Nesme-Ribes 1993; Sokoloff and Nesme-Ribes 1994). This observational fact has led to intensive theoretical efforts to explain a significant asymmetry of the sun’s surface magnetic field in the framework of the dynamo concept (see the review by Sokoloff 2004, and references therein). Note that a recent discovery (Arlt 2008, 2009) of the Staudacher’s original drawings of sunspots in late eighteenth century shows that similarly asymmetric sunspot occurrence existed also in the beginning of the Dalton minimum in 1790s (Usoskin et al. 2009c). However, the northern hemisphere dominated at that period contrary to the situation during the Maunder minimum.

4.2.2 Grand minima on a multi-millennial timescale

The presence of grand minima in solar activity on the long-term scale has been mentioned numerously (e.g., Eddy 1977b; Solanki et al. 2004; Usoskin et al. 2007; Steinhilber et al. 2012; Inceoglu et al. 2015), using the radioisotope data of $^{14}$C in tree rings and $^{10}$Be in ice cores. For example, Eddy (1977a) identified major excursions in the detrended $^{14}$C record as grand minima and maxima of solar activity and presented a list of six grand minima and five grand maxima for the last 5000 years (see Table 2). Stuiver and Braziunas (1989) and Stuiver et al. (1991) also studied grand minima as systematic excesses of the high-pass filtered $^{14}$C data and suggested that the minima are generally of two distinct types: short minima of duration 50–80 years (called Maunder-type) and longer minima collectively called Spörer-like minima. Using the same method of identifying grand minima as significant peaks in high-pass filtered $\varDelta ^{14}$C series, Voss et al. (1996) provided a list of 29 such events for the past 8000 years. A similar analysis of bumps in the $^{14}$C production rate was presented recently by Goslar (2003). However, such studies retained a qualitative element, since they are based on high-pass–filtered $^{14}$C data and thus implicitly assume that $^{14}$C variability can be divided into short-term solar variations and long-term changes attributed solely to the slowly-changing geomagnetic field. This method ignores any possible long-term changes in solar activity on timescales longer than 500 years (Voss et al. 1996). The modern approach, based on physics-based modelling (Sect. 3), allows for the quantitative reconstruction of the solar activity level in the past, and thus, for a more realistic definition of the periods of grand minima or maxima.

Table 2 Conservative list with approximate dates (in –BC/AD) of grand minima in reconstructed solar activity [1—listed in Usoskin et al. (2007); 2—listed in Inceoglu et al. (2015); 3—listed in Usoskin et al. (2016a)]

A list of 25 grand minima, identified in the quantitative solar-activity reconstruction of the last 11 000 years, shown in Fig. 20, is presented in Table 2 (after Usoskin et al. 2007, 2016a). The cumulative duration of the grand minima is about 1900 years, indicating that the sun in its present evolutionary stage spends ${\sim }{^1/_6}$ (17%) of its time in a quiet state, corresponding to grand minima. Note that the definition of grand minima is quite robust.

It was shown by Usoskin et al. (2014), using $^{14}$C data for the last three millennia, that grand minima correspond to a special mode of the solar dynamo which is clearly separated from the main mode of moderate activity. The probability density function (PDF) of the occurrence of decadal sunspot numbers in the reconstruction based on $^{14}$C for the last three millennia (Usoskin et al. 2014) is shown in Fig. 21. One can see that the PDF has a clear bimodal structure, where the main mode corresponds to the general mode of moderate activity (20–60 in decadal sunspot numbers), while the secondary maximum represents a statistically different mode of low activity (decadal sunspot numbers below 20) corresponding to Grand minima.

Fig. 21

Probability density function of the reconstructed decadal sunspot numbers for the last three millennia (grey histogram). Shown is also the best-fit bimodal Gaussian distribution (red curve with the two modes shown by dotted blue lines). The Grand minimum mode is indicated by the arrow. (Modified after Usoskin et al. 2014)

The question of whether the occurrence of grand minima in solar activity is a regular or chaotic process is important for understanding the action of the solar-dynamo machine. Even a simple deterministic numerical dynamo model can produce events comparable with grand minima (Brandenburg et al. 1989; Käpylä et al. 2016). Such models can also simulate a sequence of grand minima occurrences, which are irregular and seemingly chaotic (e.g., Jennings and Weiss 1991; Tobias et al. 1995; Covas et al. 1998). The presence of long-term dynamics in the dynamo process is often explained in terms of the $\alpha$-effect, which, being a result of the electromotive force averaged over turbulent vortices, can contain a fluctuating part (e.g., Hoyng 1993; Ossendrijver et al. 1996) leading to irregularly occurring grand minima (e.g., Brandenburg and Spiegel 2008). The present dynamo models can reproduce almost all the observed features of the solar cycle under ad hoc assumptions (e.g., Pipin et al. 2012), although it is still unclear what leads to the observed variability. Most of these models predict that the occurrence of grand minima is a purely random “memoryless” Poisson-like process, with the probability of a grand minimum occurring being constant at any given time. This unambiguously leads to the exponential shape of the waiting-time distribution (waiting time is the time interval between subsequent events) for grand minima.

Usoskin et al. (2007) performed a statistical analysis of grand minima occurrence time (Table 2) and concluded that their occurrence is not a result of long-term cyclic variations, but is defined by stochastic/chaotic processes. Moreover, waiting-time distribution deviates from the exponential law. This implies that the event occurrence is still random, but the probability is nonuniform in time and depends on the previous history. In the time series it is observed as a tendency of the events to cluster together with a relatively-short waiting time, while the clusters are separated by long event-free intervals (cf. Sect. 4.1). Such behavior can be interpreted in different ways, e.g., self-organized criticality or processes related to accumulation and release of energy. This poses a strong observational constraint on theoretical models aiming to explain the long-term evolution of solar activity (Sect. 4.4.1). However, as discussed by Moss et al. (2008) and Usoskin et al. (2009d), the observed feature can be an artefact of the small statistics (only 27 grand minima are identified during the Holocene), making this result only indicative and waiting for a more detailed investigation.

A histogram of the duration of grand minima from Table 2 is shown in Fig. 22. The mean duration is 70 year but the distribution is bimodal. The minima tend to be either of a short (30–90 years) duration similar to the Maunder minimum, or rather long (${>}100$ years), similar to the Spörer minimum, in agreement with earlier conclusions (Stuiver and Braziunas 1989). This suggests that grand minima correspond to a special state of the dynamo. Once falling into a grand minimum as a result of a stochastic/chaotic, but non-Poisson process, the dynamo is “trapped” in this state and its behavior is driven by deterministic intrinsic features.

Fig. 22

Histogram of the duration of grand minima from Table 2

4.3 Grand maxima of solar activity

4.3.1 The modern episode of active sun

In the last decades we were living in a period of a very active sun with a level of activity that is very high for the last few centuries covered by direct solar observation. The sunspot number was growing rapidly between 1900 and 1940, with more than a doubling average group sunspot number, and has remained at that high level until recently (see Fig. 1). Note that growth comes mostly from raising the cycle maximum amplitude, while sunspot activity always returns to a very low level around solar cycle minima. While the average group sunspot number (using GSN) for the period 1750–1900 was $35 \pm 9$ ($39 \pm 6$, if the Dalton minimum in 1797–1828 is not counted), it stands high at the level of $75 \pm 3$ for 1950–2000. Therefore, the modern active sun episode, which started in the 1940s, can be regarded as the modern grand maximum of solar activity, as opposed to a grand minimum (Wilson 1988b). As discussed by Clette et al. (2014, see their Figure 65), the number of spotless days during cycles 12–22 was half of that for another relatively high activity period ca. 1850. This again suggests the uniqueness of the modern grand maximum on the centennial time scale. The reality of the Modern grand maximum was independently confirmed by Ziȩba and Nieckarz (2014) who have shown, by studying active versus passive (spotless) days that cycles 17–23 were more active, compared to cycles 8–15.

Although uncertainties in sunspot numbers during the 18th and 19th centuries (see discussion in Sect. 2.2.1) make it a bit unclear on the centennial time scale, data on cosmogenic isotopes (Usoskin et al. 2003c; Solanki et al. 2004; Inceoglu et al. 2015) imply that such high activity episodes occur quite seldom.

However, as we can securely say now, after the very weak solar minimum in 2008–2009 (e.g., Gibson et al. 2011), solar activity returns to its normal moderate level in cycle # 24. Thus, the high activity episode known as the Modern grand maximum is over.

Is such high solar activity typical or is it something extraordinary? While it is broadly agreed that the modern active sun episode is a special phenomenon, the question of how (a)typical such upward bumps are from “normal” activity is a topic of hot debate.

4.3.2 Grand maxima on a multi-millennial timescale

The question of how often grand maxima occur and how strong they are, cannot be studied using the 400-year-long series of direct observations. An increase in solar activity around 1200 AD, also related to the Medieval temperature optimum, is sometimes qualitatively regarded as a grand maximum (Wilson 1988b; de Meyer 1998), but its magnitude is lower than the modern maximum (e.g., Usoskin et al. 2003c). Accordingly, it was not included in a list of grand maxima by Eddy (1977b, 1977a).

Table 3 Conservative list with approximate dates (in −BC/AD) of grand maxima in reconstructed solar activity [1—listed in Usoskin et al. (2007); 2—listed in Inceoglu et al. (2015); 3—listed in Usoskin et al. (2016a)]

A quantitative analysis is only possible using proxy data, especially cosmogenic isotope records. Using a physics-based analysis of solar-activity series reconstructed from $^{10}$Be data from polar (Greenland and Antarctica) archives, Usoskin et al. (2003c, 2004) stated that the modern maximum is unique in the last millennium. Then, using a similar analysis of the $^{14}$C calibrated series, Solanki et al. (2004) found that the modern activity burst is not unique, but a very rare event, with the previous burst occurring about 8 millennia ago. An update (Usoskin et al. 2006a) of this result, using a more precise paleo-magnetic reconstruction by Korte and Constable (2005) since 5000 BC, suggests that an increase of solar activity comparable with the modern episode might have taken place around 2000 BC, i.e., around 4 millennia ago, in agreement with more recent studies by Steinhilber et al. (2012) and Inceoglu et al. (2015). On the other hand, the definition of grand maxima is less robust than grand minima and is sensitive to other parameters such as geomagnetic field data or overall normalization (Usoskin et al. 2016a).

Keeping possible uncertainties in mind, let us consider a list of the largest grand maxima (the 50 year smoothed sunspot number stably exceeding 50), identified for the last eleven millennia using cosmogenic isotope data, as shown in Table 3. A total of 23 grand maxima have been identified with a total duration of around 1400 years, suggesting that the sun spends around 12% of its time in an active state. A statistical analysis of grand-maxima–occurrence time suggests that they do not follow long-term cyclic variations, but a clustering near highs of the Hallstatt cycle is observed (Usoskin et al. 2016a). The distribution of the waiting time between consecutive grand maxima is not unambiguously clear, but also hints at a deviation from exponential law. The duration of grand maxima has a smooth distribution, which nearly exponentially decreases towards longer intervals. Most of the reconstructed grand maxima (about 70%) were not longer than 50 years, and only five grand minima (including the modern one) have been longer than 70 years (cf. Barnard et al. 2011). Note, that the Modern grand maximum is over now and we are living during the epoch of moderate or even weak solar activity.

It is still unclear wether grand maxima correspond to a special state of solar dynamo or rather to a tail of the regular mode. Although there are some indications for the former (Usoskin et al. 2016a), they are inconclusive.

4.4 Related implications

Reconstructions of long-term solar activity have different implications in related areas of science. The results, discussed in this overview, can be used in such diverse research disciplines as theoretical astrophysics, solar-terrestrial studies, paleo-climatology, and even archeology and geology. We will not discuss all possible implications of long-term solar activity in great detail but only briefly mention them here.

4.4.1 Theoretical constrains

The basic principles of the occurrence of the 11-year Schwabe cycle are more-or-less understood in terms of the solar dynamo, which acts, in its classical form (e.g., Parker 1955), as follows (see detail in Charbonneau 2010). Differential rotation $\varOmega$ produces a toroidal magnetic field from a poloidal one, while the “$\alpha$-effect”, associated with the helicity of the velocity field or Joy’s Law tilt of active regions, produces a poloidal magnetic field from a toroidal one. This classical model results in a periodic process in the form of propagation of a toroidal field pattern in the latitudinal direction (the “butterfly diagram”). As evident from observation, the solar cycle is far from being a strictly periodic phenomenon, with essential variations in the cycle length and especially in the amplitude, varying dramatically between nearly spotless grand minima and very large values during grand maxima. The mere fact of such great variability, known from sunspot data, forced solar physicists to develop dynamo models further. Simple deterministic numerical dynamo models, developed on the basis of Parker’s migratory dynamo, can simulate events, which are seemingly comparable with grand minima/maxima occurrence (e.g., Brandenburg et al. 1989). However, since variations in the solar-activity level, as deduced from cosmogenic isotopes, appear essentially nonperiodic and irregular, appropriate models have been developed to reproduce irregularly-occurring grand minima (e.g., Jennings and Weiss 1991; Tobias et al. 1995; Covas et al. 1998). Models, including an ad hoc stochastic driver (Choudhuri 1992; Schmitt et al. 1996; Ossendrijver 2000; Weiss and Tobias 2000; Mininni et al. 2001; Charbonneau 2001; Charbonneau et al. 2004; Käpylä et al. 2016), are able to reproduce the great variability and intermittency found in the solar cycle (see the review by Charbonneau 2010). A recent statistical result of grand minima occurrence (Sect. 4.3.2) shows disagreement between observational data, depicting a degree of self-organization or “memory”, and the above dynamo model, which predicts a pure Poisson occurrence rate for grand minima (see Sect. 4.2). This poses a new constraint on the dynamo theory, responsible for long-term solar-activity variations (Sokoloff 2004; Moss et al. 2008).

In general, the following additional constraints can be posed on dynamo models aiming to describe the long-term (during the past 11 000 years) evolution of solar magnetic activity.

• The sun spends about $^3/_4$ of its time at moderate magnetic-activity levels, about $^1/_6$ of its time in a grand minimum and about $^1/_5{\,\textendash \,}^1/_{10}$ in a grand maximum. Recent solar activity corresponds to a grand maximum, which has ceased after solar cycle 23.

• Grand minima form a special, statistically significant, mode of solar dynamo. The existence of the Grand maximum mode is hinted but not conclusive.

• Occurrence of grand minima and maxima is not a result of long-term cyclic variations but is defined by stochastic/chaotic processes.

• Observed statistics of the occurrence of grand minima and maxima display deviation from a “memory-less” Poisson-like process, but tend to either cluster events together or produce long event-free periods.

  Grand minima and maxima tend to cluster around lows and highs of the ${\approx } 2400$-year Hallstatt cycle, respectively. This can be interpreted in different ways, such as self-organized criticality (e.g., Carvalho and Prado 2000), a time-dependent Poisson process (e.g., Wheatland 2003), or some memory in the driving process (e.g., Mega et al. 2003).

• Grand minima tend to be of two different types: short minima of Maunder type and long minima of Spörer type. This suggests that a grand minimum is a special state of the dynamo.

• Duration of grand maxima resemble a random Possion-like process, in contrast to grand minima.

4.4.2 Solar-terrestrial relations

The sun ultimately defines the climate on Earth supplying it with energy via radiation received by the terrestrial system, but the role of solar variability in climate variations is far from being clear. Solar variability can affect the Earth’s environment and climate in different ways (see, e.g., reviews by Haigh 2007; Gray et al. 2010). Variability of total solar irradiance (TSI) measured during recent decades is known to be too small to explain observed climate variations (e.g., Foukal et al. 2006; Fröhlich 2006; Yeo et al. 2014). On the other hand, there are other ways solar variability may affect the climate, e.g., an unknown long-term trend in TSI (Solanki and Krivova 2004; Wang et al. 2005) or a terrestrial amplifier of spectral irradiance variations (Shindell et al. 1999; Haigh et al. 2010). Uncertainties in the TSI/SSI reconstructions remain large (Schmidt et al. 2012; Yeo et al. 2014), making it difficult to assess climate models on the long-term scale. Alternatively, an indirect mechanism also driven by solar activity, such as ionization of the atmosphere by CR (Usoskin and Kovaltsov 2006) or the global terrestrial current system (Tinsley and Zhou 2006) can modify atmospheric properties, in particular cloud cover (Ney 1959; Svensmark 1998; Usoskin and Kovaltsov 2008a). Although the role of this direct mechanism is found to be small (Mironova et al. 2015), indirect effects of energetic particles may be still notable (e.g., Gray et al. 2010; Calisto et al. 2011; Martin-Puertas et al. 2012).

Accordingly, improved knowledge of the solar driver’s variability may help in disentangling various effects in the very complicated system that is the terrestrial climate (e.g., Gray et al. 2010). It is of particular importance to know the driving forces in the pre-industrial era, when all climate changes were natural. Knowledge of the natural variability can lead to an improved understanding of anthropogenic effects upon the Earth’s climate.

Studies of the long-term solar-terrestrial relations are mostly phenomenological, lacking a clear quantitative physical mechanism. Therefore, more precise knowledge of past solar activity, especially since it is accompanied by continuous efforts of the paleo-climatic community on improving climatic data sets, is crucial for improved understanding of the natural (including solar) variability of the terrestrial environment.

4.5 Summary

In this section, solar activity on a longer scale is discussed, based on recent reconstructions.

According to these reconstructions, the sun has spent about 70% of its time during the Holocene, which is ongoing, in a normal state characterized by medium solar activity. About 15–20% of the time the sun has experienced a grand minimum, while 10–15% of the time has been taken up by periods of very high activity.

One of the main features of long-term solar activity is its irregular behavior, which cannot be described by a combination of quasi-periodic processes as it includes an essentially random component.

Grand minima, whose representative is the Maunder minimum of the late seventeenth century, are typical solar phenomena. Approximately 25 grand minima can be robustly identified in solar activity reconstructions for the Holocene period. Their occurrence suggests that they appear not periodically, but tend to appear in clusters separated by 2000–2500 years (the Hallstatt cycle), and having a recurrence period of ${\approx } 210$ years (Suess/de Vries cycle) within the clusters. Grand minima tend to be of two distinct types: short (Maunder-like) and longer (Spörer-like). The appearance of grand minima can be reproduced by modern stochastic-driven dynamo models to some extent, but some problems still remain to be resolved.

The recent level of solar activity (after the 1940s) was very high, corresponding to a grand maximum, which are typical but rare events in solar behavior. However, this grand maximum has ceased after solar cycle 23. The duration of grand maxima resembles a random Possion-like process, in contrast to grand minima.

These observational features of the long-term behavior of solar activity have important implications, especially for the development of theoretical solar-dynamo models and for solar-terrestrial studies.

5 Solar energetic particles in the past

In addition to galactic cosmic rays, which are always present in the Earth’s vicinity, sometimes sporadic solar energetic particle (SEP) events with a greatly enhanced flux of less energetic particles in the interplanetary medium also occur (e.g., Klecker et al. 2006). Strong SEP events mostly originate from CME-related shocks propagating in the solar corona and interplanetary medium, that lead to effective bulk acceleration of charged particles (e.g., Cane and Lario 2006). Although these particles are significantly less energetic than GCRs, they can occasionally be accelerated to an energy reaching up to several GeV or more, which is enough to initiate the atmospheric cascade. Peak intensity of SEP flux can be very high, up to $10^{4}$ particles (with energy ${>} 30$ MeV) per cm$^{2}$ per second. In fact, the long-term average flux (or fluence) of SEP is mostly defined by rare major events, which occur a few times per solar cycle, with only minor contributions from a large number of weak events (Shea and Smart 1990, 2002). As an example, energy spectra of GCR and SEP are shown in Fig. 23 for the day of January 20, 2005, when an extreme SEP event took place. Such SEPs dominate the low-energy section of cosmic rays (below hundreds of MeV of a particle’s kinetic energy), which is crucial for the radiation environment, and play an important role in solar-terrestrial relations. For many reasons it is important to know the variations of SEPs on long-term scales.

Fig. 23

Daily fluence of solar energetic particles (dashed curve—Tylka and Dietrich 2009) and galactic cosmic rays (solid curve) for the day of January 20, 2005. Open circles represent space-borne measurements (Mewaldt 2006; Mewaldt et al. 2012)

It is not straightforward to evaluate the average SEP flux even for the modern instrumental epoch of direct space-borne measurements (e.g., Mewaldt et al. 2007). For example, estimates for the average flux of SEPs with an energy above 30 MeV (called $F_{30}$ henceforth) for individual cycles may vary by an order of magnitude, from $10\ \mathrm{cm}^{-2}\ \mathrm{s}^{-1}$ for cycle 21 up to $70\ \mathrm{cm}^{-2}\ \mathrm{s}^{-1}$ for cycle 19 (Reedy 2012). Moreover, estimates of the SEP flux were quite uncertain during the earlier years of space-borne measurements because of two effects, which are hard to account for (e.g., Reeves et al. 1992; Tylka et al. 1997). One is related to the very high flux intensities of SEPs during the peak phase of events, when a detector can be saturated because of the dead-time effect (the maximum trigger rate of the detector is exceeded). The other is related to events with high energy solar particles, which can penetrate into the detector through the walls of the collimator, leading to an enhanced effective acceptance cone with respect to the “expected” one. Since the SEP fluence is defined by major events, these effects may lead to an underestimate of the average flux of SEPs. The modern generation of detectors are better suited for measuring high fluxes. The average $F_{30}$ flux for the last five solar cycles (1954–2006) is estimated at about $35\ \mathrm{cm}^{-2}\ \mathrm{s}^{-1}$ (Smart and Shea 2002; Shea et al. 2006).

5.1 Cosmogenic isotopes

The development of the method of cosmogenic isotopes makes it possible to estimate occurrence of extreme SEP events in the past. Some earlier attempts were inconclusive. For example, Usoskin et al. (2006b) found that a typical strong SEP event leaves no distinguishable signature in $^{14}$C but may be observed from ice core $^{10}$Be records. However, the question of the possible rare occurrence of extreme SEP events on the millennial time scale is important not only from the theoretical point of view, but also for assessment of radiation risks for space-borne missions, especially manned ones. What can be the strongest SEP event originated from the sun, how often they can occur? These questions need to be answered. Several attempts have been made to evaluate that from the cosmogenic isotope data (Lingenfelter and Hudson 1980; Usoskin et al. 2006b; Webber et al. 2007), but the result was grossly uncertain (Hudson 2010; Schrijver et al. 2012), mostly because of the large model uncertainties of the radionuclide production.

A new step forward has been done recently by Usoskin and Kovaltsov (2012), who analyzed two $^{14}$C and five $^{10}$Be records over the last millennia and searched for possible signatures of extreme SEP events.

Fig. 24

Time profiles of the measured $\varDelta ^{14}$C content in Japanese cedar (M12—Miyake et al. 2012) and German oak (ETH Zürich & Mannheim AMS—Usoskin et al. 2013) trees for the period around 775 AD. Smooth black and grey lines depict a family of best fit $\varDelta ^{14}$C profiles, calculated using a family of realistic carbon cycle models for an instantaneous injection of $^{14}$C into the stratosphere (Usoskin and Kovaltsov 2012). Image after Usoskin et al. (2013)

While the response of $^{10}$Be to an SEP event is simply a 1–2-years long peak, because of the simple atmospheric transport/deposition (see Sect. 3.3.3), the response of $^{14}$C has a typical shape shown in Fig. 24—with a sharp peak and exponential decay of the length of several decades, due to the carbon cycle (see Sect. 3.2.3). A search for the available cosmogenic isotope data has been performed through millennia (Usoskin and Kovaltsov 2012; Miyake et al. 2016), looking for a potential SEP signatures, and came up with a list of candidates of extreme SEP events and assessments of their strength (Table 4).

Table 4 A list of candidates for extreme SEP events found in different cosmogenic isotope records throughout the Holocene: approximate year, dataset used (Dye3—McCracken et al. (2004); NGRIP—Berggren et al. (2009); IntCal09—Reimer et al. (2009); GRIP—Yiou et al. (1997); Dome Fuji—Horiuchi et al. (2008); South Pole—Raisbeck et al. (1990); M12—Miyake et al. (2012)), and the $F_{30}$ fluence (cm$^{-2}$)

The list includes 23 candidates for extreme SEP events with the fluence $F_{30}$ exceeding $10^{10}\ \mathrm{cm}^{-2}$, viz. the greatest fluence observed for the space era in 1960 (Shea and Smart 1990). Note that only two of these candidates appear in more than one series—the events of ca. 1460 AD and ca. 780 AD. The former had signatures in two annual $^{10}$Be series, NGRIP and Dye3. The later was observed in two $^{14}$C series, biennial M12 and 5-years IntCal13, and in quasi-decadal Dome Fuji $^{10}$Be series. The quasi-decadal South Pole $^{10}$Be series does not show an increase ca. 780 AD placing an upper limit on the strength of the event.

5.1.1 The event of 775 AD: the worst case scenario?

The event of ca. 775 AD was analyzed using biennial $^{14}$C data by Miyake et al. (2012), who suggested that the event was probably caused by $\gamma$-rays from an unknown nearby supernova. This event is confirmed by annual $^{14}$C data from a German oak tree (Usoskin et al. 2013), Russian and American tree samples (Jull et al. 2014), New Zealand trees (Güttler et al. 2013), etc., and corals from the Chinese Sea (Liu et al. 2014) According to model simulations, the production of $^{14}$C appears in agreement with that of $^{10}$Be (Usoskin et al. 2013; Melott and Thomas 2012; Pavlov et al. 2013). Although some exotic scenarios were proposed for the event: an unidentified nearby supernova (Miyake et al. 2012); a gamma-ray burst (Hambaryan and Neuhäuser 2013; Pavlov et al. 2013); or even a cometary impact on Earth (Liu et al. 2014), it is generally accepted now that it was a signature of a (probably, consequence of) extreme SEP event (Usoskin and Kovaltsov 2012; Eichler and Mordecai 2012; Usoskin et al. 2013; Melott and Thomas 2012; Thomas et al. 2013; Cliver et al. 2014). A detailed analysis performed by Mekhaldi et al. (2015) not only confirmed its solar origin but also made it possible to assess, based on data from different cosmogenic isotopes, the reconstructed integral spectrum as shown in Fig. 25 along with the fluence spectra of two extreme SEP events of the space era: the hardest event of 23-Feb-1956 (GLE # 5) with the greatest fluence of high energy SEPs; and the event of 04-Aug-1972 with the greatest measured fluence of lower energy SEPs. One can see that the energy spectrum of the 775 AD event was very hard, close to that of the 23-Feb-1956 event, but scaled up by a factor ${\approx } 40$. This implies that the fluence of high energy particles was much greater (factor of ${\approx } 40$) in 775 AD than ever observed during the space era. On the other hand, the low-energy fluence (energy range of several tens of MeV) for the 775 AD event was only a factor of two greater than that of the event of Aug-1972, suggesting that the fluence of low-energy SEP might have a natural limit (Asvestari et al. 2016), for example related to the “streaming limit” (Reames and Ng 2010). Thus, the high fluence of high energy particles does not necessarily mean a very high fluence of the lower-energy particles.

Fig. 25

Even-integrated SEP fluence spectra for the 775 AD event (Mekhaldi et al. 2015), the hardest known and the greatest soft-spectrum SEP events of 23-Feb-1956 and 04-Aug-1972, respectively (Tylka and Dietrich 2009)

The signal of the 775 AD event was so strong and clearly visible in the ice-core $^{10}$Be data that it is now used as a tie point (the point with independently known date, e.g., volcanic eruption or, as in this case, the SEP event) for more precise dating of ice cores (Sigl et al. 2015).

Another similar event was found to occur in 994 AD (Miyake et al. 2013), that was roughly half of that of 775 AD and also had a very hard spectrum (Mekhaldi et al. 2015).

Do we expect that even stronger SEP events took place in the past? The 775 AD event was observed as the sharpest peak (${\approx } 0.4$%/years) in the decadal $^{14}$C IntCal dataset, while the smaller peak (${\approx } 0.35$%/years) of the 994 AD was only barely seen in the IntCal data. Recently, Miyake et al. (2016) measured, with (bi)annual resolution, $^{14}$C around four smaller peaks (${\approx } 0.3$%/years) since 4800 BC and found no other events, suggesting for uniqueness of the 775 AD one for the last six millennia. We note that other remaining peaks in the IntCal data are smaller than the one of 775 AD. Accordingly, an event stronger than that of 775 AD could be found only in a case of an unlikely random coincidence of the event itself with an incidental drop of $^{14}$C caused by other reasons, masking the spike. In particular, the event twice as strong as the 775 AD one is hardly possible to occur since it would have produced a large spike in the IntCal data which could not be missed (see Fig. 26). Thus, the 775 AD event can securely serve as the worst case scenario of the SEP event during the entire Holocene.

Fig. 26

The record (black) of $\varDelta ^{14}$C (IntCal09 Reimer et al. 2009) throughout the Holocene, along with the expected signal (red) in the decadal $\varDelta ^{14}$C data, from a scaled 775 AD event (denoted as “E”)

5.1.2 Occurrence rate

The integral probability distribution of the occurrence of strong SEP events, as revealed from the cosmogenic isotope data, is shown in Fig. 27.

Fig. 27

Cumulative probability (with the 90% confidence interval) of occurrence of a SEP event with fluence (${>} 30$ MeV) exceeding the given value $F_{30}$, as assessed from the data for the space era 1956–2008 (black triangles), cosmogenic isotope data (blue circles), and cosmogenic data from lunar rocks (red shaded area). Modified after Kovaltsov and Usoskin (2014)

One can see that the break in the distribution marginally hinted in the directly observed SEP events at around $F_{30} = (5{\,\textendash \,}7) \times 10^{9}\ \mathrm{cm}^{-2}$ (nonproportionally fewer strong events observed) is confidently confirmed by the cosmogenic isotope data. In particular, no event with $F_{30} \,{>} 2 \times 10^{10}\ \mathrm{cm}^{-2}$ was found over the last 600 years using annually resolved $^{10}$Be data. It is noteworthy that the idea of a possible extreme Carrington SPE of 1859 AD (McCracken et al. 2001) is discarded (see also Wolff et al. 2012). On the longer time scale of 11 millennia, no event with $F_{30} \,{>}5 \times 10^{10}\ \mathrm{cm}^{-2}$ has been found. This gives a new strict observational constraint on the occurrence probability of extreme SPEs.

According to Usoskin and Kovaltsov (2012) practical limits can be set as $F_{30} \approx 1$, 2–3 and $5 \times ~10^{10}\ \mathrm{cm}^{-2}$ (10, 20–30 and 50 times greater than the SEP event of February 23, 1956), for the occurrence probability of $10^{-2}$, $10^{-3}$, and $10^{-4}\ \mathrm{years}^{-1}$, respectively. The mean SEP flux is found as ${\approx } 40$ ($\mathrm{cm}^{2}\ \mathrm{s})^{-1}$ in agreement with estimates from the lunar rocks. On average, extreme SPEs contribute about 10% to the total SEP fluence.

5.2 Lunar and meteoritic rocks

Since energy spectra of SEP and GCR are dramatically different, one may think of a natural spectrometer to separate their effects and thus evaluate their fluxes independently. A spectrometer that is able to separate cosmic rays is lunar (or meteoritic) rocks.

Fig. 28

Measured (dots) and calculated (curves) $^{14}$C activity in a lunar sample 68815 (Jull et al. 1998). The big diamond implies contamination of a thin surface layer by $^{14}$C implanted from solar wind. The dotted curve represents the expected production due to GCR, while the solid curve is the best fit SEP+GCR model production

Figure 28 depicts an example of $^{14}$C measured in a lunar sample (Jull et al. 1998). The dotted line shows the expected production of radiocarbon by GCR. The production increases with depth due to the development of a nucleonic cascade in the matter, initiated by energetic GCR particles, similar to the atmospheric cascade. Less energetic particles of solar origin produce the isotope only in upper layers of the rock, since their low energy does not allow them to initiate a cascade. On the other hand, thanks to their high flux in the lower energy range, the production of $^{14}$C in the upper layers is much higher than that from GCR. Thus, by first measuring the isotope activity in deep layers one can evaluate the average GCR flux, and then the measured excess in the upper level yields an estimate for the SEP flux in both integral intensity and spectral shape. The result is based on model computations and therefore is slightly model dependent but makes it possible to give a robust estimate of the GCR and SEP in the past.

A disadvantage of this approach is that lunar samples are not stratified and do not allow for temporal separation. The measured isotope activity is a balance between production and decay and, therefore, represents the production (and the ensuing flux) integrated over the life-time of the isotope before the sample has been measured. However, using different isotopes with different life times, one can evaluate the cosmic-ray flux integrated over different timescales.

Estimates of the average SEP flux $F_{30}$ on different timescales, as obtained from various isotopes measured in lunar samples, are collected in Table 5. Based on isotopes with different life-times (see Table 5) one can evaluate the average flux of SEP on different time scale (see Fig. 29). The average $F_{30}$ flux for the last five solar cycles (1954–2008) is consistent with the average flux estimated in the past for longer timescales from $10^{3}$ to $10^{7}$ years (cf. Reedy 2002, 2012).

Table 5 Estimates of $4\pi$ omni-directional integral (above 30 MeV) flux, $F_{30}$ in (cm$^{2}$ s)$^{-1}$, of solar energetic particles, obtained from different sources

However, this method is not able to provide an estimate of the occurrence rate of extreme SEP events. If one assumes that the entire average SEP flux is produced within one extreme event occurring at half of the isotope’s life-time ago (Reedy 1996), an upper limit for the occurrence of extreme SEP events can be placed. This is an unrealistically extreme assumption, which may lead to an overestimate by many orders of magnitude, but it sets the very conservative upper limit which cannot be exceeded.

Fig. 29

Cumulative frequency distribution of SEP events with fluences greater than $F_{10}$ (for particles with energies above 10 MeV). Red histogram: satellite-based direct observations; Blue diamonds: conservative upper limits derived from lunar isotopes (see Sect. 5.2); Blue dashed line: upper limit based on $^{14}$C record (Hudson 2010); Image reproduced by permission from Schrijver et al. (2012), copyright by AGU

A more realistic assumption is based on a a distribution of SEP events in strength, for example exponential. If applying this, the distribution of the SEP events estimated from lunar rocks appears fully consistent with the assessments based on terrestrial cosmogenic isotope data and direct data on SEP fluences for the space era (Fig. 27).

5.3 Nitrates in polar ice

It has been discussed until recently that another quantitative index of strong SEP events (with $F_{30}{>}10^{9}\ \mathrm{cm}^{-2}$) might be related to nitrate ($\mathrm {NO}_3^-$) records measured in polar ice cores. The concentration of nitrates has been measured in polar ice from both the Southern (South Pole, e.g., Dreschhoff and Zeller 1990) and Northern (Greenland, e.g., Zeller and Dreschhoff 1995; Dreschhoff and Zeller 1998) polar caps, depicting pronounced spikes associated with strong SEP events (McCracken et al. 2001). As a result of the analysis a list of large SEP events since 1560 and their fluences have been published (see Table 1 in McCracken et al. 2001) and widely used.

However, as shown by several independent recent studies (Wolff et al. 2012; Usoskin and Kovaltsov 2012) on the example of the Carrington event (September 1859), the nitrate spikes are not related to SEP events. According to McCracken et al. (2001), the nitrate spike and the associated SEP event was the strongest in the entire record ($F_{30} \approx 2 \times 10^{10}\ \mathrm{cm}^{-2}$). Wolff et al. (2012) have measured, with high resolution, nitrate content in 14 ice cores from Antarctic and Greenland for a few decades around 1859. Only one Greenland series depicts a spike which can be associated with the event, all other series have no signatures. Moreover, all similar spikes found in Greenland datasets are accompanied by chemical tracers (ammonium, formate, black carbon, etc.) clearly pointing to the anthropogenic source of nitrates—biomass burning plumes. No significant spikes have been found in the Antarctic records. Wolff et al. (2012) concluded that “Nitrate spikes cannot be used to derive the statistics of SEPs”.

This work was criticized by Smart et al. (2014), who stated that the resolution of the analyzed series was not high enough and could have led to missing the spike, which was counter-argued by Wolff et al. (2016) that even a fine time resolution does not reveal the peaks. It was also discussed theoretically (Duderstadt et al. 2016) that a realistic SEP event can hardly produce sufficient amount of nitrate to leave a strong pulse-like signature in an ice core. Usoskin and Kovaltsov (2012) calculated, from the $F_{30}$ fluence proposed by McCracken et al. (2001) for the Carrington event, the $^{10}$Be production and showed that, if the Carrington SEP event was so strong, it would have necessarily produce a spike in the annually resolved $^{10}$Be record, which however contradicts to the real data from NGRIP and Dye3 ice cores.

Thus, the nitrate record in polar ice cannot serve as an index of SEP events. On the other hand, it may be used to study long-term variability of GCR (see Sect. 3.4).

5.4 Summary

In this section, estimates of the averaged long-term flux of SEPs are discussed.

Measurements of cosmogenic isotopes with different life times in lunar and meteoritic rocks allow one to make rough estimates of the SEP flux over different timescales. The directly space-borne-measured SEP flux for past decades is broadly consistent with estimates on longer timescales—up to millions of years. The same measurements can provide a very conservative upper estimate for the occurrence rate of extreme SEP events. Terrestrial cosmogenic isotope data in dated archives (tree trunks, ice cores) give a possibility to assess the occurrence rate of strong SEP events on the time scales up to ten of millennia. Measurements of nitrates in polar ice have been shown to be an invalid index of strong SEP events in the past.

The strongest known SEP event has occurred in 775 AD as found in terrestrial cosmogenic isotope data. It can server as the worst case scenario for an extreme SEP event on the multi-millennial time scale. A smaller, but still extreme, event took place in 994 AD.

Different estimates of the extreme (quantified as the fluence of SEP with energy above 10 MeV) SEP event occurrence probability are summarized in Fig. 29.

An analysis of various kinds of data suggests that the distribution of the intensity of SEP events has a break, and the occurrence of extra-strong events (with the $F_{30}$ fluence exceeding $5 \times 10^{10}\ \mathrm{cm}^{-2}$) is unlikely on the multi-millennial time scale.

6 Conclusions

In this review the present knowledge of long-term solar activity on a multi-millennial timescale, as reconstructed using the indirect proxy method, is discussed.

Although the concept of solar activity is intuitively understandable as a deviation from the “quiet” sun concept, there is no clear definition for it, and different indices have been proposed to quantify different aspects of variable solar activity. One of the most common and practical indices is sunspot number, which forms the longest available series of direct scientific observations. While all other indices have a high correlation with sunspot numbers, dominated by the 11-year cycle, the relationship between them at other timescales (short- and long-term trends) may vary to a great extent.

On longer timescales, quantitative information of past solar activity can only be obtained using the method based upon indirect proxy, i.e., quantitative parameters, which can be measured nowadays but represent the signatures, stored in natural archives, of the different effects of solar magnetic activity in the past. Such traceable signatures can be related to nuclear or chemical effects caused by cosmic rays in the Earth’s atmosphere, lunar rocks or meteorites. The most common proxy of solar activity is formed by data from the cosmogenic radionuclides, $^{10}$Be and $^{14}$C, produced by cosmic rays in the Earth’s atmosphere and stored in independently-dated stratified natural archives, such as tree rings or ice cores. Using a recently-developed physics-based model it is now possible to reconstruct the temporal behavior of solar activity in the past, over many millennia. The most robust results can be obtained for the Holocene epoch, which started more than 11 000 years ago, whose stable climate minimizes possible uncertainties in the reconstruction. An indirect verification of long-term solar-activity reconstructions supports their veracity and confirms that variations of cosmogenic nuclides on the long-term scale (centuries to millennia) during the Holocene make a solid basis for studies of solar variability in the past. However, such reconstructions may still contain systematic uncertainties related to unknown changes in the geomagnetic field or climate of the past, especially in the early part of the Holocene.

Measurements of the concentration of different cosmogenic isotopes in lunar and meteoritic rocks make it possible to estimate the SEP flux on different timescales. Directly space-borne-measured SEP flux for recent decades is broadly consistent with estimates on longer timescales—up to millions of years. The occurrence of extra-strong events, with the fluence of SEP (with energy greater than 30 MeV) exceeding $5 \times 10^{10}\ \mathrm{cm}^{-2}$ is unlikely on the multi-millennial time scale. The SEP event of 775 AD, discovered using data of cosmogenic isotopes, was the strongest known events, which can serve as the worst case scenario for the entire Holocene.

In general, the following main features are observed in the long-term evolution of solar magnetic activity.

• Solar activity is dominated by the 11-year Schwabe cycle on an interannual timescale. Some additional longer characteristic times can be found, including the Gleissberg secular cycle, de Vries/Suess cycle, and a quasi-cycle of 2000–2400 years (Hallstatt cycle). However, all these longer cycles are intermittent and cannot be regarded as strict phase-locked periodicities.

• One of the main features of long-term solar activity is that it contains an essential chaotic/ stochastic component, which leads to irregular variations and makes solar-activity predictions impossible for a scale exceeding one solar cycle.

• The sun spends about 70% of its time at moderate magnetic activity levels, about 15–20% of its time in a grand minimum and about 10–15% in a grand maximum.

• Grand minima are a typical but rare phenomena in solar behavior. They form a distinct mode of solar dynamo. Their occurrence appears not periodically, but rather as the result of a chaotic process within clusters separated by the 2000–2500 years (around the lows of the Hallstatt cycle). Grand minima tend to be of two distinct types: short (Maunder-like) and longer (Spörer-like).

• The recent level of solar activity (after the 1940s) was very high, corresponding to a prolonged grand maximum, but it has ceased to the normal moderate level. Grand maxima are also rare and irregularly occurring events, though the exact rate of their occurrence is still a subject of debates.

These observational features of the long-term behavior of solar activity have important implications, especially for the development of theoretical solar-dynamo models and for solar-terrestrial studies.