1 Introduction

1.1 Motivation

Autonomous driving is among the most active research areas in the current automotive industry with the aim to improve various aspects of mobility and transportation. Ongoing trends towards Urbanization, Digitalization and Sustainability also result in new vehicle concepts, e.g. FlexCarFootnote 1 and U-ShiftFootnote 2. Those platforms have in common that they are highly automated and explicitly developed for operating in urban environments, for example as people mover, equipped with electric all-wheel drive and dual-axis steering focusing on high maneuverability. Urban environments are of great interest to researchers due to the high density of vehicles and specific traffic rules that have to be followed [1]. These specified conditions in city traffic also lead to new challenges regarding the motion control of vehicles demanding high position accuracy, e.g. the tracking of trajectories with large curvatures. To achieve that, the prediction of the future vehicle behavior is of great importance, especially in dangerous driving situations. With its predictive capability and the capability to explicitly handle constraints, Model predictive control is an excellent control strategy for a precise tracking of trajectories, especially in the area of the motion control of autonomous vehicles [2]. The basic idea of MPC is that using a mathematical model of the real system, its future behavior can be predicted over a time horizon of finite length.

1.2 Related work

A MPC scheme for the lateral and longitudinal control of highly automated vehicles with dual-axis steering and individual e-drive is presented in the following. In [3, 4] Fridrich et al. present a MPC approach to generate predefined driving characteristics using torque vectoring. However, the usage of MPC in this area already dates back almost two decades. In Keviczky et al. [5], present a nonlinear MPC (NMPC) controller where only the front wheel steering angle was used as a control variable for an obstacle avoidance situation, represented with a double lane change on snow with a given initial forward speed. Similarly, in [6] a steering-only MPC controller was designed for a linear time-varying (LTV) vehicle model based on successive online linearization that was also implemented for the first time on a dSPCACE rapid prototyping system with a frequency of 20 Hz. In [7] the authors showed an enhancement in the tracking performance of the MPC controller by combining steering and braking. To reduce the computational complexity of MPC algorithms, Besselmann and Morari present a hybrid MPC approach in [8]. A MPC scheme for the combined control of lateral and longitudinal dynamics can be found in [9], where the control problem is decomposed in a path following and a velocity tracking problem. The authors present the effectiveness of their MPC controller with experimental tests where the controller is executed on a dSPACE MicroAutoBox II with a sampling frequency of 25 Hz. A more recent development of MPC for the control of autonomous vehicles can be seen in [10]. The authors use a learning-based MPC scheme for autonomous racing where a single track model is used as the nominal vehicle model which is improved based on measurement data and machine learning tools.

1.3 Contribution and outline

The main contribution of this paper is the design of an output feedback MPC controller for the lateral and longitudinal control of highly-automated vehicles. The controller considers the wheel steering angle at front and rear axle as well as the individual wheel torques as control input to track a given reference trajectory as close as possible while using the full maneuverability of the vehicle with torque vectoring (TV).

In the following, the MPC prediction model is introduced in Sect. 2 and the equations of motions are derived. The MPC control problem is outlined in Sect. 3. Simulative results are shown and discussed in Sect. 4.

2 Modeling

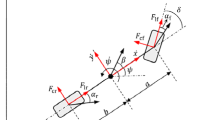
Since MPC strongly relies on a mathematical model of the vehicle, an appropriate model is fundamental to ensure good control performance. Therefore, this section describes the vehicle model used for simulations and the controller design. It is aimed to use the full maneuverability of the vehicle that is accomplished by steering both axles as well as using torque vectoring. For this purpose, a planar two-track model was used as illustrated in Fig. 1 [11, 12]. The absolute car position is denoted by the inertial coordinates X and Y while the car velocity v is given in the local vehicle frame. \(\psi\) denotes the heading angle, \(\delta\) the steering angle and \(\alpha\) the slip angle at each wheel. The lateral tire forces are denoted by \(F_{\text {lat}}\) and likewise the longitudinal ones by \(F_{\text {lon}}\). \(l_f\) and \(l_r\) denote the distance of front and rear axle to the center of gravity. \(s_f\) and \(s_r\) are the track width at front and rear axle. Throughout the paper, forces and torques acting on individual wheels will be subscripted with fl, fr, rl, rr, corresponding respectively to the front left, front right, rear left and rear right wheel. However, for ease of notation the tire quantities were generally subscribed by ij, where possible. For the derivation of the equations of motions, it was assumed that the wheel steering angle at the front tires are the same and the wheel steering angle at the rear tires were the same. Also, no resistance forces are acting on the vehicle.

2.1 Equations of motion

Fig. 1
figure 1

Two-track model

Full size image

The vehicle’s position in an absolute inertial frame are given by the equations

$$\begin{aligned} \dot{X} = \dot{x} \cos (\psi ) - \dot{y} \sin (\psi ) \end{aligned}$$
(1)
$$\begin{aligned} \dot{Y} = \dot{x} \sin (\psi ) + \dot{y} \cos (\psi ) \end{aligned}$$
(2)

The equations of motion can be derived using Newton’s second law.

$$\begin{aligned} \ddot{x}_v&= \frac{1}{m} (F_{x_{fl}}+F_{x_{fr}}+F_{x_{rl}}+F_{x_{rr}}+m \dot{y}_v \dot{\psi }_v) \end{aligned}$$
(3)
$$\begin{aligned} \ddot{y}_v&= \frac{1}{m} (F_{y_{fl}}+F_{y_{fr}}+F_{y_{rl}}+F_{y_{rr}}-m \dot{x}_v \dot{\psi }_v) \end{aligned}$$
(4)
$$\begin{aligned} \ddot{\psi }_v&= \frac{1}{I_{zz}} \bigg [ \frac{s_f}{2}(F_{x_{fr}} - F_{x_{fl}}) + \frac{s_r}{2}(F_{x_{rr}} - F_{x_{rl}}) \nonumber \\&\quad + l_f (F_{y_{fl}} - F_{y_{fr}}) + l_r (F_{y_{rl}} - F_{y_{rr}}) \bigg ] \end{aligned}$$
(5)

In (3–5) the forces acting on the tires, \(F_{x_{ij}}\) and \(F_{y_{ij}}\), are given by

$$\begin{aligned} F_{x_{ij}}&= F_{\text {lon}_{ij}} \cos (\delta _{ij}) - F_{\text {lat}_{ij}} \sin (\delta _{ij}) \end{aligned}$$
(6)
$$\begin{aligned} F_{y_{ij}}&= F_{\text {lon}_{ij}} \sin (\delta _{ij}) + F_{\text {lat}_{ij}} \cos (\delta _{ij}) \end{aligned}$$
(7)

The lateral tire forces \(F_{{\text {lat}}_{ij}}\) in (6–7) are modeled with a simplified Pacejka tire model

$$\begin{aligned} F_{{\text {lat}}_{ij}} = D_{ij} \sin (C_{ij} \arctan (B_{ij} \alpha _{ij})) \end{aligned}$$
(8)

where \(D_{ij}, C_{ij}, B_{ij}\) are specific tire constants [13] and the corresponding tire slip angle \(\alpha _{ij}\) is computed as follows:

$$\begin{aligned} \alpha _{ij}= {\left\{ \begin{array}{ll} \arctan \bigg (\frac{\dot{y}_v+l_f \dot{\psi }}{\dot{x}_v \pm \frac{s_f}{2} \dot{\psi }} \bigg ) - \delta _{ij},&{} \text {for } i = f\\ \arctan \bigg (\frac{\dot{y}_v-l_r \dot{\psi }}{\dot{x}_v \pm \frac{s_r}{2} \dot{\psi }} \bigg ) - \delta _{ij},&{} \text {for } i = r \end{array}\right. } \end{aligned}$$
(9)

The longitudinal tire forces \(F_{{\text {lon}}_{ij}}\) in (6–7) are defined as

$$\begin{aligned} F_{{\text {lon}}_{ij}} = \frac{M_{ij}}{r_{\text {dyn}}} \end{aligned}$$
(10)

where \(M_{ij}\) describe the individual wheel torques and \(r_{\text {dyn}}\) the dynamic rolling radius.

Finally, the nonlinear vehicle dynamics can be described using the Eqs. (1–10) by the following compact differential equation:

$$\begin{aligned} \dot{\mathbf{x }}&= \mathbf{f} (\mathbf{x} , \mathbf{u} ) \end{aligned}$$
(11)
$$\begin{aligned} \mathbf{y}&= \mathbf{g} (\mathbf{x} ) \nonumber \\&= \mathbf{C} \mathbf{x} \end{aligned}$$
(12)

where the state and input vector are chosen as

\(\mathbf{x} = [\dot{x}, \dot{y}, \dot{\psi }, \psi , X, Y]^T\) and \(\mathbf{u} = [\delta _f, \delta _r, M_{fl}, M_{fr}, M_{rl}, M_{rr}]^T\). The computed mean values of the wheel steering angle at the front and rear axle, \(\delta _f\) and \(\delta _r\), are then converted into their respective, absolute rack position of the steering actuator using a kinematic map. Due to the geometry of the axles, this leads to two different wheel steering angles at the left and right side that fulfills the Ackermann condition. In (12), \(\mathbf{y}\) defines the output vector that is used for feedback to track a reference trajectory. Furthermore, the output matrix in (12) is defined as

$$\begin{aligned} \mathbf{C} = \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$
(13)

3 Model predictive control problem

In this section, the MPC scheme that is used in our simulations is presented. The basic idea of MPC schemes is that using a mathematical model of the system, its future behavior over the prediction horizon N shall be predicted, such that the control actions can be chosen in a way that with respect to a quadratic cost function, the deviation of the predicted state of the system to the reference state is minimized [14, 15]. For each discrete time step this open-loop, optimal control problem (OCP) is solved until an optimal open-loop solution \(\widetilde{\mathbf{u }}^\star (\cdot \vert t) = [\widetilde{u}^\star (t \vert t), \widetilde{u}^\star (t+1 \vert t), ...,\widetilde{u}^\star (t+N-1 \vert t)]\) over N is computed. In order to close the loop, the first control action of \(\widetilde{\mathbf{u }}^\star\) is applied to the system. At the next time step \(t+1\) the new system state is measured and the optimization procedure is repeated. In this context, quantities without a “ \(\widetilde{}\) ” are real system trajectories whereas quantities with a “ \(\widetilde{}\) ” are meant to denote predicted trajectories.

Therefore, \(\widetilde{\mathbf{x }}(\cdot \vert t)\) denotes a predicted sequence at time t.

The big advantage of using a model predictive control approach is that not only nonlinear system dynamics can be considered in the controller design but also actuator and design constraints can be explicitly handled. Regarding the actuator constraints of the vehicle, it has to be mentioned that not only the magnitude of the wheel steering angle or the motor torques have to be constrained but more importantly the change of rate of these control inputs, which are typically referred to as the slew rates. However, in a discrete fashion this is not a trivial procedure that can be seen in the following equation for the control slew rate:

$$\begin{aligned} \Delta \mathbf{u }_t = \mathbf{u} _t - \mathbf{u} _{t-1} \end{aligned}$$
(14)

where \(\Delta \mathbf{u }_t\) denotes the slew rate of the control input. To compute the slew rate, the control input of the previous time step is needed. For the optimization problem, the state has to be augmented by the previous control input u and the actual control input applied to the system is then the control slew rate \(\Delta \mathbf{u }_t\). The augmented state then becomes

\(\mathbf{x} _{\text {aug}} = [\mathbf{x} \quad \mathbf{u} _{t-1}]^{T}\) and \(\mathbf{u} = \Delta \mathbf{u }_t\).

Hence, the system dynamics in (11) can be rewritten as

$$\begin{aligned} \dot{\mathbf{x }}&= \mathbf{f} (\mathbf{x} _{\text {aug}}, \Delta \mathbf{u }_t ) \end{aligned}$$
(15)
$$\begin{aligned} \mathbf{y}&= \mathbf{g} (\mathbf{x} _{\text {aug}}) \nonumber \\&= \begin{bmatrix} \begin{array}{c|c} \mathbf{C} &{} \mathbf{0} \\ \hline \mathbf{0} &{} \mathbb {I} \end{array} \end{bmatrix} \mathbf{x} _{\text {aug}} \end{aligned}$$
(16)

where \(\mathbb {I}\) is the identity matrix. For simplicity reasons, the denotation for the augmented state and the slew rate input is neglected in the following. The system dynamics in (15) is discretized over the prediction horizon N using the Euler method and a piecewise constant control parametrization is used in our approach. The discrete MPC problem is formulated as follows:

$$\begin{aligned} \min _{\widetilde{\mathbf{u }}(\cdot \vert t)} \quad&J(\mathbf{y} (t), \widetilde{\mathbf{u }}(\cdot \vert t)) \end{aligned}$$
(17a)
$$\begin{aligned} \text {s.t.} \quad&\widetilde{\mathbf{x }}_{i+1}=\widetilde{\mathbf{x }}_{i}+\Delta t\cdot \mathbf{f} (\widetilde{\mathbf{x }}_i, \widetilde{\mathbf{u }}_i),&i\in [1,N-1] \end{aligned}$$
(17b)
$$\begin{aligned}&\widetilde{\mathbf{x }}(t \vert t) = \mathbf{x} (t) \end{aligned}$$
(17c)
$$\begin{aligned}&\widetilde{\mathbf{y }}_i = \mathbf{g} (\widetilde{\mathbf{x }}_i),&i\in [1,N] \end{aligned}$$
(17d)
$$\begin{aligned}&\mathbf{u} _{\text {min}} \le \mathbf{u} _i \le \mathbf{u} _{\text {max}},&i\in [1,N-1] \end{aligned}$$
(17e)
$$\begin{aligned}&\Delta \mathbf{u} _{\text {min}} \le \Delta \mathbf{u} _i \le \Delta \mathbf{u} _{\text {max}},&i\in [1,N-1] \end{aligned}$$
(17f)

where the quadratic cost function in (17a) is chosen as

$$\begin{aligned} J(\mathbf{y} (t), \widetilde{\mathbf{u }}(\cdot \vert t))=\sum _{i=t}^{t+N-1} \Vert \mathbf{y _{ref}(t)-\widetilde{\mathbf{y }}(i \vert t)} \Vert _\mathbf{W }^2 + \Vert {\widetilde{\mathbf{u }}(i \vert t)} \Vert _\mathbf{R _{\Delta u}}^2 \end{aligned}$$
(18)

The first summand of the cost function in (18) penalizes the deviation of the predicted state trajectories to the desired reference trajectory. The second summand penalizes the predicted control effort. \(\mathbf{W}\) and \(\mathbf{R} _{\Delta u}\) are the corresponding weighting matrices for the augmented output and the control slew rate of appropriate dimensions. Since \(\mathbf{y} (t)\) is the augmented output according to (16) \(\mathbf{W}\) is defined as

$$\begin{aligned} \mathbf{W} = \begin{bmatrix} \begin{array}{c|c} \mathbf{Q} &{} \mathbf{0} \\ \hline \mathbf{0} &{} \mathbf{R} _u \end{array} \end{bmatrix} \end{aligned}$$
(19)

where \(\mathbf{Q}\) is the weight on the vehicle state and \(\mathbf{R} _u\) the weight on the magnitude of the control variables. In this work, \(\mathbf{R} _u = \mathbf{R} _{\Delta u} = \mathbf{R}\). While \(\mathbf{Q}\) is chosen to be positive semidefinite, \(\mathbf{R}\) has to be chosen positive definite since with \(R=0\) for example, a control action of infinite size would not be penalized. In (17b–17d) the constraint enforcing the system dynamics is regarded, where the initial condition in (17c) implies that the initially predicted state coincides with the current measurement of the system. A MPC controller is designed that computes the front and rear steering angle as well as the individual motor torques. Therefore, in (17e) the constraints for the magnitude and in (17f) the slew rates of these control inputs are stated. In our test vehicle, a maximum amplitude of 23° was measured for the wheel steering angle at both axles and each electric motor is able to generate 50 Nm of torque. Consequently, \(\mathbf{u} _{\text {min}} = [-23^\circ {}, -23^\circ {}, 0, 0, 0, 0]^{T}\) and \(\mathbf{u} _{\text {max}} = [23^\circ {}, 23^\circ {}, 50, 50, 50, 50]^{T}\) are used for the constraints in (17e). Furthermore, a slew rate of \(30^\circ {}\)/s for the steering angle and 25 Nm/s for the wheel torques were chosen. With an approximate steering ratio of 15 the slew rate for the wheel steering angle is \(1.5^\circ {}\)/s. Therefore, \(\Delta \mathbf{u} _{\text {min}} = [-1.5^\circ {}, -1.5^\circ {}, -25, -25, -25, -25]^{T}\) and \(\Delta \mathbf{u} _{\text {max}} = -\Delta \mathbf{u} _{\text {min}}\). The MPC problem is solved using ACADOS, a software package for efficiently solving OCPs [16, 17].

It has to be mentioned that the MPC formulation in (17a–17f) does not guarantee stability. It is a well known difficulty that to ensure closed-loop stability, the MPC control problem is usually augmented with a terminal cost and a terminal constraint set \(\mathcal {X}^f\). However, the formulation of a terminal cost can be too restrictive leading to infeasibility of the optimization problem, especially when the prediction horizon is set too short. Therefore, MPC is in practice usually implemented without a terminal constraint set and terminal cost. In [18] stability has been proven for this case by choosing the prediction horizon long enough.

4 Simulation results

The main objective of the controller is to follow a given reference trajectory as close as possible. For this purpose, the controller is tested on standard driving maneuvers, e.g. a double lane change (DLC) maneuver. To analyze the influence of torque vectoring, two controllers were compared. For the first controller, the wheel torques that are necessary to follow the reference velocity are equally distributed whereas for the second controller the wheel torques are individually computed by solving (15). In the following discussion of the results, the controller with equally distributed wheel torques is denoted by \(\text {MPC}_{1}\) and the controller using torque vectoring is denoted by \(\text {MPC}_{2}\). However, for both controllers the following MPC parameters were used in the simulation:

  • Prediction Horizon: \(N = 50\)

  • Sampling Time: \(\delta = 0.05\) s.

  • Weights on tracking error: \(Q_{\Delta Y} = 100\), \(Q_{\Delta \psi } = 10\), \(Q_{\Delta v_{x}} = 1\)

  • Weights on control magnitude: \(R_{\delta _{f}} = 10\), \(R_{\delta _{r}} = 10\), \(R_{M_{fl}} = 10^{-7}\), \(R_{M_{fr}} = 10^{-7}\), \(R_{M_{rl}} = 10^{-7}\), \(Q_{M_{rr}} = 10^{-7}\)

  • Weights on control slew rate: \(R_{\Delta \delta _{f}} = 10\), \(R_{\Delta \delta _{r}} = 10\), \(R_{\Delta M_{fl}} = 10^{-7}\), \(R_{\Delta M_{fr}} = 10^{-7}\), \(R_{\Delta M_{rl}} = 10^{-7}\), \(R_{\Delta M_{rr}} = 10^{-7}\)

In the following results the reference velocity for the DLC maneuver is set to 10 m/s and 15 m/s.

For the analysis of both controllers, first the state trajectories of the Center of Gravity (CoG) position Y(t), the orientation \(\psi (t)\) and the CoG velocity \(v_x(t)\) of the vehicle are plotted against their reference trajectories. Then the corresponding error trajectories will be evaluated and finally the control behavior is illustrated and discussed.

A starting position of \(x_{0} = -40\) m and an initial velocity of \(v_{0} = 8\) m/s is chosen to simulate a short acceleration track before entering the DLC maneuver. It can be seen in Fig. 2 that the vehicle needs quite some time to accelerate until the reference speed of \(v_{ref} = 10\) m/s is reached. This is reasonable since a pretty low slew rate constraint of 25 Nm/s was put on the wheel torques to increase speed moderately. It can be seen that the reference trajectories \(Y_{ref}(t)\) and \(\psi _{ref}(t)\) are tracked very closely. However, the differences in the performance of both controllers are illustrated in Fig. 3, where the error trajectories \(\Vert \mathbf{y _{ref}(t)-\mathbf{y} (t)} \Vert\) are compared. Here, only the interesting part in the time interval from 5 to 16 s. is shown. It can be observed that using torque vectoring the positioning accuracy can be significantly increased from a maximum lateral deviation of \(\sim\)8 cm to \(\sim\)4 cm at t = 12.7 s. Even though a higher positioning accuracy can be reached, it is interesting to see that in the time interval of 11.2 to 12.8 s the orientation error for the \(\text {MPC}_{2}\) is greater than using the pure steering controller, which is due to the fact that a greater weight was put on the positioning error. Keeping the reference velocity \(v_{ref}(t)\) constant during the DLC maneuver, it was tried to analyze the longitudinal tracking behavior of both controllers. Therefore, it is interesting to note that using torque vectoring not only a higher tracking accuracy of the reference position but also a significant better tracking of the velocity reference can be achieved. The maximum velocity error for the first controller is \(\sim\)0.2 m/s where in contrast an error of \(\sim\)0.04 m/s can be achieved using the \(\text {MPC}_{2}\) controller.

Fig. 2
figure 2

State trajectories for a DLC with \(v_{ref}=10\) m/s

Full size image
Fig. 3
figure 3

Error trajectories for a DLC with \(v_{ref}=10\) m/s

Full size image
Fig. 4
figure 4

Control trajectories for a DLC with \(v_{ref}=10\) m/s

Full size image

Looking at the control behavior of both controllers in Fig. 4, it can be observed that both controllers fully accelerate in the first two seconds until the maximum torque of 50 Nm is reached. After approximately 6 s the vehicle reaches the desired velocity before entering the maneuver. During the lane change from 6 to 14 s one can see that there are almost the same steering trajectories with only slightly higher angles for the first controller. The individual wheel torques for the first controller are identical for which reason only one dotted trajectory can be seen. During that time period, the use of torque vectoring can be clearly seen with a wheel torque magnitude of almost 0 Nm for the front right and rear right wheel and up to 30 Nm for the front left and rear left wheel when entering the right curve from 9 to 11 s. In the same fashion, the torque distribution changes in the left curve from 11 to 13 s, where the wheels on right vehicle side take the dominant part and the wheel torques on the left vehicle side drop to almost zero with a short increase at 13 s to guide the vehicle out of the lane change along the horizontal exit. An interesting observation at this point is, that the \(\text {MPC}_{2}\) controller computes almost side-wise identical wheel torques, e.g. that \(M_{fl} \approx M_{rl}\) and \(M_{fr} \approx M_{rr}\). This is due to the fact that on the one hand same weights were put on the wheel torque control inputs and on the other hand a total symmetric vehicle body was chosen which automatically leads to the conclusion that torques on the same vehicle side should be equal. By dynamically adjusting the weight parameters on the wheel torques, torque vectoring with wheel-individual torque can be reached.

However, in our tests no significant improvement of the control performance could be observed using torque vectoring with wheel-individual torques besides a strong increase in the computation time of the control variables.

For the second test an initial position of \(x_{0} = -80\) m and an initial velocity of \(v_{0} = 13\) m/s was set. In Fig. 5 can be seen that a longer acceleration track was set than before to enter the maneuver with the reference speed of \(v_{ref} = 15\) m/s. It is obvious that with the same MPC constraints as before, in this scenario higher reference deviations occur, that can especially be observed for the tracking behavior of \(\psi _{ref}(t)\) and \(v_{ref}(t)\). It can be seen that the errors in Fig. 6 are clearly increased but the overall trend is almost the same as before, where the \(\text {MPC}_{2}\) controller shows a clearly better tracking performance of the position and velocity while the \(\text {MPC}_{1}\) controller performing slightly better in tracking the orientation during the same section of the maneuver as before, between 12 and 14 s.

Comparing the control trajectories in Fig. 7 to the first scenario, it can be observed that the control behavior is more aggressive than before, where the wheel steering and torque trajectories almost look like sawtooths with their corresponding slew rate trajectories alternatingly peaking between their minimum and maximum values during the lane change. The steering trajectories of \(\text {MPC}_{1}\) and \(\text {MPC}_{2}\) are almost identical and compared to before no significant change in the steering peak can be seen. However, regarding the wheel torques it can be said that a greater difference in the side-wise identically computed wheel torques can be seen, e.g. at 11 s, where the difference in the wheel torques of the left and right vehicle side is \(\sim\)40 Nm.

Fig. 5
figure 5

State trajectories for a DLC with \(v_{ref}=15\) m/s

Full size image
Fig. 6
figure 6

Error trajectories for a DLC with \(v_{ref}=15\) m/s

Full size image
Fig. 7
figure 7

Control trajectories for a DLC with \(v_{ref}=15\) m/s

Full size image

Representative for the effectiveness of the MPC controller, the results of a DLC maneuver were presented. However, in all other tested maneuver the controller showed similar good performance. Additional maneuver, to prove the performance of the controller in further urban-like scenarios, is part of ongoing research and will be shown in experimental driving tests.

5 Conclusion and future work

In this paper, a model predictive control approach for the lateral and longitudinal control of highly automated vehicles was presented with a focus on high positioning accuracy and maneuverability, required for driving in urban environments. For this purpose, a MPC controller was designed for vehicles with front and rear steering as well as all-wheel drive. With a standard driving maneuver, the performance of the proposed controller was evaluated in simulations. It could be observed that the controller using TV led to a higher control performance with a higher accuracy in tracking the reference position and velocity. According to the main purpose of this paper, it can be concluded that using the MPC controller with TV the maneuverability of the vehicle and the reference tracking can be considerably increased while achieving a good control performance. Experimental test are yet to be performed to fully validate the effectiveness of the proposed MPC approach. Regarding future research, it is aimed to extend the proposed MPC controller in a next step with a more complex vehicle prediction model, e.g. the inclusion of braking torques as additional control inputs and the consideration of uncertainties.