Benchmark parameters of transmissions

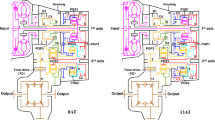
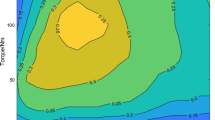
Abstract

The paper explains the influence of the transmission on the energy consumption of a vehicle. In addition to the efficiency of the transmission, the conversion quality has been introduced, which quantifies how efficiently the transmission can operate the connected drive machine. Conversion quality and transmission efficiency influence the energy consumption in different ways. Therefore, the transmission effectiveness is developed to be able to compare different transmissions directly with one another using just one parameter. The higher the transmission effectiveness, the more efficient the transmission operates in the overall context of the drive concept. Furthermore, the transmission effectiveness quantifies the consumption potential of the considered transmission concept. It is described that in the case of conventional drives, an increase in the conversion quality due to an increased ratio spread has led to reductions in energy consumption, although additional mechanical components tend to result in higher mechanical transmission losses. In the case of electrified drives, however, these correlations are reversed. As the recuperation becomes more efficient, especially through an increase in the transmission efficiency, the transmission efficiency will become increasingly important. At the same time, the electrification allows a significant improvement in the conversion quality with the same transmission concept. Due to these fundamentals, dedicated hybrid transmissions will be a key technology to further reduce the energy consumption of hybrid vehicles.