On the Test of Association Between Nonparametric Covariate and Error in Semiparametric Regression Model

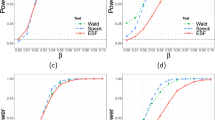
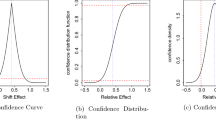
Abstract

Consider a semiparametric regression model $Y=Z\beta +m(X)+\epsilon$, with Y being the response variable, X and Z being the covariates, $\beta$ the unknown parameter, $m(\cdot )$ an unknown function preferably a non-linear one, and $\epsilon$ the random error. In this article, our objective is to test the independence between X and $\epsilon$ only, given the assumption of no relationship between Z and $\epsilon$. Using the concept of Robinson’s (Econometrica 56:931–954, 1988) technique of $\beta$ estimation at the first stage and then considering a transformed nonparametric model, test statistic is formed on the function of induced order statistics of Y. Thereafter constructing Le Cam’s contiguous alternatives, the local powers of the proposed rank-based test statistic as well as power performances of some other relevant statistics are discussed. Further, in reference to the finite sample simulation study, the power performance of newly introduced test is investigated. Finally, for a real biological data the practicability of the proposed test technique under the setting of semiparametric regression model is judged.

Appendix

1.1 Table Showing Power of Different Test Statistics for Different $\gamma$’s

See Tables 2 and 3.

Table 2 Table showing powers of $T_{n,i}$’s in Example (i) for $B=500$

Table 3 Table showing powers of $T_{n,i}$’s in Example (ii) for $B=500$

1.2 Proof of Theorem 1

The quantity $\log L_n$ can be expanded as follows.

$$\begin{aligned} \log L_{n}= & \; {} \displaystyle {\log \prod _{i=1}^{n} \frac{f_{n;X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}}\\= & \; {} \displaystyle {\log \prod _{i=1}^{n} \left \{\frac{(1-\frac{\gamma }{\sqrt{n}})f_{X,\epsilon }(x_i,e_i)+\frac{\gamma }{\sqrt{n}}k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}\right \}} \\= & \; {} \displaystyle {\sum _{i=1}^{n} \log \left \{\frac{(1-\frac{\gamma }{\sqrt{n}})f_{X,\epsilon }(x_i,e_i)+\frac{\gamma }{\sqrt{n}}k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}\right \}}. \end{aligned}$$

Now, using the Taylor expansion of $\log (1+x)$, $x>-1$, and WLLN, one can further derive $\log L_n$ as

$$\begin{aligned} \sum _{i=1}^{n} \frac{\gamma }{\sqrt{n}}\left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) -\frac{\gamma ^{2}}{2n} \sum _{i=1}^{n} \left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) ^2+O_{P}(n^{-1/2}). \end{aligned}$$

(35)

Then,

$$\begin{aligned} \log L_{n}-\sum _{i=1}^{n} \frac{\gamma }{\sqrt{n}}\left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) +\frac{\gamma ^{2}}{2n} \sum _{i=1}^{n} \left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) ^2=O_{P}(n^{-1/2})\longrightarrow 0\,\,\,as\,\,\,n\rightarrow \infty . \end{aligned}$$

Define a sequence of random variables $W_n$ as $\displaystyle {\sum _{i=1}^{n} \frac{\gamma }{\sqrt{n}}\left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) }$. With the help of Lindeberg’s condition, the asymptotic distribution of $W_n$ is developed as $\frac{W_n-E(W_n)}{\sqrt{Var(W_n)}}\overset{L}{\longrightarrow }\,\,N(0,1)$ under $H_0$, where $\displaystyle {E_{H_0}(W_n)=\sum _{i=1}^{n} \frac{\gamma }{\sqrt{n}} E_{H_0} \left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) =0}$ and

$\displaystyle {Var_{H_0}(W_n)=\frac{\gamma ^2}{n}\sum _{i=1}^{n} E_{H_0} \left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) ^{2}=\gamma ^{2}E_{H_0}\left( \frac{k_{X,\epsilon }}{f_{X,\epsilon }}-1\right) ^2}$.

Hence it can be stated that under $H_0$, $W_n\overset{L}{\longrightarrow } N\left( 0,\gamma ^{2}E_{H_0}\left( \frac{k_{X,\epsilon }}{f_{X,\epsilon }}-1\right) ^2\right)$.

Another sequence of random variables $\displaystyle {V_n=\frac{\gamma ^{2}}{2n} \sum _{i=1}^{n} \left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) ^2}$ weakly converges to $\frac{\gamma ^{2}}{2}E_{H_0}\left( \frac{k_{X,\epsilon }}{f_{X,\epsilon }}-1\right) ^2$. So, $\log L_{n}-W_{n}+V_{n}=o_p(1)$, and Slutsky’s theorem further ensures that the limiting distribution of the sequence of random variables $M_n=W_n-V_n$ converges to a random variable M such that

$$\begin{aligned} M\sim N\left( -\frac{1}{2}\gamma ^{2}E_{H_0}\left( \frac{k}{f}-1\right) ^{2}, \gamma ^{2}E_{H_0}\left( \frac{k}{f}-1\right) ^{2}\right) . \end{aligned}$$

(36)

Summing up all the facts one can conclude that $\log L_{n}-M_{n}=o_p(1)$, i.e. $\log L_{n}$ has the limiting distribution which is identical with the limiting distribution of $M_{n}$, i.e. $N(-\frac{1}{2}\sigma ,\sigma )$ where $\sigma =\gamma ^2 E_{H_0}\left( \frac{k}{f}-1\right) ^{2}$. Thereafter, the Corollary 1 of Lemma 1 is sufficient to establish the fact that $H_n$ is a contiguous sequence of alternatives due to asymptotic normality of $\log L_{n}$. Notationally one can express $F_{X,\epsilon }\triangleleft F_{n;X,\epsilon }$.

1.3 Proof of Theorem 9

• (i) The kernel of $T_{n,1}$ is $sign\{(X_{(1)}-X_{(2)})(Y^{*(2)}_{(1)}-Y^{*(2)}_{(2)})\}=f((X_{(1)},Y^{*(2)}_{(1)}),(X_{(2)},Y^{*(2)}_{(2)}))$, say.

  Define,

  $$\begin{aligned} f_{1}(x,y)= & \; {} E[f((X_{(1)},Y^{*(2)}_{(1)}),(X_{(2)},Y^{*(2)}_{(2)}))|X_{(1)}=x,Y^{*(2)}_{(1)}=y] \\= & \; {} E[sign\{(X_{(1)}-X_{(2)})(Y^{*(2)}_{(1)}-Y^{*(2)}_{(2)})\}|X_{(1)}=x,Y^{*(2)}_{(1)}=y] \\= & \; {} 2P[(X_{(1)}-X_{(2)})(Y^{*(2)}_{(1)}-Y^{*(2)}_{(2)})>0|X_{(1)}=x,Y^{*(2)}_{(1)}=y]-1. \end{aligned}$$

  Now, $E_{(X_{(1)},Y^{*(2)}_{(1)})}[f_{1}(X_{(1)},Y^{*(2)}_{(1)})]= E_{(X_{(1)},Y^{*(2)}_{(1)}),(X_{(2)},Y^{*(2)}_{(2)})}[f((X_{(1)},Y^{*(2)}_{(1)}),(X_{(2)},Y^{*(2)}_{(2)}))]=0$ under $H_0$. Then, $\sigma ^{2}_{1} = Var[f_{1}(X_{(1)},Y^{*(2)}_{(1)})]=E[f^{2}_{1}(X_{(1)},Y^{*(2)}_{(1)})]$, where $Y^{*(2)}$ has the same distribution function of $\epsilon ^{*(2)}$ as $H^{*}_{\epsilon }$ in approximate sense.

  Therefore, it is easily seen that $\sigma ^{2}_1>0$ in general; $\sigma ^{2}_{1}=0$ if the samples are either all concordant or all discordant, but this case is not considered here. Hence, by the definition of order of degeneracy of a kernel, one can conclude that f has order of degeneracy 0 as $\sigma ^{2}_{0}=0<\sigma ^{2}_{1}$.

• (ii) The variance of $T_{n,1}$ can be approximated as $\frac{4\sigma ^{2}_1}{n}$ as in Theorem 5(iii) for large n, and that converges to 0 as $n\rightarrow \infty$. Again, $E[sign\{(X_{(i)}-X_{(j)})(Y^{*(2)}_{(i)}-Y^{*(2)}_{(j)})\}]=0$ $\forall$ $1\le i<j\le n$ under $H_0$ as $P[(X_{(i)}-X_{(j)})(Y^{*(2)}_{(i)}-Y^{*(2)}_{(j)})>0]=P[(X_{(i)}-X_{(j)})(Y^{*(2)}_{(i)}-Y^{*(2)}_{(j)})<0]$ when X is independent to $Y^*$. Together they imply that $T_{n,1}$ converges to 0 in probability.

• (iii) A straightforward application of Theorem 6 is enough to prove on the asymptotic distribution of $\sqrt{n}(T_{n,1}-E(T_{n,1}))$ under $H_0$.

• (iv) As a consequence of Le Cam’s third lemma (Van der Vaart 2002; Dhar et al. 2018), the limiting distribution of $(\sqrt{n}(T_{n,1}-E(T_{n,1})), \log L_{n})$ converges to $N_{2} \left( \begin{pmatrix} 0 \\ -\frac{\sigma }{2} \end{pmatrix}, \begin{pmatrix} 4\sigma ^{2}_{1} &{} \tau \\ \tau &{} \sigma \end{pmatrix} \right) ,\,\,\sigma >0$ under $H_0$, which further implies $\sqrt{n}(T_{n,1}-E(T_{n,1}))\overset{L}{\longrightarrow } N(0+\tau , 4\sigma _1^{2})\equiv N(\tau , 4\sigma _1^{2})$ under $H_n$. We have already computed $\sigma ^{2}_1$ and it is sufficient to show that the expression of $\tau$ is identical with $\mu _1$. Note that

  $$\begin{aligned} \tau= & \; {} \displaystyle {\lim _{n\rightarrow \infty } cov_{H_0}(\sqrt{n}(T_{n,1}-E(T_{n,1})),\log L_{n})} \\= & \; {} \displaystyle {\lim _{n\rightarrow \infty } cov_{H_0}(\sqrt{n}(T_{n,1}-E(T_{n,1})), \frac{\gamma }{\sqrt{n}} \sum _{i=1}^{n} \left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) -\frac{\gamma ^{2}}{2n} \sum _{i=1}^{n} \left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) ^2+O_{P}(n^{-1/2}))} \\= & \; {} \displaystyle {\lim _{n\rightarrow \infty } E_{H_0} \left[ (T_{n,1}-E(T_{n,1}))\cdot \gamma \sum _{i=1}^{n} \left( \frac{k_{X,\epsilon }(x_i,e_i)}{f_{X,\epsilon }(x_i,e_i)}-1\right) \right] }, \end{aligned}$$

  which can be further simplified to

  $$\begin{aligned} \displaystyle {2\gamma \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } [2\int _{-\infty }^{x} \int _{-\infty }^{y} dG_X(u)dH^{*}_{\epsilon }(v)+ 2\int _{x}^{\infty } \int _{y}^{\infty } dG_X(u) dH^{*}_{\epsilon }(v)-1]dK_{X,\epsilon }(x,y)}. \end{aligned}$$

  Hence the proof.

1.4 Proof of Theorem 10

• (i) The kernel of $T_{n,2}$ as in (3.3) can be further determined as

  $$\begin{aligned}&g((X_{(1)},Y_{(1)}^{*(2)}),(X_{(2)},Y_{(2)}^{*(2)}),(X_{(3)},Y_{(3)}^{*(2)}),(X_{(4)},Y_{(4)}^{*(2)})),\,say \\&\quad =2I(|X_{(1)}-X_{(2)}|+|X_{(3)}-X_{(4)}|-|X_{(1)}-X_{(3)}|-|X_{(2)}-X_{(4)}|>0, \\&\quad |Y_{(1)}^{*(2)}-Y_{(2)}^{*(2)}|+|Y_{(3)}^{*(2)}-Y_{(4)}^{*(2)}|-|Y_{(1)}^{*(2)}-Y_{(3)}^{*(2)}|-|Y_{(2)}^{*(2)}-Y_{(4)}^{*(2)}|>0)+ \\&\quad 2I(|X_{(1)}-X_{(2)}|+|X_{(3)}-X_{(4)}|-|X_{(1)}-X_{(3)}|-|X_{(2)}-X_{(4)}|<0, \\&\quad |Y_{(1)}^{*(2)}-Y_{(2)}^{*(2)}|+|Y_{(3)}^{*(2)}-Y_{(4)}^{*(2)}|-|Y_{(1)}^{*(2)}-Y_{(3)}^{*(2)}|-|Y_{(2)}^{*(2)}-Y_{(4)}^{*(2)}|<0)-1 \\&\quad = 2P(|Y_{(1)}^{*(2)}-Y_{(2)}^{*(2)}|+|Y_{(3)}^{*(2)}-Y_{(4)}^{*(2)}|-|Y_{(1)}^{*(2)}-Y_{(3)}^{*(2)}|-|Y_{(2)}^{*(2)}-Y_{(4)}^{*(2)}|<0)-1. \end{aligned}$$

  $I(\cdot )$ being an indicator function. Define, for $c=0,\ldots ,4$, $g_c((x_{(1)},y_{(1)}^{*(2)}),\ldots ,(x_{(c)},y_{(c)}^{*(2)}))=E[g((x_{(1)},y_{(1)}^{*(2)}),\ldots ,(x_{(c)},y_{(c)}^{*(2)}),(X_{(c+1)},Y_{(c+1)}^{*(2)}),\ldots ,(X_{(4)},Y_{(4)}^{*(2)}))]$ and, $\sigma ^{2}_c = Var[g_c((X_{(1)},Y_{(1)}^{*(2)}),\ldots ,(X_{(c)},Y_{(c)}^{*(2)}))]$. Next, based upon inequalities $|Y_{(1)}^{*(2)}-Y_{(3)}^{*(2)}|\le |Y_{(1)}^{*(2)}-Y_{(2)}^{*(2)}|+|Y_{(2)}^{*(2)}-Y_{(3)}^{*(2)}|$ and $|Y_{(2)}^{*(2)}-Y_{(4)}^{*(2)}|\le |Y_{(2)}^{*(2)}-Y_{(3)}^{*(2)}|+|Y_{(3)}^{*(2)}-Y_{(4)}^{*(2)}|$, one can finally derive $P(Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)},Y_{(1)}^{*(2)}>Y_{(4)}^{*(2)})$ as

  $$\begin{aligned} P(Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)},Y_{(1)}^{*(2)}>Y_{(4)}^{*(2)}, Y_{(3)}^{*(2)}>Y_{(1)}^{*(2)})+P(Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)},Y_{(1)}^{*(2)}>Y_{(4)}^{*(2)},Y_{(3)}^{*(2)}\le Y_{(1)}^{*(2)})=\frac{1}{4!}\times 6=\frac{1}{4}. \end{aligned}$$

  Similarly, $P(Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)},Y_{(1)}^{*(2)}\le Y_{(4)}^{*(2)})=\frac{1}{4}$. Then, $P(Y_{(2)}^{*(2)}<Y_{(3)}^{*(2)})=\frac{1}{2}=P(Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)})$, implying that $2P(|Y_{(1)}^{*(2)}-Y_{(2)}^{*(2)}|+|Y_{(3)}^{*(2)}-Y_{(4)}^{*(2)}|-|Y_{(1)}^{*(2)}-Y_{(3)}^{*(2)}|-|Y_{(2)}^{*(2)}-Y_{(4)}^{*(2)}|<0)=2\min \{\frac{1}{2},\frac{1}{2}\}=1$. Hence, $E[g((X_{(1)},Y_{(1)}^{*(2)}),(X_{(2)},Y_{(2)}^{*(2)}),(X_{(3)},Y_{(3)}^{*(2)}),(X_{(4)},Y_{(4)}^{*(2)}))]=0$, and $\sigma ^{2}_1$ can be expressed as $cov[g((X_{(1)},Y_{(1)}^{*(2)}),(X_{(2)},Y_{(2)}^{*(2)}),(X_{(3)},Y_{(3)}^{*(2)}),(X_{(4)},Y_{(4)}^{*(2)}))$ which further becomes $1+4P[Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)},Y_{(5)}^{*(2)}>Y_{(6)}^{*(2)}]-2P[Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)}]-2P[Y_{(5)}^{*(2)}>Y_{(6)}^{*(2)}]$. For any distinct numbers $i_1$, $i_2$, $i_3$, $i_4\in \{1,\ldots ,7\}$, $P[Y_{(i_1)}^{*(2)}>Y_{(i_2)}^{*(2)}>Y_{(i_3)}^{*(2)}>Y_{(i_4)}^{*(2)}]=\frac{6}{4!}=\frac{1}{4}$ and eventually $P[Y_{(i_1)}^{*(2)}>Y_{(i_2)}^{*(2)}]=\frac{1}{2}$ can be obtained. Then $\sigma ^{2}_1=1+4\cdot \frac{1}{4}-2\cdot \frac{1}{2}-2\cdot \frac{1}{2}=0$ which implies that the order of degeneracy of the kernel $g(\cdot )$ is at least 1. Next, we deduce $\sigma ^{2}_2$ as $1+4P[Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)},Y_{(2)}^{*(2)}>Y_{(5)}^{*(2)}]-2P[Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)}]-2P[Y_{(2)}^{*(2)}>Y_{(5)}^{*(2)}]$. By the method of combinatorics, one can simplify it as $4\cdot 5\cdot 6 P[Y_{(2)}^{*(2)}>Y_{(3)}^{*(2)}>Y_{(5)}^{*(2)}>Y_{(6)}^{*(2)}>Y_{(4)}^{*(2)}>Y_{(1)}^{*(2)}]+4\cdot 5\cdot 6 P[Y_{(2)}^{*(2)}>Y_{(5)}^{*(2)}>Y_{(3)}^{*(2)}>Y_{(6)}^{*(2)}>Y_{(4)}^{*(2)}>Y_{(1)}^{*(2)}]=2\times \frac{4\cdot 5\cdot 6}{6!}=\frac{1}{3}$. Ultimately, one can get $\sigma ^{2}_2=1+4\cdot \frac{1}{3}-2\cdot \frac{1}{2}-2\cdot \frac{1}{2}=\frac{1}{3}>0$, henceforth $T_{n,2}$ has order of degeneracy 1.

• (ii) Using Result 1 by Bairamov et al. (2010), it is easy to verify that $(|X_{(i)}-X_{(j)}|+|X_{(k)}-X_{(l)}|-|X_{(i)}-X_{(k)}|-|X_{(j)}-X_{(l)}|)(|Y^{*(2)}_{(i)}-Y^{*(2)}_{(j)}|+|Y^{*(2)}_{(k)}-Y^{*(2)}_{(l)}|-|Y^{*(2)}_{(i)}-Y^{*(2)}_{(k)}|-|Y^{*(2)}_{(j)}-Y^{*(2)}_{(l)}|)=O_{p}(\frac{\log n}{n}),\,\,\,\forall 1\le i<j<k<l\le n$. Also, the distribution function of $(|\epsilon ^{*(2)}_{(i)}-\epsilon ^{*(2)}_{(j)}|+|\epsilon ^{*(2)}_{(k)}-\epsilon ^{*(2)}_{(l)}|-|\epsilon ^{*(2)}_{(i)}-\epsilon ^{*(2)}_{(k)}|-|\epsilon ^{*(2)}_{(j)}-\epsilon ^{*(2)}_{(l)}|)$ can be derived as $\displaystyle {\int _{-\infty }^{\infty } \Big \{H^{*}_{\epsilon }\left( v+\frac{t}{2}\right) -H^{*}_{\epsilon }\left( v-\frac{t}{2}\right) \Big \}dH^{*}_{\epsilon }(v)}$, denoted by $H^{^{*(2)}}_{\epsilon }(t)$, say, for $t\in {\mathbb {R}}$. A similar argument as done in proof of Theorem 9 can be made that the distribution function of $\epsilon ^{*(2)}$ is approximately identical with the distribution function of $Y^{*(2)}$. By Slutsky’s theorem, it is evident that $a(X_{(i)},X_{(j)},X_{(k)},X_{(l)})a(Y^{*(2)}_{(i)},Y^{*(2)}_{(j)},Y^{*(2)}_{(k)},Y^{*(2)}_{(l)})$ converges to 0 in probability $\forall$ $1\le i<j<k<l\le n$, which leads us to conclude that $T_{n,2}\overset{P}{\longrightarrow } 0$ as $n\rightarrow \infty$ further.

• (iii) Since $T_{n,2}$ has order of degeneracy 1, following the footstep of Theorem 7, it can be concluded straightaway that $n(T_{n,2}-E(T_{n,2}))$ weakly approaches towards a non-degenerate random variable of the form ${\sum _{i=1}^{\infty } \lambda _{i}(Z_i^{2}-1)}$ with $\lambda _i$’s being eigenvalues associated with l(x, y). The complete proof can be deduced by borrowing the methodologies of Serfling (1980), Lee (1990).

• (iv) Theorem 8, originally proposed by Gregory (1977), is required to complete the proof on the form of the limiting law of $n(T_{n,2}-E(T_{n,2}))$ under $H_n$.

1.5 Proof of Theorem 11

• (i) Similar proof will be carried out as in proving the order of degeneracy of $T_{n,2}$ to be 1.

• (ii) Analogous to the proof of Theorem 10(ii).

• (iii) Analogous to the proof of Theorem 10(iii).

• (iv) Analogous to the proof of Theorem 10(iv).