Binominal Mixture Lindley Distribution: Properties and Applications

Abstract

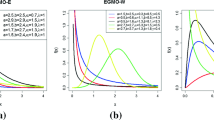
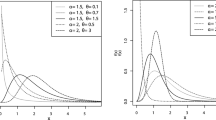
In this paper, we introduce a generalized mixture distribution, so-called the binomial mixture Lindley distribution (BMLD). The density function of this distribution is obtained by mixing binomial probabilities with gamma distribution. BMLD have various distributions as its special cases and posses various shapes for its hazard rate function including increasing, decreasing, bathtub shape and upside down bathtub shape depending on its parameters. Several mathematical, structural and statistical properties of the new distribution is presented such as moments, moment generating function, hazard rate function, vitality function, mean residual life function, inequality measures, entropy and extropy etc. The parameters of the model are estimated using the method of maximum likelihood and finally real life data sets are considered to illustrate the relevance of the new model by comparing it with some other lifetime models.

Appendix

The second partial and cross derivatives with respect to the parameters are derived as,

$$\begin{aligned} \begin{aligned}&\frac{\partial ^{2} \log l}{\partial \theta ^{2}}= \frac{2n}{(\theta +\beta )^{2}}+\frac{1}{\theta ^2}\sum \limits _{i=1}^{n}\frac{1}{(A_{i}+B_{i}+C_{i})^2}\bigg \{\Big (A_{i}+B_{i}+C_{i} \Big )\Big (\alpha _0(\alpha _0-1)A_{i}\\&\quad +(\alpha _1+1)\alpha _1 B_{i}+(\alpha _2+2)(\alpha _2+1)C_i\Big )\\&\quad - \Big (\alpha _0A_{i}+(\alpha _1+1)B_{i}+(\alpha _2+2)C_{i}\Big )^2 \bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \theta \partial \beta }= \frac{2n}{(\theta +\beta )^{2}}+\frac{1}{\theta \beta }\sum \limits _{i=1}^{n}\frac{1}{(A_{i}+B_{i}+C_{i})^2}\bigg \{(\alpha _{0}-\alpha _{1}-1) A_{i}B_{i}\\&\quad +2(\alpha _{0}-\alpha _{2}-2)A_{i}C_{i}+(\alpha _{1}-\alpha _{2}-1)B_{i}C_{i} \bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \theta \partial \alpha _{0}}= \frac{1}{\theta }\sum \limits _{i=1}^{n}\frac{A_i}{(A_{i}+B_{i}+C_{i})^2}\bigg \{\Big (A_{i}+B_{i} +C_{i}\Big )\bigg (1+\alpha _0\Big (\log (\theta x_{i})-\psi (\alpha _{0})\Big )\bigg )\\&\quad - \Big (\alpha _0A_{i}+(\alpha _1+1)B_{i}+(\alpha _2+2)C_{i}\Big ) \Big (\log (\theta x_{i})-\psi (\alpha _{0})\Big ) \bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \theta \partial \alpha _{1}}= \frac{1}{\theta }\sum \limits _{i=1}^{n}\frac{B_i}{(A_{i}+B_{i}+C_{i})^2}\bigg \{\Big (A_{i}+B_{i} +C_{i}\Big )\bigg (1+(\alpha _1+1)\Big (\log (\theta x_{i})-\psi (\alpha _{1})\Big )\bigg )\\&\quad - \Big (\alpha _0A_{i}+(\alpha _1+1)B_{i}+(\alpha _2+2)C_{i}\Big )\Big (\log (\theta x_{i})-\psi (\alpha _{1})\Big ) \bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \theta \partial \alpha _{2}}= \frac{1}{\theta }\sum \limits _{i=1}^{n}\frac{C_i}{(A_{i}+B_{i}+C_{i})^2}\bigg \{\Big (A_{i}+B_{i} +C_{i}\Big )\bigg (1+(\alpha _2+2)\Big (\log (\theta x_{i})-\psi (\alpha _{2})\Big )\bigg )\\&\quad - \Big (\alpha _0 A_{i}+(\alpha _1+1)B_{i}+(\alpha _2+2)C_{i}\Big )\Big (\log (\theta x_{i}) -\psi (\alpha _{2})\Big ) \bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \beta ^{2}}= \frac{2n}{(\theta +\beta )^{2}}+\frac{1}{\beta ^{2}}\sum \limits _{i=1}^{n}\frac{1}{(A_{i}+B_{i}+C_{i})^2}\bigg \{2A_i(A_i+B_i+C_i)-(2A_i+B_i)^2 \bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \beta \partial \alpha _{0}}= \frac{1}{\beta }\sum \limits _{i=1}^{n}\frac{A_i}{(A_{i}+B_{i}+C_{i})^2}\bigg \{\Big (\log (\theta x_{i})-\psi (\alpha _{0})\Big )\Big (B_i+2C_i\Big )\bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \beta \partial \alpha _{1}}= \frac{1}{\beta }\sum \limits _{i=1}^{n}\frac{B_i}{(A_{i}+B_{i}+C_{i})^2}\bigg \{\Big (\log (\theta x_{i})-\psi (\alpha _{1})\Big )\Big (C_i-A_i\Big )\bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \beta \partial \alpha _{2}}= \frac{1}{\beta }\sum \limits _{i=1}^{n}\frac{C_i}{(A_{i}+B_{i}+C_{i})^2}\bigg \{-\Big (\log (\theta x_{i})-\psi (\alpha _{2})\Big )\Big (2A_i+B_i\Big )\bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \alpha _{0}^{2}}= \sum \limits _{i=1}^{n}\frac{A_i}{(A_{i}+B_{i}+C_{i})^2}\bigg \{\Big (A_{i}+B_{i} +C_{i}\Big )\bigg (\Big (\log (\theta x_{i})-\psi (\alpha _{0})\Big )^{2}-\psi ^{'}(\alpha _{0})\bigg )\\&\quad - A_{i}\Big (\log (\theta x_{i})-\psi (\alpha _{0})\Big )^2 \bigg \}, \frac{\partial ^{2} \log l}{\partial \alpha _{0}\partial \alpha _{1}}\\&\quad = \sum \limits _{i=1}^{n}\frac{1}{(A_{i}+B_{i}+C_{i})^2}\bigg \{- A_{i}B_{i}\Big (\log (\theta x_{i})-\psi (\alpha _{0})\Big )\Big (\log (\theta x_{i})-\psi (\alpha _{1})\Big ) \bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \alpha _{0}\partial \alpha _{2}}= \sum \limits _{i=1}^{n}\frac{1}{(A_{i}+B_{i}+C_{i})^2}\bigg \{- A_{i}C_{i}\Big (\log (\theta x_{i})-\psi (\alpha _{0})\Big )\Big (\log (\theta x_{i})-\psi (\alpha _{2})\Big ) \bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \alpha _{1}^{2}}= \sum \limits _{i=1}^{n}\frac{B_i}{(A_{i}+B_{i}+C_{i})^2}\bigg \{\Big (A_{i}+B_{i} +C_{i}\Big )\bigg (\Big (\log (\theta x_{i})-\psi (\alpha _{1})\Big )^{2}-\psi ^{'}(\alpha _{1})\bigg )\\&\quad - B_{i}\Big (\log (\theta x_{i})-\psi (\alpha _{1})\Big )^2 \bigg \},\\&\quad \frac{\partial ^{2} \log l}{\partial \alpha _{1}\partial \alpha _{2}}= \sum \limits _{i=1}^{n}\frac{1}{(A_{i}+B_{i}+C_{i})^2}\bigg \{- B_{i}C_{i}\Big (\log (\theta x_{i})-\psi (\alpha _{1})\Big )\Big (\log (\theta x_{i})-\psi (\alpha _{2})\Big ) \bigg \} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \frac{\partial ^{2} \log l}{\partial \alpha _{2}^{2}}=&\sum \limits _{i=1}^{n}\frac{C_i}{(A_{i}+B_{i}+C_{i})^2}\bigg \{\Big (A_{i}+B_{i} +C_{i}\Big )\bigg (\Big (\log (\theta x_{i})-\psi (\alpha _{2})\Big )^{2}-\psi ^{'}(\alpha _{2})\bigg )\\&- C_{i}\Big (\log (\theta x_{i})-\psi (\alpha _{2})\Big )^2 \bigg \}. \end{aligned} \end{aligned}$$