Abstract
Monte Carlo based methods such as path tracing are widely used in movie production. To achieve low noise, they require many samples per pixel, resulting in long rendering time. To reduce the cost, one solution is Monte Carlo denoising, which renders the image with fewer samples per pixel (as little as 128) and then denoises the resulting image. Many Monte Carlo denoising methods rely on deep learning: they use convolutional neural networks to learn the relationship between noisy images and reference images, using auxiliary features such as position and normal together with image color as inputs. The network predicts kernels which are then applied to the noisy input. These methods show powerful denoising ability, but tend to lose geometric or lighting details and to blur sharp features during denoising.
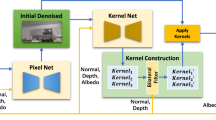
In this paper, we solve this issue by proposing a novel network structure, a new input feature—light transport covariance from path space—and an improved loss function. Our network separates feature buffers from the color buffer to enhance detail effects. The features are extracted separately and then integrated into a shallow kernel predictor. Our loss function considers perceptual loss, which also improves detail preservation. In addition, we use a light transport covariance feature in path space as one of the features, which helps to preserve illumination details. Our method denoises Monte Carlo path traced images while preserving details much better than previous methods.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Keller, A.; Fascione, L.; Fajardo, M.; Georgiev, I.; Christensen, P.; Hanika, J.; Eisenacher, C.; Nichols, G. The path tracing revolution in the movie industry. In: Proceedings of the ACM SIGGRAPH 2015 Courses, Article No. 24, 2015.
Bako, S.; Vogels, T.; McWilliams, B.; Meyer, M.; NováK, J.; Harvill, A.; Sen, P.; Derose, T.; Rousselle, F. Kernel-predicting convolutional networks for denoising Monte Carlo renderings. ACM Transactions on Graphics Vol. 36, No. 4, Article No. 97, 2017.
Vogels, T.; Rousselle, F.; McWilliams, B.; Röthlin, G.; Harvill, A.; Adler, D.; Meyer, M.; Novák, J. Denoising with kernel prediction and asymmetric loss functions. ACM Transactions on Graphics Vol. 37, No. 4, Article No. 124, 2018.
Belcour, L.; Bala, K.; Soler, C. A local frequency analysis of light scattering and absorption. ACM Transactions on Graphics Vol. 33, No. 5, Article No. 163, 2014.
Kalantari, N. K.; Bako, S.; Sen, P. A machine learning approach for filtering Monte Carlo noise. ACM Transactions on Graphics Vol. 34, No. 4, Article No. 122, 2015.
Chaitanya, C. R. A.; Kaplanyan, A. S.; Schied, C.; Salvi, M.; Lefohn, A.; Nowrouzezahrai, D.; Aila, T. Interactive reconstruction of Monte Carlo image sequences using a recurrent denoising autoencoder. ACM Transactions on Graphics Vol. 36, No. 4, Article No. 98, 2017.
Gharbi, M.; Li, T. M.; Aittala, M.; Lehtinen, J.; Durand, F. Sample-based Monte Carlo denoising using a kernel-splatting network. ACM Transactions on Graphics Vol. 38, No. 4, Article No. 125, 2019.
Yang, X.; Wang, D.; Hu, W.; Zhao, L.-J.; Yin, B.-C.; Zhang, Q.; Wei, X.-P.; Fu, H. DEMC: A deep dualencoder network for denoising Monte Carlo rendering. Journal of Computer Science and Technology Vol. 34, 1123–1135, 2019.
Sen, P.; Zwicker, M.; Rousselle, F.; Yoon, S.-E.; Kalantari, N. Denoising your Monte Carlo renders: Recent advances in image-space adaptive sampling and reconstruction. In: Proceedings of the ACM SIGGRAPH 2015 Courses, Article No. 11, 2015.
Sen, P.; Darabi, S. On filtering the noise from the random parameters in Monte Carlo rendering. ACM Transactions on Graphics Vol. 31, No. 3, Article No. 18, 2012.
Rousselle, F.; Manzi, M.; Zwicker, M. Robust denoising using feature and color information. Computer Graphics Forum Vol. 32, No. 7, 121–130, 2013.
Moon, B.; Jun, J. Y.; Lee, J.; Kim, K.; Hachisuka, T.; Yoon, S. E. Robust image denoising using a virtual flash image for Monte Carlo ray tracing. Computer Graphics Forum Vol. 32, No. 1, 139–151, 2013.
Zimmer, H.; Rousselle, F.; Jakob, W.; Wang, O.; Adler, D.; Jarosz, W.; Sorkine-Hornung, O.; Sorkine-Hornung, A. Path-space motion estimation and decomposition for robust animation filtering. Computer Graphics Forum Vol. 34, No. 4, 131–142, 2015.
Moon, B.; Carr, N.; Yoon, S.-E. Adaptive rendering based on weighted local regression. ACM Transactions on Graphics Vol. 33, No. 5, Article No. 170, 2014.
Bitterli, B.; Rousselle, F.; Moon, B.; Iglesias-Guitián, J. A.; Adler, D.; Mitchell, K.; Jarosz, W.; Novák, J. Nonlinearly weighted first-order regression for denoising Monte Carlo renderings. Computer Graphics Forum Vol. 35, No. 4, 107–117, 2016.
Moon, B.; McDonagh, S.; Mitchell, K.; Gross, M. Adaptive polynomial rendering. ACM Transactions on Graphics Vol. 35, No. 4, Article No. 40, 2016.
Boughida, M.; Boubekeur, T. Bayesian collaborative denoising for Monte Carlo rendering. Computer Graphics Forum Vol. 36, No. 4, 137–153, 2017.
Liang, Y. L.; Wang, B. B.; Wang, L.; Holzschuch, N. Fast computation of single scattering in participating media with refractive boundaries using frequency analysis. IEEE Transactions on Visualization and Computer Graphics doi: 10.1109/TVCG.2019.2909875, 2019.
Durand, F.; Holzschuch, N.; Soler, C.; Chan, E.; Sillion, F. X. A frequency analysis of light transport. ACM Transactions on Graphics Vol. 24, No. 3, 1115–1126, 2005.
Belcour, L.; Soler, C.; Subr, K.; Holzschuch, N.; Durand, F. 5D covariance tracing for efficient defocus and motion blur. ACM Transactions on Graphics Vol. 32, No. 3, Article No. 31, 2013.
Simonyan, K.; Zisserman, A. Two-stream convolutional networks for action recognition in videos. In: Proceedings of the Advances in Neural Information Processing Systems 27, 568–576, 2014.
Yang, Q. S.; Yan, P. K.; Zhang, Y. B.; Yu, H. Y.; Shi, Y. Y.; Mou, X. Q.; Kalra, M. K.; Zhang, Y.; Sun, L.; Wang, G. Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss. IEEE Transactions on Medical Imaging Vol. 37, No. 6, 1348–1357, 2018.
Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.
Bitterli, B. Tungsten renderer. Available at http://noobody.org/tungsten.html.
Bitterli, B. Rendering resources. 2016. Available at https://benediktbitterli.me/resources/.
Abadi, M.; Agarwal, A.; Barham, P. Tensorow: Large scale machine learning on heterogeneous systems. 2015. Available at http://tensorflow.org/.
Kingma, D. P.; Ba, J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In: Proceedings of the 13th International Conference on Artificial Intelligence and Statistics, 249–256, 2010.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Weiheng Lin is a master candidate in the School of Computer Science and Engineering, Nanjing University of Science and Technology (NJUST). He received his bachelor degree from NJUST in 2018. His research interests include rendering and machine learning.
Beibei Wang is an associate professor at NJUST. She received her Ph.D. degree from Shandong University in 2014 and visited Telecom ParisTech from 2012 to 2014. She worked as a postdoc in INRIA from 2015 to 2017. She joined NJUST in March 2017. Her research interests include rendering and game development.
Lu Wang is a professor at the School of Software, Shandong University. She received her Ph.D. degree from Shandong University in 2009. Her research interests include photorealistic rendering and high performance rendering.
Nicolas Holzschuch is a senior researcher at INRIA Grenoble Rhˆone- Alpes, and the scientific leader of the MAVERICK research team. He received his Ph.D. degree from Grenoble University in 1996 and his habilitation in 2007. He joined INRIA in 1997. His research interests include photorealistic rendering and real-time rendering, with an emphasis on material models and participating media.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095. To submit a manuscript, please go to https://www.editorialmanager.com/cvmj.
About this article
Cite this article
Lin, W., Wang, B., Wang, L. et al. A detail preserving neural network model for Monte Carlo denoising. Comp. Visual Media 6, 157–168 (2020). https://doi.org/10.1007/s41095-020-0167-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41095-020-0167-7