Abstract
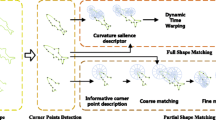
Shape matching plays an important role in various computer vision and graphics applications such as shape retrieval, object detection, image editing, image retrieval, etc. However, detecting shapes in cluttered images is still quite challenging due to the incomplete edges and changing perspective. In this paper, we propose a novel approach that can efficiently identify a queried shape in a cluttered image. The core idea is to acquire the transformation from the queried shape to the cluttered image by summarising all point-to-point transformations between the queried shape and the image. To do so, we adopt a point-based shape descriptor, the pyramid of arc-length descriptor (PAD), to identify point pairs between the queried shape and the image having similar local shapes. We further calculate the transformations between the identified point pairs based on PAD. Finally, we summarise all transformations in a 4D transformation histogram and search for the main cluster. Our method can handle both closed shapes and open curves, and is resistant to partial occlusions. Experiments show that our method can robustly detect shapes in images in the presence of partial occlusions, fragile edges, and cluttered backgrounds.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Jacobs, C. E.; Finkelstein, A.; Salesin, D. H. Fast multiresolution image querying. In: Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, 277–286, 1995.
Granlund, G. H. Fourier preprocessing for hand print character recognition. IEEE Transactions on Computers Vol. C-21, No. 2, 195–201, 1972.
Persoon, E.; Fu, K. S. Shape discrimination using Fourier descriptors. IEEE Transactions on Systems, Man, and Cybernetics Vol. 7, No. 3, 170–179, 1977.
Zhang, D.; Lu, G. Enhanced generic Fourier descriptors for object-based image retrieval. In: Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, IV-3668–IV-3671, 2002.
Mokhtarian, F.; Mackworth, A. K. A theory of multiscale, curvature-based shape representation for planar curves. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 14, No. 8, 789–805, 1992.
Mokhtarian, F.; Abbasi, S.; Kittler, J. Efficient and robust retrieval by shape content through curvature scale space. Image Databases and Multi-Media Search Vol. 8, 51–58, 1998.
Alajlan, N.; El Rube, I.; Kamel, M. S.; Freeman, G. Shape retrieval using triangle-area representation and dynamic space warping. Pattern Recognition Vol. 40, No. 7, 1911–1920, 2007.
Manay, S.; Cremers, D.; Hong, B.-W.; Yezzi, A. J.; Soatto, S. Integral invariants for shape matching. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 28, No. 10, 1602–1618, 2006.
Hong, B. W.; Soatto, S. Shape matching using multiscale integral invariants. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 37, No. 1, 151–160, 2015.
Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 24, No. 4, 509–522, 2002.
Ling, H.; Jacobs, D. W. Shape classification using the inner-distance. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 29, No. 2, 286–299, 2007.
Kwan, K. C.; Sinn, L. T.; Han, C.; Wong, T.-T.; Fu, C.-W. Pyramid of arclength descriptor for generating collage of shapes. ACM Transactions on Graphics Vol. 35, No. 6, Article No. 229, 2016.
Chuang, G. C. H.; Kuo, C. C. J. Wavelet descriptor of planar curves: Theory and applications. IEEE Transactions on Image Processing Vol. 5, No. 1, 56–70, 1996.
Tabbone, S.; Wendling, L.; Salmon, J.-P. A new shape descriptor defined on the radon transform. Computer Vision and Image Understanding Vol. 102, No. 1, 42–51, 2006.
Lee, S.-M.; Abbott, A. L.; Clark, N. A.; Araman, P. A. A shape representation for planar curves by shape signature harmonic embedding. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1940–1947, 2006.
Hu, M.-K. Visual pattern recognition by moment invariants. IRE Transactions on Information Theory Vol. 8, No. 2, 179–187, 1962.
Khotanzad, A.; Hong, Y. H. Invariant image recognition by Zernike moments. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 12, No. 5, 489–497, 1990.
Belkasim, S. O.; Shridhar, M.; Ahmadi, M. Pattern recognition with moment invariants: A comparative study and new results. Pattern Recognition Vol. 24, No. 12, 1117–1138, 1991.
Sheng, Y.; Shen, L. Orthogonal Fourier–Mellin moments for invariant pattern recognition. Journal of the Optical Society of America A Vol. 11, No. 6, 1748–1757, 1994.
Bernier, T.; Landry, J.-A. A new method for representing and matching shapes of natural objects. Pattern Recognition Vol. 36, No. 8, 1711–1723, 2003.
Mori, G.; Belongie, S.; Malik, J. Shape contexts enable efficient retrieval of similar shapes. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Vol. 1, I-723–I-730, 2001.
Mori, G.; Belongie, S.; Malik, J. Efficient shape matching using shape contexts. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 27, No. 11, 1832–1837, 2005.
Mori, G.; Malik, J. Recognizing objects in adversarial clutter: Breaking a visual CAPTCHA. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Vol. 1, I-134–I-141, 2003.
Tanase, M.; Veltkamp, R. C. Part-based shape retrieval. In: Proceedings of the 13th Annual ACM International Conference on Multimedia, 543–546, 2005
Tănase, M.; Veltkamp, R. C.; Haverkort, H. Multiple polyline to polygon matching. In: Algorithms and Computation. Lecture Notes in Computer Science, Vol. 3827. Deng, X.; Du, D. Z. Eds. Springer, Berlin, Heidelberg, 60–70, 2005.
Pickup, D.; Sun, X.; Rosin, P. L.; Martin, R. R. Skeleton-based canonical forms for non-rigid 3D shape retrieval. Computational Visual Media Vol. 2, No. 3, 231–243, 2016.
Xu, K.; Chen, K.; Fu, H.; Sun, W.-L.; Hu, S.-M. Sketch2Scene: Sketch-based co-retrieval and co-placement of 3D models. ACM Transactions on Graphics Vol. 32, No. 4, Article No. 123, 2013.
Lian, W.; Zhang, L.; Zhang, D. Rotation-invariant nonrigid point set matching in cluttered scenes. IEEE Transactions on Image Processing Vol. 21, No. 5, 2786–2797, 2012.
Thayananthan, A.; Stenger, B.; Torr, P. H. S.; Cipolla, R. Shape context and chamfer matching in cluttered scenes. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Vol. 1, I-127–I-133, 2003.
Riemenschneider, H.; Donoser, M.; Bischof, H. Using partial edge contour matches for efficient object category localization. In: Computer Vision–ECCV 2010. Lecture Notes in Computer Science, Vol. 6315. Daniilidis, K.; Maragos, P.; Paragios, N. Eds. Springer, Berlin, Heidelberg, 29–42, 2010.
Bai, X.; Li, Q.; Latecki, L. J.; Liu, W.; Tu, Z. Shape band: A deformable object detection approach. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 1335–1342, 2009.
Cheng, M.-M.; Zhang, F.-L.; Mitra, N. J.; Huang, X.; Hu, S.-M. RepFinder: Finding approximately repeated scene elements for image editing. ACM Transactions on Graphics Vol. 29, No. 4, Article No. 83, 2010.
Toshev, A.; Taskar, B.; Daniilidis, K. Shape-based object detection via boundary structure segmentation. International Journal of Computer Vision Vol. 99, No. 2, 123–146, 2012.
Chi, Y.; Leung, M. K. H. Part-based object retrieval in cluttered environment. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 29, No. 5, 890–895, 2007.
Ren, S.; He, K.; Girshick, R.; Sun, J. Faster RCNN: Towards real-time object detection with region proposal networks. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 39, No. 6, 1137–1149, 2017.
Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 779–788, 2016.
Gidaris, S.; Komodakis, N. Object detection via a multi-region and semantic segmentation-aware CNN model. In: Proceedings of the IEEE International Conference on Computer Vision, 1134–1142, 2015.
Canny, J. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. PAMI-8, No. 6, 679–698, 1986.
Cui, M.; Femiani, J.; Hu, J.; Wonka, P.; Razdan, A. Curve matching for open 2D curves. Pattern Recognition Letters Vol. 30, No. 1, 1–10, 2009.
Ferrari, V.; Fevrier, L.; Jurie, F.; Schmid, C. Groups of adjacent contour segments for object detection. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 30, No. 1, 36–51, 2008.
Jeannin, S.; Bober, M. Description of core experiments for MPEG-7 motion/shape. MPEG- 7, ISO/IEC/JTC1/SC29/WG11/MPEG99 N, 2690, 1999.
Acknowledgements
This project was supported by the Research Grants Council of the Hong Kong Special Administrative Region, under the RGC General Research Fund (Project No. CUHK 14217516).
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is published with open access at Springerlink.com
Chu Han graduated from South China Agricultural University in 2011 with a B.Sc. degree in computer science. He received his M.Phil. degree in computer science from South China University of Technology in 2014, under the supervision of Prof. Xuemiao Xu. He is now pursuing his Ph.D. degree in the Department of Computer Science and Engineering of the Chinese University of Hong Kong, under the supervision of Prof. Tien-Tsin Wong. His current research interests include computer graphics, image processing, pattern recognition, and computer vision.
Xueting Liu received her B.Eng. degree from Tsinghua University and Ph.D. degree from the Chinese University of Hong Kong in 2009 and 2014 respectively. She is currently a postdoctoral research fellow in the Department of Computer Science and Engineering of the Chinese University of Hong Kong. Her research interests include computer graphics, computer vision, computational manga and anime, and non-photorealistic rendering.
Lok Tsun Sinn graduated from the Chinese University of Hong Kong with a B.Sc. degree in computer science, and is studying for his M.Phil. degree in computer science and engineering in the same department, under the supervision of Prof. Tien-Tsin Wong.
Tien-Tsin Wong received his B.Sc., M.Phil., and Ph.D. degrees in computer science from the Chinese University of Hong Kong in 1992, 1994, and 1998, respectively. He is currently a professor in the Department of Computer Science and Engineering of the Chinese University of Hong Kong. His main research interests include computer graphics, computational manga, precomputed lighting, image-based rendering, GPU techniques, medical visualization, multimedia compression, and computer vision. He received an IEEE Transactions on Multimedia Prize Paper Award in 2005 and a Young Researcher Award in 2004.
Rights and permissions
Open Access The articles published in this journal are distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095. To submit a manuscript, please go to https://www.editorialmanager.com/cvmj.
About this article
Cite this article
Han, C., Liu, X., Sinn, L.T. et al. TransHist: Occlusion-robust shape detection in cluttered images. Comp. Visual Media 4, 161–172 (2018). https://doi.org/10.1007/s41095-018-0104-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41095-018-0104-1