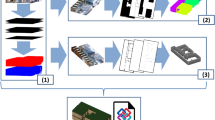
Abstract
Poisson disk sampling is an important problem in computer graphics and has a wide variety of applications in imaging, geometry, rendering, etc. In this paper, we propose a novel Poisson disk sampling algorithm based on disk packing. The key idea uses the observation that a relatively dense disk packing layout naturally satisfies the Poisson disk distribution property that each point is no closer to the others than a specified minimum distance, i.e., the Poisson disk radius. We use this property to propose a relaxation algorithm that achieves a good balance between the random and uniform properties needed for Poisson disk distributions. Our algorithm is easily adapted to image stippling by extending identical disk packing to unequal disks. Experimental results demonstrate the efficacy of our approaches.
Article PDF
Similar content being viewed by others
References
Pharr, M.; Humphreys, G. Physically Based Rendering: From Theory to Implementation. San Francisco, C A, USA: Morgan Kaufmann Publishers Inc.,2004.
Deussen, O.; Hiller, S.; Van Overveld, C.; Strothotte, T. Floating points: A method for computing stipple drawings. Computer Graphics Forum Vol. 19, No. 3, 41–50, 2000.
Secord, A. Weighted Voronoi stippling. In: Proceedings of the 2nd international symposium on Non-photorealistic animation and rendering, 37–43, 2002.
Deussen, O.; Hanrahan, P.; Lintermann, B.; Mh, R.; Pharr, M.; Prusinkiewicz, P. Realistic modeling and rendering of plant ecosystems. In: Proceedings of the 25th annual conference on Computer graphics and interactive techniques, 275–286, 1998.
Surazhsky, V.; Alliez, P.; Gotsman, C. Isotropic remeshing of surfaces: A local parameterization approach. In: 12th International Meshing Roundtable, 215–224, 2003.
Cook, R. L. Stochastic sampling in computer graphics. ACM Transactions on Graphics Vol. 5, No. 1, 51–72, 1986.
Jones, T. R. Efficient generation of Poisson-disk sampling patterns. Journal of Graphics, G PU, and Game Tools Vol. 11, No. 2, 27–36, 2006.
Dunbar, D.; Humphreys, G. A spatial data structure for fast Poisson-disk sample generation. ACM Transactions on Graphics Vol. 25, No. 3, 503–508, 2006.
White, K. B.; Cline, D.; Egbert, P. K. Poisson disk point sets by hierarchical dart throwing. In: IEEE Symposium on Interactive Ray Tracing, 129–132, 2007.
Ebeida, M. S.; Davidson, A. A.; Patney, A.; Knupp, P. M.; Mitchell, S. A.; Owens, J. D. Efficient maximal Poisson-disk sampling. In: ACM SIGGRAPH 2011 papers, Article No. 49, 2011.
Yan, D.-M.; Wonka, P. Gap processing for adaptive maximal Poisson-disk sampling. ACM Transactions on Graphics Vol. 32, No. 5, Article No. 148, 2013.
Wei, L.-Y. Parallel Poisson disk sampling. In: ACM SIGGRAPH 2008 papers, Article No. 20, 2008.
Xiang, Y.; Xin, S.-Q.; Sun, Q.; He, Y. Parallel and accurate Poisson disk sampling on arbitrary surfaces. In: SIGGRAPH Asia 2011 Sketches, Article No. 18, 2011.
Ebeida, M. S.; Mitchell, S. A.; Patney, A.; Davidson, A. A.; Owens, J. D. A simple algorithm for maximal Poisson-disk sampling in high dimensions. Computer Graphics Forum Vol. 31, No. 2, 785–794, 2012.
Gamito, M. N.; Maddock, S. C. Accurate multidimensional Poisson-disk sampling. ACM Transactions on Graphics Vol. 29, No. 1, Article No. 8, 2009.
Dippe, M. A. Z.; Wold, E. H. Antialiasing through stochastic sampling. In: Proceedings of the 12th annual conference on Computer graphics and interactive techniques, 69–78, 1985.
Cohen, M. F.; Shade, J.; Hiller, S.; Deussen, O. Wang tiles for image and texture generation. ACM Transactions on Graphics Vol. 22, No. 3, 287–294, 2003.
Ostromoukhov, V.; Donohue, C.; Jodoin, P.-M. Fast hierarchical importance sampling with blue noise properties. ACM Transactions on Graphics Vol. 23, No. 3, 488–495, 2004.
Kopf, J.; Cohen- Or, D.; Deussen, O.; Lischinski, D. Recursive Wang tiles for real-time blue noise. ACM Transactions on Graphics Vol. 25, No. 3, 509–518, 2006.
Ostromoukhov, V. Sampling with polyominoes. ACM Transactions on Graphics Vol. 26, No. 3, Article No. 78, 2007.
Lloyd, S. Least squares quantization in pcm. IEEE Transactions on Information Theory Vol. 28, No. 2, 129–137, 1982.
McCool, M.; Fiume, E. Hierarchical Poisson disk sampling distributions. In: Proceedings of the conference on Graphics interface, 94–105, 1992.
Balzer, M.; Schlömer, T.; Deussen, O. Capacity-constrained point distributions: A variant of Lloyd’s method. ACM Transactions on Graphics Vol. 28, No. 3, Article No. 86, 2009.
Chen, Z.; Yuan, Z.; Choi, Y.-K.; Liu, L.; Wang, W. Variational blue noise sampling. IEEE Transactions on Visualization and Computer Graphics Vol. 18, No. 10, 1784–1796, 2012.
Goes, F.; Breeden, K.; Ostromoukhov, V.; Desbrun, M. Blue noise through optimal transport. ACM Transactions on Graphics Vol. 31, No. 6, Article No. 171, 2012.
Zhou, Y.; Huang, H.; Wei, L.-Y.; Wang, R. Point sampling with general noise spectrum. ACM Transactions on Graphics Vol. 31, No. 4, Article No. 76, 2012.
Öztireli, A. C.; Gross, M. Analysis and synthesis of point distributions based on pair correlation. ACM Transactions on Graphics Vol. 31, No. 6, Article No. 170, 2012.
Heck, D.; Schlömer, T.; Deussen, O. Blue noise sampling with controlled aliasing. ACM Transactions on Graphics Vol. 32, No. 3, Article No. 25, 2013.
Wachtel, F.; Pilleboue, A.; Coeurjolly, D.; Breeden, K.; Singh, G.; Cathelin, G.; de Goes, F.; Desbrun, M.; Ostromoukhov, V. Fast tile-based adaptive sampling with user-specified Fourier spectra. ACM Transactions on Graphics Vol. 33, No. 4, Article No. 56, 2014.
Ebeida, M. S.; Awad, M. A.; Ge, X.; Mahmoud, A. H.; Mitchell, S. A.; Knupp, P. M.; Wei, L.-Y. Improving spatial coverage while preserving the blue noise of point sets. Computer-Aided Design Vol. 46, 25–36, 2014.
Chen, J.; Ge, X.; Wei, L.-Y.; Wang, B.; Wang, Y.; Wang, H.; Fei, Y.; Qian, K.-L.; Yong, J.-H. Wang, W. Bilateral blue noise sampling. ACM Transactions on Graphics Vol. 32, No. 6, Article No. 216, 2013.
Kepler, J. The Six-Cornered Snowflake. Oxford, UK: Clarendon Press, 1966.
Lubachevsky, B. D.; Graham, R. L. Curved hexagonal packings of equal disks in a circle. Discrete & Computational Geometry Vol. 18, No. 2, 179–194, 1997.
Szabó, P. G.; Markót, M. Cs.; Csendes, T.; Specht, E.; Casado, L. G.; Garcia, I. New Approaches to Circle Packing in a Square: With Program Codes. New York, N Y, USA: Springer-Verlag, 2007.
Graham, R. L.; Lubachevsky, B. D. Dense packings of equal disks in an equilateral triangle: From 22 to 34 and beyond. The Electronic Journal of Combinatorics Vol. 2, No. 1, A1, 1995.
Birgin, E. G.; Sobral, F. N. C. Minimizing the object dimensions in circle and sphere packing problems. Computers and Operations Research Vol. 35, No. 7, 2357–2375, 2008.
Addis, B.; Locatelli, M.; Schoen, F. Efficiently packing unequal disks in a circle. Operations Research Letters Vol. 36, No. 1, 37–42, 2008.
Pintér, J. D.; Kampas, F. J. MathOptimizer professional: Key features and illustrative applications. In: Nonconvex Optimization and Its Applications, Vol. 84 Global Optimization. Liberti, L.; Maculan, N. Eds. New York, N Y, USA: Springer-Verlag, 263–279, 2006.
Huang, W. Q.; Li, Y.; Akeb, H.; Li, C. M. Greedy algorithms for packing unequal circles into a rectangular container. Journal of the Operational Research Society Vol. 56, No. 5, 539–548, 2005.
Lu, Z.; Huang, W. PERM for solving circle packing problem. Computers & Operations Research Vol. 35, No. 5, 1742–1755, 2008.
Wang, H.; Huang, W.; Zhang, Q.; Xu, D. An improved algorithm for the packing of unequal circles within a larger containing circle. European Journal of Operational Research Vol. 141, No. 2, 440–453, 2002.
Lu, L.; Choi, Y.-K.; Sun, F.; Wang, W. Variational circle packing based on power diagram. Technical report. The University of Hong Kong, 2011. Available at http://vr.sdu.edu.cn/~lulin/CP TechReport.pdf.
Aurenhammer, F. Power diagrams: Properties, algorithms and applications. SIAM Journal on Computing Vol. 16, No. 1, 78–96, 1987.
Liu, Y.; Wang, W.; Levy, B.; Sun, F.; Yan, D.-M.; Lu, L.; Yang, C. On centroidal voronoi tessellation—energy smoothness and fast computation. ACM Transactions on Graphics Vol. 28, No. 4, Article No. 101, 2009.
Lagae, A.; Dutré, P. A comparison of methods for generating Poisson disk distributions. Computer Graphics Forum Vol. 27, No. 1, 114–129, 2008.
Fabri, A.; Pion, S. CGAL: The computational geometry algorithms library. In: Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, 538–539, 2009.
Schmaltz, C.; Gwosdek, P.; Bruhn, A.; Weickert, J. Electrostatic halftoning. Computer Graphics Forum Vol. 29, No. 8, 2313–2327, 2010.
Fattal, R. Blue-noise point sampling using kernel density model. ACM Transactions on Graphics Vol. 30, No. 4, Article No. 48, 2011.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is published with open access at Springerlink.com
Guanghui Liang received the BSEE degree in computer science and technology from Shandong University, China, in 2012. Currently, he is studying at Shandong University for a master’s degree. His research interests include computer graphics, computational geometry, and visualization.
Lin Lu is an associate professor of computer science in Shandong University, China. She got her B.Eng. (2002) and M.Eng. (2005) degrees in Shandong University, and Ph.D. (2011) degree in the University of Hong Kong, all in computer science. Her research interests include computer graphics and geometry processing.
Zhonggui Chen received B.S. and Ph.D. degrees in applied mathematics from Zhejiang University, in 2004 and 2009, respectively. Currently, he is working as an associate professor in the Department of Computer Sciences, School of Information Science and Technology, Xiamen University, China. His research interests include computer graphics and computational geometry.
Chenglei Yang is a professor at Shandong University, China. He holds a Ph.D. degree in computer science from Shandong University. His interests include human–computer interaction, virtual reality, computational geometry, and computer graphics. His work involves a variety of research topics such as data modeling and rendering, visibility computing, path planning, collision detection, cooperative design, and interaction in the domains of immersive learning systems.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liang, G., Lu, L., Chen, Z. et al. Poisson disk sampling through disk packing. Comp. Visual Media 1, 17–26 (2015). https://doi.org/10.1007/s41095-015-0003-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41095-015-0003-7