Skip to main content
SpringerLink
Log in

Multi-criteria decision making based on novel fuzzy knowledge measures

  • Original Paper
  • Published:
Granular Computing Aims and scope Submit manuscript

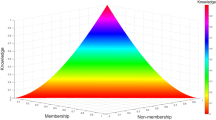
Abstract

Knowledge is related to the information considered in a particularly useful context under consideration. A knowledge measure as a dual of fuzzy entropy quantifies the knowledge associated with a fuzzy set. In this paper, a new entropy-based fuzzy knowledge measure is proposed and validated. The performance of the proposed knowledge measure is explained using two numerical examples. Furthermore, a new multi-criteria decision-making method based on the proposed knowledge measure is introduced and illustrated using a numerical example. Besides this, four new measures namely a fuzzy accuracy measure, a knowledge measure using fuzzy accuracy measure, a similarity measure, and a fuzzy information measure are derived from the proposed knowledge measure and validated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

  • Atanassov KT (1986) Intutionistic fuzzy sets. Fuzzy Sets Syst 20:87–96

    Article  Google Scholar 

  • Ohlan A (2022) Novel entropy and distance measure for interval-valued intuitionistic fuzzy sets with application in multi-criteria group decision-making. Int J Gen Syst. https://doi.org/10.1080/03081079.2022.2036138

  • Arya V, Kumar S (2021) Multi-criteria decision making problem for evaluating ERP system using entropy weighting approach and q-rung orthopair fuzzy TODIM. Granul Comput 6:977–989

    Article  Google Scholar 

  • Arya V, Kumar S (2020) Knowledge measure and entropy: a complementary concept in fuzzy theory. Granul Comput 6(3):631–643

    Article  Google Scholar 

  • Boekee DE, Vander Lubbe JCA (1980) The \(R\)-norm information measure. Inf Control 45:136–155

    Article  MathSciNet  MATH  Google Scholar 

  • Brans JP, Mareschel V (1984) PROMETHEE: a new family of outranking methods in multicriteria analysis. In: Brans JP (ed) Operational research 84. North-Holland, New York, pp 477–490

  • Benayoun R, Roy B, Sussman B (1966) ELECTRE: Une méthode pour guider le choix en présence de points de vue multiples. Note de travail 49. Direction Scientifique: SEMA-METRA International

  • Chen T, Li C (2010) Determining objective weights with intutionistic fuzzy entropy measures: a comparative analysis. Inf Sci 180:4207–4222

    Article  Google Scholar 

  • Chu ATW, Kalaba RE, Spingarn K (1979) A comparison of two methods for determining the weights of belonging to fuzzy sets. J Optim Theor App 27:531–538

    Article  MathSciNet  MATH  Google Scholar 

  • Choo EU, Wedley WC (1985) Optimal criterion weights in repetitive multicriteria decision making. J Oper Res Soc 36:983–992

    Article  MATH  Google Scholar 

  • Chen SJ, Chen SM (2001) A new method to measure the similarity between fuzzy numbers. IEEE Int Conf Fuzzy Syst 3:1123–1126

    Google Scholar 

  • Chen SM, Hsiao W-H, Jong W-T (1997) Bidirectional approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets Syst 91(3):339–353

    Article  MathSciNet  MATH  Google Scholar 

  • Chen SM, Hsiao W-H (2000) Bidirectional approximate reasoning for rule-based systems using interval-valued fuzzy sets. Fuzzy Sets Syst 113(2):185–203

    Article  MathSciNet  MATH  Google Scholar 

  • Chen SM (1997) Interval-valued fuzzy hypergraph and fuzzy partition. IEEE Trans Syst Man Cybern Part B (Cybern) 27(4):725–733

    Article  Google Scholar 

  • Luca AD, Termini S (1972) A definition of non-probabilistic entropy in the setting of fuzzy set theory. Inf Control 20:301–312

    Article  MATH  Google Scholar 

  • Fan J (2002) Some new fuzzy entropy formulas. Fuzzy Sets Syst 2002(128):277–284

    Article  MathSciNet  MATH  Google Scholar 

  • Fan ZP (1996) Complicated multiple attribute decision making: theory and applications. Ph.D. Dissertation, Northeastern university, Shenyang, China (1996)

  • Gomes LFAM, Lima MMPP (1991) Todim: basic and application to multicriteria ranking of projects with environmental impacts. Found Comput Decis Sci 16:113–127

    MATH  Google Scholar 

  • Gupta R, Kumar S (2022) Intuitionistic fuzzy scale-invariant entropy with correlation coefficients-based VIKOR approach for multi-criteria decision-making. Granul Comput 7(1):77–93

    Article  Google Scholar 

  • Havdra JH, Charvat F (1967) Quantification method classification process: concept of structural \(\alpha\)-entropy. Kybernetika 3:30–35

    MathSciNet  Google Scholar 

  • Hung WL, Yang MS (2006) Fuzzy entropy on intutionistic fuzzy sets. Int J Intell Syst 21:443–451

    Article  MATH  Google Scholar 

  • Hwang CL, Lin MJ (1987) Group decision making under multiple criteria: methods and applications. Springer, Berlin

    Book  MATH  Google Scholar 

  • Hooda DS (2004) On generalized measures of fuzzy entropy. Mathematica slovaca 54:315–325

    MathSciNet  MATH  Google Scholar 

  • Hwang CL, Yoon KP (1981) Multiple attribute decision-making: methods and applications. Springer, New York

    Book  MATH  Google Scholar 

  • Hwang CH, Yang MS (2008) On entropy of fuzzy sets. Int J Uncertain Fuzz Knowl Based Syst 16:519–527

    Article  MathSciNet  MATH  Google Scholar 

  • Joshi R, Kumar S (2016) \((R, S)\)-norm information measure and a relation between coding and questionnaire theory. Open Syst Inf Dyn 23(3):1–12

    Article  MathSciNet  MATH  Google Scholar 

  • Joshi R, Kumar S (2017) A new exponential fuzzy entropy of order-\((\alpha ,\beta )\) and its application in multiple attribute decision making. Commun Math Stat 5(2):213–229

    Article  MathSciNet  MATH  Google Scholar 

  • Joshi R, Kumar S (2018) An \((R^{\prime }, S^{\prime })\)-norm fuzzy relative information measure and its applications in strategic decision-making. Comput Appl Math 37:4518–4543

    Article  MathSciNet  MATH  Google Scholar 

  • Joshi R, Kumar S (2018) An exponential Jensen fuzzy divergence measure with applications in multiple attribute decision-making. Math Probl Eng. https://doi.org/10.1155/2018/4342098

  • Joshi R, Kumar S (2018) A new weighted \((\alpha, \beta )\)-norm information measure with applications in coding theory. Phys A Stat Mech Appl 510:538–551

    Article  MathSciNet  MATH  Google Scholar 

  • Joshi R, Kumar S (2018) A novel fuzzy decision making method using entropy weights based correlation coefficients under intuitionistic fuzzy environment. Int J Fuzzy Syst. https://doi.org/10.1007/s40815-018-0538-8

  • Joshi R, Kumar S (2018) An \((R, S)\)-norm fuzzy information measure with its applications in multiple-attribute decision-making. Comput Appl Math 37:2943–2964

    Article  MathSciNet  MATH  Google Scholar 

  • Kosko B (1986) Fuzzy entropy and conditioning. Inf Sci 40(2):165–174

    Article  MathSciNet  MATH  Google Scholar 

  • Kullback S, Leibler RA (1951) On information and sufficiency. Ann Math Stat 22:79–86

    Article  MathSciNet  MATH  Google Scholar 

  • Kerridge DF (1961) Inaccuracy and inference. J Roy Stat Soc Ser B Methodol 23:184–194

    MathSciNet  MATH  Google Scholar 

  • Kaufmann A (1975) Introduction to the theory of fuzzy subsets. Academic Press, New York, p 1975

    Google Scholar 

  • Ratika K, Kumar S (2020) A novel intuitionistic Renyi’s-Tsallis discriminant information measure and its applications in decision-making. Granul Comput 6(4):901–913

    Google Scholar 

  • Liu M, Ren H (2014) A new intutionistic fuzzy entropy and application in multi-attribute decision-making. Information 5:587–601

    Article  Google Scholar 

  • Li P, Liu B (2008) Entropy of credibility distributions for fuzzy variables. IEEE Trans Fuzzy Syst 16:123–129

    Article  Google Scholar 

  • Montes I, Pal NR, Montes S (2018) Entropy measures for Atanassov intuitionistic fuzzy sets based on divergence. Soft Comput 22:5051–5071

    Article  MATH  Google Scholar 

  • Nguyen H (2015) A new knowledge-based measure for Intuitionistic Fuzzy Sets and its application in multiple attribute group decision making. Expert Syst Appl 42(22):8766–8774

    Article  Google Scholar 

  • Pal NR, Pal SK (1989) Object background segmentation using new definitions of entropy. IEE Proc Eng 366:284–295

    Google Scholar 

  • Opricovic S (1998) Multi-criteria optimization of civil engineering systems. Ph.D. Thesis, University of Belgrade, Belgrade, Serbia

  • Opricovic S, Tzeng GH (2004) Decision aiding compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS. Eur J Oper Res 156:445–455

    Article  MATH  Google Scholar 

  • Renyi A (1961) On measures of entropy and information. In: Proceedings of 4th Barkley symposium on mathematics statistics and probability, vol 1, University of California Press, pp 547–561

  • Saaty TL (1980) The analytical hierarchy process. McGraw-Hill, New York

    MATH  Google Scholar 

  • Shannon CE (1948) A mathematical theory of communication. Bell Syst Tech J 27:379–423

    Article  MathSciNet  MATH  Google Scholar 

  • Singh S, Lalotra S, Sharma S (2019) Dual concepts in fuzzy theory: entropy and knowledge measure. https://doi.org/10.1002/int.22085

  • Smarandache F (2006) Neutrosophic set—a generalization of the intuitionistic fuzzy set. In: IEEE international conference on granular computing. https://doi.org/10.1109/GRC.2006.1635754

  • Szmidt E, Kacprzyk J, Bujnowski P (2010) On some measures of information and knowledge for intuitionistic fuzzy sets. In: 14-th international conference on IFSs, notes IFS, vol 16, no 2, pp 1–11

  • Szmidt E, Kacprzyk J, Bujnowski P (2014) How to measure the amount of knowledge conveyed by Atanassov’s intuitionistic fuzzy sets. Inf Sci 257:276–285

    Article  MathSciNet  MATH  Google Scholar 

  • Szmidt E, Kacprzyk J (2001) Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst 118(3):467–477

    Article  MathSciNet  MATH  Google Scholar 

  • Tsallis C (1988) Possible generalization of Boltzman-Gibbs statistics. J Stat Phys 52:480–487

    Article  Google Scholar 

  • Torra V, Narukawa Y (2009) On hesitant fuzzy sets and decision. In: The IEEE conference on fuzzy systems, Jeju Island, Korea, pp 1378–1382

  • Turksen IB (1986) Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst 20(2):191–210

    Article  MathSciNet  MATH  Google Scholar 

  • Verma R, Sharma BD (2011) A measure of inaccuracy between two fuzzy sets. Cybern Inf Technol 11:13–23

    MathSciNet  Google Scholar 

  • Wei CP, Wang P, Zhang YZ (2011) Entropy, similarity measure for interval-valued intuitionistic fuzzy sets and their application. Inf Sci 181(19):4273–4286

    Article  MathSciNet  MATH  Google Scholar 

  • Xia M, Xu Z (2012) Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment. Inf Fus 13:31–47

    Article  Google Scholar 

  • Ye J (2010) Fuzzy dcision-making method based on the weighted correlation coefficient under intutionistic fuzzy enviornment. Eur J Oper Res 205:202–204

    Article  Google Scholar 

  • Yu PL (1973) A class of solutions for group decision making problem. Manag Sci 19:936–946

    Article  MATH  Google Scholar 

  • Yager RR (1979) On the measure of fuzziness and negation part I: membership in the unit interval. Int J Gen Syst 5(4):221–229

    Article  MATH  Google Scholar 

  • Yager R (2020) Decision-making with measure modeled uncertain payoffs and multiple goals. Granul Comput 5(2):149–154

    Article  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inf Comput 8(3):338–353

    MATH  Google Scholar 

  • Zadeh LA (1968) Probability measures of fuzzy events. J Math Anal Appl 23:421–427

    Article  MathSciNet  MATH  Google Scholar 

  • Zavadskas EK, Kaklauskas A, Sarka V (1994) The new method of multicriteria complex proportional assessment of projects. Technol Econ Dev Econ 1(3):131–139

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, DAV University, Jalandhar, Punjab, 144012, India

    Rajesh Joshi

Authors
  1. Rajesh Joshi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rajesh Joshi.

Ethics declarations

Conflict of interests

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Joshi, R. Multi-criteria decision making based on novel fuzzy knowledge measures. Granul. Comput. 8, 253–270 (2023). https://doi.org/10.1007/s41066-022-00329-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s41066-022-00329-y

Keywords

Search

Navigation