Introduction

The dynamic analysis of multibody models is the primary approach to the study of railway vehicles running on tracks. This is also an important approach for vehicle homologation, as it is was investigated in the DynoTrain project [1], because it allows not only to reduce the need for experimental tests, thus reducing their approval costs, but also investigate the vehicle dynamics in different conditions, thus providing a means to its improvement.

The virtual homologation of railway vehicles serves not only to accept the vehicle running in a railway network, but also can be used to analyze the vehicle–track interaction. From the homologation process described in the standards [2], the vehicle behavior is assessed in terms of running safety, ride quality and track loading by characteristic values (CV) which must be within the acceptable thresholds. The use of the CV in the virtual homologation process has been demonstrated in several studies with different purposes. Polach et al. [3] presented a validation approach where the agreement between CV obtained from simulations and those obtained from experimental tests accomplish selected criteria. Magalhães et al. [4] analyzed the CV obtained from several simulations of a light rail vehicle running in a realistic track with the goal of understanding the impact of the modeling assumptions of the vehicle and the effect of the operational velocity on its acceptance for operation in a metric gauge railway track.

The dynamic analysis of a railway vehicle running in a given track requires the use of three models: vehicle; track and wheel–rail contact force. The vehicle model is characterized by a set of rigid and/or flexible bodies that are interconnected by force elements and joints. The representation of the mechanical elements that constrain the relative motion between structural elements is crucial to preserve the representativeness of the model. Springs, dampers, air springs and actuators are examples of force elements commonly used in railway vehicles. A review on modeling of these force elements is presented in the references [5]. The railway track model requires the parameterization of its geometry. In this work, the pre-processor methodology proposed by Pombo and Ambrósio [6] is used. This methodology implemented in a computational pre-processor, which describes fully the three-dimensional track and includes also the track irregularities, returns one database for each rail in which the position and orientation of the rail is given as function of the rail length. The interaction between the vehicle and the track is represented by a wheel–rail contact model [7, 8]. For studies with focus on the vehicle dynamics, the realism of the contact forces generated in the wheel–rail contact must be assessed as described in the standards [2], namely, by comparing the simulated contact forces with the experimental ones which are measured from static and dynamics tests.

The design or the modification of a vehicle depends on the approach used. Older strategies consist of using simple formulae [9], for example, it is considered only the vertical dynamics. These cases lead to lower accuracy. Nowadays, the current computer capacity allows dealing with complete and detailed numerical models. In this case, the models are simulated in batch mode, namely, under the control of an optimization method [10].

This work presents a methodology to improve the quality of a railway vehicle in terms of its running safety and ride quality [10]. The vehicle is represented by a detailed multibody model of the light rail vehicle [4]. The scenario is an existing mountainous railway track. Since the track is composed of curves of different geometry, the vehicle speed is adjusted as a function of the track length to cancel the cant deficiency [11]. The objectives of the optimal problem are based on the post-processing described in the standards [2], which involved not only the definition of novel dynamic performance indices (DP), but also the definition of a penalty term that avoids cases where the CV exceeds the limits. The selection of the design variables is based not only on easy and economical modification of existing vehicles, but also on their impact on the vehicle dynamics. The optimization tool developed here runs in successive dynamic analysis in batch mode, i.e., without requiring any manual intervention from the user, under control of the direct multisearch method [12] to identify an optimal vehicle design. The optimization results obtained with this approach demonstrate effectively that, by a small adjustment of the vehicle suspension characteristics, a better performance is obtained both in terms of running safety and ride quality.

Multibody simulation

Vehicle model

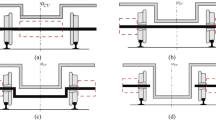
The multibody model of the light rail vehicle presented by Magalhães et al. [4] is used in this work. This vehicle is composed of a carbody that is supported by two bogies. One bogie is powered by a diesel engine, designated as motor bogie, while the other one is a trailer. Each bogie is composed of one bogie frame, two wheelsets and four axleboxes, which include the primary suspension. The carbody and bogie frames are connected by the secondary suspension elements. The suspension system of the vehicle is schematically presented in Fig. 1.

Fig. 1
figure 1

Suspension of the light rail vehicle [11]

Full size image

Two helicoidal springs, assembled vertically at each axlebox, are used to support the bogie frame. These suspension components are characterized not only by an axial stiffness, but also by a transversal stiffness [5]. For this reason, three linear force elements, with stiffness properties defined for the vertical, longitudinal and lateral directions, are used to model each helicoidal spring. The primary suspension of the light rail vehicle is also composed of two vertical guides, which are rigidly attached to the bogie frame and pass through the holes that exist in each axlebox. These elements are mainly responsible for transmitting the longitudinal and lateral forces in the primary suspension. To model the guides, cylindrical joints with clearances are used [13]. The axleboxes include tapered rolling bearings to allow and control the relative rotation between the wheelset and the axlebox. These mechanical elements are modeled here by revolute joints.

The secondary suspension of the light rail vehicle consists of a kingpin, assembled centrally at each bogie, being modeled as a cylindrical joint with bushing [13]. The carbody is supported by the bogies through four skate plates. Each skate is supported by a pair of conical rollers, which are constrained vertically by two elastic elements. Due to this configuration, only the vertical forces are transmitted between the carbody and the bogie frames by the roller-skate elements. To represent correctly the forces introduced in the horizontal plane, these suspension components are modeled here using vertical linear force elements with an abnormal length, established only for numerical purposes. Table 1 lists the suspension parameters of the light rail vehicle [4].

Table 1 Suspension parameters [4]
Full size table

Track model

To characterize the track geometry, four parameters defined as function of the track length are required: the gauge, G, which is the distance between the inner edges of the rail heads; the instantaneous radius of the track, R; the cant angle, φ, which is the track inclination with respect to the horizontal plane; the rail cant, β, which is the rail inclination with respect to the track plane. The parameters G, φ and β are depicted in Fig. 2. In nominal conditions, G and β are constant, while the curvature, i.e., the inverse of R, and φ varies with the track length, being constant in tangent and curve segments and varying linearly in transition curve segments.

Fig. 2
figure 2

Gauge (G), cant angle (φ) and rail cant (β)

Full size image

In reality, the track geometry changes over the years due to its usage, thus leading to irregularities [6]. The track irregularities can be split into four categories, namely, gauge deviation, ΔG; cant deviation, Δφ, which are depicted in Fig. 2; alignment of the left and right rails, ALLr and ALRr, depicted in Fig. 3a; and longitudinal level of the left and right rails LLLr and LLRr, shown in Fig. 3b.

Fig. 3
figure 3

a Alignment and b longitudinal level

Full size image

Wheel–rail contact model

The methodology used to calculate the contact forces follows three steps [8]: firstly, the points of contact, or the points of closest proximity, between wheels and rails are found; secondly, the creepages, i.e., the relative velocities between the wheel and rail are calculated at the points of contact; and, finally, the contact forces are determined [14], i.e., normal and tangential forces are calculated in each contact point of the wheel–rail interface. To identify the potential contact points between the wheel and the rail, the surfaces of both the wheel and rail ae parameterized according to the procedure proposed by Pombo et al. [8], in which the rail profile is swept along the track and the wheel profiles for the flange and treat are rotated about the wheel axis. For the generic representation of rail–flange or rail–treat contact points, depicted in Fig. 4, the location of the contact points, or of the points of closest proximity, are obtained by solving the system of nonlinear equations associated with each contact pair.

Fig. 4
figure 4

Wheel–rail contact model considering tread and flange contacts

Full size image

Contrary to other contact search strategies in railway dynamics, the wheel–rail interaction forces are calculated by searching the contact conditions online and not via lookup tables, using the approach proposed by Pombo et al. [8]. The introduction of the track irregularities is natural in the framework of the geometric description of the rail or wheel geometries and necessary to allow the models to be studied under realistic operation conditions. In the formulation used here, the introduction of the irregularities does not penalize the contact search algorithm. The parameterization of the wheel and rail surfaces includes not only a set of representative control points with the irregularities already applied, but also the nominal cross-sectional profiles of the wheel and rail [8] in which any geometric departure from their nominal geometries is already included. The detailed description of the formulation is presented in paper [8] and avoided here for the sake of conciseness.

Case study

In general, the dynamic analyses of railway vehicles is performed by considering initial speeds or by setting constant train velocities, and no other methods to control the speed of the vehicle are used. However, real railway tracks are characterized not only by curves with different radii and cant angles, but also by slopes that accelerate or slow down the vehicle. In this work, the light rail vehicle is simulated in a long track model constructed based on a section of an existing railway network with, approximately, 3 km of extension. A three-dimensional representation of the track is shown in Fig. 5. Note that trees with equal spacing of 10 m are placed at the side of the track to facilitate the depth perception. The nominal speed for the tangent segments is set equal to 50 km/h, while in curves the speed is defined such that the cant deficiency is null [11].

Fig. 5
figure 5

Track model obtained from experimental results measurements [3]

Full size image

Vehicle dynamic performance

International standards for railway vehicle acceptance describe procedures that quantify the vehicle in terms of running safety, ride quality and track loading [2]. In this work, the simplified method, which is applicable to vehicles already homologated, is used, but minor modifications have been applied. This method requires the lateral acceleration of the bogie frames above the outer wheelsets, and the lateral and vertical accelerations of the carbody above the bogies. Here, these quantities are obtained from the simulations, which are post-processed to obtain two sets of 16 CV, with one set being related to tangent segments, while the other is related to curve segments. Each set includes 6 CV related to running safety, while 10 CV are related to ride quality.

In this work, it is proposed to quantify the vehicle dynamic performance using two indices, DPrs and DPrq, which are the dynamic performance indices for running safety and ride quality, respectively. These quantities are defined as a weighted sum of the CV given by [10]:

$$ {\text{DP}}_{\text{rs}} = \alpha \left( {\sum\limits_{i = 1}^{6} {\omega_{{{\text{rs}},i}}^{T} {\text{CV}}_{{{\text{rs}},i}}^{T} } } \right) + \left( {1 - \alpha } \right)\left( {\sum\limits_{i = 1}^{6} {\omega_{{{\text{rs}},i}}^{C} {\text{CV}}_{{{\text{rs}},i}}^{C} } } \right), $$
(1)
$$ {\text{DP}}_{\text{rq}} = \alpha \left( {\sum\limits_{i = 1}^{10} {\omega_{{{\text{rq}},i}}^{T} {\text{CV}}_{{{\text{rq}},i}}^{T} } } \right) + \left( {1 - \alpha } \right)\left( {\sum\limits_{i = 1}^{10} {\omega_{{{\text{rq}},i}}^{C} {\text{CV}}_{{{\text{rq}},i}}^{C} } } \right), $$
(2)

where ω represents a weight for a given CV, the superscripts T and C refer to tangent and curve segments, respectively, while the subscripts rs and rq refer to running safety and ride quality; finally, α is a weight which is set equal to 0.3 to penalize more CV related to curve segments rather than CV related to tangent segments. The weights ω are defined such that higher CV with respect to their limits are more penalized.

Optimization

Design variable selection

The potential design variables are the parameters listed in Table 1, since the modification of the suspension elements is cheaper than, for example, the maintenance of the infrastructure. Among these parameters, only the ones with impact on the DPrs and DPrq are selected. This selection required several simulations of the case described in section ‘Case Study’. In each simulation, the design variables are varied, one at a time, taking 80, 90, 100, 110, and 120% of their original values. In each case, the values of DPrs and DPrq are evaluated. The maximum variation of DPrs and DPrq for each variable, defined as ΔDP(x i ), is identified and plotted in Fig. 6 as a percentage with respect to the highest value observed in all simulations. Thus, x 1 (k SS,vert), x 3 (k SS,vert) and x 6 (δ guide) are selected as design variables, since they have a higher impact on DPrs and DPrq.

Fig. 6
figure 6

Impact on the dynamic performance indices

Full size image

Optimal process

The optimal problem is written as:

$$ \begin{aligned} \hbox{min} {\mathbf{F}}\left( {\mathbf{x}} \right) &= \left[ {{\text{DP}}_{\text{rs}} \left( {\mathbf{x}} \right){\text{DP}}_{\text{rq}} \left( {\mathbf{x}} \right)p\left( {\mathbf{x}} \right)} \right], \\ & \quad {\mathbf{x}}_{\text{lower}} \le {\mathbf{x}} \le {\mathbf{x}}_{\text{upper}} \end{aligned} $$
(3)

are introduced in section ‘Vehicle Dynamic Performance’ while P the penalty term is zero, when all CV are within the threshold prescribed in the standards, and infinity otherwise. The domain of the design variables is constrained by the lower and upper bounds, x lower and x upper, respectively. x lower and x upper are defined as 80 and 180% of the original values.

The direct multisearch method (DMS) [12], which is a derivative-free method, is used to solve the multiobjective optimization problem. It is inspired by the search/poll paradigm of direct-search methods of directional type from single to multiobjective optimization and uses the concept of Pareto dominance to maintain a list of feasible non-dominated points. The new feasible points evaluated in each iteration are added to this list and the dominated ones are removed. Successful iterations correspond then to changes in the iterate list, meaning that a new feasible non-dominated point was found. Otherwise, the iteration is declared as successful.

Results

Figure 7 shows the design variable values of the points evaluated in a normalized scale, namely, x lower and x upper are zero and one, respectively. It is observed that x 1 and x 2 tend to the upper bound, while x 2 tends to the lower bound. These results suggest that the hardening of the elastic elements, the increase of the clearance of the guides and the softening of the helicoidal springs lead to an improvement of the vehicle dynamic performance. Among the points evaluated, the CV do not exceed their limits, being the Penalty term always null.

Fig. 7
figure 7

Points evaluated

Full size image

Figure 8 shows the cost of the objective functions DPrs and DPrq. All points evaluated are represented by circles (o), while the points of the Pareto front are represented by crosses (x). It is observed that the minimization of DPrs corresponds to the minimization of DPrq.

Fig. 8
figure 8

Cost of the objective functions and Pareto front

Full size image

Conclusions

A design approach based on virtual homologation is proposed in this paper. Here, the suspension of the light rail vehicle is designed by using an optimization method that performs simulations in batch mode. In each simulation performed, which represents the vehicle negotiating a real railway track with prescribed speed, the vehicle response is quantified by three terms: two novel indices related to the dynamic performance for running safety and ride quality, namely, DPrs and DPrq; and by a penalty term that allows avoiding cases where the vehicle exceeds the limits imposed by the standards [2]. The optimization results propose an optimal design for the vehicle suspension elements and also that the improvement of the DPrs corresponds to the enhancement of DPrq. It may be concluded that the optimal problem can be solved by a uniobjective optimization method. These results provide good perspectives for the application of this methodology to industrial applications, such as vehicle design and model validation.