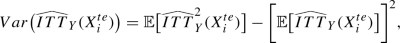Abstract
This paper provides a link between causal inference and machine learning techniques—specifically, Classification and Regression Trees—in observational studies where the receipt of the treatment is not randomized, but the assignment to the treatment can be assumed to be randomized (irregular assignment mechanism). The paper contributes to the growing applied machine learning literature on causal inference, by proposing a modified version of the Causal Tree (CT) algorithm to draw causal inference from an irregular assignment mechanism. The proposed method is developed by merging the CT approach with the instrumental variable framework to causal inference, hence the name Causal Tree with Instrumental Variable (CT-IV). An improved version, named Honest Causal Tree with Instrumental Variable (HCT-IV), able to estimate more reliably the heterogeneous causal effects, is also proposed. As compared to CT, the main strength of CT-IV and HCT-IV is that they can deal more efficiently with the heterogeneity of causal effects, as demonstrated by a series of numerical results obtained on synthetic data. Then, the proposed algorithms are used to evaluate a public policy implemented by the Tuscan Regional Administration (Italy), which aimed at easing the access to credit for small firms. In this context, HCT-IV breaks fresh ground for target-based policies, identifying interesting heterogeneous causal effects.

Similar content being viewed by others
Notes
Algorithms such the ones proposed in [6, 19] provide unit-wise estimation of the treatment effect. This feature is a very helpful tool in fields such as personalised medicine. While these techniques furnish unit level results, our proposed method is able to discriminate among bigger sub-populations. This can be useful when dealing with policy issues, since the targeted policies have to be as much general as possible. Indeed, when one needs to deliver a causal analysis to policy makers, one cannot provide unit level results since, in the spirit of the policies, the targeted intervention should be as universal as possible; in many countries, the possibility of targeted policy intervention at unit level (e.g. household, firm, organization) is ruled out to avoid personalized public spending [15, 17].
For further details on the Honest Causal Tree algorithm, the reader is referred to [8].
This problem is not really an issue in the policy-related framework studied in this paper, as explained in detail in the introduction of this paper (see Sect. 1).
See Sect. 23.6 in [25] for a discussion about the validity of the exclusion restriction, which is a common assumption in causal inference with instrumental variables. The exclusion restriction states that there is no effect of the assignment to the treatment on the outcome, in the absence of an effect of the assignment to the treatment on the treatment received [25]. This assumption is not directly testable, but there are plenty of studies in economics and social sciences where this assumption is assumed to hold. Examples can be found in fundamental econometric works such as Angrist and Imbens [1], Angrist, Imbens and Rubin [2], Angrist and Pischke [4] and Wooldridge [40]. A famous example is the study by Angrist and Kruger [3] on the effects of different lengths of schooling time on earnings later in life. The authors used as an instrumental variable, \(Z_i\), the quarter of birth of the students. Indeed, they observed that most States required pupils to enter school in the calendar year in which they turned 6, and that students were required to stay in school until the 16h birthdays. Hence, the length of time in school, which is the treatment variable \(W_i\), was a function of date of birth [4]. By exploiting the fact that there is no direct effect of date of birth on earnings, hence the exclusion restriction holds, they were able to consistently estimate the effect of schooling on earnings later in life. Moreover, another example of scenarios in which the exclusion restriction can be assumed to hold is the case of double-blind assignments [25]. In such settings, since the individuals in the study do not know whether they were assigned to the treatment group or to the control group, there is no effect of the assignment on the outcome, and all the effects on the outcome are mediated by the treatment received.
In many situations, the monotonicity assumption is reasonable [25], because the behaviour of a defier would be in contradiction to its own interest. We refer to [12] for a discussion about this issue. In particular, it is important to highlight that, in many scenarios, defiers are ruled out by not allowing individuals in the control group to have access to the treatment (and vice versa). For instance, this is the case of settings where people that are not assigned to the treatment (i.e. taking a drug, entering a job training program, undergoing a surgery) are excluded by design from the treatment (namely, they cannot possibly get the drug, enter the job program, etc.). In these scenarios of so-called one-sided non-compliance, defiers are ruled out by design. This is also the case of the application that we propose in Sect. 5.
Moreover, since the aim of the tree is to create nodes that include units with the highest index of similarity, the proposed procedure can be related to a matching procedure (see [22]).
See “Appendix A” for further details on the derivation of \(EMSE(\varOmega ^{te}, \varOmega ^{est})\) and
 .
.The comparative advantage of using the HCT-IV algorithm will be made more clear in the application part where we will compare the results from both algorithms in a case study.
The following mathematical derivation can be easily extended to the case in which \(ITT_Y(x)\) is replaced by \(\tau (x)\).
For the seek of brevity of notation, we do not include the superscript “adj” in EMSE.
The following expected value depends for its estimation on the tree \({\mathbb {T}}\). Again, to avoid burdening the terminology, we omit this dependence from the formulas.
This is due to the fact that \(ITT_{Y,i}^{te}\) comes from a sample independent of \(\varOmega ^{est}\).
This comes from the fact that one can decompose the covariance between two random variables A and B as \(Cov(AB)={\mathbb {E}}(AB)-{\mathbb {E}}(A){\mathbb {E}}(B)\). Then, \({\mathbb {E}}(AB)=Cov(AB)+{\mathbb {E}}(A){\mathbb {E}}(B)\) and, since Cov(AB) and \({\mathbb {E}}(A)\) are zero, \({\mathbb {E}}(AB)\) is zero as well.
This is derived from the fact that:
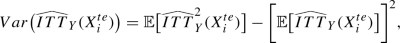
whose two members can be approximated as follows:

References
Angrist, J.D., Imbens, G.W.: Two stage least squares estimates of average causal response in models with variable treatment intensity. J. Am. Stat. Assoc. 90(430), 431–442 (1995)
Angrist, J.D., Imbens, G.W., Rubin, D.B.: Identification of causal effects using instrumental variables (with discussion). J. Am. Stat. Assoc. 91(434), 444–472 (1996)
Angrist, J.D., Keueger, A.B.: Does compulsory school attendance affect schooling and earnings? Q. J. Econ. 106(4), 979–1014 (1991)
Angrist, J.D., Pischke, J.S.: Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton University Press, Princeton (2008)
Arpino, B., Mattei, A.: Assessing the causal effects of financial aids to firms in Tuscany allowing for interference. Ann. Appl. Stat. 10(3), 1170–1194 (2016)
Athey, S., Tibshirani, J., Wager, S.: Solving Heterogeneous Estimating Equations with Gradient Forests. arXiv preprint arXiv:1610.01271 (2016)
Athey, S., Imbens, G.W.: Machine learning methods for estimating heterogeneous causal effects. Stat 1050(5), 1–26 (2015)
Athey, S., Imbens, G.W.: Recursive partitioning for heterogeneous causal effects. Proc. Natl. Acad. Sci. 113(27), 7353–7360 (2016)
Bargagli Stoffi, F., Gnecco, G.: Estimating heterogeneous causal effects in the presence of irregular assignment mechanisms. In: Proceedings of the 5th IEEE International Conference on Data Science and Advanced Analytics (IEEE DSAA 2018), p. 10, Turin, Italy, October 1st–4th (2018)
Belloni, A., Chernozhukov, V., Hansen, C.: High-dimensional methods and inference on structural and treatment effects. J. Econ. Perspect. 28(2), 29–50 (2014)
Bhattacharya, J., Vogt, W.B.: Do instrumental variables belong in propensity scores? NBER Technical Working Paper No. 343 (2009)
Bielby, R.M., House, E., Flaster, A., DesJardins, S.L.: Instrumental variables: conceptual issues and an application considering high school course taking. In: Paulsen, M.B. (ed.) Higher Education: Handbook of Theory and Research, vol. 28, pp. 263–321. Springer, Berlin (2013)
Breiman, L.: Random Forests. Mach. Learn. 45(1), 5–32 (2001)
Breiman, L., Olshen, J.H., Stone, C.J.: Classification and Regression Trees. CRC Press, Boca Raton (1984)
Brown, R., Mawson, S.: Targeted support for high growth firms: theoretical constraints, unintended consequences and future policy challenges. Environ. Plan. C Gov. Policy 34(5), 816–836 (2016)
Crump, R.K., Hotz, V.J., Imbens, G.W., Mitnik, O.A.: Nonparametric tests for treatment effect heterogeneity. Rev. Econ. Stat. 90(3), 389–405 (2008)
Devereux, S.: Is targeting ethical? Glob. Soc. Policy 16(2), 166–181 (2016)
Grimmer, J., Messing, S., Westwood, S.J.: Estimating heterogeneous treatment effects and the effects of heterogeneous treatments with ensemble methods. Polit. Anal. 25(4), 413–434 (2017)
Hahn, P.R., Murray, J.S., Carvalho, C.M.: Bayesian regression tree models for causal inference: regularization, confounding, and heterogeneous effects. arXiv preprint arXiv:1706.09523 (2017)
Hill, J.L.: Bayesian nonparametric modeling for causal inference. J. Comput. Gr. Stat. 20(1), 217–240 (2011)
Hirano, K., Imbens, G.W., Ridder, G.: Efficient estimation of average treatment effects using the estimated propensity score. Econometrica 71(4), 1161–1189 (2003)
Ho, D.E., Imai, K., King, G., Stuart, E.A.: Matching as nonparametric preprocessing for reducing model dependence in parametric causal inference. Polit. Anal. 15(3), 199–236 (2007)
Imbens, G.W.: Matching methods in practice: three examples. J. Hum. Resour. 50(2), 373–419 (2015)
Imbens, G.W., Angrist, J.D.: Identification and estimation of local average treatment effects. Econometrica 62(2), 467–475 (1994)
Imbens, G.W., Rubin, D.B.: Causal Inference for Statistics, Social, and Biomedical Sciences. An Introduction. Cambridge University Press, Cambridge (2015)
Imbens, G.W., Rubin, D.B.: Estimating outcome distributions for compliers in instrumental variables models. Rev. Econ. Stud. 64(4), 555–574 (1997)
Le Gallo, J., Páez, A.: Using synthetic variables in instrumental variable estimation of spatial series models. Environ. Plan. A 45(9), 2227–2242 (2013)
Lewbel, A.: Using heteroscedasticity to identify and estimate mismeasured and endogenous regressor models. J. Bus. Econ. Stat. 30(1), 67–80 (2012)
Mattei, A., Mauro, V.: Valutazione di Politiche per le Imprese Artigiane. Research Report, IRPET - Istituto Regionale Programmazione Economica della Toscana (2007)
Mariani, M., Mealli, F.: The effects of R&D subsidies to small and medium-sized enterprises. Evidence from a regional program. Ital. Econ. J. 4(2), 249–281 (2018)
Neyman, J.: On the two different aspects of the representative method: the method of stratified sampling and the method of purposive selection. J. R. Stat. Soc. 97(4), 558–625 (1934). https://doi.org/10.2307/2342192
Pearl, J.: Causality. Cambridge University Press, Cambridge (2009)
Rosenbaum, P., Rubin, D.B.: Assessing the sensitivity to an unobserved binary covariate in an observational study with binary outcome. J. R. Stat. Soc. Ser. B 45(2), 212–218 (1983)
Rubin, D.B.: Estimating causal effects of treatments in randomized and nonrandomized studies. J. Educ. Psychol. 66(5), 688–701 (1974)
Rubin, D.B.: Randomization analysis of experimental data: The Fisher randomization test comment. J. Am. Stat. Assoc. 75(371), 591–593 (1980)
Stock, J.H., Yogo, M.: Testing for weak instruments in linear IV regression. In: Andrews, D.W.K. (ed.) Identification and Inference for Econometric Models, pp. 80–108. Cambridge University Press, New York (2002)
Su, X., Kang, J., Fan, J., Levine, R.A., Yan, X.: Facilitating score and causal inference trees for large observational studies. J. Mach. Learn. Res. 13(Oct), 2955–2994 (2012)
Wager, S., Athey, S.: Estimation and inference of heterogeneous treatment effects using random forests. J. Am. Stat. Assoc. 113(523), 1228–1242 (2017)
Wang, G., Li, J., Hopp, W.J.: An Instrumental Variable Tree Approach for Detecting Heterogeneous Treatment Effects in Observational Studies. Technical report. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3045327 (2017)
Wooldridge, J.M.: Introductory Econometrics: A Modern Approach. Nelson Education, Scarborough (2015)
Acknowledgements
Both the authors are members of GNAMPA-INDAM (Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni - Istituto Nazionale di Alta Matematica).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper is an extension version of the DSAA’2018 paper titled “Estimating Heterogeneous Causal Effects in the Presence of Irregular Assignment Mechanisms”.
Appendices
Appendix A: Estimation of the expected mean squared error
Let \(ITT_Y(x)\) be the true intention to treat, conditional on a certain set of covariates’ values \(X_i=x\):Footnote 12
The (adjusted) Expected Mean Squared Error (henceforth, EMSEFootnote 13) is the expectation over the test sample \(\varOmega ^{te}\) and the estimation sample \(\varOmega ^{est}\) of the following adjusted Mean Squared Error (\(MSE^{adj}\)), whose precise expression is given later in equation (60):
First, the MSE can be defined as the average over the test sample of the squared error of prediction associated with the conditional estimator obtained on the estimation sample. It is expressed as:

where \(\#(\varOmega ^{te})\) is the number of observations in the test sample, \(ITT_{Y,i}\), the unit level intention to treat, is
and \(ITT_{Y,i}^{te}\) denotes its value on an element of the test sample. Following [8], we can adjust the MSE by the empirical mean (on the test sample) of \((ITT^{te}_{Y,i})^2\). Since this term does not depend on the choice of the estimator, subtracting it does not affect the way the criterion ranks different estimators [8]. The adjusted version of the MSE is the following:

Nevertheless, the unit level intention to treat \(ITT_{Y,i}^{te}\) is infeasible, since one cannot observe for the same unit i, and at the same time, the effects under its assignment to the treatment and under its assignment to the control. However, if one puts aside this problem of infeasibility for a moment, one can expand the EMSE, on a partition of a given tree \({\mathbb {T}}\), as follows:Footnote 14

Since \( {\mathbb {E}}_{i \in \varOmega ^{te}} \big [ \big (ITT_{Y,i}^{te} - ITT_Y(X_i^{te})\big )\big ]\) is zero and the covariance between the two terms \(\big (ITT_{Y,i}^{te} - ITT_Y(X_i^{te})\big )\) and  is zero,Footnote 15 then the term
is zero,Footnote 15 then the term  cancels out:Footnote 16
cancels out:Footnote 16

leading to the following:

where  denotes the conditional variance of
denotes the conditional variance of  given \(\varOmega ^{est}\).
given \(\varOmega ^{est}\).
Now it is possible to proceed with the estimation of \(EMSE^{HCT-IV}\) for the Honest Causal Tree with Instrumental Variable. For \(X_i^{te} \in {\mathbb {X}}_j\), the conditional variance in the second term of (54) can be approximated by the within-leaf conditional variance estimated on the training sample divided by the number of observations in the leaf (in the estimation sample):

The expected value can be estimated as:

where the \({\mathcal {P}}^{est}_{{\mathbb {X}}_j}\)’s are the leaf shares on the estimation sample. Assuming approximately equal leaf size, we get:

With respect to the first term in (54), \(ITT^2_Y(X_i^{te})\) can be now approximated using the square of the estimated  in the training sample minus an estimate of the within-leaf variance of
in the training sample minus an estimate of the within-leaf variance of  , obtained by taking into account the number of observations (in the training sample) in the leaf \({\mathbb {X}}_j\) associated with \(X_i^{te}\):Footnote 17
, obtained by taking into account the number of observations (in the training sample) in the leaf \({\mathbb {X}}_j\) associated with \(X_i^{te}\):Footnote 17

Assuming again that the leaves are of equal size, the expected value of \(ITT^2_Y(X_i^{te})\) in (54) can be approximated as follows:

Merging the formulas above, we get an estimator of \(EMSE^{HCT-IV} (\varOmega ^{te}, \varOmega ^{est})\) for every partition:

The first component of (55) is the conventional causal tree criterion, which rewards the partitions with a stronger heterogeneity in the causal effect, while the second component penalizes those partitions that create variance in the leaf causal estimates. This algorithm tends to balance the causal tree tendency to reward heterogeneity in the causal estimates by penalizing imprecise causal estimates within the leaves.
Moreover, one can estimate the terms \(\left( {ITT}_Y^{tr}(X_i^{tr})\right) ^2\) and  , respectively, as follows:
, respectively, as follows:

where \({\mathbb {X}}_i\) is the leaf to which \(X_i^{tr}\) is assigned by the tree \({\mathbb {T}}\), \(N_{1, {\mathbb {X}}_i}^{tr}\) is the number of units assigned to treatment within the leaf \({\mathbb {X}}_i\), \(N_{0, {\mathbb {X}}_i}^{tr}\) is the number of units assigned to control within the leaf \({\mathbb {X}}_i\), and, for a generic leaf \({\mathbb {X}}_j\) of the tree \({\mathbb {T}}\), \( s^2_{1, {\mathbb {X}}_j}\) is the within-leaf variance of \(ITT_Y\) for the units assigned to the treatment, and \( s^2_{0, {\mathbb {X}}_j}\) is the within-leaf variance of \(ITT_Y\) for the units assigned to the control.Footnote 18 Concluding, one can estimate the overall \(EMSE^{HCT-IV}\) as follows:

In practice, one can use the same sample size for both \(\varOmega ^{tr}\) and \(\varOmega ^{est}\), so the estimator above becomes:

Appendix B: Case study with causal tree with IV
Figure 2 depicts the CT-IV built using the data from the case study in Sect. 5.
Appendix C: Case study with causal tree and honest causal tree
Figures 3 and 4 depict the CT and the HCT built using the data from the case study in Sect. 5, respectively.
Rights and permissions
About this article
Cite this article
Bargagli Stoffi, F.J., Gnecco, G. Causal tree with instrumental variable: an extension of the causal tree framework to irregular assignment mechanisms. Int J Data Sci Anal 9, 315–337 (2020). https://doi.org/10.1007/s41060-019-00187-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41060-019-00187-z




 .
.