Skip to main content
SpringerLink
Log in

Elliptical modeling and pattern analysis for perturbation models and classification

  • Regular Paper
  • Published:
International Journal of Data Science and Analytics Aims and scope Submit manuscript

Abstract

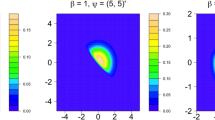
The characteristics of a feature vector in the transform domain of a perturbation model differ significantly from those of its corresponding feature vector in the input domain. These differences—caused by the perturbation techniques used for the transformation of feature patterns—degrade the performance of machine learning techniques in the transform domain. In this paper, we proposed a semi-parametric perturbation model that transforms the input feature patterns to a set of elliptical patterns and studied the performance degradation issues associated with random forest classification technique using both the input and transform domain features. Compared with the linear transformation such as principal component analysis (PCA), the proposed method requires less statistical assumptions and is highly suitable for the applications such as data privacy and security due to the difficulty of inverting the elliptical patterns from the transform domain to the input domain. In addition, we adopted a flexible block-wise dimensionality reduction step in the proposed method to accommodate the possible high-dimensional data in modern applications. We evaluated the empirical performance of the proposed method on a network intrusion data set and a biological data set, and compared the results with PCA in terms of classification performance and data privacy protection (measured by the blind source separation attack and signal interference ratio). Both results confirmed the superior performance of the proposed elliptical transformation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Aghion, P., Bloom, N., Blundell, R., Griffith, R., Howitt, P.: Competition and innovation: an inverted-u relationship. Q. J. Econ. 120(2), 701–728 (2005)

    Google Scholar 

  2. Boscolo, R., Pan, H., Roychowdhury, V.P.: Independent component analysis based on nonparametric density estimation. IEEE Trans. Neural Netw. 15(1), 55–65 (2004)

    Article  Google Scholar 

  3. Breiman, L.: Bagging predictors. Mach. Learn. 24(2), 123–140 (1996)

    MATH  MathSciNet  Google Scholar 

  4. Breiman, L.: Random forests. Mach. Learn. 45(1), 5–32 (2001)

    Article  MATH  Google Scholar 

  5. Bruce, P., Bruce, A.: Practical Statistics for Data Scientists: 50 Essential Concepts. O’Reilly Media, Inc., Sebastopol (2017)

    Google Scholar 

  6. Caiafa, C.F., Proto, A.N.: A non-gaussianity measure for blind source separation. In: Proceedings of SPARS05 (2005)

  7. Chaudhary, A., Kolhe, S., Kamal, R.: A hybrid ensemble for classification in multiclass datasets: an application to oilseed disease dataset. Comput. Electron. Agric. 124, 65–72 (2016)

    Article  Google Scholar 

  8. Chaudhuri, K., Monteleoni, C., Sarwate, A.D.: Differentially private empirical risk minimization. J. Mach. Learn. Res. 12(Mar), 1069–1109 (2011)

    MathSciNet  MATH  Google Scholar 

  9. Du, K.L., Swamy, M.: Principal component analysis. In: Neural Networks and Statistical Learning, pp. 355–405. Springer, London (2014)

  10. Fan, J., Li, R.: Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96, 1348–1360 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  11. Fienberg, S.E., Steele, R.J.: Disclosure limitation using perturbation and related methods for categorical data. J. Off. Stat. 14(4), 485–502 (1998)

    Google Scholar 

  12. Gaber, M.M., Zaslavsky, A., Krishnaswamy, S.: Mining data streams: a review. SIGMOD Rec. 34(2), 18–26 (2005). https://doi.org/10.1145/1083784.1083789

    Article  MATH  Google Scholar 

  13. Geiger, B.C.: Information loss in deterministic systems. Ph. D. Thesis, Graz University of Technology, Graz, Austria (2014)

  14. Hung, C.C., Liu, H.C., Lin, C.C., Lee, B.O.: Development and validation of the simulation-based learning evaluation scale. Nurse Educ. Today 40, 72–77 (2016)

  15. Jeyakumar, V., Li, G., Suthaharan, S.: Support vector machine classifiers with uncertain knowledge sets via robust optimization. Optimization 63(7), 1099–1116 (2014)

  16. Jin, S., Yeung, D.S., Wang, X.: Network intrusion detection in covariance feature space. Pattern Recogn. 40(8), 2185–2197 (2007

  17. Jolliffe, I.T., Cadima, J.: Principal component analysis: a review and recent developments. Philos. Trans. R. Soc. A 374(2065), 20150202 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  18. Jones, D.G., Beston, B.R., Murphy, K.M.: Novel application of principal component analysis to understanding visual cortical development. BMC Neurosci. 8(S2), P188 (2007)

    Article  Google Scholar 

  19. Lasko, T.A., Vinterbo, S.A.: Spectral anonymization of data. IEEE Trans. Knowl. Data Eng. 22(3), 437–446 (2010)

    Article  Google Scholar 

  20. Lee, S., Habeck, C., Razlighi, Q., Salthouse, T., Stern, Y.: Selective association between cortical thickness and reference abilities in normal aging. NeuroImage 142, 293–300 (2016)

    Article  Google Scholar 

  21. Lichman, M.: UCI machine learning repository (2013). http://archive.ics.uci.edu/ml. Accessed 1 Nov 2017

  22. Little, R.J.: Statistical analysis of masked data. J. Off. Stat. 9(2), 407–426 (1993)

    Google Scholar 

  23. Liu, K., Giannella, C., Kargupta, H.: A survey of attack techniques on privacy-preserving data perturbation methods. In: Aggarwal, C.C., Yu, P.S. (eds.) Privacy-Preserving Data Mining, pp. 359–381. Springer, US (2008)

  24. Muralidhar, K., Sarathy, R.: A theoretical basis for perturbation methods. Stat. Comput. 13(4), 329–335 (2003)

    Article  MathSciNet  Google Scholar 

  25. Murthy, S.K.: Automatic construction of decision trees from data: a multi-disciplinary survey. Data Min. Knowl. Discov. 2(4), 345–389 (1998)

    Article  Google Scholar 

  26. Oliveira, S.R., Zaïane, O.R.: Achieving privacy preservation when sharing data for clustering. In: Jonker, W., Petković, M. (eds.) Workshop on Secure Data Management, pp. 67–82. Springer, Berlin Heidelberg (2004)

  27. Qian, Y., Xie, H.: Drive more effective data-based innovations: enhancing the utility of secure databases. Manag. Sci. 61(3), 520–541 (2015)

    Article  Google Scholar 

  28. Rubens, N., Elahi, M., Sugiyama, M., Kaplan, D.: Recommender systems handbook. In: Ricci, F., Rokach, L., Shapira B. (eds.) Active Learning in Recommender Systems, pp. 809–846. Springer, Boston (2016)

  29. Sørensen, M., De Lathauwer, L.: Blind signal separation via tensor decomposition with Vandermonde factor: canonical polyadic decomposition. IEEE Trans. Signal Process. 61(22), 5507–5519 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  30. Suthaharan, S.: Machine Learning Models and Algorithms for Big Data Classification: Thinking with Examples for Effective Learning, vol. 36. Springer, New York (2015)

    MATH  Google Scholar 

  31. Suthaharan, S.: Support vector machine. In: Machine Learning Models and Algorithms for Big Data Classification, pp. 207–235. Springer, US (2016)

  32. Suthaharan, S., Panchagnula, T.: Relevance feature selection with data cleaning for intrusion detection system. In: Southeastcon, 2012 Proceedings of IEEE, pp. 1–6. IEEE (2012)

  33. Thrun, S., Pratt, L.: Learning to Learn. Springer, New York (2012)

    MATH  Google Scholar 

  34. Whitworth, J., Suthaharan, S.: Security problems and challenges in a machine learning-based hybrid big data processing network systems. ACM SIGMETRICS Perform. Eval. Rev. 41(4), 82–85 (2014)

    Article  Google Scholar 

  35. Zarzoso, V., Nandi, A.: Blind source separation. In: Nandi, A. (ed.) Blind Estimation Using Higher-Order Statistics, pp. 167–252. Springer, US (1999)

  36. Zumel, N., Mount, J., Porzak, J.: Practical data science with R, 1st edn. Manning, Shelter Island (2014)

Download references

Acknowledgements

This research of the first author was partially supported by the Department of Statistics, University of California at Irvine, and by the University of North Carolina at Greensboro. This material was based upon work partially supported by the National Science Foundation under Grant DMS-1638521 to the Statistical and Applied Mathematical Sciences Institute. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. Shen’s research is partially supported by Simons Foundation Award 512620. The authors thank the Editor, the Associate Editor, and the referees for their valuable comments.

Author information

Authors and Affiliations

  1. Department of Computer Science, University of North Carolina at Greensboro, Greensboro, NC, 27402, USA

    Shan Suthaharan

  2. Department of Statistics, University of California, Irvine, CA, 92697, USA

    Weining Shen

Authors
  1. Shan Suthaharan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weining Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weining Shen.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Suthaharan, S., Shen, W. Elliptical modeling and pattern analysis for perturbation models and classification. Int J Data Sci Anal 7, 103–113 (2019). https://doi.org/10.1007/s41060-018-0117-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s41060-018-0117-y

Keywords

Search

Navigation