Creep Effect on Time to Corrosion-Induced Cracking of Concrete Cover

Abstract

This paper presents an innovative method to include creep deformations in the prediction of time to corrosion-induced cover cracking. Using experimental results, creep and cracking criteria used in this method are verified. It is argued in the paper that the cover cracking problem under corrosion is close to a relaxation problem and the conventional creep formulations based on the effective elastic modulus cannot be adopted. It is found in the paper that accurate consideration of creep deformation would lead to about 30–40% longer time to cover cracking when compared to no consideration of creep deformations whilst for the currently practiced methods, the time can be up to 200% longer, which is unconservative in predicting time to cover cracking. Results in this paper open the debate on modelling of creep in the analysis of corrosion-affected structures and serve as an important step towards the accurate prediction of corrosion-induced concrete cracking.

1 Introduction

Corrosion of reinforcing steel in concrete is a significant source of deterioration and premature failure in reinforced concrete structures [1, 2]. In reinforced concrete structures, the high alkalinity of concrete material leads to the formation of a passive film at the steel-to-concrete interface, protecting the reinforcing steel from corrosion. However, this protective layer can be compromised in aggressive environments [1] due to (i) carbonation of the concrete cover, resulting in the loss of alkalinity, or (ii) chloride ingress. Carbonation generally leads to uniform corrosion over the surface of steel bars, while chloride attack results in localised (pitting) corrosion initiation.

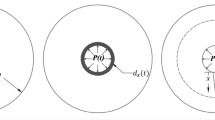
To quantitatively assess corrosion-induced damage, a multi-stage model [3,4,5], as shown in Fig. 1, has been widely accepted. In this model, the stages are identified as: (i) stress-free migration of rust products into pores at the steel–concrete interface until all these pores are filled with rust; (ii) stress generation in the concrete cover until the appearance of the first crack at the steel–concrete interface; (iii) propagation of the crack until the appearance of a concrete surface crack (some rust products may ingress into the formed cracks); and (iv) joining of cracks that may lead to concrete cover spalling or delamination.

Fig. 1

Stages of corrosion-induced damage

Excessive corrosion-induced cracking is a crucial criterion for analysing and evaluating the service life of reinforced concrete structures and is a key indicator of corrosion presence, signifying an ongoing degradation process towards the end of the service life of reinforced concrete structures. Therefore, predicting the time to cover cracking is of great interest in repair, service life prediction, and maintenance of concrete structures.

There has been a considerable amount of experimental, numerical, and analytical research on predicting the time to cover cracking [4, 6,7,8,9]. Despite these modelling advancements, the agreement between experimental and model results is generally low. An examination of these models reveals that there is no correlation between the complexity of the model and the accuracy of prediction [3, 10]. The possible sources of discrepancy between theory and observation are found to be related to [11, 12]: (i) inaccuracy in corrosion models; (ii) unknown properties of corrosion rust products; (iii) limited knowledge regarding the size of the porous band at the steel–concrete interface; (iv) limited knowledge of potential non-uniform distribution of corrosion; and (v) inaccuracy in modelling the post-cracking behaviour of concrete.

Another important source of error, which has received little attention [13], is the lack of accuracy in modelling the long-term creep deformation. Ignoring creep/relaxation leads to a global overestimate of the stress, i.e., an underestimation of deformation. Thus, creep/relaxation seems to have a negative impact on structural deformation. Limited experimental studies on the effect of creep on corrosion-induced surface cracking are available in the current literature. Experimental results have shown that a decrease in the loading rate leads to an increase in corrosion-induced crack opening [14]. This has been attributed to the creep effect. Vu et al. [15] proposed a loading rate correction factor for predicting the time to cover cracking, where a rate correction factor equal to 1.0 indicates that the rate of loading does not affect crack initiation and propagation. Using some of the available experimental data, they showed that the rate of loading, quantified as corrosion rate, has a considerable impact on the time to cover cracking, with the loading rate correction factor ranging as low as 0.5. They attributed the reduction of time to cover cracking to the dissipation of radial stress due to concrete creep and penetration of rust into crack openings. Similar results have also been reported in a more recent study on the impact of loading rate on the time to cover cracking [16].

In majority of the available models, a simplistic method is used to consider the long-term effect of creep. In this method, the concrete modulus of elasticity is replaced with an effective modulus of elasticity, E_ef, as follows

$$E_{ef} = \frac{E_c }{{1 + \phi_{cr} }}$$

(1)

where E_c is the initial modulus of elasticity and ϕ_cr is the creep coefficient accounting for the long-term deformations, which in general is a time-dependent coefficient. Consideration of the creep effect in the current literature is summarised in Table 1. It is usually assumed that this effective modulus is time-independent taking its asymptotic long-term value when t = ∞. In some studies [4] this asymptotic value was used for short and long-term tests. This is an incorrect assumption which can lead to about 200% error in prediction of time to cover cracking for accelerated corrosion tests [6].

Table 1 Treatment of long-term deformations in the current literature

As Table 1 shows, only in few studies, non-asymptotic values are used for the creep coefficient, and there has been only one time-dependent creep function [9].

There are some significant considerations when it comes to modelling long-term deformation in the analysis of corrosion-induced cracks. Firstly, corrosion loading is a displacement-based load, resembling a relaxation problem, unlike the creep problem, which is load-based. This aspect has not been addressed in the current literature. Secondly, unlike conventional problems, corrosion-induced loading is not constant; it varies with time. Solving this problem requires the accurate consideration of long-term deformation through a step-by-step time-dependent analysis.

To address these issues, this paper develops an accurate nonlinear time-dependent Finite Element (FE) model to account for long-term deformations in corrosion-induced cover cracking. Using available experimental data, the validity of the proposed model to predict long-term deformation and cracking behaviours is verified. A comparative discussion on the accuracy of some available methods in accounting for long-term deformations in the assessment of corrosion-induced time to cover cracking is then presented.

2 Corrosion-induced loading

Corrosion of steel driven by the electrochemical oxidation reactions results in various corrosion products that generally occupy larger volume than the original iron. The characteristic relative volume ratio, α_v, shows the volume ratio of the corrosion product to that of parent iron.

It is generally understood that the corrosion process, and particularly chloride-induced reinforcement corrosion, leads to a non-uniform distribution of corrosion products around the rebar perimeter [26, 27]. Several models have been presented that emphasize the non-uniform distribution of corrosion products [28,29,30]. However, in most available models for predicting the time to cover cracking, for simplicity and convenience, it is conceptually assumed that corrosion occurs uniformly around the reinforcement. As previously discussed, the non-uniformity of corrosion could be one of the major potential sources of discrepancies between models and experimental results. In the current study, where the main objective is to investigate the creep effect on the time to cover cracking, to simplify the analysis process, the conceptual uniform corrosion model is used.

As Fig. 2 shows, following corrosion initiation, the volume expansion of corrosion products begins leading to some internal pressure at the steel–concrete interface. The difference in volume of steel and rust leads to the internal pressure, p_r, at the steel–concrete interface.

Fig. 2

Rust expansion and corrosion-induced load

For a given α_v ratio, the radial thickness induced pressure, δ, at the steel–concrete interface can be expressed conceptually as follows

$$\delta = \left( {\alpha_v - 1} \right)\delta_s - \delta_0 - \delta_p$$

(2)

where δ_s is the thickness of the ring of steel loss, δ₀ is the thickness of the porous band around the steel and is δ_p is the thickness of an equivalent ring of rust penetration in pores and microcracks. To calculate the volume of rust produced, and more specifically δ_s, Faraday’s law is commonly used [4, 6, 22]. Not all the corrosion products contribute immediately to the expansive pressure on the concrete [3, 31]. Some are considered to fill the voids and pores around the reinforcing bar (Fig. 2). Once this zone is filled, volume expansion of corrosion products exerts a gradually increasing pressure on concrete surrounding the steel bar. It is believed that part of the generated corrosion rust diffuses into concrete material and the formed microcracks around the reinforcing steel and not participating in generating internal pressure at the steel–concrete interface [6, 11, 32]. Radial thickness associated with this rust penetration is denoted as δ_p.

Corrosion-induced load is an internal displacement load that follows the conceptual model shown in Eq. (2) from which the internal pressure, p_r, can be calculated. Following application of the internal δ displacement, stress relaxation occurs over time. As the corrosion-induced internal displacement is a function of time, a step-by-step time-dependent analysis will be needed to solve this relaxation problem.

3 Modelling of Long-Term Deformation

To explain the mechanism of creep in concrete structures, several theories have been proposed in the literature. In the case of short-term creep, theories such as osmotic pressure effect, solidification theory, and migration of adsorbed moisture within the capillary pores have been put forward. In the latter theory, the creep mechanism involves stress-induced water movement towards the largest diameter pores [33]. For long-term creep, micro-sliding between C–S–H particles and their own sheets has been suggested [33,34,35,36]. These mechanisms align with the mobility of water.

The analysis of long-term deflections in corrosion-induced cracking problems differs from conventional creep analysis as per the following:

• i. In conventional creep analysis, deformation increases under sustained loads, while in the corrosion-induced problem, under an imposed deformation induced by rust expansion, elastic stresses are redistributed. This is similar to relaxation problems.

• ii. In the corrosion-induced cracking problem, the internal corrosion-induced load on concrete is not constant. This load gradually increases over time, whereas in conventional creep problems, deflections increase under a constant sustained load.

• iii. In the corrosion-induced cracking problem, both tensile and compressive regions experience creep deformations. However, in conventional creep procedures, creep is predominantly under compressive stresses, as the tensile capacity of concrete is ignored.

• iv. In conventional creep problems, often used in the evaluation of long-term deflections in beams and slabs, section analysis is usually employed. In section analysis, it is assumed that the strain varies linearly across the section. By having the creep strain in the far-most fibre, the additional curvature due to creep can be easily calculated. On the other hand, there is a high spatial variation of stress in the corrosion-induced cracking problem. The problem should be solved using a more sophisticated approach that allows consideration of variation in stress in all directions.

It can, therefore, be inferred that the analysis of long-term deformations in the corrosion-induced concrete cracking problem is close to a relaxation problem but under a variable load, where spatial variation of stress relaxation needs to be accurately modelled. In the following sections, the conventional modelling of creep deformations in reinforced concrete structures is first discussed, followed by an outline of the more general procedure for considering creep deformations.

3.1 The Effective Modulus Formulation

Creep deformations occur over long-term exposure to permanent stresses. To calculate these deformations, a time-dependent analysis is required. The total strain is calculated as follows

$$\varepsilon (t) = \varepsilon_E (t) + \varepsilon_C (t) + \varepsilon_{sh} (t) + \varepsilon_T (t)$$

(3)

where ε(t), ε_E(t) and ε_C(t), ε_sh(t) and ε_T(t) are the total, instantaneous, shrinkage, creep and thermal strains, respectively, and t is time. The shrinkage and thermal strains are stress-independent, while the instantaneous and creep strains depend on stress. For constant uniaxial stress within the service loading range and by combining the stress-dependent strains and ignoring the stress-independent strains, the mechanical stress and strain can be related as follows [37]

$$\varepsilon (t) = \sigma J(t,t_0 )$$

(4)

where σ represents the stress and t₀ is the time at which the load is applied. J(t, t₀) is the so-called compliance or creep function. This function can be expressed as the sum of instant compliance and the creep compliance as follows

$$J(t,t_0 ) = \frac{1}{E(t_0 )} + C(t,t_0 ) = \frac{1 + \phi (t,t_0 )}{{E(t_0 )}}$$

(5)

E(t₀) is the elastic modulus at time of loading t₀ and ϕ is the creep function showing the ratio of creep deflection to the instant deflection. The creep function is generally given by concrete standards/guidelines. For instance, ACI 209.2R guideline [38] adopts the following function,

$$\phi (t,t_0 ) = \frac{(t - t_0 )^\psi }{{t_c + (t - t_0 )^\psi }}\phi_u$$

(6)

where t_c and ψ are the creep model parameters and t is measured in days. In the absence of more accurate experimental and field data for the creep function, the t_c and ψ parameters are recommended as 10 days and 0.60, and ϕ_u can be taken as 2.35.

Using the superposition principle, for time varying stress, the total mechanical strain can be calculated as follows

$$\varepsilon (t) = \int_0^t {J(t,\tau )\frac{\partial \sigma (\tau )}{{\partial \tau }}} d\tau$$

(7)

For isotropic materials, the uniaxial solution can be generalized to multiaxial stress states that can be used in three-dimensional analysis of structures as follows

$$\varepsilon {(}t{) = }\int_{0}^{\text{t}} {J{(}t{,}\tau {)}{\bf{B\dot{\sigma }}}{(}\tau {)}} d\tau$$

(8)

$\dot{{\varvec{\sigma}}}$ matrix is the stress tensor rate and B is the stress compliance matrix relating stress to strain in a three-dimensional state.

An approximate alternative to the direct creep analysis is to use the so-called effective modulus. For a time-interval from t₀ to t, where t₀ is the time of stress application, it can be assumed that the stress jumps right after of application of stress and remains constant till time t. By combining Eqs. (4, 5) and following some algebraic simplification, a new formulation, in which modulus of elasticity is modified is obtained as follows

$$\varepsilon (t) = \sigma J(t,t_0 ) = \sigma \frac{1 + \phi (t,t_0 )}{{E(t_0 )}} = \sigma \frac{1}{{\frac{E(t_0 )}{{1 + \phi (t,t_0 )}}}} = \frac{\sigma }{{E_{ef} (t)}}$$

(9)

where E_ef(t) is the effective elastic modulus. In practical structural analyses, in which accurate results are not required, this approximation provides a reasonable solution. If there is no aging, the results of the effective modulus are adequately accurate. A more appropriate alternative to the effective modulus is to use the age-adjusted modulus. In derivation of this modulus, it is assumed that the strain varies proportionally to J(t, t₀) as is outlined by [37]. By modification of the creep function ϕ(t, t₀), the age adjusted modulus can be derived from the effective modulus as follows

$$E_{adj} (t) = \frac{E(t_0 )}{{1 + \chi (t,t_0 )\phi (t,t_0 )}}$$

(10)

where χ(t, t₀) is a coefficient accounting for the difference between the effective and the age-adjusted moduli and normally is less than 1.0. This formulation has been adopted by the European codes such as the fib model code [39]. The effective modulus gives exact results only if the stress does not vary with time. On the other hand, in cases where the stress history can be expressed as linear functions of the relaxation function, which is proportional to inverse of the creep compliance function, the age-adjusted effective modulus gives the exact results. Such time variation is normally achieved in structures under a constant loading.

3.2 The General Formulation

Solution to the long-term deformations in corrosion-induced cracking problem requires a different approach than that used in for the conventional reinforced concrete structures. A more general method in which creep deformations are directly calculated and added to other type of deformations, see Eq. (3), is needed. Considering a general case of corrosion-induced loading as shown in Fig. 3, the load is applied in multiple steps Δt. Stress and strain increments in each step are calculated. Given the incremental load Δ[δ(t)] at each Δt time step, and by ignoring the shrinkage and thermal strains the total strain increment can be formulated as follows

$$\left\{ {\Delta \varepsilon } \right\} = \left\{ {\Delta \varepsilon_E } \right\} + \left\{ {\Delta \varepsilon_C } \right\}$$

(11)

where subscripts E and C show the mechanical and creep strains, respectively. The change in the mechanical strain can then be calculated as follows

$$\left\{ {\Delta \varepsilon_E } \right\} = \left\{ {\Delta \varepsilon } \right\} - \left\{ {\Delta \varepsilon_C } \right\}$$

(12)

Fig. 3

Corrosion-induced loading and stresses

The incremental mechanical strain can be related to incremental stress using the generalised Hook’s law as follows

$$\left\{ {\Delta \sigma } \right\} = [B]\left\{ {\Delta \varepsilon_E } \right\}$$

(13)

The compliance matrix B can be generally a function of loading, where nonlinearity in material nonlinearity can be capture through the modification of the modulus of elasticity.

By combining Eqs. (12, 13) the relationship between the total incremental stress, incremental creep strain and incremental mechanical strain can be established as follows

$$\left\{ {\Delta \sigma } \right\} = [B]\left\{ {\left\{ {\Delta \varepsilon } \right\} - \left\{ {\Delta \varepsilon_C } \right\}} \right\}$$

(14)

The total strain increment tensor can be related to total deformation. The stain tensor for a three-dimensional case can be formulated as follows

$$\varepsilon_{ij} = \frac{1}{2}\left[ {\frac{\partial u_i }{{\partial x_j }} + \frac{\partial u_j }{{\partial x_i }}} \right]$$

(15)

where i and j range from 1 to 3 indicating the three principal directions. x and u show the coordinate and deformation variable. For instance, for the cylindrical coordinate system shown in Fig. 3 used for modelling time to cover cracking, the principal coordinates are r, θ and z, and the response u is the deformation induced by corrosion.

The incremental creep strain is generally a function of some basic variables such as the effective (Von Mises) stress, σ_e, time, t, and temperature, T.

$$\Delta \varepsilon_C = f\left( {\sigma_e ,t,T} \right)$$

(16)

There are various models, e.g. time hardening and strain hardening, describing the relationship shown in Eq. (16) for different materials. Majority of these models are empirical derived from experimental creep data.

4 Modelling of Creep Effect in Corrosion-Induced Cracking

4.1 Model Geometry and Loading

Due to its simplicity and the ease of comparison with some analytical models, the conceptual thick-walled cylinder analogy is commonly used for the analysis of the corrosion-induced cracking problem. In this study, this model is employed. Nonetheless, the proposed creep analysis can be extended to more realistic models. As Fig. 4 shows, due to symmetry, only a quarter of the cylinder can be modelled. The longitudinal length, L_z, is taken as three times the radius of the thick-walled cylinder to resemble the plane strain condition. The horizontal and vertical edges of the quarter cylinder are restrained against movements normal to these edges. The ends of the cylinder are longitudinally restrained. Displacement-controlled analysis is used for the incremental nonlinear analysis, where the inner circle of the cylinder is pushed incrementally from zero to the thickness of the corrosion product ring at each time step. The thickness of the porous zone at the steel–concrete interface, δ₀ in Eq. (2), is not considered. Moreover, the ingress of rust products into concrete and the formed microcracks, δ_p in Eq. (2), are neglected.

Fig. 4

Thick-walled cylinder model

By employing the Finite Element (FE) method, the response of the thick-walled concrete cylinder with internal corrosion-induced pressure due to the applied internal deformation δ(t) = (α_v − 1) × δ_s, as shown in Fig. 4, is evaluated. Any corrosion model, e.g., the Faraday’s law can be employed to calculate thickness of steel mass loss, δ_s. Using the relationship between the average internal pressure at the steel–concrete interface (over the rebar perimeter) and time, the critical time for cover cracking can be calculated. The critical time corresponds to the attainment of the corrosion-induced maximum average pressure [6].

For the FE analysis, the commercially available software ANSYS [40] program is employed. This program has been used for modelling long-term deformations in concrete structures by many researchers [41, 42].

4.2 Elements and Meshing

The thick-walled cylinder depicted in Fig. 5a serves as the basis for FE modelling in ANSYS. As shown in Fig. 5b, SOLID65 element in ANSYS is utilised to model concrete in a three-dimensional model. The element is defined by eight nodes having three translational degrees of freedom at each node. The element has cracking and large strain capabilities. Smeared cracking can occur in three orthogonal directions.

Fig. 5

Schematic FE model and the concrete element

A mesh sensitivity analysis showed that maximum mesh size of 1.0 mm is adequate for reasonably accurate results. Due to use of radial mesh, the mesh size near steel–concrete interface, where the cracks initiate, is smaller. It is worth noting that using the force reactions at the edges of the cylinder, the pressure at the steel–concrete interface can be indirectly calculated.

4.3 Material Model

Concrete is modelled as a homogeneous isotropic material, and the [43] failure criterion is employed. To define the failure surface of the Willam-Wranke model, uniaxial tensile strength (f_t), compressive strength (f’_c), as well as the biaxial compressive strength (f_b), are required. The SOLID65 concrete element in ANSYS possesses both crushing (in compression) and cracking (in tension) capabilities. Since the problem of corrosion-induced cracking is predominantly controlled by tension and the compressive behaviour has minimal effect on the overall results, in tension, once the principal stress in an element reaches the uniaxial tensile strength (f_t), the stiffness of that element in that direction is reduced to zero.

ANSYS performs creep analysis using two different time integration methods. The Implicit creep method is robust, fast, and accurate. In this method, in each load step, the creep model is simultaneously coupled with other plasticity models. On the other hand, the Explicit method is useful when very small load steps are employed. Coupling with other plastic models is achieved through the superposition of creep strains with other strains. Currently, for the SOLID65 concrete element, only the Explicit creep model is available. In Explicit creep modelling in ANSYS, two creep equations are available: the strain hardening and the time hardening. The time hardening law, which is used in this study, is formulated as follows:

$$\dot{\varepsilon }_C = C_1 \sigma_e^{C_2 } t^{C_3 } e^{ - C_4 /T}$$

(17)

where ${\dot{\varepsilon }}_{C}$ is the creep rate, σ_e is the equivalent stress, t is time, and T is the absolute temperature. C₁, C₂, C₃ and C₄ are the model parameters. This model cannot be directly used to model creep in concrete. However, by applying some changes, it can be adopted for this purpose. Using the creep function, shown in Eq. (6), and expanding the uniaxial stress to more general effective stress the creep strain is calculated as follows

$$\varepsilon_C = \varepsilon_E \phi (t,t_0 ) = \frac{\sigma_e }{{E_c (t_0 )}}\phi (t,t_0 )$$

(18)

By differentiation with respect to time, the creep rate is calculated as follows

$$\dot{\varepsilon }_C = \frac{d\varepsilon_C }{{dt}} = \frac{\sigma_e }{{E_c (t_0 )}}\frac{d\phi (t,t_0 )}{{dt}}$$

(19)

By comparing Eqs. (17, 19), the parameters of the time hardening model are obtained as follows

$$C_4 = 0$$

(20a)

$$C_2 = C_3 = 1$$

(20b)

$$C_1 = \frac{1}{E_c (t_0 )}\frac{d\phi (t,t_0 )}{{dt}}$$

(20c)

By having the creep function ϕ(t₀, t), the C₁ coefficient can be obtained. For instance, if the ACI 209.2R guideline [38] creep function shown in Eq. (6) is used, Eq. (20c) will be as follows,

$$C_1 = \frac{1}{E_c (t_0 )}\frac{d\phi (t,t_0 )}{{tdt}} = \frac{1}{E_c (t_0 )}\frac{{\left( {t - t_0 } \right)^{\psi - 1} }}{{\left[ {t_c + \left( {t - t_0 } \right)^{\psi - 1} } \right]^2 }}\psi t_c \phi_u$$

(21)

As an alternative, if t₀ = 0 and the age dependency in the modulus of elasticity is ignored, the creep model coefficients will be as follows

$$C_4 = 0$$

(22a)

$$C_3 = \psi - 1$$

(22b)

$$C_2 = 1$$

(22c)

$$C_1 = \frac{1}{{E_{ci} }}\frac{{\left( {t - t_0 } \right)^{\psi - 1} }}{{\left[ {t_c + \left( {t - t_0 } \right)^{\psi - 1} } \right]^2 }}\psi t_c \phi_u$$

(22d)

where E_ci is the initial modulus of elasticity, i.e. at t₀ = 0. In the FE modelling in ANSYS, following Eq. (22d), the C₁ coefficient is updated at each load step.

4.4 Time-Dependent Analysis

Displacement-controlled analysis is employed for incremental nonlinear analysis, where the inner circle of the thick-walled concrete cylinder is pressed incrementally at each time step. Nonlinear structural analyses are conducted over several load steps. If necessary, sub-steps are utilized to facilitate the convergence of force and displacement in the nonlinear analysis within each time step. The use of sub-steps for convergence is automatically performed using the automatic time-stepping feature in the ANSYS program. After completing the solution and corresponding steps/sub-steps, the stiffness matrix is updated to reflect changes in the structural stiffness before proceeding to the next load step. The ANSYS program employs Newton–Raphson equilibrium iterations to adjust the structural stiffness. The Newton–Raphson iterative method ensures convergence at each displacement increment corresponding to each time step. The entire radial time-pressure of simulated samples is captured at the end of the analysis. This time-pressure response is utilized to determine the time to cover cracking.

5 Verification of Finite Element Model

To evaluate the validity and accuracy of the proposed finite element (FE) model, the numerical results should be compared with some experimental results. Due to many unknown factors involved in corrosion tests, it is preferable to compare the numerical results with test data in which pressure induced by corrosion is simulated using internal hydraulic pressure [6]. However, tests in which the gradual long-term pressure creep effect is applied are not readily available. Thus, the verification of the FE model is divided into two segments: one part verifies the FE creep modelling, while the other part verifies the FE nonlinear cracking behaviour. In the initial phase, the accuracy of the proposed creep model is assessed using creep test data on pressurized thick-walled cylinders. The geometry and boundary conditions of the considered case for verifying the creep modelling in the FE software mirror those of the thick-walled concrete cylinder used in this study. Subsequently, the ability of the developed nonlinear FE model in predicting concrete cracking is assessed using test data on concrete samples. These concrete samples are subjected to direct pressure to simulate corrosion-induced pressure resulting from rust expansion. The maximum cracking pressure predicted by the FE model is juxtaposed with the recorded pressure from the experimental data. This approach, adopted in this paper, was necessitated by the absence of long-term corrosion test data with comprehensive information.

5.1 Verification of the Creep Model

Creep of thick-walled cylinders is a classic problem and has been analytically and experimentally investigated in various studies [44, 45]. In this section, test data from [46]'s study are used to verify the creep material model employed in the proposed FE model. Creep tests were conducted on tubular specimens of an aluminium-0.07 percent titanium alloy subjected to various internal pressures at an elevated temperature of 250 degrees Celsius. Axial and diametral strains were measured during creep tests. Both the external diametral strain and the axial strain corresponding to the central 2-inch (50 mm) portion of the cylinder were recorded. Creep tests were carried out at four internal pressure levels. In this study, the specimen with an internal pressure of 590 psi (4.07 MPa) is considered. The test related to this internal pressure on the aluminium alloy is designated as Test No. 1. At this pressure level, the material behaviour remains fully elastic.

The internal diameter of the cylinder is 0.359 in (9.11 mm) and the ratio of external diameter to internal diameter and the parallel length to internal diameter are 3.13 and 22.0, respectively. Short-time, high temperature tensile properties at 250 deg C of the material showed modulus of elasticity of 4.8 × 10⁶ psi (33.10 GPa) and yield strength of 1340 psi (9.24 MPa). The Poison’s ratio is 0.32. Simple time-hardening law was used to find the best-fit parameters to the following creep rate model

$$\dot{\varepsilon }_C = A2^{n + 1} \sigma^{2n + 1} t^p$$

(23)

where A, n and p are the model parameters that were determined as 5.31 × 10^–17, 1.719 and − 0.373, respectively for low initial stresses. The variable t denotes the time which is measured in hours and σ is stress measured in psi. This model covers both the primary and secondary stages of the creep. King [45] also fitted another power function to the creep data, which only covers the second stage of creep as follows,

$$\dot{\varepsilon }_C = A2^{n + 1} \sigma^{2n + 1}$$

(24)

The best-fit data from King’s study [46] resulted in A = 1.19 × 10^–19 and n = 2.39.

Due to symmetry, only a quarter of the thick-walled cylinder specimen tested by King [46] is modelled. In Fig. 6, the meshed model and the boundary conditions are shown. Axial movement is restrained at both ends of the tube. The applied internal pressure is 590 psi (4.07 MPa). This pressure is kept constant during the creep analysis.

Fig. 6

Geometry and boundary conditions of test No. 1 from King’s study [46]

Maximum mesh size used in the FE model is 0.08 in (2 mm). Nonlinear transient creep analysis over 320 h was performed. Automatic time stepping is used to control the nonlinear FE. However, the minimum time step size is set to 1 h. Results of the external diametral strain (hoop strain at the external diameter) for both analyses along with those resulted from test are shown in Fig. 7. The FE results compare well with the test results. The results from [47] numerical method provided in [45] are also shown.

Fig. 7

Numerical and experimental results for external diametral/hoop strain

Closed-form solutions for thick-walled cylinders under internal pressure in which creep follows the model shown in Eq. (24) are available.

In what follows, the FE results of hoop stresses are also compared with these analytical solutions. In Fig. 8, comparison of the hoop stress from ANSYS results and those obtained from the analytical elastic [48] and creep [49] solutions are provided. Steady-state creep analysis is used to extract ANSYS results used to compare with the analytical results.

Fig. 8

ANSYS versus analytical hoop stress results

The results show that the proposed FE analysis predicts the hoop stresses at both elastic and long-term creep state with excellent accuracy.

5.2 Verification of the Cracking Model

To verify the cracking process in the proposed thick-walled model, the results of tests conducted by [50] are utilized. Williamson and Clark [50] investigated the cracking of cover concrete due to internal pressure induced by liquid oil, representing the pressure exerted by the expansion of corrosion products. The test specimens were 150 mm concrete cubes, with bars placed in either side or corner locations. Uniform corrosion was simulated using a hydraulic jack to pressurize a soft PVC tube inserted in the hole representing the rebar. A hand pump was incrementally used to apply pressure to the specimen until failure. The failure load was identified as the maximum load sustained by the specimen at the cracking of the cover.

In the FE modelling, the geometry of the three-dimensional experimental samples is simplified using the thick-walled cylinder model described in the previous sections. The Poisson ratio is assumed to be 0.20. The comparison of results between the proposed FE model and experimental results on cracking pressure, according to the C/D ratio of 0.5 for 8 mm and 16 mm rebar diameter, is shown in Fig. 9. It is evident from these results that the proposed FE model correlates reasonably well with the experimental data. It is worth noting that, although Williamson and Clark [50] used prismatic concrete specimens with holes representing the rebar location in their tests, the two-dimensional thick-wall cylinder model employed in the FE method could predict the cracking pressure with a reasonable accuracy.

Fig. 9

Comparison of FE and experimental results for cracked concrete samples

It is worth noting that the smeared crack model used in the SOLID65 element in ANSYS ignores the post-crack behaviour, i.e., tension softening, of concrete. If the tension softening behaviour of concrete is considered, the predicted maximum pressure would be higher than that obtained, and consequently, the results would be closer to the experimental findings. Furthermore, the simplifications employed in the thick-walled conceptual analogy are another factor that may cause deviation of FE results from the experimental ones. Confinement within a non-cylindrical reinforced concrete real model results in anisotropic response and higher internal pressure capacity.

As the current study aims to highlight the impact of different methods in modelling creep in the corrosion-induced cracking procedure, this comparative study would not be affected by the degree of accuracy in modelling the post-crack behaviour of concrete material. The proposed FE model can be extended to models with more realistic concrete material models.

6 Results and Discussion

To demonstrate applicability of the proposed procedure and to investigate the effect of creep deformations in the corrosion-induced cracking process, a numerical analysis is presented in this section. Information regarding the material models is the same as those described in the FE verification section.

6.1 Creep model

The ACI 209.2R [38] creep function, shown in Eq. (25), is employed for considering the long-term creep deformations. Age-dependency in the modulus of elasticity is not considered.

$$\phi (t,0) = \frac{{t^{0.6} }}{{10 + t^{0.6} }}\phi_u$$

(25)

where t is in days and ϕ_u = 2.35. It is assumed that the modulus of elasticity at the time of corrosion initiation equal the 28-day modulus of elasticity, and it remains unchanged afterwards. Moreover, it is assumed that prior the corrosion initiation stage, no or negligible creep deformation has occurred. Three different methods are used to model creep deformations. In the first method, as shown in Eq. (26a), creep deformations are directly calculated and added to other structural deformations. The creep deformations in this method are proportional to the effective stress, making it the most accurate in accounting for creep deformations. In the second method, a time-dependent effective modulus of elasticity, as shown in Eq. (26b), is utilized.

$${\text{Direct creep analysis:}}\;\varepsilon_C (t) = \phi (t,0)\frac{\sigma_e }{{E_{ci} }}$$

(26a)

$${\text{Variable effective modulus:}}\;E_{c,eff} (t) = \frac{{E_{ci} }}{1 + \phi (t,0)}$$

(26b)

$${\text{Long}} - {\text{term effective modulus:}}\;E_{c,eff} (t) = \frac{{E_{ci} }}{1 + \phi_u }$$

(26c)

In the third method, which is the simplest, it is assumed that the creep function takes its maximum value, ϕ_u. The modulus of elasticity, which remains constant during the cracking process, is calculated as shown in Eq. (26c).

6.2 Model Description

A typical steel bar with D = 16 mm diameter imbedded in concrete with various clear concrete covers is considered. Various concrete cover thicknesses, C, covering a wide range for C/D ratio are used. The longitudinal length L_z, shown in Fig. 4, is taken as 3(D/2 + C) to simulate a plane strain condition. To calculate the steel mass loss, the Faraday’s law is employed. Considering α_v = 3.0, the following function shows the thickness of rust layer over time

$$\delta (t) = 0.016(\alpha_v - 1)i_{corr} \left( \frac{t}{365} \right) = 63.56 \times 10^{ - 6} i_{corr} t$$

(27)

where δ is the thickness of rust layer measured in millimetre at the steel–concrete interface, the time t is in days and i_corr is the corrosion current density in μA/cm². Different values for i_corr are used in the parametric analysis presented in this study. Using fib Model Code [39], the modulus of elasticity, E_ci, and tensile strength, f_t, are calculated as follows,

$$E_{ci} = 10500\left( {f^{\prime}_c } \right)^{1/3}$$

(28a)

$$f_t = 0.3\left( {f^{\prime}_c } \right)^{2/3}$$

(28b)

In the parametric analysis, tensile strength of concrete is varied from 2.0 to 4.5 MPa and using Eqs. (28a, 28b), the compressive strength and modulus of elasticity are backcalculated. It is assumed that the Poisson ratio of concrete, v_c, is 0.20. For the base case study, the rebar diameter, D, concrete cover, C and the tensile strength of concrete, f_t, are taken as 16 mm, 32 mm and 3.5 MPa, respectively, and the corrosion current density, i_corr, is also taken as 0.5 µA/cm².

In the FE model, the maximum mesh size is set to 1 mm. The analysis time is chosen in such a way that the critical time to cover cracking, which correspond to the maximum corrosion-induced average pressure, is attained before this time runs out. A time interval of 0.25 days is chosen for the transient FE analysis. Displacement-controlled analysis is used for all the three creep models. Following the corrosion-induced deformation, δ(t), the internal surface is monotonically pushed.

6.3 Results

To find the time to cover cracking the criterion proposed by [6] is employed. According to this criterion, the critical time to cover cracking corresponds to the maximum radial pressure at the steel–concrete interface. A typical curve showing the relationship between the internal pressure and time is shown in Fig. 10a. Three important stages can be identified on this curve. Following a linear elastic response, the first crack occurs at the steel–concrete interface, as can be seen in Fig. 10b. Then, the crack front gradually propagates outward until the maximum internal pressure is attained. The hoop stress distribution at the critical state is shown in Fig. 10c.

Fig. 10

Typical nonlinear FE results considering the creep deformations

After attainment of the maximum pressure, the crack front rapidly propagates until it reaches the concrete surface as is shown in Fig. 10a. The results indicate that the critical time to reach maximum pressure is about 134.75 days, while the time at which the surface crack appears is 174.50 days.

For further analysis, Fig. 11 presents the nonlinear response of a typical thick-walled cylinder based on different considered creep methods, along with the elastic response. The dot points indicate the critical state, characterized by the maximum radial pressure. The time to cover cracking for the elastic response, direct creep analysis, variable effective modulus, and long-term effective modulus are 98.25, 134.75, 260, and 329 days, respectively. The results reveal that, compared to direct creep analysis, both effective modulus methods overestimate the time to cover cracking by a significant margin. This overestimation is linked to the overestimation of stress relaxation.

Fig. 11

Typical results of thick-walled cylinder based on different methods

As depicted in Fig. 11, the maximum radial pressure—and consequently, the state of stress—is the same for all the considered methods. This pressure is controlled by force equilibrium, which remains consistent across all methods. However, due to different stress relaxation formulations, the maximum radial pressure is attained at different times. The total hoop strain, representing the sum of elastic and creep strains, at the critical time to cover cracking is also illustrated in Fig. 11a–d. The hoop strains are generally larger for the effective modulus methods than for the direct creep analysis method. This difference is attributed to the overestimation of relaxation in effective modulus methods.

Analytical solution for thick-walled cylinders under elastic plane strain assumption are available [51]. The internal radial pressure, p_r, and the internal radial deformation, δ_r, are related as follows,

$$p_r = E_r \delta_r = \frac{{E_c \left[ {(b/a)^2 - 1} \right]}}{{(1 + v_c )\left[ {1 - 2v_c + (b/a)^2 } \right]a}}\delta_r = 3502.38\,\delta_r$$

(29)

where E_r is the bulk radial modulus. Note that a = D/2 = 8 mm, b = C + D/2 = 40 mm and E_c = 35,864 MPa. In Fig. 11, the elastic line representing Eq. (29) is shown. There is an excellent agreement between the elastic FE results and the analytical solution. This verifies the adequacy of the established geometrical model in representing the plane strain condition.

To quantify the difference, for all the three methods, the equivalent bulk radial modulus is calculated. Based on the results shown in Fig. 11, this modulus represents the slope of the p_r-δ_r lines. For direct creep analysis, variable effective modulus, and the long-term effective modulus, the radial bulk moduli are 2513.16, 1045.84 and 1317.91 N/mm³, respectively. Normalising these moduli to the elastic bulk modulus results in ratios of 0.718, 0.376 and 0.299, respectively. It should be noted that for the long-term effective modulus method, this ratio can be easily calculated as 1/(1 + ϕ_u) = 1/(1 + 2.35) = 0.298.

The difference in the relaxed stresses resulted from the direct creep analysis is more than twice that of the long-term effective modulus, which is commonly used in evaluation of time to cover cracking.

In some studies [4, 7, 8], the time to cover cracking is considered as the time of surface crack appearance. For further comparison, the simple criterion used by Liu and Weyers [7] is employed to calculate the time to cover cracking. According to this criterion, which is based on a simple force equilibrium at the maximum pressure state, the entire concrete cover reaches the concrete tensile capacity, f_t. For the current typical case, this pressure is calculated as follows

$$p_r = \frac{2C}{D}f_t = 2(\frac{32}{{16}})(3.5) = 14\,{\text{MPa}}$$

(30)

To obtain the radial deformation that corresponds to this pressure, Liu and Weyers [7] employed the elastic solution for the thick-walled cylinder under plane stress condition. Here, the elastic solution under the plane strain assumption, as shown in Eq. (29), is utilized. The critical radial deformation is calculated as follows

$$\delta_r = \frac{p_r }{{3502.38}} = \frac{14}{{3502.38}} = 0.004\,{\text{mm}}$$

(31)

To account for the effect of long-term deformations, Liu and Weyers [7] suggested a simple long-term effective modulus of elasticity. Due to the linear relationship between the initial and effective moduli of elasticity, the final time to cover cracking can be simply multiplied by a factor of (1 + ϕ_u) = 3.35. Finally, using the calculated critical radial deformation δ_r, and by employing an empirical or theoretical corrosion model, the time to cover cracking can be determined. Liu and Weyers [7] utilised an empirical nonlinear corrosion model; however, for convenience, Faraday’s model shown in Eq. (27), is employed here.

$$t_{cr} = \frac{\delta_r }{{63.56 \times 10^{ - 6} i_{corr} }} = \frac{0.004}{{63.56 \times 10^{ - 6} \times 0.5}} = 125.78\,{\text{day}}$$

(32)

Now, applying the 3.35 long-term factor results in a critical time of 421.36 days. It should be noted that the criterion proposed by Liu and Weyers is based on the appearance of a surface crack, not the maximum pressure. This value is more than twice the 174.5 days obtained from the direct creep analysis method (Fig. 10).

The typical evolution of elastic and creep hoop strains at the steel–concrete surface is depicted in Fig. 10a. The results accurately illustrate that once the first crack appears at the steel–concrete interface, there will be negligible creep strain, as creep does not occur in an opening crack. Additionally, due to crack opening, the elastic strain rate increases. For further comparison, Fig. 12a displays the variation of hoop strain across the concrete thickness at the critical time to cover cracking. In comparison to the direct creep analysis method, both effective modulus methods considerably overestimate the hoop strain. The ratio of hoop strain obtained from all the considered methods to that of the elastic response is presented in Fig. 12b. This ratio remains constant across the concrete cover thickness in effective modulus methods, while for direct creep analysis, it gradually decreases by about 10% from the inner side of the cylinder to the outer side. This variation is more realistic than the constant ratio obtained from methods based on effective modulus. The inner side of the cylinder experiences larger strains throughout the loading, leading to a higher accumulation of creep strain, which is proportional to the elastic strain, in this region. Furthermore, the evolution of elastic strains and their effect on creep strain, which is proportional to the updated elastic strain, is not considered in effective modulus methods. It should be noted that the variation of hoop stress at the critical state is the same for all methods, including the elastic response.

Fig. 12

Distribution of the hoop strain at the attainment of maximum pressure

For various geometrical dimensions and material properties, the results of internal radial pressure can be analysed, and the critical time to cover cracking can be calculated. In Fig. 13a, b, the time to cover cracking as a function of concrete cover, C, and concrete tensile strength, f_t, is shown. The corrosion current density is 0.50 µA/cm². In comparison with the effective modulus methods, the prediction in the direct creep analysis method is closer to the elastic result. The average ratio of predicted time to cover cracking by direct creep analysis, variable effective modulus, and long-term effective modulus to that of the elastic response is 1.37, 2.67, and 3.35, respectively. This shows that the results of the long-term effective modulus, commonly used in predicting the time to cover cracking, are more than twice those predicted by the accurate creep analysis method. This is a significant outcome, rendering the effective modulus of elasticity a method with a considerable error in predicting the time to cover cracking. Similar results for other geometrical dimensions and material properties are obtained and, for the sake of brevity, are not presented here.

Fig. 13

Time to cover cracking for different geometrical and material properties

Another important factor in assessing the time to cover cracking is the corrosion current density, which controls the rate of loading. In Fig. 14, for a typical case, the ratio of the time to cover cracking predicted by the considered creep analysis methods to that of the elastic response is shown as a function of corrosion current density. For the long-term effective modulus, this ratio simply equals 1 + ϕ_u = 3.35, while for the other two methods, it varies with the corrosion current density. As long-term deformations are time-dependent, any variation in the loading rate affects the results. For higher corrosion current densities, i.e., more severe corrosion rates, a shorter time for concrete cover cracking is needed. Therefore, it is expected that over this shorter time, fewer long-term deformations occur. The results in Fig. 14 conform to this expectation. However, the time-dependent effective modulus is very sensitive to the corrosion rate, while the creep analysis method shows much less sensitivity. As previously discussed, in the variable effective modulus method, the interaction between creep and elastic strains is not considered, leading to the overestimation of creep deformations.

Fig. 14

Effect of corrosion current density on the time to cover cracking

7 Conclusion

In this paper, major issues with the current treatment of creep deformations in predicting the time to cover cracking have been discussed. An accurate procedure for modelling creep deformations and the concrete cracking process has been developed and verified using experimental data. Comparison of the developed procedure with current methods for treating creep deformations in predicting the time to cover cracking has shown that current methods based on effective modulus are not suitable. This is attributed to the fact that the problem of corrosion-induced cracking is like a relaxation problem under a monotonically increasing displacement, while the current methods are designed to calculate creep deformations under sustained loads. The study reveals that accurate consideration of creep deformation would lead to about 30–40% longer time to cover cracking compared to not considering creep deformations. In contrast, for current methods based on effective modulus, the time can be up to 200% longer, which is unconservative in predicting time to cover cracking. It has also been observed that the degree of increased time varies with the rate of corrosion, though not considerably. The results of this study initiate a debate on the modelling of long-term effects of creep in the analysis of corrosion-affected structures and serve as a step toward the accurate prediction of corrosion-induced cracking of concrete cover.