Skip to main content
SpringerLink
Log in

Accuracy of Numerical Simulation in Asymmetric Compound Channels

  • Research Paper
  • Published:
International Journal of Civil Engineering Aims and scope Submit manuscript

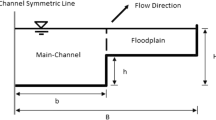
Abstract

In the recent years, compound channels received more attention in hydraulic engineering for their role in estimating and calculating the hydraulic parameters of natural rivers. Usually, for determination of the hydraulic parameters of compound channels, physical models are used which have cost and time assumption. According to the wide usage of numerical modeling in hydraulic engineering, this paper aims to evaluate the accuracy of numerical models in compound channels by simulating the hydraulic parameters in nine different types of compound channels and to compare them with experimental data. These simulations can show the interaction between velocity and vorticity and other hydraulic parameters by using contours and graphs along the channel length which help to have more and better understanding about their changes. Numerical simulations were performed using the renormalization-group turbulence model and volume-of-fluid free surface model for determining the level of fluid. Values of convergence ratio and the grid convergence index were calculated for evaluating the extrapolated values from numerical modeling and the sensitivity of the model solution to the numerical discretization, respectively, which indicates a proper validation of grid spacing and refinement selection for optimizing the calculation process. The comparison between numerical and experimental results shows a good agreement. The extracted numerical results show that by changing the floodplain width and depth, the water surface level changes 4–20% and 5–34%, respectively. Moreover, the numerical results show an increment of 20 and 145% in Froude and Weber numbers in floodplains, respectively, because of increment of velocity in floodplain.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

Abbreviations

A :

The fractional area open to flow

B :

Width of main channel

B o :

Width of upstream channel

B f :

Width of floodplain

D :

Hydraulic diameter

f i :

The result corresponding to the different mesh sizes

F SOR :

The time rate of change of the volume fraction of fluid associated with the mass source for fluid

Fr :

Froude number

f x , f y and f z :

Viscous accelerations

g :

Earth gravity

G x , G y and G z :

Body accelerations

H :

Main channel water depth

K :

The turbulence kinetic energy

Q 1 :

Mean main channel volumetric flow rate

Q 2 :

Mean floodplain volumetric flow rate

Q 3 :

Mean full cross-sectional volumetric flow rate

R ’ :

Refinement factor

R :

The center of mass of a body

R c :

The convergence ratio

R DIF :

A turbulent diffusion term

R SOR :

A mass source

u w, v w and w w :

The velocity of source component

u s, v s and w s :

The velocity of the fluid at the surface of the source relative to the source itself

V :

Mean cross-sectional velocity

V F :

The fractional volume open to flow

We :

Weber number

x, y and z :

Coordinate directions

u, v and w :

Velocity components

Y f :

Floodplain water depth

Y r :

The ratio of floodplain water depth and main channel water depth

Z :

Step height

θ 1 :

Entrance angles

θ 2 :

Entrance angles

ρ :

The fluid density

ε i + 1,i :

The relative deviation

ε :

Dissipation rate

v t :

Eddy viscosity

v :

The kinematic viscosity

Δh :

The grid spacing

σ :

Surface tension

References

  1. Knight DW, Brown FA (2001) Resistance studies of overbank flow in rivers with sediment using the flood channel facility. J Hydraul Res 39(3):283–301

    Article  Google Scholar 

  2. Karamisheva RD, Lyness JF, Myers WRC, Cassells JBC, O’Sullivan J (2006) Overbank flow depth prediction in alluvial compound channels. Proc Ice Water Manag 159(3):195–205

    Google Scholar 

  3. Carollo FG, Ferro V, Termini D (2002) Flow velocity measurements in vegetated channels. J Hydraul Eng 128(7):669–673

    Article  Google Scholar 

  4. Seckin G (2004) A comparison of one-dimensional methods for estimating discharge capacity of straight compound channels. Can J Civ Eng 31(4):619–631

    Article  Google Scholar 

  5. Al-Khatib IA, Dweik AA, Gogus M (2012) Evaluation of separate channel methods for discharge computation in asymmetric compound channels. Flow Meas Instrum 24:19–25

    Article  Google Scholar 

  6. Luo EC (2011) Apparent shear stress in symmetric-straight compound-channel flow. Int J Environ Prot 1(2):28–32

    Google Scholar 

  7. Bousmar D, Wilkin N, Jacquemart JH, Zech Y (2004) Overbank flow in symmetrically narrowing floodplains. J Hydraul Eng 130(4):305–312

    Article  Google Scholar 

  8. Rezaei B, Knight DW (2011) Overbank flow in compound channels with nonprismatic floodplains. J Hydraul Eng 137(8):815–824

    Article  Google Scholar 

  9. Meile T, Boillat J, Schleiss A (2011) Flow resistance caused by large-scale bank roughness in a channel. J Hydraul Eng 137(12):1588–1597

    Article  Google Scholar 

  10. Sahu M, Mahapatra SS, Biswal KC, Khatua KK (2014) Prediction of flow resistance in a compound open channel. J Hydroinform 16(1):19

    Article  Google Scholar 

  11. Hosseini SM (2004) Equations for discharge calculation in compound channels having homogeneous roughness. Iran J Sci Technol 28(B5):538–546

    Google Scholar 

  12. Sahu M, Khatua KK, Mahapatra SS (2011) A neural network approach for prediction of discharge in straight compound open channel flow. Flow Meas Instrum 22(5):438–446

    Article  Google Scholar 

  13. Zeng YH, Guymer I, Spence KJ, Huai WX (2012) Application of analytical solutions in trapezoidal compound channel flow. River Res Appl 28(1):53–61

    Article  Google Scholar 

  14. Zahiri A, Dehghani AA (2009) Flow discharge determination in straight compound channels using ANNs. Int Sci Index 3(10):12–15

    Google Scholar 

  15. Chau KW, Jiang YW (2004) A three-dimensional pollutant transport model in orthogonal curvilinear and sigma coordinate system for Pearl river estuary. Int J Environ Pollut 21(2):188–198

    Article  Google Scholar 

  16. Chau KW, Jiang YW (2001) 3D numerical model for Pearl River estuary. J Hydraul Eng 127(1):72–82

    Article  Google Scholar 

  17. Yazdi J, Sarkardeh H, Azamathulla HM, Ghani AA (2010) 3D simulation of flow around a single spur dike with free-surface flow. Int J River Basin Manag 8(1):55–62

    Article  Google Scholar 

  18. Rahimzadeh H, Maghsoodi R, Sarkardeh H, Tavakkol S (2012) Simulating flow over circular spillways by using different turbulence models. Eng Appl Comput Fluid Mech 6(1):100–109

    Google Scholar 

  19. Maghsoodi R, Roozgar MS, Sarkardeh H, Azamathulla HM (2012) 3D-simulation of flow over submerged weirs. Int J Model Simul 32(4):237–245

    Google Scholar 

  20. Sarkardeh H, Zarrati AR, Jabbari E, Marosi M (2014) Numerical simulation and analysis of flow in a reservoir in the presence of vortex. J Eng Appl Comput Fluid Mech 8(4):598–608

    Google Scholar 

  21. Maghsoodi R, Roozgar MS, Chau KW, Sarkardeh H (2012) 3D simulation of dam break flows. Dam Eng 23(2):53–60

    Google Scholar 

  22. Atabay S, Knight DW, Seckin G (2005) Effects of overbank flow on fluvial sediment transport rates. Proc Ice Water Manag 158(1):25–34

    Google Scholar 

  23. Maghrebi MF, Ball JE (2006) New method for estimation of discharge. J Hydraul Eng 132(10):1044–1051

    Article  Google Scholar 

  24. Jan C, Chang CF (2009) Experiments on discharge equations of compound broad crested weirs. J Irrig Drain Eng 135(4):511–515

    Article  Google Scholar 

  25. Nguyen VT, Moreno CS, Lyu S (2014) Numerical simulation of sediment transport and bed morphology around Gangjeong Weir on Nakdong River. KSCE J Civ Eng 19(7):2291–2297

    Article  Google Scholar 

  26. Nazari O, Jabbari E, Sarkardeh H (2015) Dynamic pressure analysis at chute flip buckets of five dam model studies. Int J Civ Eng 13(1A):45–54

    Google Scholar 

  27. Kazemi F, Khodashenas SR, Sarkardeh H (2016) Experimental study of pressure fluctuation in stilling basins. Int J Civ Eng 14(1):13–21

    Article  Google Scholar 

  28. Fazel Z, Fazelian M, Sarkardeh H (2016) Development of a device for measuring air-water flow characteristics. Int J Civ Eng 15(1):45–54

    Google Scholar 

  29. Ferziger JH, Peri M (2002) Computational method for fluid dynamics. Springer, Berlin

    Book  Google Scholar 

  30. Thanh NC, Ling-Ling W (2015) Physical and numerical model of flow through a spillway with a breast wall. KSCE J Civ Eng 19(7):2317–2324

    Article  Google Scholar 

  31. Gaulke D, Dreyer ME (2015) CFD simulation of capillary transport of liquid between parallel perforated plates using Flow 3D. Microgravity Sci Technol 27(4):261–271

    Article  Google Scholar 

  32. Abbaspour A, Hashemi-kia S (2014) Numerical investigation of turbulent open channel flow with semi-cylindrical rough beds. KSCE J Civ Eng 18(7):2252–2260

    Article  Google Scholar 

  33. Kang H (2013) Flow characteristics and morphological changes in open-channel flows with alternative vegetation zones. KSCE J Civ Eng 17(5):1157–1165

    Article  Google Scholar 

  34. Al-khatib IA, Hassan HA, Abaza KA (2013) Application and validation of regression analysis in prediction of discharge in asymmetric compound channel. J Irrig Drain Eng 139:542–550

    Article  Google Scholar 

  35. Shahheidari H, Nodoshan EJ, Barati R, Moghadam MA (2015) Discharge coefficient and energy dissipation over stepped spillway under skimming flow regime. KSCE J Civ Eng 19(4):1174–1182

    Article  Google Scholar 

  36. Ali MSM, Doolan CJ, Wheatley V (2009) Grid convergence study for a two dimensional simulation of flow around square cylinder at a low reynolds number. In: Proceeding of 7th International Conference on CFD in the Minerals and Process Industries, CSIRO, Melbourne, Australia, pp 1–6

  37. Aydin MC, Ozturk M (2009) Verification and validation of a computational fluid dynamics (CFD) model for air entrainment at spillway aerators. Can J Civ Eng 36(5):826–836

    Article  Google Scholar 

  38. Wilcox DC (2007) Turbulence modeling for CFD, 3rd edn. DCW Ind Inc, California

    Google Scholar 

  39. Kumbhakar M, Ghoshal K (2016) Two dimensional velocity distribution in open channels using Renyi entropy. Phys A 450:465–559

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Faculty of Engineering, Hakim Sabzevari University, Tohid Shahr, P.O. Box 9617976487, Sabzevar, Iran

    Sayed-Abdul-Hamid Sajjadi, Sayed-Hamed Sajjadi & Hamed Sarkardeh

Authors
  1. Sayed-Abdul-Hamid Sajjadi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sayed-Hamed Sajjadi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hamed Sarkardeh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hamed Sarkardeh.

Ethics declarations

Funding

No fund available in this research work.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sajjadi, SAH., Sajjadi, SH. & Sarkardeh, H. Accuracy of Numerical Simulation in Asymmetric Compound Channels. Int J Civ Eng 16, 155–167 (2018). https://doi.org/10.1007/s40999-016-0113-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40999-016-0113-3

Keywords

Search

Navigation