Abstract
In this paper, we present a distributed model predictive control strategy for discrete-time interconnected linear systems. The overall system is composed of a number of discrete-time interconnected linear subsystems. The MPC controllers of subsystems communicate their information to handle the interconnection effects. It is known that distributed MPC relies on communication networks to transmit and share information among subsystems. Communication delays, resulting in delayed information exchange among subsystems, may inhibit the use of any distributed MPC approach. To address this problem, a delay handling mechanism is employed. Besides, it is showed that the proposed method guarantees input-to-state stability characterization for both local subsystems and the global system under some predetermined assumptions. The simulation results are exploited to illustrate the effectiveness of the proposed method.

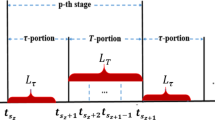
(Reproduced with permission from Li and Shi 2013)

















Similar content being viewed by others
References
Abu-Ayyad M, Dubay R (2007) Real-time comparison of a number of predictive controllers. ISA Trans 46:411–418
Camacho EF, Alba CB (2013) Model predictive control. Springer, New York
Camponogara E, Jia D, Krogh BH, Talukdar S (2002) Distributed model predictive control. Control Syst IEEE 22:44–52
Christofides PD, Liu J, De La Pena DM (2011) Conclusions. In: Networked and distributed predictive control. Methods and nonlinear process network applications. Advances in industrial control. Springer, London, pp 219–220
Christofides PD, Scattolini R, de la Pena DM, Liu J (2013) Distributed model predictive control: a tutorial review and future research directions. Comput Chem Eng 51:21–41
Dunbar WB, Murray RM (2006) Distributed receding horizon control for multi-vehicle formation stabilization. Automatica 42:549–558
Ferrara A, Sacone S, Siri S (2014) Distributed model predictive control for MLD systems: application to freeway ramp metering. Am Control Conf (ACC) 2014:5294–5299
Figueroa J, Biagiola S, Alvarez M, Castro L, Agamennoni O (2013) Robust model predictive control of a Wiener-like system. J Franklin Inst 350:556–574
Findeisen R, Imsland L, Allgower F, Foss BA (2003) State and output feedback nonlinear model predictive control: an overview. Eur J Control 9:190–206
Franco E, Magni L, Parisini T, Polycarpou MM, Raimondo DM (2008) Cooperative constrained control of distributed agents with nonlinear dynamics and delayed information exchange: a stabilizing receding-horizon approach. Autom Control IEEE Trans 53:324–338
Franzè G, Tedesco F, Famularo D (2015) Model predictive control for constrained networked systems subject to data losses. Automatica 54:272–278
Gao H, Chen T (2007) Networked based H-inf output tracking control. IEEE Trans Autom Control 52:2070–2084
Gu B, Gupta YP (2008) Control of nonlinear processes by using linear model predictive control algorithms. ISA Trans 47:211–216
Heidarinejad M, Liu J, de la Pena DM, Davis JF, Christofides PD (2011) Handling communication disruptions in distributed model predictive control. J Process Control 21:173–181
Hosseini I, Naghavi SV, Safavi AA (2016) Distributed model predictive control of discrete-time interconnected systems with time delays. In: 2016 24th Iranian conference on electrical engineering (ICEE), pp 477–483
Kazempour F, Ghaisari J (2013) Stability analysis of model-based networked distributed control systems. J Process Control 23:444–452
Keviczky T, Borrelli F, Balas GJ (2006) Decentralized receding horizon control for large scale dynamically decoupled systems. Automatica 42:2105–2115
Li H, Shi Y (2013) Distributed model predictive control of constrained nonlinear systems with communication delays. Syst Control Lett 62:819–826
Li H, Shi Y (2014a) Robust distributed model predictive control of constrained continuous-time nonlinear systems: a robustness constraint approach. IEEE Trans Autom Control 59:1673–1678
Li H, Shi Y (2014b) Distributed receding horizon control of large-scale nonlinear systems: handling communication delays and disturbances. Automatica 50:1264–1271
Li H, Shi Y (2017) Robust receding horizon control for networked and distributed nonlinear systems. Springer, New York
Liu X, Shi Y, Constantinescu D (2016a) Robust distributed model predictive control of constrained continuous-time nonlinear systems using two-layer invariant sets. J Dyn Syst Meas Control 138:061004
Liu M, Shi Y, Liu X (2016b) Distributed MPC of aggregated heterogeneous thermostatically controlled loads in smart grid. IEEE Trans Ind Electron 63:1120–1129
Müller MA, Reble M, Allgöwer F (2012) Cooperative control of dynamically decoupled systems via distributed model predictive control. Int J Robust Nonlinear Control 22:1376–1397
Naghavi SV, Safavi A, Kazerooni M (2014) Decentralized fault tolerant model predictive control of discrete-time interconnected nonlinear systems. J Franklin Inst 351:1644–1656
Naghavi SV, Naghavi SV, Safavi A, Safavi A, Khooban MH, Khooban MH, Pourdehi S, Pourdehi S, Ghaffari V, Ghaffari V (2016) A robust control strategy for a class of distributed network with transmission delays: LMI-based model predictive controller. COMPEL Int J Comput Math Electric Electron Eng 35:1786–1813
Nikolakopoulos G, Dritsas L, Delshad SS (2014) Combined networked switching output feedback control with-region stability for performance improvement. Int J Control 87:1172–1180
Pang ZH, Liu GP, Zhou D, Sun D (2016) Data-based predictive control for networked nonlinear systems with network-induced delay and packet dropout. IEEE Trans Ind Electron 63:1249–1257
Qin SJ, Badgwell TA (2003) A survey of industrial model predictive control technology. Control Eng Pract 11:733–764
Rahideh A, Shaheed MH (2011) Stable model predictive control for a nonlinear system. J Franklin Inst 348:1983–2004
Ren M, Zhang J, Jiang M, Yu M, Xu J (2015) Minimum entropy control for non-gaussian stochastic networked control systems and its application to a networked dc motor control system. IEEE Trans Control Syst Technol 23:406–411
Richards A, How J (2007) Robust distributed model predictive control. Int J Control 80:1517–1531
Scattolini R (2009) Architectures for distributed and hierarchical model predictive control—a review. J Process Control 19:723–731
Seuret A, Hetel L, Daafouz J, Johansson KH (2016) Delays and networked control systems. Springer, New York
Shafiee G, Arefi M, Jahed-Motlagh M, Jalali A (2006) Model predictive control of a highly nonlinear process based on piecewise linear Wiener models. In: 2006 1ST IEEE international conference on e-learning in industrial electronics, pp 113–118
Shafiee G, Arefi M, Jahed-Motlagh M, Jalali A (2008) Nonlinear predictive control of a polymerization reactor based on piecewise linear Wiener model. Chem Eng J 143:282–292
Venkat AN, Hiskens IA, Rawlings JB, Wright SJ (2008) Distributed MPC strategies with application to power system automatic generation control. Control Syst Technol IEEE Trans 16:1192–1206
Xia Y-Q, Gao Y-L, Yan L-P, Fu M-Y (2015) Recent progress in networked control systems—a survey. Int J Autom Comput 12:343–367
Zhang B, Yang W, Zong H, Wu Z, Zhang W (2011) A novel predictive control algorithm and robust stability criteria for integrating processes. ISA Trans 50:454–460
Zhang L, Gao H, Kaynak O (2013) Network-induced constraints in networked control systems—a survey. IEEE Trans Ind Inf 9:403–416
Zheng Y, Li S, Li N (2011) Distributed model predictive control over network information exchange for large-scale systems. Control Eng Pract 19:757–769
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
One can use the following proposition to extend the results to nonlinear case:
Problem 2 (Naghavi et al. 2014)
Let \(\alpha_{3i} \in K_{\infty } ,J_{{{\text{MPC}}i}} ( \cdot )\) in (5.7) and a CLF \(V_{i} (.)\,\) be given for the \(i\)th subsystem. At time k measure the state \(x_{i} (k)\,\) and minimize the cost \(J_{{\rm MPC}i} (.)\) over \(\bar{U}_{i} (k): = (\bar{u}_{i} (k\left| {k),\bar{u}_{i} (k + 1|k), \ldots ,\bar{u}_{i} (k + N_{c} - 1} \right|k))\) subject to the following constraints
Note that \(\bar{u}_{i} \left( {k |k} \right) = u_{i} (k\)).
Let \(\pi_{o} (x_{i} (k)): = \left\{ {u_{i} (k)\left| {\varPsi \;{\text{holds}}} \right.} \right\}\) and \(x_{i} (k + 1)\, \in \,f_{oi} (x_{i} (k),\pi_{o} (x_{i} (k))): = \,\left\{ {f_{i} (x_{i} (k),u_{i} (k))\left| {u_{i} } \right. \in \pi_{o} (x_{i} (k))} \right\}\) denote the difference inclusion corresponding to the system without considering the disturbance in a closed loop with the set of feasible solutions obtained by solving Problem 1 at each instant \(k \in Z_{ + }\).
Theorem 2
(Naghavi et al. 2014) Let\(\alpha_{1i} (s) = a_{i} s^{{\delta_{i} }} ,\alpha_{2i} (s) = b_{i} s^{{\delta_{i} }} ,\alpha_{3i} (s) = c_{i} s^{{\delta_{i} }}\)for some\(a_{i} ,b_{i} ,c_{i} ,\delta_{i} \in R_{ + }\), \(b_{i} \ge c_{i}\), continuous and convex CLFs\(V_{i} ( \cdot )\)and costs\(J_{{{\text{MPC}}i}} ( \cdot )\)be given for all systems indexed by\(i = 1,2, \ldots ,n\). Suppose Problem 1 is feasible for each subsystem\(i = 1,2, \ldots ,n\)and for all states\(x_{i} \in X_{i}\). Then, each ith subsystem is ISS (\(X_{i} ,\,\,W_{i}\)) and the global interconnected dynamically coupled nonlinear system described by the collection of difference inclusions
is ISS(X,W).
Rights and permissions
About this article
Cite this article
Hosseini, I., Naghavi, S.V. & Safavi, A.A. Distributed Model Predictive Control Strategy for a Class of Interconnected Discrete-Time Systems with Communication Delay. Iran J Sci Technol Trans Electr Eng 43, 267–276 (2019). https://doi.org/10.1007/s40998-018-0085-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40998-018-0085-1