Skip to main content
SpringerLink
Log in

Nonlinear Forced Vibration of Thermally Postbuckled Double-Layered Triangular Graphene Sheet with Clamped Boundary Conditions

  • Research Paper
  • Published:
Iranian Journal of Science and Technology, Transactions of Mechanical Engineering Aims and scope Submit manuscript

Abstract

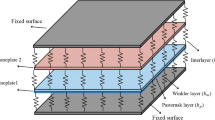
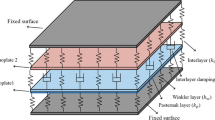
In the present research, vibration behavior is presented for a thermally postbuckled double-layered triangular graphene sheet (DLTGS). The DLTGS is modeled as a nonlocal orthotropic plate and contains small-scale effects. The formulations are based on the Kirchhoff’s plate theory, and a nonlinearity of von Karman-type is considered in strain–displacement relations. The thermal effects and van der Waals forces between layers are also included and some of the material properties are assumed to be temperature-dependent. A semi-analytical solution is obtained using the multiple time scales method. The effects of variation of small-scale parameter to the natural frequencies, deflections and response curve of DLTGS are analyzed, and the numerical results are obtained from the nonlocal plate model. Numerical results are compared with those of similar researches. Effects of various parameters on the postbuckled vibration of DLTGS in thermal environments such as scale parameter and thermal load are presented. The stability and occurrence of the internal resonance between vibration modes around a stable buckled configuration is investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Andrew A (1997) Active control of buckling using piezo-ceramic actuators. Xerox Palo Alto Research Center, N00014-00092-J-04097

  • Anlas G, Elbeyli O (2002) Nonlinear vibrations of a simply supported rectangular metallic plate subjected to transverse harmonic excitation in the presence of a one-to-one internal resonance. Nonlinear Dyn 30:1–28

    Article  MATH  Google Scholar 

  • Ansari R, Faraji Oskouie M, Gholami R, Sadeghi F (2016) Thermo-electro-mechanical vibration of postbuckled piezoelectric Timoshenko nanobeams based on the nonlocal elasticity theory. Compos B Eng 89:316–327

    Article  Google Scholar 

  • Ansari R, Gholami R (2016a) Nonlocal free vibration in the pre- and postbuckled states of magneto-electro-thermo elastic rectangular nanoplates with various edge conditions. Smart Mater Struct 25(9):095033

    Article  Google Scholar 

  • Ansari R, Gholami R (2016b) Size-dependent modeling of the free vibration characteristics of postbuckled third-order shear deformable rectangular nanoplates based on the surface stress elasticity theory. Compos Part B 95:301–316

    Article  Google Scholar 

  • Ansari R, Pourashraf T, Gholami R (2015) An exact solution for the nonlinear forced vibration of functionally graded nanobeams in thermal environment based on surface elasticity theory. Thin-Walled Struct 93:169–176

    Article  Google Scholar 

  • Askari H, Saadatnia Z, Esmailzadeh E, Younesian D (2014) Multi-frequency excitation of stiffened triangular plates for large amplitude oscillations. J Sound Vib 333:5817–5835

    Article  Google Scholar 

  • Beni AA, Malekzadeh P (2012) Nonlocal free vibration of orthotropic non-prismatic skew nanoplates. Compos Struct 94:3215–3222

    Article  Google Scholar 

  • Biswas P, Kapoor P (1984) Nonlinear free vibrations of triangular plates at elevated temperature. J Indian Inst Sci 65(8):29–37

    MATH  Google Scholar 

  • Chang SI, Bajaj AK, Krousgrill CM (1993) Non-linear vibrations and chaos in harmonically excited rectangular plates with one-to-one internal resonance. Nonlinear Dyn 4:433–460

    Article  Google Scholar 

  • Chen Z, Zhang C, Wu Q, Li K, Tan L (2015) Application of triangular silver nanoplates for colorimetric detection of H2O2. Sens Actuators B Chem. https://doi.org/10.1016/j.snb.2015.05.085

    Article  Google Scholar 

  • Cheung YK, Zhou D (2002) Three-dimensional vibration analysis of cantileveredand completely free isosceles triangular plates. Int J Solids Struct 39:673–687

    Article  MATH  Google Scholar 

  • Emam SA, Nayfeh AH (2004) On the nonlinear dynamics of a buckled beam subjected to a primary-resonance excitation. Nonlinear Dyn 35:1–17

    Article  MATH  Google Scholar 

  • Emam SA, Nayfeh AH (2013) Non-linear response of buckled beam to 1:1 and 3:1 internal resonance. Int J Non-Linear Mech 52:12–25

    Article  Google Scholar 

  • Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54:4703–4710

    Article  Google Scholar 

  • Eringen AC (2002) Nonlocal continuum field theories. Springer, New York

    MATH  Google Scholar 

  • Farokhi H, Ghayesh MH, Amabili M (2013) Nonlinear resonant behavior of microbeams over the buckled state. Appl. Phys. A 113:297–307

    Article  Google Scholar 

  • Gholami R, Ansari R (2019) Nonlinear stability and vibration of pre/post-buckled multilayer FG-GPLRPC rectangular plates. Appl Math Model 65:627–660

    Article  MathSciNet  MATH  Google Scholar 

  • Gholami Y, Ansari R, Gholami R, Rouhi H (2018) Analyzing primary resonant dynamics of functionally graded nanoplates based on a surface third-order shear deformation model. Thin-Walled Struct 131:487–499

    Article  Google Scholar 

  • López-Suárez M, Abadal G, Gammaitoni L, Rurali R (2015) Noise energy harvesting in buckled BN nanoribbons from molecular dynamics. Nano Energy 15:329–334

    Article  Google Scholar 

  • Na K-S, Kim J-H (2006) Thermal postbuckling investigations of functionally graded plates using 3-D finite element method. Finite Elem Anal Des 42:749–756

    Article  Google Scholar 

  • Nallim LG, Luccioni BM, Grossi RO (2005) Vibration of general triangular composite plates with elastically restrained edges. Thin-Walled Struct 43:1711–1745

    Article  Google Scholar 

  • Nayfeh AH, Emam SA (2008) Exact solution and stability of postbuckling configurations of beams. Nonlinear Dyn 54:395–408

    Article  MathSciNet  MATH  Google Scholar 

  • Nayfeh AH, Mook DT (1995) Non-linear oscillations. Wiley, New York

    Book  Google Scholar 

  • Nazemnezhad R (2015) Nonlocal Timoshenko beam model for considering shear effect of van der Waals interactions on free vibration of multilayer graphene nanoribbons. Compos Struct. https://doi.org/10.1016/j.compstruct.2015.07.108

    Article  Google Scholar 

  • Paik JK, Anil K, Amballi T, Kim BJ (2001) Large deflection orthotropic plate approach to develop ultimate strength formulations for stiffened panels under combined biaxial compression/tension and lateral pressure. Thin-Walled Struct 39:215–246

    Article  Google Scholar 

  • Pradhan SC, Phadikar JK (2009) Nonlocal elasticity theory for vibration of nanoplates. J Sound Vib 325:206–223

    Article  Google Scholar 

  • Reddy JN (2007) Theory and analysis of elastic plates and shels, 2nd edn. Taylor & Francis Group, New York

    Google Scholar 

  • Setoodeh AR, Rezae M (2017) Large amplitude free vibration analysis of functionally graded nano/micro beams on nonlinear elastic foundation. Struct Eng Mech 61(2):209–220

    Article  Google Scholar 

  • Setoodeh AR, Khosrownejad M, Malekzadeh P (2011) Exact nonlocal solution for postbuckling of single-walled carbon nanotubes. Physica E 43:1730–1737

    Article  Google Scholar 

  • Shen L, Shen HS, Zhang CL (2010) Nonlocal plate model for nonlinear vibration of single layer graphene sheets in thermal environments. Comput Mater Sci 48:680–685

    Article  Google Scholar 

  • Shen H-S, Xu Y-M, Zhang C-L (2013) Prediction of nonlinear vibration of bilayer graphene sheets in thermal environments via molecular dynamics simulations and nonlocal elasticity. Comput Methods Appl Mech Eng 267:458–470

    Article  MathSciNet  MATH  Google Scholar 

  • Shi JX, Ni QQ, Lei XW, Natsuki T (2012) Nonlocal vibration of embedded double-layer graphene nanoribbons in in-phase and anti-phase modes. Physica E 44:1136–1141

    Article  Google Scholar 

  • Terrones M, Botello-Méndez AR, Campos-Delgado J, Lopez-Urias F, Vega-Cantú YI, Rodríguez-Macías FJ, Elías AL, Munoz-Sandoval E, Cano-Márquez AG, Charlier JC, Terrones H (2010) Graphene and graphite nanoribbons: morphology, properties, synthesis, defects and applications. Nano Today 5:351–372

    Article  Google Scholar 

  • Varzandian GA, Ziaee S (2017) Analytical solution of non-linear free vibration of thin rectangular nano plates with various boundary conditions based on non-local theory. Amirkabir J Mech Eng 48(4):331–346

    Google Scholar 

  • Ventsel E, Krauthammer T (2001) Thin Plates and Shells: theory, analysis and applications. Marcell Dekker Inc., New York

    Book  Google Scholar 

  • Wang Y-Z, Li F-M (2014) Nonlinear primary resonance of nano beam with axial initial load by nonlocal continuum theory. Int J Non-Linear Mech 61:74–79

    Article  Google Scholar 

  • Wang YZ, Li FM, Kishimoto K (2011a) Thermal effects on vibration properties of double-layered nanoplates at small scales. Compo Part B 42(5):1311–1317

    Article  Google Scholar 

  • Wang J, He X, Kitipornchai S, Zhang H (2011b) Geometrical nonlinear free vibration of multi-layered graphene sheets. J Phys D Appl Phys 44:135401–135409

    Article  Google Scholar 

  • Wijaya YN, Kim J, Choi WM, Park SH, Kim MH (2017) Systematic study of triangular silver nanoplates: one-pot green synthesis, chemical stability, and sensing application. Nanoscale. https://doi.org/10.1039/c7nr03077k

    Article  Google Scholar 

  • Yamaki N, Chiba M (1983) Nonlinear vibrations of a clamped rectangular plate with initial deflection and initial edge displacement part I: theory. Thin-Walled Struct 1:3–29

    Article  Google Scholar 

  • Zhang XF, Li WL (2015) Vibration of arbitrarily-shaped triangular plates with elastically restrained edges. J Sound Vib 357:195–206

    Article  Google Scholar 

  • Zhang J, Sun Y, Zhang H, Xu B, Zhang H, Song D (2013) Preparation and application of triangular silver nanoplates/chitosan composite in surface plasmon resonance biosensing. Anal Chim Acta 769:114–120

    Article  Google Scholar 

  • Zhang LW, Lei ZX, Liew KM (2015) Free vibration analysis of functionally graded carbon nanotube-reinforced composite triangular plates using the FSDT and element-free IMLS-Ritz method. Compos Struct 120:189–199

    Article  Google Scholar 

  • Zhang LW, Zhang Y, Zou GL, Liew KM (2016a) Free vibration analysis of triangular CNT-reinforced composite plates subjected to in-plane stresses using FSDT element-free method. Compos Struct 149:247–260

    Article  Google Scholar 

  • Zhang LW, Liu WH, Liew KM (2016b) Geometrically nonlinear large deformation analysis of triangular CNT-reinforced composite plates. Int J Non-Linear Mech 86:122–132

    Article  Google Scholar 

  • Zhou D, Liu W, Yang Q (2008) Three-dimensional vibration analysis of cantilevered skew plates. J Sound Vib 313:134–148

    Article  Google Scholar 

Download references

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, Yasouj University, Yasouj, Iran

    G. A. Varzandian, S. Ziaee & A. Niknejad

  2. School of Mechanical Engineering, Shiraz University, Shiraz, Iran

    M. Farid

Authors
  1. G. A. Varzandian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Ziaee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Farid
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. Niknejad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Ziaee.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Varzandian, G.A., Ziaee, S., Farid, M. et al. Nonlinear Forced Vibration of Thermally Postbuckled Double-Layered Triangular Graphene Sheet with Clamped Boundary Conditions. Iran J Sci Technol Trans Mech Eng 45, 581–595 (2021). https://doi.org/10.1007/s40997-019-00325-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40997-019-00325-9

Keywords

Search

Navigation