Abstract
Accurate forecasting of streamflow data over daily timescales is a critical problem for the long-term management of water resources, agricultural uses, and many more purposes. This study proposes a new hybrid approach that combines the Robust Local Mean Decomposition (RLMD) method and the Artificial Neural Network (ANN) method for the prediction of streamflow data. Monthly streamflow data were split into the training and the testing part firstly and threefold cross-validation was performed to obtain a more reliable model. After building of the model using the training data, the proposed model was tested on the testing data. Also to compare the performance of the RLMD–ANN model and the Support Vector Regression (SVR) model, Long Short-Term Memory Networks (LSTM) were used for forecasting of subband signal and streamflow data. Also, the hybrid Empirical Mode Decomposition (EMD) model and hybrid Autoregressive Integrated Moving Average (ARIMA) model were used for comparison of the proposed model. Therefore, the RLMD–ANN model was compared with RLMD–SVR, RLMD–LSTM, EMD–ANN, Additive–ARIMA–ANN, ANN, SVR, and LSTM models. The numerical results of the study were assessed concerning the Mean Square Error (MSE), Mean Absolute Error (MAE), Determination Coefficient (R2), Correlation Coefficient (R), and Kruskal–Wallis test was used to indicate whether the results are statically significant. One- to three-ahead forecast and one–two inputs were applied to the models. The mean one-ahead forecasting performance of the three folds was calculated for two inputs with MSE, MAE, R2, and R parameters as 0.0060, 0.0522, 0.7342, and 0.8532 respectively. The obtained results show that the novel RLMD–ANN model is a reliable, efficient, and high-performant model for forecasting streamflow data.










Similar content being viewed by others
Change history
17 February 2022
A Correction to this paper has been published: https://doi.org/10.1007/s40996-022-00843-8
References
Alobaidi MH, Meguid MH, Chebana F (2020) Varying-parameter modeling within ensemble architecture: application to extended streamflow forecasting. J Hydrol 582:124511.
Ali M, Prasad R, Xiang Y, Yaseen ZM (2020) Complete ensemble empirical mode decomposition hybridized with random forest and kernel ridge regression model for monthly rainfall forecasts. Jf Hydrol 584:124647
Apaydin H, Sibtain M (2021) A multivariate streamflow forecasting model by integrating improved complete ensemble empirical mode decomposition with additive noise, sample entropy, Gini index and sequence-to-sequence approaches. J Hydrol 603:126831.
Bergmeir C, Benítez JM (2012) On the use of cross-validation for time series predictor evaluation. Inf Sci 191:192–213
Box GEP, Jenkins GM (1970) Time series analysis: forecasting and control. Holden-Day, San Francisco
Cheng M, Fang F, Kinouchi T, Navon IM, Pain CC (2020). Long lead-time daily and monthly streamflow forecasting using machine learning methods. J Hydrol 590:125376.
Chu H, Wei J, Wu W, Jiang Y, Chu Q, Meng X (2021) A classification-based deep belief networks model framework for daily streamflow forecasting. J Hydrol 595:125967.
Dragomiretskiy K, Zosso D (2014) Variational mode decomposition. IEEE Trans Signal Process, 62.
Fan RE, Chen PH, Lin CJ (2005) Working set selection using second order information for training support vector machines. J Mach Learn Res 6:1871–1918
Fan RE, Chen PH, Lin CJ (2006) A study on SMO-type decomposition methods for support vector machines. IEEE Trans Neural Netw 17:893–908
Freire PKMM, Santos CAG, Silva GBL (2019) Analysis of the use of discrete wavelet transforms coupled with ANN for short-term streamflow forecasting. Appl Soft Comput 80:494–505
Ghorbani MA, Deo RC, Kim S, Kashani MH, Karimi V, Izadkhah M (2020) Development and evaluation of the cascade correlation neural network and the random forest models for river stage and river flow prediction in Australia. Soft Comput, pp 1–12.
Ghorbani MA, Karimi V, Ruskeepää H, Sivakumar B, Pham QB, Mohammadi F, Yasmin N (2021) Application of complex networks for monthly rainfall dynamics over central Vietnam. Stoch Env Res Risk Assess 35(3):535–548
Hadi SJ, Tombul M (2018) Monthly streamflow forecasting using continuous wavelet and multi-gene genetic programming combination. J Hydrol 561:674–687
Hagan MT, Demuth HB, Beale MH (1996) Neural network design. PWS Publishing, Boston.
Haykin S (1994) Neural networks: a comprehensive foundation. Macmillan College Publishing Company Inc., New
Hochreiter S, Schmidhuber J (1997) Long short-term memory. Neural Comput 9(8):1735–1780
Huang TM, Kecman V, Kopriva I (2006) Kernel Based Algorithms for Mining Huge Data Sets: Supervised, Semi-Supervised, and Unsupervised Learning. Springer, New York
Huang NE, Shen Z, Long SR (1999) A new view of nonlinear water waves: the Hilbert spectrum. Annu Rev Fluid Mech 31:417–457
Humphrey GB, Gibbs MS, Dandy GC, Maier HR (2016) A hybrid approach to monthly streamflow forecasting: Integrating hydrological model outputs into a Bayesian artificial neural network. J Hydrol 540:623–640
Hyndman RJ, Athanasopoulos G (2018) Forecasting: Principles and Practice. Monash University, Australia
Ibrahim KSMH, Huang YF, Ahmed AN, Koo CH, El-Shafie A (2022) A review of the hybrid artificial intelligence and optimization modelling of hydrological streamflow forecasting. Alex Eng J 61(1):279–303
Kasiviswanathan KS, He J, Sudheer KP, Tay JH (2016) Potential application of wavelet neural network ensemble to forecast streamflow for flood management. J Hydrol 536:161–173
Kisi O, Latifoğlu L, Latifoglu F (2014) Investigation of empirical mode decomposition in forecasting of hydrological time series. Water Resour Manage 28:4045–4057
Liu Z, Jina Y, Zuo MJ, Feng Z (2017) Time-frequency representation based on robust local mean decomposition for multicomponent AM-FM signal analysis. Mech Syst Signal Process 95:468–487
Marques CAF, Ferreira JA, Rocha A, Castanheira JM, Melo-Gonçalves P, Vaz N, Dias JM (2006) Singular spectrum analysis and forecasting of hydrological time series. Phys Chem Earth, Parts a/b/c 31(18):1172–1179
Marquardt DW (1963) An algorithm for least-squares estimation of nonlinear parameters. J Soc Ind Appl Math 11:431–441
Ni L, Wang D, Singh VP, Wu J, Wang Y, Tao Y, Zhang J (2019) Streamflow and rainfall forecasting by two long short-term memory-based models. J Hydrol, 124296 (in press).
Niu WJ, Feng ZK (2021) Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management. Sustain Cities Soc 64:102562.
Nourani V, Andalib G, Sadikoglu F (2017) Multi-station streamflow forecasting using wavelet denoising and artificial intelligence models. Procedia Computer Sci 120:617–624
Panigrahi S, Behera HS (2017) A hybrid ETS–ANN model for time series forecasting. Eng Appl Artif Intell 66:49–59
Purohit SK, Panigrahi S, Sethy PK, Behera SK (2021) Time series forecasting of price of agricultural products using hybrid methods. Appl Artificial Intell, pp 1–19
Platt J (1999) Sequential minimal optimization: a fast algorithm for training support vector machines. Technical Report MSR-TR-98–14.
Ren D, Yang S, Wu Z, Yan G (2012) Research on end effect of LMD based time-frequency analysis in rotating machinery fault diagnosis. China Mech. Eng 8:951–956
Sahoo A, Samantaray S, Ghose DK (2019) Stream flow forecasting in Mahanadi River Basin using Artificial Neural Networks. Procedia Comp Sci 157:168–174
Siddiqi TA, Ashraf S, Khan SA, Iqbal MJ (2021) Estimation of data-driven streamflow predicting models using machine learning methods. Arab J Geosci 14(11):1–9
Smith JS (2005) The local mean decomposition and its application to EEG perception data. J R Soc Interface 2:443–454
Solomatine D, See LM, Abrahart RJ (2008) Practical hydroinformatics computational intelligence and technological developments in water applications, Water Science and Technology Library.
Tongal H, Booij MJ (2018) Simulation and forecasting of streamflows using machine learning models coupled with base flow separation. J Hydrol 564:266–282
Vapnik VN (1995) The nature of statistical learning theory. Springer, New York
Wang H, Wang C, Wang Y, Gao X, Yua C (2017) Bayesian forecasting and uncertainty quantifying of stream flows using Metropolis-Hastings Markov Chain Monte Carlo algorithm. J Hydrol 549:476–483
https://www.dsi.gov.tr/faaliyetler/akim-gozlem-yilliklari. Accessed Feb 2020
Yaseen ZM, Ebtehaj I, Bonakdari H, Deod RC, Mehr AD, Mohtar WHM, Diop L, El-shafi A, Singhi VP (2017) Novel approach for streamflow forecasting using a hybrid ANFIS-FFA model. J Hydrol 554:263–276
Yaseen ZM, El-Shafie A, Othman Jaafar, Haitham Abdulmohsin Afan, Khamis Naba Sayl (2015) Artificial intelligence based models for stream-flow forecasting: 2000–2015. J Hydrol 530:829–844
Yaseen ZM, Jafar O, Deo RC et al (2016) Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J Hydrol 542:603–614
Yu C, Li Y, Zhang M (2017) An improved Wavelet Transform using Singular Spectrum Analysis for wind speed forecasting based on Elman Neural Network. Energy Convers Manage 148:895–904
Yu X, Zhang X, Qin H (2018) A data-driven model based on Fourier transform and support vector regression for monthly reservoir inflow forecasting. J Hydro-environment Res 18:12–24
Zhang X, Peng Y, Zhang C, Wang B (2015) Are hybrid models integrated with data preprocessing techniques suitable for monthly streamflow forecasting? Some experiment evidences. J Hydrol 30(2015):137–152
Zuo G, Luo J, Ni W, Lian Y, He X (2020) Decomposition ensemble model based on variational mode decomposition and long short-term memory for streamflow forecasting. J Hydrol 585:124776
Author information
Authors and Affiliations
Corresponding author
Additional information
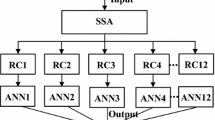
The original Online version of this article was revised : The caption to Fig 2 has been incorrectly published.
Rights and permissions
About this article
Cite this article
Latifoğlu, L. The Performance Analysis of Robust Local Mean Mode Decomposition Method for Forecasting of Hydrological Time Series. Iran J Sci Technol Trans Civ Eng 46, 3453–3472 (2022). https://doi.org/10.1007/s40996-021-00809-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40996-021-00809-2