Skip to main content
SpringerLink
Log in

RETRACTED ARTICLE:An Intelligent Algorithm Optimum for Building Design of Fuzzy Structures

  • Research Paper
  • Published:
Iranian Journal of Science and Technology, Transactions of Civil Engineering Aims and scope Submit manuscript

This article was retracted on 10 December 2023

This article has been updated

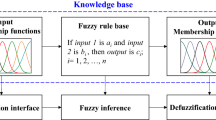
Abstract

Optimum structural design of composites is a research subject that has drawn the attention of many researchers for more than 40 years with a growing interest. In many cases, the loads acting on a composite structure may not be known precisely. Therefore, to design a fuzzy intelligent system, the datasets including general information about MDOF systems subjected to different earthquakes were used. The proportional major operation of the designed fuzzy system based on solving linear matrix inequality method optimized and derived by stability analysis of the system behavior. Because the design of efficient and high-performance structural systems is of fundamental interest to engineers, systematic methodologies are to be used for the combined structural and active control system synthesis in many applications. Based on the relaxed method, the intelligent approach can be stabilized by regulating appropriately the parameters of high-frequency injection. If the frequency is high enough, the trajectory of the closed-loop system and that of its corresponding model—the closed-loop fuzzy relaxed system can be made as close as desired. Thus, the closed-loop system’s behavior can be rigorously predicted by establishing the stability of the closed-loop fuzzy relaxed system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Change history

References

  • Azevedo A, Rezende SM (1991) Controlling chaos in spin-wave instabilities. Phys Rev Lett 66:1342–1345

    Article  Google Scholar 

  • Chen BS, Wang WJ (1990) Robust stabilization of nonlinearly perturbed large-scale systems by decentralized observer-controller compensators. Automatica 26:1035–1041

    Article  Google Scholar 

  • Chu SC, Tsai PW (2007) Computational intelligence based on behaviors of cats. Int J Innov Comput Inf Control 3(1):163–173

    Google Scholar 

  • Chu SC, Tsai PW, Pan JS (2006) Cat swarm optimization. In: Proceedings of trends in artificial intelligence, 9th Pacific Rim international conference on artificial intelligence, Guilin, China, pp 854–858

  • Colet P, Braiman Y (1996) Control of chaos in multimode solid state lasers by the use of small periodic perturbations. Phys Rev E 53:200–206

    Article  Google Scholar 

  • Desoer CA, Shahruz SM (1986) Stability of the dithered nonlinear system with backlash or hysteresis. Int J Control 43:1045–1060

    Article  MathSciNet  Google Scholar 

  • Harms VW (1979) Design criteria for floating tire breakwaters. J Waterw Port Coast Ocean Div ASCE 105(2):149–170

    Article  Google Scholar 

  • Hwang CC, Chow HY, Wang YK (1996) A new feedback control of a modified Chua’s circuit system. Phys D 92:95–100

    Article  Google Scholar 

  • Jabbari F, Sehmitendorf WE, Yang JN (1995) H∞ control for seismic excited buildings with acceleration feedback. J Eng Mech 21:994–1002

    Article  Google Scholar 

  • Kapitaniak T, Kocarev LJ, Chua LO (1993) Controlling chaos without feedback and control signals. Int J Bifurc Chaos 3:459–468

    Article  Google Scholar 

  • Kickert WJM, Mamdani EH (1978) Analysis of a fuzzy logic controller. Fuzzy Sets Syst 1(1):29–44

    Article  Google Scholar 

  • Liu SC, Lin SF (2012) LMI-based robust sliding control for mismatched uncertain nonlinear systems using fuzzy models. Int J Robust Nonlinear Control 22(16):1827–1836

    Article  MathSciNet  Google Scholar 

  • Liu SC, Lin SF (2013) Robust sliding control for mismatched uncertain fuzzy time-delay systems using linear matrix inequality approach. J Chin Inst Eng 36(5):589–597

    Article  Google Scholar 

  • Lu LT, Chiang WL, Tang JP (1998) LQG/LTR control methodology in active structure control. J Eng Mech ASCE 124(4):446–454

    Article  Google Scholar 

  • Mossaheb S (1983) Application of a method of averaging to the study of dithers in nonlinear systems. Int J Control 38:557–576

    Article  MathSciNet  Google Scholar 

  • Ott E, Grebogi C, Yorke JA (1990) Controlling chaos. Phys Rev Lett 64:1196–1199

    Article  MathSciNet  Google Scholar 

  • Schmitendorf WE, Jabbari F, Yang JN (1994) Robust control techniques for buildings under earthquake excitation. Earthq Eng Struct Dyn 23:539–552

    Article  Google Scholar 

  • Shen W, Zhu S, Zhu H, Xu Y-L (2016) Electromagnetic energy harvesting from structural vibrations during earthquakes. Smart Struct Syst 18(449–470):32

    Google Scholar 

  • Singer J, Wang YT, Bau HH (1991) Experimental control of chaos. Phys Rev Lett 66:1123–1125

    Article  Google Scholar 

  • Steinberg AM, Kadushin I (1973) Stabilization of nonlinear systems with dither control. J Math Anal Appl 43:273–284

    Article  MathSciNet  Google Scholar 

  • Takagi T, Sugeno M (1985) Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern 1:116–132

    Article  Google Scholar 

  • Tanaka K, Wang HO (2001) Fuzzy control systems design and analysis. Wiley, New York

    Book  Google Scholar 

  • Tose AR (1994) Nonlinear feedback for controlling the Lorenz equation. Phys Rev E 50:2339–2342

    Article  Google Scholar 

  • Tsai PW, Pan JS, Liao BY, Tsai MJ, Istanda V (2012) Bat algorithm inspired algorithm for solving numerical optimization problems. Appl Mech Mater 148:134–137

    Google Scholar 

  • Wang HO, Abed EH (1995) Bifurcation control of a chaotic system. Automatica 31:1213–1226

    Article  MathSciNet  Google Scholar 

  • Wang HO, Tanaka K, Griffin MF (1996) An approach to fuzzy control of nonlinear systems: stability and design issues. IEEE Trans Fuzzy Syst 4:14–23

    Article  Google Scholar 

  • Yamamoto T, Yoshida A, Ijima T (1982) Dynamics of elastically moored floating objects. In: Kirk CL (ed) Dynamic analysis of offshore structures. CML, Southampton, pp 106–113

    Google Scholar 

  • Zames G, Shneydor NA (1976) Dither in nonlinear systems. IEEE Trans Autom Control 21:660–667

    Article  MathSciNet  Google Scholar 

  • Zames G, Shneydor NA (1977) Structural stabilization on quenching by dither in nonlinear systems. IEEE Trans Autom Control 22:353–361

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Information Technology, Ton Duc Thang University, 19 Nguyen Huu Tho Street, Tan Phong Ward, District 7, Ho Chi Minh City, 700000, Vietnam

    Tim Chen

  2. Department of Mathematics and Informatics, Shymkent University, Zhibek Zholy koshesi, 131, Shymkent, South Kazakhstan, Kazakhstan

    Sinngiresu Rao & Ramazaov Tlekkabul Sabitovich

  3. Department of Computer Science and Engineering, BRAC University, 66 Mohakhali, Dhaka, 1212, Bangladesh

    C. Y. J. Chen

  4. Faculty of Management Science, Covenant University, 10 Idiroko Road, Canaan Land, Ota, Ogun State, Nigeria

    C. Y. J. Chen

Authors
  1. Tim Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sinngiresu Rao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ramazaov Tlekkabul Sabitovich
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. C. Y. J. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to C. Y. J. Chen.

Additional information

This article has been retracted. Please see the retraction notice for more detail: https://doi.org/10.1007/s40996-023-01303-7"

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, T., Rao, S., Sabitovich, R.T. et al. RETRACTED ARTICLE:An Intelligent Algorithm Optimum for Building Design of Fuzzy Structures. Iran J Sci Technol Trans Civ Eng 44, 523–531 (2020). https://doi.org/10.1007/s40996-019-00251-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40996-019-00251-5

Keywords

Search

Navigation