Abstract
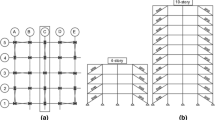
The energy approach is useful to understand the behavior of structural systems subjected to strong ground motions. In this research, the energy responses from the buckling-restrained braced frames as well as dual systems subjected to the NF and FF earthquakes are investigated and compared. The dual systems consist of reinforced concrete wall and buckling-restrained braces within steel frame adjacent to the wall. The considered structures are designed according to the current codes using the response spectrum analysis. Nonlinear numerical models were created in which the walls were made of fiber element model. The inelastic energy, input energy, kinetic energy, elastic strain energy and damping energy demand were investigated by implementing nonlinear time-history analysis. Also, the inelastic energy distribution pattern along the height was studied. The results show that for both near-field and far-field sets, the maximum inelastic energy dissipation demand belongs to the BRBFs compared to dual system. The wall existence caused the maximum inelastic energy demand to reduce and also leads to more balanced inelastic energy demand along the height of the structure.

















Similar content being viewed by others
References
ACI 318-11. 2011. Building code requirements for structural concrete and commentary. ACI Committee 318: Farmington Hills
Aiken ID, Mahin SA, Uriz P (2002) Large-scale testing of buckling-restrained braced frames. In: Proceedings of the Japan passive control symposium, Tokyo Institute of Technology, Japan, pp 35–44
AISC (2010) Seismic provision for structural steel buildings. American Institute of Steel Construction, Chicago, p 2005
Applied Technology Council (2010) ATC-72: modeling and acceptance criteria for seismic design and analysis of tall buildings. ATC, Redwood City, CA
Ariyaratana CA, Fahnestock LA (2011) Evaluation of buckling-restrained braced frame seismic performance considering reserve strength. Eng Struct 33:77–89
ASCE, SEI 7 (2010) Minimum design loads for buildings and other structures. American Society of Civil Engineers, Reston
Beiraghi H (2017) Earthquake effects on the energy demand of tall reinforced concrete walls with buckling-restrained brace outriggers. Struct Eng Mech 63(4):521–536
Beiraghi H, Siahpolo N (2016) Seismic assessment of RC core-wall building capable of three plastic hinges with outrigger. Struct Des Tall Spec Build. https://doi.org/10.1002/tal.1306
Beiraghi H, Kheyroddin A, Kafi MA (2015) Nonlinear fiber element analysis of a reinforced concrete shear wall subjected to earthquake records. Trans Civil Eng 39(2):409–422
Beiraghi H, Kheyroddin A, Kafi MA (2016a) Energy dissipation of tall core-wall structures with multi-plastic hinges subjected to forward directivity near-fault and far-fault earthquakes. Struct Des Tall Spec Build 25(15):801–820
Beiraghi H, Kheyroddin A, Kafi MA (2016b) Forward directivity near-fault and far-fault ground motion effects on the behavior of reinforced concrete wall tall buildings with one and more plastic hinges. Struct Des Tall Spec Build 25(11):519–539
Beiraghi H, Kheyroddin A, Kafi MA (2016c) Effect of record scaling on the behavior of reinforced concrete core-wall buildings subjected to near-fault and far-fault earthquakes. Sci Iran 24(3):884–899
Black C, Makris N, Aiken I (2002) Component testing, stability analysis and characterization of buckling-restrained braces. Report No. PEER-2002/08, Pacific Earthquake Engineering Research Center, University of California, Berkeley, CA, USA
Chopra AK (2001) Dynamics of structures. Prentice-Hall, New Jersey
Erochko J, Christopoulos C, Tremblay R, Choi H (2011) Residual drift response of SMRFs and BRB Frames in steel buildings designed according to ASCE 7-05. J Struct Eng 137(5):589–599
Fajfar P (1992) Equivalent ductility factors, taking into account low-cycle fatigue. Earthq Eng Struct Dyn 23:507–521
FEMA P695 (2009) Quantification of building seismic performance factors (ATC-63 project). Federal Emergency Management Agency, Washington DC
Ghodsi T, Ruiz JF, Massie C, Chen Y (2010) Pacific earthquake engineering research/seismic safety commission tall building design case study. Struct Des Tall Spec Build 19(2):197–256
Jones P, Zareian F (2013) Seismic response of a 40-storey buckling-restrained braced frame designed for the Los Angeles region. Struct Des Tall Spec Build 22(3):291–299. https://doi.org/10.1002/tal.687
Judd J, Phillips A, Eatherton M, Charney F, Marinovic I, Hyder C (2015) Subassemblage testing of all-steel web-restrained braces. STESSA, Shanghai
Kalkan E, Kunnath SK (2006) Effects of fling-step and forward directivity on the seismic response of buildings. Earthq Spectra 22(2):367–390
Khashaee P, Mohraz B, Sadek F, Lew HS, Gross JL (2003) Distribution of earthquake input energy in structures. Report no. NISTIR 6903. Gaithersburg: Building and Fire Research Laboratory, National Institute of Standards and Technology
Kiggins S, Uang CM (2006) Reducing residual drift of buckling-restrained braced frames as a dual system. Eng Struct 28:1525–1532
Kuwamura H, Galambos TV (1989) Earthquake load for structural reliability. J Struct Eng, ASCE 115(6):1446–1462
LATBSDC (2011) An alternative procedure for seismic analysis and design of tall buildings located in the Los Angeles region. Los Angeles Tall Buildings Structural Design Council, Los Angeles
Luco N, Cornell A (2007) Structure-specific scalar intensity measures for near source and ordinary earthquake ground motions. Earthq Spectra 23(2):357–392
Mander JB, Priestley MJN, Park R (1988) Theoretical stress–strain model for confined concrete. ASCE J Struct Eng 114(8):1804–1826
Nguyen AH, Chintanapakdee C, Hayashikawa T (2010) Assessment of current nonlinear static procedures for seismic evaluation of BRBF buildings. J Constr Steel Res 66(8–9):1118–1127
NIST (2015) Seismic design of steel buckling-restrained braced frames: a guide for practicing engineers, GCR 15-917-34, NEHRP Seismic Design Technical Brief No. 11, produced by the Applied Technology Council and the Consortium of Universities for Research in Earthquake Engineering for the National Institute of Standards and Technology, Gaithersburg, MD
Orakcal K, Wallace JW (2006) Flexural modeling of reinforced concrete walls-experimental verification. ACI Struct J 103(2):196–206
Paulay T, Priestley MJN (1992) Seismic design of reinforced concrete and masonry buildings. Wiley, Hoboken
PERFORM-3D (2006) Nonlinear analysis and performance assessment for 3D structures, V. 4, user guide. Computers and Structures Inc, Berkeley
PERFORM-3D (2011) Nonlinear analysis and performance assessment for 3D structures, V.4.0.3. Computers and Structures Inc, Berkeley
Sabelli R (2001) “Research on improving the design and analysis of earthquake-resistant steel braced frames”, The 2000 NEHRP Professional Fellowship Report. Earthquake Engineering Research Institute, Oakland
Sabelli R, Mahin S, Chang C (2003) Seismic demands on steel braced frame buildings with buckling-restrained braces. Eng Struct 25:655–666
Sahoo DR, Chao S (2010) Performance-based plastic design method for buckling-restrained braced frames. Eng Struct 32:2950–2958
Teran-Gilmore A (1998) A parametric approach to performance-based numerical seismic design. Earthq Spectra 14(3):501–520
Tjhin T, Aschheim M, Wallace J (2007) Yield displacement-based seismic design of RC wall buildings. Eng Struct. https://doi.org/10.1016/j.engstruct.2006.10.022
Tremblay R, Bolduc P, Neville R, DeVall R (2006) Seismic testing and performance of buckling restrained bracing systems. Can J Civ Eng 33:183–198
Tsai K-C, Hsiao P-C (2008) Pseudo-dynamic test of a full-scale CFT/BRB frame—Part II: seismic performance of buckling-restrained braces and connections. Earthq Eng Struct Dyn 37:1099–1115
Uang CM, Bertero VV (1997) Seismic response of an instrumented 13-story steel frame building damaged in the 1994 Northridge earthquake. Earthq Spectra 13(1):131–148
Uriz P, Mahin SA (2008) Toward earthquake-resistant design of concentrically braced steel-frame structures, PEER 2008/08. Pacific Earthquake Engineering Research Center, University of California, Berkeley
Watanabe A (1992) Development of composite brace with a large ductility. In: Proceedings of the U.S.-Japan workshop on composite and hybrid structures, Berkeley, CA, September 10-12, Goel S. and Yamanouchi, H. (ed.)
Watanabe A, Hitomi Y, Saeki E, Wada A, Fujimoto M (1988) Properties of brace encased in buckling-restraining concrete and steel tube. In: Proceedings of the 9th world conference on earthquake engineering, Tokyo-Kyoto, Japan
Wu A-C, Lin P-C, Tsai K-C (2014) High-mode buckling responses of buckling-restrained brace core plates. Earthq Eng Struct Dyn, 43: 375–393. Accessed August 2015, http://onlinelibrary.wiley.com/doi/10.1002/eqe.2349/ abstract, https://doi.org/10.1002/eqe.2349
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Beiraghi, H. Energy Dissipation of Reinforced Concrete Wall Combined with Buckling-Restrained Braces Subjected to Near- and Far-Fault Earthquakes. Iran J Sci Technol Trans Civ Eng 42, 345–359 (2018). https://doi.org/10.1007/s40996-018-0109-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40996-018-0109-0