Skip to main content
SpringerLink
Log in

A Simplified SPH Method for Simulation of Free Surface Flows

  • Research Paper
  • Published:
Iranian Journal of Science and Technology, Transactions of Civil Engineering Aims and scope Submit manuscript

Abstract

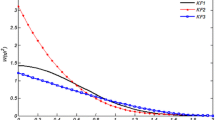
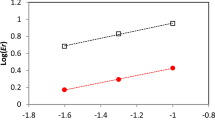
In this study, SPH formulations are simplified based on straightforward mathematical operations for simulation of free surface flows. Satisfaction of boundary conditions, especially Neumann boundary conditions, is of great importance in accuracy of numerical methods. Employing dummy particles which are placed outside of wall boundaries is one of the simplest methods for imposing Neumann boundary conditions in which pressure of a dummy particle is set to that of a wall particle in the normal direction of the wall boundaries. In fact, dummy particles prevent fluid particles from penetration walls by imposing a repulsive pressure force. In spite of the simplicity of the method, initial placement of several lines of dummy particles can be difficult, especially for non-geometric computational domains. In this research, two different strategies are proposed and employed in which the wall conditions are modeled without the need of dummy particles. In the first strategy, contribution of dummy particles is indirectly included in the numerical computations based on their priori known positions. In the second and main strategy, dummy particles are entirely excluded from the computations and the wall conditions can be modeled only with the wall particles. The efficiency and accuracy of both strategies in modeling of the wall conditions are tested for simulation of dam-break flow using a well-known spline kernel function. It is found that water penetration across the walls is occurred for a certain range of radius of support domain, especially when the second strategy is employed. A new kernel function with steeper shape in comparison with the spline function is introduced here to prevent water penetration even for the second strategy. The efficiency of the proposed kernel function is tested by two free surface problems of dam break and Scott Russell wave generator.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  • Ataie-Ashtiani B, Shobeyri G (2008) Numerical simulation of landslide impulsive waves by incompressible smoothed particle hydrodynamics. Int J Numer Meth Fluids 56(2):209–232

    Article  MathSciNet  MATH  Google Scholar 

  • Ataie-Ashtiani B, Shobeyri G, Farhadi L (2008) Modified incompressible SPH method for simulating free surface problems. Fluid Dyn Res 40(9):637–661

    Article  MATH  Google Scholar 

  • Atluri SN, Zhu T (1998) A new meshless local Petrov–Galerkin (MPLG) approach in computational mechanics. Comput Mech 22:117–127

    Article  MathSciNet  MATH  Google Scholar 

  • Belytschko T, Lu YY, Gu L (1994) Element-free Galerkin methods. Int J Numer Meth Eng 37:229–256

    Article  MathSciNet  MATH  Google Scholar 

  • Bonet J, Kulasegaram S (1999) Variational and momentum preserving aspects of smoothed particle hydrodynamics (SPH) formulations. Comput Methods Appl Mech 180:97–115

    Article  Google Scholar 

  • Bonet J, Lok T (2000) Correction and stabilization of smoothed particle hydrodynamics methods with applications in metal forming simulations. Int J Numer Methods Eng 47:1189–1214

    Article  MATH  Google Scholar 

  • Chiaki G, Yoshida N (2015) Particle splitting in smoothed particle hydrodynamics based on Voronoi diagram. Mon Not R Astron Soc 451(4):3955–3963

    Article  Google Scholar 

  • Cueto-Felgueroso L, Colominas I, Mosqueira G (2004) On the Galerkin formulation of the smoothed particle hydrodynamics method. Int J Numer Meth Eng 60(9):1475–1512

    Article  MathSciNet  MATH  Google Scholar 

  • Gingold RA, Monaghan JJ (1977) Smoothed particle hydrodynamics: theory and application to non spherical stars. Mon Not R Astron Soc 181:375–389

    Article  MATH  Google Scholar 

  • Gui Q, Dong P, Shao S (2015) Numerical study of PPE source term errors in the incompressible SPH models. Int J Numer Meth Fluids 77(6):358–379

    Article  MathSciNet  Google Scholar 

  • Harlow FH, Welch JE (1965) Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. J Phys Fluids 8(12):322–332

    MathSciNet  MATH  Google Scholar 

  • Heb S, Springel V (2010) Particle hydrodynamics with tessellation techniques. Mon Not R Astron Soc 406(4):2289–2311

    Article  Google Scholar 

  • Hirt CW, Nichols BD (1981) Volume of fluid (VOF) method for the dynamics of free boundaries. J Comput Phys 39:201–225

    Article  MATH  Google Scholar 

  • Koshizuka S, Oka Y (1996) Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl Sci Eng 123:421–434

    Article  Google Scholar 

  • Koshizuka S, Nobe A, Oka Y (1998) Numerical analysis of breaking waves using the moving particle semi-implicit method. Int J Numer Meth Fluids 26:751–769

    Article  MATH  Google Scholar 

  • Liu GR (2003) Mesh free methods: moving beyond the finite element method. Chemical Rubber, Boca Raton

    MATH  Google Scholar 

  • Liu X, Lin P, Shao S (2014) An ISPH simulation of coupled structure interaction with free surface flows. J Fluids Struct 48:46–61

    Article  Google Scholar 

  • Lo EYM, Shao SD (2002) Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl Ocean Res 24(5):275–286

    Article  Google Scholar 

  • Martin JC, Moyce WJ (1952) An experimental study of the collapse of liquid columns on a rigid horizontal plane. Philos Trans R Soc Lond Ser A 244:312–324

    Article  Google Scholar 

  • Monaghan JJ (1994) Simulating free surface flows with SPH. J Comput Phys 110:399–406

    Article  MATH  Google Scholar 

  • Monaghan JJ (1996) Gravity currents and solitary waves. Physica D 98:523–533

    Article  MATH  Google Scholar 

  • Monaghan JJ (2000) SPH without a tensile instability. J Comput Phys 159(2):290–311

    Article  MATH  Google Scholar 

  • Monaghan JJ, Kos A (2000) Scott Russell’s wave generator. Phys Fluids 12:622–630

    Article  MathSciNet  MATH  Google Scholar 

  • Monaghan JJ, Kos A, Issa N (2003) Fluid motion generated by impact. J Waterway Port Coast Ocean Eng 129(6):250–259

    Article  Google Scholar 

  • Onate E, Idelson S, Zienkiewicz OC, Taylorm RL, Sacco C (1996) A stabilized finite point method for analysis of fluid mechanics problems. Comput Methods Appl Mech Eng 139:315–346

    Article  MathSciNet  Google Scholar 

  • Shao SD (2012) Incompressible smoothed particle hydrodynamics simulation of multifluid flows. Int J Numer Meth Fluids 69(11):1715–1735

    Article  MathSciNet  MATH  Google Scholar 

  • Shao SD, Lo EYM (2003) Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv Water Resour 26(7):787–800

    Article  Google Scholar 

  • Shobeyri G, Afshar MH (2010) Simulating free surface problems using discrete least squares meshless method. Comput Fluids 39:461–470

    Article  MATH  Google Scholar 

  • Shobeyri G, Afshar MH (2012) Corrected discrete least square meshless method for simulating free surface flows. Eng Anal Bound Elem Method 36:1581–1594

    Article  MathSciNet  MATH  Google Scholar 

  • Shobeyri G, Ardakani RR (2017) Improving accuracy of SPH method using Voronoi Diagram. Iran J Sci Technol Trans Civ Eng 41:345–350

    Article  Google Scholar 

  • Sussman M (2003) A second order coupled level set and volume-of-fluid method for computing growth and collapse of vapor bubbles. J Comput Phys 187:110–136

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Allaodoleh Semnani Institute of Higher Education (ASIHE), Garmsar, Iran

    Gholamreza Shobeyri

Authors
  1. Gholamreza Shobeyri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gholamreza Shobeyri.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shobeyri, G. A Simplified SPH Method for Simulation of Free Surface Flows. Iran J Sci Technol Trans Civ Eng 42, 245–258 (2018). https://doi.org/10.1007/s40996-018-0103-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40996-018-0103-6

Keywords

Search

Navigation