Skip to main content
SpringerLink
Log in

Assessing Absolute Maximum Vibration Amplitude of a Rectangular Plate Subjected to a Moving Mass

  • Research Paper
  • Published:
Iranian Journal of Science and Technology, Transactions of Civil Engineering Aims and scope Submit manuscript

Abstract

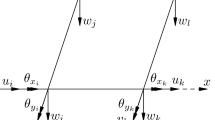
Dynamic behavior of bridges under moving loads is a challenging engineering problem, which has attracted a great interest in a myriad of papers and books in structural dynamics field. In case of a slab-type bridge, a plate influenced by a traversing mass can reflect the full two-dimensional mechanical behavior of the supporting structure. This paper investigates absolute maximum response amplitude of a plate-type structure subject to a moving mass. To this end, the absolute maximum dynamic deflection of a rectangular plate under a moving mass is sought at all interior points of it, while the existing literature is restricted to capturing maximum values at the plate center point. Unlike the conventional methods that seek maximum dynamic response at the center point of the plate, extracting absolute maximum response—which does not necessarily take place at the center point—is an onerous task and computationally demanding. According to the findings of the current paper, accurate values of the plate maximum vibration amplitude significantly differ from those maximum responses obtained at the plate center point.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Akin JE, Mofid M (1989) Numerical solution for response of beams with moving mass. J Struct Eng 115(1):120–131

    Article  Google Scholar 

  • Amiri JV et al (2013) Vibration analysis of a Mindlin elastic plate under a moving mass excitation by eigenfunction expansion method. Thin Walled Struct 62:53–64

    Article  Google Scholar 

  • Azam SE et al (2013) Dynamic response of Timoshenko beam under moving mass. Sci Iran Trans A Civ Eng 20(1):50–56

    MathSciNet  Google Scholar 

  • Beskou ND, Theodorakopoulos DD (2011) Dynamic effects of moving loads on road pavements: a review. Soil Dyn Earthq Eng 31(4):547–567

    Article  Google Scholar 

  • Biondi B et al (2004) Methods for calculating bending moment and shear force in moving mass problem. J Vib Acoust 126(4):542–552

    Article  Google Scholar 

  • de Oliveira FM, Greco M (2014) Nonlinear dynamic analysis of beams with layered cross sections under moving masses. J Braz Soc Mech Sci Eng 37(2):451–462

    Article  Google Scholar 

  • Dyniewicz B, Bajer CI (2010) New feature of the solution of a Timoshenko beam carrying the moving mass particle. Arch Mech 62(5):327–341

    MathSciNet  MATH  Google Scholar 

  • Ebrahimi M et al (2015) Dynamic behavior of a multispan continuous beam traversed by a moving oscillator. Acta Mech 226(12):4247–4257

    Article  MathSciNet  MATH  Google Scholar 

  • Eftekhari SA, Jafari AA (2014) A mixed method for forced vibration of multi-span rectangular plates carrying moving masses. Arab J Sci Eng 39(4):3225–3250

    Article  Google Scholar 

  • Enshaeian A, Rofooei FR (2014) Geometrically nonlinear rectangular simply supported plates subjected to a moving mass. Acta Mech 225(2):595–608

    Article  MathSciNet  MATH  Google Scholar 

  • Esen İ (2013) A new finite element for transverse vibration of rectangular thin plates under a moving mass. Finite Elem Anal Des 66:26–35

    Article  MathSciNet  MATH  Google Scholar 

  • Esen İ (2015) A new FEM procedure for transverse and longitudinal vibration analysis of thin rectangular plates subjected to a variable velocity moving load along an arbitrary trajectory. Lat Am J Solids Struct 12(4):808–830

    Article  Google Scholar 

  • Frýba L (1999) Vibration of solids and structures under moving loads. Thomas Telford, London

    Book  MATH  Google Scholar 

  • Ghazvini T et al (2016) Dynamic response analysis of a thin rectangular plate of varying thickness to a traveling inertial load. J Braz Soc Mech Sci Eng 38(2):403–411

    Article  Google Scholar 

  • Hassanabadi ME et al (2013) A new Orthonormal Polynomial Series Expansion method in vibration analysis of thin beams with non-uniform thickness. Appl Math Model 37(18):8543–8556

    Article  MathSciNet  Google Scholar 

  • Hassanabadi ME et al (2014) On the vibration of a thin rectangular plate carrying a moving oscillator. Sci Iran Trans A Civ Eng 21(2):284–294

    Google Scholar 

  • Hassanabadi ME et al (2016) Resonance of a rectangular plate influenced by sequential moving masses. Coupled Syst Mech 5(1):87–100

    Article  Google Scholar 

  • Ichikawa M et al (2000) Vibration analysis of the continuous beam subjected to a moving mass. J Sound Vib 230(3):493–506

    Article  Google Scholar 

  • Lotfollahi-Yaghin MA et al (2015) On the absolute maximum dynamic response of a beam subjected to a moving mass. Struct Eng Mech 54(1):55–67

    Article  Google Scholar 

  • Malekzadeh P, Monajjemzadeh SM (2015) Nonlinear response of functionally graded plates under moving load. Thin Walled Struct 96:120–129

    Article  Google Scholar 

  • Mamandi A, Mohsenzadeh R, Kargarnovin MH (2015) Nonlinear dynamic analysis of a rectangular plate subjected to accelerated/decelerated moving load. J Theor Appl Mech 53(1):151–166

    Article  Google Scholar 

  • Nikkhoo A et al (2014) Vibration of a thin rectangular plate subjected to series of moving inertial loads. Mech Res Commun 55:105–113

    Article  Google Scholar 

  • Nikkhoo A et al (2015) Simplified modeling of beam vibrations induced by a moving mass by regression analysis. Acta Mech 226(7):2147–2157

    Article  MathSciNet  MATH  Google Scholar 

  • Nikkhoo et al (2016) On the computation of moving mass/beam interaction utilizing a semi-analytical method. J Braz Soc Mech Sci Eng 38(3):761–771

    Article  Google Scholar 

  • Olsson M (1991) On the fundamental moving load problem. J Sound Vib 145(2):299–307

    Article  MathSciNet  Google Scholar 

  • Ouyang H (2011) Moving-load dynamic problems: a tutorial (with a brief overview). Mech Syst Signal Process 25(6):2039–2060. doi:10.1016/j.ymssp.2010.12.010

    Article  MathSciNet  Google Scholar 

  • Pesterev AV, Bergman LA (1998) A contribution to the moving mass problem. J Vib Acoust 120(3):824–826

    Article  Google Scholar 

  • Shadnam et al (2001) On the dynamic response of rectangular plate, with moving mass. Thin Walled Struct 39(9):797–806

    Article  Google Scholar 

  • Şimşek M, Kocatürk T (2009) Nonlinear dynamic analysis of an eccentrically prestressed damped beam under a concentrated moving harmonic load. J Sound Vib 320(1–2):235–253

    Google Scholar 

  • Soedel W (2004) Vibration of shells and plates. Marcel Dekker, New York

    MATH  Google Scholar 

  • Stăncioiu D et al (2008) Vibration of a beam excited by a moving oscillator considering separation and reattachment. J Sound Vib 310(4–5):1128–1140. doi:10.1016/j.jsv.2007.08.019

    Article  Google Scholar 

  • Wu JJ (2007) Vibration analyses of an inclined flat plate subjected to moving loads. J Sound Vib 299(1–2):373–387

    Article  Google Scholar 

  • Yamchelou MT, Nouri GR (2016) Spectral analysis of dynamic response of a thin beam subjected to a varying speed moving mass. J Mech Sci Technol 30(7):3009–3017

    Article  Google Scholar 

  • Yang B et al (2000) Direct numerical procedure for solution of moving oscillator problems. J Eng Mech 126(5):462–469

    Article  Google Scholar 

  • Yang YB et al (2004) Vehicle-bridge interaction dynamics. World Scientific, Singapore

    Book  Google Scholar 

  • Yavari A et al (2002) Discrete element analysis of dynamic response of Timoshenko beams under moving mass. Adv Eng Softw 33(3):143–153

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Civil Engineering, Kharazmi University, Tehran, Iran

    Morteza Tahmasebi Yamchelou

  2. Department of Civil Engineering, Rasht Branch, Islamic Azad University, 3516-41335, Rasht, Iran

    Iman Mohammadpour Nikbin

  3. Department of Civil Engineering, Deilaman Institute of Higher Education, Lahijan, Iran

    Homam Zareian & Shahin Charkhtab

Authors
  1. Morteza Tahmasebi Yamchelou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Iman Mohammadpour Nikbin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Homam Zareian
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shahin Charkhtab
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Iman Mohammadpour Nikbin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yamchelou, M.T., Nikbin, I.M., Zareian, H. et al. Assessing Absolute Maximum Vibration Amplitude of a Rectangular Plate Subjected to a Moving Mass. Iran J Sci Technol Trans Civ Eng 41, 135–147 (2017). https://doi.org/10.1007/s40996-017-0055-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40996-017-0055-2

Keywords

Search

Navigation