Skip to main content
SpringerLink
Log in

Comparative analysis of the nonlinear unified strength criterion for rocks and other three-dimensional Hoek–Brown strength criteria

  • Original Article
  • Published:
Geomechanics and Geophysics for Geo-Energy and Geo-Resources Aims and scope Submit manuscript

Abstract

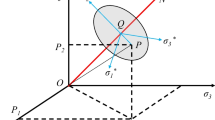
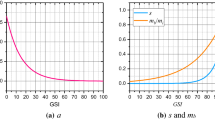
The Hoek–Brown strength criterion, which has been widely used in rock engineering, is one of the most influential rock strength criteria. Because this criterion does not take into account the effect of intermediate principal stress and because there are deficiencies in the theory and its practical application, for nearly 30 years many scholars have carried out research related to this topic. Yu and Zan took the advantages of the unified strength theory and integrated this theory with the Hoek–Brown strength criterion, thereby proposing the nonlinear unified strength criterion for rocks. This criterion takes into account the difference between the tensile strength and the compressive strength of rock, i.e. the intermediate principal stress effect, and the researchers determined that the limit loci in the meridian plane are nonlinear. The parameters of the nonlinear unified strength criterion are the same as those of the Hoek–Brown strength criterion obtained from conventional triaxial tests for rock blocks. The current study compared and analyzed the relationship between the nonlinear unified strength criterion and other three-dimensional Hoek–Brown strength criteria proposed by Pan and Hudson, Zhang and Zhu, and Jiang. Using the comparison of failure limit lines of the various strength criteria in the π-plane, the nonlinear unified strength criterion is superior to other strength criteria. Using the 1stOpt software of the general global optimization algorithm to fit the strength criterion parameters, the comparison of the results of the nonlinear unified strength criterion with the true triaxial test data from six types of rocks shows good agreement, and the true triaxial test of rock strength can be evaluated with high accuracy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Benz T, Schwab R, Kauther RA, Vermeer PA (2008) A Hoek–Brown criterion with intrinsic material strength factorization. Int J Rock Mech Min Sci 45:210–222. doi:10.1016/j.ijrmms.2007.05.003

    Article  Google Scholar 

  • Chang C, Haimson B (2000) True triaxial strength and deformability of the German Continental Deep Drilling Program (KTB) deep hole amphibolite. J Geophys Res 105:18999–19013. doi:10.1029/2000JB900184

    Article  Google Scholar 

  • Haimson BC, Chang C (2000) Anew true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of Westerly granite. Int J Rock Mech Min Sci 37:285–296. doi:10.1016/S1365-1609(99)00106-9

    Article  Google Scholar 

  • Hoek E, Brown ET (1980) Empirical strength criterion for rock masses. J Geotech Eng ASCE 106:1013–1035

    Google Scholar 

  • Hoek E, Wood D, Shah S (1992) A modified Hoek–Brown criterion for jointed rock masses. In: Hudson JA (ed) Proceedings of the rock characterization, symposium of ISRM. British Geotechnical Society, London, pp 209–214

  • Hoek E, Carranza-Torres CT, Corkum B (2002) Hoek–Brown failure criterion—2002 edition. In: Hammah R, Bawden W, Curran J, Telesnicki M (eds) Proceedings of the Fifth North American rock mechanics symposium (NARMS-TAC). University of Toronto Press, Toronto, pp 267–273

  • Jiang H (2015) A simple convenient three-dimensional Hoek–Brown criterion for rocks. Chin J Rock Mech Eng 34(Suppl1):2996–3004 (in Chinese)

    Google Scholar 

  • Jiang H, Wang XW, Xie YL (2011) New strength criteria for rocks under polyaxial compression. Can Geotech J 48:1233–1245. doi:10.1139/t11-034

    Article  Google Scholar 

  • Lu XY, Zhu HL, Lu XL, Liu JM, Zhou Y, Li XG (2015) A study on the inner surface pressure distribution of fluid in ninety degree elbow pipe. AMM 713–715:34–38. doi:10.4028/www.scientific.net/AMM.713-715.34

    Article  Google Scholar 

  • Mehranpour MH, Kulatilake PHSW (2016) Comparison of six major intact rock failure criteria using a particle flow approach under true-triaxial stress condition. Geomech Geophys Geo Energy Geo Res 2(4):203–229. doi:10.1007/s40948-016-0030-6

    Article  Google Scholar 

  • Mogi K (1971) Fracture and flow of rocks under high triaxial compression. J Geophys Res 76:1255–1269. doi:10.1029/JB076i005p01255

    Article  Google Scholar 

  • Mogi K (2007) Experimental rock mechanics. Taylor and Francis, London, p 64

    Google Scholar 

  • Pan X, Hudson JA (1988) A simplified three dimensional Hoek–Brown yield criterion. In: Romana M (ed) Rock mechanics and power plants. Balkema, Rotterdam, pp 95–103

    Google Scholar 

  • Shi XC, Meng YF, Li G (2011) Comparative analyses of several rock strength criteria. Rock Soil Mech 32(Suppl 1):209–216 (in Chinese)

    Google Scholar 

  • Shi XC, Yang X, Meng YF, Li G (2016) Modified Hoek–Brown failure criterion for anisotropic rocks. Environ Earth Sci 75:995. doi:10.1007/s12665-016-5810-3

    Article  Google Scholar 

  • Single B, Goel RK, Mehrotra VK, Garg SK, Allu MR (1998) Effect of intermediate principal stress on strength of anisotropic rock mass. Tunn Undergr Space Technol 13:71–79. doi:10.1016/S0886-7798(98)00023-6

    Article  Google Scholar 

  • Vásárhelyi B, Kovács L, Török Á (2016) Analysing the modified Hoek–Brown failure criteria using Hungarian granitic rocks. Geomech Geophys Geo Energy Geo Res 2(2):131–136. doi:10.1007/s40948-016-0021-7

    Article  Google Scholar 

  • Wang R, Kemeny JM (1995) A new empirical criterion for rock under polyaxial compressive stresses. In: Daemen S (ed) Rock mechanics. Balkema, Rotterdam, pp 453–458

    Google Scholar 

  • You M (2011) Comparison of the accuracy of some conventional triaxial strength criteria for intact rock. Int J Rock Mech Min Sci 48:852–863. doi:10.1016/j.ijrmms.2011.05.006

    Article  Google Scholar 

  • Yu MH (2011) New system of strength theory: theory, development and application, 2nd edn. Xi an Jiao Tong University Press, Xi an, pp 75–95 (in Chinese)

    Google Scholar 

  • Yu MH, Zan YW, Zhao J, Yoshimine M (2002) A unified strength criterion for rock material. Int J Rock Mech Min Sci 39:975–989. doi:10.1016/S1365-1609(02)00097-7

    Article  Google Scholar 

  • Zan YW, Yu MH, Wang SJ (2002) Nonlinear unified strength criterion of rock. Chin J Rock Mech Eng 21:1435–1441 (in Chinese)

    Google Scholar 

  • Zhang LY, Zhu HH (2007) Three-dimensional Hoek–Brown strength criterion for rocks. J Geotech Geoenviron Eng 133:1128–1135. doi:10.1061/(ASCE)1090-0241(2007)133:9(1128)

    Article  Google Scholar 

  • Zhang YP, Cao P, Dong LJ (2010) A robust regression model and its application in calculating shear strength of rock. Sci Technol Rev 28:91–95 (in Chinese)

  • Zhang H, Liu J, Cao Y, Wang Y (2013) Effects of particle size on lignite reverse flotation kinetics in the presence of sodium chloride. Powder Technol 246:658–663

    Article  Google Scholar 

Download references

Acknowledgements

We acknowledge our gratitude toward the sponsors of the work presented in this paper: the MOE’s Program for Changjiang Scholars and the Innovative Research Team (IRT13092).

Author information

Authors and Affiliations

  1. School of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu, 611756, Sichuan, China

    Qun Yang & YueWen Zan

  2. College of Physics and Engineering Technology, Chengdu Normal University, Chengdu, 611130, Sichuan, China

    Qun Yang

  3. Sichuan Vocational and Technical College of Communications, Chengdu, 611130, Sichuan, China

    Li Guang Xie

Authors
  1. Qun Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. YueWen Zan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Li Guang Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to YueWen Zan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Q., Zan, Y. & Xie, L.G. Comparative analysis of the nonlinear unified strength criterion for rocks and other three-dimensional Hoek–Brown strength criteria. Geomech. Geophys. Geo-energ. Geo-resour. 4, 29–37 (2018). https://doi.org/10.1007/s40948-017-0072-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40948-017-0072-4

Keywords

Search

Navigation