Effect of circumferential sealant joints and metal supporting frames on the buckling behavior of glass panels subjected to in-plane shear loads

Abstract

In this paper, the structural stability of adhesively supported glass panels subjected to in-plane shear walls is assessed by means of extended finite-element (FE) investigations and analytical methods. Based on past research projects, careful consideration is given to glass panels with two-side circumferential linear adhesive connections and supporting metal frames, which are frequently used in practice for facades and building envelopes. In accordance with earlier research contributions, the effects deriving from adhesive connections and supporting frames of various stiffnesses are highlighted in terms of expected Euler’s critical shear loads and ultimate buckling resistances. Further extended nonlinear incremental studies are then discussed, and the major structural effects deriving from the interaction between the glass sheets, the circumferential adhesive joints, the supporting metal frames and additional small steel supports often used to transfer the maximum compressive reaction forces to the structural background are properly highlighted. As shown, compared to classical theories of ideally simply supported or fully clamped panels under the action of in-plane shear loads, the actual boundary conditions should be carefully taken into account. At the same time, the effects deriving from multiple combinations of several geometrical and mechanical aspects should be properly assessed. In the specific case, numerically derived buckling coefficients and fitting curves of practical use are proposed for an appropriate calculation of the expected Euler’s critical load for the studied configurations. Finally, the application and validity of a normalized Eurocode-based design buckling curve recalled from literature is also assessed. Based on the rather good agreement between FE and analytical calculations, the same approach is then proposed as practical and suitable design method for the studied loading and boundary conditions.

Introduction

Glass panels are widely used in modern buildings as structural elements. Frequent applications in façade envelopes, for example, involve the use of glass panels spanning from floor to floor (e.g. restrained at the level of foundation and roof) able to ensure lightness, transparency and energy efficiency to wide surfaces and interiors. Often, the same glass panels are used for architectural and comfort requirements, but especially in the form of ‘glass shear walls’ able to ensure stabilization and stiffening contributions to entire buildings. As a result, their design and calculation strictly depends on a complex structural interaction between the glass panels themselves and their connections to the substructures, namely consisting in glued connections, adhesive joints and special metal fasteners, steel or aluminum frames, as well as timber framing systems.

Huveners (2009) experimentally investigated the structural behavior of glass panels subjected to in plane shear loads and circumferentially glued to metal frameworks. Mocibob (2008) focused on experimental and finite-element (FE) numerical investigation of the structural behavior of laminated glass panels under in plane shear loads. In that work, careful consideration was spent for glass walls point supported to the substructure by means of metal fasteners, as well as to glass panels linearly supported at the top and bottom edges via partially rigid, adhesive joints. Nhamoinesu and Overend (2012) analyzed, by means of experiments and analytical models, the mechanical properties of several adhesives for facades applications, highlighting their effectiveness as linear load-bearing connections under the action of short-duration loads. Van Lancker et al. (2014) assessed the rotational stiffening contribution of linear adhesive joints used to provide the structural interaction between glass panels and cold-formed steel profiles.

Wellershoff (2008) studied via experiments and numerical simulations the buckling response of glass panels under in-plane shear and linearly supported along the four edges. Antolinc et al. (2014) investigated, by means of full-scale shake-table experiments, the seismic capacity of glass walls interacting with timber frames. Further research studies related to the in-plane shear resistance of steel-glass or timber-glass composite walls are discussed in Memari et al. (2003), Krstevska et al. (2013), Bârnaure and Voiculescu (2013) and Ber et al. (2014).

Analytical and FE numerical studies were proposed in Bedon and Amadio (2012) for the assessment of the buckling response and resistance of glass panels simply supported along the four edges, under the action of in-plane shear loads. Based on a further validation of a simplified equivalent thickness approach, the study was then extended in Amadio and Bedon (2013) to laminated glass panels composed of two (or three) glass sheets and one (or two) viscoelastic PVB films. A Eurocode-based design curve was also proposed as rational buckling design procedure for the examined loading and boundary conditions, while in Bedon and Amadio (2014) a normalized resisting domain was presented for the buckling verification of the same panels under the combined action of in-plane shear and compressive loads.

In this research project, the buckling response of glass panels subjected to in-plane shear loads only, with two-side linear circumferential sealant joints along the four edges and supporting metal frames, is investigated by means of extended FE parametric simulations (ABAQUS), analytical methods derived from past literature contributions (Amadio and Bedon 2013) and classical theories (Timoshenko and Gere 1961; Bulson 1970). Throughout the extended parametric studies, numerically derived buckling coefficients and corresponding fitting curves of practical use are first proposed. As shown, due to the interaction of glass panels with small steel supports, in-plane flexible sealant joints and supporting frames with mullions of variable out-of-plane bending stiffness, the expected Euler’s critical loads can be markedly lower than classical theory estimations obtained for ideally simply supported or fully clamped plates. As result, appropriate analytical methods are required for a correct prediction of the expected theoretical buckling resistance.

Further extended nonlinear incremental simulations (INLS) are then carried out on the same assembled structural systems, so that the effects deriving from multiple aspects (e.g. the mechanical behavior of the involved materials, initial geometrical imperfections, possible small gaps at the interface between the glass panels edges and the compressive steel supports, etc.) could be properly emphasized. The Eurocode-based buckling design method proposed in Amadio and Bedon (2013) for the stability check of ideally simply supported glass panels affected by initial imperfections of maximum amplitude up to 1/1000 the panel height is then recalled. Based on parametric FE estimations partially discussed in this paper, its applicability and general validity for the studied loading and boundary condition is assessed. As shown, due to appropriate estimation of the actual buckling coefficients, a rather close agreement is found between past findings and the current study, hence suggesting the use of the same normalized design buckling curve as suitable tool for practical buckling design calculations.

Theoretical background and field of study

Shear buckling of isotropic plates

The buckling behavior of isotropic plates, simply supported along the four edges and subjected to in-plane shear loads has been widely investigated over the last decades, due to the large application of various panel typologies as shear stiffeners for structural, naval, aerospace engineering applications (Ore and Durban 1989; Kosteletos 1992; Machimdamrong et al. 2004; Amani et al. 2011; Uymaz and Aydogdu 2013, etc.).

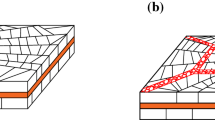
With reference to Fig. 1, for a given monolithic panel with $b\times H$ the global dimensions; t the thickness; $E,\,\nu$ the Young’s modulus and Poisson’ ratio, analytical calculations are usually performed by taking into account classical formulations derived from literature (Timoshenko and Gere 1961). In the hypotheses that

• (i) the material has an elastic, homogeneous, isotropic behavior

• (ii) the panel is initially perfectly flat and its thickness is small, compared to the global dimensions

• (iii) the strains due to deflection in the middle surface are negligible, compared to strains due to bending

• (iv) deformations are such that straight lines initially normal to the middle surface remain straight and normal

the critical shear load $V_{cr}^{(E)}$ is in fact given by:

$$\begin{aligned} V_{cr}^{(E)} =\frac{\pi ^{2}D}{b^{2}}\hbox { }k_\tau . \end{aligned}$$

(1)

In Eq. (1), $D={Ebt^{3}}/{12(1-\nu ^{2})}$ denotes the bending stiffness of the panel, while $k_\tau$ is a well-known buckling coefficient expressed as a function of the assigned boundary conditions and the aspect ratio $\alpha =H/b$.

Fig. 1

Shear buckling of monolithic plates. a Reference configuration, b classical buckling coefficients $k_{\tau }$ for various boundary configurations

For panels with fully simply supported edges (‘ss-ss’, Fig. 1b) or continuously clamped edges (‘cc-cc’, Fig. 1b), for example, $k_\tau$ is given respectively by (Timoshenko and Gere 1961):

$$\begin{aligned} k_\tau =\left\{ {\begin{array}{l@{\quad }l} 4.00+\frac{5.34}{\alpha ^{2}}&{}\alpha \le 1 \\ 5.34+\frac{4.00}{\alpha ^{2}}&{} \alpha >1 \\ \end{array}} \right. \end{aligned}$$

(2)

and

$$\begin{aligned} k_\tau =\left\{ {\begin{array}{l@{\quad }l} 5.60+\frac{8.98}{\alpha ^{2}}&{}\alpha \le 1 \\ 8.98+\frac{5.60}{\alpha ^{2}}&{} \alpha >1 \\ \end{array}} \right. . \end{aligned}$$

(3)

In the case of plates with clamps along two opposite edges and continuous simply supports on the other two edges, conversely, $k_\tau$ can be calculated by means of Eqs. (4) or (5), depending on the application of restraints. For long edges clamped (‘cc-ss’, Fig. 1b) or short edges clamped (‘ss-cc’, Fig. 1b), specifically (Bulson 1970):

$$\begin{aligned} k_\tau =\left\{ {\begin{array}{l@{\quad }l} \frac{8.98}{\alpha ^{2}}+5.61-1.99\alpha &{}\alpha \le 1 \\ 8.98+\frac{5.61}{\alpha ^{2}}-\frac{1.99}{\alpha ^{3}}&{} \alpha >1 \\ \end{array}} \right. \end{aligned}$$

(4)

and

$$\begin{aligned} k_\tau =\left\{ {\begin{array}{l@{\quad }l} \frac{5.34}{\alpha ^{2}}+\frac{2.31}{\alpha }-3.44+9.39\alpha &{} \alpha \le 1 \\ 5.34+\frac{2.31}{\alpha }-\frac{3.44}{\alpha ^{2}}+\frac{8.39}{\alpha ^{3}}&{} \alpha >1 \\ \end{array}} \right. \end{aligned}$$

(5)

Existing buckling design method for simply supported structural glass panels

While the accurate calculation of the critical shear load $V_{cr,0}^{(E)}$ for a given structural element represents an important information for the assessment of its load carrying capacities and theoretical buckling resistance, the same critical load provide only approximate estimation of the actual buckling resistance of a given structural element or system.

More refined analytical models and design methods are in fact required, in order to properly take into account the possible decrease of the theoretical critical shear load $V_{cr,0}^{(E)}$ due to several geometrical and mechanical aspects, like for example initial imperfections, material constitutive behaviors, eccentricities, specific boundary conditions, etc.

In the case of panels composed of glass, for example, a normalized design buckling curve developed in accordance with current standards for steel structures [e.g. the Eurocode 3 (UNI-EN 1993-1-1 2005)] was presented in Amadio and Bedon (2013) as simplified verification approach for panels composed both of monolithic or laminated cross-sections. The mentioned design approach, validated also towards experimental studies available in past research projects [e.g. (Wellershoff 2008)], was proposed so that the buckling shear strength of a glass panel with general geometrical properties and possible initial geometrical imperfections could be calculated.

For this purpose, let us briefly consider the $b\times H,t$-thick monolithic panel of Fig. 1a composed of glass [with $E_g =E$ the Young’s modulus and $\nu _g =\nu$ the Poisson’s ratio (EN 572-2 2004)]. The panel is ideally continuously supported along the four edges and subjected to in-plane shear loads V only.

In accordance with Amadio and Bedon (2013), its shear buckling collapse should be properly prevented by limiting the applied loads V, so that they could not exceed the corresponding buckling strength $V_{b,Rd}$:

$$\begin{aligned} V=V_{Ed} \le V_{b,Rd} =\chi \frac{A\tau _{Rk}}{\gamma _M}, \end{aligned}$$

(6)

where $A=bt$ is the cross-sectional area, $\gamma _M = 1.40$ is a safety coefficient,

$$\begin{aligned} \chi =\frac{1}{\Phi +\sqrt{\Phi ^{2}-\bar{\lambda } ^{2}}},\quad \hbox { for }\chi \le 1, \end{aligned}$$

(7)

is a buckling reduction factor, with

$$\begin{aligned}&\Phi =0.5 [1+{\upalpha }_{\mathrm{imp}} (\bar{\uplambda }-{\upalpha } _0 )+\bar{\uplambda }^{2}],\nonumber \\&{\upalpha }_{\mathrm{imp}} =0.49 \quad \hbox {and} \quad {\upalpha }_0=0.50 \end{aligned}$$

(8)

calibrated imperfection factors, able to take into account the effects of initial geometrical imperfections of maximum amplitude up to $u_{0,\max } =H/{1000}$, and

$$\begin{aligned} \bar{\uplambda }=\bar{\uplambda }_V =\sqrt{\frac{A\,\tau _{Rk} }{V_{cr}^{(E)} }}\quad \hbox {is a normalized slenderness ratio.}\nonumber \\ \end{aligned}$$

(9)

In Eq. (9), $\tau _{Rk}$ denotes the characteristic shear strength of glass, which is reasonably assumed equal to its nominal characteristic tensile strength $\sigma _{Rk}$ (EN 572-2 2004). The Euler’s critical shear load $V_{cr,0}^{(E)}$ of Eq. (9), conversely, can be calculated on the base of classical shear buckling theory, that is by means of Eqs. (1) and (2).

Validation of the mentioned analytical method, as shown in Amadio and Bedon (2013), highlighted that the same approach can be applied to laminated glass panels composed of 2 or 3 glass plies (Fig. 2), by simply replacing the nominal thickness t with a properly calibrated equivalent thickness $t_{eq,w}$. In this case, the accuracy of the method depends on the mechanical characterization of the interlayer foils used to bond together the glass plies, which are typically characterized by strong degradation of the shear modulus $G_{\mathrm{int}}$ with long term loads and high temperatures (Callewaert et al. 2011; Galuppi and Royer 2012; Bittner et al. 2014; Liu et al. 2014; Andreozzi et al. 2014).

Fig. 2

Schematic cross-section for laminated glass elements composed by a 2 or b 3 glass plies

For a given loading condition (e.g. load duration $t_L$ and reference temperature T), it was in fact shown in Amadio and Bedon (2013) and Bedon and Amadio (2015) that the bending stiffness of the assigned LG section can described by taking into account—to describe the viscoelastic behavior of interlayers—the shear stiffness $G_{\mathrm{int}}=f\left( {t_L ,T}\right)$ and calculating the equivalent fully monolithic thickness $t_{eq,w}$ as (2 glass layers):

$$\begin{aligned} t_{eq,w} =\root 3 \of {2t^{3}+12\Gamma J_s}, \end{aligned}$$

(10)

with:

$$\begin{aligned}&0\le \Gamma =\frac{1}{1+\pi ^{2}\beta \frac{E_g \hbox { }t\hbox { }t_{\mathrm{int}} }{2G_{\mathrm{int}} b^{2}}}\le 1 \end{aligned}$$

(11)

$$\begin{aligned}&J_s =\frac{t}{2}\left( {t+t_{\mathrm{int}} } \right) ^{2} \end{aligned}$$

(12)

$$\begin{aligned}&\beta =\frac{5.25}{\alpha ^{2}}+7.32 \end{aligned}$$

(13)

or (3 glass layers):

$$\begin{aligned} t_{eq,w} =\root 3 \of {2t_1^3 +t_2^3 +12\Gamma J_s }, \end{aligned}$$

(14)

with:

$$\begin{aligned}&J_s = 2t_1 t_{s;1}^2 \end{aligned}$$

(15)

$$\begin{aligned}&t_{s;1} = 0.5t_1 +t_{\mathrm{int}} +0.5t_2 \end{aligned}$$

(16)

$$\begin{aligned}&t_s = t_1 +2t_{\mathrm{int}} +t_2 \end{aligned}$$

(17)

In Eq. (11), $G_{\mathrm{int}}=f\left( {t_L ,T}\right)$ is the elastic shear modulus of the adopted interlayer, derived from master curves available in literature for PVB or SG foils for the assigned load duration and temperature condition (e.g. Bennison et al. 1999).

Depending on the assigned geometrical and mechanical properties, the shear transfer coefficient $\varGamma$ of Eq. (11) is then able to take into account the effects deriving from the presence of a partially rigid shear connection between the glass plies, namely comprised between the well-known limit conditions identified by the ‘abs’ layered limit ($\Gamma =0$, when $G_{\mathrm{int}} \rightarrow 0$) or by the ‘full’ monolithic limit ($\Gamma =1$, when $G_{\mathrm{int}} \rightarrow \infty$).

Shear glass panels under various boundary conditions

Although the validation of the design method recalled in Sect. 2.2 demonstrated general applicability to monolithic or LG glass panels subjected to in-plane shear loads, the main limit of the same approach is that—as in the case of shear plate buckling in general—it takes into account ideal boundary conditions only.

In current practice, when glass panels are used as stiffeners and carrying load elements in buildings, several solutions are used in fact to provide a structural interaction between the glass panels themselves and the supporting systems (e.g. metal frames).

Huveners (2009), for example, investigated by means of experiments and analytical methods the structural behavior of glass panels used as shear stiffeners for steel façade frameworks. In that case, each glass panel was assumed circumferentially connected to a metal framework by means of an adhesive connection. Both one-side or two-side adhesive epoxy resin joints were investigated (Fig. 3a, b, respectively). Design recommendations were also provided for the application of adhesively supported glass panels as stabilizers for buildings, by taking into account a double criterion able to limit maximum stresses and displacements. Laufs [Fig. 3c, (Laufs 2000)] studied the structural capacities of linear, one-side adhesive joints introduced along two edges only of the panels (e.g. the horizontal top and bottom edges). In that case, to kept fix the position of the glass panels, additional steel setting blocks were introduced between the panel edges and the frameworks.

Fig. 3

Examples of adhesive connections for glass panels and cladding walls. a, b One-side or two-side adhesive joints for circumferentially supported panels (Huveners 2009). Horizontal crosssection. c, d One-side adhesive joints for glass panels linearly supported along the top and bottom edges only ((Laufs 2000) and (Mocibob 2008) respectively). Vertical cross-section.

Also Mocibob [Fig. 3d, (Mocibob 2008) and Fig. 4, case ‘A’] analyzed the stabilizing effect of glass walls spanning from floor to floor in facades and building envelopes, and restrained to the substructure by means of linear structural sealant joints (introduced along the top and bottom edges only) able to interact with steel angular profiles rigidly connected to the structural background. In that case, the actual position of the glass panel within the steel devices was then kept constant by means of setting blocks (e.g. spacers) able to ensure possible rotations of the panel itself, as well as to avoid possible splitting and crushing mechanisms in the adhesive layers. In order to properly transfer the compressive reaction forces from the glass panels—through the sealant connection—to the steel supporting profiles and hence to the substructure, additional small unilateral steel supports were also introduced near the corners of the top and bottom edges (Figs. 3d, 4, case ‘A’). The gaps between these small steel supports, the glass edges and the frame transoms were then filled with mortar (Figs. 3d, 4, case ‘A’).

Fig. 4

Reference limit configurations for continuously restrained, frame-supported glass panels under in-plane shear loads. a fully deformable mullions, b fully rigid mullions

In this paper, based on past analytical and numerical studies discussed in Amadio and Bedon (2013), extended FE investigations are dedicated to the shear buckling response of glass panels circumferentially restrained by means of structural sealant joints and interacting with metal supporting frames. In accordance with Mocibob (2008), the frame transoms are assumed composed of two angular steel profiles able to prevent possible out-of-plane displacements to the panel’ top and bottom edges (Figs. 3d, 4, case ‘A’).

The same solution is also applied to the frame mullions, where possible compressive reaction forces are transmitted from the glass panel to the adjacent mullions by means of small unilateral steel supports (Fig. 4, case ‘B’). While it is expected that the fully frame-supported glass panel of Fig. 4 (case ‘B’) would behave as a plate fully clamped along the four edges, the effective interaction between the panel and the supporting system (e.g. the frame, the sealant joints and the setting blocks) is assessed in this work by means of extended FE parametric investigations. The stiffening and strengthening contribution of metal frames with mullions of variable out-of-plane bending stiffness—compared to the glass panel rigidity—as well as further possible combinations of geometrical and mechanical aspects (e.g. the presence and position of small unilateral steel supports, the strengthening contribution of continuous sealant joints, etc.) are also emphasized. By assuming the case ‘A’ of Fig. 4 as a ‘lower limit condition’, as far as the bending stiffness of mullions increases, as shown, the typical glass panel depicted in Fig. 4‘A’ manifests a structural response which is markedly affected by the contribution of the mullions themselves. Careful consideration, however, should be dedicated to correctly estimate the effective shear buckling resistance deriving from the actual boundary restraints and the assigned material mechanical properties.

General finite element (FE) numerical approach

FE solving method

Linear bifurcation analyses (LBA) were first performed, in order to qualitative investigate the global behavior of the examined panels, as well as to highlight the general effect deriving from circumferential joints interacting with partially flexurally rigid supporting frames under the action of in-plane shear loads V applied along the top and bottom edges of each ‘composite’ system.

In a second phase, by properly modifying the typical FE-models discussed in Sect. 3.2, nonlinear incremental simulations (INLS) were also carried out on the same panels (see Sect. 5), in order to more accurately assess the typical buckling response and possible failure mechanisms for the studied loading and boundary configurations.

FE model assembly

The typical FE-model adopted throughout the extended LBA numerical investigations partly discussed in this paper was implemented in the ABAQUS/Standard computer software (2010) and consisted of 4-node shell elements composed of glass and characterized by an monolithic thickness t, representative of both fully monolithic glass panes as well as LG panels composed of 2 or 3 glass plies. In the latter case, the corresponding equivalent monolithic thickness was calculated according to Eqs. (10) and (14). In terms of mechanical characterization of glass, a indefinitely linear elastic material, with $E_g = 70\hbox {GPa},\,\nu _g = 0.23,\,\rho _g = 2490\hbox { kg/m}^{3}$, was used.

The supporting frame was described in each FE-model in the form of B31 beam elements with assigned ‘general’ cross-section characterized by infinite axial EA and torsional $GJ_t$ stiffnesses. A simple ‘join’ connector was assigned at the intercepting end nodes of transoms and mullions, so that their relative displacements could be fully prevented. In terms of bending stiffness of the frame components, an infinite flexural stiffness was considered for the transoms ($EI_t =\infty$), since well representative of a fully rigid connection between each glass panel and the structural background (e.g. a concrete slab, for glass panels spanning from floor to floor), while a specific flexural stiffness $EI_m$, with $0\le EI_m \le \infty$, was taken into account in each separate simulation, in order to assess the effects deriving from flexible or almost rigid mullions. An indefinitely linear elastic behavior was taken into account for the frame components throughout the parametric numerical study ($E_s = 210\, \hbox {GPa},\,\nu _s = 0.3$ and $\rho _s = 7850\,\hbox { kg/m}^{3}$), while out-of-plane displacements were prevented for all the transoms nodes $(U_z =0)$.

Fig. 5

Detail of the typical FE model for a glass panel circumferentially restrained subjected to in-plane shear loads

Each glass panel was then properly restrained along the edges, so that in accordance with Figs. 3d and 4 the effects deriving from linear sealant joints interposed between the panel edges and the supporting frame could be properly highlighted. A set of ‘slide-plane’ connectors available in the ABAQUS library was used (Fig. 5), since the effect of the assumed connector typology, when properly calibrated, is the same of a flexible restraint towards two in-plane translational deformations ($U_x$ and $U_y$), together with possible separate rotational restraints for the three $R_x ,\, R_y ,\,R_z$ components. In this work, the‘slide-plane’ connectors were orientated so that their translational restraints could be activate in the $\left( {x,y} \right)$ plane of the glass panel (detail of Fig. 5). While keeping a fully rigid out-of-plane restraint along the panel edges (e.g. $K_z =\infty$, in order to properly describe the effect of setting blocks and the position of the glass panel, with respect to the supporting steel frame), the in-plane elastic stiffness $K=K_x =K_y$ per unit-of-length of each connector, representative of the shear stiffness of the structural sealant layers, was properly calibrated. Its final value—comprehensive of the joint stiffness on both the sides of each panel (Fig. 3d)—was in fact calculated by taking into account the mesh reference size $l_{mesh}$ of each FE-model, the modulus of elasticity $E_{joint} = 2.4\,\hbox {MPa}$ of a common sealant for structural glass applications (Mocibob 2008) and the nominal cross-section $t_{joint} \times h_{joint}$ of a single joint layer [$t_{joint}= 9.5\,\hbox {mm}$ and $h_{joint} = 40\,\hbox {mm}$ for preliminary LBA simulations, in accordance with Mocibob (2008)]. For linear bifurcation analyses (LBA) purposes, a linear elastic mechanical behavior was then assigned to these connectors, by taking into account the so calculated in-plane elastic stiffness per unit-of-length K.

Concerning the rotational restraints provided by the same ‘slide-plane’ connectors to each panel, a fully clamped condition was assumed towards possible out-of-plane deformations of the panel edges, with respect to the frame components, in order to properly simulate the interaction between the glass panel edges and the adjacent setting blocks/metal profiles $(R_x =R_y =\infty )$. For the same reason, additional unilateral, point connectors able to sustain compressive loads only, were also introduced along all the four edges, to reproduce the effects deriving from the point steel supports (Fig. 3d). In accordance with the design solution proposed in Mocibob (2008) and also investigated in Bedon and Amadio (2015), these steel supports were positioned at a fixed distance $d_{support} =b/5$ from the corners of each panel (Fig. 4), with $b_{support} = 100\hbox {mm}$ the reference size of each setting block.

Discussion of LBA parametric numerical results

A wide set of geometrical and mechanical configurations was taken into account throughout the parametric LBA simulations, in order to highlighting the sensitivity of the Euler’s shear buckling resistance $V_{cr,0}^{(E)}$ of the examined panels to the aspect ratio $\alpha$, slenderness $\bar{\lambda }$, frame bending stiffness, joint stiffness, etc.

Square glass panels

Some results are proposed in Fig. 6, in the form of numerically derived $k_\tau$ buckling coefficients, as a function of the $R_{EI}$ out-of-plane bending stiffness ratio, where:

$$\begin{aligned} R_{EI} =\frac{2EI_m }{EI_g }, \end{aligned}$$

(18)

and

$$\begin{aligned} EI_g =E_g \cdot \frac{bt^{3}}{12} \end{aligned}$$

(19)

is the flexural stiffness of the glass panel, with $EI_m$ the bending stiffness of the supporting mullions.

Fig. 6

LBA numerically derived buckling coefficients $k_{\tau }$ for square glass panels with two-side circumferential sealant joints, setting blocks, unilateral steel supports and frame with mullions of variable out-of-plane bending stiffness (ABAQUS/Standard)

All the proposed $k_\tau$ values, specifically, are calculated by means of Eq. (1), on the base of the assigned geometrical properties and the corresponding LBA predicted fundamental critical loads $\left( {V_{cr,0}^{(E)}}\right) _{LBA}$.

As highlighted in Fig. 6, a totally different response was found for glass panels with fixed geometry, a given linear connection along the four edges (e.g. constant $E_{joint},\,t_{joint}, \,h_{joint}$ parameters) and supporting mullions with assigned bending stiffness $EI_m$. The numerically derived $k_\tau$ coefficients of Fig. 6 are in fact clearly comprised between two well-defined limit values, e.g. a lower limit $\left( {k_\tau } \right) _0$ and an upper limit $\left( {k_\tau } \right) _{\max }$. While $\left( {k_\tau } \right) _0$ strictly depends on the top and bottom linear supports only (e.g. mullions with negligible bending stiffness and null strengthening contribution), the upper limit $\left( {k_\tau } \right) _{\max }$ is associated to glass panels supported along the four edges by a circumferential sealant joint and an infinitely rigid frame. In this latter case, consequently, the flexibility of the panel strictly depends on the linear sealant joints and the compressive steel supports only. The points A, B, C of Fig. 6 are associated to well-distinguishable buckling coefficients $k_\tau$ and corresponding Euler’s critical loads $\left( {V_{cr,0}^{(E)} } \right) _{LBA}$, but also specific overall behaviors. As shown in Fig. 7, it can be seen for the same panel geometry that as far as the bending stiffness of mullions increases, both the expected deformed shape and the corresponding distribution of principal stresses in glass modify.

Fig. 7

Qualitative effects of the mullion out-of-plane bending stiffness on the buckling response of glass panels subjected to in-plane shear, supported by circumferential two-side sealant joints and metal frames. Red-to-blue contour plot of (i) out-of-plane displacements and (ii) maximum principal stresses on the top glass surface (blue $=$ compression; red $=$ tension). ABAQUS/Standard. a REI $=$ 0, b REI $=$ 1, c REI $=$ 50. (Color figure online)

Figure 7a is in fact associated to a panel without supporting mullions $(R_{EI} =0)$ and is characterized by maximum out-of-plane displacements at mid-span that are almost uniformly distributed along the transversal section of the panel, due to the lack of restraints along the vertical edges. When the stiffening contribution of mullions is comparable to a fully rigid restraint against out-of-plane deformations $(R_{EI} =\infty )$, conversely, the obtained deformed shape and stress distribution on glass are almost comparable to the qualitative response of a fully linearly supported glass panel (Fig. 7c and point C of Fig. 6). All the intermediate conditions (Figs. 7b, 6, point B), finally, are characterized by fundamental deformed shapes typically identified as an interpolation of the limit configurations, and an expected theoretical shear buckling resistance that can be markedly higher, compared to the laterally unrestrained panel.

An important aspect emphasized by Fig. 6 is that the upper limit $\left( {k_\tau } \right) _{\max }$—despite the presence of rotational restraints (e.g. the lateral setting blocks) and an almost rigid supporting frame able to fully prevent possible out-of-plane deformations along the panel edges—is markedly lower than the ‘ss-ss’ theoretical buckling coefficient $k_\tau$ [Eq. (2)] and almost one half the corresponding ‘cc-cc’ value [Eq. (3)]. The reason of this large discrepancy between the estimated $k_\tau$ coefficients and the $k_\tau$ values associated to ideal linear simply supports or continuous clamps respectively, as highlighted by parametric LBA simulations and INL analyses (see also Sect. 5)—is primarily given by the additional point steel supports introduced between the glass panels and the frame, to transfer the compressive reaction forces to the substructure. As also discussed in Mocibob (2008) and recalled in Bedon and Amadio (2015), under the action of in-plane shear loads V the active point steel supports involve in fact the occurrence of a compressed diagonal in the glass panel, hence resulting in premature buckling failure of the system—compared to ideally simply supported or clamped configurations—and in a substantial modification of the expected buckling coefficients $k_\tau$. Parametric simulations also highlighted that the modification of the LBA predicted $k_\tau$ coefficients, for the studied case, depends on the presence of linear sealant joints acting as flexible translational restraints between the glass panel edges and the supporting frame. A general dependency of the $k_\tau$ coefficients from a combination of geometrical and mechanical aspects is thus expected.

Rectangular glass panels

LBA estimations obtained for rectangular glass panels generally confirmed the same trend of square panels.

In accordance with Fig. 6, all the performed simulations highlighted in fact that as far as the $R_{EI}$ ratio is lower than $\approx$0.1, the supporting mullions provide almost null stiffening and strengthening contribution to the laterally unrestrained panels $(k_\tau \approx \left( {k_\tau }\right) _0)$. Conversely, when the $R_{EI}$ ratio exceeds the reference value $\approx$50, further increase in the frame stiffness does not provide additional beneficial contribution to the glass-steel assembled system $(k_\tau \rightarrow \left( {k_\tau } \right) _{\max })$. Major modifications in terms of overall buckling response and ultimate buckling resistance are consequently expected in the range $0.1<R_{EI} <50$.

Some LBA parametric results are proposed in Fig. 8, for glass panels with various aspect ratios $\alpha$ (with $1\,\mathrm{{m}}\le H\le 3\,\mathrm{{m}}$), nominal glass thickness $t= 10\,\mathrm {mm}$ (with $8\,\mathrm{{mm}}\le t\le 35\,\mathrm{{mm}}$ the thickness range considered through the full parametric numerical investigation) and variable $R_{EI}$ ratios. LBA numerical predictions are compared in the form of ${k_\tau }/{\left( {k_\tau } \right) }_0$ ratio, as a function of $R_{EI}$. As shown, as far as the aspect ratio $\alpha$ increases, for a given $R_{EI}$ value, the beneficial contribution of mullions increases, hence confirming their important stabilizing effect. Since the proposed LBA estimations are also strictly related to the stiffness of the used sealant joints $(E_{joint},\,h_{joint},\,t_{joint})$, however, analytical models and fitting curves of general validity are required for practical purposes.

Fig. 8

Variation of the LBA numerically derived buckling coefficients $k_{\tau }$ for glass panels with two-side circumferential sealant joints, setting blocks, unilateral steel supports and frame with mullions of variable out-of-plane bending stiffness (ABAQUS/Standard), as a function of the $R_{EI}$ ratio

Derivation of $k_{\tau }$ buckling curves

In order to identify a general correlation between geometrical and mechanical properties of glass panels, sealant joints, point steel supports and supporting frames, further extended LBA parametric studies were carried out.

In this case, together with a wide set of glass panel’ geometries and mullion’ stiffness combinations $(t,\,H,\,b,\,EI_m)$, variations in terms of in-plane stiffness per unit-of-length of the sealant joints were also taken into account $(E_{joint}, \,t_{joint},\,h_{joint})$. Exemplificative comparisons are proposed in Fig. 9, where LBA numerically derived $k_\tau$ buckling curves are proposed for glass panels with variable $R_{EI}$ ratios and a given sealant joint in-plane stiffness.

Fig. 9

LBA numerically derived (ABAQUS/Standard) $k_{\tau }$ buckling coefficients for glass panels with two-side circumferential sealant joints, setting blocks, unilateral steel supports and frames with mullions of variable out-of-plane bending, under the action of in-plane shear loads

In accordance with Fig. 9, LBA simulations highlighted that the upper limit buckling curve $(R_{EI}>50)$ is generally defined by:

$$\begin{aligned} \left( {k_\tau } \right) _{\max } =A\cdot B^{\frac{1}{\alpha }} , \end{aligned}$$

(20)

where the constants A and B depend on the sealant joint in-plane stiffness [$A= 3.24$ and $B= 2.54$, in Fig. 9 ($E_{joint}= 2.4\,\hbox {MPa}, h_{joint} = 40\,\hbox {mm}, t_{joint} = 9.5\,\hbox {mm}$)]. An accurate calculation of the upper limit curve, consequently, should be able to properly take into account the effects deriving from the interaction between a given glass panel and the used adhesive joints. Comparative LBA calculations highlighted that—for most of the $E_{joint} ,\,h_{joint} , \,t_{joint}$ solutions of practical interest for glass applications—the constant A almost linearly depends on the in-plane stiffness of the adhesive joints:

$$\begin{aligned} A=\frac{K_{joint} }{c_1 }+1.86, \end{aligned}$$

(21)

with $c_1 =1.98\hbox { N/mm}^{2}$,

while

$$\begin{aligned} B=\frac{1}{c_2 \cdot K_{joint} +0.24}, \end{aligned}$$

(22)

with

$$\begin{aligned} K_{joint} =n\cdot \left( {\frac{E_{joint} }{2\cdot \left( {1+\nu _{joint} } \right) }\frac{h_{joint} }{t_{joint} }} \right) \end{aligned}$$

(23)

in $[\hbox {N/mm}^{2}],\,\nu _{joint} =0.49$ and $n=1$ or 2 for adhesive joints applied on a single or both the glass panel sides respectively and $c_2 =0.028\hbox { N/mm}^{2}$.

The lower limit curve of Fig. 9 $(R_{EI} =0)$, conversely, is given by:

$$\begin{aligned} \left( {k_\tau } \right) _0 =\frac{k_\tau ^*}{\alpha ^{2.55}}, \end{aligned}$$

(24)

with

$$\begin{aligned} k_\tau ^*=\frac{K_{joint} }{c_3 }+4.6, \end{aligned}$$

(25)

$K_{joint}$ calculated by means of Eq. (24) and $c_3 =12.2\hbox { N/mm}^{2}$.

In this latter case, Eqs. (25) and (26) are in close agreement with findings presented in Mocibob (2008) and Bedon and Amadio (2015), that is with past research projects related to glass panels subjected to in-plane shear loads V and linearly supported along the top and bottom edges only (Fig. 4a), that is with vertical unrestrained edges. As far as the $R_{EI}$ ratio modifies between $\approx$0.1 and $\approx$50, the $k_\tau$ buckling curves proposed in Fig. 9 present almost a variable trend up to $R_{EI} \approx 10$, that is an almost direct proportionality between the $R_{EI}$ parameter and the corresponding $k_\tau$ coefficients.

When $R_{EI}$ is comprised between $\approx$10 and $\approx$50, conversely, the stiffening contribution of the supporting frame manifests a more than linear proportionality increase for long panels ($\alpha >2.5)$, e.g. the higher is the aspect ratio $\alpha$ and the largest is the expected stabilizing contribution provided by the bracing mullions of assigned bending stiffness $EI_m$, compared to short panels. As a result, the $k_\tau$ buckling curves show a progressive transition from an exponential form comparable to Eq. (25) towards a fitting curve agreeing with Eq. (21). In order to properly estimate the $k_\tau$ coefficient for a generic panel geometry, frame stiffness and joint stiffness, consequently, it is clear that approximate analytical equations of general validity could represent a practical tool of large use in practice.

In this work, LBA parametric estimations were used to derive generalized fitting curves for $k_\tau$ buckling coefficients of general glass panels with variable $R_{EI}$ and $K_{joint}$ parameters. Based on Fig. 9, specifically, approximate equations were extrapolated so that the upper limit curve $\left( {k_\tau } \right) _{\max }$ and all the intermediate configurations could be calculated in the same form of the lower limit curve associated to glass panels with unrestrained vertical edges [Eq. (25)].

Manipulation of parametric LBA predictions highlighted that the upper limit curve of Fig. 9 $(R_{EI}= 50)$ is well approximated by:

$$\begin{aligned} \left( {k_\tau } \right) _{\max } =\frac{k_\tau ^*}{\alpha ^{0.7}}, \end{aligned}$$

(26)

where

$$\begin{aligned} k_\tau ^*=\frac{K_{joint} }{c_3 }+7.78, \end{aligned}$$

(27)

with $K_{joint}$ given by Eq. (24) and $c_3$ in Eq. (26), represents the intercepting value between the $\left( {k_\tau } \right) _{\max }$ curve and the y-axis $(\upalpha = 1)$.

All the intermediate conditions comprised between the upper and limit $k_\tau$ curves $(0.1<R_{EI}<50)$, at the same time, can be rationally expressed in the form:

$$\begin{aligned} k_\tau =\frac{C}{\alpha ^{D}} \end{aligned}$$

(28)

where the constants C and D should properly take into account the effects deriving from the structural interaction between a given glass panel geometry $(EI_g)$, the supporting frame $(EI_m)$ and the interposed sealant joints $(E_{joint})$.

Parametric LBA calculations and analytical comparisons highlighted that the transition of the $k_\tau$ buckling curves between the lower [Eq. (25) and upper Eq. (27)] fitting curves is well represented by Eq. (29), when $(0.1<R_{EI} <50)$:

$$\begin{aligned} C= & {} X+0.39\cdot \ln \left( {R_{EI} } \right) , \end{aligned}$$

(29)

$$\begin{aligned} X= & {} c_4 \cdot K_{joint} +6.67 \end{aligned}$$

(30)

with $c_4= 0.03\hbox { N/mm}^{2}$, and

$$\begin{aligned} D=\frac{1}{0.04\cdot R_{EI} +0.365} \end{aligned}$$

(31)

Comparisons between the LBA numerically calculated $k_\tau$ buckling coefficients and the corresponding approximated fitting curves given by Eq. (29) are proposed in Fig. 10, while in Fig. 11 the $C,\, X,\,D$ parameters approximated by Eqs. (30), (31), (32) are shown, together with the corresponding LBA estimations.

Fig. 10

Examples of fitting curves for the calculation of the buckling coefficients $k_{\tau }$, compared to LBA results (ABAQUS/Standard)

Fig. 11

Fitting curves for the calculation of the buckling coefficients $k_{\tau }$, compared to LBA results (ABAQUS/Standard). Parameters a C [Eq. (30)], b X [Eq. (31)] and c D [Eq. (32)]

As shown, the proposed Equations generally provide close agreement with LBA calculations for the majority of the configurations of practical interest for structural glass applications (Fig. 12). Once the $k_\tau$ buckling coefficient for a given geometrical and mechanical configuration is calculated by means of Eq. (29), consequently, the corresponding Euler’s critical load $V_{cr,0}^{(E)}$ can be rationally estimated by means of Eq. (1).

Based on this simplified approach, the flexural contribution of the frame mullions is fully neglected as far as $R_{EI}<0.1$. In accordance with Figs. 6 and 8, however, this assumption is rationally justified by the almost null modification of the estimated $k_\tau$ coefficients [less than 4 % of $k_\tau$ increase, for all the studied configurations, compared to glass panels with laterally unrestrained vertical edges $(R_{EI} =0)$].

Incremental nonlinear simulations (INLS)

FE-model updating and solving method

Based on the preliminary assessment of the buckling response of the studied panels by means of LBA parametric studies, further numerical investigations where then carried out in the form of more refined nonlinear incremental simulations (INLS).

Fig. 12

Comparisons between LBA numerically derived (ABAQUS/Standard) and approximated $k_{\tau }$ buckling coefficients [Eq. (29)]

Since the Euler’s critical loads $V_{cr,0}^{(E)}$ provide only approximate estimations of the actual shear buckling resistance of the studied panels—being not able to take into account the effects deriving from initial geometrical imperfections, brittle tensile failure of glass, possible collapse of the sealant joints, etc. —it is clear that accurate analytical models are required for appropriate design calculations. At the same time, the validity of the buckling design approach recalled in Sect. 2 for ideally simply supported glass panels must be properly assessed for the specific boundary condition.

For this purpose, the FE-models described in Sect. 3 were first properly updated, so that more accurate mechanical behaviors could be taken into account.

Regarding the mechanical characterization of the ‘slide-plane’ connectors representative of the structural sealant joints, for example, a brittle linear elastic constitutive behavior was used, so that—based on a reference ultimate deformation $d_u$ and an assigned ultimate tensile stress $\sigma _u$—the so calibrated connectors could be considered well representative of possible failure mechanisms occurring in the sealant joints. Specifically, in accordance with some reference values available in literature for the maximum elongation allowed to structural sealants of practical use for glass components (Dow Corning 2011; Henkel 2012; Bostik 2008) and shear test experiments on sealant joints (Belis and Bedon 2014), an ultimate displacement $d_u$ corresponding to a maximum elongation $\varepsilon _u = 400\,\%$ was taken into account. At the same time, the ultimate tensile stress was kept equal to $\sigma _u = 0.94\,\hbox {MPa}$ (Belis and Bedon 2014), that is in close agreement with ultimate tensile resistances of common sealant joints (with $\sigma _{u,nom} = 1.06\,\hbox {MPa}$ and $\sigma _{u,nom} = 1.2\,\hbox {MPa}$ the nominal values given in Henkel (2012) and Bostik (2008) respectively). Throughout the parametric study, based on (Dow Corning 2011; Henkel 2012; Bostik 2008; Belis and Bedon 2014; Mocibob 2008), the adhesive Young’s modulus was also modified in the range $\approx$ 0 $\le E_{joint} \le 4\,\hbox {MPa}$, so that a wide set of configurations of practical interest could be taken into account. Concerning the size of the adhesive layers, based on (Mocibob 2008), $h_{joint}$ and $t_{joint}$ were kept equal to 40 and 9.5 mm respectively and $n=2$.

The unilateral connectors representative of the compressive point steel supports (Fig. 5) were then replaced by more refined FE details (Fig. 13). Small steel supports composed of 8-node solid elements (with $E_s= 210\,\hbox {GPa},\,\nu _s = 0.3,\,\rho _s = 7850\, \hbox {kg/m}^{3}$) were in fact introduced in each FE-model. A frictionless surface-to-surface interaction was also assigned to the glass edge nodes and the steel support surface involved in a possible contact with glass, so that when applying the linearly increasing in-plane shear loads V, both the physical detachment of the glass panel from the steel supports (e.g. due to in-plane deformations allowed by the flexible sealant joints) or any possible crushing due to contact between them could be taken into account. Key parameters for the so modelled steel supports were the block size $(b_{support})$, their distance from the panel corners of the glass panel $(d_{support})$ and any possible gap $(h_{gap})$ between the glass panel edge and the contact surface of each steel support. In accordance with Mocibob (2008), $b_{support}$ and $d_{support}$ were kept equal to 100 mm and b / 5 respectively. The gap effects, with $h_{gap}$ initially set equal to 0 (e.g. direct contact between the glass panel and the steel supports), were then also assessed.

Fig. 13

Schematic representation of a glass panel corner with unilateral steel supports (detail)

For each of the performed INLS simulations, the tested panels were also subjected to initial geometrical imperfections obtained as scaled fundamental shapes derived from corresponding LBA simulations. In accordance with Bedon and Amadio (2012), the maximum amplitude $u_{0,\max }$ of these initial geometrical imperfections was assumed equal to H / 1000 the panel height. At the same time, to properly assess the effective overall response and buckling resistance of the so assembled structural systems, careful consideration was paid during INLS investigations to multiple aspects, like for example the occurrence of:

• (i) tensile cracking of glass: this possible buckling failure configuration was manually checked, during each INLS, and identified as the first attainment of maximum principal stresses $\sigma _{\max } =\sigma _{\max }^{(+)}$ at least equal to the characteristic tensile strength of glass $\sigma _{Rk}$ [with $\sigma _{Rk} = 45\hbox {MPa},\,70\hbox {MPa}$ and 120MPa for annealed (AN), heat strengthened (HS) or fully tempered (FT) glass types respectively (EN 572-2 2004)];

• (ii) crushing in glass: the occurrence of compressive failure mechanisms in glass near the unilateral point steel supports [e.g. where the maximum compressive reaction forces are transferred from the glass panel to the structural background) was also monitored, and identified as the first attainment of maximum compressive stresses $\sigma _{\max }^{(-)}$ in the glass panel exceeding a conventional nominal compressive resistance of glass $\sigma _{Rk}^{(-)*}$ assumed equal to half the theoretical one $\sigma _{Rk}^{(-)}\,(\sigma _{Rk}^{(-)*} =0.5\cdot \sigma _{Rk}^{(-)} = 500\hbox {MPa}$ (EN 572-2 2004)];

• (iii) maximum deformations: in accordance with Amadio and Bedon (2013), the maximum out-of-plane displacement $u_{\max }$ were monitored and the maximum envelope of out-of-plane deformations was continuously measured;

• (iv) failure in the sealant joints, due to the first attainment of (a) maximum in-plane deformations $d_{\max }$ exceeding the assigned limit value $d_u$ or (b) maximum tensile stresses exceeding the corresponding ultimate value $\sigma _u$.

Discussion of results

Some comparative results are proposed in Figs. 14 and 15, for glass panels circumferentially restrained by frames with mullions of variable out-of-plane bending stiffness and adhesive joints with constant geometrical and mechanical properties ($E_{joint}= 2.4\hbox {MPa},\,h_{joint} = 40\,\hbox {mm},\,t_{joint} = 9.5\,\hbox {mm}$, with $h_{gap} = 0$). In Fig. 14, the monitored out-of-plane displacement ratios (e.g. the maximum envelopes of relative out-of-plane deformations $\left( {u_{\max }-u_{0,\max }}\right)$ on the whole glass surface, divided by the panel height H) are proposed as a function of the in-plane shear loads V. The plots (b) and (c), otherwise, propose the envelopes of maximum tensile (b) and compressive (c) stresses on glass, as a function of the applied loads V.

Fig. 14

Shear buckling response of a glass panels with two-side circumferential sealant joints, setting blocks, unilateral steel supports and metal frames with mullions of variable out-of-plane bending stiffness (ABAQUS/Standard). Applied shear load versus the maximum a out-of-plane displacement ratios b tensile stresses and c compressive stresses on glass (ABAQUS/Standard)

Fig. 15

Vectorial distribution of maximum tensile and compressive stresses in the glass panel, at a given maximum out-of-plane deformation $((\mu _{\max }-\mu _{0,\max })/H=0.01)$, in presence of metal frames with mullions of variable out-of-plane bending stiffness (ABAQUS/Standard). a $R_{EI}=1^{-5}$, b $R_{EI}=1^{-1}$, c $R_{EI}=1^{5}$

In Fig. 15, finally, the vectorial distribution of maximum tensile and compressive stresses in glass is proposed for some configurations selected from Fig. 14a, at a given maximum deformation $({\left( {u_{\max } -u_{0,\max } } \right) }/H=0.01)$.

From both the Figures, the effects deriving from a progressively increased out-of-plane bending stiffness in the supporting mullions can be clearly noticed. Rather close agreement with the corresponding LBA estimations was also found. For all the plots collected in Fig. 14a, the Euler’s critical load $V_{cr,0}^{(E)}$ coincides in fact with the asymptotical value (e.g. when $R_{EI}$ is small) or with the first inflection point (in presence of stiffer frames) of the proposed load—out-of-plane displacement curves.

Figure 14 again highlights that the strengthening and stiffening contribution due to the supporting frame has major evidence within a well defined range of $R_{EI}$ values. As far as $R_{EI}$ increases, possible out-of-plane deformations along the vertical edges are prevented and the out-of-plane stiffness of the assembled system globally increases, hence resulting in higher tensile resistance (Fig. 14b) but also in the occurrence of increasingly higher compressive stresses near the point steel supports (Fig. 14b). Extremely flexible or rigid mullions, otherwise, do not affect further the overall response of the studied panels, in terms of deformations and stress distributions in glass.

Important modifications in the obtained buckling results of INLS were also found when assigning a small gap between the panels edges and the unilateral steel supports in contact with glass. Examples are shown in Fig. 16, where for a given frame-supported glass panel the $h_{gap}$ size is modified between 0 (e.g. direct contact) and 20mm. For all the examined configurations, results are proposed as non-dimensional maximum envelopes of out-of-plane (a) and in-plane displacement ratios (b), as well as maximum tensile (c) and compressive (d) stresses in glass, as a function of the applied shear load V (with $R_{EI} =0$).

Fig. 16

Effect of gaps between the glass panel edges and the unilateral steel supports. a Applied load as a function of the maximum a out-of-plane displacement ratio, b in-plane displacement ratio, c tensile and d compressive stresses in glass (ABAQUS/Standard)

Based on comparisons collected in Fig. 16, it can be seen that the gaps between the glass panels edges and the point steel supports could have beneficial structural effects. Due to the presence of in-plane flexible sealant joints, when $h_{gap} \ne 0$, the glass panel can in fact undergo small in-plane deformations, with respect to the supporting frame and the point steel supports. As far as contact does not occur between glass and these steel supports, major effects of gaps manifest in terms of higher stiffness (Fig. 16a), and lower tensile/compressive stresses in glass (Fig. 16c, d), compared to $h_{gap} =0$.

Application of the existing buckling design approach to circumferentially restrained glass panels

Final assessment was performed towards the design buckling method recalled in Sect. 2 for the stability check of glass panels continuously restrained by means of structural sealant joints and supporting frames.

Parametric results of INLS are collected in Fig. 17, in non-dimensional form, as a function of the numerically derived $\chi$ reduction factor and $\bar{\lambda }$ slenderness ratio. For clarity of presentation, FE estimations are divided in Fig. 17a, b, for panels with laterally unrestrained vertical edges (e.g. $R_{EI} =0$) and panels supported by bracing mullions of variable out-of-plane bending stiffness $(0.1<R_{EI} <50)$, respectively.

Fig. 17

Design buckling curve for glass panels with two-side circumferential adhesive joints, setting blocks, unilateral steel supports and metal frames with mullions of variable out-of-plane bending stiffness, under the action of in-plane shear loads $(\mu _{0,\max })/H=1000)$

In both the cases, $\chi$ is calculated as:

$$\begin{aligned} \chi =\chi ^{*}=\frac{V_u }{\sigma _{Rk} \cdot A} \end{aligned}$$

(32)

where

$$\begin{aligned} V_u =\min \left( {V_u^{tens} ;\hbox { }V_u^{comp} ;\hbox { }V_u^{disp}} \right) \end{aligned}$$

(33)

denotes the ultimate buckling resistance of each panel, $\sigma _{Rk}$ the nominal characteristic tensile resistance associated to AN, HS or FT glass types respectively and A the cross sectional area of each panel.

For each simulation, the ultimate shear loads $V_u^{tens},\, V_u^{comp},\,V_u^{disp}$ of Eq. (31) were identified in accordance with Sect. 5.1 (bullet points (i), (ii) and (iii) respectively). In the latter case, for buckling design purposes, a reference limit deformation ratio $R_{u_{\lim }} ={\left( {u_{\max } -u_{0,\max } } \right) }/H=0.0033$ was taken into account (Amadio and Bedon 2013).

At the same time,

$$\begin{aligned} \bar{\lambda } =\bar{\lambda } ^{*}=\sqrt{\frac{A\hbox { }\sigma _{Rk} }{\left( {V_{cr,0}^{(E)} } \right) _{LBA} }} \end{aligned}$$

(34)

of Fig. 17 is the slenderness ratio, calculated in accordance with Eq. (9).

The collected INLS non-dimensional results generally highlighted, compared to glass panels deprived of bracing mullions, that the presence of a frame with assigned bending rigidity typically manifests in the form of decrease of slenderness ratio $\bar{\lambda }$ and increase of the corresponding buckling reduction factor $\chi$. This main effect is rather in close agreement with FE results discussed also in Sects. 4 and 5.

As far as the reference initial geometrical imperfections are assumed with a maximum amplitude up to $u_{0,\max } =H/{1000}$, moreover, the Eurocode-based design curve proposed in Eq. (7) can still represent a practical tool for the shear buckling verification of glass panels in the examined boundary condition. This effect mainly derives from the calibrated imperfection factors $\alpha _0$ and $\alpha _{imp}$, as well as from the accurate estimation—in terms of buckling coefficients $k_\tau$ and corresponding Euler’s critical loads $V_{cr,0}^{(E)}$—of the theoretical buckling resistance for the studied systems.

Conclusions

In this paper, the buckling response of glass panels circumferentially restrained by means of structural sealant joints and supporting metal frames under the action of in-plane shear loads has been investigated. Extended FE numerical simulations have been carried out, both in the form of linear bifurcation analyses and nonlinear incremental simulations. In the first case, the effects of metal frames, sealant joints and point steel supports on the overall buckling response have been highlighted. Fitting curves able to give accurate predictions of the expected buckling coefficients $k_{\tau }$, hence the corresponding Euler’s critical loads, have been proposed for glass panels with general geometrical properties, circumferentially supported by continuous sealant joints and metal frames with mullions of variable out-of-plane stiffness. In order to assess in detail the effective ultimate buckling resistance of the same assembled systems, wide series of nonlinear geometrical imperfections have then been performed. In this latter case, careful attention has been paid to the effects deriving from several geometrical and mechanical aspects, like for example possible initial geometrical imperfections, as well as possible failure mechanisms due to tensile cracking of glass or crushing mechanisms along the glass panel ends (e.g. near the unilateral point steel supports, where the maximum compressive reactions are transferred to the structural background), damage in the sealant joints.

Finally, a normalized Eurocode-based design curve proposed in past research projects for the buckling design of glass panels ideally simply supported along the four edges and subjected to in-plane shear loads has also been recalled. Its general validity and applicability to the studied loading and boundary condition has been properly assessed. As shown, due to imperfection factors calibrated on a reference initial imperfection of maximum amplitude up to 1/1000 the panel height, the same analytical method can provide close agreement with the corresponding FE estimations, hence representing a practical tool for buckling design purposes.