A Global Linearization Approach to Control and State Estimation of a Voltage Source Converter: HVDC System

Abstract

A control method is developed for the VSC-HVDC system, that is for an AC to DC voltage source converter connected to the electricity grid through a high voltage DC transmission line terminating at an inverter. By showing that the VSC-HVDC system is a differentially flat one, its transformation to the linear canonical form becomes possible. This is a global input–output linearization procedure that results into an equivalent dynamic model of the VSC-HVDC system for which the design of a state feedback controller becomes possible. Moreover, to estimate and compensate for modeling uncertainty terms and perturbation inputs exerted on the VSC-HVDC model it is proposed to include in the control loop a disturbance observer that is based on the Derivative-free nonlinear Kalman Filter. This filtering method makes use of the linearized equivalent model of the VSC-HVDC system and of an inverse transformation which is based on differential flatness theory and which finally provides estimates of the state variables of the initial nonlinear model. The performance of the proposed VSC-HVDC control scheme is evaluated through simulation experiments.

Introduction

The integration of renewable energy sources in the electricity grid has imposed in several cases the development of methods for power transmission through AC to DC and DC to AC conversion, and with the intervention of high voltage DC (HVDC) lines. Towards the design of more efficient control schemes for VSC-HVDC grid connections the following results can be noted: in [1–3] $H_{\infty }$ control has been proposed for high voltage direct current links. In [4, 5] and [6] input–output linearization of the voltage converter (VSC) and HVDC link is performed and accordingly a state feedback controller is developed. In [7] and [8] feedback linearization is performed to model of multiple HVDC links and subsequently optimal control is applied. In [9] a decentralized PI passivity-based controller is developed for high-voltage direct current transmission systems. Moreover, in [10] model predictive control and decentralized PID control is applied to the system of multiple HVDC links. In [11] a sliding-mode control method has been developed for the VSC-HVDC model. Finally, in [12] flatness-based control is proposed for the HVDC dynamics considering that the latter is described by a PDE model, while in [13] a feedforward-feedback control scheme is implemented for active power control in VSC-HVDC.

The present paper proposes a global linearization approach, through differential flatness theory, for the problem of nonlinear feedback control and state estimation of a voltage source converter—HVDC line system. First, the dynamic model of this electric power transmission system is considered. This comprises the state-space equations of an AC to DC voltage source converter, that is connected to the rest of the grid through an HVDC line terminating at an inverter. This dynamic model describes the stages of transmission of electric power from a power generator to the rest of the grid, through the intervention of an HVDC line. Next, it is shown that this model is a differentially flat one, which means that all its state variables and its control inputs can be expressed as differential functions of one specific state variable of the model, which the so-called flat output. By proving that differential flatness properties hold for the electric power transmission system it is also shown that the initial nonlinear VSC-HVDC state-space model can be written into the linear canonical (Brunovsky) form. This is a global (exact) linearization procedure, that is valid throughout the entire state-space of the VSC-HVDC system and which is not based on approximate truncation of nonlinearities. For the latter description of the system’s dynamics the design of a feedback controller becomes possible, thus permitting to make the voltage output at the inverter’s side track any reference setpoint [14–16].

Another problem that has to be dealt with in the design of the feedback control scheme is that the control loop is subject to modelling uncertainty and external disturbances. To estimate and compensate for these perturbation terms it is proposed to include in the control loop a disturbance observer that is based on the Derivative-free nonlinear Kalman Filter. Actually, the Derivative-free nonlinear Kalman Filter consists of the Kalman Filter recursion applied to the linearized equivalent model of the VSC-HVDC and of an inverse transformation based again on differential flatness theory which enables to obtain estimates for the state variables of the initial nonlinear model. The inclusion of an additional term in the control input, based on the identification of these exogenous or endogenous perturbations, makes possible their compensation and improves the robustness of the control loop [14, 15]. The performance of the considered control scheme for the VSC-HVDC system is evaluated through simulation experiments.

The structure of the paper is as follows: in “Modelling of the VSC-HVDC Transmission System” section, the model of the dynamics of the VSC-HVDC system is provided. In “Differential flatness of the VSC-HVDC System” section, the differential flatness properties of the VSC-HVDC system are shown. In “Flatness-based Control of the VSC-HVDC System” section, a flatness-based controller is designed for the VSC-HVDC model and its stability and convergence properties are proven. In “Compensation of Disturbances Using the Derivative-free Nonlinear Kalman Filter” section, the Derivative-free nonlinear Kalman Filter is included in the control loop as a disturbance observer, thus enabling to estimate and compensate for modeling uncertainties and external disturbances. In “Simulation Tests” section, the performance of the proposed control scheme is tested through simulation experiments. Finally, in “Conclusions” section concluding remarks are stated. Finally, in an Appendix that is given at the end of the mansucript Lie algrebra-based linearization of the VSC-HVC system is performed, leading to an additional global linearization-based control of this power transmission system.

Fig. 1

Transmission system comprising a voltage source converter (VSC), a high voltage DC line (HVDC) and an inverter

Modelling of the VSC-HVDC Transmission System

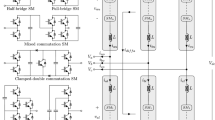
By connecting the three-phase voltage source converter, which is found at the generator’s side with the three-phase inverter which is found at the load’s side through an HVDC line (see Fig. 1) the high voltage DC transmission system is formed. Moreover, by applying Kirchhoff’s voltage and current laws the dynamics of the HVDC line is obtained. Thus at the converter’s side it holds

$$\begin{aligned} {C_1}{\dot{V}_{{DC}_1}}=-{1 \over Z_L}V_{{DC}_1}+{1 \over Z_L}V_{{DC}_2}+{3 \over 4}{i_d}{u_1}+{3 \over 4}{i_q}{u_2} \end{aligned}$$

(1)

where $Z_L$ is the impedance of the transmission line (Fig. 2). Here $Z_L$ is considered to consist of only a resistance part (if inductance part is also included in the transmission line’s dynamics then a higher order state-space model for the VSC-HVDC system will be obtained). It is also possible to model the transmission line’s dynamics as a distributed parameters system, however this latter assumption will not be followed in this manuscript.

At the inverter’s side it holds

$$\begin{aligned} {C_2}\dot{V}_{{DC}_2}={1 \over Z_L}V_{{DC}_1}-{1 \over Z_L}V_{{DC}_2} \end{aligned}$$

(2)

The state-space model of the VSC-HVDC transmission line, can be obtained using established models about the dynamics of the voltage source converter [17–23]:

$$\begin{aligned}&L{\dot{i}_d}=-R{i_d}+L{\omega }{i_q}+v_d-{V_{{DC}_1} \over 2}{u_1} \nonumber \\&L{\dot{i}_q}=-L{\omega }{i_d}-R{i_q}+v_q-{V_{{DC}_1} \over 2}{u_2} \nonumber \\&{C_{DC_2}}{\dot{V}_{{DC}_2}}={1 \over {Z_L}}V_{{DC}_1}-{1 \over {Z_L}}V_{{DC}_2} \nonumber \\&{C_{DC_1}}{\dot{V}_{{DC}_1}}=-{1 \over {Z_L}}V_{{DC}_1}+{1 \over {Z_L}}V_{{DC}_2}+{3 \over 4}{i_d}{u_1}+{3 \over 4}{i_q}{u_2}\nonumber \\ \end{aligned}$$

(3)

Fig. 2

Components of the high voltage DC line (HVDC)

By defining the new state vector of the VSC-HVDC system as $x=[x_1.x_2,x_3,x_4]^T=[i_d,i_q,V_{{DC}_2},V_{{DC}_1}]$ one obtains the state-space description

$$\begin{aligned}&L{\dot{x}_1}=-R{x_1}+L{\omega }{x_2}+v_d-{x_{4} \over 2}{u_1} \nonumber \\&L{\dot{x}_2}=-L{\omega }{x_1}-R{x_2}+v_q-{x_{4} \over 2}{u_2} \nonumber \\&{C_{DC_2}}{\dot{x}_3}={1 \over {Z_L}}{x_4}-{1 \over {Z_L}}{x_3} \nonumber \\&{C_{DC_1}}{\dot{x}_4}=-{1 \over {Z_L}}{x_4}+{1 \over {Z_L}}{x_3}+{3 \over 4}{x_1}{u_1} \nonumber \\&\qquad +\,{3 \over 4}{x_2}{u_2} \end{aligned}$$

(4)

which can be also written in matrix form

$$\begin{aligned} \begin{pmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{pmatrix}= & {} \begin{pmatrix} -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L} \\ -{\omega }{x_1}-{R \over L}{x_2}+{v_q \over L} \\ {1 \over {{Z_L}C_{{DC}_2}}}{x_4}-{1 \over {{Z_L}C_{{DC}_2}}}{x_3} \\ -{1 \over {{Z_L}C_{{DC}_1}}}{x_4}+{1 \over {{Z_L}C_{{DC}_1}}}{x_3} \end{pmatrix} \\&+\begin{pmatrix} -{x_{4} \over {2L}} &{} 0 \\ 0 &{} -{x_{4} \over {2L}} \\ 0 &{} 0 \\ {3 \over {4C_{{DC}_1}}}{x_1} &{} {3 \over {4C_{{DC}_1}}}{x_2} \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \end{pmatrix} \end{aligned}$$

(5)

while, as in the case of the stand-alone VSC the output of the voltage source converter is taken to be

$$\begin{aligned} h=\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}= \begin{pmatrix} e_c \\ i_q \end{pmatrix}= \begin{pmatrix} {3 \over 4}L\left( x_1^2+x_2^2\right) +{C_{{DC}_2} \over 2}{x_3^2} \\ x_2 \end{pmatrix} \end{aligned}$$

(6)

Consequently, the VSC-HVDC system is written again in the state-space form

$$\begin{aligned} \dot{x}= & {} f(x)+G(x)u \nonumber \\ y= & {} h(x) \end{aligned}$$

(7)

where f(x), G(x) and h(x) are given by

$$\begin{aligned} f(x)= & {} \begin{pmatrix} -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L} \\ -{\omega }{x_1}-{R \over L}{x_2}+{v_q \over L} \\ {1 \over {{Z_L}C_{{DC}_2}}}{x_4}-{1 \over {{Z_L}C_{{DC}_2}}}{x_3} \\ -{1 \over {{Z_L}C_{{DC}_1}}}{x_4}+{1 \over {{Z_L}C_{{DC}_1}}}{x_3} \end{pmatrix} \nonumber \\ G(x)= & {} \begin{pmatrix} -{x_{4} \over {2L}} &{} 0 \\ 0 &{} -{x_{4} \over {2L}} \\ 0 &{} 0 \\ {3 \over {4C_{{DC}_1}}}{x_1} &{} {3 \over {4C_{{DC}_1}}}{x_2} \end{pmatrix} \end{aligned}$$

(8)

$$\begin{aligned} h(x)= & {} \begin{pmatrix} {3 \over 4}L\left( x_1^2+x_2^2\right) +{C_{DC_2} \over 2}{x_3^2} \\ x_3 \end{pmatrix} \end{aligned}$$

(9)

Remark 1

The impedance of the line can be considered to consist of both a resistance part and of an inductance part. Should one have adopted this description the dynamic model of the HVDC-VSC system would not be described by Eq. (4) but would be given a higher-order state-space description. Besides, in such a case it would be necessary to consider as state variables the derivatives of the control inputs and to perform dynamic feedback linearization in place of static feedback linearization. In several research articles, the assumption made is that for short transmission lines (up to tens of Km) the line can be modeled by only a resistance part (see Ref. [24]).

Remark 2

The modelling of the VSC-HVDC system takes into account the dynamics of the AC to DC voltage source converter and the dynamics of the transmission line. The dynamics of the inverter can be considered in Eq (2) by including a current variable $i_D$ in its right part, which denotes the current that becomes input to the inverter. However, one can also consider this current term as unmodelled dynamics which is described by the disturbance terms $\tilde{d}_1$ and $\tilde{d}_2$ appearing in Eqs. (69) and (70). It has been explained that by using a Kalman Filter-based disturbance observer in the control loop the effects of such disturbance terms can be estimated and annihilated. Consequently, the model of the third line of the VSC-HVDC system is adequate if current $i_D$ is taken to be a disturbance parameter that will be compensated by the robustness of the controller. Moreover, by considering that the right part of the equation in the third row of Eq. (3) is completed by the load current $i_D$ (the latter is taken to be a disturbance input to the model), it is assured that even in the steady-state $V_{{dc}_1}$ will be greater than $V_{{dc}_2}$.

Differential Flatness of the VSC-HVDC System

Next, it will be shown that the dynamic model of the voltage source converter is a differentially flat one, i.e. it holds that all state variables and its control inputs can be written as functions of the flat outputs and their derivatives [25–31]. Moreover, it will be shown that by expressing the elements of the state vector as functions of the flat outputs and their derivatives one obtains a transformation of the VSC-HVDC model into the linear canonical (Brunovsky) form.

The dynamic model of the joint VSC-HVDC dynamics has been defined as

$$\begin{aligned} \dot{x}_1= & {} -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L}-{x_4 \over {2L}}u_1 \end{aligned}$$

(10)

$$\begin{aligned} \dot{x}_2= & {} -{\omega }{x_1}-{R \over L}{x_2}+{v_q \over L}-{x_4 \over {2L}}u_2 \end{aligned}$$

(11)

$$\begin{aligned} \dot{x}_3= & {} {1 \over {{Z_L}{C_{{DC}_2}}}}x_4-{1 \over {{Z_L}{C_{{DC}_2}}}}x_3 \end{aligned}$$

(12)

$$\begin{aligned} \dot{x}_4= & {} -{1 \over {{Z_L}{C_{{DC}_1}}}}x_4+{1 \over {{Z_L}{C_{{DC}_1}}}}x_3+{{3{x_1}} \over {4{C_{{DC}_1}}}}u_1 \nonumber \\&+\, {{3{x_2}} \over {4{C_{{DC}_1}}}}u_2 \end{aligned}$$

(13)

The flat output of the system is taken to be $y_f=[y_{f_1},y_{f_2}]^T$, where

$$\begin{aligned} y_{f_1}= & {} {{3L} \over 4}\left( x_1^2+x_2^2\right) +{{C_{{DC}_1}} \over 2}{x_4^2} \end{aligned}$$

(14)

$$\begin{aligned} y_{f_2}= & {} x_3 \end{aligned}$$

(15)

By deriving Eq. (14) with respect to time one obtains

$$\begin{aligned} {\dot{y}_{f_1}}= & {} {{3L} \over 2}{x_1}{\dot{x}_1}+{{3L} \over 2}{x_2}{\dot{x}_2}+{C_{{DC}_1}}{x_4}{\dot{x}_4}\,{\Rightarrow } \nonumber \\ {\dot{y}_{f_1}}= & {} {{3L} \over 2}{x_1}\left[ -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L}-{{x_4} \over {2L}}{u_1}\right] \nonumber \\&+\,{{3L} \over 2}{x_2}\left[ -{R \over L}{x_2}-{\omega }{x_1}+{v_q \over L}-{x_4 \over {2L}}u_2\right] \nonumber \\&+\,{C_{{DC}_1}}{x_4}\left[ -{1 \over {{Z_L}{C_{{DC}_1}}}}x_4+\,{1 \over {{Z_L}{C_{{DC}_1}}}}x_3 \right. \nonumber \\&\left. +\,{{3{x_1}} \over {4{C_{{DC}_1}}}}u_1+{{3{x_2}} \over {4{C_{{DC}_1}}}}u_2\right] \end{aligned}$$

(16)

Using that $v_d$ is constant (d-axis component of the grid voltage) and $v_q=0$, and after intermediate computations one obtains

$$\begin{aligned} {\dot{y}_{f_1}}=-{{3R} \over 2}\left( x_1^2+x_2^2\right) +{{3{x_1}} \over 2}{v_d}-{{x_4^2} \over {Z_L}}+{{{x_3}{x_4}} \over {Z_L}} \end{aligned}$$

(17)

From Eq. (12) one has

$$\begin{aligned} {x_4}= & {} ({Z_L}{C_{{DC}_2}})\left[ \dot{x}_3+{1 \over {{Z_L}{C_{{DC}_2}}}}{x_3}\right] {\Rightarrow } \nonumber \\ {x_4}= & {} ({Z_L}{C_{{DC}_2}})\left[ {\dot{y}_{f_2}}+{1 \over {{Z_L}{C_{{DC}_2}}}}{y_{f_2}}\right] {\Rightarrow } \nonumber \\ {x_4}= & {} {f_a}(y_f,\dot{y}_f) \end{aligned}$$

(18)

which means that state variable $x_4$ is a function of the flat output and of its derivatives. Moreover, from Eq. (14) one gets

$$\begin{aligned} \left( x_1^2+x_2^2\right)= & {} {4 \over {3L}}\left[ {y_{f_1}}-{{C_{{DC}_1}} \over 2}{x_4^2}\right] {\Rightarrow } \nonumber \\ \left( x_1^2+x_2^2\right)= & {} f_b(y_f,\dot{y}_f) \end{aligned}$$

(19)

Next, using Eq. (17) one has

$$\begin{aligned} x_1= & {} {2 \over {3{v_d}}}\left\{ {\dot{y}_{f_1}}+{{3R} \over 2}\left( x_1^2+x_2^2\right) +{{x_4^2} \over {Z_L}}-{{{x_3}{x_4}} \over {Z_L}}\right\} {\Rightarrow } \nonumber \\ x_1= & {} {2 \over {3{v_d}}}\left\{ {\dot{y}_{f_1}}+{{3R} \over 2}f_b(y_f,\dot{y}_f)+{{x_4^2} \over {Z_L}}-{{{y_{f_2}}{x_4}} \over {Z_L}}\right\} \end{aligned}$$

(20)

Using Eq. (18) in Eq. (20) one finally gets that state variable $x_1$ is a function of the flat output and its derivatives

$$\begin{aligned} x_1=f_c(y_f, \dot{y}_f) \end{aligned}$$

(21)

Moreover, from Eqs. (19) and (21) it holds $(x_1^2+x_2^2)=f_b(y_f,\dot{y}_f)$ and $x_1=f_c(y_f,\dot{y}_f)$. Thus by solving with respect to $x_2$ one gets

$$\begin{aligned} {x_2^2}= & {} f_b(y_f,\dot{y}_f)-f_c^2(y_f,\dot{y}_f)\, {\Rightarrow } \nonumber \\ x_2= & {} \sqrt{|f_b(y_f,\dot{y}_f)-f_c^2(y_f.\dot{y}_f)|}\, {\Rightarrow } \nonumber \\ x_2= & {} {f_d}(y_f,\dot{y}_f) \end{aligned}$$

(22)

which means that state variable $x_2$ is also a function of the flat output and of its derivatives. Next by solving Eq. (10) with respect to the control input $u_1$ and Eq. (11) with respect to the control input $u_2$ one obtains

$$\begin{aligned} u_1= & {} {{2L} \over {x_4}}\left\{ \dot{x}_1+{R \over L}x_1-{\omega }x_2-{v_d \over L}\right\} \end{aligned}$$

(23)

$$\begin{aligned} u_2= & {} {{2L} \over {x_4}}\left\{ \dot{x}_2+{\omega }{x_1}+{R \over L}{x_2}-{v_q \over L}\right\} \end{aligned}$$

(24)

Using Eqs. (21), (22 and (18) in Eq. (23) it can be concluded that

$$\begin{aligned} u_1=f_e(y_f,\dot{y}_f) \end{aligned}$$

(25)

Similarly, using Eqs. (21), (22 and (18) in Eq. (24) it can be concluded that

$$\begin{aligned} u_2=f_g(y_f,\dot{y}_f) \end{aligned}$$

(26)

Consequently, all state variables and the control inputs of the VSC-HVDC model can be written as differential functions of the flat output $y_f=[y_{f_1},y_{f_2}]^T$. Thus the VSC-HVDC system is a differentially flat one.

Flatness-Based Control of the VSC-HVDC System

Next, a flatness-based controller will be designed for the VSC-HVDC system. Using Eq. (16) and deriving $\dot{y}_{f_1}$ once more with respect to time one gets

$$\begin{aligned} {\ddot{y}_{f_1}}= & {} -{{3R} \over 2}(2{x_1}{\dot{x}_1}+2{x_2}\dot{x}_2)+3{{\dot{x}_1} \over 2}{v_d}-{2{x_4}{\dot{x}_4} \over {Z_L}} \nonumber \\&+{{{\dot{x}_3}{x_4}} \over Z_L}+{{{x_3}{\dot{x}_4}} \over {Z_L}}{\Rightarrow } \nonumber \\ {\ddot{y}_{f_1}}= & {} \left( -3R{x_1}+{{3{v_d}} \over 2}\right) \left[ -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L}-{x_4 \over {2L}}u_1\right] \nonumber \\&-3R{x_2}\left[ -{\omega }{x_1}+{R \over L}{x_2}+{v_q \over L}-{x_4 \over {2L}}u_2\right] \nonumber \\&+{x_4 \over Z_L}\left( {x_4 \over {{Z_L}{C_{{DC}_2}}}}-{x_3 \over {{Z_L}{C_{{DC}_2}}}}\right) \nonumber \\&+\left( -{{2{x+4}} \over {Z_L}}+{x_3 \over Z_L}\right) \nonumber \\&\left[ -{x_4 \over {{Z_L}{C_{{DC}_1}}}}+{x_3 \over {{Z_L}{C_{{DC}_1}}}}+{{3{x_1}} \over {4{C_{{DC}_1}}}}u_1 +{{3{x_2}} \over {4{C_{{DC}_1}}}}u_2\right] \nonumber \\ \end{aligned}$$

(27)

which after intermediate computations gives

$$\begin{aligned} {\ddot{y}_{f_1}}= & {} \left[ {{3{R^2}} \over L}\left( x_1^2+x_2^2\right) -{{6{R}{x_1}{v_d}} \over L}+{{3{\omega }{v_d}{x_2}} \over 2}+{{3{v_d^2}} \over {4}} \right. \nonumber \\&+\,{{2{x_4^2}} \over {{Z_L^2}{C_{{DC}_1}}}}-{{2{x_1}{x_4}} \over {{Z_L^2}{C_{{DC}_1}}}}+{{x_4^2} \over {{Z_L^2}{C_{{DC}_2}}}}-{{{x_3}{x_4}} \over {{Z_L^2}{C_{{DC}_2}}}} \nonumber \\&\left. -\,{{{x_3}{x_4}} \over {{Z_L^2}{C_{{DC}_1}}}}+-{{{x_3^2}} \over {{Z_L^2}{C_{{DC}_1}}}}\right] \nonumber \\&+ \left[ {{3R{x_1}{x_4}} \over {2L}}-{{3{v_d}{x_4}} \over {4L}}-{6{{x_1}{x_4}} \over {4{Z_L}C_{{DC}_1}}}+{{3{x_1}{x_3}} \over {4{Z_L}{C_{{DC}_1}}}}\right] u_1 \nonumber \\&+\left[ {{3R{x_2}{x_4}} \over {2L}}-{{6{x_2}{x_4}} \over {4{Z_L}{C_{{DC}_1}}}}+{{3{x_2}{x_3}} \over {4{Z_L}{C_{{DC}_1}}}}\right] u_2 \end{aligned}$$

(28)

Equation (28) can be also written in the concise form

$$\begin{aligned} {\ddot{y}_{f_1}}={L_f^2}{h_1}(x)+{L_{g_1}}{L_f}{h_1(x)}u_1+{L_{g_2}}{L_f}{h_1(x)}u_2 \end{aligned}$$

(29)

Functions ${L_f^2}{h_1}(x)$, ${L_{g_1}}{L_f}{h_1(x)}$ and ${L_{g_2}}{L_f}{h_1(x)}$ are defined in detail in Eqs. (69), (70) and (72) respectively, which have been provided in Appendix. Additionally, from the second component of the flat outputs vector given in Eq. (15) one gets

$$\begin{aligned} y_{f_2}= & {} x_2\, {\Rightarrow } \,\dot{y}_{f_3}=\dot{x}_3\, {\Rightarrow }\, \nonumber \\ {\dot{y}_{f_2}}= & {} {1 \over {{Z_L}{C_{{DC}_2}}}}{x_4}-{1 \over {{Z_L}{C_{{DC}_2}}}}{x_3} \end{aligned}$$

(30)

By deriving once more the above relation with respect to time one gets

$$\begin{aligned} {\ddot{y}_{f_2}}={1 \over {{Z_L}{C_{{DC}_2}}}}\dot{x}_4-{1 \over {{Z_L}{C_{{DC}_2}}}}\dot{x}_3 \end{aligned}$$

(31)

Next, by substituting Eqs. (12) and (13) into Eq. (31) one arrives at

$$\begin{aligned} {\ddot{y}_{f_2}}= & {} {1 \over {{Z_L}{C_{{DC}_2}}}}\left[ -{1 \over {{Z_L}{C_{{DC}_1}}}}x_4+{1 \over {{Z_L}{C_{{DC}_1}}}}x_3 \right. \nonumber \\&\left. +{{3{x_1}} \over {4{C_{{DC}_1}}}}u_1+{{3{x_2}} \over {4{C_{{DC}_1}}}}u_2\right] \nonumber \\&-{1 \over {{Z_L}{C_{{DC}_2}}}}\left[ {1 \over {{Z_L}{C_{{DC}_2}}}}x_4-{1 \over {{Z_L}{C_{{DC}_2}}}}x_3\right] \end{aligned}$$

(32)

which after intermediate operations gives

$$\begin{aligned} \ddot{y_{f_2}}= & {} \left[ -{x_4 \over {{Z_L^2}{C_{{DC}_1}}{C_{{DC}_2}}}}+{x_3 \over {{Z_L^2}{C_{{DC}_1}}{C_{{DC}_2}}}}-{x_4 \over {{Z_L^2}{C_{{DC}_2}}^2}} \right. \nonumber \\&\left. +\,{x_3 \over {{Z_L^2}{C_{{DC}_2}}^2}}\right] \nonumber \\&+{{3{x_1}} \over {{4{Z_L}{C_{{DC}_1}}{C_{{DC}_2}}}}}u_1+{{3{x_2}} \over {{4{Z_L}{C_{{DC}_1}}{C_{{DC}_2}}}}}u_2 \end{aligned}$$

(33)

which can be also written in the more concise form

$$\begin{aligned} {\ddot{y}_{f_2}}={L_f^2}{h_2}(x)+{L_{g_1}}{L_f}{h_2(x)}u_1+{L_{g_2}}{L_f}{h_2(x)}u_2 \end{aligned}$$

(34)

Functions ${L_f^2}{h_2}(x)$, ${L_{g_1}}{L_f}{h_2(x)}$ and ${L_{g_2}}{L_f}{h_2(x)}$ are defined in detail in Eqs. (74), (75) and (76) respectively, which have been provided in Appendix. Next, Eqs. (29) and (28) are written in matrix form

$$\begin{aligned} \begin{pmatrix} {\ddot{y}_{f_1}}\\ {\ddot{y}_{f_1}} \end{pmatrix}= & {} \begin{pmatrix} {L_f^2}h_1(x)\\ {L_f^2}h_2(x) \end{pmatrix}+ \begin{pmatrix} {L_{g_1}}{L_f}h_1(x) &{} {L_{g_2}}{L_f}h_1(x) \\ {L_{g_1}}{L_f}h_2(x) &{} {L_{g_2}}{L_f}h_2(x) \end{pmatrix} \nonumber \\&\begin{pmatrix} u_1 \\ u_2 \end{pmatrix} \end{aligned}$$

(35)

By defining the new control inputs $v_1={L_f^2}{h_1}(x)+{L_{g_1}}{L_f}{h_1(x)}u_1+{L_{g_2}}{L_f}{h_1(x)}u_2$ and $v_2={L_f^2}{h_2}(x)+{L_{g_1}}{L_f}{h_2(x)}u_1+{L_{g_2}}{L_f}{h_2(x)}u_2$ one arrives at the linearized and decoupled description of the dynamics of the VSC-HVDC model

$$\begin{aligned} \ddot{y}_{f_1}= & {} v_1 \nonumber \\ \ddot{y}_{f_2}= & {} v_2 \end{aligned}$$

(36)

Moreover, by defining the following vectors and matrices

$$\begin{aligned} \tilde{y}_f= & {} \begin{pmatrix} y_{f_1} \\ y_{f_2} \end{pmatrix} \quad \tilde{f}= \begin{pmatrix} {L_f^2}h_1(x) \\ {L_f^2}h_2(x) \end{pmatrix} \nonumber \\ \tilde{M}= & {} \begin{pmatrix} {L_{g_1}}{L_f}h_1(x) &{} {L_{g_2}}{L_f}h_1(x) \\ {L_{g_1}}{L_f}h_2(x) &{} {L_{g_2}}{L_f}h_2(x) \end{pmatrix} \quad \tilde{v} = \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} \end{aligned}$$

(37)

one obtains the following matrix-form description of the system’s dynamics

$$\begin{aligned} \ddot{\tilde{y}}_f=\tilde{f}+\tilde{M}\tilde{u}\, { \Rightarrow }\, \tilde{u}={\tilde{M}^{-1}}[\tilde{v}-f] \end{aligned}$$

(38)

where $\tilde{u}$ is the control input that is actually exerted on the VSC-HVDC system, while the transformed control input $\tilde{v}$ is given by

$$\begin{aligned} \tilde{v}=\ddot{\tilde{y}}_f^d-{K_d}\left( \dot{\tilde{y}}_f-\dot{\tilde{y}}_f^d\right) -{K_p}\left( \tilde{y}_f-\tilde{y}_f^d\right) \end{aligned}$$

(39)

For the linearized model of the VSC-HVDC dynamics one can also obtain a description in the linear canonical (Brunovsky) form. The following state variables are defined: $z_1=y_{f_1}$, $z_2=\dot{y}_{f_1}$, $z_3=y_{f_2}$ and $z_4=\dot{y}_{f_2}$. This results in the following state-space description

$$\begin{aligned} \dot{z}_1= & {} z_2 \nonumber \\ \dot{z}_2= & {} {L_f^2}{h_1}(x)+{L_{g_1}}{L_f}{h_1}(x)u_1+{L_{g_2}}{L_f}{h_1}(x)u_2 \nonumber \\ \dot{z}_3= & {} z_4 \nonumber \\ \dot{z}_4= & {} {L_f^2}{h_2}(x)+{L_{g_1}}{L_f}{h_2}(x)u_1+{L_{g_2}}{L_f}{h_2}(x)u_2 \end{aligned}$$

(40)

The previous state-space description results also in the linear canonical (Brunovsky) form:

$$\begin{aligned} \begin{pmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \dot{z}_3 \\ \dot{z}_4 \end{pmatrix}= \begin{pmatrix} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \end{pmatrix}+ \begin{pmatrix} 0 &{} 0 \\ 1 &{} 0 \\ 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} \end{aligned}$$

(41)

and since the measurable variables for this system are taken to be $z_1=y_{f_1}$ and $z_3=y_{f_2}$ the associated measurement equation becomes

$$\begin{aligned} \begin{pmatrix} z_1^{m} \\ z_3^{m} \end{pmatrix}= \begin{pmatrix} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \end{pmatrix} \end{aligned}$$

(42)

By defining the new control inputs

$$\begin{aligned} v_1= & {} {L_f^2}h_1(x)+{L_{g_1}}{L_f}{h_1(x)}u_1+{L_{g_2}}{L_f}{h_1(x)}u_2 \nonumber \\ v_2= & {} {L_f^2}h_1(x)+{L_{g_1}}{L_f}{h_1(x)}u_1+{L_{g_2}}{L_f}{h_1(x)}u_2 \end{aligned}$$

(43)

the VSC-HVDC system is written in the chain of integrators form

$$\begin{aligned} \ddot{z}_1= & {} v_1 \nonumber \\ \ddot{z}_1= & {} v_2 \end{aligned}$$

(44)

Moreover, by defining the feedback control inputs

$$\begin{aligned} v_1= & {} \ddot{z}_1^d-k_d^1\left( \dot{z}_1-\dot{z}_1^d\right) -k_p^1\left( z_1-z_1^d\right) \nonumber \\ v_2= & {} \ddot{z}_2^d-k_d^2\left( \dot{z}_2-\dot{z}_2^d\right) -k_p^2\left( z_2-z_2^d\right) \end{aligned}$$

(45)

The tracking error dynamics for the closed loop becomes $\ddot{e}_1+{k_d^1}\dot{e}_1+{k_p^1}e_1=0$ and $\ddot{e}_2+{k_d^2}\dot{e}_2+{k_p^2}e_2=0$. By selecting the feedback gains $k_p^1$, $k_d^1$ and $k_p^2$, $k_d^2$ such that the associated characteristic polynomials to be Hurwitz ones, one has the tracking error dynamics $lim_{t{\rightarrow }\infty }e_1(t)=0$ and $lim_{t{\rightarrow }\infty }e_2(t)=0$. It is possible to experiment with different values of the gains $k_p^1$, $k_d^1$ and $k_p^2$, $k_d^2$ within the ranges that assure the stability of the control loop, so as to achieve certain performance indexes (such as overshoot or settling time).

To compute the control input that is actually applied to the VSC-HVDC model one proceeds as follows: Eqs. (43) and (44) are rewritten in the matrix form

$$\begin{aligned} \ddot{\tilde{y}}_f=\tilde{f}+\tilde{M}\tilde{u} \end{aligned}$$

(46)

where

$$\begin{aligned} \tilde{y}_f= & {} \begin{pmatrix} y_{f_1} \\ y_{f_2} \end{pmatrix} \quad \tilde{f}= \begin{pmatrix} {L_f^2}h_1(x) \\ {L_f^2}h_2(x) \end{pmatrix} \nonumber \\ \tilde{M}= & {} \begin{pmatrix} {L_{g_1}}{L_f}h_1(x) &{} {L_{g_2}}{L_f}h_1(x) \\ {L_{g_1}}{L_f}h_2(x) &{} {L_{g_2}}{L_f}h_2(x) \end{pmatrix} \quad \tilde{v}= \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} \end{aligned}$$

(47)

Using the above, the control input that should be exerted on the VSC-HVDC model is for eliminating the tracking error is

$$\begin{aligned} \tilde{u}=\tilde{M}^{-1}[\tilde{v}-\tilde{f}] \end{aligned}$$

(48)

Compensation of Disturbances Using the Derivative-Free Nonlinear Kalman Filter

Next, it is assumed that the VSC-HVDC model is subjected to additive input disturbances, that is

$$\begin{aligned} \ddot{y}_{f_1}= & {} {L_f^2}{h_1}(x)+{L_{g_1}}{L_f}h_1(x)u_1+{L_{g_2}}{L_f}h_1(x)u_2+\tilde{d}_1 \nonumber \\ \ddot{y}_{f_2}= & {} {L_f^2}{h_2}(x)+{L_{g_1}}{L_f}h_2(x)u_1 \nonumber \\&+{L_{g_2}}{L_f}h_2(x)u_2+\tilde{d}_2 \end{aligned}$$

(49)

or equivalently

$$\begin{aligned} \ddot{y}_{f_1}= & {} v_1+\tilde{d}_1 \nonumber \\ \ddot{y}_{f_2}= & {} v_2+\tilde{d}_2 \end{aligned}$$

(50)

Moreover, it is considered that the disturbance inputs can be described by their n-th order derivative. This is because each function can be described either by its mathematical equations or equivalently by its derivatives and the associated initial conditions. However, in the studied case there will be finally no use of initial conditions because the disturbance function will be estimated by the Kalman Filter which is not dependent on the processing of initial conditions. Without loss of generality it is assumed that the additive disturbance terms $\tilde{d}_i, \ i=1,2$ are described by the signal’s second order derivative, that is

$$\begin{aligned} \ddot{\tilde{d}}_1=f_{d_1} \qquad \ddot{\tilde{d}}_2=f_{d_2} \end{aligned}$$

(51)

Then by defining the new state variables $z_1=y_{f_1}$, $z_2=\dot{y}_{f_1}$, $z_3=y_{f_2}$, $z_4=\dot{y}_{f_2}$, $z_5=\tilde{d}_1$, $z_6=\dot{\tilde{d}}_1$, $z_7=\tilde{d}_2$, $z_8=z_6=\dot{\tilde{d}}_2$ one obtains the following extended state-space description of the system

$$\begin{aligned} \begin{pmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \dot{z}_3 \\ \dot{z}_4 \\ \dot{z}_5 \\ \dot{z}_6 \\ \dot{z}_7 \\ \dot{z}_8 \end{pmatrix}= \begin{pmatrix} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ z_5 \\ z_6 \\ z_7 \\ z_8 \end{pmatrix}+ \begin{pmatrix} 0 &{} 0 \\ 1 &{} 0 \\ 0 &{} 0 \\ 0 &{} 1 \\ 0 &{} 0 \\ 0 &{} 0 \\ 0 &{} 0 \\ 0 &{} 0 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} \end{aligned}$$

(52)

while by denoting the extended state vector $z_e=[z_1,z_2,z_3,z_4, z_5,z_6,z_7,z_8]^T$, the measurement equation for the extended system becomes

$$\begin{aligned} \begin{pmatrix} z_1^{m} \\ z_3^{m} \end{pmatrix}= \begin{pmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} z_e \end{aligned}$$

(53)

According to the above the extended state-space model of the VSC-HVDC system is written in the linear matrix from

$$\begin{aligned} \dot{z}_e= & {} Az_e+Bv \nonumber \\ z_e^{m}= & {} Cz_e \end{aligned}$$

(54)

For the extended state-space model of the VSC-HVDC system it is possible to perform simultaneously states and disturbances estimation using the Derivative-free nonlinear Kalman Filter. The latter consists of the Kalman Filter recursion on the linearized equivalent model of the VSC-HVDC system and of an inverse transformation, based on the results of “Differential flatness of the VSC-HVDC system” section which allows to obtain estimates of the state variables of the initial nonlinear model described in Eqs. (10)– (13). The filter’s algorithm uses the discrete time equivalents of the previously defined matrices A, B and C, which are denoted as $A_d$, $B_d$ and $C_d$ respectively. The proposed filtering method consists of a measurement update and a time update stage [32–34]:

Measurement update

$$\begin{aligned} K(k)= & {} {P^{-}}(k){C_d^T}[{C_d}P(k){C_d^T}+R(k)]^{-1} \nonumber \\ \hat{z}_e(k)= & {} \hat{z}_e^{-}(k)+K(k)[z_e^m(k)-{C_d}\hat{z}_e^{-}(k)] \nonumber \\ P(k)= & {} P^{-}(k)-K(k){C_d}P^{-}(k) \end{aligned}$$

(55)

Time update

$$\begin{aligned} P^{-}(k+1)= & {} {A_d}P(k){A_d^T}+Q(k) \nonumber \\ \hat{z}^{-}(k+1)= & {} {A_d}\hat{z}(k)+{B_d}v(k) \end{aligned}$$

(56)

where Q(k) and R(k) stand for process and measurement noise covariance matrices. After estimating the disturbance inputs , that is $\hat{z}_5=\hat{\tilde{d}}_1$ and $\hat{z}_7=\hat{\tilde{d}}_2$ the control input that is applied to VSC-HVDC system is modified as follows:

$$\begin{aligned} v_1^{*}= & {} v_1-\hat{z}_5 \nonumber \\ v_2^{*}= & {} v_2-\hat{z}_7 \end{aligned}$$

(57)

Thus, with respect to Eq. (50), the closed-loop dynamics becomes

$$\begin{aligned} \ddot{y}_{f_1}= & {} v_1-\hat{z}_5+\tilde{d}_1 \nonumber \\ \ddot{y}_{f_2}= & {} v_2-\hat{z}_7+\tilde{d}_2 \end{aligned}$$

(58)

Remark 3

Control based on differential flatness theory implements actually a global linearization method. Through a change of variables (diffeomorphism) the initial nonlinear state-space model of the system is transformed into an equivalent linear one. Unlike approximate linearization methods this new description is not only valid round local linearization points but can be extended throughout the state-space of dynamical system. Besides, unlike local linearization, such a global linearization method does not introduce any numerical errors and consequently the associated feedback control and filtering schemes are more robust.

Remark 4

The outputs defined in Eq. (6) are the input–output linearizing outputs of the VSC-HVDC model. The flat outputs of the model are also those described by Eq. (6). Through successive derivation of these outputs one arrives at the input–output linearized model of Eqs. (35) and (36). There is not a standard procedure for selecting the linearizing outputs of a system, as there is no standard procedure for selecting a Lyapunov function. However, once such outputs are found the system can be transformed into the linear canonical form, where both the solution of the control and of the filtering (estimation) problem become easier.

Simulation Tests

The performance of the control loop for the VSC-HVDC system was tested through simulation experiments. The associated results are presented in Figs. 3, 4, 5, 6 and 7. Actually, in Figs. 3a, 4a, 5a, 6a and 7a the convergence of the real state variables of the system $x_i, \ i=1,\cdots ,4$ to their reference setpoints is presented. Additionally, in Figs. 3b, 4b, 5b, 6b and 7b the estimated disturbance inputs of the VSC-HVDC model are plotted. Moreover, diagrams of the variation of the system’s control inputs are provided. In the aforementioned diagrams, the per unit (p.u.) measurement system has been used. It can be observed that through the proposed control scheme, the state variables of the VSC-HVDC system converge fast to the reference setpoints. Furthermore, the performance of the control loop is improved against external disturbances by including in it the Derivative-free nonlinear Kalman Filter. By functioning as a disturbance observer the filter enables to estimate in real-time additive disturbance inputs that affect the VSC-HVDC model and subsequently to compensate for them.

Fig. 3

a Convergence of the state vector elements $x_i, \ i=1,\ldots ,4$ to the associated reference setpoint No 1 for the initial nonlinear model of the VSC-HVDC system, b estimation of disturbance input $\tilde{d}$ on the VSC-HVDC model and variation of control inputs $u_i, \ i=1,2$

Fig. 4

a Convergence of the state vector elements $x_i, \ i=1,\ldots ,4$ to the associated reference setpoint No 2 for the initial nonlinear model of the VSC-HVDC system, b estimation of disturbance input $\tilde{d}$ on the VSC-HVDC model and variation of control inputs $u_i, \ i=1,2$

Fig. 5

a Convergence of the state vector elements $x_i, \ i=1,\ldots ,4$ to the associated reference setpoint No 3 for the initial nonlinear model of the VSC-HVDC system, b estimation of disturbance input $\tilde{d}$ on the VSC-HVDC model and variation of control inputs $u_i, \ i=1,2$

Fig. 6

a Convergence of the state vector elements $x_i, \ i=1,\ldots ,4$ to the associated reference setpoint No 4 for the initial nonlinear model of the VSC-HVDC system, b estimation of disturbance input $\tilde{d}$ on the VSC-HVDC model and variation of control inputs $u_i, \ i=1,2$

Fig. 7

a Convergence of the state vector elements $x_i, \ i=1,\ldots ,4$ to the associated reference setpoint No 5 for the initial nonlinear model of the VSC-HVDC system, b estimation of disturbance input $\tilde{d}$ on the VSC-HVDC model and variation of control inputs $u_i, \ i=1,2$

Remark 5

The vector control approach which is implemented through PID controllers is unsuitable, because it is not of proven stability while its robustness cannot be assured. Taking into account that the dynamic model of the VSC-HVDC system is characterized by parametric uncertainties and external perturbations and that it functions under varying conditions, the performance of vector control becomes questionable and consequently such a controller is not recommended for the VSC-HVDC model.

Remark 6

Comparing to nonlinear feedback control approaches which are based on approximate linearization of the VSC-HVDC system (round local operating points), the proposed flatness-based control method is assessed as follows: (i) it performs global linearization which is valid through the entire state-space of the systems dynamic model. This is done with the use of state variables’ transformations (diffeomorphisms), (ii) it does not introduce any modelling error. On the contrary, approximate linearization methods coming from the application of Taylor series expansion induce cumulative modelling errors which affect the robustness of the control loop, (iii) the proposed flatness-based control method does not require the computation of Jacobian matrices, and thus in the case of electric power systems of high dimensionality a cumbersome computational procedure is avoided, (iv) unlike control based on approximate linearization, the proposed flatness-based control does not have to compensate for the effects of the cumulative linearization error and thus the robustness of the control loop is improved, (v) unlike control based on approximate linearization, the proposed flatness-based control does not require the solution of Riccati equations, which means that for systems of high dimensionality a cumbersome computational procedure is again avoided.

Conclusions

A new method of nonlinear control of high voltage direct current (HVDC) links in the electric power system has been developed using differential flatness theory. It has been proven that the model of the joint dynamics between the AC to DC voltage source converter and the DC transmission line that constitute the VSC-HVDC link is a differentially flat one. This means that all state variables and the control inputs of this model (IGBT currents at the converter) can be finally written as differential functions of an algebraic variable which is the flat output. The differential flatness property of the VSC-HVDC model enables its transformation to the linear canonical (Brunovsky) form. This is a global linearization approach that remains valid for the complete state space of the VSC-HVDC system and which does not introduce any numerical errors or approximations. For the latter description of the system’s dynamics the design of a state feedback controller becomes easy.

Another problem that had to be dealt with in the design of the feedback control loop was that of estimation and compensation of the disturbances that affected the VSC-HVDC model. To this end a disturbance observer has been included in the control scheme. The observer was based on the Derivative-free nonlinear Kalman Filter, that is on the Kalman Filter recursion that was applied on the linear equivalent of the VSC-HVDC model. Moreover, the filter comprised an inverse transformation that was based on differential flatness theory and which enabled to obtain estimates for the state variables of the initial nonlinear VSC-HVDC model. The efficiency of the state estimation-based control scheme for VSC-HVDC links was tested through simulation experiments. The proposed method is a reliable solution to this type of control problems appearing in the smart grid and in the connection of renewable energy sources with the electricity network.

Appendix

Lie Algebra-Based Linearization of the VSC-HVDC Dynamics

First, it will be shown that input–output linearization of the VSC-HVDC system can be succeeded with the use of Lie algebra methods. Using Lie derivatives the following state variables are defined $z_1=h_1(x)$, $z_2={L_f}{h_1}(x)$, $z_3=h_2(x)$ and $z_4={L_f}{h_2}(x)$. It holds that:

$$\begin{aligned} z_2= & {} {L_f}{h_1}(x){\Rightarrow }{z_2}={{{\partial }{h_1}} \over {{\partial }x_1}}f_1+{{{\partial }{h_1}} \over {{\partial }x_2}}f_2+{{{\partial }{h_1}} \over {{\partial }x_3}}f_3 \nonumber \\&+{{{\partial }{h_1}} \over {{\partial }x_4}}f_4 \end{aligned}$$

(59)

Thus, one gets

$$\begin{aligned} {L_f}{h_1}(x)= & {} {{3L} \over 2}{x_1}\left[ -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L}\right] \nonumber \\&+{{3L} \over 2}{x_2} \left[ -{\omega }{x_1}-{R \over L}{x_2}+{v_q \over L}\right] \nonumber \\&+ 0\left[ {1 \over {{Z_L}C_{{DC}_2}}}{x_4}-{1 \over {{Z_L}C_{{DC}_2}}}{x_3}\right] \nonumber \\&+ {C_{{DC}_1}}{x_4}\left[ -{1 \over {{Z_L}C_{{DC}_1}}}{x_4}+{1 \over {{Z_L}C_{{DC}_1}}}{x_3}\right] \end{aligned}$$

(60)

which after intermediate computations gives

$$\begin{aligned} {L_f}{h_1}(x)=-{{3R} \over 2}\left( x_1^2+x_2^2\right) +{{3{v_d}} \over 2}{x_1}-{{x_4^2} \over {Z_L}}+{{{x_3}{x_4}} \over {Z_L}} \end{aligned}$$

(61)

Moreover, it holds that

$$\begin{aligned} {L_{g_1}}{h_1}(x)= & {} {{{\partial }{h_1}} \over {{\partial }{x_1}}}g_{11}+{{{\partial }{h_1}} \over {{\partial }{x_2}}}g_{12}+ {{{\partial }{h_1}} \over {{\partial }{x_3}}}g_{13}+{{{\partial }{h_1}} \over {{\partial }{x_4}}}g_{14}{\Rightarrow } \nonumber \\ {L_{g_1}}{h_1}(x)= & {} {{3L} \over 2}{x_1}{\cdot }\left( -{{x_4} \over {2L}}\right) +{{3L} \over 2}{x_2}{\cdot }0+0{\cdot }0 \nonumber \\&+({C_{{DC}_1}}{x_4}){\cdot }\left( {{3{x_1}} \over {4{C_{{DC}_1}}}}\right) {\Rightarrow } \nonumber \\ {L_{g_1}}{h_1}(x)= & {} -{{3{{x_1}{x_4}}} \over 4}+{{3{{x_1}{x_4}}} \over 4}{\Rightarrow }{L_{g_1}}{h_1}(x)=0 \end{aligned}$$

(62)

Similarly, one obtains

$$\begin{aligned} {L_{g_2}}{h_1}(x)= & {} {{{\partial }{h_1}} \over {{\partial }{x_1}}}g_{21}+{{{\partial }{h_1}} \over {{\partial }{x_2}}}g_{22}+ {{{\partial }{h_1}} \over {{\partial }{x_3}}}g_{23}+{{{\partial }{h_1}} \over {{\partial }{x_4}}}g_{24}{\Rightarrow } \nonumber \\ {L_{g_2}}{h_1}(x)= & {} {{3L} \over 2}{x_1}{\cdot }0+{{3L} \over 2}{x_2}{\cdot }\left( -{{x_4} \over {2L}}\right) +0{\cdot }0 \nonumber \\&+\,{C_{{DC}_1}}{x_4}\left( {{3{x_2}} \over {4C_{{DC}_1}}}\right) {\Rightarrow } \nonumber \\ {L_{g_2}}{h_1}(x)= & {} -{{3{{x_2}{x_4}}} \over 4}+{{3{{x_2}{x_4}}} \over 4}\,{\Rightarrow }\;{L_{g_2}}{h_1}(x)=0 \end{aligned}$$

(63)

Next, the Lie derivatives of the second flat output are computed:

$$\begin{aligned} z_4= & {} {L_f}{h_2}(x){\Rightarrow }z_4={{{\partial }{h_2}} \over {{\partial }{x_1}}}f_1+{{{\partial }{h_2}} \over {{\partial }{x_2}}}f_2+{{{\partial }{h_2}} \over {{\partial }{x_3}}}f_3 \nonumber \\&+{{{\partial }{h_2}} \over {{\partial }{x_4}}}f_4 \end{aligned}$$

(64)

which gives

$$\begin{aligned} {L_f}{h_2}(x)= & {} 0{\cdot }f_1+0{\cdot }f_2+1{\cdot }{f_3}+0{\cdot }f_4{\Rightarrow } \nonumber \\ {L_f}{h_2}(x)= & {} {1 \over {Z_L}{C_{{DC}_2}}}{x_4}-{1 \over {Z_L}{C_{{DC}_2}}}{x_3} \end{aligned}$$

(65)

and in a similar manner one gets

$$\begin{aligned} {{L_{g_1}}}h_2(x)= & {} {{{\partial }{h_2}} \over {{\partial }{x_1}}}g_{11}+{{{\partial }{h_2}} \over {{\partial }{x_2}}}g_{12}+{{{\partial }{h_2}} \over {{\partial }{x_3}}}g_{13}+{{{\partial }{h_2}} \over {{\partial }{x_4}}}g_{14}\;{\Rightarrow } \nonumber \\ {{L_{g_1}}}h_2(x)= & {} 0{\cdot }g_{11}+0{\cdot }g_{12}+1{\cdot }g_{13}+0{\cdot }g_{14}{\Rightarrow } \nonumber \\ {{L_{g_1}}}h_2(x)= & {} 0 \end{aligned}$$

(66)

while it also holds

$$\begin{aligned} {{L_{g_2}}}h_2(x)= & {} {{{\partial }{h_2}} \over {{\partial }{x_1}}}g_{21}+{{{\partial }{h_2}} \over {{\partial }{x_2}}}g_{22}+{{{\partial }{h_2}} \over {{\partial }{x_3}}}g_{23}+{{{\partial }{h_2}} \over {{\partial }{x_4}}}g_{24}{\Rightarrow } \nonumber \\ {{L_{g_2}}}h_2(x)= & {} 0{\cdot }g_{21}+0{\cdot }g_{22}+1{\cdot }g_{23}+0{\cdot }g_{24}{\Rightarrow } \nonumber \\ {{L_{g_2}}}h_2(x)= & {} 0 \end{aligned}$$

(67)

In the following, higher order Lie derivatives of the system are computed:

$$\begin{aligned} {L_f^2}h_1(x)= & {} \left( -3R{x_1}+{{3{v_d}} \over 2}\right) \left[ -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L}\right] \nonumber \\&-3R{x_2}\left[ -{\omega }{x_1}-{R \over L}{x_2}+{v_q \over L}\right] \nonumber \\&+{x_4 \over Z_L}\left[ {1 \over {{Z_L}{C_{{DC}_2}}}}{x_4}-{1 \over {{Z_L}{C_{{DC}_2}}}}{x_3}\right] \nonumber \\&\left( -{{2{x_4}} \over {Z_L}}+{x_3 \over Z_L}\right) \left[ -{1 \over {{Z_L}{C_{{DC}_1}}}}{x_4} \right. \nonumber \\&\left. +{1 \over {{Z_L}{C_{{DC}_1}}}}{x_3}\right] \end{aligned}$$

(68)

After performing intermediate computations, the previous relation gives

$$\begin{aligned} {L_f^2}{h_1}(x)= & {} {{3{R^2}} \over L}\left( x_1^2+x_2^2\right) -{{6{R}{x_1}{v_d}} \over L}+{{3{\omega }{v_d}{x_2}} \over 2}+{{3{v_d^2}} \over {4}} \nonumber \\&+{{2{x_4^2}} \over {{Z_L^2}{C_{{DC}_1}}}}-{{2{x_1}{x_4}} \over {{Z_L^2}{C_{{DC}_1}}}}+{{x_4^2} \over {{Z_L^2}{C_{{DC}_2}}}} \nonumber \\&-{{{x_3}{x_4}} \over {{Z_L^2}{C_{{DC}_2}}}}-{{{x_3}{x_4}} \over {{Z_L^2}{C_{{DC}_1}}}}+-{{{x_3^2}} \over {{Z_L^2}{C_{{DC}_1}}}} \end{aligned}$$

(69)

In a similar manner one computes:

$$\begin{aligned} \quad {L_{g_1}}{L_f}{h_1}(x)= & {} {L_{g_1}}{z_2}{\Rightarrow }{L_{g_1}}{L_f}{h_1}(x)\nonumber \\= & {} {{{\partial }{z_2}} \over {{\partial }{x_1}}}g_{11}+{{{\partial }{z_2}} \over {{\partial }{x_2}}}g_{12} \nonumber \\&+{{{\partial }{z_2}} \over {{\partial }{x_3}}}g_{13}+{{{\partial }{z_2}} \over {{\partial }{x_4}}}g_{14}{\Rightarrow } \nonumber \\ {L_{g_1}}{L_f}{h_1}(x)= & {} \left( -3R{x_1}+{{3{v_d}} \over 2}\right) {\cdot }\left( -{x_4 \over {2L}}\right) \nonumber \\&+\,(-3R{x_2}{\cdot }0)+{x_4 \over Z_L}{\cdot }0 \nonumber \\&+\,\left( -{{2{x_4}} \over Z_L}+{x_3 \over Z_L}\right) {{3{x_1}} \over {4C_{{DC}_1}}}{\Rightarrow } \nonumber \\ {L_{g_1}}{L_f}{h_1}(x)= & {} {{{3R}{x_1}{x_4}} \over {2L}}-{{3{v_d}{x_4}} \over {4L}} \nonumber \\&-{{6{x_1}{x_4}} \over {{4}{Z_L}{C_{{DC}_1}}}} +{{3{x_1}{x_3}} \over {4{Z_L}{C_{{DC}_1}}}} \end{aligned}$$

(70)

while it also holds

$$\begin{aligned} {L_{g_2}}{L_f}{h_1}(x)= & {} {L_{g_2}}{z_2}{\Rightarrow }{L_{g_2}}{L_f}{h_2}(x)={{{\partial }{z_2}} \over {{\partial }{x_1}}}g_{21}+{{{\partial }{z_2}} \over {{\partial }{x_2}}}g_{22} \nonumber \\&+{{{\partial }{z_2}} \over {{\partial }{x_3}}}g_{23}+{{{\partial }{z_2}} \over {{\partial }{x_4}}}g_{24}{\Rightarrow } \nonumber \\ {L_{g_2}}{L_f}{h_1}(x)= & {} \left( -3R{x_1}+{{3{v_d}} \over 2}\right) {\cdot }0-(3R{x_2})\cdot \left( -{{x_4} \over {2L}}\right) \nonumber \\&+{x_4 \over Z_L}{\cdot }0+\left( -{{2{x_4}} \over Z_L}+{x_3 \over Z_L}\right) {\cdot }\left( {{3{x_2}} \over {4C_{{DC}_1}}}\right) \nonumber \\ \end{aligned}$$

(71)

which finally gives

$$\begin{aligned} {L_{g_2}}{L_f}{h_1}(x)={{3R{x_2}{x_4}} \over {2L}}-{{6{x_2}{x_4}} \over {4{Z_L}{C_{{DC}_1}}}}+{{3{x_2}{x_3}} \over {4{Z_L}{C_{{DC}_1}}}} \end{aligned}$$

(72)

Following the same approach one computes

$$\begin{aligned} {L_f^2}{h_2}(x)= & {} {L_f}{z_4}{\Rightarrow }{L_f^2}{h_2}(x)={{{\partial }{z_4}} \over {{\partial }{x_1}}}f_1+{{{\partial }{z_4}} \over {{\partial }{x_2}}}f_2+{{{\partial }{z_4}} \over {{\partial }{x_3}}}f_3 \nonumber \\&+{{{\partial }{z_4}} \over {{\partial }{x_4}}}f_4{\Rightarrow } \nonumber \\ {L_f^2}{h_2}(x)= & {} 0{\cdot }f_1+0{\cdot }f_2\nonumber \\&-{1 \over {{Z_L}{C_{{DC}_2}}}}\left[ {1 \over {{Z_L}{C_{{DC}_2}}}}{x_4}-{1 \over {{Z_L}{C_{{DC}_2}}}}{x_3}\right] \nonumber \\&+{1 \over {{Z_L}{C_{{DC}_2}}}}\left[ -{1 \over {{Z_L}{C_{{DC}_1}}}}{x_4}+{1 \over {{Z_L}{C_{{DC}_1}}}}{x_3}\right] \nonumber \\ \end{aligned}$$

(73)

which after intermediate operations gives

$$\begin{aligned} {L_f^2}{h_2}(x)= & {} -{x_4 \over {{Z_L^2}{C_{{DC}_2}^2}}}+{x_3 \over {{Z_L^2}{C_{{DC}_2}^2}}}-{x_4 \over {{Z_L^2}{C_{{DC}_1}}{C_{{DC}_2}}}} \nonumber \\&+{x_3 \over {{Z_L^2}{C_{{DC}_1}}{C_{{DC}_2}}}} \end{aligned}$$

(74)

In a similar manner one computes

$$\begin{aligned} {L_{g_1}}{L_f}{h_2}(x)= & {} {L_{g_1}}{z_4}{\Rightarrow }{L_{g_1}}{L_f}{h_2}(x)={{{\partial }{z_4}} \over {{\partial }{x_1}}}g_{11}+{{{\partial }{z_4}} \over {{\partial }{x_2}}}g_{12} \nonumber \\&+{{{\partial }{z_4}} \over {{\partial }{x_3}}}g_{13}+{{{\partial }{z_4}} \over {{\partial }{x_4}}}g_{14}{\Rightarrow } \nonumber \\ {L_{g_1}}{L_f}{h_2}(x)= & {} 0{\cdot }g_{11}+0{\cdot }g_{12}-{1 \over {{Z_L}{C_{{DC}_2}}}}{\cdot }0 \nonumber \\&+{1 \over {{Z_L}{C_{{DC}_2}}}}{\cdot }\left( {{3{x_1}} \over {4C_{{DC}_1}}}\right) {\Rightarrow } \nonumber \\ {L_{g_1}}{L_f}{h_2}(x)= & {} {{3{x_1}} \over {4{Z_L}{C_{{DC}_1}}{C_{{DC}_2}}}} \end{aligned}$$

(75)

Finally, by applying the same method one computes

$$\begin{aligned} {L_{g_2}}{L_f}{h_2}(x)= & {} {L_{g_2}}{z_4}{\Rightarrow }{L_{g_2}}{L_f}{h_2}(x)={{{\partial }{z_4}} \over {{\partial }{x_1}}}g_{21}+{{{\partial }{z_4}} \over {{\partial }{x_2}}}g_{22} \nonumber \\&+{{{\partial }{z_4}} \over {{\partial }{x_3}}}g_{23}+{{{\partial }{z_4}} \over {{\partial }{x_4}}}g_{24}{\Rightarrow } \nonumber \\ {L_{g_2}}{L_f}{h_2}(x)= & {} 0{\cdot }g_{21}+0{\cdot }g_{22}-{1 \over {{Z_L}{C_{{DC}_2}}}}{\cdot }0 \nonumber \\&+{1 \over {{Z_L}{C_{{DC}_2}}}}{\cdot }\left( {{3{x_2}} \over {4C_{{DC}_1}}}\right) {\Rightarrow } \nonumber \\ {L_{g_2}}{L_f}{h_2}(x)= & {} {{3{x_2}} \over {4{Z_L}{C_{{DC}_1}}{C_{{DC}_2}}}} \end{aligned}$$

(76)

It can be confirmed that it holds

$$\begin{aligned} \dot{z}_1= & {} z_2 \nonumber \\ \dot{z}_2= & {} {L_f^2}h_1(x)+{L_{g_1}}{L_f}{h_1(x)}u_1+{L_{g_2}}{L_f}{h_1(x)}u_2 \nonumber \\ \dot{z}_3= & {} z_4 \nonumber \\ \dot{z}_4= & {} {L_f^2}h_2(x)+{L_{g_1}}{L_f}{h_2(x)}u_1+{L_{g_2}}{L_f}{h_2(x)}u_2 \end{aligned}$$

(77)

The input–output linearized model takes the form

$$\begin{aligned} \dot{z}_1= & {} {L_f^2}h_1(x)+{L_{g_1}}{L_f}{h_1(x)}u_1+{L_{g_2}}{L_f}{h_1(x)}u_2 \nonumber \\ \dot{z}_2= & {} {L_f^2}h_2(x)+{L_{g_1}}{L_f}{h_2(x)}u_1+{L_{g_2}}{L_f}{h_2(x)}u_2 \end{aligned}$$

(78)

By defining the new control inputs

$$\begin{aligned} v_1= & {} {L_f^2}h_1(x)+{L_{g_1}}{L_f}{h_1(x)}u_1+{L_{g_2}}{L_f}{h_1(x)}u_2 \nonumber \\ v_2= & {} {L_f^2}h_1(x)+{L_{g_1}}{L_f}{h_1(x)}u_1+{L_{g_2}}{L_f}{h_1(x)}u_2 \end{aligned}$$

(79)

the VSC-HVDC system is written in the chain of integrators form

$$\begin{aligned} \ddot{z}_1= & {} v_1 \nonumber \\ \ddot{z}_1= & {} v_2 \end{aligned}$$

(80)

Moreover, by defining the feedback control inputs

$$\begin{aligned} v_1= & {} \ddot{z}_1^d-k_d^1(\dot{z}_1-\dot{z}_1^d)-k_p^1\left( z_1-z_1^d\right) \nonumber \\ v_2= & {} \ddot{z}_2^d-k_d^2(\dot{z}_2-\dot{z}_2^d)-k_p^2\left( z_2-z_2^d\right) \end{aligned}$$

(81)

The tracking error dynamics for the closed loop becomes $\ddot{e}_1+{k_d^1}\dot{e}_1+{k_p^1}e_1=0$ and $\ddot{e}_2+{k_d^2}\dot{e}_2+{k_p^2}e_2=0$. By selecting the feedback gains $k_p^1$, $k_d^1$ and $k_p^2$, $k_d^2$ such the associated characteristic polynomials to be Hurwitz ones, one has the tracking error dynamics $lim_{t{\rightarrow }\infty }e_1(t)=0$ and $lim_{t{\rightarrow }\infty }e_2(t)=0$.

To compute the control input that is actually applied to the VSC-HVDC model one proceeds as follows: Eq. (78) is rewritten in the matrix form

$$\begin{aligned} \ddot{\tilde{y}}_f=\tilde{f}+\tilde{M}\tilde{u} \end{aligned}$$

(82)

where

$$\begin{aligned} \tilde{y}_f= & {} \begin{pmatrix} y_{f_1} \\ y_{f_2} \end{pmatrix} \quad \tilde{f}= \begin{pmatrix} {L_f^2}h_1(x) \\ {L_f^2}h_2(x) \end{pmatrix} \nonumber \\ \tilde{M}= & {} \begin{pmatrix} {L_{g_1}}{L_f}h_1(x) &{} {L_{g_2}}{L_f}h_1(x) \\ {L_{g_1}}{L_f}h_2(x) &{} {L_{g_2}}{L_f}h_2(x) \end{pmatrix} \quad \tilde{v}= \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} \end{aligned}$$

(83)

Using the above, the control input that should be exerted on the VSC-HVDC model is for eliminating the tracking error is

$$\begin{aligned} \tilde{u}=\tilde{M}^{-1}[\tilde{v}-\tilde{f}] \end{aligned}$$

(84)