Abstract
In many countries of the developing world, it is difficult to conduct large-scale household travel surveys to collect data for travel behaviour model estimation and application. This paper focuses on two candidate solutions to the problem: (1) developing models that can be applied for prediction using secondary data collected for other purposes and include socio-demographic information but do not include transport specific information such as the car and/or transit pass ownership (e.g. census, public health records, etc.), (2) ‘borrowing’ a model developed using data from a similar city within the same region. In the first approach, we investigate the feasibility of developing car trip generation models which imputes the car ownership variable with estimated car ownership propensities. The proposed framework is applied in two East African cities, Nairobi and Dar-es-Salaam. The estimation results indicate that for both cities the proposed approach outperforms the models that exclude the car ownership variable. In the second approach, we investigate the spatial transferability of the models developed in the first approach between the two cities to evaluate if it is justified to apply models from one developing country to another in the absence of local models. Results indicate that though some of the estimated parameters are not significantly different from each other between the two cities, statistical tests do not support direct transferability of all the models from Nairobi to Dar-es-Salaam or vice versa. However, interestingly, the simpler model (which excludes car-ownership) outperforms the model with imputed car ownership propensity in terms of transferability. These findings provide useful insights into the development of trip generation models under data constraints which can practically be very useful for developing countries.
Similar content being viewed by others
Introduction
In recent years, developing countries have witnessed speedy urbanisation, improvements in living standards and significant growths in economic activities. As a consequence, there has been a substantial increase in disposable household income levels [8] which has led to a significant increase in car ownership levels in most of the countries. The increased car ownership levels, coupled with increased economic activities, have led to an increase in the overall numbers of car trips, which has contributed to increased traffic congestion, energy consumption, and air pollution, particularly in big cities [10].
Given the important role of the trip generation component in transport planning, there has been numerous research studies investigating the relative contribution of different factors on trip generation [1, 15, 32, 38, 44]. However, these studies are conducted in the context of developed countries, and the findings as well as the methodologies are not directly applicable to developing countries due to substantial differences in the socio-economic conditions and data issues. Trip generation studies in developing countries on the other hand are still limited, primarily due to the lack of data for calibrating and applying the trip generation models. But there are often secondary datasets available in developing countries, which have detailed socio-demographic information (e.g. census, public health records, etc.). However, in most cases they lack car ownership information—which has been found to be a critical variable in trip generation models. Although there are examples of trip generation models without the car ownership explanatory variable in the context of developing countries (e.g. [42], there is a substantial risk that this introduces a strong correlation between the error term of the model and the rest of the explanatory variables. Such omission can, therefore, lead to endogeneity and bias in the estimates [43]. Consequently, it is critical that the relationship between trip generation and car ownership, as well as the influence of other exogenous factors, is well represented to mitigate the endogeneity problem.
Furthermore, the relationship between car ownership and trip generation is more complex than usually presented. While ownership of car offers increased flexibility and mobility, people with increased mobility needs are likely to be more prone to own cars (provided that they can afford). This can lead to potential simultaneity between the two decisions and can lead to endogeneity, where an explanatory variable (car ownership) is influenced by the dependent variable (trip generation) [43]. Where attempts have been made to address this issue, it has been hypothesised that current car ownership is influenced by trip generation from a previous period, reflecting the “learning from experience idea” [26]. The development or application of such models, however, requires panel data, which are difficult to find in developing countries since there is rarely any initiative to systematically document travel survey records [36]. To the best of our knowledge, there has not been any previous research that investigates how a robust and dependable trip generation model can be developed in the context of developing countries amid these data limitations.
On the other hand, ‘borrowing’ models from similar settings also hold the promise for overcoming the issues arising from the absence of dependable travel behaviour data for developing local models. But though there has been substantial research on transferability of models developed for one location to another in the context of developed countries (see [40] for a detailed synthesis), this has not been investigated rigorously in the context of developing countries.
In this research, we address these research gaps in the following two ways:
-
exploring candidate model structures to address the issue of unavailability of a key variable in the application context (car ownership in this case);
-
investigating the spatial transferability of these model structures to evaluate if it is justified to apply models from one developing country to another in the absence of local models.
The models are estimated using household survey data collected from two East African cities, Nairobi, Kenya, in 2004 [22], and Dar-es-Salaam, Tanzania, in 2007 [23]. Given their geographical proximity, similarities in their socio-economic structure, and their fairly similar transport systems [21], it is expected that there will be some similarities in the travel behaviour of the two cities, which prompts us to investigate the spatial transferability of the models between the two cities.
In this regard, two different model structures (i.e. one sequential and one simultaneous structure) are developed and their performances are compared against models where all the variables are observed. The spatial transferability of each of these model structures is then tested to investigate which one is more transferrable to the other city. It may be noted that we focus on car trips (as opposed to the total number of trips) because private cars are the key contributors to congestion in both cities [22, 23].
The rest of the paper is arranged as follows: a review of literature on trip generation, vehicle ownership models and spatial transferability are presented first. This is followed by a description of the modelling methodology and the details of the data for each city. The empirical findings are presented next, followed by the key findings and directions for future research.
Literature Review
This section briefly reviews literature on trip generation and car ownership models and that on spatial transferability of models.
Previous Trip Generation and Car Ownership Studies
As mentioned, the positive influence of car ownership on trip generation has already been established in previous research [1, 15, 32, 38, 44]. Among other factors, household income has been found to positively influence trip generation [15, 26, 32, 38]. Golob [19] explained that the positive influence of income on trip generation could be a second-order influence derived from the positive influence of income on vehicle ownership, which in turn positively influences trip generation. It has, however, also been previously argued that both income and vehicle ownership have separate positive influences on trip generation [44]. In regard to Wootton and Pick’s findings, it can be argued that car ownership depends more on long-term income while trip generation expenses often depend more on daily disposable income. The other household socio-economic/demographic key exogenous factors previously found to affect trip generation include: household size [1, 12, 15, 38]; age, gender and family structure [32]; number of children and students [5]; employment-related variables [1, 5, 12, 15]; number of driving licence-holding members [5, 12, 32] and aggregate variables such as population density [32, 38].
In the case of car ownership, household income and the number of driving licence-holding members have been found to have a consistent positive influence on the number of cars owned by a household [31]. The other key household socio-economic/demographic exogenous factors previously considered to affect car ownership include household size, number of children, accessibility measures [31]; the number of workers in a household [7, 14, 33, 37–39], age and gender of the household members [37], and family structure [7, 14, 33]. Aggregate variables such as population density [24, 38, 45] and residential density [33, 39] have also been previously considered as explanatory variables.
Most of the previous studies encountered in this field have employed discrete choice methods in estimating car ownership [7, 14, 26, 31, 37, 39, 45] and trip generation [1, 32]. Obviously, there are other studies that have used different techniques such as linear regression [24, 38, 42] and structural equations [19, 20], but discrete choice methods are more appropriate for this study since they are able to represent a decision maker’s choice from a set of discrete alternatives, where at least one and only one can be chosen at a time [6].
Based on the sample studies above, it is noted that both car ownership and trip generation largely depend on similar explanatory variables. As earlier mentioned, this points to the fact that arbitrary omission of the car ownership variable in trip generation models increases the risk of endogeneity due to variable omission [43]. That aside, this is also used to our advantage in scenarios where there is lack of car ownership data in the application context, without needing a new set of explanatory variables. A possible way is provided in a study [38] where the influence of vehicle ownership is incorporated into a ‘vehicle use model’ using a separately estimated vehicle ownership model based on a largely similar set of explanatory variables. The setback is that this study uses linear regression models which are not suitable for developing disaggregate car ownership or car trip generation models.
Structures of State-of-the-Art Trip Generation and Car Ownership Models
Most previous studies have used discrete choice methods for modelling car ownership and trip generation decisions due to the discrete nature of the explanatory variables. Discrete choice models can generally be divided into unordered response or ordered response models. Depending on the nature of the study, previous vehicle ownership studies have used both unordered [7, 14, 33, 45] and ordered [7, 29, 31, 37, 39] response models, while most previous trip generation studies have used ordered response models [1, 32].
Although it is possible to use both unordered and ordered response models, car ownership level and trip generation choices are incremental by nature which makes ordered response models more appropriate. Modelling these as ordered choices means acknowledging that there is a correlation between the alternative choices for each case (See [6] for details). With ordered response models, it is also possible to conduct multivariate analysis for cases with more than one dependent variable [35]. This has previously been used to jointly model household car and motorcycle ownership levels in Asia using bivariate ordered response probit (BOP) models [37]. However, to the best of our knowledge, no previous study has investigated the possibility of jointly modelling car ownership and car trip generation using the BOP model, and this study addresses this research gap among others.
Spatial Transferability of Trip Generation and Car Ownership Models
From the onset, we highlight the difference between model transfer and transferability, with the former simply being an act of transferring models between contexts and the latter being the degree of success with which a model estimated for a given context explains behaviour in another context [34].
Transferability can be investigated between different time periods within the same area (temporal transferability) or between different geographical areas (spatial transferability) or both [1, 9, 17, 40]. Previous studies have established that spatial transferability of trip generation [1, 11, 34, 41, 42] and car ownership [37] models can be reasonably achieved. This is, however, is not always the case; for example, in a study [13], satisfactory spatial transferability of trip generation was not achieved on an account of underlying differences between London and Tel-Aviv city structures.
Transferability improves when models are developed at a disaggregate level [30]. It has been argued that preference for disaggregate models is due to the observation that they do not depend on unique zone definitions [42]. It is, however, difficult to achieve flawless model transferability and, therefore, the aim usually is to make as much improvement in transferability as possible [27].
Various methods have been developed to test model transferability and these include the t-ratio for the difference between parameters [18], the transferability test statistic [2, 18], the transfer index [28], and the transfer rho-square [18]. By and large, of the methods presented above, the transferability index seems to be the most effective measure for ranking the transferability of alternative model structures based on how close the calculated indices are to one. This is discussed further in “Evaluating Spatial Transferability”.
Methodology
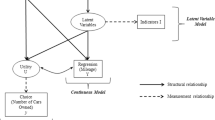
Based on the review of literature (“Structures of State-of-the-Art Trip Generation and Car Ownership Models”), we use ordered response models which assume that every individual has latent car ownership and trip making propensities which are functions of their demographics. These propensities are then converted to discrete car ownership levels and trips using estimated cut-off points.
Model Structures
The model system consists of two submodels, one for car ownership, and the other for trip generation.
Car ownership submodel:
Trip generation submodel:
where \(y_{1n}^{*}\) and \(y_{2n}^{*}\) are the car ownership and trip generation propensities, respectively, for household \(n\); \(x_{1n}\) and \(x_{2n}\) are vectors of the car ownership and trip generation explanatory variables, while \(\beta_{1}\) and \(\beta_{2}\) are the respective parameter vectors. \(y_{1n}\) is the observed car ownership for \(n\), which is different from \(y_{1n}^{*}\), the estimated car ownership propensity. \(y_{2n}\) denotes the observed car trips for \(n\). The corresponding parameters \(\gamma\) and \(\lambda\) are mutually exclusive depending on the model being estimated as described in the next paragraph. The \(\mu\) s are the threshold parameters.
The three models estimated below are expressed as special cases of the two submodels.
Base model This model is applicable for the case where car ownership data are available, and the number of cars owned (\(y_{1n}\)) is directly used as an explanatory variable. Hence, in the model formulation, Eqs. (1c) and (1d) are used and, \(\gamma\) is estimated, but \(\lambda\) is fixed to zero. A variation of the model without the car-ownership variable has been tested as well.
Sequential model This model accounts for situations where car ownership data are available in the estimation context but missing in the application context, and attempts to address this issue using the estimated car ownership propensity.Footnote 1 In this formulation, the car ownership submodel (Eqs. (1a) and (1b)) is estimated followed by the trip generation submodel (Eqs. (1c) and (1d)). The car ownership propensity \(y_{1n}^{*}\) is derived from the car ownership submodel \(y_{1n}^{*}\) and utilised in the trip generation submodel; \(\lambda\) is estimated, and \(\gamma\) is fixed to zero.
For the base and the sequential models, the car ownership and the trip generation probabilities can be estimated using the ordered response probit model as follows:
where \(\varPhi ( \cdot )\) is a standard normal cumulative distribution function, and \(P_{{n,y_{a} }}\) is the probability of household \(n\) falling in category \(y_{a}\); a = 1 for the car ownership submodel, and 2 for the trip generation submodel.
The models are estimated using the maximum likelihood estimator. Equation (2b) presents the log-likelihood function:
where \(Z_{{n,y_{a} }} = 1\) if and only when household n is in category \(y_{a}\) and 0 otherwise. It may be noted that for the base model, we only estimate the trip generation submodel, while for the sequential model, we sequentially estimate the car ownership and the trip generation submodels.
Simultaneous model In this model, the car ownership and the trip generation submodels are estimated jointly. This model thus attempts to address the simultaneity problem between car ownership and trip generation, as well as car ownership data shortages in the application context. Here again, the car ownership propensity \(y_{1n}^{*}\) is calculated in the car ownership submodel and utilised in the trip generation submodel, where \(\lambda\) is estimated, and \(\gamma\) is fixed to zero. However, the car ownership and the trip generation probabilities are jointly estimated using the bivariate ordered response probit model as follows [35]:
where \(P_{{n, y_{1} y_{2} }}\) is the probability of household \(n\) owning \(y_{1}\) cars and making \(y_{2}\) car trips, \(\varPhi_{2}\) a bivariate standard normal cumulative distribution function, \(\widetilde{\rho } = \zeta (\lambda + {\text{corr}})\), \(\zeta = \frac{1}{{\sqrt {1 + 2 \cdot \lambda \cdot {\text{corr}} + \lambda^{2} } }}\), and \({\text{corr}}\) is the correlation between \(\varepsilon_{1n}\) and \(\varepsilon_{2n}\).
Equation (2d) presents the log-likelihood functions for the simultaneous model [35]:
where \(Z_{{n,y_{1} y_{2} }} = 1\) if and only when household n owns \(y_{1}\) cars and makes \(y_{2}\) car trips, otherwise it is equal to zero.
An important point worth noting is that for the sequential estimation, only the deterministic component of car ownership propensity is entered in the trip generation model (and used in subsequent forecasting), while for the simultaneous estimation, both the deterministic and the stochastic components of the variable contribute to the model used for forecasting.
Evaluating Spatial Transferability
Three model structures have been specified starting with the base model (the simplest of all), followed by the more complex sequential and simultaneous model structures. Although it is generally assumed that better specified models tend to be more transferrable, this needs to be investigated using the available transferability metrics as it is difficult to assess this from the model specifications alone.
Spatial transferability of the individual parameters is checked by testing whether or not there is a significant difference between the parameter estimates of equivalent variables in the two cities (Eq. 3a) [18]. Minimum and maximum t-ratio values of − 1.96 and 1.96 corresponding to the 95% confidence interval are taken as the critical values:
where \(\widehat{\beta }_{{{\text{trans}},k}}\) and \(\widehat{\beta }_{{{\text{appl}},k}}\) are the estimates for the k th parameter in the transferred and application areas, \(t_{{{\text{trans}},k}}\) and \(t_{{{\text{appl}},k}}\) the respective t ratios of the parameter estimates, and \(t_{{{\text{diff}},k}}\) is the t-ratio for the difference between parameters.
Global measures of model transferability are also obtained using the transferability index (TI) (Eq. 3b) [28]:
where \(LL_{\text{appl}} (\widehat{\beta }_{\text{trans}} )\) is the log-likelihood on the application context data with transferred context parameters, \(LL_{\text{appl}} (\widehat{\beta }_{\text{appl}} )\) the log-likelihood on the application context data with application context parameters, and \(LL_{\text{appl}} (C)\) is the log-likelihood of the application context model with constants only.
A TI value of one indicates perfect transferability, while a value of zero indicates complete non-transferability. This metric is suitable for comparing the transferability of alternative model structures; however, there is no specific lower limit to judge whether the reported transferability is good or not. Equation 3b means that a higher \(LL_{\text{appl}} (\widehat{\beta }_{\text{trans}} )\) always results in a higher TI.
Data
The data used for this study were collected from the cities of Nairobi (Kenya) and Dar-es-Salaam (Tanzania) in 2004 and 2007, respectively. Figure 1 shows the study area locations.

Source: http://www.unima-usa.org/
Study area locations
The surveys were conducted by face to face interviews of household members aged 5 years and above (in Nairobi) and 6 years and above (in Dar-es-Salaam). A total number of 8588 and 7676 valid household observations were made in Nairobi and Dar-es-Salaam representing sampling rates of approximately 1.3% and 1.1%, respectively. Table 1 presents a brief description of the data while Fig. 2 presents variation of household car trip generation rates with key household descriptors. Though the trends are not identical, in general, the possibility of households making increased numbers of car trips increases with household car ownership, household income, the number of licence holders and the number of workers in both cities (Fig. 2a–d). From Fig. 2a in particular, it may be noted that there is a small proportion of households that reported that they do not own a car and yet had car trip origins. This could be because they had access to office cars for work (and for private usage as well in some cases) which are not reported in the numbers of cars owned. These trends are all in agreement with intuitive reasoning. A high number of cars owned are likely to increase the possibility of car use. High income is expected to be highly correlated with high disposable income for spending on private car travel. A high number of driving licence holders would most likely increase the possibility of the available cars being driven. High numbers of workers in a household are likely to lead to increase household travel activity in general and possibly car trip generation rates in particular. The other explanatory variables considered to be important are household size and house ownership.
Apart from private car trips, the mode share of walking trips is approximately equal to that of public transport, which is largely under private control in both cities [22]. Public transport in Nairobi comprises of both large buses and minibuses (matatus), while that in Dar-es-Salaam largely comprises of minibuses; however, both cities had no option for rail transport at the time of data collection.
Although public transport is privately controlled, there is a fare setting procedure for large buses and minibuses in both cities, which is managed by transport operator associations [21]. However, public transport operations are largely flexible, with no adherence to departure timetables, which could be one of the issues discouraging high-income individuals from using public transport in both cities.
Results
Estimation Results
The estimates and the summary statistics for all the three model structures are presented in Tables 2 and 3, respectively. In addition to the three models, we estimated the base model (without the car ownership variable) for comparison purposes. The summary statistics of these models are presented in Table 3.
Positive parameter estimates imply that an increase in any of these explanatory variables increases the propensity of household car trip generation or ownership, while the reverse is true for negative parameter estimates. The same interpretation applies to the relative parameter magnitudes of the dummies associated with the same explanatory variable. For all the three models, most of the parameter signs and relative magnitudes are in agreement with intuitive reasoning. One of the exceptions is parameters associated with the number of workers per household in the car ownership submodels of the sequential and the simultaneous models in both cities, indicating that households with more working members sometimes have fewer cars. The reason for this unusual behaviour needs further investigation; however, a possible interpretation is that household income is much more important and the total number of working members may include low-income workers (who do not contribute to the car ownership). The other exceptions relate to the relative magnitudes of parameters associated with the number of workers per household (for the trip generation submodel of the sequential model in Dar-es-Salaam), and the number of cars owned per household (for the base model in both cities). The estimates do not have a monotonically increasing trend with respect to the number of workers or cars owned. However, this problem is not found in the simultaneous model, thereby supporting its theoretical superiority.
The scalar quantity ‘lambda’ in the sequential and the simultaneous models, which relates the household car ownership propensity to household car trip rates, is positive as expected. However, it is noted that whereas ‘lambda’ is significant in Nairobi, it is insignificant in Dar-es-Salaam. One interpretation is the poorer model fit of the car ownership submodel in Dar-es-Salaam, due in part to more unevenly distributed car ownership such as extremely larger share of 0 car household (see Table 1). However, it is good to keep this since this is a key variable in the present research. Similarly, the correlation parameter (corr) in the simultaneous model is positive in both cities, signifying a positive correlation between household car ownership propensity and household car trip generation as expected.
For model comparison in terms of the measures of fit, we separately analyse the car ownership and the trip generation submodels since some model structures have both submodels, while others do not. For the sequential model, the convergence log-likelihoods of the two submodels are determined in a straightforward manner; however, for the simultaneous model, which reports the joint car ownership/trip generation probabilities, the convergence log-likelihoods of the different submodels need to be computed outside the estimation process. To do this, we sum the joint car ownership/trip generation probabilities along the number of trip dimensions (for the trip generation submodel), and along the number of car dimensions (for the car ownership submodel). For example, to obtain the probability of making 0 trips, we sum the joint probabilities of (0 cars, 0 trips), (1 car, 0 trips), (2 cars, 0 trips) and (3+ cars, 0 trips), while to obtain the probability of owning 0 cars, we sum the joint probabilities of (0 cars, 0 trips), (0 cars, 1 trip), (0 cars, 2 trips) and (0 cars, 3+ trips). We then apply these unconditional probabilities to the appropriate version of the log-likelihood function in Eq. (2b).
A comparison of the trip generation submodels in terms of the adjusted rho-square values shows that the sequential and the simultaneous models perform worse than the base model containing the observed car ownership variable. This is because the base model uses actual car ownership levels which are not subject to estimation errors such as the latent car ownership propensities in the sequential and the simultaneous models. This might also relate to the discrete nature of the relationship between car ownership and usage. The dummy coding in the base model shows that the difference in the parameter estimates between 0 and 1 car(s) owned is much higher than those between 1 and 3+ car(s). This suggests that although people might use company cars or used cars as passengers, households without cars are likely to use cars less frequently. A dummy coding used in the base model is appropriate to express this, but a continuous variable expressed by latent propensity to car ownership is less suitable in this regard. However, both the sequential and the simultaneous models outperform a version of the base model where the car ownership variable is totally excluded, especially in Nairobi where the differences in the convergence log-likelihoods are more pronounced. This signifies that the inclusion of latent car ownership propensity is better than total exclusion of the car ownership variable.
A comparison of the sequential and the simultaneous models shows that the performance of simultaneous models is a little worse than that of the sequential model for both the car ownership and the trip generation submodels. One explanation for this is the very low statistical significance of the correlation term (corr) in both cities (see the simultaneous model results in Table 2), which points to the possibility that accounting for simultaneity is not critical for the study area; however, further investigation is needed using panel data, where households are investigated over a given period of time as this would reveal more behavioural aspects of the car ownership/trip generation relationship.
Evaluation of Spatial Transferability
The parameter signs for each of the three models are similar across both cities which is an indication of similarities in car ownership and trip generation behaviour. Analysis of the t-statistics for the difference between parameters (headed by ‘t-stat. diff’ in Table 2) reveals that most of the parameter estimates for all the three models have insignificant differences in magnitude which indicates that they are individually transferrable between the two cities. It is noted that the monthly household income parameter is the least transferable potentially due to difficulties in categorising the income data for the two cities into equivalent income groups which lead to the use of a continuous income variable.
In terms of the overall spatial transferability, Table 4 presents the transferability indices for all the estimated models. Transferability is tested in both directions by applying the Nairobi parameters to the Dar-es-Salaam data (column headed by ‘application to Dar-es-Salaam’) and by applying the Dar-es-Salaam parameters to the Nairobi data (column headed by ‘application to Nairobi’). For each direction, we compare the likelihood ratio of the transferred and the local model with respect to local model having constants only using the transferability index (TI) (see Eq. (3b)). A higher TI indicates higher transferability.
With respect to the trip generation submodel, the base models (both with and without the car ownership variable) produce the highest TI values (the highest LL values with transferred parameters; see Eq. 3b) in both directions compared to the rest of the models. The higher transferability of the base models might relate to their simple model structure, which only relies on the observed variables. On the other hand, the sequential and the simultaneous models, which contain a variable that is already subject to estimation errors in the local context (i.e. the car ownership propensity) are likely to perform even worse when transferred as expected.Footnote 2
The critical point now is the trade-off between local model performance and spatial transferability, when faced with possible data limitations in the application context. In this study, we see that although exclusion of the car ownership variable from the base model structure leads to poor performance in the local context, when compared to models using the estimated car ownership propensity (i.e. the sequential and the simultaneous models. See Table 3), the base model without the car ownership variable is more spatially transferrable. This might relate to the choice of explanatory variables. Explanatory variables in the car trip generation submodel (except the car ownership variable) are also included in the car ownership submodel. The contribution of car ownership propensity in the car trip generation submodel consists of these explanatory variables and the other variables included only in the car ownership submodel. If the contribution from the other variables is limited, the base model (without the car ownership variable) might work as a reduced form of the sequential and simultaneous models.
Therefore, for situations where data shortages of particular variables are expected in a different geographical area, and yet the spatial transferability of the models is an important issue, it may be better to develop models excluding those particular variables, although this comes at a risk of endogeneity due to variable omission. At this point, it is also worth noting that although the complex model structures have been found to be the least transferrable, the better transferability of the simultaneous model over the sequential model implies that although the correlation term was not statistically significant (see Table 2), the superior correlation structure of the model makes it more transferrable. Alluding to earlier, better specification of the car ownership submodel could lead to different conclusions on the transferability of the complex model structures and needs to be investigated further using alternative datasets with more explanatory variables.
Policy Implications and Concluding Remarks
This study has investigated the feasibility of different model structures aimed at addressing the issue of unavailability of data on a key variable in the application context.
The key findings together with their policy implications are as follows.
-
The inclusion of latent variables as a proxy for the missing variables is better than total exclusion of the variables with respect to model fit to the estimation dataset. Models considering endogeneity and simultaneity have stronger theoretical underpinning which is supported by the better goodness-of-fit with the data. In addition, the simultaneous model produced intuitive estimates as mentioned in “Estimation Results”.
-
The similarity in travel behaviour across different cities within the same region (as assessed from the statistically insignificant differences in the parameter values) is encouraging, and shows that we should not rule out the possibility of transferring the models between the cities. In this particular study, we note that while there is a high risk of endogeneity due to omission of the car ownership variable in both cities, the benefits accrued from the spatial transferability of models excluding the car ownership variable overrides the need to address this limitation through complex model structures. There is a need for further investigations using alternative datasets with more explanatory variables to examine if this finding can be generalised.
The results of the current models, however, show some minor inconsistencies with intuitive reasoning in terms of the relative parameter magnitudes of some variables, which are an important topic of future research to ascertain the unique characteristics of the study areas. Also, our comparison between the sequential and the simultaneous models indicates that accounting for the simultaneity between car ownership and trip generation is not critical for the two cities; however, further investigation is needed (potentially using panel data) to see if this finding can be generalised across other cities of the developing world. Further, in this case, car ownership information has been assumed to be available for model estimation and unavailable in the application context. However, in more limiting situations, such information may be completely unavailable, which may necessitate the development of hybrid models as a possible direction of future research. Last, in the present study, we use the same model specifications in all three cases for the sake of comparability. It is, therefore, not possible to provide a detailed conceptual or theoretical guidance on the optimum model specification based on our empirical findings. This can be a topic of future research where the effect of model specification on transferability is investigated using a larger number of datasets with varying characteristics. It will be also interesting to investigate methods to increase spatial transferability of the models by methods such as Bayesian updating and joint context estimation (e.g. [16]).
Notes
Availability of car ownership data in estimation context is less of a concern, since researchers can ensure that the car ownership field is included in the survey during primary data collection. However, the information is typically not collected during census or wide-scale data collection.
Model specification is largely driven by the characteristics of the estimation dataset. Therefore, though on one hand, it is expected that better specified models will be more transferrable (as reported by [4, 17, 25]), there is risk that the model with better specification is actually overfitting the estimation data. If the latter is true, the transferability results will not be better compared to a simpler model where there is less risk of overfitting (as reported by [3]. Further, the simpler specification can indeed score better in the tests because of less number of parameters (and less differences in likelihood values between the estimation and application context models). Given these inherent complexities, we believe it is not possible to provide a detailed conceptual or theoretical guidance on the optimum model specification based on our empirical findings.
References
Agyemang-Duah K, Hall FL (1997) Spatial transferability of an ordered response model of trip generation. Transp Res Part A 31:389–402
Atherton TJ, Ben-Akiva ME (1976) Transferability and updating of disaggregate travel demand models. Transp Res Rec 610:12–18
Badoe D, Miller E (1995) Analysis of the temporal transferability of disaggregate work trip mode choice models. Transp Res Rec 1493:1–11
Badoe D, Miller E (1995) Comparison of alternative methods for updating disaggregate logit mode choice models. Transp Res Record 1493:90–100
Badoe D, Chen C (2004) Modeling trip generation with data from single and two independent cross-sectional travel surveys. J Urban Plan Dev 130:167–174
Ben-Akiva ME, Lerman SR (1985) Discrete choice analysis: theory and application to travel demand. MIT Press, Cambridge
Bhat CR, Pulugurta V (1998) A comparison of two alternative behavioral choice mechanisms for household auto ownership decisions. Transp Res Part B 32:61–75
Bolt J, Zanden JLV (2013) The first update of the Maddison project: re-estimating growth before 1820. Maddison-Project Working Paper WP-4, University of Groningen. https://www.rug.nl/ggdc/historicaldevelopment/maddison/publications/wp4.pdf. Accessed 15 Apr 2019
Bowman JL, Bradley M, Castiglione J, Yoder SL (2014) Making advanced travel forecasting models affordable through model transferability. 93rd Transportation Research Board Annual Meeting, Washington DC, USA
Button K, Ngoe N, Hine J (1993) Modelling vehicle ownership and use in low income countries. J Transp Econ Policy 27(1):51–67
Caldwell LC, Demetsky MJ (1980) Transferability of trip generation models. Transp Res Rec 751:56–62
Cotrus AV, Prashker JN, Shiftan Y (2005) Spatial and temporal transferability of trip generation demand models in Israel. J Transp Stat 8:37–56
Daor E (1981) The transferability of independent variables in trip generation models. Planning and Transport Res and Comp, Sum Ann Mtg, Proc, 1981 London. PTRC Education and Research Services, Ltd., pp 235–252
Deka D (2002) Transit availability and automobile ownership some policy implications. J Plan Educ Res 21:285–300
Douglas A (1973) Home-based trip end models—a comparison between category analysis and regression analysis procedures. Transportation 2:53–70
Flavia A, Choudhury C (2019) Temporal transferability of vehicle ownership models in the developing world: case study of Dhaka, Bangladesh. Transp Res Rec. https://doi.org/10.1177/0361198119836760
Fox J, Daly A, Hess S, Miller E (2014) Temporal transferability of models of mode-destination choice for the Greater Toronto and Hamilton Area. J Transp Land Use 7:41–62
Galbraith RA, Hensher DA (1982) Intra-metropolitan transferability of mode choice models. J Transp Econ Policy 16(1):7–29
Golob TF (1989) The causal influences of income and car ownership on trip generation by mode. J Transp Econ Policy 141–162
Golob TF, van Wissen L (1989) A joint household travel distance generation and car ownership model. Transp Res Part B 23:471–491
Gwilliam K (2011) Africa’s transport infrastructure mainstreaming maintenance and management. The International Bank for Reconstruction and Development, The World Bank, Washington, DC
JICA (2006) The study on master plan for urban transport in the Nairobi Metropolitan Area in the Republic of Kenya (SDJR06-41). Japan International Co-operation Agency (JICA), Nairobi
JICA (2008) Dar-es-Salaam transport policy and system development master plan. Japan International Co-operation Agency (JICA), Dar-es-Salaam
Kain JF, Beesley M (1965) Forecasting car ownership and use. Urban Stud 2:163–185
Karsamaa N, Pursula M (1997) Empirical studies of transferability of Helsinki metropolitan area travel forecasting models. Transp Res Record 1607:38–44
Kitamura R (2009) A dynamic model system of household car ownership, trip generation, and modal split: model development and simulation experiment. Transportation 36:711–732
Koppelman F, Kuah G, Wilmot C (1985) Transfer model updating with disaggregate data. Transp Res Record 1037:102–107
Koppelman FS, Wilmot CG (1982) Transferability analysis of disaggregate choice models. Transp Res Record 895:18–24
Matas A, Raymond JL, Roig JL (2009) Car ownership and access to jobs in Spain. Transp Res A Policy Pract 43(6):607–617
Ortúzar JDD, Willumsen LG (2011) Modelling transport. Wiley, Hoboken
Pendyala RM, Kostyniuk LP, Goulias KG (1995) A repeated cross-sectional evaluation of car ownership. Transportation 22:165–184
Pettersson P, Schmöcker J-D (2010) Active ageing in developing countries?—trip generation and tour complexity of older people in Metro Manila. J Transp Geogr 18:613–623
Potoglou D, Susilo YO (2008) Comparison of vehicle-ownership models. Transp Res Record 2076:97–105
Rose G, Koppelman FS (1984) Transferability of disaggregate trip generation models. In: Proceedings of the 9th international symposium of transportation and traffic theory, pp 471–491
Sajaia Z (2008) Maximum likelihood estimation of a bivariate ordered probit model: implementation and Monte Carlo simulations. Stata J 4:1–18
San Santoso D, Tsunokawa K (2005) Spatial transferability and updating analysis of mode choice models in developing countries. Transp Plan Technol 28:341–358
Sanko N, Dissanayake D, Kurauchi S, Maesoba H, Yamamoto T, Morikawa T (2014) Household car and motorcycle ownership in Bangkok and Kuala Lumpur in comparison with Nagoya. Transp A 10:187–213
Schimek P (1996) Household motor vehicle ownership and use: how much does residential density matter? Transp Res Record 1552:120–125
Senbil M, Zhang J, Fujiwara A (2007) Motorization in Asia. IATSS Res 31:46
Sikder S, Pinjari AR, Srinivasan S, Nowrouzian R (2013) Spatial transferability of travel forecasting models: a review and synthesis. Int J Adv Eng Sci Appl Math 5:104–128
Walker W, Olanipekun O (1989) Interregional stability of household trip generation rates from the 1986 New Jersey Home Interview Survey. Transp Res Rec 1220:47–57
Wilmot CG (1995) Evidence on transferability of trip-generation models. J Transp Eng 121:405–410
Wooldridge J (2012) Introductory econometrics: a modern approach. South-Western Cengage Learning, Mason
Wootton H, Pick G (1967) A model for trips generated by households. J Transp Econ Policy 1(2):137–153
Yamamoto T (2009) Comparative analysis of household car, motorcycle and bicycle ownership between Osaka metropolitan area, Japan and Kuala Lumpur, Malaysia. Transportation 36:351–366
Acknowledgements
The authors would like to thank JICA for providing the data and technical reports used in this study. The lead author acknowledges the support of the Commonwealth Scholarship Commission for conducting the research.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bwambale, A., Choudhury, C.F. & Sanko, N. Car Trip Generation Models in the Developing World: Data Issues and Spatial Transferability. Transp. in Dev. Econ. 5, 10 (2019). https://doi.org/10.1007/s40890-019-0075-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40890-019-0075-7