Abstract
We prove that every toric quiver flag variety Y is isomorphic to a fine moduli space of cyclic modules over the algebra \(\mathrm{End}(T)\) for some tilting bundle T on Y. This generalises the well-known fact that  can be recovered from the endomorphism algebra of
can be recovered from the endomorphism algebra of  .
.
Similar content being viewed by others
1 Introduction
Nakajima [8, Section 3] introduced certain framed moduli spaces associated to a quiver, and the first author showed that these ‘quiver flag varieties’ admit a tilting bundle [3], generalising the construction of Beilinson [1] and Kapranov [6]. Here we extend this link further in the toric case by showing that every toric quiver flag variety can be reconstructed as a fine moduli space of cyclic modules over the endomorphism algebra of the tilting bundle.
Before stating the main result we recall the construction and basic geometric properties of quiver flag varieties, also known as ‘framed quiver moduli’; references for this material include Nakajima [8, Section 3], Reineke [9] and Craw [3]. Let \(\Bbbk \) be an algebraically closed field of characteristic zero and let Q be a finite, connected, acyclic quiver with a unique source. Write  for the vertex set, where 0 is the source, and \(Q_1\) for the arrow set, where for each \(a\in Q_1\) we write \(\mathrm{h}(a)\) and \(\mathrm{t}(a)\) for the head and tail of a respectively. Fix a dimension vector
for the vertex set, where 0 is the source, and \(Q_1\) for the arrow set, where for each \(a\in Q_1\) we write \(\mathrm{h}(a)\) and \(\mathrm{t}(a)\) for the head and tail of a respectively. Fix a dimension vector  satisfying
satisfying  . The group
. The group  acts by conjugation on the space
acts by conjugation on the space  of representations of Q of dimension vector \(\underline{r}\), and we define the quiver flag variety associated to the pair \((Q,\underline{r})\) to be the GIT quotient
of representations of Q of dimension vector \(\underline{r}\), and we define the quiver flag variety associated to the pair \((Q,\underline{r})\) to be the GIT quotient

for the special choice of linearisation  . This GIT quotient is non-empty if and only if the inequality
. This GIT quotient is non-empty if and only if the inequality

holds for each \(i>0\), in which case Y is a smooth Mori Dream Space of dimension  . In fact, Y can be obtained from a tower of Grassmann-bundles
. In fact, Y can be obtained from a tower of Grassmann-bundles

where at each stage, \(Y_i\) is isomorphic to the Grassmannian of rank \(r_i\) quotients of a fixed locally-free sheaf of rank \(s_i\) on \(Y_{i-1}\); see [3, Theorem 3.3]. Hereafter we assume that the inequality (1) is strict for each \(i>0\) to avoid degeneracy in the tower.
Quiver flag varieties naturally carry a collection of vector bundles \(\mathscr {W}_1,\dots , \mathscr {W}_\ell \) that determine many of their algebraic invariants. Indeed, for \(i>0\), the Grassmann-bundle \(Y_i\) over \(Y_{i-1}\) carries a tautological quotient bundle \(\mathscr {V}_i\) of rank \(r_i\), and we write  for the globally-generated bundle of rank \(r_i\) on Y obtained as the pullback under the morphism \(\pi _i:Y\rightarrow Y_i\) in the tower. It follows from the construction that the invertible sheaves
for the globally-generated bundle of rank \(r_i\) on Y obtained as the pullback under the morphism \(\pi _i:Y\rightarrow Y_i\) in the tower. It follows from the construction that the invertible sheaves  provide an integral basis for the Picard group of Y. More generally, the results of Beilinson [1] and Kapranov [6] extend to all quiver flag varieties as follows. Let
provide an integral basis for the Picard group of Y. More generally, the results of Beilinson [1] and Kapranov [6] extend to all quiver flag varieties as follows. Let  denote the set of Young diagrams with no more than k columns and l rows. Recall that for any vector bundle \(\mathscr {W}\) of rank r and for
denote the set of Young diagrams with no more than k columns and l rows. Recall that for any vector bundle \(\mathscr {W}\) of rank r and for  , we obtain a vector bundle
, we obtain a vector bundle  whose fibre over each point is the irreducible
whose fibre over each point is the irreducible  -module of highest weight \(\lambda \).
-module of highest weight \(\lambda \).
Theorem 1.1
([3]) The vector bundle on Y given by

is a tilting bundle. In particular, the bounded derived category of coherent sheaves on Y is equivalent to the bounded derived category of finite-dimensional modules over  .
.
This result answered affirmatively the question of Nakajima [8, Problem 3.10].
We now describe our main result. Work of Bergman and Proudfoot [2, Theorem 2.4] compares any smooth projective variety admitting a tilting bundle to a fine moduli space of modules over the endomorphism algebra. To define the relevant moduli space for the tilting bundle E from (3), list the indecomposable summands as \(E_0, E_1,\dots , E_n\) with  , and consider the dimension vector
, and consider the dimension vector  satisfying
satisfying  for all \(0\leqslant j\leqslant n\). For a special choice of ‘0-generated’ stability condition \(\theta \) (see Sect. 2), we consider the fine moduli space \(\mathscr {M}(A,\varvec{\mathrm v},\theta )\) of isomorphism classes of \(\theta \)-stable A-modules of dimension vector \(\varvec{\mathrm v}\) that was constructed by King [7] using GIT. Since each bundle
for all \(0\leqslant j\leqslant n\). For a special choice of ‘0-generated’ stability condition \(\theta \) (see Sect. 2), we consider the fine moduli space \(\mathscr {M}(A,\varvec{\mathrm v},\theta )\) of isomorphism classes of \(\theta \)-stable A-modules of dimension vector \(\varvec{\mathrm v}\) that was constructed by King [7] using GIT. Since each bundle  is globally-generated, an observation of Craw et al. [4, Theorem 1.1] induces a universal morphism
is globally-generated, an observation of Craw et al. [4, Theorem 1.1] induces a universal morphism
and in our case this is a closed immersion. In fact, [2, Theorem 2.4] implies that \(f_E\) identifies Y with a connected component of \(\mathscr {M}(A,\varvec{\mathrm v},\theta )\), because Y is smooth, E is a tilting bundle, and our stability condition \(\theta \) is ‘great’.
Our main result concerns the special case when  for all \(1\leqslant i\leqslant \ell \), in which case G is an algebraic torus and therefore Y is a toric variety; we call Y a toric quiver flag variety. The toric fan \(\Sigma \) can be described directly in this case (see [5, p. 1517]), and Y is a tower of projective space bundles via (2). We can say the following:
for all \(1\leqslant i\leqslant \ell \), in which case G is an algebraic torus and therefore Y is a toric variety; we call Y a toric quiver flag variety. The toric fan \(\Sigma \) can be described directly in this case (see [5, p. 1517]), and Y is a tower of projective space bundles via (2). We can say the following:
Theorem 1.2
Let Y be a toric quiver flag variety. The morphism  from (4) is an isomorphism.
from (4) is an isomorphism.
As a result, toric quiver flag varieties provide a new class of examples where the programme of Bergman and Proudfoot [2] can be carried out in full, enabling one to reconstruct the variety from the tilting bundle. The special case where Y is isomorphic to projective space recovers the well-known result that  can be reconstructed from the tilting bundle
can be reconstructed from the tilting bundle  of Beilinson [1]. Theorem 1.2 therefore provides further evidence that toric quiver flag varieties provide good multigraded analogues of projective space.
of Beilinson [1]. Theorem 1.2 therefore provides further evidence that toric quiver flag varieties provide good multigraded analogues of projective space.
2 The reduction step
Our assumption gives  for \(1\leqslant i\leqslant \ell \), so the tilting bundle from (3) is simply the direct sum of line bundles
for \(1\leqslant i\leqslant \ell \), so the tilting bundle from (3) is simply the direct sum of line bundles

on Y. Set  , and list the indecomposable summands from (5) as \(E_0, \dots , E_{n}\) with
, and list the indecomposable summands from (5) as \(E_0, \dots , E_{n}\) with  . Consider the endomorphism algebra
. Consider the endomorphism algebra  and the dimension vector
and the dimension vector  .
.
The moduli space that features in Theorem 1.2 is an example of those constructed originally by King [7]. To introduce our choice of stability condition, first set  . An A-module
. An A-module  of dimension vector \(\varvec{\mathrm v}\) is \(\theta ^\prime \)-stable iff M is generated as an A-module by any nonzero element of \(M_0\); any such stability condition is called 0-generated. Since \(\varvec{\mathrm v}\) is primitive and since every \(\theta ^\prime \)-semistable A-module of dimension vector \(\varvec{\mathrm v}\) is \(\theta ^\prime \)-stable (see, for example, [5, Proof of Proposition 3.8]), King [7, Proposition 5.3] constructs the fine moduli space \(\mathscr {M}(A,\varvec{\mathrm v},\theta ^\prime )\) of isomorphism classes of \(\theta ^\prime \)-stable A-modules of dimension vector \(\varvec{\mathrm v}\) as a GIT quotient. In particular, \(\mathscr {M}(A,\varvec{\mathrm v},\theta ^\prime )\) comes with an ample bundle \(\mathscr {O}(1)\). Let \(k\geqslant 1\) denote the smallest positive integer such that
of dimension vector \(\varvec{\mathrm v}\) is \(\theta ^\prime \)-stable iff M is generated as an A-module by any nonzero element of \(M_0\); any such stability condition is called 0-generated. Since \(\varvec{\mathrm v}\) is primitive and since every \(\theta ^\prime \)-semistable A-module of dimension vector \(\varvec{\mathrm v}\) is \(\theta ^\prime \)-stable (see, for example, [5, Proof of Proposition 3.8]), King [7, Proposition 5.3] constructs the fine moduli space \(\mathscr {M}(A,\varvec{\mathrm v},\theta ^\prime )\) of isomorphism classes of \(\theta ^\prime \)-stable A-modules of dimension vector \(\varvec{\mathrm v}\) as a GIT quotient. In particular, \(\mathscr {M}(A,\varvec{\mathrm v},\theta ^\prime )\) comes with an ample bundle \(\mathscr {O}(1)\). Let \(k\geqslant 1\) denote the smallest positive integer such that  is very ample. Then
is very ample. Then  is also a 0-generated stability condition, and we consider the fine moduli space \(\mathscr {M}(A,\varvec{\mathrm v}, \theta )\) of \(\theta \)-stable A-modules of dimension vector \(\varvec{\mathrm v}\); this moduli space is the ‘multigraded linear series’ of E in the sense of [4, Definition 2.5].
is also a 0-generated stability condition, and we consider the fine moduli space \(\mathscr {M}(A,\varvec{\mathrm v}, \theta )\) of \(\theta \)-stable A-modules of dimension vector \(\varvec{\mathrm v}\); this moduli space is the ‘multigraded linear series’ of E in the sense of [4, Definition 2.5].
Since each indecomposable summand of E from (5) is globally-generated, we deduce from [4, Theorem 2.6] that the universal property of \(\mathscr {M}(A,\varvec{\mathrm v}, \theta )\) gives a morphism
and, moreover, \(f_E\) is a closed immersion because the line bundle  is very ample. This puts us in the situation studied by Craw and Smith [5], where it is possible to give an explicit GIT quotient description for both the moduli space \(\mathscr {M}(A,\varvec{\mathrm v},\theta )\) and the image of the universal morphism \(f_E\). Theorem 1.2 will follow once we prove that these two GIT quotients coincide.
is very ample. This puts us in the situation studied by Craw and Smith [5], where it is possible to give an explicit GIT quotient description for both the moduli space \(\mathscr {M}(A,\varvec{\mathrm v},\theta )\) and the image of the universal morphism \(f_E\). Theorem 1.2 will follow once we prove that these two GIT quotients coincide.
To describe \(\mathscr {M}(A,\varvec{\mathrm v},\theta )\) as a GIT quotient, we first present the algebra \(A=\mathrm{End}_{\mathscr {O}_Y}(E)\) using the bound quiver of sections \((Q^\prime \!,R)\) as follows. The quiver \(Q^\prime \) has vertex set  and an arrow from vertex i to j for each irreducible, torus-invariant section of
and an arrow from vertex i to j for each irreducible, torus-invariant section of  , i.e., the corresponding homomorphism from \(E_i\) to
, i.e., the corresponding homomorphism from \(E_i\) to  does not factor through some \(E_k\) with \(k \ne i, j\). To each arrow \(a\in Q^\prime _1\) we associate the corresponding torus-invariant ‘labeling divisor’ \(\mathrm{div}(a)\in \mathbb {N}^{\Sigma (1)}\), where \(\Sigma (1)\) denotes the set of rays of the fan of Y. The two-sided ideal
does not factor through some \(E_k\) with \(k \ne i, j\). To each arrow \(a\in Q^\prime _1\) we associate the corresponding torus-invariant ‘labeling divisor’ \(\mathrm{div}(a)\in \mathbb {N}^{\Sigma (1)}\), where \(\Sigma (1)\) denotes the set of rays of the fan of Y. The two-sided ideal

in \(\Bbbk Q^\prime \) satisfies  (see [5, Proposition 3.3]). Denote the coordinate ring of \(\mathbb {A}^{Q^\prime _1}_\Bbbk \) by
(see [5, Proposition 3.3]). Denote the coordinate ring of \(\mathbb {A}^{Q^\prime _1}_\Bbbk \) by  , where a ranges over \(Q^\prime _1\). The ideal R in the noncommutative ring \(\Bbbk Q^\prime \) determines an ideal in
, where a ranges over \(Q^\prime _1\). The ideal R in the noncommutative ring \(\Bbbk Q^\prime \) determines an ideal in  given by
given by

where the support of a path \(\mathrm{supp}(p)\) is simply the set of arrows that make up the path. This ideal is homogeneous with respect to the action of  by conjugation. It now follows directly from the definition of King [7] that
by conjugation. It now follows directly from the definition of King [7] that

where  denotes the \(k\theta \)-graded piece. In fact, [5, Proposition 3.8] implies that \(\mathscr {M}(A,\varvec{\mathrm v},\theta )\) is the geometric quotient of
denotes the \(k\theta \)-graded piece. In fact, [5, Proposition 3.8] implies that \(\mathscr {M}(A,\varvec{\mathrm v},\theta )\) is the geometric quotient of  by the action of T, where
by the action of T, where

is the irrelevant ideal in  that cuts out the \(\theta \)-unstable locus in \(\mathbb {A}_\Bbbk ^{\!Q^\prime _1}\).
that cuts out the \(\theta \)-unstable locus in \(\mathbb {A}_\Bbbk ^{\!Q^\prime _1}\).
Our task is to compare (7) with the GIT quotient description of the image of \(f_E\). For this, define a map  by setting \(\pi (\chi _a)=(\chi _{\mathrm{h}(a)}-\chi _{\mathrm{t}(a)},\mathrm{div}(a))\), where \(\chi _a\) for \(a\in Q^\prime _1\) and \(\chi _i\) for \(i\in Q^\prime _0\) denote the characteristic functions. The T-homogeneous ideal
by setting \(\pi (\chi _a)=(\chi _{\mathrm{h}(a)}-\chi _{\mathrm{t}(a)},\mathrm{div}(a))\), where \(\chi _a\) for \(a\in Q^\prime _1\) and \(\chi _i\) for \(i\in Q^\prime _0\) denote the characteristic functions. The T-homogeneous ideal

contains \(I_R\) from (6), and [5, Proposition 4.3] establishes that the image of the universal morphism \(f_E\) is isomorphic to the geometric quotient of  by the action of T.
by the action of T.
Proposition 2.1
Suppose that the T-orbit of every closed point of  contains a closed point of
contains a closed point of  . Then Theorem 1.2 holds.
. Then Theorem 1.2 holds.
Proof
The inclusion \(\mathbb {V}(I_{Q^\prime })\subseteq \mathbb {V}(I_R)\) always holds, and the assumption ensures that  , so the closed immersion \(f_E\) is surjective. \(\square \)
, so the closed immersion \(f_E\) is surjective. \(\square \)
In Sect. 4 we prove that the assumption of Proposition 2.1 holds for every toric quiver flag variety Y. To illustrate the strategy, we recall the following well-known construction of  using Beilinson’s tilting bundle.
using Beilinson’s tilting bundle.
Example 2.2
For the acyclic quiver Q with vertex set  and \(n+1\) arrows from 0 to 1, the toric quiver flag variety Y is isomorphic to
and \(n+1\) arrows from 0 to 1, the toric quiver flag variety Y is isomorphic to  and the quiver of sections \(Q^\prime \) for the tilting bundle
and the quiver of sections \(Q^\prime \) for the tilting bundle  is shown in Fig. 1; note that Q is a subquiver of \(Q^\prime \). For each \(1\leqslant m\leqslant n\) and each ray \(\rho \in \Sigma (1)\) in the fan of
is shown in Fig. 1; note that Q is a subquiver of \(Q^\prime \). For each \(1\leqslant m\leqslant n\) and each ray \(\rho \in \Sigma (1)\) in the fan of  defining a torus-invariant divisor
defining a torus-invariant divisor  , let \(a_\rho ^m\) denote the arrow with head at m and labeling divisor
, let \(a_\rho ^m\) denote the arrow with head at m and labeling divisor  . Writing
. Writing  for the variable associated to the arrow \(a_\rho ^m\), we have
for the variable associated to the arrow \(a_\rho ^m\), we have

We claim that a point  lies in the same T-orbit as the point \((v_\rho ^m)\) with components
lies in the same T-orbit as the point \((v_\rho ^m)\) with components  for all \(1\leqslant m\leqslant n\) and \(\rho \in \Sigma (1)\). Clearly
for all \(1\leqslant m\leqslant n\) and \(\rho \in \Sigma (1)\). Clearly  , so the claim and Proposition 2.1 show that Theorem 1.2 holds for
, so the claim and Proposition 2.1 show that Theorem 1.2 holds for  .
.
To prove the claim, note that since \((w_\rho ^m)\not \in \mathbb {V}(B_{Q^\prime })\), the T-action allows us to assume that for all \(1\leqslant m\leqslant n\) there exists \(\rho (m)\in \Sigma (1)\) such that  . Then
. Then  , and (10) implies that
, and (10) implies that  for all \(\rho \in \Sigma (1)\). The case \(\rho =\rho (2)\) gives
for all \(\rho \in \Sigma (1)\). The case \(\rho =\rho (2)\) gives  , so
, so
Let the one-dimensional subgroup  scale by
scale by  at vertex 2 to obtain a point in the same T-orbit as \((w_\rho ^m)\) whose components agree with those of \((v_\rho ^m)\) for \(m=1,2\). Repeating at each successive vertex shows that \((v_\rho ^m)\) and \((w_\rho ^m)\) lie in the same T-orbit as claimed.
at vertex 2 to obtain a point in the same T-orbit as \((w_\rho ^m)\) whose components agree with those of \((v_\rho ^m)\) for \(m=1,2\). Repeating at each successive vertex shows that \((v_\rho ^m)\) and \((w_\rho ^m)\) lie in the same T-orbit as claimed.
3 The tilting quiver
Before establishing that the assumption of Proposition 2.1 holds for every toric quiver flag variety, we describe the tilting quiver \(Q^\prime \) in detail (see Example 3.3).
For the vertex set \(Q^\prime _0\), recall that the line bundles \(\mathscr {W}_1, \dots , \mathscr {W}_\ell \) provide an integral basis for \(\mathrm{Pic}(Y)\cong \mathbb {Z}^{\ell }\). Since \(Q^\prime _0\) is defined by the summands  of the tilting bundle E from (5), it is convenient to realise \(Q^\prime _0\) as the set of lattice points of a cuboid in
of the tilting bundle E from (5), it is convenient to realise \(Q^\prime _0\) as the set of lattice points of a cuboid in  of dimension \(\ell \) with side lengths \(s_1-1,\dots ,s_{\ell }-1\). We label the vertex for
of dimension \(\ell \) with side lengths \(s_1-1,\dots ,s_{\ell }-1\). We label the vertex for  by the corresponding lattice point
by the corresponding lattice point  , giving
, giving

We introduce a total order on \(Q^\prime _0\): for  ,
,  , write \(k<m\) if
, write \(k<m\) if  for the largest index i satisfying
for the largest index i satisfying  .
.
For the arrow set \(Q^\prime _1\), note first that Q is the quiver of sections of  , so the arrows in Q correspond precisely to the torus-invariant prime divisors in Y [5, Remark 3.9]. For \(\rho \in \Sigma (1)\) we write
, so the arrows in Q correspond precisely to the torus-invariant prime divisors in Y [5, Remark 3.9]. For \(\rho \in \Sigma (1)\) we write  for the arrow corresponding to the divisor of zeros
for the arrow corresponding to the divisor of zeros  of a torus-invariant section of
of a torus-invariant section of  . Each \(a_\rho \) may be regarded as an arrow in \(Q^\prime \), so we may identify Q with a complete subquiver of \(Q^\prime \) that we call the base quiver in \(Q^\prime \). More generally, translating each \(a_\rho \) around the cuboid described in the preceding paragraph (so that the head and tail lie in \(Q^\prime _0\)) produces arrows in \(Q^\prime \) that we denote
. Each \(a_\rho \) may be regarded as an arrow in \(Q^\prime \), so we may identify Q with a complete subquiver of \(Q^\prime \) that we call the base quiver in \(Q^\prime \). More generally, translating each \(a_\rho \) around the cuboid described in the preceding paragraph (so that the head and tail lie in \(Q^\prime _0\)) produces arrows in \(Q^\prime \) that we denote  for \(m=\mathrm{h}(a_\rho ^m)\) and
for \(m=\mathrm{h}(a_\rho ^m)\) and  . In fact, we have the following:
. In fact, we have the following:
Lemma 3.1
Every arrow \(a\in Q^\prime _1\) is of the form \(a=a^m_\rho \), where \(m=\mathrm{h}(a)\) and  .
.
Proof
For \(a\in Q^\prime _1\), write  and
and  , so \(\mathrm{div}(a)\) is the divisor of zeros of a section of
, so \(\mathrm{div}(a)\) is the divisor of zeros of a section of  . In terms of prime divisors, we have
. In terms of prime divisors, we have

Let \(1\leqslant k\leqslant \ell \) be the largest value such that  for some \(\rho \in \Sigma (1)\) satisfying \(k=\mathrm{h}(a_\rho )\in Q_0\). Note that
for some \(\rho \in \Sigma (1)\) satisfying \(k=\mathrm{h}(a_\rho )\in Q_0\). Note that  , and moreover,
, and moreover,  . Since \(\mathrm{div}(a)\) is irreducible, translating \(a_\rho \) so that the tail is at vertex \(m^\prime \) forces the head to lie outside the cuboid, giving
. Since \(\mathrm{div}(a)\) is irreducible, translating \(a_\rho \) so that the tail is at vertex \(m^\prime \) forces the head to lie outside the cuboid, giving  or
or  ; similarly, translating \(a_\rho \) so that the head is at m forces the tail to lie outside the cuboid, giving
; similarly, translating \(a_\rho \) so that the head is at m forces the tail to lie outside the cuboid, giving  or
or  . Since
. Since  , both
, both  and
and  must hold, so
must hold, so  . As a result, there must exist \(\sigma \in \Sigma (1)\) satisfying
. As a result, there must exist \(\sigma \in \Sigma (1)\) satisfying  for \(j=\mathrm{h}(a_{\sigma })\). If we set
for \(j=\mathrm{h}(a_{\sigma })\). If we set  and repeat the argument above, we deduce that
and repeat the argument above, we deduce that  . Continuing in this way, we eventually find \(\tau \in \Sigma (1)\) such that
. Continuing in this way, we eventually find \(\tau \in \Sigma (1)\) such that  with \(\mathrm{h}(a_\tau ) = 1\) and \(\mathrm{t}(a_\tau )=0\). But then
with \(\mathrm{h}(a_\tau ) = 1\) and \(\mathrm{t}(a_\tau )=0\). But then  , so we can place a translation of \(a_\tau \) with head at m and tail in the cuboid (or tail at \(m^\prime \) and head in the cuboid). This shows \(\mathrm{div}(a)\) is reducible, a contradiction. \(\square \)
, so we can place a translation of \(a_\tau \) with head at m and tail in the cuboid (or tail at \(m^\prime \) and head in the cuboid). This shows \(\mathrm{div}(a)\) is reducible, a contradiction. \(\square \)
Remark 3.2
Since Q is the quiver of sections of  , the vertices of the base quiver are the vertices
, the vertices of the base quiver are the vertices  , where \(e_i\) denotes the \(i^{\text {th}}\) standard basis vector for \(i>0\), and where
, where \(e_i\) denotes the \(i^{\text {th}}\) standard basis vector for \(i>0\), and where  .
.
The next example illustrates how the base quiver sits inside \(Q^\prime \).
Example 3.3
The quiver Q shown in Fig. 2, (a) defines the toric quiver flag variety  where
where  ; the colours of the arrows indicate the distinct labeling divisors. We have
; the colours of the arrows indicate the distinct labeling divisors. We have  and
and  , so the tilting quiver \(Q^\prime \) has 12 vertices shown in Fig. 2, (b) using the ordering described above. Note that the base quiver is the complete subquiver of \(Q^\prime \) whose vertices are shown in bold in Fig. 2 (b). The colour of each arrow of \(Q^\prime \) is determined by its unique translate arrow from the base quiver.
, so the tilting quiver \(Q^\prime \) has 12 vertices shown in Fig. 2, (b) using the ordering described above. Note that the base quiver is the complete subquiver of \(Q^\prime \) whose vertices are shown in bold in Fig. 2 (b). The colour of each arrow of \(Q^\prime \) is determined by its unique translate arrow from the base quiver.
4 Proof of Theorem 1.2
In light of Lemma 3.1, each point of \(\mathbb {A}^{\!Q^\prime _1}_\Bbbk \) is a tuple \((w_\rho ^m)\) where \(w_\rho ^m\in \Bbbk \) for \(\rho \in \Sigma (1)\) and for all relevant \(m\in Q^\prime _0\). Motivated by Example 2.2, we associate to \((w_\rho ^m)\in \mathbb {A}^{\!Q^\prime _1}_\Bbbk \) an auxiliary point \((v_\rho ^m)\in \mathbb {V}(I_{Q^\prime })\subseteq \mathbb {A}^{\!Q^\prime _1}_\Bbbk \) whose components satisfy

where for \(\rho \in \Sigma (1)\) we write  for the component of the point \((w_\rho ^m)\) corresponding to the unique arrow \(a_\rho \) in the base quiver satisfying
for the component of the point \((w_\rho ^m)\) corresponding to the unique arrow \(a_\rho \) in the base quiver satisfying  .
.
Lemma 4.1
If \((w_\rho ^m)\not \in \mathbb {V}(B_{Q^\prime })\), then \((v_\rho ^m)\not \in \mathbb {V}(B_{Q^\prime })\).
Proof
Fix  and let \(1\leqslant j\leqslant \ell \) be minimal such that
and let \(1\leqslant j\leqslant \ell \) be minimal such that  . Then for all \(\rho \) satisfying \(\mathrm{h}(a_\rho )=j\in Q_0\), the arrow \(a_\rho ^m\) obtained by translating \(a_\rho \) until the head lies at m is an arrow of \(Q^\prime \). At least one of the values
. Then for all \(\rho \) satisfying \(\mathrm{h}(a_\rho )=j\in Q_0\), the arrow \(a_\rho ^m\) obtained by translating \(a_\rho \) until the head lies at m is an arrow of \(Q^\prime \). At least one of the values  is nonzero by assumption, and hence for this value of \(\rho \) we have
is nonzero by assumption, and hence for this value of \(\rho \) we have  as required. \(\square \)
as required. \(\square \)
We now establish notation for the proof of Theorem 1.2. For any  , let
, let  denote the bound quiver of sections of the line bundles
denote the bound quiver of sections of the line bundles on Y with
on Y with  . Explicitly,
. Explicitly,  is the complete subquiver of \(Q^\prime \) with vertex set
is the complete subquiver of \(Q^\prime \) with vertex set  , and the ideal of relations
, and the ideal of relations  satisfies
satisfies

As in Sect. 2, the coordinate ring  of the affine space
of the affine space  contains ideals
contains ideals  and
and  defined as in Eqs. (6), (8) and (9) respectively, each of which is homogeneous with respect to the action of
defined as in Eqs. (6), (8) and (9) respectively, each of which is homogeneous with respect to the action of  by conjugation. The projection onto the coordinates indexed by arrows \(a_\rho ^m\) satisfying \(m\leqslant k\), denoted
by conjugation. The projection onto the coordinates indexed by arrows \(a_\rho ^m\) satisfying \(m\leqslant k\), denoted

is equivariant with respect to the actions of T and  . Notice that
. Notice that  ,
,  and
and  .
.
Proof of Theorem 1.2
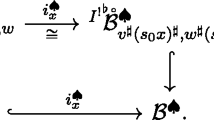
Fix a point  and the corresponding point
and the corresponding point  whose components are defined in equation (11). Since \(w\not \in \mathbb {V}(B_{Q^\prime })\), the action of T enables us to assume that for all \(m\in Q^\prime _0\) there exists \(\rho (m)\in \Sigma (1)\) such that
whose components are defined in equation (11). Since \(w\not \in \mathbb {V}(B_{Q^\prime })\), the action of T enables us to assume that for all \(m\in Q^\prime _0\) there exists \(\rho (m)\in \Sigma (1)\) such that  . In particular, \(v_{\rho (m)}^m=1\) for all relevant \(m\in Q^\prime _0\). Now, for
. In particular, \(v_{\rho (m)}^m=1\) for all relevant \(m\in Q^\prime _0\). Now, for  , the morphism \(\pi _k\) from (12) sends the points w and v to
, the morphism \(\pi _k\) from (12) sends the points w and v to

respectively. We claim that \(\pi _k(v)\) lies in the  -orbit of \(\pi _k(w)\). Given the claim, the special case
-orbit of \(\pi _k(w)\). Given the claim, the special case  shows that the point v lies in the T-orbit of the point w, so Theorem 1.2 follows immediately from Proposition 2.1.
shows that the point v lies in the T-orbit of the point w, so Theorem 1.2 follows immediately from Proposition 2.1.
We prove the claim by induction on the vertex  using the total order on \(Q^\prime _0\) from Sect. 3. The case \(k=e_0\) is immediate, and for
using the total order on \(Q^\prime _0\) from Sect. 3. The case \(k=e_0\) is immediate, and for  the claim follows from Example 2.2; hereafter we assume that \(\ell \geqslant 2\). Suppose the claim holds for all \(m<k\), so we may assume that
the claim follows from Example 2.2; hereafter we assume that \(\ell \geqslant 2\). Suppose the claim holds for all \(m<k\), so we may assume that  for all \(m<k\). It is enough to show for all \(\rho \in \Sigma (1)\), that
for all \(m<k\). It is enough to show for all \(\rho \in \Sigma (1)\), that  and
and

because then we may let the one-dimensional subgroup  scale by
scale by  at vertex k. Before establishing the claim (13), we introduce some notation that we use in the proof.
at vertex k. Before establishing the claim (13), we introduce some notation that we use in the proof.
Notation 4.2
-
(a)
Recall from Sect. 3 that vertices of the tilting quiver \(Q^\prime \) are elements
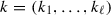 in the lattice \(\mathbb {Z}^\ell \), so
in the lattice \(\mathbb {Z}^\ell \), so  for \(1\leqslant i\leqslant \ell \). Note also (see Remark 3.2) that the standard basis vectors \(e_1,\dots , e_\ell \) of \(\mathbb {Z}^\ell \) denote certain vertices of \(Q^\prime \). This notation is standard and we hope that no confusion arises in what follows.
for \(1\leqslant i\leqslant \ell \). Note also (see Remark 3.2) that the standard basis vectors \(e_1,\dots , e_\ell \) of \(\mathbb {Z}^\ell \) denote certain vertices of \(Q^\prime \). This notation is standard and we hope that no confusion arises in what follows. -
(b)
It is convenient to distinguish certain elements of \(Q_0\) and \(\mathbb {Z}^\ell \).
-
First we distinguish certain elements of the vertex set
 of the original quiver. For the ray
of the original quiver. For the ray 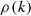 appearing in (13), define \(0\leqslant \alpha <\beta \leqslant \ell \) by
appearing in (13), define \(0\leqslant \alpha <\beta \leqslant \ell \) by 
where
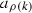 is the arrow in the original quiver Q satisfying
is the arrow in the original quiver Q satisfying  . Also, let \(1\leqslant \delta \leqslant \ell \) be minimal such that the induction vertex
. Also, let \(1\leqslant \delta \leqslant \ell \) be minimal such that the induction vertex  satisfies
satisfies  , and define \(0\leqslant \gamma <\delta \) by setting
, and define \(0\leqslant \gamma <\delta \) by setting 
Minimality of \(\delta \) implies that either \(\gamma =0\) or
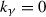 and, moreover, that \(\delta \leqslant \beta \).
and, moreover, that \(\delta \leqslant \beta \). -
Next we introduce certain elements of \(\mathbb {Z}^\ell \). For any ray \(\rho \in \Sigma (1)\), define

where \(a_\rho \) is the arrow in the original quiver satisfying
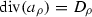 (recall that
(recall that  ). In particular, by the previous bullet point we have $$\begin{aligned} \underline{d}(\rho (k))=e_\beta -e_\alpha \quad \text {and}\quad \underline{d}(\rho (e_\delta ))=e_\delta -e_\gamma . \end{aligned}$$
). In particular, by the previous bullet point we have $$\begin{aligned} \underline{d}(\rho (k))=e_\beta -e_\alpha \quad \text {and}\quad \underline{d}(\rho (e_\delta ))=e_\delta -e_\gamma . \end{aligned}$$
-
We now return to the proof of the claim (13), treating the cases \(\delta <\beta \) and \(\delta =\beta \) separately.
Case 1: Suppose first that \(\delta <\beta \). In this case we proceed in three steps:
Step 1: Show that equation (13) holds for \(\rho =\rho (e_\delta )\) when \(\gamma =\alpha =0\) or \(\gamma \ne \alpha \). We use generators of the ideal  corresponding to pairs of paths in
corresponding to pairs of paths in  with head at k. Consider paths of length two as in Fig. 3, where for now we substitute
with head at k. Consider paths of length two as in Fig. 3, where for now we substitute  and \(\rho (e_\delta )\) in place of \(\rho _1\) and \(\rho _2\). In this case, we claim that each vertex in Fig. 3 lies in the quiver
and \(\rho (e_\delta )\) in place of \(\rho _1\) and \(\rho _2\). In this case, we claim that each vertex in Fig. 3 lies in the quiver  . Indeed,
. Indeed,  , so its head k and tail \(k-e_\beta +e_\alpha \) lie in
, so its head k and tail \(k-e_\beta +e_\alpha \) lie in  ; this implies
; this implies  and either \(\alpha =0\) or
and either \(\alpha =0\) or  . Also,
. Also,  and either \(\gamma =0\) or
and either \(\gamma =0\) or  , so \(k-\underline{d}(\rho (e_\delta ))\) is equal to \(k-e_\delta +e_\gamma \), which lies in the quiver
, so \(k-\underline{d}(\rho (e_\delta ))\) is equal to \(k-e_\delta +e_\gamma \), which lies in the quiver  . For the fourth vertex in Fig. 3, either:
. For the fourth vertex in Fig. 3, either:
-
(i)
\(\gamma =\alpha =0\), giving
 , and the inequalities
, and the inequalities 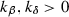 imply that the fourth vertex
imply that the fourth vertex  lies in
lies in  as claimed; or
as claimed; or -
(ii)
\(\gamma \ne \alpha \), and since \(\gamma<\delta <\beta \), the fourth vertex \(k-e_\beta +e_\alpha -e_\delta +e_\gamma \) lies in
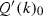 because
because  , either \(\alpha =0\) or \(k_\alpha < s_\alpha -1\) and either \(\gamma =0\) or
, either \(\alpha =0\) or \(k_\alpha < s_\alpha -1\) and either \(\gamma =0\) or  .
.
Figure 3 therefore determines a binomial in  which implies that
which implies that

Our induction assumption gives  for all \(m<k\), and since
for all \(m<k\), and since  , we have
, we have  . In particular,
. In particular,  and
and

which establishes equation (13) for \(\rho =\rho (e_\delta )\) when \(\gamma =\alpha =0\) or \(\gamma \ne \alpha \).
Step 2: Show that equation (13) holds for \(\rho =\rho (e_\delta )\) when \(\gamma =\alpha \ne 0\). Since  , the method from Step 1 applies verbatim unless
, the method from Step 1 applies verbatim unless  . In this case, define \(0\leqslant \varepsilon < \gamma \) by
. In this case, define \(0\leqslant \varepsilon < \gamma \) by

giving \(\underline{d}(\rho (e_\gamma ))=e_\gamma -e_\varepsilon \). Consider paths of length three as in Fig. 4, where for now we substitute  and \(\rho (e_\gamma )\) in place of \(\rho _1,\rho _2\) and \(\rho _3\). Again, we claim that each vertex in Fig. 4 lies in the quiver
and \(\rho (e_\gamma )\) in place of \(\rho _1,\rho _2\) and \(\rho _3\). Again, we claim that each vertex in Fig. 4 lies in the quiver  ; the proof is similar to that from Step 1 (here, minimality of \(\delta \) implies \(\varepsilon =0\) or
; the proof is similar to that from Step 1 (here, minimality of \(\delta \) implies \(\varepsilon =0\) or  , and we use the inequalities \(\varepsilon<\gamma<\delta <\beta \)). Thus we obtain a binomial in
, and we use the inequalities \(\varepsilon<\gamma<\delta <\beta \)). Thus we obtain a binomial in  which, applying the inductive assumption
which, applying the inductive assumption  for all \(m<k\), gives
for all \(m<k\), gives

Since  , we have
, we have  and
and  which implies that equation (13) holds for \(\rho =\rho (e_\delta )\).
which implies that equation (13) holds for \(\rho =\rho (e_\delta )\).
Step 3: Show that equation (13) holds for all \(\rho \in \Sigma (1)\). Consider any arrow \(a_\rho ^k\) in \(Q^\prime \) with head at k. The vertices

satisfy \(\underline{d}(\rho )=e_\mu -e_\lambda \) with \(0\leqslant \lambda <\mu \leqslant \ell \). We proceed using the approach from Steps 1–2:
-
(i)
If \(\mu \ne \beta \), then we substitute \(\rho \) and
 in place of \(\rho _1\) and \(\rho _2\) in Fig. 3 as in Step 1, unless \(\lambda =\alpha \ne 0\) and \(s_\alpha =2\) in which case we substitute \(\rho (e_\alpha )\) in place of \(\rho _3\) in Fig. 4 as in Step 2. In either case, we obtain an equation relating components of \(w_k\) which, after applying the inductive hypothesis if necessary, becomes
in place of \(\rho _1\) and \(\rho _2\) in Fig. 3 as in Step 1, unless \(\lambda =\alpha \ne 0\) and \(s_\alpha =2\) in which case we substitute \(\rho (e_\alpha )\) in place of \(\rho _3\) in Fig. 4 as in Step 2. In either case, we obtain an equation relating components of \(w_k\) which, after applying the inductive hypothesis if necessary, becomes 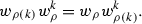
Steps 1 and 2 established
 , and
, and  , so equation (13) holds.
, so equation (13) holds. -
(ii)
Otherwise, \(\mu =\beta \). Substitute \(\rho (e_\delta )\) and \(\rho \) in place of \(\rho _1\) and \(\rho _2\) in Fig. 3 as in Step 1, unless \(\lambda =\gamma \ne 0\) and
 in which case we substitute \(\rho (e_\gamma )\) in place of \(\rho _3\) in Fig. 4 as in Step 2. As in part \((\mathrm {i})\) above, we obtain an equation which simplifies to
in which case we substitute \(\rho (e_\gamma )\) in place of \(\rho _3\) in Fig. 4 as in Step 2. As in part \((\mathrm {i})\) above, we obtain an equation which simplifies to 
Steps 1 and 2 established
 , so equation (13) follows.
, so equation (13) follows.
This completes the proof of equation (13) in Case 1.
Case 2: Suppose instead that \(\delta =\beta \). If  then the proof is identical to Case 1. If on the other hand
then the proof is identical to Case 1. If on the other hand  , then the vertex
, then the vertex  that plays a key role in Case 1 does not lie in
that plays a key role in Case 1 does not lie in  . In the special case that \(k=e_\delta \), making k a vertex of the base quiver, then we have
. In the special case that \(k=e_\delta \), making k a vertex of the base quiver, then we have  for all relevant \(\rho \in \Sigma (1)\) and there is nothing to prove. If \(k\ne e_\delta \), we introduce another useful vertex of the original quiver: let \(\xi \) be minimal such that \(\delta <\xi \leqslant \ell \) and
for all relevant \(\rho \in \Sigma (1)\) and there is nothing to prove. If \(k\ne e_\delta \), we introduce another useful vertex of the original quiver: let \(\xi \) be minimal such that \(\delta <\xi \leqslant \ell \) and  , and define \(0\leqslant \eta <\xi \) by setting
, and define \(0\leqslant \eta <\xi \) by setting

giving \(\underline{d}(\rho (e_\xi ))=e_\xi -e_\eta \). We treat the cases \(\eta \ne \delta \) and \(\eta =\delta \) separately.
Subcase 2A: If  , then either \(\eta =0\) or
, then either \(\eta =0\) or  , so \(k-\underline{d}(\rho (e_\xi )) = k-e_\xi +e_\eta \) is a vertex of
, so \(k-\underline{d}(\rho (e_\xi )) = k-e_\xi +e_\eta \) is a vertex of  . We may now proceed just as in Case 1 except that \(\rho (e_\xi )\) replaces \(\rho (e_\delta )\) throughout (so \(\xi \) and \(\eta \) replace \(\delta \) and \(\gamma \) respectively).
. We may now proceed just as in Case 1 except that \(\rho (e_\xi )\) replaces \(\rho (e_\delta )\) throughout (so \(\xi \) and \(\eta \) replace \(\delta \) and \(\gamma \) respectively).
Subcase 2B: Suppose instead that  . We have already reduced to the case
. We have already reduced to the case  . If
. If  then once again, \(k-\underline{d}(\rho (e_\xi )) = k-e_\xi +e_\delta \) is a vertex of
then once again, \(k-\underline{d}(\rho (e_\xi )) = k-e_\xi +e_\delta \) is a vertex of  and we proceed as in Case 1 with \(\rho (e_\xi )\) replacing \(\rho (e_\delta )\) throughout. If
and we proceed as in Case 1 with \(\rho (e_\xi )\) replacing \(\rho (e_\delta )\) throughout. If  , then we proceed as follows:
, then we proceed as follows:
Step 1: Show that  . If \(\gamma \ne \alpha \) or \(\gamma =\alpha =0\), then we use Fig. 4 with
. If \(\gamma \ne \alpha \) or \(\gamma =\alpha =0\), then we use Fig. 4 with  ,
,  and
and  to obtain the equation
to obtain the equation

which gives  . Otherwise, \(\gamma =\alpha \ne 0\), giving
. Otherwise, \(\gamma =\alpha \ne 0\), giving  . It may be that
. It may be that  , in which case
, in which case  and hence
and hence  as required. If
as required. If  , then consider the pair of paths of length four as in Fig. 5, where we substitute
, then consider the pair of paths of length four as in Fig. 5, where we substitute  and \(\rho (e_\gamma )\) in place of \(\rho _1,\dots ,\rho _4\) (in fact, both paths pass through the same set of vertices in this case).
and \(\rho (e_\gamma )\) in place of \(\rho _1,\dots ,\rho _4\) (in fact, both paths pass through the same set of vertices in this case).
We obtain the equation

which gives  and completes Step 1.
and completes Step 1.
Step 2: Show that equation (13) holds for all \(\rho \in \Sigma (1)\). For any  , the vertices
, the vertices

satisfy \(\underline{d}(\rho )=e_\mu -e_\lambda \) with \(0\leqslant \lambda <\mu \leqslant \ell \).
-
(i)
If \(\mu >\delta \), use Fig. 3 with
 and
and  , unless \(\lambda =\alpha \ne 0\) and
, unless \(\lambda =\alpha \ne 0\) and 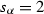 in which case use Fig. 4 with the addition of
in which case use Fig. 4 with the addition of  . Either way, we obtain the equation
. Either way, we obtain the equation  which, since
which, since 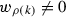 by Step 1, gives (13).
by Step 1, gives (13). -
(ii)
If \(\mu =\delta \), use Fig. 4 with
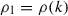 ,
, 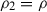 and
and  unless \(\lambda =\alpha \ne 0\) and
unless \(\lambda =\alpha \ne 0\) and 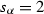 in which case use Fig. 5 with the addition of
in which case use Fig. 5 with the addition of 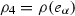 . Either way, we obtain
. Either way, we obtain  which, since
which, since  by Step 1, gives (13).
by Step 1, gives (13).
This concludes the proof in Case 2, and completes the proof of Theorem 1.2. \(\square \)
Remark 4.3
Our approach relies on the explicit description of the image of the morphism \(f_E\) in Theorem 1.2 as the GIT quotient \(\mathbb {V}(I_{Q^\prime })/\!\!/\!_\theta T\), see [5, Theorem 1.1]. We do not at present have a similar description in the non-toric setting.
Example 4.4
We conclude with an example to illustrate the proof of Theorem 1.2. Let Q and \(Q^\prime \) be the quivers in Fig. 2, so \(\ell =3\). Suppose \(k=(0,1,1)\in Q^\prime _0\), so \(\delta =2\). The three arrows with head at k have tails at (1, 1, 0) (light blue), (0, 0, 1) (red) and (1, 0, 1) (blue), and we label the corresponding rays \(\rho _1, \rho _2\) and \(\rho _3\) respectively. We now illustrate in two different situations why  and why the equation
and why the equation  from (13) holds for \(\rho =\rho _1, \rho _2, \rho _3\).
from (13) holds for \(\rho =\rho _1, \rho _2, \rho _3\).

-
(a)
Suppose that
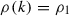 . Then \(\beta =3\) and \(\alpha =1\) (see Fig. 2, (a)), and
. Then \(\beta =3\) and \(\alpha =1\) (see Fig. 2, (a)), and  . Suppose \(\rho (e_\delta )=\rho (e_2)=\rho _2\) so that \(\gamma =0\) and
. Suppose \(\rho (e_\delta )=\rho (e_2)=\rho _2\) so that \(\gamma =0\) and 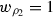 . This is an example of Case 1 as \(\delta <\beta \), and since \(\gamma =0\) we require only Step 1. In this case Fig. 3 becomes
. This is an example of Case 1 as \(\delta <\beta \), and since \(\gamma =0\) we require only Step 1. In this case Fig. 3 becomes 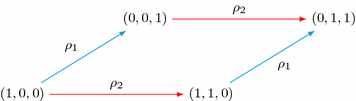
and the relation gives the equation
 . Moreover,
. Moreover, 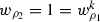 implies
implies  and
and 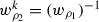 which establishes (13) for \(\rho =\rho _1, \rho _2\). The remaining arrow \(a^k_{\rho _3}\) with head at k requires Step 3, and in this case for \(\rho =\rho _3\) we have \(\mu =2\) and \(\lambda =1\). Since
which establishes (13) for \(\rho =\rho _1, \rho _2\). The remaining arrow \(a^k_{\rho _3}\) with head at k requires Step 3, and in this case for \(\rho =\rho _3\) we have \(\mu =2\) and \(\lambda =1\). Since  and
and  , we require Step 3 (i) to deduce
, we require Step 3 (i) to deduce  . This implies
. This implies  , establishing (13) for \(\rho =\rho _3\).
, establishing (13) for \(\rho =\rho _3\). -
(b)
Suppose
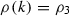 , so \(\beta =2\),
, so \(\beta =2\),  and
and  . Suppose that \(\rho (e_2)=\rho _2\), so \(\gamma =0\) and
. Suppose that \(\rho (e_2)=\rho _2\), so \(\gamma =0\) and 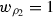 . Since \(\delta =\beta \) and
. Since \(\delta =\beta \) and  , this is an example of Case 2. Since \(k\ne e_2\), we compute \(\xi =3\). Write \(\rho _4\) for the label of the pink arrow with head at (0, 0, 1) and tail at (0, 1, 0), and suppose \(\rho (e_3)=\rho _4\). Then \(\eta =\mathrm{t}(a_{\rho _4})=2\) and
, this is an example of Case 2. Since \(k\ne e_2\), we compute \(\xi =3\). Write \(\rho _4\) for the label of the pink arrow with head at (0, 0, 1) and tail at (0, 1, 0), and suppose \(\rho (e_3)=\rho _4\). Then \(\eta =\mathrm{t}(a_{\rho _4})=2\) and  . Since \(\eta =\delta \) and
. Since \(\eta =\delta \) and  , we require Subcase 2B. Following Step 1, since \(\gamma =0\) we use Fig. 4 as shown below. This yields the equation
, we require Subcase 2B. Following Step 1, since \(\gamma =0\) we use Fig. 4 as shown below. This yields the equation 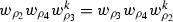 which simplifies
which simplifies 
to \(1=w_{\rho _3} w^k_{\rho _2}\), giving
 as required. Step 2 of Subcase 2B establishes (13) for \(\rho =\rho _1,\rho _2,\rho _3\): we already know this for \(\rho =\rho _3\) by assumption; the case \(\rho =\rho _2\) is provided by Step 1 since
as required. Step 2 of Subcase 2B establishes (13) for \(\rho =\rho _1,\rho _2,\rho _3\): we already know this for \(\rho =\rho _3\) by assumption; the case \(\rho =\rho _2\) is provided by Step 1 since  ; and the case \(\rho =\rho _1\) is a simple application of Step 2 (i), where we apply Fig. 3 to the rectangle with vertices (2, 0, 0), (1, 1, 0), (1, 0, 1), k and arrows labelled \(\rho _1\) and \(\rho _3\).
; and the case \(\rho =\rho _1\) is a simple application of Step 2 (i), where we apply Fig. 3 to the rectangle with vertices (2, 0, 0), (1, 1, 0), (1, 0, 1), k and arrows labelled \(\rho _1\) and \(\rho _3\).
References
Beilinson, A.A.: Coherent sheaves on \(\mathbb{P}^{n}\) and problems of linear algebra. Funct. Anal. Appl. 12(3), 214–216 (1978)
Bergman, A., Proudfoot, N.J.: Moduli spaces for Bondal quivers. Pacific J. Math. 237(2), 201–221 (2008)
Craw, A.: Quiver flag varieties and multigraded linear series. Duke Math. J. 156(3), 469–500 (2011)
Craw, A., Ito, Y., Karmazyn, J.: Multigraded linear series and recollement (2017). arXiv:1701.01679 (to appear in Math. Z.)
Craw, A., Smith, G.G.: Projective toric varieties as fine moduli spaces of quiver representations. Amer. J. Math. 130(6), 1509–1534 (2008)
Kapranov, M.M.: On the derived categories of coherent sheaves on some homogeneous spaces. Invent. Math. 92(3), 479–508 (1988)
King, A.D.: Moduli of representations of finite-dimensional algebras. Quart. J. Math. Oxford Ser. 45(180), 515–530 (1994)
Nakajima, H.: Varieties associated with quivers. In: Bautista, R., Martínez-Villa, R., de La Pena, J.A. (eds.) Representation Theory of Algebras and Related Topics. CMS Conference Proceedings, vol. 19, pp. 139–157. American Mathematical Society, Providence (1996)
Reineke, M.: Framed quiver moduli, cohomology, and quantum groups. J. Algebra 320(1), 94–115 (2008)
Acknowledgements
We thank the anonymous referee for a number of helpful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
The first author was supported in part by EPSRC Grant EP/J019410/1, and the second author is supported by a doctoral studentship from EPSRC.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Craw, A., Green, J. Reconstructing toric quiver flag varieties from a tilting bundle. European Journal of Mathematics 4, 185–199 (2018). https://doi.org/10.1007/s40879-017-0194-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0194-9


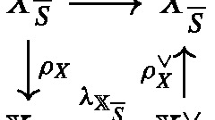


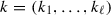 in the lattice
in the lattice  for
for  of the original quiver. For the ray
of the original quiver. For the ray 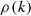 appearing in (
appearing in (
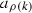 is the arrow in the original quiver Q satisfying
is the arrow in the original quiver Q satisfying  . Also, let
. Also, let  satisfies
satisfies  , and define
, and define 
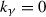 and, moreover, that
and, moreover, that 
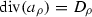 (recall that
(recall that  ). In particular, by the previous bullet point we have
). In particular, by the previous bullet point we have 
 , and the inequalities
, and the inequalities 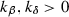 imply that the fourth vertex
imply that the fourth vertex  lies in
lies in  as claimed; or
as claimed; or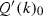 because
because  , either
, either  .
.
 in place of
in place of 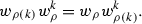
 , and
, and  , so equation (
, so equation ( in which case we substitute
in which case we substitute 
 , so equation (
, so equation ( and
and  , unless
, unless 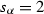 in which case use Fig.
in which case use Fig.  . Either way, we obtain the equation
. Either way, we obtain the equation  which, since
which, since 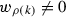 by Step 1, gives (
by Step 1, gives (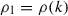 ,
, 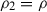 and
and  unless
unless 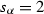 in which case use Fig.
in which case use Fig. 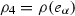 . Either way, we obtain
. Either way, we obtain  which, since
which, since  by Step 1, gives (
by Step 1, gives (
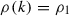 . Then
. Then  . Suppose
. Suppose 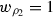 . This is an example of Case 1 as
. This is an example of Case 1 as 
 . Moreover,
. Moreover, 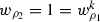 implies
implies  and
and 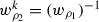 which establishes (
which establishes ( and
and  , we require Step 3 (i) to deduce
, we require Step 3 (i) to deduce  . This implies
. This implies  , establishing (
, establishing (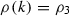 , so
, so  and
and  . Suppose that
. Suppose that 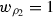 . Since
. Since  , this is an example of Case 2. Since
, this is an example of Case 2. Since  . Since
. Since  , we require Subcase 2B. Following Step 1, since
, we require Subcase 2B. Following Step 1, since 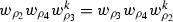 which simplifies
which simplifies 
 as required. Step 2 of Subcase 2B establishes (
as required. Step 2 of Subcase 2B establishes ( ; and the case
; and the case