Abstract
We extend Ferrand’s results about pushouts of schemes to the category of algebraic spaces.
Similar content being viewed by others
1 Introduction
In [3], Ferrand studied schematic pushouts of the form  , where \(f:T\rightarrow Y\) is an affine morphism and \(g:T\hookrightarrow Z\) is a closed immersion. When f is finite such pushout is called pinching or pinching of Z with respect to f. Although studying pinchings was, probably, Ferrand’s main motivation, he realized that the “right generality”, which allows one to prove all the fundamental results, is obtained by weakening the finiteness assumption on f. In the current paper we study the case of algebraic spaces Y, Z, and T with the same assumptions on f and g. We call such a triple \({\mathscr {P}}=(T;Y,Z)\) a Ferrand pushout datum. If \({\mathscr {P}}\) admits a pushout X in the category of algebraic spaces such that the morphisms \(Y\rightarrow X\) and \(Z\rightarrow X\) are affine then
, where \(f:T\rightarrow Y\) is an affine morphism and \(g:T\hookrightarrow Z\) is a closed immersion. When f is finite such pushout is called pinching or pinching of Z with respect to f. Although studying pinchings was, probably, Ferrand’s main motivation, he realized that the “right generality”, which allows one to prove all the fundamental results, is obtained by weakening the finiteness assumption on f. In the current paper we study the case of algebraic spaces Y, Z, and T with the same assumptions on f and g. We call such a triple \({\mathscr {P}}=(T;Y,Z)\) a Ferrand pushout datum. If \({\mathscr {P}}\) admits a pushout X in the category of algebraic spaces such that the morphisms \(Y\rightarrow X\) and \(Z\rightarrow X\) are affine then  is called a Ferrand pushout.
is called a Ferrand pushout.
1.1 Motivation
Let \(g:T\hookrightarrow Z\) be a closed immersion. If \(f:T\rightarrow Y\) is also a closed immersion, then the pinching  can be viewed as the scheme obtained by gluing Y and Z along the closed subscheme T.
can be viewed as the scheme obtained by gluing Y and Z along the closed subscheme T.
A more interesting and less intuitive case is the case when f is an affine open immersion, or, more generally, a pro-open immersion; e.g., the embedding of the generic point. In this case we call the Ferrand pushout a composition, and say that X is obtained by composing Y and Z along T. At first glance, gluing an open subscheme of Y to a closed subscheme of Z may seem unnatural. For example, such pushout is usually non-noetherian even if Y and Z are. Nevertheless, compositions naturally appear in the theory of valued rings and schemes over them. For example, any valuation ring of non-zero finite height is composed of valuation rings of height one, and on the geometric side this corresponds to the composition of spectra of valuation rings of height one. More generally, compositions of schemes appear in applications of valuation theory to algebraic geometry, such as the study of relative Riemann–Zariski spaces and the proof of Nagata’s compactification theorem by the first author [9, Section 2.3]. Similarly, Rydh uses compositions in his work [7, Section 6] on Nagata’s compactification of certain classes of algebraic stacks.
In the sequel papers [10, 11] we define valuation algebraic spaces, and use them to study RZ spaces in the category of algebraic spaces, obtaining, as an application, a new proof of Nagata’s compactification for algebraic spaces. Composing valuation algebraic spaces plays an important technical role in these papers. Although we only use compositions in our applications, and the proofs are slightly easier when f is a monomorphism, we decided to study arbitrary Ferrand pushouts in the category of algebraic spaces because the main results hold true in this generality, and the additional arguments needed for this case are not very involved.
Curiously enough, the only published proof of Nagata’s compactification for algebraic spaces does not involve compositions but makes a serious use of pinchings, see [2, Theorem 2.2.2]. Our results, in particular, subsume that theorem.
1.2 Main results
1.2.1 Properties of Ferrand pushouts
We say that a Ferrand pushout datum \({\mathscr {P}}\) is affine if Y, Z and T are so. It is easy to see that if the Ferrand pushout  is a scheme (resp. affine) then \({\mathscr {P}}\) possesses an open affine covering \({\mathscr {P}}=\bigcup _i{\mathscr {P}}_i\) (resp. \({\mathscr {P}}\) is affine). In Theorem 4.3 we prove that, conversely, if \({\mathscr {P}}\) possesses an open affine covering then there exists a Ferrand pushout
is a scheme (resp. affine) then \({\mathscr {P}}\) possesses an open affine covering \({\mathscr {P}}=\bigcup _i{\mathscr {P}}_i\) (resp. \({\mathscr {P}}\) is affine). In Theorem 4.3 we prove that, conversely, if \({\mathscr {P}}\) possesses an open affine covering then there exists a Ferrand pushout  , and if \({\mathscr {P}}\) is affine then so is X. A closely related Theorem 4.5 asserts that the pushouts of schemes constructed by Ferrand in [3] are, in fact, pushouts in the category of all algebraic spaces.
, and if \({\mathscr {P}}\) is affine then so is X. A closely related Theorem 4.5 asserts that the pushouts of schemes constructed by Ferrand in [3] are, in fact, pushouts in the category of all algebraic spaces.
The following properties of Ferrand pushout  are established in Theorem 4.8: (i) the pushout is compatible with topological realizations, i.e.,
are established in Theorem 4.8: (i) the pushout is compatible with topological realizations, i.e.,  , (ii)
, (ii)  , (iii) set-theoretically, X is the disjoint union of its closed subspace Y and open subspace
, (iii) set-theoretically, X is the disjoint union of its closed subspace Y and open subspace  .
.
Claim (i) is extended to other topologies in Theorem 6.4. Moreover, pullback and Ferrand pushout induce equivalences of categories of flat X-schemes and effective flat pushout data over \({\mathscr {P}}\), which preserve various properties of morphisms.
Finally, by Theorem 6.6, certain properties of morphisms hold for \(Z\rightarrow X\) if and only if they hold for \(T\rightarrow Y\); and by Theorem 6.8, certain properties relative to a base space hold for  if and only if they hold for \({\mathscr {P}}\).
if and only if they hold for \({\mathscr {P}}\).
1.2.2 Existence of Ferrand pushouts
We prove in Theorem 6.2 that the Ferrand pushout  exists if and only if the pushout datum \({\mathscr {P}}=(T;Y,Z)\) admits an affine étale covering
exists if and only if the pushout datum \({\mathscr {P}}=(T;Y,Z)\) admits an affine étale covering  , i.e., affine étale coverings
, i.e., affine étale coverings  ,
,  , and
, and  with identifications
with identifications  . Whether such coverings exist is an innocent-looking problem, which seems to be rather difficult. It is closely related to the lifting problem for étale morphisms
. Whether such coverings exist is an innocent-looking problem, which seems to be rather difficult. It is closely related to the lifting problem for étale morphisms  with respect to a closed immersion \(T\hookrightarrow Z\), see Section 5.2. We managed to solve the latter problem for ind-quasi-affine Z, but the general case remains open. Consequently, we prove in Theorem 5.8 that an étale affine covering exists in the following cases: (i) Z is ind-quasi-affine, (ii) the pushout is a pinching, (iii) Z is decent and |T| is finite and discrete. We do not know a single example of Ferrand pushout datum that admits no affine étale covering.
with respect to a closed immersion \(T\hookrightarrow Z\), see Section 5.2. We managed to solve the latter problem for ind-quasi-affine Z, but the general case remains open. Consequently, we prove in Theorem 5.8 that an étale affine covering exists in the following cases: (i) Z is ind-quasi-affine, (ii) the pushout is a pinching, (iii) Z is decent and |T| is finite and discrete. We do not know a single example of Ferrand pushout datum that admits no affine étale covering.
Remark 1.1
(i) Theorem 5.8 (i) is the main geometric input in our approach, which, in particular, is used to prove that affine Ferrand pushouts are pushouts in the category of all algebraic spaces (surjectivity of \(\psi \) in the proof of Theorem 4.3).
(ii) Existence of pinchings in the non-noetherian case is a new result. Artin proved in [1, Theorem 6.1] that pinchings always exist in the noetherian case, see also [2, Theorem 2.2.2] for a more complete claim. Artin’s proof uses his algebraization criteria, so the noetherian assumption cannot be eliminated. Note also that pinchings (and all Ferrand pushouts) are only compatible with flat base changes, so one cannot deduce the non-noetherian case by approximating  by noetherian algebraic spaces. A simpler proof of existence of pinchings, based on construction of an étale affine covering, was given by Kollár in [6, Theorem 38]. Although the noetherian assumption is made in loc.cit. too, it can be easily removed. Our proof in the case of pinchings is a variation on Kollár’s one.
by noetherian algebraic spaces. A simpler proof of existence of pinchings, based on construction of an étale affine covering, was given by Kollár in [6, Theorem 38]. Although the noetherian assumption is made in loc.cit. too, it can be easily removed. Our proof in the case of pinchings is a variation on Kollár’s one.
1.3 Plan of the paper
The paper is written using the language of pushout data and their morphisms, see Section 2.2.1. Preliminary results on general pushouts and affine Ferrand pushouts are collected in Sects. 2–3. Most of this material is known, in particular, we recall Ferrand’s results. In Section 4, we start by constructing pushouts for \({\mathscr {P}}\) admitting open affine coverings, see Lemma 4.1 and Theorem 4.3, and then extend this to the case when \({\mathscr {P}}\) possesses only an étale affine covering  such that each
such that each  possesses an open affine covering. The latter condition is removed in Theorem 6.2 since it is always satisfied, but to prove this, we must study existence of étale affine coverings in Section 5. Finally, Section 6 is devoted to proving finer criteria for existence of pushouts, see Theorem 6.2, and studying how various properties of spaces and morphisms descend through pushouts, see Theorems 6.4, 6.6 and 6.8.
possesses an open affine covering. The latter condition is removed in Theorem 6.2 since it is always satisfied, but to prove this, we must study existence of étale affine coverings in Section 5. Finally, Section 6 is devoted to proving finer criteria for existence of pushouts, see Theorem 6.2, and studying how various properties of spaces and morphisms descend through pushouts, see Theorems 6.4, 6.6 and 6.8.
2 Preliminaries
2.1 Algebraic spaces
We adopt the definitions, notation, and conventions of [8]. In particular, we do not assume that algebraic spaces are quasi-separated.
2.1.1 Coverings and presentations
By an affine covering of an algebraic space X in a given topology \(\tau \) we mean a \(\tau \)-covering  such that all \(U_i\) are affine. For a \(\tau \)-covering
such that all \(U_i\) are affine. For a \(\tau \)-covering  , set \(U=\coprod _i U_i\) and
, set \(U=\coprod _i U_i\) and  . Then \(R\rightrightarrows U\) is a \(\tau \)-equivalence relation, and \(X=U/R\). If U is a scheme then so is R, and we say that \(R\rightrightarrows U\) is a \(\tau \)-presentation of X.
. Then \(R\rightrightarrows U\) is a \(\tau \)-equivalence relation, and \(X=U/R\). If U is a scheme then so is R, and we say that \(R\rightrightarrows U\) is a \(\tau \)-presentation of X.
2.1.2 Ind-quasi-affine morphisms
Recall that a scheme X is called ind-quasi-affine if every quasi-compact open of X is quasi-affine. Similarly, a morphism of schemes \(X\rightarrow Y\) is called ind-quasi-affine if the pullback of an open affine is ind-quasi-affine. It is shown in [8, Tag:0AP5] that ind-quasi-affiness is stable under base change, fpqc local on the base, and that any separated locally quasi-finite morphism is ind-quasi-affine. We say that a morphism of algebraic spaces \(X\rightarrow Y\) is ind-quasi-affine if for any morphism \(Z\rightarrow Y\) with an affine source the pullback  is ind-quasi-affine. The next properties follow easily from [8, Tags:0AP5,02X4,0418]:
is ind-quasi-affine. The next properties follow easily from [8, Tags:0AP5,02X4,0418]:
Lemma 2.1
(i) Any separated locally quasi-finite morphism is ind-quasi-affine. In particular, so is the diagonal  of an algebraic space X.
of an algebraic space X.
(ii) If Y is ind-quasi-affine then so is any morphism \(Y\rightarrow X\).
2.1.3 Zariski points
Recall that a point of an algebraic space X is an equivalence class of morphisms  , where F is a field, and two maps are equivalent if and only if they are dominated by a third map. A point x is called a Zariski point if its class contains a quasi-compact monomorphism. Recall that X is called decent in [8, Tag:03I8] if all its points are Zariski points; e.g., quasi-separated spaces are decent by [8, Tag:03JX]. It follows from [8, Tag:0BBN] that if x is a Zariski point, and
, where F is a field, and two maps are equivalent if and only if they are dominated by a third map. A point x is called a Zariski point if its class contains a quasi-compact monomorphism. Recall that X is called decent in [8, Tag:03I8] if all its points are Zariski points; e.g., quasi-separated spaces are decent by [8, Tag:03JX]. It follows from [8, Tag:0BBN] that if x is a Zariski point, and  is its quasi-compact monomorphic representative then (a) any representative of x factors through f, and (b) f factors through an étale presentation. Thus, the quasi-compact monomorphic representative of x is unique up-to an isomorphism, and by abuse of language, we will not distinguish between x and
is its quasi-compact monomorphic representative then (a) any representative of x factors through f, and (b) f factors through an étale presentation. Thus, the quasi-compact monomorphic representative of x is unique up-to an isomorphism, and by abuse of language, we will not distinguish between x and  , and will call F the residue field of
x.
, and will call F the residue field of
x.
2.1.4 A criterion for being a monomorphism
Lemma 2.2
Assume that \(h:Y\rightarrow X\) is a representable morphism locally of finite type and \(g:X'\rightarrow X\) is any surjective morphism. Then h is a monomorphism if and only if so is  .
.
Proof
Monomorphisms are stable under arbitrary base changes, thus one direction is clear. By [8, Tag:042Q], we may assume that X and \(X'\) are schemes, and hence so is Y. For any point  the base change
the base change  is a monomorphism. It then follows by fpqc descent that the same is true for
is a monomorphism. It then follows by fpqc descent that the same is true for  for \(x=g(x')\). Since g is surjective, the restriction of h over any point of X is a monomorphism, hence h is a monomorphism by [5, \(\mathrm IV_4\), 17.2.6].\(\square \)
for \(x=g(x')\). Since g is surjective, the restriction of h over any point of X is a monomorphism, hence h is a monomorphism by [5, \(\mathrm IV_4\), 17.2.6].\(\square \)
2.2 General pushouts
2.2.1 Pushout data
Let \({\mathfrak C}\) be one of the following categories: affine schemes, schemes, or algebraic spaces. By a pushout datum \({\mathscr {P}}\) in \({\mathfrak C}\) we mean a diagram
where  , and f, g are separated morphisms. The colimit of \({\mathscr {P}}\) in \({\mathfrak C}\) is called the pushout of Y and Z with respect to T, and is denoted by
, and f, g are separated morphisms. The colimit of \({\mathscr {P}}\) in \({\mathfrak C}\) is called the pushout of Y and Z with respect to T, and is denoted by  or
or  . By abuse of notation, we often refer to \({\mathscr {P}}\) as a triple (T; Y, Z), omitting the morphisms in the notation. If \({\mathfrak C}\) is our default category of algebraic spaces we omit \({\mathfrak C}\) in the notation \(\amalg ^{\mathfrak C}\).
. By abuse of notation, we often refer to \({\mathscr {P}}\) as a triple (T; Y, Z), omitting the morphisms in the notation. If \({\mathfrak C}\) is our default category of algebraic spaces we omit \({\mathfrak C}\) in the notation \(\amalg ^{\mathfrak C}\).
Remark 2.3
It often happens that two geometric categories \({\mathfrak C}\subset {\mathfrak C}'\) possess different pushouts  and
and  , i.e., the natural \({\mathfrak C}'\)-morphism
, i.e., the natural \({\mathfrak C}'\)-morphism  is not an isomorphism. A classical example of this phenomenon is a quotient stack \(X'\) and its coarse moduli space X. Another example is the pushout of
is not an isomorphism. A classical example of this phenomenon is a quotient stack \(X'\) and its coarse moduli space X. Another example is the pushout of  and
and  along
along  . While in the category of k-schemes the pushout is the projective line, in the category of k-affine schemes it is just a point. We will see that Ferrand pushouts are more stable, and, in particular, an affine Ferrand pushout is the pushout in the category of all algebraic spaces.
. While in the category of k-schemes the pushout is the projective line, in the category of k-affine schemes it is just a point. We will see that Ferrand pushouts are more stable, and, in particular, an affine Ferrand pushout is the pushout in the category of all algebraic spaces.
Consider a commutative diagram of pushout data \({\mathscr {P}}\) and \({\mathscr {P}}'\)

If both squares are cartesian then \(\phi :{\mathscr {P}}\rightarrow {\mathscr {P}}'\) is called a morphism of pushout data. If  and
and  then \(\phi :{\mathscr {P}}\rightarrow U\) is called a map from the pushout datum \({\mathscr {P}}\) to the algebraic space U. Plainly, a composition of morphisms is a morphism, and the composition of a morphism and a map is a map.
then \(\phi :{\mathscr {P}}\rightarrow U\) is called a map from the pushout datum \({\mathscr {P}}\) to the algebraic space U. Plainly, a composition of morphisms is a morphism, and the composition of a morphism and a map is a map.
The cartesian condition is rather restrictive. For instance, if  is the product defined componentwise, then the natural projections
is the product defined componentwise, then the natural projections  are usually not morphisms. However, one easily checks that the category of pushout data admits fiber products, which are nothing but componentwise fiber products. Moreover, if \({\mathscr {P}}\rightarrow U\) is a map and
are usually not morphisms. However, one easily checks that the category of pushout data admits fiber products, which are nothing but componentwise fiber products. Moreover, if \({\mathscr {P}}\rightarrow U\) is a map and  is a morphism of algebraic spaces then
is a morphism of algebraic spaces then  is a morphism, where
is a morphism, where  is defined componentwise.
is defined componentwise.
Unless explicitly said to the contrary, we say that a diagram of pushout data (resp. a pushout datum) possesses certain property if all its components do. In particular, if \({\mathfrak C}\) is the category of algebraic spaces then we define affine pushout data, étale morphisms, fppf affine covers, etc., via this rule.
Remark 2.4
Since the category of pushout data admits no products one should be careful while defining equivalence relation. So, by an fppf or étale equivalence relation we mean two morphisms \({\mathscr {P}}_1\rightrightarrows {\mathscr {P}}_0\) defining fppf or étale equivalence relations on the \(T_i,Y_i\), and \(Z_i\) components.
Lemma 2.5
Let \({\mathscr {P}}_1\rightrightarrows {\mathscr {P}}_0\) be an fppf equivalence relation. Set \(Y=Y_0/Y_1\), \(Z=Z_0/Z_1\), \(T=T_0/T_1\), and \({\mathscr {P}}={\mathscr {P}}_0/{\mathscr {P}}_1=(T;Y,Z)\). Then Y, Z, T are algebraic spaces, the commutative diagram \({\mathscr {P}}_0\rightarrow {\mathscr {P}}\) is a morphism, and  .
.
Proof
By Artin’s theorem [8, Tag:04S6], Y, Z, and T are algebraic spaces. Thus, the last two assertions follow from [8, Tag:07S3].\(\square \)
2.2.2 Quasi-coherent modules, pullback and pushforward functors
For any pushout datum \({\mathscr {P}}=(T;Y,Z)\) set \({\mathscr {O}}_{\mathscr {P}}=({\mathscr {O}}_T;{\mathscr {O}}_Y,{\mathscr {O}}_Z)\). A quasi-coherent \({\mathscr {O}}_{\mathscr {P}}\)-module \({\mathscr {F}}\) is a triple of quasi-coherent modules \(({\mathscr {F}}_T;{\mathscr {F}}_Y,{\mathscr {F}}_Z)\) with isomorphisms \(\alpha _{\mathscr {F}}:f^*({\mathscr {F}}_Y)\rightarrow {\mathscr {F}}_T\) and \(\beta _{\mathscr {F}}:g^*({\mathscr {F}}_Z)\rightarrow {\mathscr {F}}_T\). This agrees with the usual definition of modules over algebraic spaces if \(Y=T=Z\). An \({\mathscr {O}}_{\mathscr {P}}\)-module is flat, finitely generated, etc., if all its components are. A morphism of modules is a triple of morphism compatible with the homomorphisms \(\alpha _\bullet \) and \(\beta _\bullet \). This defines a category \(\mathrm{QCoh}_{\mathscr {P}}\).
For a map \(\phi :{\mathscr {P}}\rightarrow U\) from a pushout datum to an algebraic space we have the pullback functor \(\phi ^*:\mathrm{QCoh}_U\rightarrow \mathrm{QCoh}_{{\mathscr {P}}}\) defined componentwise.
Lemma 2.6
Let \(\phi :(T;Y,Z)\rightarrow U\) be a map from a pushout datum to an algebraic space. Then \(\phi ^*\) admits right adjoint \(\phi _*\), which is given by the formula

Proof
Pick \({\mathscr {G}}\in \mathrm{QCoh}_U\). To give a homomorphism \(\phi ^*({\mathscr {G}})\rightarrow {\mathscr {F}}\) is the same as to give compatible homomorphisms from \({\mathscr {G}}\) to \(\phi _{Y*}({\mathscr {F}}_Y),\phi _{Z*}({\mathscr {F}}_Z)\) and \(\phi _{T*}({\mathscr {F}}_T)\), which is equivalent to giving a homomorphism  . \(\square \)
. \(\square \)
Remark 2.7
A similar theory applies to the categories of quasi-coherent algebras verbatim, so we omit the details.
3 Affine Ferrand pushouts
3.1 Terminology
A pushout datum \({\mathscr {P}}=(T;Y,Z)\) is called Ferrand if \(T\rightarrow Y\) is affine and \(T\rightarrow Z\) is a closed immersion. In the category of schemes such pushouts were introduced and studied extensively by Ferrand [3]. If the pushout  exists and the morphisms \(Y\rightarrow X\) and \(Z\rightarrow X\) are affine then we say that X is a Ferrand pushout and the Ferrand pushout datum \({\mathscr {P}}\) is effective.
exists and the morphisms \(Y\rightarrow X\) and \(Z\rightarrow X\) are affine then we say that X is a Ferrand pushout and the Ferrand pushout datum \({\mathscr {P}}\) is effective.
If all components of a Ferrand pushout datum \({\mathscr {P}}\) are affine then we say that \({\mathscr {P}}\) is an affine Ferrand pushout datum and  is the affine Ferrand pushout. We will prove in Theorem 4.3 that
is the affine Ferrand pushout. We will prove in Theorem 4.3 that  , so it is, in fact, Ferrand pushout of \({\mathscr {P}}\), but we have to distinguish the two notions until then.
, so it is, in fact, Ferrand pushout of \({\mathscr {P}}\), but we have to distinguish the two notions until then.
3.2 Ferrand diagrams of rings
3.2.1 Definition
Let \(B\rightarrow K\leftarrow C\) be homomorphisms of rings such that \(C\rightarrow K\) is surjective. Set  , and consider the commutative diagrams
, and consider the commutative diagrams

where the right diagram is the diagram of the corresponding spectra. We say that the left cartesian square is a Ferrand diagram of rings.
3.2.2 Conductor
The ideal  is called the conductor of the Ferrand diagram. Note that \(\phi \) induces an isomorphism
is called the conductor of the Ferrand diagram. Note that \(\phi \) induces an isomorphism  , and the diagram is completely determined by \(\phi \) and I. Vice versa, for a homomorphism \(\phi :A\rightarrow C\) and an ideal \(I\subset A\) such that
, and the diagram is completely determined by \(\phi \) and I. Vice versa, for a homomorphism \(\phi :A\rightarrow C\) and an ideal \(I\subset A\) such that  is an ideal of C, set \(B=A/I\), \(K=C/I\). Then the corresponding diagram is Ferrand.
is an ideal of C, set \(B=A/I\), \(K=C/I\). Then the corresponding diagram is Ferrand.
3.2.3 Basic properties
By a bicartesian square we mean a square diagram which is both cartesian and cocartesian.
Lemma 3.1
Let assumptions and notation be as in diagram (1). Then,
-
(i)
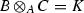 , so Ferrand diagrams are bicartesian.
, so Ferrand diagrams are bicartesian. -
(ii)
If \(A\rightarrow A'\) is flat then the diagram (1)
 is Ferrand.
is Ferrand. -
(iii)
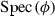 induces an isomorphism of open subschemes
induces an isomorphism of open subschemes  .
.
Proof
(i) Let I be the conductor. Then  .
.
(ii) The sequence  is exact, hence by the flatness assumption so is
is exact, hence by the flatness assumption so is  , where
, where  . Thus,
. Thus,  , and the diagram (1)
, and the diagram (1) is Ferrand.
is Ferrand.
(iii) By (ii),  for any \(f\in A\). Thus, for \(f\in I\), \(B_f=K_f=0\), \(A_f=C_f\), and so \(Z_f=X_f\). Hence
for any \(f\in A\). Thus, for \(f\in I\), \(B_f=K_f=0\), \(A_f=C_f\), and so \(Z_f=X_f\). Hence  .\(\square \)
.\(\square \)
Example 3.2
If  ,
,  ,
,  , and the map \(C\rightarrow K\) sends y to 0, then
, and the map \(C\rightarrow K\) sends y to 0, then  , and the conductor ideal is
, and the conductor ideal is  . Notice that A is not noetherian even though B, C, and K are so.
. Notice that A is not noetherian even though B, C, and K are so.
3.3 Affine Ferrand pushouts
3.3.1 Basic properties
In general, affine pushouts  may contain almost no information about the components of \({\mathscr {P}}\), cf. Remark 2.3. However, affine Ferrand pushouts behave much better:
may contain almost no information about the components of \({\mathscr {P}}\), cf. Remark 2.3. However, affine Ferrand pushouts behave much better:
Proposition 3.3
Let  be an affine Ferrand pushout. Then,
be an affine Ferrand pushout. Then,
-
(i)
The topological pushout
 is naturally homeomorphic to |X|,
is naturally homeomorphic to |X|, -
(ii)
 ,
, -
(iii)
\(Y\rightarrow X\) is a closed immersion,
 is an open immersion, and \(|X|=|Y|\amalg |U|\) set-theoretically.
is an open immersion, and \(|X|=|Y|\amalg |U|\) set-theoretically.
Proof
Assertion (i) follows from [3, Theorem 5.1 and Scholie 4.3], and assertions (ii)–(iii) follow from Lemma 3.1.\(\square \)
3.3.2 Liftings of semivaluations
Assume that \(T\rightarrow Y\) is an open immersion, in particular, the pushout is a composition. Then Proposition 3.3 (i) implies that the topological space |X| is glued from its open subspace |Z| and closed subspace |Y| along |T|. In particular, for any \(z\in |Z|\) with a specialization \(y\in |Y|\) there exists a point \(t\in |T|\) with \(y\preceq t\preceq z\). Thus, any continuous map from a topological space totally ordered by the specialization relation to |X| for which the preimage of |Y| consists of at most one point factors through |Z|. For example, in the situation of Example 3.2, a map  from a valuation scheme factors through Z if and only if \(f^*x\) is invertible. If \(f^*x\) is not invertible then the valuation of \(f^*x\) is strictly positive, and since the valuation of \(f^*(x^{-n}y)\) is non-negative, the valuation of \(f^*y\) is strictly greater than the valuation of \(f^*x^n\) for all n. Thus, \(\sqrt{f^*I}=\sqrt{(f^*x^ny)_{n\in {\mathbb Z}}}\varsubsetneq (f^*x)\subseteq m_R\), and since radical ideals in valuation rings are prime we obtain that \(f^{-1}(Y)\) contains at least two points. The following strengthening of this fact will be used to show that Ferrand pushouts preserve separatedness.
from a valuation scheme factors through Z if and only if \(f^*x\) is invertible. If \(f^*x\) is not invertible then the valuation of \(f^*x\) is strictly positive, and since the valuation of \(f^*(x^{-n}y)\) is non-negative, the valuation of \(f^*y\) is strictly greater than the valuation of \(f^*x^n\) for all n. Thus, \(\sqrt{f^*I}=\sqrt{(f^*x^ny)_{n\in {\mathbb Z}}}\varsubsetneq (f^*x)\subseteq m_R\), and since radical ideals in valuation rings are prime we obtain that \(f^{-1}(Y)\) contains at least two points. The following strengthening of this fact will be used to show that Ferrand pushouts preserve separatedness.
Lemma 3.4
Let assumptions and notation be as in diagram (1). Assume that R is a valuation ring of non-zero height, i.e., R is not a field,  , \(s\in S\) the closed point, and \(f:S\rightarrow X\) a morphism such that \(f^{-1}(Y)=\{s\}\). Then f admits a unique lifting \(g:S\rightarrow Z\), and the latter morphism satisfies \(g^{-1}(T)=\{s\}\).
, \(s\in S\) the closed point, and \(f:S\rightarrow X\) a morphism such that \(f^{-1}(Y)=\{s\}\). Then f admits a unique lifting \(g:S\rightarrow Z\), and the latter morphism satisfies \(g^{-1}(T)=\{s\}\).
Proof
The uniqueness of lifting follows from the separatedness of \(Z\rightarrow X\), and \(g^{-1}(T)=f^{-1}(Y)=\{s\}\) because  . Thus, let us prove the existence.
. Thus, let us prove the existence.
Let \(\eta \in X\) be the image of the generic point of S. Then  and
and  is a valuation ring. Since f factors through a morphism
is a valuation ring. Since f factors through a morphism  , it suffices to lift \(f'\) to Z. Thus, after replacing R with \(R'\) we may assume that R is a valuation ring of \(k(\eta )\). By our assumptions
, it suffices to lift \(f'\) to Z. Thus, after replacing R with \(R'\) we may assume that R is a valuation ring of \(k(\eta )\). By our assumptions  , hence the homomorphism \(A\rightarrow k(\eta )\) factors through the homomorphism \(C\rightarrow k(\eta )\), and we should only prove that the image \(C(\eta )\subset k(\eta )\) of C lies in R.
, hence the homomorphism \(A\rightarrow k(\eta )\) factors through the homomorphism \(C\rightarrow k(\eta )\), and we should only prove that the image \(C(\eta )\subset k(\eta )\) of C lies in R.
Assume to the contrary that some \(x\in C\) is mapped to  . Then
. Then  lies in the maximal ideal \(m_R\). Let \(I\subset A\) be the conductor of the diagram. Since \(f^{-1}(Y)=\{s\}\), the radical of
lies in the maximal ideal \(m_R\). Let \(I\subset A\) be the conductor of the diagram. Since \(f^{-1}(Y)=\{s\}\), the radical of  coincides with \(m_R\). In particular, there exists \(n\geqslant 1\) such that
coincides with \(m_R\). In particular, there exists \(n\geqslant 1\) such that  , and hence
, and hence  , which is a contradiction.\(\square \)
, which is a contradiction.\(\square \)
Recall that a ring A is Prüfer if and only if all its localizations are valuation rings. So, the following is an immediate consequence of Lemma 3.4.
Corollary 3.5
Let assumptions and notation be as in diagram (1). Assume that R is a Prüfer ring such that  has no isolated points, and \(f:S\rightarrow X\) is a morphism such that the preimage of Y is contained in the set of closed points of S. Then f admits a unique lifting to a morphism \(g:S\rightarrow Z\).
has no isolated points, and \(f:S\rightarrow X\) is a morphism such that the preimage of Y is contained in the set of closed points of S. Then f admits a unique lifting to a morphism \(g:S\rightarrow Z\).
3.3.3 Descent of properties through \(\phi _*\)
Assume that  is a Ferrand affine pushout, and let \(\phi :{\mathscr {P}}\rightarrow X\) be the natural map. While the pullback preserves all natural properties of modules, the situation with the pushforward is more delicate. When working on [9] the first author learned from Rydh the following example, in which finite presentation is not respected by \(\phi _*\).
is a Ferrand affine pushout, and let \(\phi :{\mathscr {P}}\rightarrow X\) be the natural map. While the pullback preserves all natural properties of modules, the situation with the pushforward is more delicate. When working on [9] the first author learned from Rydh the following example, in which finite presentation is not respected by \(\phi _*\).
Example 3.6
Let k be a field. Consider discrete valuation rings  and \(C=K[y]_{(y)}\), where \(K=k(x)\). In particular,
and \(C=K[y]_{(y)}\), where \(K=k(x)\). In particular,  . Then their composition A is the preimage of B in C, which is a valuation ring of height two. In fact, A is the valuation ring of k(x, y) such that \(|y|\ll |x|\ll 1\), where the valuation is written multiplicatively. Note that \(C=A_x\) and \(B=A/I\), where \(I=yC\) is the conductor of the corresponding Ferrand diagram.
. Then their composition A is the preimage of B in C, which is a valuation ring of height two. In fact, A is the valuation ring of k(x, y) such that \(|y|\ll |x|\ll 1\), where the valuation is written multiplicatively. Note that \(C=A_x\) and \(B=A/I\), where \(I=yC\) is the conductor of the corresponding Ferrand diagram.
Set \(I_n=x^{-n}yA\), and note that \(I=\bigcup _n I_n\) is not finitely generated as an ideal of A because \(I_n\varsubsetneq I_{n+1}\) for any n. In particular,  is finitely generated but not finitely presented over A, while \(A'_n=A/I_n\) are finitely presented. Note that the B-module
is finitely generated but not finitely presented over A, while \(A'_n=A/I_n\) are finitely presented. Note that the B-module  , the C-module
, the C-module  , and the K-module
, and the K-module  are finitely presented and independent of n. In particular,
are finitely presented and independent of n. In particular,  , and we obtain the following pathologies: \(\phi _*\) takes the finitely presented \({\mathscr {O}}_{\mathscr {P}}\)-module \((K'_n;B'_n,C'_n)\) to the non-finitely presented A-module \(A'\), and the natural homomorphism \(A'_n\rightarrow \phi _*\phi ^*(A'_n)=A'\) is not injective.
, and we obtain the following pathologies: \(\phi _*\) takes the finitely presented \({\mathscr {O}}_{\mathscr {P}}\)-module \((K'_n;B'_n,C'_n)\) to the non-finitely presented A-module \(A'\), and the natural homomorphism \(A'_n\rightarrow \phi _*\phi ^*(A'_n)=A'\) is not injective.
On the positive side, we have the following list of properties respected by \(\phi _*\):
Proposition 3.7
Let \(\phi :{\mathscr {P}}\rightarrow X\) be as in Section 3.3.3, and let \((\dag )\) be one of the following properties of quasi-coherent modules (resp. algebras): being (i) flat, (ii) finitely generated, (iii) flat and finitely presented. Then, both \(\phi _*\) and \(\phi ^*\) preserve \((\dag )\).
Proof
For modules, the assertion was proved by Ferrand [3, Theorem 2.2 (iv)] (one uses the fact that a flat finitely presented module is nothing but a projective module of finite type). Obviously, this also covers (i) for algebras.
To prove (ii) and (iii) for algebras, let \(A'\) be an A-algebra,  , and
, and  . In (ii) we should prove that if \(B'\) and \(C'\) are finitely generated then \(A'\) is finitely generated. Obviously, there exists a finitely generated A-subalgebra \(A''\subset A'\) such that the homomorphisms
. In (ii) we should prove that if \(B'\) and \(C'\) are finitely generated then \(A'\) is finitely generated. Obviously, there exists a finitely generated A-subalgebra \(A''\subset A'\) such that the homomorphisms  and
and  are surjective. Since \(\phi ^*\) is right exact, this implies that \(\phi ^*(A'/A'')=0\), and then
are surjective. Since \(\phi ^*\) is right exact, this implies that \(\phi ^*(A'/A'')=0\), and then  by [3, Theorem 2.2 (ii)].
by [3, Theorem 2.2 (ii)].
Finally, assume that \(B'\) and \(C'\) are flat and finitely presented. Then \(A'\) is A-flat by (i), and finitely generated over A by (ii). It remains to prove that it is finitely presented over A. Pick a surjective A-homomorphism  , and let us prove that
, and let us prove that  is finitely generated. By (ii) for modules, it suffices to show that
is finitely generated. By (ii) for modules, it suffices to show that  and
and  are finitely generated. Since \(A'\) is A-flat, \(I_A\) is flat too. Therefore,
are finitely generated. Since \(A'\) is A-flat, \(I_A\) is flat too. Therefore,  and
and  , where
, where  and
and  are the base changes of \(f_A\). Thus, \(I_B\) and \(I_C\) are finitely generated modules since \(B'\) and \(C'\) are finitely presented.\(\square \)
are the base changes of \(f_A\). Thus, \(I_B\) and \(I_C\) are finitely generated modules since \(B'\) and \(C'\) are finitely presented.\(\square \)
3.3.4 Adjunctions
Proposition 3.8
Let \(\phi :{\mathscr {P}}\rightarrow X\) be as in Section 3.3.3. Then,
-
(i)
The adjunction \(\phi ^*\phi _*({\mathscr {M}})\rightarrow {\mathscr {M}}\) is an isomorphism for any quasi-coherent \({\mathscr {O}}_{\mathscr {P}}\)-module (resp. \({\mathscr {O}}_{\mathscr {P}}\)-algebra) \({\mathscr {M}}\).
-
(ii)
If \({\mathscr {F}}\) is a flat quasi-coherent \({\mathscr {O}}_X\)-module (resp. \({\mathscr {O}}_X\)-algebra) then the adjunction \({\mathscr {F}}\rightarrow \phi _*\phi ^*({\mathscr {F}})\) is an isomorphism.
Proof
Obviously, it suffices to prove the proposition for modules, and in this case (i) is proved in [3, Theorem 2.2 (i)]. As for (ii), one should check that any flat A-module M satisfies  , and this is done by tensoring the exact sequence
, and this is done by tensoring the exact sequence  with M.\(\square \)
with M.\(\square \)
Propositions 3.7 and 3.8 immediately imply the following result.
Corollary 3.9
The functors \(\phi _*\) and \(\phi ^*\) establish essentially inverse equivalences between the categories of flat modules (resp. algebras) over \({\mathscr {O}}_X\) and \({\mathscr {O}}_{\mathscr {P}}\). Moreover, these functors establish equivalences of the full subcategories consisting of flat and finitely generated modules (resp. algebras), and of flat and finitely presented modules (resp. algebras).
Remark 3.10
One cannot remove the flatness assumption in Corollary 3.9. For example, in the situation described in Example 3.6, the finitely presented A-module \(A'_n\) is not contained in the essential image of \(\phi _*\). Indeed, if  for a \({\mathscr {P}}\)-module M then
for a \({\mathscr {P}}\)-module M then  by Proposition 3.8 (i), and so
by Proposition 3.8 (i), and so  . But we saw in Example 3.6 that the cyclic modules \(\phi _*\phi ^*(A'_n)=A'\) and \(A'_n\) are not isomorphic.
. But we saw in Example 3.6 that the cyclic modules \(\phi _*\phi ^*(A'_n)=A'\) and \(A'_n\) are not isomorphic.
3.4 Equivalence of categories
Assume that  and \(\phi :{\mathscr {P}}\rightarrow X\) is the natural map. Then by \(\phi ^{-1}\) we denote the pullback functors from the category of X-spaces to the category of pushout data over \({\mathscr {P}}\), i.e.,
and \(\phi :{\mathscr {P}}\rightarrow X\) is the natural map. Then by \(\phi ^{-1}\) we denote the pullback functors from the category of X-spaces to the category of pushout data over \({\mathscr {P}}\), i.e.,  .
.
Lemma 3.11
If \({\mathscr {P}}\) is an affine Ferrand pushout datum,  , and \({\mathfrak C}\) and \({\mathfrak D}\) the categories of affine flat schemes (resp. pushout data) over X (resp. \({\mathscr {P}}\mathrm{)}\) then,
, and \({\mathfrak C}\) and \({\mathfrak D}\) the categories of affine flat schemes (resp. pushout data) over X (resp. \({\mathscr {P}}\mathrm{)}\) then,
-
(i)
\(\phi ^{-1}:{\mathfrak C}\rightarrow {\mathfrak D}\) and \(\amalg ^{\mathfrak {Aff}}:{\mathfrak D}\rightarrow {\mathfrak C}\) are essentially inverse equivalences.
-
(ii)
Both \(\phi ^{-1}\) and \(\amalg ^\mathfrak {Aff}\) preserve the following properties of morphisms: being (a) surjective, (b) étale, (c) flat, (d) finite type, (e) flat and finitely presented.
Proof
(i) follows from Corollary 3.9 by passing to spectra since \(\phi ^{-1}\) corresponds to \(\phi ^*\) and \(\amalg ^{\mathfrak {Aff}}\) corresponds to \(\phi _*\) by Lemma 2.6.
(ii) Clearly, \(\phi ^{-1}\) respects all five properties, so let us prove that they are also respected by \(\amalg ^{\mathfrak {Aff}}\). Cases (c)–(e) follow from Corollary 3.9. Recall that a finitely presented flat morphism is étale if and only if so are its fibers. Thus, case (b) follows from (e), since the morphism  is surjective by Proposition 3.3. In the same fashion, case (a) follows from the surjectivity of h.\( \square \)
is surjective by Proposition 3.3. In the same fashion, case (a) follows from the surjectivity of h.\( \square \)
4 General Ferrand pushouts
Now let us study general Ferrand pushouts. At one place we will have to use a result on existence of étale affine coverings of pushouts, whose proof is postponed until Section 5 for expositional reasons.
4.1 Zariski globalization of \(\amalg ^\mathfrak {Aff}\)
Our first goal is to globalize the functor \(\amalg ^\mathfrak {Aff}\) with respect to Zariski topology.
Lemma 4.1
There exists a unique extension of \(\amalg ^\mathfrak {Aff}\) to a functor \(\amalg ^\mathfrak {Sch}\) that associates a scheme to a Ferrand pushout datum possessing an open affine covering, and takes open coverings to open coverings.
Proof
Let \({\mathscr {P}}\) be a Ferrand pushout datum with an open affine covering  . We claim that each intersection \({\mathscr {P}}_{ij}\) possesses an open affine covering
. We claim that each intersection \({\mathscr {P}}_{ij}\) possesses an open affine covering  . Indeed, \({\mathscr {P}}_{ij}\) is open in \({\mathscr {P}}_i\), hence by Proposition 3.3 (i) it is the pullback of an open subscheme \(X_{ij}\) of
. Indeed, \({\mathscr {P}}_{ij}\) is open in \({\mathscr {P}}_i\), hence by Proposition 3.3 (i) it is the pullback of an open subscheme \(X_{ij}\) of  . Take an open affine covering \(\{X_{ijk}\}_k\) of \(X_{ij}\) and define \({\mathscr {P}}_{ijk}\) to be its pullback to \({\mathscr {P}}_{ij}\).
. Take an open affine covering \(\{X_{ijk}\}_k\) of \(X_{ij}\) and define \({\mathscr {P}}_{ijk}\) to be its pullback to \({\mathscr {P}}_{ij}\).
At this stage, uniqueness of \(\amalg ^\mathfrak {Sch}\) is clear: for each \({\mathscr {P}}_{ij}\) fix an open affine covering  of \({\mathscr {P}}_{ij}\) and glue
of \({\mathscr {P}}_{ij}\) and glue  from the affine schemes \(X_i\) along the open subschemes
from the affine schemes \(X_i\) along the open subschemes  . To prove existence one should check independence of the construction of choices. In fact, it suffices to check that one can replace the affine covering \(\{{\mathscr {P}}_i\}_i\) with its refinement, which is clear.\(\square \)
. To prove existence one should check independence of the construction of choices. In fact, it suffices to check that one can replace the affine covering \(\{{\mathscr {P}}_i\}_i\) with its refinement, which is clear.\(\square \)
Ferrand proved that  is the pushout of \({\mathscr {P}}\) in the category of schemes, which implies that so is
is the pushout of \({\mathscr {P}}\) in the category of schemes, which implies that so is  ; thereby justifying the notation. We shall not use this, and instead we we will prove directly that
; thereby justifying the notation. We shall not use this, and instead we we will prove directly that  is the pushout in the category of all algebraic spaces. Let us start with a necessary auxiliary result.
is the pushout in the category of all algebraic spaces. Let us start with a necessary auxiliary result.
Lemma 4.2
Assume that \({\mathscr {P}}\) is a Ferrand pushout datum that admits an open affine covering and  . Let \({\mathfrak C}\) be the category of flat schemes over X (with arbitrary morphisms between them), and \({\mathfrak D}\) the category of flat Ferrand pushout data over \({\mathscr {P}}\) that possess an open affine covering. Then,
. Let \({\mathfrak C}\) be the category of flat schemes over X (with arbitrary morphisms between them), and \({\mathfrak D}\) the category of flat Ferrand pushout data over \({\mathscr {P}}\) that possess an open affine covering. Then,
-
(i)
The natural map \(\phi :{\mathscr {P}}\rightarrow X\) is affine,
 , \(Y\rightarrow X\) is a closed immersion,
, \(Y\rightarrow X\) is a closed immersion,  is an open immersion,
is an open immersion,  , and \(|X|=|Y|\amalg |U|\) set-theoretically.
, and \(|X|=|Y|\amalg |U|\) set-theoretically. -
(ii)
The functors \(\phi ^{-1}:{\mathfrak C}\rightarrow {\mathfrak D}\) and \(\amalg ^\mathfrak {Sch}:{\mathfrak D}\rightarrow {\mathfrak C}\) are essentially inverse equivalences. In particular, they preserve products, and \({\mathfrak D}\) admits finite products.
-
(iii)
Both \(\phi ^{-1}:{\mathfrak C}\rightarrow {\mathfrak D}\) and \(\amalg ^\mathfrak {Sch}:{\mathfrak D}\rightarrow {\mathfrak C}\) preserve the following properties of morphisms: being (a) surjective, (b) étale, (c) flat, (d) locally of finite type, (e) flat and locally of finite presentation.
Proof
(i) Let  be an open affine covering of \({\mathscr {P}}\). Set
be an open affine covering of \({\mathscr {P}}\). Set  . Then, by the construction of \(\amalg ^\mathfrak {Sch}\), the map \({\mathscr {P}}\rightarrow X\) is glued on the base from the affine maps \({\mathscr {P}}_i\rightarrow X_i\). The other claims now follow from Proposition 3.3.
. Then, by the construction of \(\amalg ^\mathfrak {Sch}\), the map \({\mathscr {P}}\rightarrow X\) is glued on the base from the affine maps \({\mathscr {P}}_i\rightarrow X_i\). The other claims now follow from Proposition 3.3.
(ii) We shall prove that  for an X-flat scheme \(X'\) and
for an X-flat scheme \(X'\) and  for an appropriate \({\mathscr {P}}\)-pushout datum. Both functors are compatible with localizations, hence it suffices to consider the case when \(X,X'\!,{\mathscr {P}}\) and \({\mathscr {P}}'\) are affine, but this case is covered by Lemma 3.11 (i).
for an appropriate \({\mathscr {P}}\)-pushout datum. Both functors are compatible with localizations, hence it suffices to consider the case when \(X,X'\!,{\mathscr {P}}\) and \({\mathscr {P}}'\) are affine, but this case is covered by Lemma 3.11 (i).
(iii) Properties (b)–(e) are Zariski local on the target and on the source, hence the assertion follows from Lemma 3.11 (ii). Finally, the claim about surjectivity follows from the surjectivity of  .\(\square \)
.\(\square \)
4.2 Schematic case
In the proof of the following theorem, given an algebraic space U and a pushout datum \({\mathscr {P}}\), denote by \(h_U({\mathscr {P}})\) the set of maps \({\mathscr {P}}\rightarrow U\). Thus, a morphism \({\mathscr {P}}\rightarrow X\) represents the pushout of \({\mathscr {P}}\) if and only if the natural map \(\psi :h_U(X)\rightarrow h_U({\mathscr {P}})\) is bijective for any  .
.
Theorem 4.3
Let \({\mathscr {P}}\) be a Ferrand pushout datum that admits an open affine covering and  . Then \({\mathscr {P}}\) is effective and
. Then \({\mathscr {P}}\) is effective and  .
.
Proof
It suffices to show that  since the morphism \({\mathscr {P}}\rightarrow X\) is affine by Lemma 4.2 (i). First, let us reduce to the case when \({\mathscr {P}}\) is affine. If
since the morphism \({\mathscr {P}}\rightarrow X\) is affine by Lemma 4.2 (i). First, let us reduce to the case when \({\mathscr {P}}\) is affine. If  is an open affine covering of \({\mathscr {P}}\) then we showed in the proof of Lemma 4.1 that each \({\mathscr {P}}_{ij}\) possesses an open affine covering
is an open affine covering of \({\mathscr {P}}\) then we showed in the proof of Lemma 4.1 that each \({\mathscr {P}}_{ij}\) possesses an open affine covering  and X is glued from
and X is glued from  along the unions of
along the unions of  . In other words, \({\mathscr {P}}=\mathrm{colim}_{\mathscr {D}}{\mathscr {P}}_*\) and \(X=\mathrm{colim}_{\mathscr {D}}X_*\), where \({\mathscr {D}}\) denotes the diagram of arrows \((ijk)\rightarrow l\) with \(i,j\in I\), \(k\in K_{ij}\) and \(l\in \{i,j\}\). Since colimits commute, if the theorem holds for affine pushouts then
. In other words, \({\mathscr {P}}=\mathrm{colim}_{\mathscr {D}}{\mathscr {P}}_*\) and \(X=\mathrm{colim}_{\mathscr {D}}X_*\), where \({\mathscr {D}}\) denotes the diagram of arrows \((ijk)\rightarrow l\) with \(i,j\in I\), \(k\in K_{ij}\) and \(l\in \{i,j\}\). Since colimits commute, if the theorem holds for affine pushouts then  .
.
Assume now, that \({\mathscr {P}}\) is affine, and hence  . We shall show that the natural map \(\psi :h_U(X)\rightarrow h_U({\mathscr {P}})\) is bijective for any algebraic space U. Since X, Y, Z, T are affine, \(h_U(X)=\lim _W h_W(X)\) and \(h_U({\mathscr {P}})=\lim _W h_W({\mathscr {P}})\), where the limits are taken over all open quasi-compact subsets \(W\subseteq U\). Thus, we may assume that U is quasi-compact. Fix an étale covering \(U_0\rightarrow U\) with an affine source.
. We shall show that the natural map \(\psi :h_U(X)\rightarrow h_U({\mathscr {P}})\) is bijective for any algebraic space U. Since X, Y, Z, T are affine, \(h_U(X)=\lim _W h_W(X)\) and \(h_U({\mathscr {P}})=\lim _W h_W({\mathscr {P}})\), where the limits are taken over all open quasi-compact subsets \(W\subseteq U\). Thus, we may assume that U is quasi-compact. Fix an étale covering \(U_0\rightarrow U\) with an affine source.
Injectivity of
\(\psi \): Pick \(h_1,h_2\in h_U(X)\) and assume that \(\psi (h_1)=\psi (h_2)\). Set  and
and  . Since \(X'_{0i}\) are schemes and
. Since \(X'_{0i}\) are schemes and  , it follows from Lemma 4.2 (ii) that \(X_{01}'\simeq X_{02}'\), which we denote simply by \(X_0'\). Since \(X'_0\) is quasi-compact there exists a surjective étale morphism \(X_0\rightarrow X_0'\) with an affine source. Set
, it follows from Lemma 4.2 (ii) that \(X_{01}'\simeq X_{02}'\), which we denote simply by \(X_0'\). Since \(X'_0\) is quasi-compact there exists a surjective étale morphism \(X_0\rightarrow X_0'\) with an affine source. Set  , then
, then  by Lemma 4.2 (ii). Consider the commutative diagram
by Lemma 4.2 (ii). Consider the commutative diagram

It is enough to prove that the base change morphisms \(X'_0\rightrightarrows U_0\) coincide, or, equivalently, that the two composed morphisms \(X_0\rightarrow X'_0\rightrightarrows U_0\) coincide. But, the composed map \({\mathscr {P}}_0\rightarrow {\mathscr {P}}'_0\rightarrow U_0\) factors uniquely through  since \(U_0\) is affine, and hence \(h_1=h_2\).
since \(U_0\) is affine, and hence \(h_1=h_2\).
Surjectivity of
\(\psi \): Let \({\alpha }\in h_U({\mathscr {P}})\) be arbitrary, and set  . Then \(Z'_0\) is an ind-quasi-affine scheme and hence \({\mathscr {P}}'_0\) possesses an étale affine covering \({\mathscr {P}}_0\rightarrow {\mathscr {P}}'_0\) by Corollary 5.10. Set
. Then \(Z'_0\) is an ind-quasi-affine scheme and hence \({\mathscr {P}}'_0\) possesses an étale affine covering \({\mathscr {P}}_0\rightarrow {\mathscr {P}}'_0\) by Corollary 5.10. Set  and
and  for \(i=0,1\), then \({\mathscr {P}}_0\rightarrow U_0\) factors through a morphism \(h_0:X_0\rightarrow U_0\). Note that \(X_1\rightrightarrows X_0\) is an étale equivalence relation with quotient X because \(X_0\rightarrow X\) is an étale covering by Lemma 4.2 (iii) and
for \(i=0,1\), then \({\mathscr {P}}_0\rightarrow U_0\) factors through a morphism \(h_0:X_0\rightarrow U_0\). Note that \(X_1\rightrightarrows X_0\) is an étale equivalence relation with quotient X because \(X_0\rightarrow X\) is an étale covering by Lemma 4.2 (iii) and  by Lemma 4.2 (ii). Consider the commutative diagram
by Lemma 4.2 (ii). Consider the commutative diagram

The compositions of \({\mathscr {P}}_1\rightarrow X_1\) with the two composed morphisms \(X_1\rightrightarrows X_0\rightarrow U_0\rightarrow U\) coincide. Thus, the two morphisms \(X_1\rightrightarrows U\) coincide by the injectivity of \(\psi _1:h_U(X_1)\rightarrow h_U({\mathscr {P}}_1)\). Hence the morphism \(X_0\rightarrow U\) induces a morphism \(h:X\rightarrow U\) since \(X=X_0/X_1\). It remains to verify that \(\psi (h)=\alpha \). By the construction  , where \(\pi :{\mathscr {P}}_0\rightarrow {\mathscr {P}}\) is the étale covering. Thus
, where \(\pi :{\mathscr {P}}_0\rightarrow {\mathscr {P}}\) is the étale covering. Thus  , and we are done.\(\square \)
, and we are done.\(\square \)
4.2.1 Ferrand pushouts of schemes
For completeness, we compare our results to Ferrand’s. This will not be used, so uninterested reader can skip to Section 4.3. By Theorem 4.3, Ferrand pushout of an affine scheme is affine. On the other hand, it is easy to give examples of Ferrand pushouts of schemes which are not schemes.
Example 4.4
Assume that Z is a scheme,  a closed subscheme admitting no open affine neighborhood, and \(f:T\rightarrow Y\) a morphism such that \(f(t_1)\) and \(f(t_2)\) have a common specialization \(y\in Y\). In Theorem 6.2 (ii), we will establish criteria that guarantee the existence of the Ferrand pushout
a closed subscheme admitting no open affine neighborhood, and \(f:T\rightarrow Y\) a morphism such that \(f(t_1)\) and \(f(t_2)\) have a common specialization \(y\in Y\). In Theorem 6.2 (ii), we will establish criteria that guarantee the existence of the Ferrand pushout  of this kind even for compositions (f is an open immersion) and pinchings (f is finite). For any neighborhood \(U\subseteq X\) of the image of y, its preimage in Z contains T. In particular, U is not affine, and hence X is not a scheme.
of this kind even for compositions (f is an open immersion) and pinchings (f is finite). For any neighborhood \(U\subseteq X\) of the image of y, its preimage in Z contains T. In particular, U is not affine, and hence X is not a scheme.
Consider the following condition (\(\dag \)) on a Ferrand pushout datum \({\mathscr {P}}=(T;Y,Z)\): (a) X, Y and Z are schemes, (b) the pushout X of \({\mathscr {P}}\) in the category of locally ringed spaces is a scheme, (c) the morphism \(Z\rightarrow X\) is affine, and (d) the morphism \(Y\rightarrow X\) is a closed immersion. In [3, Theorem 7.1], Ferrand found a necessary and sufficient condition for (\(\dag \)) to hold. One can also relate (\(\dag \)) to general Ferrand pushouts as follows:
Theorem 4.5
Let \({\mathscr {P}}=(T;Y,Z)\) be a Ferrand pushout datum. Then the following conditions are equivalent:
-
(i)
\({\mathscr {P}}\) satisfies Ferrand’s condition (\(\dag \)).
-
(ii)
\({\mathscr {P}}\) is effective in the category of algebraic spaces and
 is a scheme.
is a scheme. -
(iii)
\({\mathscr {P}}\) possesses an open affine covering.
Proof
Assume (i) holds, and let X be the schematic pushout of \({\mathscr {P}}\). Since the morphism \({\mathscr {P}}\rightarrow X\) is affine, any affine open covering of X induces an open affine covering of \({\mathscr {P}}\), and we obtain (iii). Theorem 4.3 provides the implication (iii) \(\Rightarrow \) (ii). Finally, if (ii) holds then an open affine covering of  induces such a covering of \({\mathscr {P}}\), hence
induces such a covering of \({\mathscr {P}}\), hence  by Theorem 4.3. Working locally it suffices to check \((\dag )\) when \({\mathscr {P}}\) is affine, but this is covered by [3, Theorem 5.1].\(\square \)
by Theorem 4.3. Working locally it suffices to check \((\dag )\) when \({\mathscr {P}}\) is affine, but this is covered by [3, Theorem 5.1].\(\square \)
4.3 Pushout of equivalence relations
General Ferrand pushouts are “glued” from the schematic ones by use of étale equivalence relations. The following lemma plays a central role in our construction.
Lemma 4.6
Let \(p_{1,2}:{\mathscr {P}}_1\rightrightarrows {\mathscr {P}}_0\) be an fppf equivalence relation of Ferrand pushout data. Assume that \({\mathscr {P}}_i\) admit open affine coverings, and set  . Then the induced morphisms \(q_{1,2}:X_1\rightrightarrows X_0\) form an fppf equivalence relation.
. Then the induced morphisms \(q_{1,2}:X_1\rightrightarrows X_0\) form an fppf equivalence relation.
Proof
We have an fppf groupoid of pushout data \((p_1,p_2,m,i,\delta )\), where

satisfy all usual compatibilities, such as  , etc.; see [8, Section 35.11, Tag:0231]. Since \(\amalg ^\mathfrak {Sch}\) respects flat fiber products by Lemma 4.2 (ii), it takes this groupoid to an fppf groupoid of schemes
, etc.; see [8, Section 35.11, Tag:0231]. Since \(\amalg ^\mathfrak {Sch}\) respects flat fiber products by Lemma 4.2 (ii), it takes this groupoid to an fppf groupoid of schemes  . It remains to check that the latter groupoid is, in fact, an equivalence relation, that is, the diagonal
. It remains to check that the latter groupoid is, in fact, an equivalence relation, that is, the diagonal  is a monomorphism.
is a monomorphism.
Set  . Then \(U_i\rightarrow X_i\) is an open immersion and
. Then \(U_i\rightarrow X_i\) is an open immersion and  by Lemma 4.2 (i). Notice that h is locally of finite type. Indeed it is the composition of
by Lemma 4.2 (i). Notice that h is locally of finite type. Indeed it is the composition of  and
and  , where the first morphism is locally of finite type, and the second morphism is locally of finite presentation. Thus, by Lemma 2.2, it is sufficient to show that the base change of h with respect to the surjective morphism
, where the first morphism is locally of finite type, and the second morphism is locally of finite presentation. Thus, by Lemma 2.2, it is sufficient to show that the base change of h with respect to the surjective morphism  is a monomorphism.
is a monomorphism.
The base changes of h to  and
and  are monomorphisms, in fact empty morphisms, because their sources are supported on \(U_1\cap Y_1\). By definition, \(Y_1\rightrightarrows Y_0\) and \(Z_1\rightrightarrows Z_0\) are equivalence relations, hence
are monomorphisms, in fact empty morphisms, because their sources are supported on \(U_1\cap Y_1\). By definition, \(Y_1\rightrightarrows Y_0\) and \(Z_1\rightrightarrows Z_0\) are equivalence relations, hence  and
and  are monomorphisms. Note that
are monomorphisms. Note that

is a base change of h. Since \(Y_1\rightarrow X_1\) is a monomorphism (even a closed immersion), the diagonal  is an isomorphism, and hence \(h_Y=h'_Y\) is the base change of h. Although a similar claim fails for \(Z_i\), it does hold for \(U_i\), and hence
is an isomorphism, and hence \(h_Y=h'_Y\) is the base change of h. Although a similar claim fails for \(Z_i\), it does hold for \(U_i\), and hence  is a base change of h. On the other hand, \(h_U\) is also the base change of \(h_Z\), hence a monomorphism, which completes the proof.\(\square \)
is a base change of h. On the other hand, \(h_U\) is also the base change of \(h_Z\), hence a monomorphism, which completes the proof.\(\square \)
4.4 General pushouts
Now, we can attack the general case.
Theorem 4.7
Let \({\mathscr {P}}=(T;Y,Z)\) be a Ferrand pushout datum. Then,
-
(i)
The following conditions are equivalent: \((\mathrm{a})\) \({\mathscr {P}}\) is effective, \((\mathrm{b})\) there exists an étale presentation \({\mathscr {P}}={\mathscr {P}}_0/{\mathscr {P}}_1\) such that both \({\mathscr {P}}_0\) and \({\mathscr {P}}_1\) admit open affine coverings, \((\mathrm{c})\) same as \((\mathrm{b})\) with an fppf presentation \({\mathscr {P}}={\mathscr {P}}_0/{\mathscr {P}}_1\).
-
(ii)
In the situation of \((\mathrm{c})\) set
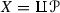 and
and  . Then \(X_1\rightrightarrows X_0\) is an fppf equivalence relation, \(X=X_0/X_1\), and
. Then \(X_1\rightrightarrows X_0\) is an fppf equivalence relation, \(X=X_0/X_1\), and  .
.
Proof
(a) \(\Rightarrow \) (b): Pick an étale presentation \(X_0/X_1\) of  , and set
, and set  . Then \({\mathscr {P}}_0/{\mathscr {P}}_1\) is an étale presentation of \({\mathscr {P}}\), and open affine coverings of \(X_i\) pull back to open affine coverings of \({\mathscr {P}}_i\) since the maps \({\mathscr {P}}_i\rightarrow X_i\) are affine.
. Then \({\mathscr {P}}_0/{\mathscr {P}}_1\) is an étale presentation of \({\mathscr {P}}\), and open affine coverings of \(X_i\) pull back to open affine coverings of \({\mathscr {P}}_i\) since the maps \({\mathscr {P}}_i\rightarrow X_i\) are affine.
It remains to show that (c) implies (a) and the assertion of (ii). Let \({\mathscr {P}}_0/{\mathscr {P}}_1\) be an fppf presentation of \({\mathscr {P}}\) such that \({\mathscr {P}}_i\) possess open affine coverings. Set  and recall that
and recall that  by Theorem 4.3. Since colimits commute,
by Theorem 4.3. Since colimits commute,

Furthermore, \(X_1\rightrightarrows X_0\) is an fppf equivalence relation by Lemma 4.6, hence \(X=X_0/X_1\) is the pushout of \({\mathscr {P}}\). Finally, since by Lemma 4.2 (ii),  (with respect to either projection \({\mathscr {P}}_1\rightarrow {\mathscr {P}}_0\)), it follows that
(with respect to either projection \({\mathscr {P}}_1\rightarrow {\mathscr {P}}_0\)), it follows that  by flat descent and then clearly
by flat descent and then clearly  . In particular, the map \({\mathscr {P}}\rightarrow X\) is affine by flat descent since \({\mathscr {P}}_0\rightarrow X_0\) is affine, thereby proving that \({\mathscr {P}}\) is effective.\(\square \)
. In particular, the map \({\mathscr {P}}\rightarrow X\) is affine by flat descent since \({\mathscr {P}}_0\rightarrow X_0\) is affine, thereby proving that \({\mathscr {P}}\) is effective.\(\square \)
Theorem 4.8
Let \({\mathscr {P}}=(T;Y,Z)\) be an effective Ferrand pushout datum,  , and \(\phi :{\mathscr {P}}\rightarrow X\) the natural map. Then,
, and \(\phi :{\mathscr {P}}\rightarrow X\) the natural map. Then,
-
(i)
The topological pushout
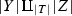 is naturally homeomorphic to |X|.
is naturally homeomorphic to |X|. -
(ii)
 .
. -
(iii)
\(Y\rightarrow X\) is a closed immersion,
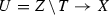 is an open immersion, and
is an open immersion, and  set-theoretically.
set-theoretically.
Proof
By Theorem 4.7, there exists an étale presentation \({\mathscr {P}}={\mathscr {P}}_0/{\mathscr {P}}_1\) such that \({\mathscr {P}}_i\) admit open affine coverings, and \(X=X_0/X_1\) and  , where
, where  . Using flat descent this reduces all claims to the case of the pushout
. Using flat descent this reduces all claims to the case of the pushout  . It remains to recall that
. It remains to recall that  and use Lemma 4.2 (i).\(\square \)
and use Lemma 4.2 (i).\(\square \)
5 Affine presentations
Existence of \(\tau \)-affine coverings was important in our construction of pushouts. In particular, existence of an étale affine covering of \({\mathscr {P}}\) is necessary for \({\mathscr {P}}\) to be effective, and we will prove later that it is also sufficient. Unfortunately, we were unable to verify the existence of such coverings in general, but at least we shall establish some non-trivial criteria in this section.
5.1 Relation to lifting problems
A \(\tau \)-affine covering  is nothing but a pair of \(\tau \)-affine coverings
is nothing but a pair of \(\tau \)-affine coverings  and
and  that agree over T. In many cases, the requirement that a covering of T is the pull-back of a covering of Y is very restrictive, e.g., this is the case if Y is a point. Therefore our strategy for constructing
that agree over T. In many cases, the requirement that a covering of T is the pull-back of a covering of Y is very restrictive, e.g., this is the case if Y is a point. Therefore our strategy for constructing  is always to start with a fine enough \(\tau \)-affine covering
is always to start with a fine enough \(\tau \)-affine covering  and to lift its base change
and to lift its base change  to a \(\tau \)-affine covering of Z.
to a \(\tau \)-affine covering of Z.
5.1.1 Pinchings
Pinchings are the main case where one can seriously profit from playing also with affine coverings of Y. This was used by Kollár in [6, Section 42] to give an elementary proof that any pinching datum possesses an étale affine covering (the noetherian assumption in loc.cit. is not essential and can be removed easily). A conceptual way to say that there are many étale coverings of T coming from Y is as follows.
Lemma 5.1
Assume that \(f:T\rightarrow Y\) is a finite morphism of algebraic spaces. Then étale coverings of the form  , where
, where  is an étale covering, are cofinal among all étale coverings of T.
is an étale covering, are cofinal among all étale coverings of T.
Proof
If  is a surjective étale morphism, then it is sufficient to prove the lemma for the base change
is a surjective étale morphism, then it is sufficient to prove the lemma for the base change  of f, since étale coverings of T that factor through \(T'\) form a cofinal family. Thus, we may assume that Y and T are schemes.
of f, since étale coverings of T that factor through \(T'\) form a cofinal family. Thus, we may assume that Y and T are schemes.
Fix an étale morphism \(g:U\rightarrow T\), and let \(y\in g(U)\) be any point. It is sufficient to find an étale neighborhood \(W\rightarrow Y\) of y such that  factors through U. Let
factors through U. Let  be the strict henselization of the local scheme \(Y_y\). By [5, \(\mathrm IV_4\), 18.8.10],
be the strict henselization of the local scheme \(Y_y\). By [5, \(\mathrm IV_4\), 18.8.10],  is a disjoint union of strict henselizations of T at closed points, and hence \({\overline{T}}\rightarrow T\) factors through \(U\rightarrow T\). It remains to note that
is a disjoint union of strict henselizations of T at closed points, and hence \({\overline{T}}\rightarrow T\) factors through \(U\rightarrow T\). It remains to note that  is the limit of Y-étale schemes
is the limit of Y-étale schemes  , hence \({\overline{T}}\) is the limit of T-étale schemes
, hence \({\overline{T}}\) is the limit of T-étale schemes  and by [5, \(\mathrm IV_3\), 8.14.2], the T-morphism \({\overline{T}}\rightarrow U\) factors through some
and by [5, \(\mathrm IV_3\), 8.14.2], the T-morphism \({\overline{T}}\rightarrow U\) factors through some  .\(\square \)
.\(\square \)
5.1.2 General case
For general Ferrand pushout data, we have only the following trivial result.
Lemma 5.2
Let \({\mathscr {P}}=(T;Y,Z)\) be a Ferrand pushout datum. If any étale morphism  with an affine source lifts to an étale morphism
with an affine source lifts to an étale morphism  with an affine source, in the sense that
with an affine source, in the sense that  , then \({\mathscr {P}}\) admits an étale affine covering.
, then \({\mathscr {P}}\) admits an étale affine covering.
Proof
Pick an étale affine covering  . Then its pullback
. Then its pullback  is an étale affine covering that can be lifted to an étale family
is an étale affine covering that can be lifted to an étale family  such that \(Z_i\) are affine schemes. Since \(T\hookrightarrow Z\) is a closed immersion, its complement is open, and we can pick an étale affine covering
such that \(Z_i\) are affine schemes. Since \(T\hookrightarrow Z\) is a closed immersion, its complement is open, and we can pick an étale affine covering  . Then
. Then  is an étale affine covering of Z. For any \(j\in J\) set
is an étale affine covering of Z. For any \(j\in J\) set  ,
,  , and for \(k\in I\cup J\) set \({\mathscr {P}}_k=(T_k;Y_k,Z_k)\). Then
, and for \(k\in I\cup J\) set \({\mathscr {P}}_k=(T_k;Y_k,Z_k)\). Then  is the required covering.\(\square \)
is the required covering.\(\square \)
5.2 Affine lifting problem
Assume that \(T\hookrightarrow Z\) is a closed immersion of algebraic spaces. By a lifting of an étale algebraic T-space \(T'\) to Z we mean any étale algebraic Z-space \(Z'\) with  . Lemma 5.2 provides a motivation to raise the following affine lifting question:
. Lemma 5.2 provides a motivation to raise the following affine lifting question:
Question 5.3
(AL) Assume that \(T\hookrightarrow Z\) is a closed immersion of algebraic spaces. Given an étale morphism \(T'\rightarrow T\) with an affine source, does there exist a lifting  with an affine source.
with an affine source.
In fact, this problem is equivalent to the combination of two particular cases, a lifting question and a henselization question:
Question 5.4
Assume that \(T\hookrightarrow Z\) is a closed immersion of algebraic spaces.
-
(L)
If \(T'\) is affine and
 is étale then does it admit a lifting to Z?
is étale then does it admit a lifting to Z? -
(H)
If T is affine, can one factor \(T\rightarrow Z\) through an affine \(Z'\) étale over Z?
Remark 5.5
(i) Question (H) is, closely related to the following fundamental open question about henselian schemes, cf. Conjecture B in [4, Remark 1.23 (ii)]: Does there exist a non-affine henselian scheme with affine closed fiber?
(ii) We will prove below that the affine lifting question has affirmative answer in the ind-quasi-affine case and in the case of a discrete T, but we do not know what happens with either (L) or (H) for more general spaces T and Z.
Lemma 5.6
(AL) has affirmative answer if Z is decent and |T| is discrete.
Proof
We shall find a lifting  for an étale morphism
for an étale morphism  with an affine source. Clearly, we may replace Z with a neighborhood \(g(T')\). Thus, since \(g(T')\) is quasi-compact, we may assume that so is Z, and hence |T| is finite. Now, it is clear that it suffices to solve the lifting problem for each connected component of T, hence we may assume in the sequel that |T| is a point.
with an affine source. Clearly, we may replace Z with a neighborhood \(g(T')\). Thus, since \(g(T')\) is quasi-compact, we may assume that so is Z, and hence |T| is finite. Now, it is clear that it suffices to solve the lifting problem for each connected component of T, hence we may assume in the sequel that |T| is a point.
By [8, Tag:0ABT], T is decent, and hence a scheme by [8, Tag:047Z]. Let z be the reduction of T, then \(z\rightarrow Z\) is a closed Zariski point. By [8, Tag:0BBP], there exists an elementary affine étale neighborhood \(f:(U,u)\rightarrow (Z,z)\) of z, i.e., U is affine, \(u=f^{-1}(z)\), and \(k(z)=k(u)\). Since the diagonal component  is the only component of
is the only component of  containing a preimage of z, it follows easily that any morphism \(h:S\rightarrow Z\) with \(h(S)=z\) factors through U. In particular, we obtain a factorization \(T\rightarrow U\rightarrow Z\). Since \(T'\) is discrete, we can use the local description of étale morphisms [5, \(\mathrm IV_4\), 18.4.6], to lift the étale morphism
containing a preimage of z, it follows easily that any morphism \(h:S\rightarrow Z\) with \(h(S)=z\) factors through U. In particular, we obtain a factorization \(T\rightarrow U\rightarrow Z\). Since \(T'\) is discrete, we can use the local description of étale morphisms [5, \(\mathrm IV_4\), 18.4.6], to lift the étale morphism  to an affine étale morphism
to an affine étale morphism  . Then the composition
. Then the composition  is as needed.\(\square \)
is as needed.\(\square \)
Theorem 5.7
(AL) has affirmative answer if Z is an ind-quasi-affine scheme.
Proof
If Z is affine then the result is known, see [8, Tag:04D1]. We shall mention that our original argument in this case was rather involved and made a use of Elkik’s lifting theorem. We are grateful to Aise Johan de Jong who pointed out to us that the assertion in this case is elementary.
By quasi-compactness, if \(T'\) is affine then its image is contained in a quasi-affine open subscheme of Z. Thus, we may assume that Z is quasi-affine, and hence an open subscheme of the affine hull \({\overline{Z}}\). Let \({\overline{T}}\) be the schematic closure of T in \({\overline{Z}}\); we aware the reader that the morphism from the affine hull of T to \({\overline{T}}\) does not have to be an open immersion. By the affine case, the étale morphism  lifts to an étale morphism
lifts to an étale morphism  with an affine source. The closed set
with an affine source. The closed set  is disjoint from \(T'\), and the latter is quasi-compact. Hence there exists a basic open affine \(Z'\subseteq {\overline{Z}}{}'\) containing \(T'\), which is disjoint from V. Thus, the étale morphism
is disjoint from \(T'\), and the latter is quasi-compact. Hence there exists a basic open affine \(Z'\subseteq {\overline{Z}}{}'\) containing \(T'\), which is disjoint from V. Thus, the étale morphism  factors through Z, and
factors through Z, and  is the required lifting of f.\(\square \)
is the required lifting of f.\(\square \)
5.3 Existence of étale affine coverings
Using the lifting results we have proved above, existence of étale affine coverings can be established in the following cases.
Theorem 5.8
A Ferrand pushout datum \({\mathscr {P}}=(T;Y,Z)\) possesses an étale affine covering  if one of the following conditions is satisfied:
if one of the following conditions is satisfied:
-
(i)
Z is an ind-quasi-affine scheme,
-
(ii)
\({\mathscr {P}}\) is a pinching datum, i.e., \(f:T\rightarrow Y\) is finite.
-
(iii)
Z is decent and |T| is discrete.
Proof
In view of Lemma 5.2, we see that (i) follows from Theorem 5.7 and (iii) follows from Lemma 5.6. In the case of a pinching datum, choose an étale affine covering  , and use Lemma 5.1 to find an étale affine covering
, and use Lemma 5.1 to find an étale affine covering  such that its pullback
such that its pullback  factors through the pullback
factors through the pullback  of
of  . Then
. Then  can be lifted to
can be lifted to  by Theorem 5.7. Thus, by setting \({\mathscr {P}}_i=(T_i;Y_i,Z_i)\) we obtain the desired étale affine covering of \({\mathscr {P}}\).\(\square \)
by Theorem 5.7. Thus, by setting \({\mathscr {P}}_i=(T_i;Y_i,Z_i)\) we obtain the desired étale affine covering of \({\mathscr {P}}\).\(\square \)
Remark 5.9
For shortness, we used Theorem 5.7 to construct étale affine coverings of pinching data. This is not necessary and can be bypassed by a simple local argument that only uses Lemma 5.2, see [6, Section 42].
Corollary 5.10
Let \(f:{\mathscr {P}}\rightarrow {\widetilde{\mathscr {P}}}\) be a morphism of Ferrand pushout data with an ind-quasi-affine \(f_Z:Z\rightarrow {\widetilde{Z}}\). If \({\widetilde{\mathscr {P}}}\) admits an étale (resp. flat) affine covering then so does \({\mathscr {P}}\).
Proof
Let  be an étale (resp. flat) affine covering of \({\widetilde{\mathscr {P}}}\). Set
be an étale (resp. flat) affine covering of \({\widetilde{\mathscr {P}}}\). Set  . Then
. Then  is an étale (resp. flat) covering. Since \(f_Z\) is ind-quasi-affine, so are its base changes \(Z_i\rightarrow {\widetilde{Z}}_i\), and hence also \(Z_i\). By Theorem 5.8 (i), all \({\mathscr {P}}_i\) admit étale affine coverings
is an étale (resp. flat) covering. Since \(f_Z\) is ind-quasi-affine, so are its base changes \(Z_i\rightarrow {\widetilde{Z}}_i\), and hence also \(Z_i\). By Theorem 5.8 (i), all \({\mathscr {P}}_i\) admit étale affine coverings  . Hence
. Hence  is the desired covering.\(\square \)
is the desired covering.\(\square \)
6 Properties of Ferrand pushouts
In this section we study properties of spaces and morphisms preserved by the Ferrand pushout functor.
6.1 Absolute properties
We start with properties of spaces.
Theorem 6.1
Let \({\mathscr {P}}\) be an effective Ferrand pushout datum, and set  . Let \((\dag )\) be any of the following properties: \(\mathrm{(a)}\) being affine, \(\mathrm{(b)}\) possessing an open affine covering, \(\mathrm{(c)}\) being separated, \(\mathrm{(d)}\) being quasi-compact, \(\mathrm{(e)}\) being quasi-separated. Then \({\mathscr {P}}\) satisfies \((\dag )\) if and only if so does X.
. Let \((\dag )\) be any of the following properties: \(\mathrm{(a)}\) being affine, \(\mathrm{(b)}\) possessing an open affine covering, \(\mathrm{(c)}\) being separated, \(\mathrm{(d)}\) being quasi-compact, \(\mathrm{(e)}\) being quasi-separated. Then \({\mathscr {P}}\) satisfies \((\dag )\) if and only if so does X.
Proof
If X satisfies \((\dag )\) then so does \({\mathscr {P}}\) since \({\mathscr {P}}\rightarrow X\) is affine. Now, the assertion of the theorem for properties (a) and (b) follows from Theorem 4.3, and for property (d) the assertion is clear since  is surjective by Theorem 4.8.
is surjective by Theorem 4.8.
(e) Assume that \({\mathscr {P}}\) is quasi-separated, and let \(X_i,{\mathscr {P}}_i\) be as in Theorem 4.7. In particular, \(X=X_1/X_0\),  , and
, and  , where
, where  and
and  . We shall show that the diagonal
. We shall show that the diagonal  is quasi-compact. The morphism \(W\rightarrow X\) is affine, hence quasi-compact, and it is surjective by Theorem 4.8. Thus, it suffices to show the quasi-compactness of the base change
is quasi-compact. The morphism \(W\rightarrow X\) is affine, hence quasi-compact, and it is surjective by Theorem 4.8. Thus, it suffices to show the quasi-compactness of the base change  . Since limits are preserved under base changes,
. Since limits are preserved under base changes,  is the morphism
is the morphism  . And the latter is quasi-compact since W is quasi-separated.
. And the latter is quasi-compact since W is quasi-separated.
(c) Assume that \({\mathscr {P}}=(T;Y,Z)\) is separated. Then X is quasi-separated by (e). Consider a valuation ring R with fraction field K, and let  be a morphism. By the valuative criterion of separatedness [8, Tag:03KV], it is sufficient to show that if
be a morphism. By the valuative criterion of separatedness [8, Tag:03KV], it is sufficient to show that if  extend i then \(f=g\). Recall that
extend i then \(f=g\). Recall that  , where
, where  , and \(Y\rightarrow X\) is a closed immersion by Theorem 4.8 (iii). If \(i(\eta )\in Y\) then the morphisms f, g factor through Y since \(Y\rightarrow X\) is a closed immersion, and hence \(f=g\) by the separatedness of Y. So, we may assume that \(i(\eta )\in U\).
, and \(Y\rightarrow X\) is a closed immersion by Theorem 4.8 (iii). If \(i(\eta )\in Y\) then the morphisms f, g factor through Y since \(Y\rightarrow X\) is a closed immersion, and hence \(f=g\) by the separatedness of Y. So, we may assume that \(i(\eta )\in U\).
Since \(f^{-1}(Y)\) and \(g^{-1}(Y)\) are closed subschemes of S, one of them contains the other (we use here the fact that the ideals of R are linearly ordered with respect to inclusion). Without loss of generality we assume that \(f^{-1}(Y)\) is the larger subscheme and denote its generic point by \(\varepsilon \). Note that \(\varepsilon \ne \eta \), hence the localization \(S_\varepsilon \) is a valuation ring of non-zero height. We claim that \(f(\varepsilon )\in T\) and \(g(\varepsilon )\in T\). Pick an étale affine covering  , and set
, and set  ,
,  . Then
. Then  by Theorem 4.3, and
by Theorem 4.3, and  by Theorem 4.7 (ii). Set
by Theorem 4.7 (ii). Set  , and
, and  . Both \(S'\) and \(S''\) are disjoint unions of affine étale schemes over \(S_\varepsilon \), hence disjoint unions of spectra of Prüfer rings. By our construction, the preimages of \(Y'\) in both \(S'\) and \(S''\) are contained in the preimage of \(\varepsilon \). Hence the morphisms
. Both \(S'\) and \(S''\) are disjoint unions of affine étale schemes over \(S_\varepsilon \), hence disjoint unions of spectra of Prüfer rings. By our construction, the preimages of \(Y'\) in both \(S'\) and \(S''\) are contained in the preimage of \(\varepsilon \). Hence the morphisms  factor uniquely through \(Z'\) by Corollary 3.5. In particular, \(f(\varepsilon )\in T\) and \(g(\varepsilon )\in T\).
factor uniquely through \(Z'\) by Corollary 3.5. In particular, \(f(\varepsilon )\in T\) and \(g(\varepsilon )\in T\).
We proved that f and g take \(S_\varepsilon \) to Z, hence their restrictions onto \(S_\varepsilon \) coincide by the separatedness of Z. Let W be the closed subscheme of S with generic point \(\varepsilon \). Since f and g take W to the separated subspace \(Y\hookrightarrow X\) and coincide on the generic point, it follows that \(f|_W=g|_W\). It remains to note that S is the composition of \(S_\varepsilon \) and W along \(\varepsilon \). So,  by Theorem 4.3, and hence \(f=g\).\(\square \)
by Theorem 4.3, and hence \(f=g\).\(\square \)
6.2 Criterion of effectivity
Theorem 4.7 (i) provides a criterion of effectivity of Ferrand pushout data, but it is not so convenient. Our next aim is to strengthen it by removing the assumption on \({\mathscr {P}}_1\).
Theorem 6.2
Let \({\mathscr {P}}\) be a Ferrand pushout datum, then
-
(i)
\({\mathscr {P}}\) is effective if and only if it admits an étale affine covering
 . Moreover, if \({\mathscr {P}}_0=\coprod _i{\mathscr {W}}_i\) and
. Moreover, if \({\mathscr {P}}_0=\coprod _i{\mathscr {W}}_i\) and  then \({\mathscr {P}}_1\) possesses an open affine covering and hence the assertion of Theorem 4.7 (ii) holds.
then \({\mathscr {P}}_1\) possesses an open affine covering and hence the assertion of Theorem 4.7 (ii) holds. -
(ii)
\({\mathscr {P}}\) is effective in either of the following cases: (a) Z is decent and |T| is discrete, (b) \(T\rightarrow Y\) is finite, (c) Z is ind-quasi-affine, (d) there exists a morphism \({\mathscr {P}}\rightarrow {\mathscr {P}}'\) such that \({\mathscr {P}}'\) is effective, and \(Z\rightarrow Z'\) is ind-quasi-affine.
Proof
Assertion (ii) follows from (i), Theorem 5.8, and Corollary 5.10.
(i) If \({\mathscr {P}}\) is effective then the assertion is clear since  is affine. Let now
is affine. Let now  be an étale affine covering, \({\mathscr {P}}_0=\coprod _i{\mathscr {W}}_i\), and
be an étale affine covering, \({\mathscr {P}}_0=\coprod _i{\mathscr {W}}_i\), and  . By Theorem 4.7, it suffices to prove that \({\mathscr {P}}_1\) possesses an open affine covering. To do so, we shall show that \({\mathscr {P}}_1\) is effective, and
. By Theorem 4.7, it suffices to prove that \({\mathscr {P}}_1\) possesses an open affine covering. To do so, we shall show that \({\mathscr {P}}_1\) is effective, and  is a scheme, since then pulling back an open affine covering from \(X_1\) will do the trick.
is a scheme, since then pulling back an open affine covering from \(X_1\) will do the trick.
We start with effectivity. Since \({\mathscr {P}}_0\rightarrow {\mathscr {P}}\) is ind-quasi-affine, so is its base change \({\mathscr {P}}_1\rightarrow {\mathscr {P}}_0\), and hence so is \(Z_1\). Thus, \({\mathscr {P}}_1\) admits an étale affine covering  by Corollary 5.10. Set \({\mathscr {Q}}_0=\coprod _j {\mathscr {U}}_j\), and
by Corollary 5.10. Set \({\mathscr {Q}}_0=\coprod _j {\mathscr {U}}_j\), and  . Since \({\mathscr {P}}_1\) is separated, both \({\mathscr {Q}}_i\) admit open affine coverings, and hence are effective. Set
. Since \({\mathscr {P}}_1\) is separated, both \({\mathscr {Q}}_i\) admit open affine coverings, and hence are effective. Set  . Then by Theorems 4.3 and 4.7 (ii), \({\mathscr {P}}_1\) is effective, \(X_1=Y_0/Y_1\), and
. Then by Theorems 4.3 and 4.7 (ii), \({\mathscr {P}}_1\) is effective, \(X_1=Y_0/Y_1\), and  .
.
Let us now show that \(X_1\) is a scheme. Set  , and consider the morphisms \(Y_i\rightarrow X_0\) and \(X_1\rightarrow X_0\) induced by the first projection \(p_1:{\mathscr {P}}_1\rightarrow {\mathscr {P}}_0\). By Lemma 4.2 (ii),
, and consider the morphisms \(Y_i\rightarrow X_0\) and \(X_1\rightarrow X_0\) induced by the first projection \(p_1:{\mathscr {P}}_1\rightarrow {\mathscr {P}}_0\). By Lemma 4.2 (ii),  for \(i=0,1\), and it follows by flat descent that
for \(i=0,1\), and it follows by flat descent that  . In addition, the morphisms \(Y_i\rightarrow X_0\) are étale by Lemma 4.2 (iii), hence so is \(X_1\rightarrow X_0\). By Theorem 6.1, the space \(X_1\) is separated, and hence a scheme by [8, Tag:082J].\(\square \)
. In addition, the morphisms \(Y_i\rightarrow X_0\) are étale by Lemma 4.2 (iii), hence so is \(X_1\rightarrow X_0\). By Theorem 6.1, the space \(X_1\) is separated, and hence a scheme by [8, Tag:082J].\(\square \)
Remark 6.3
(i) Our proof of the fact that \({\mathscr {P}}_1\) admits an open affine covering is very indirect and rather involved. We construct an étale affine covering, feed it into Theorem 4.7, and then apply Zariski’s main theorem for algebraic spaces to show that the pushout is, in fact, a scheme. It is an interesting question whether one can show directly (and hopefully simpler) that \({\mathscr {P}}_1\) possesses an open affine covering, and whether one can extend the theorem to fppf affine coverings.
(ii) We do not know if this criterion can be made more explicit. We do not even know if there exist non-effective data. Note that Ferrand describes in [3, Theorem 7.1] such a criterion in the category of schemes, which essentially reduces to the existence of an open affine covering. In particular, one obtains a source of examples which are non-effective in the category of schemes. However, many of these examples are effective in the category of algebraic spaces, e.g., Example 4.4, and it is not clear whether one can use this to construct a Ferrand pushout datum, which is not effective in the algebraic spaces.
6.3 Descent of properties through Ferrand pushouts
6.3.1 Equivalence of categories
Lemmas 3.11 and 4.2 extend to the case of general Ferrand pushouts. This is one of the main results on Ferrand pushouts, so we provide a more complete list of properties they respect. A morphism of Ferrand pushout data  is called a pro-open immersion if it is isomorphic to the filtered projective limit of a family of open immersions (at least a priori, this condition is stronger than the componentwise condition).
is called a pro-open immersion if it is isomorphic to the filtered projective limit of a family of open immersions (at least a priori, this condition is stronger than the componentwise condition).
Theorem 6.4
Assume that \({\mathscr {P}}\) is an effective Ferrand pushout datum,  and \(\phi :{\mathscr {P}}\rightarrow X\) is the natural map. Let \({\mathfrak C}\) and \({\mathfrak D}\) be the categories of flat algebraic spaces over X and of effective flat Ferrand pushout data over \({\mathscr {P}}\), respectively. Then,
and \(\phi :{\mathscr {P}}\rightarrow X\) is the natural map. Let \({\mathfrak C}\) and \({\mathfrak D}\) be the categories of flat algebraic spaces over X and of effective flat Ferrand pushout data over \({\mathscr {P}}\), respectively. Then,
-
(I)
The functors \(\phi ^{-1}:{\mathfrak C}\rightarrow {\mathfrak D}\) and \(\amalg :{\mathfrak D}\rightarrow {\mathfrak C}\) are essentially inverse equivalences.
-
(II)
The functors \(\phi ^{-1}:{\mathfrak C}\rightarrow {\mathfrak D}\) and \(\amalg :{\mathfrak D}\rightarrow {\mathfrak C}\) preserve the following properties of morphisms: (a) surjective, (b) quasi-compact, (c) open immersion, (d) étale, (e) smooth, (f) flat, (g) locally of finite type, (h) flat and locally of finite presentation, (i) finite type, (j) flat and of finite presentation, (k) pro-open immersion. In particular, \(\phi ^{-1}\) and \(\amalg \) respect Zariski, étale, fppf and fpqc topologies on \({\mathfrak C}\) and \({\mathfrak D}\).
Proof
(I) Let us prove that if \(X'\) is in \({\mathfrak C}\) and  then
then  . Assume first that X is a scheme. Choose an étale presentation
. Assume first that X is a scheme. Choose an étale presentation  and set
and set  , obtaining the following diagram with cartesian squares:
, obtaining the following diagram with cartesian squares:

Applying Lemma 4.2 (ii) to the right diagram we obtain that  and hence
and hence  by Theorem 4.7 (ii).
by Theorem 4.7 (ii).
In general, find a presentation \(X=X_0/X_1\), and set  ,
,  and
and  . Then
. Then  by the above case and it follows by a simple diagram chase and compatibility of colimits that
by the above case and it follows by a simple diagram chase and compatibility of colimits that  .
.
Vice versa, let us prove that if \({\mathscr {P}}'\) is in \({\mathscr {D}}\) and  then
then  . We will distinguish two special cases: (A) \({\mathscr {P}}\) has an open affine covering, (B) \({\mathscr {P}}'\) has an open affine covering. First, let us reduce the general case to case (B). Pick an étale affine covering
. We will distinguish two special cases: (A) \({\mathscr {P}}\) has an open affine covering, (B) \({\mathscr {P}}'\) has an open affine covering. First, let us reduce the general case to case (B). Pick an étale affine covering  , and set \({\mathscr {P}}'_0=\coprod _i{\mathscr {W}}_i\). Then
, and set \({\mathscr {P}}'_0=\coprod _i{\mathscr {W}}_i\). Then  admits an open affine covering by Theorem 6.2 (i). By Theorem 4.7 (ii), setting
admits an open affine covering by Theorem 6.2 (i). By Theorem 4.7 (ii), setting  , we obtain a commutative diagram as above for which \(X'=X'_0/X'_1\) and squares (1), (2) are cartesian. If the assertion is true in case (B) then (23) is also cartesian, and hence (3) is cartesian by flat descent of fiber products. Furthermore, the same argument proves the assertion in case (A) unconditionally because in the latter case (23) is cartesian by Lemma 4.2 (ii).
, we obtain a commutative diagram as above for which \(X'=X'_0/X'_1\) and squares (1), (2) are cartesian. If the assertion is true in case (B) then (23) is also cartesian, and hence (3) is cartesian by flat descent of fiber products. Furthermore, the same argument proves the assertion in case (A) unconditionally because in the latter case (23) is cartesian by Lemma 4.2 (ii).
Now, let us establish case (B). By Theorem 6.2 (i), there exists an étale presentation \({\mathscr {P}}={\mathscr {P}}_0/{\mathscr {P}}_1\), where \({\mathscr {P}}_i\) possess open affine coverings. Then  are effective by Theorem 6.2 (ii)(d). Set
are effective by Theorem 6.2 (ii)(d). Set  and
and  . By case (A),
. By case (A),  , and by Lemma 4.2 (ii),
, and by Lemma 4.2 (ii),  . The assertion now follows by descent of fiber products.
. The assertion now follows by descent of fiber products.
(II) Properties (f)–(h) are étale local on the target and source, hence in these cases the assertion follows by descent from Lemma 4.2 (iii). The assertion for properties (a), (b) is clear since the morphism  is surjective and quasi-compact, and hence a morphism of X-schemes is surjective (resp. quasi-compact) if and only if so is its base change with respect to h. A morphism f satisfies (c), (d) or (e) if and only if f is flat, locally of finite presentation, and its fibers satisfy the same property. Therefore, the case of (c), (d) and (e) follows from (h) and the surjectivity of h. Property (i) (resp. (j)) is the combination of (b) and (g) (resp. (b) and (h)). Finally, if
is surjective and quasi-compact, and hence a morphism of X-schemes is surjective (resp. quasi-compact) if and only if so is its base change with respect to h. A morphism f satisfies (c), (d) or (e) if and only if f is flat, locally of finite presentation, and its fibers satisfy the same property. Therefore, the case of (c), (d) and (e) follows from (h) and the surjectivity of h. Property (i) (resp. (j)) is the combination of (b) and (g) (resp. (b) and (h)). Finally, if  for a family of open immersions \({\mathscr {P}}_i\hookrightarrow {\mathscr {P}}\) then it is also the limit in the category \({\mathfrak D}\), and hence
for a family of open immersions \({\mathscr {P}}_i\hookrightarrow {\mathscr {P}}\) then it is also the limit in the category \({\mathfrak D}\), and hence  is the limit in \({\mathfrak C}\) of the open subspaces
is the limit in \({\mathfrak C}\) of the open subspaces  of X. Clearly,
of X. Clearly,  in the category of algebraic spaces, and hence
in the category of algebraic spaces, and hence  is a pro-open immersion.\(\square \)
is a pro-open immersion.\(\square \)
Corollary 6.5
If \({\mathscr {P}}\) is an effective Ferrand pushout datum, and  , then the categories of flat \({\mathscr {O}}_X\)-modules and flat \({\mathscr {O}}_{\mathscr {P}}\)-modules are naturally equivalent. Furthermore, the equivalence preserves the finite presentation property.
, then the categories of flat \({\mathscr {O}}_X\)-modules and flat \({\mathscr {O}}_{\mathscr {P}}\)-modules are naturally equivalent. Furthermore, the equivalence preserves the finite presentation property.
Proof
Pick an étale affine covering  , and set \({\mathscr {P}}_0=\coprod _i{\mathscr {U}}_i\). Then by Theorem 6.2 (i),
, and set \({\mathscr {P}}_0=\coprod _i{\mathscr {U}}_i\). Then by Theorem 6.2 (i),  possesses an open affine covering, and hence
possesses an open affine covering, and hence  by Theorem 4.3. Thus, the result follows by flat descent, since \(X=X_0/X_1\) and \({\mathscr {P}}={\mathscr {P}}_0/{\mathscr {P}}_1\) by Theorem 4.7, and the assertion of the corollary holds true for \(({\mathscr {P}}_i, X_i)\) by Corollary 3.9.\(\square \)
by Theorem 4.3. Thus, the result follows by flat descent, since \(X=X_0/X_1\) and \({\mathscr {P}}={\mathscr {P}}_0/{\mathscr {P}}_1\) by Theorem 4.7, and the assertion of the corollary holds true for \(({\mathscr {P}}_i, X_i)\) by Corollary 3.9.\(\square \)
6.3.2 The morphism \(Z\rightarrow X\)
Our next aim is to compare properties of the morphisms \(T\rightarrow Y\) and \(Z\rightarrow X\) for a Ferrand pushout  .
.
Theorem 6.6
Let  be a Ferrand pushout, and \((\dag )\) one of the following properties: being open immersion, pro-open immersion, schematically dominant, finite, quasi-finite, finite type. Then \(Z\rightarrow X\) satisfies \((\dag )\) if and only if so does \(T\rightarrow Y\).
be a Ferrand pushout, and \((\dag )\) one of the following properties: being open immersion, pro-open immersion, schematically dominant, finite, quasi-finite, finite type. Then \(Z\rightarrow X\) satisfies \((\dag )\) if and only if so does \(T\rightarrow Y\).
Proof
Only the inverse implication needs a proof since \(T\rightarrow Y\) is a base change of \(Z\rightarrow X\). If \(T\rightarrow Y\) is a (pro-)open immersion then  and hence
and hence  is a morphism of pushout data. Since h is a (pro-)open immersion,
is a morphism of pushout data. Since h is a (pro-)open immersion,  is a (pro-)open immersion by Theorem 6.4 (II). The remaining four properties can be checked étale locally on X, so we may assume that \({\mathscr {P}}\) and X are affine by Theorems 4.7 and 4.3. The case of schematic dominance follows from [3, Proposition 5.6 (2)] and the remaining three cases follow from [3, Proposition 5.6 (3)].\(\square \)
is a (pro-)open immersion by Theorem 6.4 (II). The remaining four properties can be checked étale locally on X, so we may assume that \({\mathscr {P}}\) and X are affine by Theorems 4.7 and 4.3. The case of schematic dominance follows from [3, Proposition 5.6 (2)] and the remaining three cases follow from [3, Proposition 5.6 (3)].\(\square \)
Remark 6.7
(i) In the case of pro-open immersions, Theorem 6.6 actually asserts that if  is a composition then \(Z\rightarrow X\) is a pro-open immersion. This justifies the terminology, since X is “composed” from a closed subspace Y and a pro-open subspace Z.
is a composition then \(Z\rightarrow X\) is a pro-open immersion. This justifies the terminology, since X is “composed” from a closed subspace Y and a pro-open subspace Z.
(ii) The assertion of Theorem 6.6 fails for \((\dag )\) being étale or flat even for pinchings. For example, if Z is a smooth curve over a field k,  ,
,  consists of two k-points, and \(T\rightarrow Y\) is the projection, then X is a nodal curve. So, \(T\rightarrow Y\) is split étale, but \(Z\rightarrow X\) is not even flat.
consists of two k-points, and \(T\rightarrow Y\) is the projection, then X is a nodal curve. So, \(T\rightarrow Y\) is split étale, but \(Z\rightarrow X\) is not even flat.
6.4 S-properties
Note that even a composition of varieties over a field can be non-noetherian. In particular, the property of being of finite type over S is not respected by Ferrand pushouts. Here is a list of few S-properties that are respected.
Theorem 6.8
Let \({\mathscr {P}}\) be an effective Ferrand pushout datum over an algebraic space S, and set  . Let \((\dag )\) be any of the following properties relative to S: being (a) affine, (b) separated, (c) quasi-compact, (d) quasi-separated. Then \({\mathscr {P}}\) satisfies \((\dag )\) if and only if so does X.
. Let \((\dag )\) be any of the following properties relative to S: being (a) affine, (b) separated, (c) quasi-compact, (d) quasi-separated. Then \({\mathscr {P}}\) satisfies \((\dag )\) if and only if so does X.
Proof
Only the direct implication requires a proof. All properties are étale-local on S, and if  is an étale morphism,
is an étale morphism,  , and
, and  , then
, then  by Theorem 6.4 (I). Therefore, we may assume that S is affine, and the result follows from Theorem 6.1.\(\square \)
by Theorem 6.4 (I). Therefore, we may assume that S is affine, and the result follows from Theorem 6.1.\(\square \)
References
Artin, M.: Algebraization of formal moduli. II. Existence of modifications. Ann. of Math. 91(1), 88–135 (1970)
Conrad, B., Lieblich, M., Olsson, M.: Nagata compactification for algebraic spaces. J. Inst. Math. Jussieu 11(4), 747–814 (2012)
Ferrand, D.: Conducteur, descente et pincement. Bull. Soc. Math. France 131(4), 553–585 (2003)
Greco, S., Strano, R.: Quasicoherent sheaves over affine Hensel schemes. Trans. Amer. Math. Soc. 268(2), 445–465 (1981)
Grothendieck, A.: Éléments de Géométrie Algébrique. Institut des Hautes Études Scitifiques, Paris (1960–1967)
Kollár, J.: Quotients by finite equivalence relations. In: Caporaso, L., McKernan, J., Mustata, M., Popa, M. (eds.) Current Developments in Algebraic Geometry. Mathematical Sciences Research Institute Publications, vol. 59, pp. 227–256. Cambridge University Press, Cambridge (2012)
Rydh, D.: Compactification of tame Deligne–Mumford stacks (2010). http://www.math.kth.se/~dary/tamecompactification20110517.pdf
Stacks Project. http://stacks.math.columbia.edu
Temkin, M.: Relative Riemann–Zariski spaces. Israel J. Math. 185, 1–42 (2011)
Temkin, M., Tyomkin, I.: Prüfer algebraic spaces. Math. Z. doi:10.1007/s00209-016-1748-0
Temkin, M., Tyomkin, I.: On relative birational geometry and Nagata’s compactification for algebraic spaces (2013). arXiv:1311.6308
Acknowledgments
We are grateful to Yakov Varshavsky for helpful discussions, and to an anonymous referee for valuable remarks, and for suggesting not to restrict the generality to the case of quasi-compact and quasi-separated algebraic spaces.
Author information
Authors and Affiliations
Corresponding author
Additional information
Both authors were supported by the Israel Science Foundation (Grant No. 1018/11). The second author was also partially supported by the European FP7 IRG Grant No. 248826.
Rights and permissions
About this article
Cite this article
Temkin, M., Tyomkin, I. Ferrand pushouts for algebraic spaces. European Journal of Mathematics 2, 960–983 (2016). https://doi.org/10.1007/s40879-016-0115-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-016-0115-3




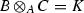 , so Ferrand diagrams are bicartesian.
, so Ferrand diagrams are bicartesian. is Ferrand.
is Ferrand.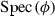 induces an isomorphism of open subschemes
induces an isomorphism of open subschemes 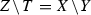 .
. is naturally homeomorphic to |X|,
is naturally homeomorphic to |X|, ,
, is an open immersion, and
is an open immersion, and  ,
,  is an open immersion,
is an open immersion,  , and
, and 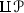 is a scheme.
is a scheme.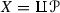 and
and  . Then
. Then  .
.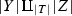 is naturally homeomorphic to |X|.
is naturally homeomorphic to |X|. .
.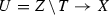 is an open immersion, and
is an open immersion, and  set-theoretically.
set-theoretically. is étale then does it admit a lifting to Z?
is étale then does it admit a lifting to Z? . Moreover, if
. Moreover, if  then
then