Abstract
In this paper, we apply some methods from ring theory to the framework of prime ideals in tensor triangulated categories developed by Balmer. Given a thick tensor ideal \({\mathscr {A}}\) and a multiplicatively closed family \({\mathscr {S}}\) of objects in a tensor triangulated category \(({\mathscr {C}}, \otimes ,1)\), we say that a prime ideal \({\mathscr {P}}\) realizes \(({\mathscr {A}},{\mathscr {S}})\) if \({\mathscr {P}}\supseteq {\mathscr {A}}\) and \({\mathscr {P}}\cap {\mathscr {S}}=\varnothing \). Analogously to the results of Bergman with ordinary rings, we show how to construct a realization of a family \(\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I}\) of such pairs indexed by a finite chain I, i.e., a collection \(\{{\mathscr {P}}_i\}_{i\in I}\) of prime ideals such that each \({\mathscr {P}}_i\) realizes \(({\mathscr {A}}_i,{\mathscr {S}}_i)\) and  for each \(i\leqslant j\) in I. Thereafter we obtain conditions on a family \({\mathfrak {F}} \) of thick tensor ideals of \(({\mathscr {C}},\otimes ,1)\) so that any ideal that is maximal with respect to not being contained in \({\mathfrak {F}}\) must be prime. This extends the Prime Ideal Principle of Lam and Reyes from commutative algebra. We also combine these methods to consider realizations of templates \(\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I}\), where each \({\mathscr {A}}_i\) is a thick tensor ideal and each \({\mathfrak {F}}_i\) is a family of thick tensor ideals that is also a monoidal semifilter.
for each \(i\leqslant j\) in I. Thereafter we obtain conditions on a family \({\mathfrak {F}} \) of thick tensor ideals of \(({\mathscr {C}},\otimes ,1)\) so that any ideal that is maximal with respect to not being contained in \({\mathfrak {F}}\) must be prime. This extends the Prime Ideal Principle of Lam and Reyes from commutative algebra. We also combine these methods to consider realizations of templates \(\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I}\), where each \({\mathscr {A}}_i\) is a thick tensor ideal and each \({\mathfrak {F}}_i\) is a family of thick tensor ideals that is also a monoidal semifilter.
Similar content being viewed by others
1 Introduction
Triangulated categories were introduced by Verdier [37] and have since assumed an increasing significance in several fields of modern mathematics; from algebraic geometry to motives and homotopy theory, modular representation theory and noncommutative geometry. Additionally, a triangulated category appearing in these areas is often gifted with a tensor structure, making it into a tensor triangulated category, i.e., a symmetric monoidal category \(({\mathscr {C}},\otimes ,1)\) such that \({\mathscr {C}}\) is triangulated and  is exact in both variables. The classification of thick subcategories is a common theme that runs through the work of Devinatz et al. [17] in homotopy theory, that of Thomason [36] in algebraic geometry, the work of Benson et al. [11] in modular representation theory and that of Friedlander and Pevtsova with finite group schemes [19]. Tensor triangular geometry developed by Balmer (see [1–5, 8]) unites these classifications in terms of classification of thick tensor ideal subcategories in a tensor triangulated category (also see further work by Balmer and Favi [9, 10]).
is exact in both variables. The classification of thick subcategories is a common theme that runs through the work of Devinatz et al. [17] in homotopy theory, that of Thomason [36] in algebraic geometry, the work of Benson et al. [11] in modular representation theory and that of Friedlander and Pevtsova with finite group schemes [19]. Tensor triangular geometry developed by Balmer (see [1–5, 8]) unites these classifications in terms of classification of thick tensor ideal subcategories in a tensor triangulated category (also see further work by Balmer and Favi [9, 10]).
Given a tensor triangulated category \(({\mathscr {C}},\otimes ,1)\), Balmer [1] associates to it a spectrum  consisting of prime ideals of \({\mathscr {C}}\). A thick tensor ideal \({\mathscr {P}}\) (see Definition 2.1) in \(({\mathscr {C}},\otimes ,1)\) is called prime if
consisting of prime ideals of \({\mathscr {C}}\). A thick tensor ideal \({\mathscr {P}}\) (see Definition 2.1) in \(({\mathscr {C}},\otimes ,1)\) is called prime if  for any objects \(a,b \in {\mathscr {C}}\) implies that at least one of a, b lies in \({\mathscr {P}}\). Then
for any objects \(a,b \in {\mathscr {C}}\) implies that at least one of a, b lies in \({\mathscr {P}}\). Then  is equipped with a Zariski topology and the support theory obtained by associating to each object \(a\in {\mathscr {C}}\) the closed subset
is equipped with a Zariski topology and the support theory obtained by associating to each object \(a\in {\mathscr {C}}\) the closed subset  unites various support theories in algebraic geometry, modular representation theory and homotopy theory. Further, support theory for a tensor triangulated category \(({\mathscr {C}},\otimes ,1)\) acting on a triangulated category \({\mathscr {M}}\) has been developed by Stevenson [34]. Stevenson’s work in [34] may be viewed as categorification of some of the work of Benson, Iyengar and Krause [12–14] in the case of actions of the unbounded derived category
unites various support theories in algebraic geometry, modular representation theory and homotopy theory. Further, support theory for a tensor triangulated category \(({\mathscr {C}},\otimes ,1)\) acting on a triangulated category \({\mathscr {M}}\) has been developed by Stevenson [34]. Stevenson’s work in [34] may be viewed as categorification of some of the work of Benson, Iyengar and Krause [12–14] in the case of actions of the unbounded derived category  for a commutative noetherian ring R. Tensor triangular geometry has further emerged as an object of study in its own right: for instance, Balmer [6] introduced Chow groups of rigid tensor triangulated categories and properties of these Chow groups have been studied in detail by Klein [23, 24]. For further work in tensor triangular geometry, we refer the reader, for example, to Dell’Ambrogio and Stevenson [16], Peter [28], Sanders [31], Stevenson [35] and Xu [38].
for a commutative noetherian ring R. Tensor triangular geometry has further emerged as an object of study in its own right: for instance, Balmer [6] introduced Chow groups of rigid tensor triangulated categories and properties of these Chow groups have been studied in detail by Klein [23, 24]. For further work in tensor triangular geometry, we refer the reader, for example, to Dell’Ambrogio and Stevenson [16], Peter [28], Sanders [31], Stevenson [35] and Xu [38].
The purpose of this paper is to bring some methods in ring theory to the framework of tensor triangulated categories. Let R be an ordinary commutative ring, A be an ideal in R and let \(S\subseteq R\) be a multiplicatively closed subset. Then, Bergman [15] refers to a prime ideal P such that \(P\supseteq A\) and \(P\cap S=\varnothing \) as a realization of the pair (A, S) and says that  . More generally, if \((I,\leqslant )\) is a partially ordered set, Bergman [15] has studied conditions under which a template \(\{(A_i,S_i)\}_{i\in I}\) of such pairs indexed by I admits a realization, i.e., a family \(\{P_i\}_{i\in I}\) of prime ideals such that \(P_i\) realizes \((A_i,S_i)\) and \(P_i\subseteq P_j\) whenever \(i\leqslant j\) in I (see also further work by Sharma [33]). In [1, Lemma 2.2], Balmer shows that if \({\mathscr {A}}\) is a thick tensor ideal in \(({\mathscr {C}}, \otimes ,1)\) and \({\mathscr {S}}\) is a multiplicatively closed family of objects of \({\mathscr {C}}\) such that \({\mathscr {A}}\cap {\mathscr {S}}=\varnothing \), there exists a prime ideal \({\mathscr {P}}\supseteq {\mathscr {A}}\) satisfying \({\mathscr {P}} \cap {\mathscr {S}}=\varnothing \). Our first main aim in this paper is to formulate conditions analogous to those of Bergman [15] for construction of realizations of certain templates \(\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I}\), where each \({\mathscr {A}}_i\) is a thick tensor ideal in \(({\mathscr {C}},\otimes ,1)\) and each \({\mathscr {S}}_i\) is a multiplicatively closed family of objects of \({\mathscr {C}}\).
. More generally, if \((I,\leqslant )\) is a partially ordered set, Bergman [15] has studied conditions under which a template \(\{(A_i,S_i)\}_{i\in I}\) of such pairs indexed by I admits a realization, i.e., a family \(\{P_i\}_{i\in I}\) of prime ideals such that \(P_i\) realizes \((A_i,S_i)\) and \(P_i\subseteq P_j\) whenever \(i\leqslant j\) in I (see also further work by Sharma [33]). In [1, Lemma 2.2], Balmer shows that if \({\mathscr {A}}\) is a thick tensor ideal in \(({\mathscr {C}}, \otimes ,1)\) and \({\mathscr {S}}\) is a multiplicatively closed family of objects of \({\mathscr {C}}\) such that \({\mathscr {A}}\cap {\mathscr {S}}=\varnothing \), there exists a prime ideal \({\mathscr {P}}\supseteq {\mathscr {A}}\) satisfying \({\mathscr {P}} \cap {\mathscr {S}}=\varnothing \). Our first main aim in this paper is to formulate conditions analogous to those of Bergman [15] for construction of realizations of certain templates \(\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I}\), where each \({\mathscr {A}}_i\) is a thick tensor ideal in \(({\mathscr {C}},\otimes ,1)\) and each \({\mathscr {S}}_i\) is a multiplicatively closed family of objects of \({\mathscr {C}}\).
We start in Sect. 2 by defining a relation \(\preccurlyeq \) among pairs such that  if every prime ideal
if every prime ideal  realizing
realizing  contains a prime ideal \({\mathscr {P}}\) realizing the pair \(({\mathscr {A}}, {\mathscr {S}})\). Thereafter, given a template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I}\) indexed by a finite decreasing chain I, we show that its realizations can be described in terms of realizations of a template
contains a prime ideal \({\mathscr {P}}\) realizing the pair \(({\mathscr {A}}, {\mathscr {S}})\). Thereafter, given a template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I}\) indexed by a finite decreasing chain I, we show that its realizations can be described in terms of realizations of a template  satisfying
satisfying  for each \(i\leqslant j\) in I. Under certain finiteness conditions on the pairs in T, we construct a template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i,{\mathscr {T}}_i)\}_{i\in I}\) such that for any fixed \(i_0\in I\), we can start with a prime ideal \({\mathscr {P}} \) realizing the pair \(({\mathscr {B}}_{i_0},{\mathscr {T}}_{i_0})\) and obtain a realization \(\{{\mathscr {P}}_i\}_{i\in I}\) of T with \({\mathscr {P}}_{i_0}={\mathscr {P}}\). Further, looking at the subsets of the form
for each \(i\leqslant j\) in I. Under certain finiteness conditions on the pairs in T, we construct a template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i,{\mathscr {T}}_i)\}_{i\in I}\) such that for any fixed \(i_0\in I\), we can start with a prime ideal \({\mathscr {P}} \) realizing the pair \(({\mathscr {B}}_{i_0},{\mathscr {T}}_{i_0})\) and obtain a realization \(\{{\mathscr {P}}_i\}_{i\in I}\) of T with \({\mathscr {P}}_{i_0}={\mathscr {P}}\). Further, looking at the subsets of the form  themselves, we show that these are exactly the convex subsets of
themselves, we show that these are exactly the convex subsets of  , i.e., subsets
, i.e., subsets  satisfying the property that if \(\bigcup _{{\mathscr {P}} \in {\mathfrak {X}}}{\mathscr {P}}\subseteq {\mathscr {Q}} \subseteq \bigcup _{{\mathscr {P}}\in {\mathfrak {X}}}{\mathscr {P}}\), then \({\mathscr {Q}}\in {\mathfrak {X}}\). We also give necessary and sufficient conditions for a family of finite chains of prime ideals to be a collection of realizations of such template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I}\).
satisfying the property that if \(\bigcup _{{\mathscr {P}} \in {\mathfrak {X}}}{\mathscr {P}}\subseteq {\mathscr {Q}} \subseteq \bigcup _{{\mathscr {P}}\in {\mathfrak {X}}}{\mathscr {P}}\), then \({\mathscr {Q}}\in {\mathfrak {X}}\). We also give necessary and sufficient conditions for a family of finite chains of prime ideals to be a collection of realizations of such template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I}\).
Since  is a spectral space, following Hochster [21], we know that it is equipped with an inverse topology where the open sets
is a spectral space, following Hochster [21], we know that it is equipped with an inverse topology where the open sets  are given by arbitrary unions
are given by arbitrary unions  with each
with each  open and quasi-compact in
open and quasi-compact in  . Then,
. Then,  equipped with this inverse topology is denoted by
equipped with this inverse topology is denoted by  Then, [4, Theorem 14] may be restated as follows: to every thick tensor ideal \({\mathscr {I}}\) in \(({\mathscr {C}},\otimes ,1)\) there is associated the closed subspace
Then, [4, Theorem 14] may be restated as follows: to every thick tensor ideal \({\mathscr {I}}\) in \(({\mathscr {C}},\otimes ,1)\) there is associated the closed subspace

of  . Then, [4, Theorem 14] shows that (1) gives a one-to-one order reversing correspondence between the radical thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) and the closed subspaces of
. Then, [4, Theorem 14] shows that (1) gives a one-to-one order reversing correspondence between the radical thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) and the closed subspaces of  . We have restated this theorem in terms of an order reversing correspondence with closed subspaces (rather than the order preserving correspondence with open subspaces expressed in [4, Theorem 14]) in order to have a comforting similarity with the standard Nullstellensatz. In fact, if X is a topologically noetherian scheme, using the fact that there is a homeomorphism
. We have restated this theorem in terms of an order reversing correspondence with closed subspaces (rather than the order preserving correspondence with open subspaces expressed in [4, Theorem 14]) in order to have a comforting similarity with the standard Nullstellensatz. In fact, if X is a topologically noetherian scheme, using the fact that there is a homeomorphism  (see [1, Corollary 5.6]), we see that the theorem gives us a correspondence between (radical) thick tensor ideals in
(see [1, Corollary 5.6]), we see that the theorem gives us a correspondence between (radical) thick tensor ideals in  and closed subspaces of X in the inverse topology. We can build on this idea in two ways: first, we can think about the constructible topology on X, because the constructible topology on a spectral space always coincides with the constructible topology on its inverse (see, for instance, [18, Corollary 4.8]). Secondly, we can think about the closed irreducible subspaces of the scheme X in inverse topology. More generally, for the tensor triangulated category \({\mathscr {C}}\), we show that subsets of the form
and closed subspaces of X in the inverse topology. We can build on this idea in two ways: first, we can think about the constructible topology on X, because the constructible topology on a spectral space always coincides with the constructible topology on its inverse (see, for instance, [18, Corollary 4.8]). Secondly, we can think about the closed irreducible subspaces of the scheme X in inverse topology. More generally, for the tensor triangulated category \({\mathscr {C}}\), we show that subsets of the form  , which we have previously characterized as the convex subsets of
, which we have previously characterized as the convex subsets of  , are pro-constructible subsets of
, are pro-constructible subsets of  . Then, the subspaces
. Then, the subspaces  themselves become spectral spaces in the induced topology. Further, if \({\mathscr {C}}\) is assumed to be topologically noetherian (see [2, Definition 3.13]), i.e.,
themselves become spectral spaces in the induced topology. Further, if \({\mathscr {C}}\) is assumed to be topologically noetherian (see [2, Definition 3.13]), i.e.,  is a noetherian space, then the constructible topology on
is a noetherian space, then the constructible topology on  has a basis of subsets of the form
has a basis of subsets of the form  . Further, we show that any closed subspace of
. Further, we show that any closed subspace of  in the constructible topology may be expressed as a union of subspaces of the form
in the constructible topology may be expressed as a union of subspaces of the form  .
.
On the other hand, suppose that \({\mathfrak {F}}^*\) is a family of closed subspaces of  such that \(\varnothing \in {\mathfrak {F}}^*\) and \({\mathfrak {F}}^*\) is closed under finite unions. Then, it is clear that any closed subspace
such that \(\varnothing \in {\mathfrak {F}}^*\) and \({\mathfrak {F}}^*\) is closed under finite unions. Then, it is clear that any closed subspace  that is minimal with respect to not being in \({\mathfrak {F}}^*\) must be irreducible. If
that is minimal with respect to not being in \({\mathfrak {F}}^*\) must be irreducible. If  for a topologically noetherian scheme X, then such \(K_0\) will correspond to a closed irreducible subspace of X in inverse topology. Now, a collection \({\mathfrak {F}}\) of thick tensor ideals of \(({\mathscr {C}},\otimes ,1)\) will be referred to as a monoidal family if \({\mathscr {C}}\in {\mathfrak {F}}\) and
for a topologically noetherian scheme X, then such \(K_0\) will correspond to a closed irreducible subspace of X in inverse topology. Now, a collection \({\mathfrak {F}}\) of thick tensor ideals of \(({\mathscr {C}},\otimes ,1)\) will be referred to as a monoidal family if \({\mathscr {C}}\in {\mathfrak {F}}\) and  for every \({\mathscr {I}}_1\), \({\mathscr {I}}_2\in {\mathfrak {F}}\) (see Definition 3.1). Since
for every \({\mathscr {I}}_1\), \({\mathscr {I}}_2\in {\mathfrak {F}}\) (see Definition 3.1). Since  for thick tensor ideals \({\mathscr {I}}_1,{\mathscr {I}}_2\) in \({\mathscr {C}}\), using the correspondence above, we can translate this fact as follows: let \({\mathfrak {F}}\) be a monoidal family of radical ideals in \({\mathscr {C}}\) such that \({\mathscr {C}}\in {\mathfrak {F}}\) and let \({\mathscr {I}}_0\) be a radical ideal that is maximal with respect to being a radical ideal not contained in \({\mathfrak {F}}\). Then, if \({\mathscr {J}},{\mathscr {K}}\) are radical ideals such that
for thick tensor ideals \({\mathscr {I}}_1,{\mathscr {I}}_2\) in \({\mathscr {C}}\), using the correspondence above, we can translate this fact as follows: let \({\mathfrak {F}}\) be a monoidal family of radical ideals in \({\mathscr {C}}\) such that \({\mathscr {C}}\in {\mathfrak {F}}\) and let \({\mathscr {I}}_0\) be a radical ideal that is maximal with respect to being a radical ideal not contained in \({\mathfrak {F}}\). Then, if \({\mathscr {J}},{\mathscr {K}}\) are radical ideals such that  , we must have either \({\mathscr {I}}_0\supseteq {\mathscr {J}}\) or \({\mathscr {I}}_0\supseteq {\mathscr {K}}\). However, this statement does not seem very satisfactory and we would like to obtain better results on families of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\). We therefore use some methods from commutative algebra, where there are several results of the type “maximal implies prime”. For example, given an R-module M, an ideal \(I\subseteq R\) that is maximal among annihilators of non-zero elements of M must be prime. In [25], Lam and Reyes unified such results in the form of a “Prime Ideal Principle”, i.e., criteria on a family \({\mathscr {F}}\) of ideals in R such that an ideal I that is maximal with respect to not being in \({\mathscr {F}}\) must be prime (see also further work by Lam and Reyes [26] and Reyes [29, 30]). Then, the main purpose of Sect. 3 is to construct an analogous Prime Ideal Principle for thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) (see Theorem 3.5). For any thick tensor ideal \({\mathscr {I}}\) and any collection X of objects of \({\mathscr {C}}\), we set
, we must have either \({\mathscr {I}}_0\supseteq {\mathscr {J}}\) or \({\mathscr {I}}_0\supseteq {\mathscr {K}}\). However, this statement does not seem very satisfactory and we would like to obtain better results on families of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\). We therefore use some methods from commutative algebra, where there are several results of the type “maximal implies prime”. For example, given an R-module M, an ideal \(I\subseteq R\) that is maximal among annihilators of non-zero elements of M must be prime. In [25], Lam and Reyes unified such results in the form of a “Prime Ideal Principle”, i.e., criteria on a family \({\mathscr {F}}\) of ideals in R such that an ideal I that is maximal with respect to not being in \({\mathscr {F}}\) must be prime (see also further work by Lam and Reyes [26] and Reyes [29, 30]). Then, the main purpose of Sect. 3 is to construct an analogous Prime Ideal Principle for thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) (see Theorem 3.5). For any thick tensor ideal \({\mathscr {I}}\) and any collection X of objects of \({\mathscr {C}}\), we set

Similarly to the terminology of Lam and Reyes [25], we say that a family \({\mathfrak {F}}\) of thick tensor ideals is an Oka family (resp. an Ako family) if given objects \(a,b\in {\mathscr {C}}\) and a thick tensor ideal \({\mathscr {I}}\) in \(({\mathscr {C}},\otimes ,1)\), then  and
and  implies \({\mathscr {I}} \in {\mathfrak {F}}\) (resp.
implies \({\mathscr {I}} \in {\mathfrak {F}}\) (resp.  and
and  implies
implies  ). Thereafter, we show that any family \({\mathfrak {F}}\) of thick tensor ideals that is either Oka or Ako must satisfy the Prime Ideal Principle. In particular, if \({\mathscr {S}}\) is a multiplicatively closed family of objects of \({\mathscr {C}}\), we show that the family
). Thereafter, we show that any family \({\mathfrak {F}}\) of thick tensor ideals that is either Oka or Ako must satisfy the Prime Ideal Principle. In particular, if \({\mathscr {S}}\) is a multiplicatively closed family of objects of \({\mathscr {C}}\), we show that the family

is an Oka family (as well as an Ako family) and hence any thick tensor ideal maximal with respect to being disjoint from \({\mathscr {S}}\) must be prime. In fact, \({\mathfrak {F}}_{{\mathscr {S}}}\) is also a monoidal semifilter (see Definition 3.1), i.e., the product of any two thick tensor ideals in \({\mathfrak {F}}_{{\mathscr {S}}}\) lies in \({\mathfrak {F}}_{{\mathscr {S}}}\) and, given any \({\mathscr {I}}\in {\mathfrak {F}}_{{\mathscr {S}}}\), any thick tensor ideal \({\mathscr {J}}\supseteq {\mathscr {I}}\) also lies in \({\mathfrak {F}}_{{\mathscr {S}}}\). From Theorem 3.5, a monoidal semifilter \({\mathfrak {F}}\) is both an Oka family and an Ako family. We also prove other results from [25] in the framework of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\), such as any ideal that is maximal among thick tensor ideals satisfying  for each \(n\geqslant 0\) must be prime. Using the notion from Stevenson [34] of a tensor triangulated category \(({\mathscr {C}},\otimes ,1)\) having a module action on a triangulated category \({\mathscr {M}}\), we show that a thick tensor ideal that is maximal among annihilators of non-zero objects of \({\mathscr {M}}\) is also prime.
for each \(n\geqslant 0\) must be prime. Using the notion from Stevenson [34] of a tensor triangulated category \(({\mathscr {C}},\otimes ,1)\) having a module action on a triangulated category \({\mathscr {M}}\), we show that a thick tensor ideal that is maximal among annihilators of non-zero objects of \({\mathscr {M}}\) is also prime.
In Sect. 4, we combine the methods of Sects. 2 and 3. We consider pairs \(({\mathscr {A}},{\mathfrak {F}})\) such that \({\mathscr {A}}\) is a thick tensor ideal and \({\mathfrak {F}}\) is a monoidal semifilter. Further, we assume that any non-empty increasing chain of ideals in the complement  of \({\mathfrak {F}}\) has an upper bound in
of \({\mathfrak {F}}\) has an upper bound in  (see Definition 4.1), whence it follows that if \({\mathscr {A}}\notin {\mathfrak {F}}\), there always exists a prime ideal \({\mathscr {P}}\supseteq {\mathscr {A}}\) such that \({\mathscr {P}}\notin {\mathfrak {F}}\). We refer to such prime ideal \({\mathscr {P}}\) as a realization of \(({\mathscr {A}},{\mathfrak {F}})\). Accordingly, we can define realizations of templates \(\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I}\) indexed by a partially ordered set I. As in Sect. 2, we define a relation \(\preccurlyeq \) among pairs such that
(see Definition 4.1), whence it follows that if \({\mathscr {A}}\notin {\mathfrak {F}}\), there always exists a prime ideal \({\mathscr {P}}\supseteq {\mathscr {A}}\) such that \({\mathscr {P}}\notin {\mathfrak {F}}\). We refer to such prime ideal \({\mathscr {P}}\) as a realization of \(({\mathscr {A}},{\mathfrak {F}})\). Accordingly, we can define realizations of templates \(\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I}\) indexed by a partially ordered set I. As in Sect. 2, we define a relation \(\preccurlyeq \) among pairs such that  if every prime ideal
if every prime ideal  realizing
realizing  contains a prime ideal \({\mathscr {P}}\) realizing \(({\mathscr {A}},{\mathfrak {F}})\). We show how to construct realizations of a template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I}\) indexed by a finite decreasing chain I by replacing it with a template
contains a prime ideal \({\mathscr {P}}\) realizing \(({\mathscr {A}},{\mathfrak {F}})\). We show how to construct realizations of a template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I}\) indexed by a finite decreasing chain I by replacing it with a template  that satisfies
that satisfies  for each \(i\leqslant j\) in I. Again, under certain finiteness conditions, we construct a template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i, {\mathfrak {G}}_i)\}_{i\in I}\) such that for any chosen \(i_0\in I\), we can start with a prime ideal \({\mathscr {P}}\) realizing \(({\mathscr {B}}_{i_0}, {\mathfrak {G}}_{i_0})\) and obtain a realization \(\{{\mathscr {P}}_i\}_{i\in I}\) of T such that \({\mathscr {P}}_{i_0}={\mathscr {P}}\). Towards the end of Sect. 4, we also construct realizations for templates indexed by finite descending trees.
for each \(i\leqslant j\) in I. Again, under certain finiteness conditions, we construct a template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i, {\mathfrak {G}}_i)\}_{i\in I}\) such that for any chosen \(i_0\in I\), we can start with a prime ideal \({\mathscr {P}}\) realizing \(({\mathscr {B}}_{i_0}, {\mathfrak {G}}_{i_0})\) and obtain a realization \(\{{\mathscr {P}}_i\}_{i\in I}\) of T such that \({\mathscr {P}}_{i_0}={\mathscr {P}}\). Towards the end of Sect. 4, we also construct realizations for templates indexed by finite descending trees.
Finally, in Sect. 5, we assume that all thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) are radical, i.e.,  for all thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\). In fact, this property is quite common in examples of tensor triangulated categories (see [1, Remark 4.3]). For us, the key consequence of this assumption is that it implies
for all thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\). In fact, this property is quite common in examples of tensor triangulated categories (see [1, Remark 4.3]). For us, the key consequence of this assumption is that it implies  for all thick tensor ideals \({\mathscr {I}}\) and \({\mathscr {J}}\). We then show that all thick tensor ideals being radical, every monoidal family \({\mathfrak {F}}\) of thick tensor ideals satisfies the Prime Ideal Principle, i.e., any ideal that is maximal with respect to not being in \({\mathfrak {F}}\) must be prime. Accordingly, we show that any ideal in \(({\mathscr {C}},\otimes ,1)\) that is maximal with respect to not being principal is prime. An analogous result holds for ideals that are maximal with respect to not being generated by a set of cardinality \(\leqslant \alpha \) for some infinite cardinal \(\alpha \). Thereafter, we formulate conditions for the construction of realizations of certain templates \(\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I}\) indexed by an infinite decreasing chain I. We conclude by showing how we can construct families \({\mathfrak {F}}^*\) of closed subspaces of
for all thick tensor ideals \({\mathscr {I}}\) and \({\mathscr {J}}\). We then show that all thick tensor ideals being radical, every monoidal family \({\mathfrak {F}}\) of thick tensor ideals satisfies the Prime Ideal Principle, i.e., any ideal that is maximal with respect to not being in \({\mathfrak {F}}\) must be prime. Accordingly, we show that any ideal in \(({\mathscr {C}},\otimes ,1)\) that is maximal with respect to not being principal is prime. An analogous result holds for ideals that are maximal with respect to not being generated by a set of cardinality \(\leqslant \alpha \) for some infinite cardinal \(\alpha \). Thereafter, we formulate conditions for the construction of realizations of certain templates \(\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I}\) indexed by an infinite decreasing chain I. We conclude by showing how we can construct families \({\mathfrak {F}}^*\) of closed subspaces of  that are not closed under finite unions such that any closed subspace that is minimal with respect to not being in \({\mathfrak {F}}^*\) is irreducible. This is done with the help of Ako families of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\).
that are not closed under finite unions such that any closed subspace that is minimal with respect to not being in \({\mathfrak {F}}^*\) is irreducible. This is done with the help of Ako families of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\).
We mention here that in [8], Balmer has proved a Going-Up Theorem in tensor triangular geometry with profound connections to Quillen stratification in modular representation theory. When \({\mathscr {C}}\) is idempotent-complete, Balmer’s result (see [8, Section 1.5]) gives going-up and incomparability results for prime ideals in the spectra of categories of modules over tt-rings in \(({\mathscr {C}},\otimes ,1)\). The tt-rings are commutative ring objects in \(({\mathscr {C}},\otimes ,1)\) that are also separable in a suitable sense (see [8, Section 2] for details). As such, it is hoped that the methods in this paper can be developed in the future to study prime ideals in the spectra of categories of modules over tt-rings, thus using tensor triangular geometry to obtain further connections between classical commutative algebra and modular representation theory. For more on tt-rings in \(({\mathscr {C}},\otimes ,1)\), we also refer the reader to Balmer [7].
In this paper, we will always assume that our categories are essentially small. Further, by abuse of notation, for any category \({\mathscr {D}}\), we will always write \(x\in {\mathscr {D}}\) to mean that x is an object of \({\mathscr {D}}\).
2 Prime ideals in \(({\mathscr {C}},\otimes ,1)\) and realizations of pairs
Throughout this section and the rest of this paper, \(({\mathscr {C}},\otimes ,1)\) will be a symmetric monoidal category with \({\mathscr {C}}\) also having the structure of a triangulated category (see [37]). Further, we will always assume that the symmetric monoidal tensor product  is exact in each variable and the category \({\mathscr {C}}\) contains all finite direct sums. We will say that \(({\mathscr {C}},\otimes ,1)\) is a tensor triangulated category. Further, a tensor triangulated functor \(F:({\mathscr {C}},\otimes ,1)\rightarrow ({\mathscr {D}},\otimes ,1)\) between tensor triangulated categories \({\mathscr {C}}\) and \({\mathscr {D}}\) will be an exact functor
\(F:{\mathscr {C}}\rightarrow {\mathscr {D}}\) that preserves the symmetric monoidal product and carries the unit object in \({\mathscr {C}}\) to the unit object in \({\mathscr {D}}\). Unless otherwise mentioned, we do not require our tensor triangulated categories to satisfy the additional axioms due to May [27].
is exact in each variable and the category \({\mathscr {C}}\) contains all finite direct sums. We will say that \(({\mathscr {C}},\otimes ,1)\) is a tensor triangulated category. Further, a tensor triangulated functor \(F:({\mathscr {C}},\otimes ,1)\rightarrow ({\mathscr {D}},\otimes ,1)\) between tensor triangulated categories \({\mathscr {C}}\) and \({\mathscr {D}}\) will be an exact functor
\(F:{\mathscr {C}}\rightarrow {\mathscr {D}}\) that preserves the symmetric monoidal product and carries the unit object in \({\mathscr {C}}\) to the unit object in \({\mathscr {D}}\). Unless otherwise mentioned, we do not require our tensor triangulated categories to satisfy the additional axioms due to May [27].
Given an object a in the triangulated category \({\mathscr {C}}\), we will denote the translation of a in \({\mathscr {C}}\) by \(\mathrm{T}a\). We now recall from Balmer [1] the notion of a prime ideal in the tensor triangulated category \(({\mathscr {C}},\otimes ,1)\).
Definition 2.1
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category as given above and let \({\mathscr {A}}\) be a full subcategory of \({\mathscr {C}}\) containing 0. Then, \({\mathscr {A}}\) will be called a thick tensor ideal if it satisfies the following conditions:
-
The subcategory \({\mathscr {A}}\) is triangulated, i.e. if \(a\rightarrow b\rightarrow c\rightarrow \mathrm{T}a\) is a distinguished triangle in \({\mathscr {C}}\) and any two of a, b and c lie in \({\mathscr {A}}\), so does the third.
-
The subcategory \({\mathscr {A}}\) is thick, i.e., if \(a\in {\mathscr {A}}\) splits in \({\mathscr {C}}\) as a direct sum
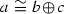 , both direct summands b and c lie in \({\mathscr {A}}\).
, both direct summands b and c lie in \({\mathscr {A}}\). -
The subcategory \({\mathscr {A}}\) is a tensor ideal, i.e., if \(a\in {\mathscr {A}}\) and \(b\in {\mathscr {C}}\), then we must have
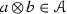 .
.
We will use the expression  to mean that \({\mathscr {A}}\) is a thick tensor ideal of \(({\mathscr {C}},\otimes ,1)\). Given thick tensor ideals \({\mathscr {A}}\),
to mean that \({\mathscr {A}}\) is a thick tensor ideal of \(({\mathscr {C}},\otimes ,1)\). Given thick tensor ideals \({\mathscr {A}}\),  , we will denote by \({\mathscr {A}}+{\mathscr {B}}\) the smallest thick tensor ideal containing both \({\mathscr {A}}\) and \({\mathscr {B}}\).
, we will denote by \({\mathscr {A}}+{\mathscr {B}}\) the smallest thick tensor ideal containing both \({\mathscr {A}}\) and \({\mathscr {B}}\).
Finally, if \({\mathscr {P}}\) is a proper thick tensor ideal in \(({\mathscr {C}},\otimes ,1)\), \({\mathscr {P}}\) is said to be prime if

A family \({\mathscr {S}}\) of objects of \({\mathscr {C}}\) will be said to be multiplicatively closed if \(1\in {\mathscr {S}}\) and for any \(a,b\in {\mathscr {S}}\), we have  . We will work with pairs \(({\mathscr {A}},{\mathscr {S}})\), where \({\mathscr {A}}\) is a thick tensor ideal and \({\mathscr {S}}\) is a multiplicatively closed family of objects of \({\mathscr {C}}\). From [1, Lemma 2.2], we know that if \(({\mathscr {A}},{\mathscr {S}})\) is such pair with \({\mathscr {A}}\cap {\mathscr {S}}=\varnothing \), there always exists a prime ideal \({\mathscr {P}}\) such that \({\mathscr {A}}\subseteq {\mathscr {P}}\) and \({\mathscr {P}}\cap {\mathscr {S}}=\varnothing \). We start with a prime avoidance result for the category \(({\mathscr {C}},\otimes ,1)\).
. We will work with pairs \(({\mathscr {A}},{\mathscr {S}})\), where \({\mathscr {A}}\) is a thick tensor ideal and \({\mathscr {S}}\) is a multiplicatively closed family of objects of \({\mathscr {C}}\). From [1, Lemma 2.2], we know that if \(({\mathscr {A}},{\mathscr {S}})\) is such pair with \({\mathscr {A}}\cap {\mathscr {S}}=\varnothing \), there always exists a prime ideal \({\mathscr {P}}\) such that \({\mathscr {A}}\subseteq {\mathscr {P}}\) and \({\mathscr {P}}\cap {\mathscr {S}}=\varnothing \). We start with a prime avoidance result for the category \(({\mathscr {C}},\otimes ,1)\).
Proposition 2.2
Let \({\mathscr {A}}\) be a thick tensor ideal of \(({\mathscr {C}},\otimes ,1)\) that is contained in the union  of finitely many prime ideals \({\mathscr {P}}_i\). Then, there exists some \(1\leqslant i\leqslant n\) such that \({\mathscr {A}}\subseteq {\mathscr {P}}_i\).
of finitely many prime ideals \({\mathscr {P}}_i\). Then, there exists some \(1\leqslant i\leqslant n\) such that \({\mathscr {A}}\subseteq {\mathscr {P}}_i\).
Proof
We proceed by induction on n. The result is obvious for \(n=1\). We suppose that the result holds for all integers up to \(n-1\) and consider some  . Suppose that we can choose some object \(a_j\in {\mathscr {A}}\) for each \(1\leqslant j\leqslant n\) such that
. Suppose that we can choose some object \(a_j\in {\mathscr {A}}\) for each \(1\leqslant j\leqslant n\) such that  and
and  . We consider the object
. We consider the object  (since \({\mathscr {A}}\) is triangulated, it is easy to check that it contains direct sums).
(since \({\mathscr {A}}\) is triangulated, it is easy to check that it contains direct sums).
Now suppose that  . Then, since
. Then, since  is thick, we must have
is thick, we must have  . However, this is impossible, since
. However, this is impossible, since  is prime and we have chosen
is prime and we have chosen  for all \(1\leqslant i\leqslant n-1\). On the other hand, if \(a\in {\mathscr {P}}_i\) for some \(1\leqslant i\leqslant n-1\), it follows that \(a_n\in {\mathscr {P}}_i\) which is also a contradiction. This contradicts the fact that
for all \(1\leqslant i\leqslant n-1\). On the other hand, if \(a\in {\mathscr {P}}_i\) for some \(1\leqslant i\leqslant n-1\), it follows that \(a_n\in {\mathscr {P}}_i\) which is also a contradiction. This contradicts the fact that  . Hence, it follows that the thick tensor ideal \({\mathscr {A}}\) is already contained in the union of some proper subcollection of \(\{{\mathscr {P}}_i\}_{1\leqslant i\leqslant n}\). Using the induction assumption, the result follows. \(\square \)
. Hence, it follows that the thick tensor ideal \({\mathscr {A}}\) is already contained in the union of some proper subcollection of \(\{{\mathscr {P}}_i\}_{1\leqslant i\leqslant n}\). Using the induction assumption, the result follows. \(\square \)
Analogously to the terminology of Bergman [15, Definition 7], we now introduce the following definition.
Definition 2.3
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category as given above. Let \(({\mathscr {A}}, {\mathscr {S}})\) be a pair such that \({\mathscr {A}}\) is a thick tensor ideal and \({\mathscr {S}}\) is a multiplicatively closed family of objects of \({\mathscr {C}}\). Then, a prime ideal \({\mathscr {P}}\) in \({\mathscr {C}}\) is said to be a realization of the pair
\(({\mathscr {A}},{\mathscr {S}})\) if \({\mathscr {A}}\subseteq {\mathscr {P}}\) and \({\mathscr {P}}\cap {\mathscr {S}}=\varnothing \). The collection of all realizations of such a pair \(({\mathscr {A}},{\mathscr {S}})\) will be denoted by  . Further, we let \({\mathscr {M}}{({\mathscr {A}},{\mathscr {S}})}\) be the multiplicatively closed family given by the complement of
. Further, we let \({\mathscr {M}}{({\mathscr {A}},{\mathscr {S}})}\) be the multiplicatively closed family given by the complement of  .
.
More generally, let \((I,\leqslant )\) be a partially ordered set. By a template
T indexed by I, we will mean a family \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I}\) of pairs indexed by I. Then, we will say that a collection \(\{{\mathscr {P}}_i\}_{i\in I}\) of prime ideals in \({\mathscr {C}}\) is a realization of the template
T if each \({\mathscr {P}}_i\) realizes the pair \(({\mathscr {A}}_i,{\mathscr {S}}_i)\) and  for every \(i\leqslant j\) in I.
for every \(i\leqslant j\) in I.
Given a thick tensor ideal \({\mathscr {A}}\) and a multiplicatively closed family \({\mathscr {S}}\), we define  to be the full subcategory of \({\mathscr {C}}\) consisting of the following objects:
to be the full subcategory of \({\mathscr {C}}\) consisting of the following objects:

Lemma 2.4
Let \({\mathscr {A}}\) be a thick tensor ideal and \({\mathscr {S}}\) be a multiplicatively closed family. Then, the full subcategory  as defined in (2) determines a thick tensor ideal in \(({\mathscr {C}},\otimes ,1)\) containing \({\mathscr {A}}\).
as defined in (2) determines a thick tensor ideal in \(({\mathscr {C}},\otimes ,1)\) containing \({\mathscr {A}}\).
Proof
From the definition in (2), it is clear that the full subcategory  contains \({\mathscr {A}}\) and that given any
contains \({\mathscr {A}}\) and that given any  and
and  , we must have
, we must have  . In order to check that
. In order to check that  is thick, consider some
is thick, consider some  such that a decomposes as a direct sum
such that a decomposes as a direct sum  . We know that there exists \(s\in {\mathscr {S}}\) such that
. We know that there exists \(s\in {\mathscr {S}}\) such that  . It follows that
. It follows that

Since \({\mathscr {A}}\) is thick, it now follows that  , whence we have
, whence we have  . Finally, we consider a distinguished triangle
. Finally, we consider a distinguished triangle
where two out of a, b, c lie in  . For the sake of definiteness, suppose that
. For the sake of definiteness, suppose that  and choose \(s,t\in S\) such that
and choose \(s,t\in S\) such that  . Since S is multiplicatively closed and
. Since S is multiplicatively closed and  is exact in both variables, we have a new distinguished triangle
is exact in both variables, we have a new distinguished triangle

in \({\mathscr {C}}\). Since  , we see that
, we see that  and we have
and we have  . This proves the result. \(\square \)
. This proves the result. \(\square \)
We note here that, by Definition 2.1, every thick tensor ideal is a full subcategory of \({\mathscr {C}}\). Hence,  . Further, given any thick tensor ideal \({\mathscr {A}}\) and a multiplicatively closed family of objects \({\mathscr {S}}\), it is clear that
. Further, given any thick tensor ideal \({\mathscr {A}}\) and a multiplicatively closed family of objects \({\mathscr {S}}\), it is clear that  is also a multiplicatively closed family of objects. Given multiplicatively closed families
is also a multiplicatively closed family of objects. Given multiplicatively closed families  , we can also form the multiplicatively closed family
, we can also form the multiplicatively closed family  . In order to understand realizations of chains, we will need the following result.
. In order to understand realizations of chains, we will need the following result.
Proposition 2.5
Let \(({\mathscr {A}},{\mathscr {S}})\) be a pair such that \({\mathscr {A}}\) is a thick tensor ideal and \({\mathscr {S}}\) is a multiplicatively closed family of objects of \({\mathscr {C}}\). Then, we have:
-
(a)
A prime ideal \({\mathscr {P}}\) contains
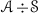 if and only if it contains a prime ideal realizing \(({\mathscr {A}},{\mathscr {S}})\).
if and only if it contains a prime ideal realizing \(({\mathscr {A}},{\mathscr {S}})\). -
(b)
If a prime ideal \({\mathscr {P}}\) is contained in a prime ideal that realizes \(({\mathscr {A}},{\mathscr {S}})\), then \({\mathscr {P}}\) must be disjoint from
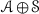 .
. -
(c)
Suppose that
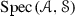 is finite. Then, a prime ideal \({\mathscr {P}}\) is contained in a prime ideal realizing \(({\mathscr {A}},{\mathscr {S}})\) if and only if \({\mathscr {P}}\) is disjoint from \({\mathscr {M}}({\mathscr {A}},{\mathscr {S}})\).
is finite. Then, a prime ideal \({\mathscr {P}}\) is contained in a prime ideal realizing \(({\mathscr {A}},{\mathscr {S}})\) if and only if \({\mathscr {P}}\) is disjoint from \({\mathscr {M}}({\mathscr {A}},{\mathscr {S}})\).
Proof
(a) From the definition of  it is clear that any prime ideal \({\mathscr {Q}}\) realizing \(({\mathscr {A}},{\mathscr {S}})\) also contains
it is clear that any prime ideal \({\mathscr {Q}}\) realizing \(({\mathscr {A}},{\mathscr {S}})\) also contains  . Hence, so does any prime ideal containing \({\mathscr {Q}}\). Conversely, if \({\mathscr {P}}\) is a prime ideal containing
. Hence, so does any prime ideal containing \({\mathscr {Q}}\). Conversely, if \({\mathscr {P}}\) is a prime ideal containing  , it follows that
, it follows that  whence it follows that \({\mathscr {S}}({\mathscr {C}}-{\mathscr {P}})\cap {\mathscr {A}}=\varnothing \). Accordingly, we can choose a prime ideal \({\mathscr {Q}}\) such that \({\mathscr {Q}}\cap {\mathscr {S}}({\mathscr {C}}-{\mathscr {P}})=\varnothing \) and \({\mathscr {A}}\subseteq {\mathscr {Q}}\). Since \({\mathscr {Q}}\cap {\mathscr {S}}\subseteq {\mathscr {Q}}\cap {\mathscr {S}}({\mathscr {C}}-{\mathscr {P}})=\varnothing \), we know that \({\mathscr {Q}}\) realizes \(({\mathscr {A}},{\mathscr {S}})\). Finally, since \({\mathscr {Q}}\cap ({\mathscr {C}}-{\mathscr {P}})\subseteq {\mathscr {Q}}\cap {\mathscr {S}}({\mathscr {C}}-{\mathscr {P}})=\varnothing \), it follows that \({\mathscr {Q}}\subseteq {\mathscr {P}}\).
whence it follows that \({\mathscr {S}}({\mathscr {C}}-{\mathscr {P}})\cap {\mathscr {A}}=\varnothing \). Accordingly, we can choose a prime ideal \({\mathscr {Q}}\) such that \({\mathscr {Q}}\cap {\mathscr {S}}({\mathscr {C}}-{\mathscr {P}})=\varnothing \) and \({\mathscr {A}}\subseteq {\mathscr {Q}}\). Since \({\mathscr {Q}}\cap {\mathscr {S}}\subseteq {\mathscr {Q}}\cap {\mathscr {S}}({\mathscr {C}}-{\mathscr {P}})=\varnothing \), we know that \({\mathscr {Q}}\) realizes \(({\mathscr {A}},{\mathscr {S}})\). Finally, since \({\mathscr {Q}}\cap ({\mathscr {C}}-{\mathscr {P}})\subseteq {\mathscr {Q}}\cap {\mathscr {S}}({\mathscr {C}}-{\mathscr {P}})=\varnothing \), it follows that \({\mathscr {Q}}\subseteq {\mathscr {P}}\).
(b) Suppose that \({\mathscr {Q}}\) realizes \(({\mathscr {A}},{\mathscr {S}})\) and let \(a\in {\mathscr {A}}\), \(s\in {\mathscr {S}}\) be such that  . Since \({\mathscr {Q}}\) is thick, this implies that \(s\in {\mathscr {Q}}\) which is a contradiction. Hence,
. Since \({\mathscr {Q}}\) is thick, this implies that \(s\in {\mathscr {Q}}\) which is a contradiction. Hence,  and hence any prime ideal contained in \({\mathscr {Q}}\) is also disjoint from
and hence any prime ideal contained in \({\mathscr {Q}}\) is also disjoint from  .
.
(c) Suppose that \({\mathscr {P}}\subseteq {\mathscr {Q}}\) for some  . Then,
. Then,  and hence \({\mathscr {P}}\cap {\mathscr {M}}({\mathscr {A}},{\mathscr {S}})=\varnothing \). Conversely, if \({\mathscr {P}}\cap {\mathscr {M}}({\mathscr {A}},{\mathscr {S}})=\varnothing \), then
and hence \({\mathscr {P}}\cap {\mathscr {M}}({\mathscr {A}},{\mathscr {S}})=\varnothing \). Conversely, if \({\mathscr {P}}\cap {\mathscr {M}}({\mathscr {A}},{\mathscr {S}})=\varnothing \), then  . However, since
. However, since  is finite, it follows from the prime avoidance result in Proposition 2.2 that \({\mathscr {P}}\subseteq {\mathscr {Q}}\) for some
is finite, it follows from the prime avoidance result in Proposition 2.2 that \({\mathscr {P}}\subseteq {\mathscr {Q}}\) for some  . \(\square \)
. \(\square \)
Definition 2.6
Let \(({\mathscr {A}},{\mathscr {S}})\) and  be two pairs as in Definition 2.3. Then, we will say that
be two pairs as in Definition 2.3. Then, we will say that  if every prime ideal
if every prime ideal  realizing the pair
realizing the pair  contains a prime ideal \({\mathscr {P}}\) realizing \(({\mathscr {A}},{\mathscr {S}})\).
contains a prime ideal \({\mathscr {P}}\) realizing \(({\mathscr {A}},{\mathscr {S}})\).
We now recall from [1, Section 4] that, given any thick tensor ideal \({\mathscr {I}}\), we can define its radical
 as follows:
as follows:

Then, from [1, Lemma 4.2], we know that  is also a thick tensor ideal and indeed
is also a thick tensor ideal and indeed  is given by the intersection
is given by the intersection  of all prime ideals containing \({\mathscr {I}}\).
of all prime ideals containing \({\mathscr {I}}\).
Proposition 2.7
Let \(({\mathscr {A}},{\mathscr {S}})\) and  be two pairs. Then, the following are equivalent:
be two pairs. Then, the following are equivalent:
-
(a)
The pairs are related as
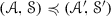 , i.e., any prime ideal realizing
, i.e., any prime ideal realizing 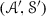 contains a prime ideal realizing \(({\mathscr {A}},{\mathscr {S}})\).
contains a prime ideal realizing \(({\mathscr {A}},{\mathscr {S}})\). -
(b)
The radical of
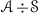 is contained in the radical of
is contained in the radical of 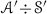 , i.e.,
, i.e.,  .
.
Proof
(b) \(\Rightarrow \) (a). Suppose that  and let
and let  be a prime ideal realizing
be a prime ideal realizing  . Then,
. Then,  and
and  being prime, we get
being prime, we get  . Then, we have
. Then, we have

and it follows from Proposition 2.5 that  contains a prime ideal realizing the pair \(({\mathscr {A}},{\mathscr {S}})\).
contains a prime ideal realizing the pair \(({\mathscr {A}},{\mathscr {S}})\).
(a) \(\Rightarrow \) (b). Consider any prime ideal  such that
such that  . Then, from Proposition 2.5, we know that
. Then, from Proposition 2.5, we know that  contains a prime ideal
contains a prime ideal  realizing
realizing  . By assumption, there exists a prime ideal
. By assumption, there exists a prime ideal  such that \({\mathscr {P}}\) realizes \(({\mathscr {A}},{\mathscr {S}})\). Hence,
such that \({\mathscr {P}}\) realizes \(({\mathscr {A}},{\mathscr {S}})\). Hence,  and therefore
and therefore  for any prime ideal
for any prime ideal  containing
containing  . It now follows that
. It now follows that  .\(\square \)
.\(\square \)
Remark 2.8
We note that \(\preccurlyeq \) is not a partial order relation. In particular, if  and
and  , we do get
, we do get  but not necessarily that
but not necessarily that  . However, it is clear that \(\preccurlyeq \) is reflexive and transitive.
. However, it is clear that \(\preccurlyeq \) is reflexive and transitive.
We now start by considering realizations of templates \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{1\leqslant i\leqslant n}\) indexed by a finite chain of length \(n\geqslant 1\). In particular, if the pairs in the finite chain template also satisfy

it is clear how to find a realization of such template: we choose any prime ideal \({\mathscr {P}}_1\) realizing \(({\mathscr {A}}_1,{\mathscr {S}}_1)\). Then, since  , we can choose a prime ideal \({\mathscr {P}}_{2}\subseteq {\mathscr {P}}_1\) such that \({\mathscr {P}}_{2}\) realizes \(({\mathscr {A}}_{2},{\mathscr {S}}_{2})\) and so on. We will now show that given any finite chain template, its realizations can be described in terms of realizations of a chain template satisfying the condition in (3). Given a partially ordered set \((I,\leqslant )\), we will denote by \(I^\mathrm{op}\) the partially ordered set obtained by reversing all order relations in I.
, we can choose a prime ideal \({\mathscr {P}}_{2}\subseteq {\mathscr {P}}_1\) such that \({\mathscr {P}}_{2}\) realizes \(({\mathscr {A}}_{2},{\mathscr {S}}_{2})\) and so on. We will now show that given any finite chain template, its realizations can be described in terms of realizations of a chain template satisfying the condition in (3). Given a partially ordered set \((I,\leqslant )\), we will denote by \(I^\mathrm{op}\) the partially ordered set obtained by reversing all order relations in I.
Proposition 2.9
Let \(n\geqslant 1\) and let \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) be a finite chain template indexed by the opposite \(I^\mathrm{op}\) of the ordered set \(I=\{1<2<\cdots <n\}\). We define \(\{{\mathscr {B}}_i\}_{1\leqslant i\leqslant n}\) inductively by letting \({\mathscr {B}}_n ={\mathscr {A}}_n\) and setting

Then, we have:
-
(a)
A chain
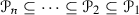 is a realization of the template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) if and only if it is also a realization of the template
is a realization of the template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) if and only if it is also a realization of the template 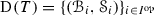 .
. -
(b)
The template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) has a realization if and only if \({\mathscr {B}}_1\cap {\mathscr {S}}_1=\varnothing \), i.e.
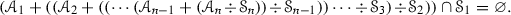
Proof
(a) Let  be a realization of the template T. We know that \({\mathscr {B}}_n={\mathscr {A}}_n\) and hence
be a realization of the template T. We know that \({\mathscr {B}}_n={\mathscr {A}}_n\) and hence  realizes \((\mathscr {B}_n,{\mathscr {S}}_n)\). Now suppose that \({\mathscr {P}}_i\) realizes \(({\mathscr {B}}_i,{\mathscr {S}}_i)\) for each \(n\geqslant i>j\) for some given j. Then, since
realizes \((\mathscr {B}_n,{\mathscr {S}}_n)\). Now suppose that \({\mathscr {P}}_i\) realizes \(({\mathscr {B}}_i,{\mathscr {S}}_i)\) for each \(n\geqslant i>j\) for some given j. Then, since  and
and  realizes
realizes  , it follows from Proposition 2.5 that
, it follows from Proposition 2.5 that  . Since
. Since  realizes
realizes  , we already know that
, we already know that  and
and  . From (4), it follows that
. From (4), it follows that  and
and  , i.e.,
, i.e.,  realizes the pair
realizes the pair  . This proves the result by induction.
. This proves the result by induction.
Conversely, let  be a realization of the template
be a realization of the template  . Then, for each \(1\leqslant i\leqslant n\), we know that \({\mathscr {P}}_i\) realizes the pair \(({\mathscr {B}}_i,{\mathscr {S}}_i)\). From (4), it is clear that \({\mathscr {A}}_i\subseteq {\mathscr {B}}_i\) and hence \({\mathscr {P}}_i\) realizes the pair \(({\mathscr {A}}_i,{\mathscr {S}}_i)\).
. Then, for each \(1\leqslant i\leqslant n\), we know that \({\mathscr {P}}_i\) realizes the pair \(({\mathscr {B}}_i,{\mathscr {S}}_i)\). From (4), it is clear that \({\mathscr {A}}_i\subseteq {\mathscr {B}}_i\) and hence \({\mathscr {P}}_i\) realizes the pair \(({\mathscr {A}}_i,{\mathscr {S}}_i)\).
(b) From part (a), it is clear that the template T can be realized if and only if the template  can be realized. In particular, this means that if T has a realization, the pair \(({\mathscr {B}}_1,{\mathscr {S}}_1)\) can be realized and we must have \({\mathscr {B}}_1\cap {\mathscr {S}}_1=\varnothing \). Conversely, if \({\mathscr {B}}_1\cap {\mathscr {S}}_1=\varnothing \), we can choose a prime ideal \({\mathscr {P}}_1\) realizing \(({\mathscr {B}}_1,{\mathscr {S}}_1)\). From (4), it follows that
can be realized. In particular, this means that if T has a realization, the pair \(({\mathscr {B}}_1,{\mathscr {S}}_1)\) can be realized and we must have \({\mathscr {B}}_1\cap {\mathscr {S}}_1=\varnothing \). Conversely, if \({\mathscr {B}}_1\cap {\mathscr {S}}_1=\varnothing \), we can choose a prime ideal \({\mathscr {P}}_1\) realizing \(({\mathscr {B}}_1,{\mathscr {S}}_1)\). From (4), it follows that

From (5) it is clear that  and hence it follows from Proposition 2.7 that
and hence it follows from Proposition 2.7 that

Thus, we can form a realization  of the template
of the template  (and hence of T) starting from
(and hence of T) starting from  . \(\square \)
. \(\square \)
From now onwards, we will say that two templates indexed by the same partially ordered set are equivalent if they have the same realizations. In Proposition 2.9, we have shown that the finite chain template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) indexed by the opposite \(I^\mathrm{op}\) of \(I=\{1<2<\cdots <n\}\) is equivalent to the modified chain template  . Further, since the modified chain template
. Further, since the modified chain template  satisfies
satisfies

we can start with an arbitrary realization \({\mathscr {P}}_1\) of \(({\mathscr {B}}_1,{\mathscr {S}}_1)\) and pick a prime ideal \({\mathscr {P}}_2\subseteq {\mathscr {P}}_1\) realizing \(({\mathscr {B}}_2,{\mathscr {S}}_2)\) and so on to obtain a realization  of
of  . However, if we started with an arbitrary realization say
. However, if we started with an arbitrary realization say  of \(({\mathscr {B}}_2,{\mathscr {S}}_2)\), it is not necessary that we can find some prime
of \(({\mathscr {B}}_2,{\mathscr {S}}_2)\), it is not necessary that we can find some prime  realizing \(({\mathscr {B}}_1,{\mathscr {S}}_1)\), i.e., the process of realizing a finite chain in Proposition 2.9 can proceed in one direction only. We will now show that under certain finiteness conditions, we can construct a template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i,{\mathscr {T}}_i)\}_{i\in I^\mathrm{op}}\) equivalent to T such that starting from any arbitrary realization \({\mathscr {Q}}_j\) of some
realizing \(({\mathscr {B}}_1,{\mathscr {S}}_1)\), i.e., the process of realizing a finite chain in Proposition 2.9 can proceed in one direction only. We will now show that under certain finiteness conditions, we can construct a template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i,{\mathscr {T}}_i)\}_{i\in I^\mathrm{op}}\) equivalent to T such that starting from any arbitrary realization \({\mathscr {Q}}_j\) of some  , we can proceed in both directions to form a realization
, we can proceed in both directions to form a realization  of \({\mathscr {D}}(T)\). Since \({\mathscr {D}}(T)\) is equivalent to the template T, this also becomes a realization of T.
of \({\mathscr {D}}(T)\). Since \({\mathscr {D}}(T)\) is equivalent to the template T, this also becomes a realization of T.
Proposition 2.10
Let \(n\geqslant 1\) and let \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) be a finite chain template indexed by the opposite of the ordered set \(I=\{1<2<\cdots <n\}\). Suppose that for each \(1\leqslant i\leqslant n\),  is a finite set. We define \(\{{\mathscr {B}}_i\}_{1\leqslant i\leqslant n}\) inductively by letting \({\mathscr {B}}_n ={\mathscr {A}}_n\) and setting
is a finite set. We define \(\{{\mathscr {B}}_i\}_{1\leqslant i\leqslant n}\) inductively by letting \({\mathscr {B}}_n ={\mathscr {A}}_n\) and setting

On the other hand, we define \(\{{\mathscr {T}}_i\}_{1\leqslant i\leqslant n}\) inductively by letting \({\mathscr {T}}_1={\mathscr {S}}_1\) and setting \({\mathscr {T}}_{i+1}\) to be the product of the multiplicatively closed families

Then, we have:
-
(a)
A chain \({\mathscr {Q}}_n\subseteq \dots \subseteq {\mathscr {Q}}_2\subseteq {\mathscr {Q}}_1\) of prime ideals is a realization of the template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) if and only if it is also a realization of the template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i,{\mathscr {T}}_i)\}_{i\in I^\mathrm{op}}\), i.e., the templates T and \({\mathscr {D}}(T)\) are equivalent.
-
(b)
Fix any integer \(j\in \{1,2,\dots ,n\}\). Then, the template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) has a realization if and only if
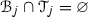 .
.
Proof
(a) Let \({\mathscr {Q}}_n\subseteq \cdots \subseteq {\mathscr {Q}}_2\subseteq {\mathscr {Q}}_1\) be a realization of the template T. From the proof of Proposition 2.9 (a), we know that each \({\mathscr {B}}_i\subseteq {\mathscr {Q}}_i\). By definition, we know that \({\mathscr {T}}_1={\mathscr {S}}_1\) and hence \({\mathscr {Q}}_1\cap {\mathscr {T}}_1=\varnothing \). We now suppose that \({\mathscr {Q}}_i\cap {\mathscr {T}}_i=\varnothing \) for each \(1\leqslant i\leqslant j\) for some given j. We know that \({\mathscr {Q}}_{j+1}\) realizes \(({\mathscr {A}}_{j+1},{\mathscr {S}}_{j+1})\) and hence \({\mathscr {Q}}_{j+1}\cap {\mathscr {S}}_{j+1} =\varnothing \). Further, since \({\mathscr {Q}}_{j+1}\subseteq {\mathscr {Q}}_j\) and  (i.e.,
(i.e.,  ), we have
), we have

Since \({\mathscr {Q}}_{j+1}\) is a prime ideal,  . Hence, each \({\mathscr {Q}}_i\) realizes the pair
. Hence, each \({\mathscr {Q}}_i\) realizes the pair  .
.
Conversely, let \({\mathscr {Q}}_n\subseteq \cdots \subseteq {\mathscr {Q}}_2\subseteq {\mathscr {Q}}_1\) be a realization of the template \({\mathscr {D}}(T)\). Then, for each \(1\leqslant i\leqslant n\), we know that \({\mathscr {Q}}_i\) realizes the pair \(({\mathscr {B}}_i,{\mathscr {T}}_i)\). From (6) and (7), it is clear that each \({\mathscr {A}}_i\subseteq {\mathscr {B}}_i\) and \({\mathscr {S}}_i\subseteq {\mathscr {T}}_i\). Hence, each \({\mathscr {Q}}_i\) realizes the pair \(({\mathscr {A}}_i,{\mathscr {S}}_i)\).
(b) We fix some \(j\in \{1,2,\dots ,n\}\). From part (a), it is clear that the template T can be realized if and only if the template \( {\mathscr {D}}(T)\) can be realized. In particular, this means that if T has a realization, the pair  can be realized and we must have
can be realized and we must have  . Conversely, if
. Conversely, if  , we choose some \({\mathscr {Q}}_j\) realizing
, we choose some \({\mathscr {Q}}_j\) realizing  . Then, we have
. Then, we have

and it follows from Proposition 2.5 (a) that there exists a prime ideal \({\mathscr {Q}}_{j+1}\subseteq {\mathscr {Q}}_j\) realizing  . Further, since \({\mathscr {Q}}_{j+1}\subseteq {\mathscr {Q}}_j\) and \({\mathscr {Q}}_j\) realizes
. Further, since \({\mathscr {Q}}_{j+1}\subseteq {\mathscr {Q}}_j\) and \({\mathscr {Q}}_j\) realizes  , we see that
, we see that  . Accordingly,
. Accordingly,  , i.e.,
, i.e.,  realizes
realizes  . On the other hand, from (7), we have
. On the other hand, from (7), we have

Since  , we see that
, we see that  is finite. From (8), we see that
is finite. From (8), we see that  and it follows from Proposition 2.5 (c) that we can choose a prime ideal \({\mathscr {Q}}_{j-1}\supseteq {\mathscr {Q}}_j\) realizing
and it follows from Proposition 2.5 (c) that we can choose a prime ideal \({\mathscr {Q}}_{j-1}\supseteq {\mathscr {Q}}_j\) realizing  . Further, since \({\mathscr {Q}}_j\) realizes
. Further, since \({\mathscr {Q}}_j\) realizes  (as \({\mathscr {Q}}_j\) realizes
(as \({\mathscr {Q}}_j\) realizes  and
and  ) and \({\mathscr {Q}}_{j-1}\) contains \({\mathscr {Q}}_j\), it follows from Proposition 2.5 (a) that \({\mathscr {Q}}_{j-1}\) contains
) and \({\mathscr {Q}}_{j-1}\) contains \({\mathscr {Q}}_j\), it follows from Proposition 2.5 (a) that \({\mathscr {Q}}_{j-1}\) contains  . Consequently, we have
. Consequently, we have

Hence, \({\mathscr {Q}}_{j-1}\) realizes  . Accordingly, starting from \({\mathscr {Q}}_j\) we can proceed in both directions to give a realization \({\mathscr {Q}}_n\subseteq \cdots \subseteq {\mathscr {Q}}_2\subseteq {\mathscr {Q}}_1\) of \({\mathscr {D}}(T)\). From part (a), it follows that this is also a realization of the template T. \(\square \)
. Accordingly, starting from \({\mathscr {Q}}_j\) we can proceed in both directions to give a realization \({\mathscr {Q}}_n\subseteq \cdots \subseteq {\mathscr {Q}}_2\subseteq {\mathscr {Q}}_1\) of \({\mathscr {D}}(T)\). From part (a), it follows that this is also a realization of the template T. \(\square \)
The next result will explain what kinds of collections of prime ideals may arise as  for some pair \(({\mathscr {A}},{\mathscr {S}})\).
for some pair \(({\mathscr {A}},{\mathscr {S}})\).
Proposition 2.11
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category and let \({\mathfrak {X}}\) be a collection of prime ideals of \(({\mathscr {C}},\otimes ,1)\). Then, the following are equivalent:
-
(a)
The family
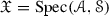 for some thick tensor ideal \({\mathscr {A}}\) and some multiplicatively closed family of objects \({\mathscr {S}}\).
for some thick tensor ideal \({\mathscr {A}}\) and some multiplicatively closed family of objects \({\mathscr {S}}\). -
(b)
The family \({\mathfrak {X}}\) satisfies the following property: given a prime ideal \({\mathscr {Q}}\) such that
 (9)
(9)then \({\mathscr {Q}}\in {\mathfrak {X}}\).
Proof
(a) \(\Rightarrow \) (b). Since each \({\mathscr {P}}\in {\mathfrak {X}}\) realizes the pair \(({\mathscr {A}}, {\mathscr {S}})\), we have \({\mathscr {A}}\subseteq \bigcap _{{\mathscr {P}}\in {\mathfrak {X}}}{\mathscr {P}}\) and \({\mathscr {S}}\cap \bigcup _{{\mathscr {P}}\in {\mathfrak {X}}}{\mathscr {P}}=\varnothing \). Hence, if a prime ideal \({\mathscr {Q}}\) satisfies the condition in (9), then \({\mathscr {Q}}\) realizes \(({\mathscr {A}},{\mathscr {S}})\), i.e.,  .
.
(b) \(\Rightarrow \) (a). Given a collection \({\mathfrak {X}}\) of prime ideals satisfying the condition in (b), we set

Then, a prime ideal \({\mathscr {Q}}\) realizes \(({\mathscr {A}},{\mathscr {S}})\) if and only if it satisfies (9). Hence, \({\mathfrak {X}}\) may be expressed as  . \(\square \)
. \(\square \)
A collection \({\mathfrak {X}}\) of prime ideals of \(({\mathscr {C}},\otimes ,1)\) satisfying condition (b) in Proposition 2.11 will be referred to as a convex set. Under the finiteness conditions from Proposition 2.10, we will now characterize the families of chains of prime ideals that realize a given finite chain template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\).
Proposition 2.12
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category and fix some \(n\geqslant 1\). We consider decreasing chains of length n consisting of prime ideals of \({\mathscr {C}}\)

Let \({\mathfrak {X}}\) be a collection of such chains of prime ideals and for any \(1\leqslant j\leqslant n\), we denote by \({\mathfrak {X}}_j\) the collection of prime ideals arising as the j-th element of a chain in \({\mathfrak {X}}\). Then, the following are equivalent:
-
(a)
\({\mathfrak {X}}\) is a collection of realizations of a finite chain template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) indexed by the opposite \(I^\mathrm{op}\) of the ordered set \(I=\{1<2<\cdots <n\}\) such that each
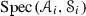 is a finite set.
is a finite set. -
(b)
For each \(1\leqslant j\leqslant n\), \({\mathfrak {X}}_j\) is a finite convex set of prime ideals of \(({\mathscr {C}},\otimes ,1)\). Further, \({\mathfrak {X}}\) consists of all chains of prime ideals whose i-th element is in \({\mathfrak {X}}_i\) for each \(1\leqslant i\leqslant n\). In other words, we have
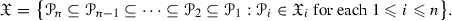 (10)
(10)
Proof
(a) \(\Rightarrow \) (b). Let \({\mathfrak {X}}\) be a collection of realizations of \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\). Since each  is finite, we can construct the equivalent modified template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i,{\mathscr {T}}_i)\}_{i\in I^\mathrm{op}}\) as defined in Proposition 2.10. Fix some j and choose some prime ideal \({\mathscr {P}}\in {\mathfrak {X}}_j\). Then, there exists a realization
is finite, we can construct the equivalent modified template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i,{\mathscr {T}}_i)\}_{i\in I^\mathrm{op}}\) as defined in Proposition 2.10. Fix some j and choose some prime ideal \({\mathscr {P}}\in {\mathfrak {X}}_j\). Then, there exists a realization  of T such that
of T such that  . Since T is equivalent to the template \({\mathscr {D}}(T)\), we see that
. Since T is equivalent to the template \({\mathscr {D}}(T)\), we see that  realizes
realizes  and hence
and hence  . Conversely, given any prime
. Conversely, given any prime  , we can construct as in the proof of Proposition 2.10 a realization
, we can construct as in the proof of Proposition 2.10 a realization  of T such that
of T such that  . Hence,
. Hence,  and each \({\mathfrak {X}}_j\) is a finite convex set. Finally, any chain
and each \({\mathfrak {X}}_j\) is a finite convex set. Finally, any chain  such that each
such that each  is a realization of \({\mathscr {D}}(T)=\{({\mathscr {B}}_i,{\mathscr {T}}_i)\}_{i\in I^\mathrm{op}}\) and hence of T. Therefore, the collection of realizations \({\mathfrak {X}}\) of T must be given by
is a realization of \({\mathscr {D}}(T)=\{({\mathscr {B}}_i,{\mathscr {T}}_i)\}_{i\in I^\mathrm{op}}\) and hence of T. Therefore, the collection of realizations \({\mathfrak {X}}\) of T must be given by

(b) \(\Rightarrow \) (a). We define a template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\) as follows:

From the proof of Proposition 2.11, we know that  . Hence, any chain
. Hence, any chain  of prime ideals drawn from the set
of prime ideals drawn from the set

must be a realization of the template \(T=\{({\mathscr {A}}_i,{\mathscr {S}}_i)\}_{i\in I^\mathrm{op}}\). Conversely, given any realization  of T, we know that each
of T, we know that each  and hence condition (10) ensures that this chain lies in \({\mathfrak {X}}\). Finally, since each \({\mathfrak {X}}_i\) is finite, so is each
and hence condition (10) ensures that this chain lies in \({\mathfrak {X}}\). Finally, since each \({\mathfrak {X}}_i\) is finite, so is each  . \(\square \)
. \(\square \)
We have described in Proposition 2.11 that the subsets  are exactly the convex subsets of
are exactly the convex subsets of  . Following Balmer [1, Section 2], the space
. Following Balmer [1, Section 2], the space  is endowed with a Zariski topology with the closed subsets being given by
is endowed with a Zariski topology with the closed subsets being given by

for each family \({\mathscr {X}}\subseteq {\mathscr {C}}\) of objects of \({\mathscr {C}}\). Then, open sets of  are of the form
are of the form  for \({\mathscr {X}}\subseteq {\mathscr {C}}\). Further, we know from [4, Proposition 11] that the spectrum
for \({\mathscr {X}}\subseteq {\mathscr {C}}\). Further, we know from [4, Proposition 11] that the spectrum  becomes a spectral space in the sense of Hochster [21]. We will now show that the subsets
becomes a spectral space in the sense of Hochster [21]. We will now show that the subsets  (which are the convex subsets of
(which are the convex subsets of  ) are related to constructible subsets of the spectral space
) are related to constructible subsets of the spectral space  . Since
. Since  is a spectral space, every constructible subset
is a spectral space, every constructible subset  is of the form
is of the form

(see, for instance, [32, Section 2]) with each \(U_i\) and each  quasi-compact and open in
quasi-compact and open in  . From [1, Proposition 2.14], we know that each quasi-compact open subset of
. From [1, Proposition 2.14], we know that each quasi-compact open subset of  is of the form
is of the form  for some \(a\in {\mathscr {C}}\). Further, we note that a thick tensor ideal \({\mathscr {A}}\) contains a finite set
for some \(a\in {\mathscr {C}}\). Further, we note that a thick tensor ideal \({\mathscr {A}}\) contains a finite set  of objects of \({\mathscr {C}}\) if and only if it contains the direct sum
of objects of \({\mathscr {C}}\) if and only if it contains the direct sum  , i.e., every finitely generated thick tensor ideal is principal.
, i.e., every finitely generated thick tensor ideal is principal.
We will say that a multiplicatively closed family \({\mathscr {S}}\) is finitely generated if there exists a finite set  of objects of \({\mathscr {C}}\) such that \({\mathscr {S}}\) is the smallest multiplicatively closed family containing all objects in
of objects of \({\mathscr {C}}\) such that \({\mathscr {S}}\) is the smallest multiplicatively closed family containing all objects in  .
.
Proposition 2.13
-
(a)
Given a finitely generated (hence principal) thick tensor ideal \({\mathscr {A}}\) and a finitely generated multiplicatively closed family \({\mathscr {S}}\),
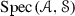 is a constructible subset of
is a constructible subset of 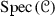 .
. -
(b)
Every convex subset of
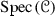 is pro-constructible, i.e., it may be expressed as an intersection of a family of constructible subsets of
is pro-constructible, i.e., it may be expressed as an intersection of a family of constructible subsets of 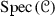 .
. -
(c)
For any thick tensor ideal \({\mathscr {A}}\) and any multiplicatively closed family \({\mathscr {S}}\), the subset
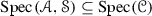 is a spectral space, i.e.,
is a spectral space, i.e., 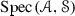 is quasi-compact, quasi-separated, has a basis of quasi-compact open subsets and every non-empty irreducible closed subset has a unique generic point.
is quasi-compact, quasi-separated, has a basis of quasi-compact open subsets and every non-empty irreducible closed subset has a unique generic point.
Proof
(a) Since \({\mathscr {S}}\) is finitely generated, we can choose a finite set of objects  such that \({\mathscr {S}}\) is the smallest multiplicatively closed family containing all objects in
such that \({\mathscr {S}}\) is the smallest multiplicatively closed family containing all objects in  . Then, it is clear that for any object \(s\in {\mathscr {S}}\), we can choose non-negative integers \(e_1,e_2, \dots , e_k\) such that
. Then, it is clear that for any object \(s\in {\mathscr {S}}\), we can choose non-negative integers \(e_1,e_2, \dots , e_k\) such that  . We now set \(s_0=\bigotimes _{i=1}^k s_i\) and see that \(Z({\mathscr {S}})=Z(s_0)\). Then,
. We now set \(s_0=\bigotimes _{i=1}^k s_i\) and see that \(Z({\mathscr {S}})=Z(s_0)\). Then,  is quasi-compact and open in
is quasi-compact and open in  . Further, if \({\mathscr {A}}\) is generated by the object \(a\in {\mathscr {C}}\), it is clear that we may express
. Further, if \({\mathscr {A}}\) is generated by the object \(a\in {\mathscr {C}}\), it is clear that we may express  . Hence,
. Hence,  is constructible.
is constructible.
(b) From Proposition 2.11, we know that each convex subset of  is of the form
is of the form  for some thick tensor ideal \({\mathscr {A}}\) and some multiplicatively closed family \({\mathscr {S}}\). We now express
for some thick tensor ideal \({\mathscr {A}}\) and some multiplicatively closed family \({\mathscr {S}}\). We now express  . Since each \(U(a)\cap Z(s)\) is constructible, it follows that the intersection
. Since each \(U(a)\cap Z(s)\) is constructible, it follows that the intersection  is pro-constructible.
is pro-constructible.
(c) follows from the fact that a pro-constructible subspace of a spectral space is always spectral in the induced subspace topology (see, for instance, [32, Section 2]).\(\square \)
For the final result of this section, we will restrict ourselves to tensor triangulated categories that are topologically noetherian (see [2, Definition 3.13]), i.e.,  is a noetherian topological space. This happens, for instance, when X is a topologically noetherian scheme and
is a noetherian topological space. This happens, for instance, when X is a topologically noetherian scheme and  , i.e., the derived category of perfect complexes over X (see [1, Corollary 5.6]). We denote by
, i.e., the derived category of perfect complexes over X (see [1, Corollary 5.6]). We denote by  the space
the space  equipped with the constructible topology. From Proposition 2.13 we know that for any thick tensor ideal \({\mathscr {A}}\) and any multiplicatively closed family \({\mathscr {S}}\),
equipped with the constructible topology. From Proposition 2.13 we know that for any thick tensor ideal \({\mathscr {A}}\) and any multiplicatively closed family \({\mathscr {S}}\),  is pro-constructible. Equivalently, since
is pro-constructible. Equivalently, since  is a spectral space,
is a spectral space,  is closed in
is closed in  .
.
Corollary 2.14
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category that is topologically noetherian, i.e.,  is a noetherian space.
is a noetherian space.
-
(a)
Given a finitely generated (hence principal) thick tensor ideal \({\mathscr {A}}\) and a multiplicatively closed family \({\mathscr {S}}\),
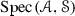 is a constructible subset of
is a constructible subset of 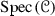 . Further, such subsets form a basis for the constructible topology on
. Further, such subsets form a basis for the constructible topology on 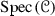 .
. -
(b)
Any closed subset of
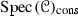 may be expressed as a union
may be expressed as a union 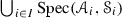 with each \({\mathscr {A}}_i\) a thick tensor ideal and each \({\mathscr {S}}_i\) a multiplicatively closed family.
with each \({\mathscr {A}}_i\) a thick tensor ideal and each \({\mathscr {S}}_i\) a multiplicatively closed family.
Proof
(a) Since  is noetherian, the open subset
is noetherian, the open subset  is quasi-compact. If we choose an object \(a\in {\mathscr {A}}\) generating \({\mathscr {A}}\), we can express
is quasi-compact. If we choose an object \(a\in {\mathscr {A}}\) generating \({\mathscr {A}}\), we can express  . Hence,
. Hence,  is constructible. Further, let \({\mathscr {X}}\) and \({\mathscr {Y}}\) be families of objects and consider the constructible subset \(U({\mathscr {X}})\cap Z({\mathscr {Y}})\). From the definition of \(U({\mathscr {X}})\), it is clear that \(U({\mathscr {X}})=\bigcup _{x\in {\mathscr {X}}}U(x)\) and hence we have
is constructible. Further, let \({\mathscr {X}}\) and \({\mathscr {Y}}\) be families of objects and consider the constructible subset \(U({\mathscr {X}})\cap Z({\mathscr {Y}})\). From the definition of \(U({\mathscr {X}})\), it is clear that \(U({\mathscr {X}})=\bigcup _{x\in {\mathscr {X}}}U(x)\) and hence we have

where (x) is the ideal generated by x and \(M({\mathscr {Y}})\) is the smallest multiplicatively closed family containing \({\mathscr {Y}}\). Further, every open in  being quasi-compact, the open sets in the constructible topology on
being quasi-compact, the open sets in the constructible topology on  are simply the unions of constructible subsets. Thus, subsets of the form
are simply the unions of constructible subsets. Thus, subsets of the form  with \({\mathscr {A}}\) finitely generated form a basis for the constructible topology on
with \({\mathscr {A}}\) finitely generated form a basis for the constructible topology on  .
.
(b) Since  is spectral, a subset of
is spectral, a subset of  is closed if and only if it is pro-constructible, i.e., it is the intersection of a family of constructible subsets. Let us consider a family
is closed if and only if it is pro-constructible, i.e., it is the intersection of a family of constructible subsets. Let us consider a family  , \(j\in J\), with each
, \(j\in J\), with each  a constructible set. Let \({\mathscr {B}}=\sum _{j\in J} {\mathscr {A}}_j\) be the smallest ideal containing each of the ideals \({\mathscr {A}}_j\) and let \({\mathscr {T}}\) be the smallest multiplicatively closed family containing each of the families
a constructible set. Let \({\mathscr {B}}=\sum _{j\in J} {\mathscr {A}}_j\) be the smallest ideal containing each of the ideals \({\mathscr {A}}_j\) and let \({\mathscr {T}}\) be the smallest multiplicatively closed family containing each of the families  . Then, it is clear that
. Then, it is clear that  . Combining with the fact (from part (a)) that any constructible subset may be expressed as a union of constructible sets of the form
. Combining with the fact (from part (a)) that any constructible subset may be expressed as a union of constructible sets of the form  , we obtain the result. \(\square \)
, we obtain the result. \(\square \)
For a topologically noetherian scheme, we know that there is a homeomorphism  of X with the spectrum of the derived category of perfect complexes (see [1, Corollary 5.6]). Then, Corollary 2.14 gives us an understanding of the constructible topology on such a scheme in terms of the subsets
of X with the spectrum of the derived category of perfect complexes (see [1, Corollary 5.6]). Then, Corollary 2.14 gives us an understanding of the constructible topology on such a scheme in terms of the subsets  for the tensor triangulated category
for the tensor triangulated category  .
.
3 Oka families and a Prime Ideal Principle for tensor triangulated categories
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category as before. As mentioned in the introduction, [4, Theorem 14] shows that the association

gives a one-to-one order reversing correspondence between radical thick tensor ideals in \({\mathscr {C}}\) and closed subspaces of  , where
, where  denotes the spectrum of \({\mathscr {C}}\) equipped with the inverse topology. In particular, if X is a topologically noetherian scheme and we take
denotes the spectrum of \({\mathscr {C}}\) equipped with the inverse topology. In particular, if X is a topologically noetherian scheme and we take  , the derived category of perfect complexes on X, we know that there is a homeomorphism
, the derived category of perfect complexes on X, we know that there is a homeomorphism  (see [1, Corollary 5.6]) and hence radical thick tensor ideals in
(see [1, Corollary 5.6]) and hence radical thick tensor ideals in  correspond to closed subspaces of X in the inverse topology. We have restated [4, Theorem 14] as an order-reversing correspondence with closed subspaces rather than as an order-preserving correspondence with open subspaces in order to make it look more similar to the standard Nullstellensatz. As such, this leads us to think about the irreducible closed subspaces of X in the inverse topology. More generally, let \({\mathfrak {F}}^*\) be a family of closed subspaces of
correspond to closed subspaces of X in the inverse topology. We have restated [4, Theorem 14] as an order-reversing correspondence with closed subspaces rather than as an order-preserving correspondence with open subspaces in order to make it look more similar to the standard Nullstellensatz. As such, this leads us to think about the irreducible closed subspaces of X in the inverse topology. More generally, let \({\mathfrak {F}}^*\) be a family of closed subspaces of  such that \(\varnothing \in {\mathfrak {F}}^*\) and suppose that \({\mathfrak {F}}^*\) is closed under finite unions. Then, if we consider a closed subspace
such that \(\varnothing \in {\mathfrak {F}}^*\) and suppose that \({\mathfrak {F}}^*\) is closed under finite unions. Then, if we consider a closed subspace  such that \(K_0\) is minimal with respect to not being in
such that \(K_0\) is minimal with respect to not being in  , it is clear that \(K_0\) is irreducible. Using the correspondence in (11), we have a radical thick tensor ideal \({\mathscr {I}}_0\) such that
, it is clear that \(K_0\) is irreducible. Using the correspondence in (11), we have a radical thick tensor ideal \({\mathscr {I}}_0\) such that  . Translated in terms of ideals in \({\mathscr {C}}\), we have a family \({\mathfrak {F}} \) of radical ideals and \({\mathscr {I}}_0\) is maximal with respect to being a radical ideal not contained in \({\mathfrak {F}}\). Then, it follows that if \({\mathscr {J}},{\mathscr {K}}\) are radical ideals such that
. Translated in terms of ideals in \({\mathscr {C}}\), we have a family \({\mathfrak {F}} \) of radical ideals and \({\mathscr {I}}_0\) is maximal with respect to being a radical ideal not contained in \({\mathfrak {F}}\). Then, it follows that if \({\mathscr {J}},{\mathscr {K}}\) are radical ideals such that  , we must have either \({\mathscr {I}}_0\supseteq {\mathscr {J}}\) or \({\mathscr {I}}_0\supseteq {\mathscr {K}}\). However, we would like to have better results along these lines on families of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\).
, we must have either \({\mathscr {I}}_0\supseteq {\mathscr {J}}\) or \({\mathscr {I}}_0\supseteq {\mathscr {K}}\). However, we would like to have better results along these lines on families of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\).
Accordingly, we turn to some methods from commutative algebra, where there are several well known results of the kind “maximal implies prime”. For example, given a commutative ring R and an R-module M, an ideal I that is maximal among annihilators of non-zero elements of M must be prime (see, for example, [20, Proposition 3.12]). In [25], Lam and Reyes gave a criterion that unifies these results, i.e., conditions on a family \({\mathscr {F}}\) of ideals in a ring such that any ideal that is maximal with respect to not being contained in \({\mathscr {F}}\) must be prime. They referred to this as the “Prime Ideal Principle”. Using the Prime Ideal Principle, the authors in [25] were also able to uncover several new results of a similar nature (see also further work in Lam and Reyes [26] and Reyes [29, 30]). The purpose of this section is to construct an analogous Prime Ideal Principle for thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\).
We will need to introduce some notation: if \({\mathscr {I}},{\mathscr {J}}\) are thick tensor ideals in \({\mathscr {C}}\), we set  , i.e., the smallest thick tensor ideal containing both \({\mathscr {I}}\) and \({\mathscr {J}}\). We may easily verify that
, i.e., the smallest thick tensor ideal containing both \({\mathscr {I}}\) and \({\mathscr {J}}\). We may easily verify that  is the smallest thick tensor ideal containing all direct sums
is the smallest thick tensor ideal containing all direct sums  where \(x\in {\mathscr {I}}\) and \(y\in {\mathscr {J}}\). Given an object \(a\in {\mathscr {C}}\), we write
where \(x\in {\mathscr {I}}\) and \(y\in {\mathscr {J}}\). Given an object \(a\in {\mathscr {C}}\), we write  for the smallest thick tensor ideal containing both \({\mathscr {I}}\) and a. For any collection X of objects of \({\mathscr {C}}\), we set
for the smallest thick tensor ideal containing both \({\mathscr {I}}\) and a. For any collection X of objects of \({\mathscr {C}}\), we set

It may be easily verified that  contains 0 and satisfies the three conditions in Definition 2.1, i.e.,
contains 0 and satisfies the three conditions in Definition 2.1, i.e.,  is a thick tensor ideal. When
is a thick tensor ideal. When  is a singleton, we will denote
is a singleton, we will denote  simply by
simply by  . When X happens to be a multiplicatively closed family, we note that
. When X happens to be a multiplicatively closed family, we note that  defined in (12) is not necessarily equal to
defined in (12) is not necessarily equal to  as defined in (2).
as defined in (2).
Further, given a thick tensor ideal \({\mathscr {I}}\) and an object \(a\in {\mathscr {C}}\), we will denote by  the smallest thick tensor ideal containing all objects
the smallest thick tensor ideal containing all objects  , where \(x\in {\mathscr {I}}\). Similarly, given thick tensor ideals \({\mathscr {I}}_1,{\mathscr {I}}_2\), we denote by
, where \(x\in {\mathscr {I}}\). Similarly, given thick tensor ideals \({\mathscr {I}}_1,{\mathscr {I}}_2\), we denote by  the smallest thick tensor ideal containing all objects
the smallest thick tensor ideal containing all objects  , where \(x_1\in {\mathscr {I}}_1\) and \(x_2\in {\mathscr {I}}_2\). In a manner analogous to [25], we will now define Oka families and Ako families of ideals in \(({\mathscr {C}},\otimes ,1)\).
, where \(x_1\in {\mathscr {I}}_1\) and \(x_2\in {\mathscr {I}}_2\). In a manner analogous to [25], we will now define Oka families and Ako families of ideals in \(({\mathscr {C}},\otimes ,1)\).
Definition 3.1
Let \({\mathfrak {F}}\) be a family of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) such that \({\mathscr {C}}\in {\mathfrak {F}}\). In what follows, let \({\mathscr {I}}\), \({\mathscr {J}}\) be thick tensor ideals in \({\mathscr {C}}\). Then, we will say that
-
\({\mathfrak {F}}\) is a semifilter if \({\mathscr {I}}\subseteq {\mathscr {J}}\) and \({\mathscr {I}}\in {\mathfrak {F}}\) implies that \({\mathscr {J}}\in {\mathfrak {F}}\).
-
\({\mathfrak {F}}\) is a filter if it is a semifilter and for any ideals \({\mathscr {I}},{\mathscr {J}}\in {\mathfrak {F}}\), the intersection \({\mathscr {I}}\cap {\mathscr {J}}\in {\mathfrak {F}}\).
-
\({\mathfrak {F}}\) is monoidal if \({\mathscr {I}}\), \({\mathscr {J}}\in {\mathfrak {F}}\) implies that
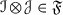 .
. -
\({\mathfrak {F}}\) is an Oka family (resp. a strongly Oka family) if
 for some object \(a\in {\mathscr {C}}\) (resp.
for some object \(a\in {\mathscr {C}}\) (resp. 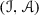 ,
, 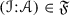 for some ideal
for some ideal 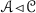 ) implies that \({\mathscr {I}}\in {\mathfrak {F}}\).
) implies that \({\mathscr {I}}\in {\mathfrak {F}}\). -
\({\mathfrak {F}}\) is an Ako family (resp. a strongly Ako family) if
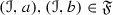 for objects \(a,b\in {\mathscr {C}}\) (resp.
for objects \(a,b\in {\mathscr {C}}\) (resp. 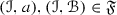 for some object \(a\in {\mathscr {C}}\) and some ideal
for some object \(a\in {\mathscr {C}}\) and some ideal 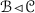 ) implies that
) implies that 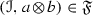 (resp.
(resp. 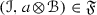 ).
).
We will say that a family \({\mathfrak {F}}\) of thick tensor ideals satisfies the “Prime Ideal Principle” if any ideal that is maximal with respect to not being in \({\mathfrak {F}}\) is also prime. We will now prove the main Prime Ideal Principle for ideals in \(({\mathscr {C}},\otimes ,1)\).
Proposition 3.2
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category and let \({\mathfrak {F}}\) be a family of thick tensor ideals in \({\mathscr {C}}\) such that \({\mathscr {C}}\in {\mathfrak {F}}\). Let \({\mathscr {I}}\) be a thick tensor ideal of \(({\mathscr {C}},\otimes ,1)\) that is maximal with respect to not being contained in \({\mathfrak {F}}\). Then:
-
(a)
If \({\mathfrak {F}}\) is an Oka family of ideals, then \({\mathscr {I}}\) is a prime ideal.
-
(b)
If \({\mathfrak {F}}\) is an Ako family of ideals, then \({\mathscr {I}}\) is a prime ideal.
-
(c)
In other words, if \({\mathfrak {F}}\) is either an Oka family or an Ako family, \({\mathfrak {F}}\) satisfies the “Prime Ideal Principle”, i.e., any ideal that is maximal with respect to not being in \({\mathfrak {F}}\) must be prime.
Proof
(a) We know that \({\mathfrak {F}}\) is an Oka family. Suppose that \({\mathscr {I}}\) is not a prime ideal, i.e., we can choose \(a,b\in {\mathscr {C}}\) such that  but \(a\notin {\mathscr {I}}\) and \(b\notin {\mathscr {I}}\). Then, we note that
but \(a\notin {\mathscr {I}}\) and \(b\notin {\mathscr {I}}\). Then, we note that  because the latter contains b and
because the latter contains b and  because \(a\notin {\mathscr {I}}\). However, since \({\mathscr {I}}\) is maximal with respect to not being contained in \({\mathfrak {F}}\), we must have
because \(a\notin {\mathscr {I}}\). However, since \({\mathscr {I}}\) is maximal with respect to not being contained in \({\mathfrak {F}}\), we must have  and
and  . Since \({\mathfrak {F}}\) is an Oka family, we conclude that \({\mathscr {I}}\in {\mathfrak {F}}\), which is a contradiction.
. Since \({\mathfrak {F}}\) is an Oka family, we conclude that \({\mathscr {I}}\in {\mathfrak {F}}\), which is a contradiction.
(b) Again, we suppose that \({\mathscr {I}}\) is not prime and choose \(a,b\in {\mathscr {C}}\) such that  but \(a\notin {\mathscr {I}}\) and \(b\notin {\mathscr {I}}\). As in part (a), we see that
but \(a\notin {\mathscr {I}}\) and \(b\notin {\mathscr {I}}\). As in part (a), we see that  and
and  because \(a,b\notin {\mathscr {I}}\). Then, \({\mathscr {I}}\) being maximal with respect to not being contained in \({\mathfrak {F}}\), we must have
because \(a,b\notin {\mathscr {I}}\). Then, \({\mathscr {I}}\) being maximal with respect to not being contained in \({\mathfrak {F}}\), we must have  . Since \({\mathfrak {F}}\) is an Ako family, this implies that
. Since \({\mathfrak {F}}\) is an Ako family, this implies that  . But since
. But since  , we have
, we have  , which is a contradiction. \(\square \)
, which is a contradiction. \(\square \)
In order to proceed further, we will need a more explicit description of the thick tensor ideal generated by a collection X of objects in \({\mathscr {C}}\). For a collection X of objects of \({\mathscr {C}}\), we denote by \(\widetilde{X}\) the smallest thick tensor ideal containing all objects of X. Note that, by definition, thick tensor ideals are full subcategories and hence it is enough to describe the objects of \(\widetilde{X}\). For any collection X of objects of \({\mathscr {C}}\), we now set

From (13), it is clear that \(\overline{\overline{X}}=\overline{X}\). For a collection X of objects of \({\mathscr {C}}\), we also consider \(\mathrm{\Delta }(X)\), the collection of all objects \(a\in {\mathscr {C}}\) such that there exist \(b,c\in X\) with a, b, c forming a distinguished triangle (in some order). We are now ready to describe the thick tensor ideal \(\widetilde{X}\) more explicitly.
Proposition 3.3
Let X be a collection of objects in \(({\mathscr {C}},\otimes ,1)\). We set \(X_0=X\) and inductively define
Then, the smallest thick tensor ideal \(\widetilde{X}\) containing all objects in X is given by the union of the increasing chain
Proof
From the definitions in (13) and (14), it is clear that each  . We set
. We set

In order to prove the result, it suffices to show that \(X'\) is itself a thick tensor ideal. We now consider some \(x\in X'\) and choose \(i\geqslant 0\) such that  . Hence, there exist \(a\in X_i\) and \(b,c\in {\mathscr {C}}\) such that
. Hence, there exist \(a\in X_i\) and \(b,c\in {\mathscr {C}}\) such that  . Then, for any \(y\in {\mathscr {C}}\), it is clear that
. Then, for any \(y\in {\mathscr {C}}\), it is clear that  and hence
and hence  . Further, if x splits as
. Further, if x splits as  , we have
, we have  with \(a\in X_i\) and hence both
with \(a\in X_i\) and hence both  . Finally, we consider a distinguished triangle
. Finally, we consider a distinguished triangle
and assume for the sake of definiteness that  . Then, we can choose \(j\geqslant 0\) large enough so that
. Then, we can choose \(j\geqslant 0\) large enough so that  . From (14), it follows that
. From (14), it follows that  and hence
and hence  . We have shown that \(X'\) is a thick tensor ideal. \(\square \)
. We have shown that \(X'\) is a thick tensor ideal. \(\square \)
We remark here that, in particular, if we apply the explicit description in Proposition 3.3 to the case of a thick tensor ideal generated by a single object, it follows from Definition 3.1 that a strongly Oka family is also an Oka family.
Lemma 3.4
Let \({\mathscr {I}}\) (resp. \({\mathscr {J}})\) be a thick tensor ideal of \(({\mathscr {C}},\otimes ,1)\) that is generated by  (resp. \(Y=\{y_j\}_{j\in J})\). Then, the thick tensor ideal
(resp. \(Y=\{y_j\}_{j\in J})\). Then, the thick tensor ideal  is generated by the collection
is generated by the collection  .
.
Proof
We consider some thick tensor ideal \({\mathscr {K}}\) containing all objects of the form  . It suffices to show that \({\mathscr {K}}\) contains all objects of the form
. It suffices to show that \({\mathscr {K}}\) contains all objects of the form  with \(x\in {\mathscr {I}}\) and \(y\in {\mathscr {J}}\). We start by fixing some \(j\in J\). Then, we know that
with \(x\in {\mathscr {I}}\) and \(y\in {\mathscr {J}}\). We start by fixing some \(j\in J\). Then, we know that  for each \(i\in I\). We now use the notation of Proposition 3.3 and set \(X_0=X\). Then, we know from Proposition 3.3 that the ideal \({\mathscr {I}}\) may be described as the union
for each \(i\in I\). We now use the notation of Proposition 3.3 and set \(X_0=X\). Then, we know from Proposition 3.3 that the ideal \({\mathscr {I}}\) may be described as the union

We now consider some  . From (13), we know that there exist \(x\in X_0=X\) and \(b,c\in {\mathscr {C}}\) such that
. From (13), we know that there exist \(x\in X_0=X\) and \(b,c\in {\mathscr {C}}\) such that  . Then,
. Then,  . Since
. Since  , it follows that
, it follows that  for each
for each  . We will now proceed by induction. Suppose that
. We will now proceed by induction. Suppose that  for every
for every  and \(n\leqslant N\) for some given \(N\geqslant 0\). We consider some
and \(n\leqslant N\) for some given \(N\geqslant 0\). We consider some  . By definition,
. By definition,  and hence \(x'\) is a part of a distinguished triangle two of whose objects are already in
and hence \(x'\) is a part of a distinguished triangle two of whose objects are already in  . For the sake of definiteness, we assume that we have a distinguished triangle
. For the sake of definiteness, we assume that we have a distinguished triangle

with  . Since
. Since  is exact in both variables, we have an induced distinguished triangle
is exact in both variables, we have an induced distinguished triangle

Since  , it follows that
, it follows that  for each
for each  . Repeating the reasoning for \(X_0\), we now see that
. Repeating the reasoning for \(X_0\), we now see that  for each
for each  . By induction, it follows that
. By induction, it follows that  for each \(x\in {\mathscr {I}}\). Now since \(\{y_j\}_{j\in J}\) generate \({\mathscr {J}}\), it follows similarly that
for each \(x\in {\mathscr {I}}\). Now since \(\{y_j\}_{j\in J}\) generate \({\mathscr {J}}\), it follows similarly that  for each \(x\in {\mathscr {I}}\), \(y\in {\mathscr {J}}\). \(\square \)
for each \(x\in {\mathscr {I}}\), \(y\in {\mathscr {J}}\). \(\square \)
We remark here that it follows from the proof of Lemma 3.4 and Definition 3.1 that a strongly Ako family is also an Ako family.
Theorem 3.5
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category as above and let \({\mathfrak {F}}\) be a family of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) such that \({\mathscr {C}}\in {\mathfrak {F}}\). Consider the following conditions:
-
(P1)
\({\mathfrak {F}}\) is a monoidal filter.
-
(P2)
\({\mathfrak {F}}\) is monoidal and, given thick tensor ideals \({\mathscr {I}},{\mathscr {J}}\) with \({\mathscr {J}}\in {\mathfrak {F}}\) and
 , we must have \({\mathscr {I}}\in {\mathfrak {F}}\).
, we must have \({\mathscr {I}}\in {\mathfrak {F}}\). -
(P3)
For thick tensor ideals \({\mathscr {I}},{\mathscr {A}},{\mathscr {B}}\) such that
 , we must have
, we must have  .
. -
(Q1)
\({\mathfrak {F}}\) is a monoidal semifilter.
-
(Q2)
\({\mathfrak {F}}\) is monoidal and, given thick tensor ideals \({\mathscr {I}},{\mathscr {J}}\) with \({\mathscr {J}}\in {\mathfrak {F}}\) and \({\mathscr {I}}\supseteq {\mathscr {J}}\supseteq {\mathscr {I}}^n\) for some \(n>1\), we must have \({\mathscr {I}}\in {\mathfrak {F}}\).
-
(Q3)
If \({\mathscr {A}},{\mathscr {B}}\in {\mathfrak {F}}\) and \({\mathscr {I}}\) is a thick tensor ideal such that
 , we must have \({\mathscr {I}}\in {\mathfrak {F}}\).
, we must have \({\mathscr {I}}\in {\mathfrak {F}}\).
Then, we have:
-
(a)
The following chart of implications holds:
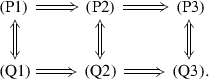
-
(b)
We have the following implications:

In particular, a family \({\mathfrak {F}}\) satisfying condition (P3) also satisfies the Prime Ideal Principle, i.e., any ideal maximal with respect to not being in \({\mathfrak {F}}\) must be prime.
Proof
(a) For thick tensor ideals \({\mathscr {I}},{\mathscr {J}}\), it is clear that  and hence it follows from Definition 3.1 that (P1) \(\Leftrightarrow \) (Q1). Further, it is obvious that (Q2) \(\Rightarrow \) (P2).
and hence it follows from Definition 3.1 that (P1) \(\Leftrightarrow \) (Q1). Further, it is obvious that (Q2) \(\Rightarrow \) (P2).
(Q1) \(\Rightarrow \) (Q2). Since \({\mathfrak {F}}\) is a semifilter, whenever we have \({\mathscr {I}}\supseteq {\mathscr {J}}\) with \({\mathscr {J}} \in {\mathfrak {F}}\), we see that \({\mathscr {I}}\in {\mathfrak {F}}\).
(P2) \(\Rightarrow \) (P3). We consider thick tensor ideals \({\mathscr {I}},{\mathscr {A}},{\mathscr {B}}\) with  . Since \({\mathfrak {F}}\) is monoidal, we have
. Since \({\mathfrak {F}}\) is monoidal, we have  . Further, since
. Further, since  and
and  , we have
, we have

On the other hand, we know that  (resp.
(resp.  ) is generated by objects of the form
) is generated by objects of the form  with \(x\in {\mathscr {I}}\), \(a\in {\mathscr {A}}\) (resp.
with \(x\in {\mathscr {I}}\), \(a\in {\mathscr {A}}\) (resp.  with \(y\in {\mathscr {I}}\), \(b\in {\mathscr {B}}\)). From Lemma 3.4, it follows that
with \(y\in {\mathscr {I}}\), \(b\in {\mathscr {B}}\)). From Lemma 3.4, it follows that  is generated by objects of the form
is generated by objects of the form

\(x,y\in {\mathscr {I}}\), \(a\in {\mathscr {A}}\), \(b\in {\mathscr {B}}\). Since any element of the form in (16) is in  , we have
, we have

From (15) and (17) and applying condition (P2), we see that  . This proves (P3).
. This proves (P3).
(P2) \(\Rightarrow \) (Q2). We suppose that there exist thick tensor ideals \({\mathscr {I}},{\mathscr {J}}\) with \({\mathscr {I}}\notin {\mathfrak {F}}\), \({\mathscr {J}}\in {\mathfrak {F}}\) and \({\mathscr {I}}\supseteq {\mathscr {J}}\supseteq {\mathscr {I}}^n\) for some \(n>1\). Then, there is a largest integer \(k\geqslant 1\) such that  . By Lemma 3.4, \(({\mathscr {J}}+{\mathscr {I}}^k)^2\) is generated by objects of the form
. By Lemma 3.4, \(({\mathscr {J}}+{\mathscr {I}}^k)^2\) is generated by objects of the form  with
with  and
and  . Any such object lies in \({\mathscr {J}}+{\mathscr {I}}^{k+1}\) and hence we have
. Any such object lies in \({\mathscr {J}}+{\mathscr {I}}^{k+1}\) and hence we have

Since  , it follows from condition (P2) that
, it follows from condition (P2) that  which is a contradiction.
which is a contradiction.
(P3) \(\Rightarrow \) (Q3). Let \({\mathscr {A}},{\mathscr {B}}\in {\mathfrak {F}}\) and suppose that  . Then,
. Then,  and
and  and hence it follows from (P3) that
and hence it follows from (P3) that  . But since
. But since  , we have
, we have  .
.
(Q3) \(\Rightarrow \) (P3). Suppose that  . It is clear that we have
. It is clear that we have  . As in (17), we can show that
. As in (17), we can show that  . From condition (Q3), it now follows that
. From condition (Q3), it now follows that  .
.
(b) We assume condition (P3). To show that \({\mathfrak {F}}\) is strongly Ako, we consider \(a\in {\mathscr {C}}\) and thick tensor ideals \({\mathscr {I}},{\mathscr {B}}\) such that  . Let \({\mathscr {A}}\) be the thick tensor ideal generated by a. Then,
. Let \({\mathscr {A}}\) be the thick tensor ideal generated by a. Then,  lies in \({\mathfrak {F}}\) and it follows from (P3) that
lies in \({\mathfrak {F}}\) and it follows from (P3) that  . From Lemma 3.4, it is clear that
. From Lemma 3.4, it is clear that  . Hence,
. Hence,  and \({\mathfrak {F}}\) is strongly Ako.
and \({\mathfrak {F}}\) is strongly Ako.
In order to show that \({\mathfrak {F}}\) is strongly Oka, we consider ideals \({\mathscr {I}},{\mathscr {A}}\) with  ,
,  . We now set
. We now set  . Then, it is clear that
. Then, it is clear that  and it follows from condition (P3) that
and it follows from condition (P3) that  . From the definition in (12), we know that if \(a\in {\mathscr {A}}\) and
. From the definition in (12), we know that if \(a\in {\mathscr {A}}\) and  , we must have
, we must have  and hence
and hence  . It follows that
. It follows that  and \({\mathfrak {F}}\) is strongly Oka. We have also noted before that strongly Oka families are also Oka and hence it follows from Proposition 3.2 that \({\mathfrak {F}}\) satisfies the Prime Ideal Principle.
and \({\mathfrak {F}}\) is strongly Oka. We have also noted before that strongly Oka families are also Oka and hence it follows from Proposition 3.2 that \({\mathfrak {F}}\) satisfies the Prime Ideal Principle.
It remains to show that strongly Ako families are also Oka. Let \({\mathfrak {F}}\) be strongly Ako and suppose that  . We set
. We set  . Again since
. Again since  , we see that
, we see that  . But
. But  and hence
and hence  and hence \({\mathfrak {F}}\) is Oka. \(\square \)
and hence \({\mathfrak {F}}\) is Oka. \(\square \)
For the rest of this section, we shall construct various families of thick tensor ideals that satisfy the Prime Ideal Principle.
Proposition 3.6
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category as above. Let \({\mathfrak {F}}_1\) and \({\mathfrak {F}}_2\) be families of thick tensor ideals in \({\mathscr {C}}\) such that \({\mathfrak {F}}_1\) is monoidal and \({\mathfrak {F}}_2\) is closed under finite intersections. Consider the family

Then, \({\mathfrak {F}}\) is both a strongly Oka family and a strongly Ako family. In particular, \({\mathfrak {F}}\) satisfies the Prime Ideal Principle.
Proof
We will show that \({\mathfrak {F}}\) satisfies condition (Q3) in Theorem 3.5. By Theorem 3.5 (b), condition (P3) which is equivalent to (Q3) will then imply that \({\mathfrak {F}}\) is a strongly Oka and a strongly Ako family.
We choose \({\mathscr {A}},{\mathscr {B}}\in {\mathfrak {F}}\) and consider a thick tensor ideal \({\mathscr {I}}\) satisfying  . If either \({\mathscr {A}}={\mathscr {C}}\) or \({\mathscr {B}}={\mathscr {C}}\), the result is obvious. Hence, we suppose that \({\mathscr {A}}\ne {\mathscr {C}}\) and \({\mathscr {B}} \ne {\mathscr {C}}\) and choose \({\mathscr {J}}_1,{\mathscr {K}}_1\in {\mathfrak {F}}_1\) and \({\mathscr {J}}_2,{\mathscr {K}}_2\in {\mathfrak {F}}_2\) such that
. If either \({\mathscr {A}}={\mathscr {C}}\) or \({\mathscr {B}}={\mathscr {C}}\), the result is obvious. Hence, we suppose that \({\mathscr {A}}\ne {\mathscr {C}}\) and \({\mathscr {B}} \ne {\mathscr {C}}\) and choose \({\mathscr {J}}_1,{\mathscr {K}}_1\in {\mathfrak {F}}_1\) and \({\mathscr {J}}_2,{\mathscr {K}}_2\in {\mathfrak {F}}_2\) such that
It now follows that

Since \({\mathfrak {F}}_1\) is monoidal and \({\mathfrak {F}}_2\) is closed under finite intersections, we see that  and \({\mathscr {J}}_2\cap {\mathscr {K}}_2\in {\mathfrak {F}}_2\). Hence, it follows from the definition in (18) that \({\mathscr {I}}\in {\mathfrak {F}}\). \(\square \)
and \({\mathscr {J}}_2\cap {\mathscr {K}}_2\in {\mathfrak {F}}_2\). Hence, it follows from the definition in (18) that \({\mathscr {I}}\in {\mathfrak {F}}\). \(\square \)
Corollary 3.7
-
(a)
Let \({\mathscr {J}}\), \({\mathscr {K}}\) be thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\). Consider the following family of ideals:
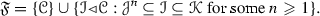
Then, \({\mathfrak {F}}\) satisfies the Prime Ideal Principle, i.e., any thick tensor ideal that is maximal with respect to not being in \({\mathfrak {F}}\) must be prime.
-
(b)
Let \(\{{\mathscr {J}}_j\}_{j\in J}\) be a family of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\). Then, any ideal that is maximal with respect to not containing a finite product of
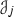 is prime.
is prime.
Proof
(a) We set  and \({\mathfrak {F}}_2=\{{\mathscr {K}}\}\). Then, \({\mathfrak {F}}_1\) is monoidal and \({\mathfrak {F}}_2\) is closed under finite intersections. Now applying Proposition 3.6, we see that \({\mathfrak {F}}\) satisfies the Prime Ideal Principle.
and \({\mathfrak {F}}_2=\{{\mathscr {K}}\}\). Then, \({\mathfrak {F}}_1\) is monoidal and \({\mathfrak {F}}_2\) is closed under finite intersections. Now applying Proposition 3.6, we see that \({\mathfrak {F}}\) satisfies the Prime Ideal Principle.
(b) We set  and \({\mathfrak {F}}_2=\{{\mathscr {C}}\}\). It is clear that \({\mathfrak {F}}_1\) is monoidal and \({\mathfrak {F}}_2\) is closed under finite intersections. The result now follows from Proposition 3.6. \(\square \)
and \({\mathfrak {F}}_2=\{{\mathscr {C}}\}\). It is clear that \({\mathfrak {F}}_1\) is monoidal and \({\mathfrak {F}}_2\) is closed under finite intersections. The result now follows from Proposition 3.6. \(\square \)
Proposition 3.8
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category and let \({\mathscr {S}}\) be a multiplicatively closed family of objects of \({\mathscr {C}}\). Then:
-
(a)
A thick tensor ideal that is maximal with respect to being disjoint from \({\mathscr {S}}\) is also prime.
-
(b)
A thick tensor ideal that is maximal among ideals \({\mathscr {I}}\) satisfying
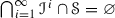 is also prime.
is also prime. -
(c)
Let \({\mathfrak {F}}\) be a monoidal semifilter. Then, a thick tensor ideal that is maximal among ideals \({\mathscr {I}}\) satisfying
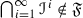 is also prime.
is also prime.
Proof
(a) We consider the family

It is clear that \({\mathfrak {F}}_{{\mathscr {S}}}\) is a semifilter. Further, if we choose \(x\in {\mathscr {I}}\cap {\mathscr {S}}\), \(y\in {\mathscr {J}}\cap {\mathscr {S}}\) for thick tensor ideals \({\mathscr {I}},{\mathscr {J}}\in {\mathfrak {F}}_{{\mathscr {S}}}\), it follows that  . Thus, \({\mathfrak {F}}_{{\mathscr {S}}}\) is also monoidal and we see that it satisfies condition (Q1) in Theorem 3.5. Hence, \({\mathfrak {F}}_{{\mathscr {S}}}\) satisfies the Prime Ideal Principle.
. Thus, \({\mathfrak {F}}_{{\mathscr {S}}}\) is also monoidal and we see that it satisfies condition (Q1) in Theorem 3.5. Hence, \({\mathfrak {F}}_{{\mathscr {S}}}\) satisfies the Prime Ideal Principle.
(c) Given the monoidal semifilter \({\mathfrak {F}}\), we consider

Since \({\mathfrak {F}}\) is a semifilter, it is clear that so is \({\mathfrak {F}}_\infty \). We consider \({\mathscr {I}},{\mathscr {J}}\in {\mathfrak {F}}_\infty \) and note that

Since \({\mathfrak {F}}\) is a semifilter, it follows that  and hence
and hence  . Hence, \({\mathfrak {F}}_\infty \) is a monoidal semifilter and satisfies the Prime Ideal Principle.
. Hence, \({\mathfrak {F}}_\infty \) is a monoidal semifilter and satisfies the Prime Ideal Principle.
(b) follows by applying the result of (c) with \({\mathfrak {F}}={\mathfrak {F}}_{{\mathscr {S}}}\). \(\square \)
Remark 3.9
We mention here that the result of part (a) of Proposition 3.8 is already known as a special case of [1, Lemma 2.2].
The next result will deal with thick tensor ideals that are annihilators of objects from categories that are “modules” over the tensor triangulated category \(({\mathscr {C}},\otimes ,1)\). For this, we recall that Stevenson [34, Definition 3.2] has introduced module actions for a tensor triangulated category \(({\mathscr {C}},\otimes ,1)\) on a triangulated category \({\mathscr {M}}\). More explicitly, a module over \(({\mathscr {C}},\otimes ,1)\) consists of a triangulated category \({\mathscr {M}}\) along with an action

that is exact in both variables; in other words, for any \(a\in {\mathscr {C}}\) and \(m\in {\mathscr {M}}\), the functors  and
and  are exact. Further, the action in (19) satisfies appropriate associative, distributive and unit properties and is well behaved with respect to the translation operator on the triangulated category \({\mathscr {M}}\) (see [34, Definition 3.2]). For a detailed study on modules over tensor triangulated categories, we refer the reader to [34].
are exact. Further, the action in (19) satisfies appropriate associative, distributive and unit properties and is well behaved with respect to the translation operator on the triangulated category \({\mathscr {M}}\) (see [34, Definition 3.2]). For a detailed study on modules over tensor triangulated categories, we refer the reader to [34].
Given an object \(m\in {\mathscr {M}}\), we let the annihilator  be the collection of all objects \(a\in {\mathscr {C}}\) such that
be the collection of all objects \(a\in {\mathscr {C}}\) such that  . Given that the action
. Given that the action  in (19) is exact in both variables, it is clear that
in (19) is exact in both variables, it is clear that  is actually a thick tensor ideal.
is actually a thick tensor ideal.
Proposition 3.10
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category and let \({\mathscr {M}}\) be a triangulated category that has the structure of a \({\mathscr {C}}\)-module.
-
(a)
Let \({\mathscr {S}}\) be a multiplicatively closed family of objects in \(({\mathscr {C}},\otimes ,1)\). Consider the following family of thick tensor ideals:
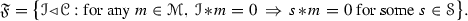 (20)
(20)Then, \({\mathfrak {F}}\) is a strongly Ako semifilter. In particular, the family \({\mathfrak {F}}\) satisfies the Prime Ideal Principle.
-
(b)
A thick tensor ideal of \(({\mathscr {C}},\otimes ,1)\) that is maximal among the annihilators of non-zero objects of \({\mathscr {M}}\) is also prime.
Proof
(a) It is immediate from (20) that \({\mathfrak {F}}\) is a semifilter. To show that \({\mathfrak {F}}\) is strongly Ako, we choose thick tensor ideals \({\mathscr {I}}\),  and some object \(a\in {\mathscr {C}}\) such that
and some object \(a\in {\mathscr {C}}\) such that  ,
,  . Suppose that
. Suppose that  for some \(m\in {\mathscr {M}}\). Then,
for some \(m\in {\mathscr {M}}\). Then,  and hence
and hence  . Since
. Since  , we conclude that there exists some \(s\in {\mathscr {S}}\) such that
, we conclude that there exists some \(s\in {\mathscr {S}}\) such that  . It follows that
. It follows that  .
.
On the other hand, since  , we have
, we have  . Then,
. Then,  . Since
. Since  , it follows that there exists
, it follows that there exists  such that
such that  . Finally, since \({\mathscr {S}}\) is multiplicatively closed, we know that
. Finally, since \({\mathscr {S}}\) is multiplicatively closed, we know that  . This shows that
. This shows that  and hence \({\mathfrak {F}}\) is strongly Ako. In particular, it now follows from Theorem 3.5 (b) that \({\mathfrak {F}}\) satisfies the Prime Ideal Principle.
and hence \({\mathfrak {F}}\) is strongly Ako. In particular, it now follows from Theorem 3.5 (b) that \({\mathfrak {F}}\) satisfies the Prime Ideal Principle.
(b) In particular, we take \({\mathscr {S}}=\{1\}\). Then, from the definition in (20), it is clear that

In part (a), we have shown that \({\mathfrak {F}}\) satisfies the Prime Ideal Principle. Hence, if \({\mathscr {I}}\) is maximal with respect to being contained in some  with \(m\ne 0\), it must be prime. Finally, it is clear that an ideal is maximal with respect to being contained in some
with \(m\ne 0\), it must be prime. Finally, it is clear that an ideal is maximal with respect to being contained in some  with \(m\ne 0\) if and only if it is maximal among the annihiliators of non-zero objects of \({\mathscr {M}}\). \(\square \)
with \(m\ne 0\) if and only if it is maximal among the annihiliators of non-zero objects of \({\mathscr {M}}\). \(\square \)
Analogously to the usual definition in commutative algebra, we will say that a thick tensor ideal \({\mathscr {I}}\) in \(({\mathscr {C}},\otimes ,1)\) is essential if it has non-trivial intersection with every non-zero thick tensor ideal in \(({\mathscr {C}},\otimes ,1)\). Further, as in [1, Corollary 2.4], an object \(a\in {\mathscr {C}}\) will be called \(\otimes \)-nilpotent if there exists an integer \(n>0\) such that  . As such, we will say that \(({\mathscr {C}},\otimes ,1)\) is \(\otimes \)-reduced if it has no non-zero \(\otimes \)-nilpotent objects. We now have the following result.
. As such, we will say that \(({\mathscr {C}},\otimes ,1)\) is \(\otimes \)-reduced if it has no non-zero \(\otimes \)-nilpotent objects. We now have the following result.
Proposition 3.11
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category and let \({\mathfrak {F}}\) be the family of essential thick tensor ideals of \(({\mathscr {C}},\otimes ,1)\). Then, if \(({\mathscr {C}},\otimes ,1)\) is \(\otimes \)-reduced, \({\mathfrak {F}}\) is a monoidal semifilter. In particular, a thick tensor ideal of \(({\mathscr {C}},\otimes ,1)\) that is maximal with respect to not being essential must be prime.
Proof
If \({\mathscr {I}}\in {\mathfrak {F}}\) is an essential ideal and \({\mathscr {J}}\) is a thick tensor ideal containing \({\mathscr {I}}\), it is clear that \({\mathscr {J}}\) is also essential. Hence, \({\mathfrak {F}}\) is a semifilter.
We now suppose that \({\mathscr {I}}_1,{\mathscr {I}}_2\in {\mathfrak {F}}\) and consider some non-zero thick tensor ideal \({\mathscr {A}}\). Since \({\mathscr {I}}_1\) is essential, we can choose \(0\ne x\in {\mathscr {I}}_1\cap {\mathscr {A}}\). We now consider the thick tensor ideal (x) generated by x. Now since \({\mathscr {I}}_2\) is essential, we may choose \(0\ne y\in (x)\cap {\mathscr {I}}_2\) and consider  . Since \(({\mathscr {C}},\otimes ,1)\) is \(\otimes \)-reduced, it follows that
. Since \(({\mathscr {C}},\otimes ,1)\) is \(\otimes \)-reduced, it follows that  . This shows that
. This shows that  is essential and hence \({\mathfrak {F}}\) is a monoidal semifilter. It now follows from Theorem 3.5 that any ideal that is maximal with respect to not being essential is also prime. \(\square \)
is essential and hence \({\mathfrak {F}}\) is a monoidal semifilter. It now follows from Theorem 3.5 that any ideal that is maximal with respect to not being essential is also prime. \(\square \)
Proposition 3.12
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category. Then, an ideal that is maximal among thick tensor ideals \({\mathscr {I}}\) satisfying  for each \(n\geqslant 0\) must be prime.
for each \(n\geqslant 0\) must be prime.
Proof
We will show that the following family of thick tensor ideals:

is an Oka family by showing that it satisfies condition (Q2) in Theorem 3.5. If \({\mathscr {J}},{\mathscr {K}} \in {\mathfrak {F}}\), we can choose N large enough so that  and
and  . It follows that we have
. It follows that we have  and hence \({\mathfrak {F}}\) is monoidal.
and hence \({\mathfrak {F}}\) is monoidal.
We now consider a thick tensor ideal \({\mathscr {I}}\) such that there exists \(n>1\) with \({\mathscr {I}}\supseteq {\mathscr {J}} \supseteq {\mathscr {I}}^{\otimes n}\) and \({\mathscr {J}}\in {\mathfrak {F}}\). We choose \(m\geqslant 0\) such that  . Then, we have
. Then, we have

By reasoning similar to (21), we see that  and hence
and hence  . Since \(n>1\), we now have
. Since \(n>1\), we now have

Then, \({\mathscr {I}}\in {\mathfrak {F}}\) and the family \({\mathfrak {F}}\) satisfies condition (Q2) in Theorem 3.5. As such, \({\mathfrak {F}}\) satisfies the Prime Ideal Principle. \(\square \)
4 Monoidal semifilters of ideals and realizations of pairs
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category as before. In Sect. 2, we considered pairs \(({\mathscr {A}},{\mathscr {S}})\), where \({\mathscr {A}}\) is a thick tensor ideal and \({\mathscr {S}}\) is a multiplicatively closed family of objects of \({\mathscr {C}}\). In Sect. 3, we have already seen that for such a multiplicatively closed family \({\mathscr {S}}\), we can define

Then, \({\mathfrak {F}}_S\) turns out to be a monoidal semifilter (and hence an Oka family) of ideals in \({\mathscr {C}}\). More generally, in this section, we will consider pairs \(({\mathscr {A}},{\mathfrak {F}})\), where \({\mathscr {A}}\) is a thick tensor ideal and \({\mathfrak {F}}\) is a monoidal semifilter. Our purpose is to study realizations of templates of such pairs in a manner similar to Sect. 2.
Definition 4.1
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category as before. We consider a pair \(({\mathscr {A}},{\mathfrak {F}})\) satisfying the following conditions:
-
\({\mathscr {A}}\) is a thick tensor ideal in \(({\mathscr {C}},\otimes ,1)\).
-
\({\mathfrak {F}}\) is a family of thick tensor ideals that is a monoidal semifilter.
-
Let
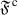 denote the collection of all thick tensor ideals of \(({\mathscr {C}},\otimes ,1)\) not contained in \({\mathfrak {F}}\). Then, every non-empty increasing chain of ideals in
denote the collection of all thick tensor ideals of \(({\mathscr {C}},\otimes ,1)\) not contained in \({\mathfrak {F}}\). Then, every non-empty increasing chain of ideals in  has an upper bound in
has an upper bound in 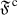 .
.
Then, we will say that a prime ideal \({\mathscr {P}}\) is a realization of the pair
\(({\mathscr {A}},{\mathfrak {F}})\) if \({\mathscr {A}}\subseteq {\mathscr {P}}\) and \({\mathscr {P}}\not \in \mathfrak {F}\). We let  denote the collection of all prime ideals realizing the pair \(({\mathscr {A}},{\mathfrak {F}})\). Further, we let \({\mathscr {M}}{({\mathscr {A}},{\mathfrak {F}})}\) be the multiplicatively closed family given by the complement of
denote the collection of all prime ideals realizing the pair \(({\mathscr {A}},{\mathfrak {F}})\). Further, we let \({\mathscr {M}}{({\mathscr {A}},{\mathfrak {F}})}\) be the multiplicatively closed family given by the complement of  .
.
More generally, let \((I,\leqslant )\) be a partially ordered set and let \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I}\) be a collection of such pairs indexed by I. Then, we will say that a collection \(\{{\mathscr {P}}_i\}_{i\in I}\) of prime ideals in \({\mathscr {C}}\) is a realization of the template
T if each \({\mathscr {P}}_i\) realizes the pair \(({\mathscr {A}}_i,{\mathfrak {F}}_i)\) and  for every \(i\leqslant j\) in I.
for every \(i\leqslant j\) in I.
Henceforth, we will only consider pairs \(({\mathscr {A}},{\mathfrak {F}})\) as in Definition 4.1. Further, since \({\mathfrak {F}}\) is a semifilter, it is clear that if there exists a prime ideal \({\mathscr {P}}\) realizing a pair \(({\mathscr {A}},{\mathfrak {F}})\), we must have \({\mathscr {A}}\notin {\mathfrak {F}}\).
Proposition 4.2
Let \(({\mathscr {A}},{\mathfrak {F}})\) be a pair as in Definition 4.1. Suppose that \({\mathscr {A}}\notin {\mathfrak {F}}\). Then, there always exists a prime ideal in \(({\mathscr {C}},\otimes ,1)\) that realizes the pair \(({\mathscr {A}},{\mathfrak {F}})\).
Proof
From Theorem 3.5, we know that a thick tensor ideal that is maximal with respect to not being in the monoidal semifilter \({\mathfrak {F}}\) must be prime. Further, since every increasing chain of ideals in  has an upper bound in
has an upper bound in  , given that \({\mathscr {A}}\notin {\mathfrak {F}}\), it follows from Zorn’s lemma that \({\mathscr {A}}\) must be contained in a thick tensor ideal \({\mathscr {P}}\) that is maximal with respect to not being in \({\mathfrak {F}}\). Then, \({\mathscr {P}}\) is a prime ideal realizing the pair \(({\mathscr {A}},{\mathfrak {F}})\).\(\square \)
, given that \({\mathscr {A}}\notin {\mathfrak {F}}\), it follows from Zorn’s lemma that \({\mathscr {A}}\) must be contained in a thick tensor ideal \({\mathscr {P}}\) that is maximal with respect to not being in \({\mathfrak {F}}\). Then, \({\mathscr {P}}\) is a prime ideal realizing the pair \(({\mathscr {A}},{\mathfrak {F}})\).\(\square \)
Remark 4.3
In particular, let \({\mathscr {S}}\) be a multiplicatively closed family of objects of \({\mathscr {C}}\) and set  as in (22). It is clear that the union of any chain of ideals in the complement
as in (22). It is clear that the union of any chain of ideals in the complement  of \({\mathfrak {F}}_{{\mathscr {S}}}\) lies in
of \({\mathfrak {F}}_{{\mathscr {S}}}\) lies in  . Then, if \({\mathscr {A}}\) is a thick tensor ideal such that \({\mathscr {A}}\cap {\mathscr {S}}=\varnothing \), i.e., \({\mathscr {A}}\notin {\mathfrak {F}}_{{\mathscr {S}}}\), it follows from Proposition 4.2 that we can find a prime ideal \({\mathscr {P}}\) realizing the pair \(({\mathscr {A}},{\mathfrak {F}}_{{\mathscr {S}}})\). This allows us to recover [1, Lemma 2.2] as a special case.
. Then, if \({\mathscr {A}}\) is a thick tensor ideal such that \({\mathscr {A}}\cap {\mathscr {S}}=\varnothing \), i.e., \({\mathscr {A}}\notin {\mathfrak {F}}_{{\mathscr {S}}}\), it follows from Proposition 4.2 that we can find a prime ideal \({\mathscr {P}}\) realizing the pair \(({\mathscr {A}},{\mathfrak {F}}_{{\mathscr {S}}})\). This allows us to recover [1, Lemma 2.2] as a special case.
Lemma 4.4
Let \({\mathscr {A}}\) be a thick tensor ideal and let \({\mathfrak {F}}\) be a monoidal semifilter. Consider the full subcategory  of \({\mathscr {C}}\) defined by
of \({\mathscr {C}}\) defined by

Then,  is a thick tensor ideal in \(({\mathscr {C}},\otimes ,1)\).
is a thick tensor ideal in \(({\mathscr {C}},\otimes ,1)\).
Proof
From (23), it is clear that if  , then
, then  for any
for any  . Now, suppose that
. Now, suppose that  splits as
splits as  . We choose \({\mathscr {I}}\in {\mathfrak {F}}\) such that
. We choose \({\mathscr {I}}\in {\mathfrak {F}}\) such that  . Then, for any \(x\in {\mathscr {I}}\), we have
. Then, for any \(x\in {\mathscr {I}}\), we have

Since  and \({\mathscr {A}}\) is thick, it follows that
and \({\mathscr {A}}\) is thick, it follows that  and
and  for any \(x\in {\mathscr {I}}\). Hence,
for any \(x\in {\mathscr {I}}\). Hence,  and
and  and we see that
and we see that  . Finally, we consider a distinguished triangle
. Finally, we consider a distinguished triangle
where two out of a, b, c lie in  . For the sake of definiteness, suppose that
. For the sake of definiteness, suppose that  . We now choose ideals \({\mathscr {I}}_1,{\mathscr {I}}_2\in {\mathfrak {F}}\) such that
. We now choose ideals \({\mathscr {I}}_1,{\mathscr {I}}_2\in {\mathfrak {F}}\) such that  . Then, it is clear that
. Then, it is clear that  and
and  . We choose
. We choose  and consider the induced triangle
and consider the induced triangle

It follows from (24) that  for each
for each  . Hence,
. Hence,  . Since \({\mathfrak {F}}\) is a monoidal family, we know that
. Since \({\mathfrak {F}}\) is a monoidal family, we know that  and hence
and hence  . \(\square \)
. \(\square \)
Lemma 4.5
Let \({\mathscr {S}}\) be a multiplicatively closed family of objects of \({\mathscr {C}}\) and let \({\mathfrak {F}}\) be a monoidal semifilter. Suppose that every non-empty increasing chain of ideals in  has an upper bound in
has an upper bound in  . Consider the family
. Consider the family  of ideals of \({\mathscr {C}}\) defined by
of ideals of \({\mathscr {C}}\) defined by

Then,  is a monoidal semifilter. Further, every non-empty increasing chain of ideals in the complement
is a monoidal semifilter. Further, every non-empty increasing chain of ideals in the complement  of
of  has an upper bound in
has an upper bound in  .
.
Proof
From the definition in (25), it is clear that if \({\mathscr {I}}\subseteq {\mathscr {J}}\) and  , then
, then  . Further, let
. Further, let  and choose \({\mathscr {I}}'_1,{\mathscr {I}}'_2\in {\mathfrak {F}}\) as well as \(s_1,s_2\in {\mathscr {S}}\) such that
and choose \({\mathscr {I}}'_1,{\mathscr {I}}'_2\in {\mathfrak {F}}\) as well as \(s_1,s_2\in {\mathscr {S}}\) such that  ,
,  . Since \({\mathscr {S}}\) is multiplicatively closed, we have
. Since \({\mathscr {S}}\) is multiplicatively closed, we have  . Then
. Then

Since \({\mathfrak {F}}\) is a monoidal semifilter, we know that  and it now follows from (26) that
and it now follows from (26) that  .
.
Finally, let \(\{{\mathscr {J}}_n\}_{n\in N}\) be an increasing chain of ideals in  indexed by a totally ordered set \((N,\leqslant )\) and consider
indexed by a totally ordered set \((N,\leqslant )\) and consider  . Suppose that
. Suppose that  , i.e., there exists \(s\in {\mathscr {S}}\) and
, i.e., there exists \(s\in {\mathscr {S}}\) and  such that
such that  . We now consider
. We now consider

as in (12). We know that each  and
and  are thick tensor ideals. Further, it is also clear that
are thick tensor ideals. Further, it is also clear that

We claim that each ideal  . Indeed if
. Indeed if  for some \(n\in N\), we have
for some \(n\in N\), we have  and it follows from the definition in (25) that
and it follows from the definition in (25) that  , which is a contradiction. Accordingly,
, which is a contradiction. Accordingly,  is an increasing chain of ideals in
is an increasing chain of ideals in  and therefore we can choose an upper bound
and therefore we can choose an upper bound  for
for  . Then, we have
. Then, we have

Since \({\mathfrak {F}}\) is a semifilter and \({\mathscr {K}}\notin {\mathfrak {F}}\), it follows from (27) that  . We now recall that
. We now recall that  is such that
is such that  from which it follows that
from which it follows that  . Since \({\mathfrak {F}}\) is a semifilter, it now follows that
. Since \({\mathfrak {F}}\) is a semifilter, it now follows that  , which is a contradiction. Hence, we must have
, which is a contradiction. Hence, we must have  and thus \({\mathscr {J}}\) becomes an upper bound for the system \(\{{\mathscr {J}}_n\}_{n\in N}\) in
and thus \({\mathscr {J}}\) becomes an upper bound for the system \(\{{\mathscr {J}}_n\}_{n\in N}\) in  .\(\square \)
.\(\square \)
Proposition 4.6
-
(a)
Let \(({\mathscr {A}},{\mathfrak {F}})\) be a pair and let \({\mathscr {Q}}\) be any prime ideal in \(({\mathscr {C}},\otimes ,1)\). Then, \({\mathscr {Q}}\) contains a prime ideal realizing the pair \(({\mathscr {A}},{\mathfrak {F}})\) if and only if
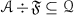 .
. -
(b)
Let \(({\mathscr {A}},{\mathfrak {F}})\) be a pair such that
 is finite. Then, a prime ideal \({\mathscr {P}}\) is contained in a prime ideal realizing \(({\mathscr {A}},{\mathfrak {F}})\) if and only if \({\mathscr {P}}\) is disjoint from \({\mathscr {M}}({\mathscr {A}},{\mathfrak {F}})\).
is finite. Then, a prime ideal \({\mathscr {P}}\) is contained in a prime ideal realizing \(({\mathscr {A}},{\mathfrak {F}})\) if and only if \({\mathscr {P}}\) is disjoint from \({\mathscr {M}}({\mathscr {A}},{\mathfrak {F}})\).
Proof
(a) Let \({\mathscr {P}}\) be a prime ideal realizing the pair \(({\mathscr {A}},{\mathfrak {F}})\). Choose any  and some \({\mathscr {I}}\in {\mathfrak {F}}\) such that
and some \({\mathscr {I}}\in {\mathfrak {F}}\) such that  . Then,
. Then,  . Suppose that \(a\notin {\mathscr {P}}\). Then, for any \(x\in {\mathscr {I}}\), we have
. Suppose that \(a\notin {\mathscr {P}}\). Then, for any \(x\in {\mathscr {I}}\), we have  and hence \(x\in {\mathscr {P}}\). Hence, \({\mathscr {I}}\subseteq {\mathscr {P}}\). Since \({\mathfrak {F}}\) is a semifilter and \({\mathscr {I}}\in {\mathfrak {F}}\), it now follows that \({\mathscr {P}}\in {\mathfrak {F}}\) which is a contradiction. Hence,
and hence \(x\in {\mathscr {P}}\). Hence, \({\mathscr {I}}\subseteq {\mathscr {P}}\). Since \({\mathfrak {F}}\) is a semifilter and \({\mathscr {I}}\in {\mathfrak {F}}\), it now follows that \({\mathscr {P}}\in {\mathfrak {F}}\) which is a contradiction. Hence,  is contained in \({\mathscr {P}}\) and hence in any prime ideal \({\mathscr {Q}}\) containing \({\mathscr {P}}\).
is contained in \({\mathscr {P}}\) and hence in any prime ideal \({\mathscr {Q}}\) containing \({\mathscr {P}}\).
Conversely, suppose that  . We claim that
. We claim that  . Otherwise, there exists \({\mathscr {I}}\in {\mathfrak {F}}\) and \(s\notin {\mathscr {Q}}\) such that
. Otherwise, there exists \({\mathscr {I}}\in {\mathfrak {F}}\) and \(s\notin {\mathscr {Q}}\) such that  , i.e.,
, i.e.,  which is a contradiction. Further, from Lemma 4.5, we know that any increasing chain of ideals in
which is a contradiction. Further, from Lemma 4.5, we know that any increasing chain of ideals in  has an upper bound in
has an upper bound in  . Accordingly, we choose a prime ideal \({\mathscr {P}}\) realizing the pair
. Accordingly, we choose a prime ideal \({\mathscr {P}}\) realizing the pair  . Now suppose that there exists some \(x\in {\mathscr {P}}\cap ({\mathscr {C}}-{\mathscr {Q}})\) and take any
. Now suppose that there exists some \(x\in {\mathscr {P}}\cap ({\mathscr {C}}-{\mathscr {Q}})\) and take any  . Then,
. Then,  and hence
and hence  , which is a contradiction. Hence, \({\mathscr {P}}\subseteq {\mathscr {Q}}\).
, which is a contradiction. Hence, \({\mathscr {P}}\subseteq {\mathscr {Q}}\).
(b) Suppose that we have prime ideals \({\mathscr {P}}\subseteq {\mathscr {Q}}\) such that \({\mathscr {Q}}\) realizes \(({\mathscr {A}},{\mathfrak {F}})\). Then,  and hence \({\mathscr {P}}\cap {\mathscr {M}}({\mathscr {A}},{\mathfrak {F}})=\varnothing \). On the other hand, suppose that \({\mathscr {P}}\cap {\mathscr {M}}({\mathscr {A}},{\mathfrak {F}})=\varnothing \), i.e.,
and hence \({\mathscr {P}}\cap {\mathscr {M}}({\mathscr {A}},{\mathfrak {F}})=\varnothing \). On the other hand, suppose that \({\mathscr {P}}\cap {\mathscr {M}}({\mathscr {A}},{\mathfrak {F}})=\varnothing \), i.e.,  . Since
. Since  is finite, it follows from Proposition 2.2 that \({\mathscr {P}}\subseteq {\mathscr {Q}}\) for some
is finite, it follows from Proposition 2.2 that \({\mathscr {P}}\subseteq {\mathscr {Q}}\) for some  . \(\square \)
. \(\square \)
Definition 4.7
Let \(({\mathscr {A}},{\mathfrak {F}})\) and  be two pairs as in Definition 4.1. Then, we will say that
be two pairs as in Definition 4.1. Then, we will say that  if every prime ideal
if every prime ideal  realizing the pair
realizing the pair  contains a prime ideal \({\mathscr {P}}\) that realizes \(({\mathscr {A}},{\mathfrak {F}})\).
contains a prime ideal \({\mathscr {P}}\) that realizes \(({\mathscr {A}},{\mathfrak {F}})\).
Proposition 4.8
Let \(({\mathscr {A}},{\mathfrak {F}})\) and  be two pairs. Then, the following are equivalent:
be two pairs. Then, the following are equivalent:
-
(a)
We have
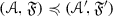 , i.e., any prime ideal that realizes
, i.e., any prime ideal that realizes 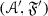 contains a prime ideal that realizes \(({\mathscr {A}},{\mathfrak {F}})\).
contains a prime ideal that realizes \(({\mathscr {A}},{\mathfrak {F}})\). -
(b)
The radical of
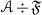 is contained in the radical of
is contained in the radical of 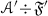 , i.e.,
, i.e.,  .
.
Proof
(b) \(\Rightarrow \) (a). Suppose that  and let
and let  be a prime ideal realizing
be a prime ideal realizing  . Then, we see that
. Then, we see that

and it follows from Proposition 4.6 that  contains a prime ideal realizing the pair \(({\mathscr {A}},{\mathfrak {F}})\).
contains a prime ideal realizing the pair \(({\mathscr {A}},{\mathfrak {F}})\).
(a) \(\Rightarrow \) (b). Consider any prime ideal  such that
such that  (if there is no such prime ideal
(if there is no such prime ideal  , then
, then  and we are done). Then, from Proposition 4.6, we know that
and we are done). Then, from Proposition 4.6, we know that  contains a prime ideal
contains a prime ideal  realizing
realizing  . By assumption, there exists a prime ideal
. By assumption, there exists a prime ideal  such that \({\mathscr {P}}\) realizes \(({\mathscr {A}},{\mathfrak {F}})\). Hence,
such that \({\mathscr {P}}\) realizes \(({\mathscr {A}},{\mathfrak {F}})\). Hence,  and therefore
and therefore  for any prime ideal
for any prime ideal  containing
containing  . It now follows that
. It now follows that  . \(\square \)
. \(\square \)
For the rest of this section, we will say that two templates indexed by the same partially ordered set are equivalent if they have the same realizations. As with pairs in Sect. 2, we will now show how to construct realizations of a finite chain template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{1\leqslant i\leqslant n}\) by showing that it is equivalent to a template  satisfying the additional condition that
satisfying the additional condition that
From Proposition 4.8, it is clear how one can construct a realization of a template of the form (28) starting with a realization \({\mathscr {P}}_1\) of \(({\mathscr {B}}_1,{\mathfrak {F}}_1)\).
Proposition 4.9
Let \(n\geqslant 1\) and let \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) be a finite chain template indexed by the opposite \(I^\mathrm{op}\) of the ordered set \(I=\{1<2<\cdots <n\}\). We define \(\{{\mathscr {B}}_i\}_{1\leqslant i\leqslant n}\) inductively by letting \({\mathscr {B}}_n ={\mathscr {A}}_n\) and setting

Then, we have:
-
(a)
A chain
 is a realization of the template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) if and only if it is also a realization of the template
is a realization of the template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) if and only if it is also a realization of the template 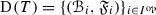 .
. -
(b)
The template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) has a realization if and only if \({\mathscr {B}}_1\notin {\mathfrak {F}}_1\), i.e.,
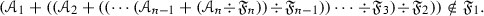
Proof
(a) Suppose that  is a realization of the template
is a realization of the template  . From (29), it is clear that each \( {\mathscr {A}}_i\subseteq {\mathscr {B}}_i\) and hence \({\mathscr {P}}_i\) realizes the pair \(({\mathscr {A}}_i,{\mathfrak {F}}_i)\). Hence,
. From (29), it is clear that each \( {\mathscr {A}}_i\subseteq {\mathscr {B}}_i\) and hence \({\mathscr {P}}_i\) realizes the pair \(({\mathscr {A}}_i,{\mathfrak {F}}_i)\). Hence,  is a realization of T.
is a realization of T.
Conversely, suppose that  is a realization of T. By definition, we know that \({\mathscr {B}}_n={\mathscr {A}}_n\) and hence
is a realization of T. By definition, we know that \({\mathscr {B}}_n={\mathscr {A}}_n\) and hence  . Suppose that \({\mathscr {B}}_i\subseteq {\mathscr {P}}_i\) for all \(n\geqslant i>j\) for some fixed j. Since
. Suppose that \({\mathscr {B}}_i\subseteq {\mathscr {P}}_i\) for all \(n\geqslant i>j\) for some fixed j. Since  and \({\mathscr {P}}_{j+1}\) realizes
and \({\mathscr {P}}_{j+1}\) realizes  , it follows from Proposition 4.6 (a) that
, it follows from Proposition 4.6 (a) that  . Further, \({\mathscr {A}}_j\subseteq {\mathscr {P}}_{j}\) because
. Further, \({\mathscr {A}}_j\subseteq {\mathscr {P}}_{j}\) because  realizes
realizes  . Hence,
. Hence,  and
and  realizes the pair
realizes the pair  . Hence,
. Hence,  becomes a realization of
becomes a realization of  .
.
(b) We claim that \(({\mathscr {B}}_{i+1},{\mathfrak {F}}_{i+1})\preccurlyeq ({\mathscr {B}}_i,{\mathfrak {F}}_i)\) for each \(1\leqslant i <n\). For this, we note that

Hence,  and it follows from Proposition 4.8 that
and it follows from Proposition 4.8 that  . Now suppose that \({\mathscr {B}}_1\notin {\mathfrak {F}}_1\). Then, using Proposition 4.2, we can obtain a prime ideal \({\mathscr {P}}_1\) realizing \(({\mathscr {B}}_1,{\mathfrak {F}}_1)\). Since the template
. Now suppose that \({\mathscr {B}}_1\notin {\mathfrak {F}}_1\). Then, using Proposition 4.2, we can obtain a prime ideal \({\mathscr {P}}_1\) realizing \(({\mathscr {B}}_1,{\mathfrak {F}}_1)\). Since the template  , satisfies condition (28), we can now obtain a realization
, satisfies condition (28), we can now obtain a realization  of
of  starting from \({\mathscr {P}}_1\).
starting from \({\mathscr {P}}_1\).
Conversely, suppose that the template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) is realizable. From part (a), it follows that the template  is also realizable and in particular this means that the pair \(({\mathscr {B}}_1,{\mathfrak {F}}_1)\) is realizable. Hence, we must have \({\mathscr {B}}_1\notin {\mathfrak {F}}_1\). \(\square \)
is also realizable and in particular this means that the pair \(({\mathscr {B}}_1,{\mathfrak {F}}_1)\) is realizable. Hence, we must have \({\mathscr {B}}_1\notin {\mathfrak {F}}_1\). \(\square \)
Let \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) be a template as above. We will now show that under certain finiteness conditions, we may construct a template \({\mathscr {D}}(T)=\{({\mathscr {B}}_i, {\mathfrak {G}}_i)\}_{i\in I^\mathrm{op}}\) equivalent to T such that if we start with an arbitrary realization \({\mathscr {Q}}_j\) of some pair  , we can expand it in both directions to form a realization \({\mathscr {Q}}_n\subseteq \dots \subseteq {\mathscr {Q}}_j\subseteq \dots \subseteq {\mathscr {Q}}_1\) of \({\mathscr {D}}(T)\). We notice that since \({\mathscr {D}}(T)\) is equivalent to T, the latter becomes a realization of T.
, we can expand it in both directions to form a realization \({\mathscr {Q}}_n\subseteq \dots \subseteq {\mathscr {Q}}_j\subseteq \dots \subseteq {\mathscr {Q}}_1\) of \({\mathscr {D}}(T)\). We notice that since \({\mathscr {D}}(T)\) is equivalent to T, the latter becomes a realization of T.
Proposition 4.10
Let \(n\geqslant 1\) and let \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) be a finite chain template indexed by the opposite \(I^\mathrm{op}\) of the ordered set \(I=\{1<2<\cdots <n\}\). Suppose that for each \(1\leqslant i\leqslant n\),  is a finite set. We define \(\{{\mathscr {B}}_i\}_{1\leqslant i\leqslant n}\) inductively by letting \({\mathscr {B}}_n ={\mathscr {A}}_n\) and setting
is a finite set. We define \(\{{\mathscr {B}}_i\}_{1\leqslant i\leqslant n}\) inductively by letting \({\mathscr {B}}_n ={\mathscr {A}}_n\) and setting

On the other hand, we define \(\{{\mathfrak {G}}_i\}_{1\leqslant i\leqslant n}\) inductively by letting \({\mathfrak {G}}_1={\mathfrak {F}}_1\) and setting \({\mathfrak {G}}_{i+1}\) to be

Then, we have:
-
(a)
The templates T and \({\mathscr {D}}(T)\) are equivalent.
-
(b)
Choose any integer \(j\in \{1,2,\dots ,n\}\). Then, the template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) has a realization if and only if
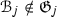 .
.
Proof
(a) Suppose that \({\mathscr {Q}}_n\subseteq \dots \subseteq {\mathscr {Q}}_2\subseteq {\mathscr {Q}}_1\) is a realization of \({\mathscr {D}}(T)\). From (30) and (31), it is clear that each \({\mathscr {A}}_i\subseteq {\mathscr {B}}_i\) and \({\mathfrak {F}}_i\subseteq {\mathfrak {G}}_i\). Since each \({\mathscr {Q}}_i\) realizes the pair \(({\mathscr {B}}_i,{\mathfrak {G}}_i)\), we see that it also realizes \(({\mathscr {A}}_i,{\mathfrak {F}}_i)\).
Conversely, let \({\mathscr {Q}}_n\subseteq \cdots \subseteq {\mathscr {Q}}_2\subseteq {\mathscr {Q}}_1\) be a realization of T. From the proof of Proposition 4.9 (a), we see that each \({\mathscr {B}}_i\subseteq {\mathscr {Q}}_i\). By definition, we know that \({\mathfrak {G}}_1={\mathfrak {F}}_1\) and hence \({\mathscr {Q}}_1\notin {\mathfrak {G}}_1\). To proceed by induction, we now suppose that \({\mathscr {Q}}_i\notin {\mathfrak {G}}_i\) for all \(1\leqslant i\leqslant j\) for some fixed j. Then, since \({\mathscr {Q}}_{j+1}\subseteq {\mathscr {Q}}_j\) and  , we have
, we have

Now if  , it follows from (25) that there exists
, it follows from (25) that there exists  and
and  such that
such that  . Since \({\mathscr {Q}}_{j+1}\) is a prime ideal, it now follows from (32) that
. Since \({\mathscr {Q}}_{j+1}\) is a prime ideal, it now follows from (32) that  . But, \({\mathfrak {F}}_{j+1}\) being a semifilter,
. But, \({\mathfrak {F}}_{j+1}\) being a semifilter,  implies that \({\mathscr {Q}}_{j+1}\in {\mathfrak {F}}_{j+1}\), which is a contradiction. Hence,
implies that \({\mathscr {Q}}_{j+1}\in {\mathfrak {F}}_{j+1}\), which is a contradiction. Hence,  and \({\mathscr {Q}}_{j+1}\) realizes the pair
and \({\mathscr {Q}}_{j+1}\) realizes the pair  .
.
(b) We choose some \(j\in \{1,2,\dots ,n\}\). From part (a), we know that if T has a realization, so does \( {\mathscr {D}}(T)\). Hence, the pair  can be realized and we must have
can be realized and we must have  . Conversely, suppose that
. Conversely, suppose that  and choose some prime ideal \({\mathscr {Q}}_j\) realizing
and choose some prime ideal \({\mathscr {Q}}_j\) realizing  . Then, we have
. Then, we have

and it follows from Proposition 4.6 (a) that there exists a prime ideal \({\mathscr {Q}}_{j+1}\subseteq {\mathscr {Q}}_j\) realizing  . Further, as in part (a), we see that
. Further, as in part (a), we see that  and hence
and hence  , i.e., \({\mathscr {Q}}_{j+1}\) realizes
, i.e., \({\mathscr {Q}}_{j+1}\) realizes  . On the other hand, if \(j>1\), we have from (31)
. On the other hand, if \(j>1\), we have from (31)

Since  , it follows that
, it follows that  must be finite. From (33), we see that
must be finite. From (33), we see that  and it follows from Proposition 4.6 (b) that there exists a prime \({\mathscr {Q}}_{j-1}\supseteq {\mathscr {Q}}_j\) realizing
and it follows from Proposition 4.6 (b) that there exists a prime \({\mathscr {Q}}_{j-1}\supseteq {\mathscr {Q}}_j\) realizing  . Again, since \({\mathscr {Q}}_j\) realizes
. Again, since \({\mathscr {Q}}_j\) realizes  , Proposition 4.6 (a) implies that
, Proposition 4.6 (a) implies that  . Hence,
. Hence,

and \({\mathscr {Q}}_{j-1}\) realizes  . Accordingly, starting from \({\mathscr {Q}}_j\) we can proceed in both directions to give a realization \({\mathscr {Q}}_n\subseteq \dots \subseteq {\mathscr {Q}}_2\subseteq {\mathscr {Q}}_1\) of the template \({\mathscr {D}}(T)\) (and hence of T).\(\square \)
. Accordingly, starting from \({\mathscr {Q}}_j\) we can proceed in both directions to give a realization \({\mathscr {Q}}_n\subseteq \dots \subseteq {\mathscr {Q}}_2\subseteq {\mathscr {Q}}_1\) of the template \({\mathscr {D}}(T)\) (and hence of T).\(\square \)
Remark 4.11
In the proof above, we note that the finiteness condition is only used in part (b), i.e., the templates T and \({\mathscr {D}}(T)\) are always equivalent.
For the final result of this section, we will consider finite descending trees. Given a finite descending tree \(\mathbb T\), a node at the k-th level of \(\mathbb T\) will be denoted by a multi-index \(I=(i_1,\dots ,i_k)\) with k-coordinates. If this node I has n(I) branches, these branch nodes will be denoted by multi-indices \((I,l)=(i_1,\dots ,i_k,l)\), with l varying from 1 to n(I). The root node appearing at the top will be denoted by (1). Then, if there are n(1) branches leading out of the root node, these branches will be labelled as \((1,1),(1,2),\dots ,(1,n(1))\). The following diagram illustrates our labeling scheme for the nodes of such a tree \(\mathbb T\).

We make \(\mathbb T\) partially ordered by setting the branch nodes \((I,i)\leqslant I\), \(1\leqslant i\leqslant n(I)\), for each node I and consider templates of pairs indexed by \(\mathbb T\).
Proposition 4.12
Let \(\{({\mathscr {A}}_I,{\mathfrak {F}}_I)\}_{I\in \mathbb T}\) be a template indexed by a finite descending tree \(\mathbb T\). For each node I of the tree that has no further branches, we set \({\mathscr {B}}_I={\mathscr {A}}_I\). Then, we define \({\mathscr {B}}_I\) for each multi-index \(I\in \mathbb T\) inductively by setting

where the sum is taken over all nodes \((I,1),(I,2),\dots ,(I,n(I))\) immediately below the node I. Then, the template \(\{({\mathscr {A}}_I,{\mathfrak {F}}_I)\}_{I\in \mathbb T}\) has a realization if and only if \({\mathscr {B}}_{(1)}\notin {\mathfrak {F}}_{(1)}\).
Proof
“If part”: we claim that starting with any prime ideal realizing \(({\mathscr {B}}_{(1)},{\mathfrak {F}}_{(1)})\), we can obtain a realization of the entire template \(\{({\mathscr {A}}_I,{\mathfrak {F}}_I)\}_{I\in \mathbb T}\). We prove this by induction on \(|\mathbb T|\), the number of nodes in the tree \(\mathbb T\). This is obvious if \(|\mathbb T|=1\) and we assume that it holds for all trees with fewer than \(|\mathbb T|\) nodes. Since \({\mathscr {B}}_{(1)}\notin {\mathfrak {F}}_{(1)}\), we can choose a prime \({\mathscr {P}}_{(1)}\) realizing \(({\mathscr {B}}_{(1)},{\mathfrak {F}}_{(1)})\). From the definition in (34), we know that \({\mathscr {A}}_{(1)}\subseteq {\mathscr {B}}_{(1)}\) and each  for each node (I, i) immediately below the root node. Hence, \({\mathscr {P}}_{(1)}\) realizes \(({\mathscr {A}}_{(1)},{\mathfrak {F}}_{(1)})\) and contains prime ideals \({\mathscr {P}}_{(1,i)}\) realizing \(({\mathscr {B}}_{(1,i)}, {\mathfrak {F}}_{(1,i)})\) for each \(1\leqslant i\leqslant n(1)\). Now, n(1) different subtrees \(\mathbb T_1\), ..., \(\mathbb T_{n(1)}\) obtained by cutting off the root node all have strictly less than \(|\mathbb T|\) nodes. By the induction assumption, it follows that starting from each \({\mathscr {P}}_{(1,i)}\), we may obtain a realization of the subtree \(\mathbb T_i\). This proves the result.
for each node (I, i) immediately below the root node. Hence, \({\mathscr {P}}_{(1)}\) realizes \(({\mathscr {A}}_{(1)},{\mathfrak {F}}_{(1)})\) and contains prime ideals \({\mathscr {P}}_{(1,i)}\) realizing \(({\mathscr {B}}_{(1,i)}, {\mathfrak {F}}_{(1,i)})\) for each \(1\leqslant i\leqslant n(1)\). Now, n(1) different subtrees \(\mathbb T_1\), ..., \(\mathbb T_{n(1)}\) obtained by cutting off the root node all have strictly less than \(|\mathbb T|\) nodes. By the induction assumption, it follows that starting from each \({\mathscr {P}}_{(1,i)}\), we may obtain a realization of the subtree \(\mathbb T_i\). This proves the result.
For the “only if” part, we can reverse our arguments and prove by induction the claim that if \(\{{\mathscr {P}}_I\}_{I\in \mathbb T}\) is a realization of \(\{({\mathscr {A}}_I,{\mathfrak {F}}_I)\}_{I\in \mathbb T}\), \({\mathscr {P}}_{(1)}\) must be a realization of \(({\mathscr {B}}_{(1)},{\mathfrak {F}}_{(1)})\). Hence, \({\mathscr {B}}_{(1)}\notin {\mathfrak {F}}_{(1)}\). \(\square \)
5 Monoidal families and the Prime Ideal Principle
In this final section of the paper, we shall assume that the tensor triangulated category \(({\mathscr {C}},\otimes ,1)\) has the additional property that all thick tensor ideals are radical, i.e., for any thick tensor ideal \({\mathscr {I}}\) in \(({\mathscr {C}},\otimes ,1)\), we have  . This additional assumption is equivalent (see [1, Proposition 4.4]) to the assumption that for any object \(a\in {\mathscr {C}}\), a lies in the ideal generated by the object
. This additional assumption is equivalent (see [1, Proposition 4.4]) to the assumption that for any object \(a\in {\mathscr {C}}\), a lies in the ideal generated by the object  . In fact, it is very frequent for all thick tensor ideals to be radical (see [1, Remark 4.3] and [22, Lemma A.2.6]). In particular, this assumption holds in rigid tensor triangulated categories (see [34, Section 2]). For us, the key consequence of this assumption is the following fact.
. In fact, it is very frequent for all thick tensor ideals to be radical (see [1, Remark 4.3] and [22, Lemma A.2.6]). In particular, this assumption holds in rigid tensor triangulated categories (see [34, Section 2]). For us, the key consequence of this assumption is the following fact.
Proposition 5.1
-
(a)
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category such that every thick tensor ideal is a radical ideal. Then, for any thick tensor ideals \({\mathscr {I}}\) and \({\mathscr {J}}\), we have
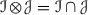 .
. -
(b)
Let \({\mathfrak {F}}\) be a family of thick tensor ideals such that \({\mathscr {C}}\in {\mathfrak {F}}\). Then, if \({\mathfrak {F}}\) is monoidal, the family \({\mathfrak {F}}\) is a strongly Oka and a strongly Ako family. In particular, \({\mathfrak {F}}\) satisfies the Prime Ideal Principle.
Proof
(a) It is clear that  . We choose some object \(a\in {\mathscr {I}}\cap {\mathscr {J}}\). Then,
. We choose some object \(a\in {\mathscr {I}}\cap {\mathscr {J}}\). Then,  . Since all thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) are radical, it follows that a lies in the ideal generated by
. Since all thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) are radical, it follows that a lies in the ideal generated by  . We conclude that
. We conclude that  and hence
and hence  .
.
(b) We will show that \({\mathfrak {F}}\) is strongly Oka and strongly Ako by showing that it satisfies condition (Q3) in Theorem 3.5. For this, we consider thick tensor ideals \({\mathscr {A}},{\mathscr {B}}\in {\mathfrak {F}}\) and some ideal \({\mathscr {I}}\) such that  . From part (a), it follows that
. From part (a), it follows that  . By assumption, \({\mathfrak {F}}\) is monoidal and hence
. By assumption, \({\mathfrak {F}}\) is monoidal and hence  . Hence, the family \({\mathfrak {F}}\) satisfies condition (Q3) in Theorem 3.5. \(\square \)
. Hence, the family \({\mathfrak {F}}\) satisfies condition (Q3) in Theorem 3.5. \(\square \)
Remark 5.2
Proposition 5.1 (b) may also be proved as follows: all thick tensor ideals being radical, [4, Theorem 14] now gives us a correspondence between closed subspaces of  and all ideals in \({\mathscr {C}}\). As such, if \({\mathfrak {F}}\) is a monoidal family, then
and all ideals in \({\mathscr {C}}\). As such, if \({\mathfrak {F}}\) is a monoidal family, then  is closed under finite unions and hence any closed subspace of
is closed under finite unions and hence any closed subspace of  that is minimal with respect to not being in \({\mathfrak {F}}^*\) must be irreducible.
that is minimal with respect to not being in \({\mathfrak {F}}^*\) must be irreducible.
Proposition 5.3
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category such that every thick tensor ideal is a radical ideal. Then:
-
(a)
Let \({\mathscr {I}}\) be a thick tensor ideal that is maximal with respect to being non-principal. Then \({\mathscr {I}}\) is prime.
-
(b)
Let \(\alpha \) be an infinite cardinal and let \({\mathfrak {F}}_\alpha \) denote the family of thick tensor ideals \({\mathscr {I}}\) having a generating set \(G_{{\mathscr {I}}}\) of cardinality \(|G_{{\mathscr {I}}}|\leqslant \alpha \). Then, any ideal that is maximal with respect to not being in \({\mathfrak {F}}_\alpha \) is prime.
Proof
(a) Using Proposition 5.1 (b), it is enough to show that the collection of principal ideals is monoidal. If we have principal ideals \({\mathscr {I}}=(x)\) and \({\mathscr {J}}=(y)\) generated by objects \(x,y\in {\mathscr {C}}\) respectively, it follows from Lemma 3.4 that  is the principal ideal generated by
is the principal ideal generated by  . Hence, the family of principal ideals is monoidal and satisfies the Prime Ideal Principle. The result of part (b) follows similarly.\(\square \)
. Hence, the family of principal ideals is monoidal and satisfies the Prime Ideal Principle. The result of part (b) follows similarly.\(\square \)
Using the same approach as in Proposition 5.3, we can prove the following more general result.
Proposition 5.4
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category such that every thick tensor ideal is radical. Let \({\mathscr {S}}\) be a multiplicatively closed family of objects of \({\mathscr {C}}\) containing 1 and also possibly 0. For any infinite cardinal \(\alpha \), let \({\mathfrak {G}}_{\leqslant \alpha }^{{\mathscr {S}}}\) (resp. \({\mathfrak {G}}_{<\alpha }^{{\mathscr {S}}})\) denote the family of thick tensor ideals \({\mathscr {I}}\) having a generating set \(G_{{\mathscr {I}}}\subseteq {\mathscr {S}}\) such that \(|G_{{\mathscr {I}}}|\leqslant \alpha \) (resp. \(|G_{{\mathscr {I}}}|<\alpha )\). Then, any ideal that is maximal with respect to not being in \({\mathfrak {G}}_{\leqslant \alpha }^{{\mathscr {S}}}\) (resp. \({\mathfrak {G}}_{<\alpha }^{{\mathscr {S}}})\) is prime.
Proof
We consider thick tensor ideals \({\mathscr {I}},{\mathscr {J}}\in {\mathfrak {G}}_{\leqslant \alpha }^{{\mathscr {S}}}\) with respective generating sets  , \(G_{{\mathscr {J}}}=\{y_j\}_{j\in J}\subseteq {\mathscr {S}}\) of cardinality \(\leqslant \alpha \). Since \({\mathscr {S}}\) is multiplicatively closed, we see that each
, \(G_{{\mathscr {J}}}=\{y_j\}_{j\in J}\subseteq {\mathscr {S}}\) of cardinality \(\leqslant \alpha \). Since \({\mathscr {S}}\) is multiplicatively closed, we see that each  . It then follows from Lemma 3.4 that
. It then follows from Lemma 3.4 that  may be generated by the set
may be generated by the set  of cardinality
of cardinality  . Hence, \({\mathfrak {G}}_{\leqslant \alpha }^{{\mathscr {S}}}\) is a monoidal family and satisfies the Prime Ideal Principle. The case of \({\mathfrak {G}}_{<\alpha }^{{\mathscr {S}}}\) follows similarly. \(\square \)
. Hence, \({\mathfrak {G}}_{\leqslant \alpha }^{{\mathscr {S}}}\) is a monoidal family and satisfies the Prime Ideal Principle. The case of \({\mathfrak {G}}_{<\alpha }^{{\mathscr {S}}}\) follows similarly. \(\square \)
Proposition 5.5
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category such that every thick tensor ideal is radical. Then:
-
(a)
Let \({\mathfrak {F}}\) be a monoidal semifilter. Then, the family
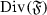 defined by
defined by 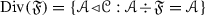
is a strongly Oka family and satisfies the Prime Ideal Principle.
-
(b)
Let \({\mathscr {S}}\) be a multiplicatively closed family of objects of \({\mathscr {C}}\) such that \(1\in {\mathscr {S}}\) and \(0\notin {\mathscr {S}}\). Then, the family is a strongly Oka family and satisfies the Prime Ideal Principle.
Proof
(a) From Proposition 5.1, it suffices to show that  is monoidal. Given any thick tensor ideals \({\mathscr {A}},{\mathscr {B}}\), it is clear from the definition in (23) that
is monoidal. Given any thick tensor ideals \({\mathscr {A}},{\mathscr {B}}\), it is clear from the definition in (23) that  . Conversely, choose an object
. Conversely, choose an object  . Then, there exist \({\mathscr {I}},{\mathscr {J}}\in {\mathfrak {F}}\) such that
. Then, there exist \({\mathscr {I}},{\mathscr {J}}\in {\mathfrak {F}}\) such that  and
and  . It follows that
. It follows that  . Since \({\mathfrak {F}}\) is monoidal,
. Since \({\mathfrak {F}}\) is monoidal,  and hence
and hence  . Since all ideals in \(({\mathscr {C}},\otimes ,1)\) are radical, it now follows that
. Since all ideals in \(({\mathscr {C}},\otimes ,1)\) are radical, it now follows that  . Hence,
. Hence,

In particular, if  , (35) reduces to
, (35) reduces to  . Hence,
. Hence,  and
and  is monoidal. Finally, part (b) follows from part (a) by setting \({\mathfrak {F}}= {\mathfrak {F}}_{{\mathscr {S}}}\) where
is monoidal. Finally, part (b) follows from part (a) by setting \({\mathfrak {F}}= {\mathfrak {F}}_{{\mathscr {S}}}\) where  . \(\square \)
. \(\square \)
Proposition 5.6
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category such that every thick tensor ideal is a radical ideal. Let \({\mathscr {I}}\) be a thick tensor ideal. Then:
-
(a)
The family \({\mathfrak {F}}_{{\mathscr {I}}}\) of thick tensor ideals containing \({\mathscr {I}}\) is a monoidal semifilter. In particular, any ideal of \(({\mathscr {C}},\otimes ,1)\) that is maximal with respect to not containing \({\mathscr {I}}\) must be prime.
-
(b)
Suppose that \({\mathscr {I}}\) is a finitely generated (hence principal) ideal. Then, any non-empty increasing chain of ideals in the complement
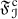 of \({\mathfrak {F}}_{{\mathscr {I}}}\) has an upper bound in
of \({\mathfrak {F}}_{{\mathscr {I}}}\) has an upper bound in 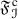 .
.
Proof
(a) It is clear that \({\mathfrak {F}}_{{\mathscr {I}}}\) is a semifilter. Further, if \({\mathscr {I}}\subseteq {\mathscr {A}}\) and \({\mathscr {I}}\subseteq {\mathscr {B}}\) for some \({\mathscr {A}},{\mathscr {B}}\in {\mathfrak {F}}_{{\mathscr {I}}}\), we have  . Hence, \({\mathfrak {F}}_{{\mathscr {I}}}\) is also monoidal.
. Hence, \({\mathfrak {F}}_{{\mathscr {I}}}\) is also monoidal.
(b) Suppose that \({\mathscr {I}}\) is generated by an object x. We consider an increasing chain \(\{{\mathscr {J}}_j\}_{j\in N}\) of ideals in  indexed by a totally ordered set \((N,\leqslant )\) and the union \({\mathscr {J}}=\bigcup _{j\in N}{\mathscr {J}}_j\). Now, if \({\mathscr {J}}\in {\mathfrak {F}}_{{\mathscr {I}}}\), there exists \(n \in N\) large enough such that \(x\in {\mathscr {J}}_n\). Hence, \({\mathscr {I}}\subseteq {\mathscr {J}}_n\) and \({\mathscr {J}}_n\in {\mathfrak {F}}_{{\mathscr {I}}}\), which is a contradiction. We conclude that \({\mathscr {J}}\notin {\mathfrak {F}}_{{\mathscr {I}}}\). \(\square \)
indexed by a totally ordered set \((N,\leqslant )\) and the union \({\mathscr {J}}=\bigcup _{j\in N}{\mathscr {J}}_j\). Now, if \({\mathscr {J}}\in {\mathfrak {F}}_{{\mathscr {I}}}\), there exists \(n \in N\) large enough such that \(x\in {\mathscr {J}}_n\). Hence, \({\mathscr {I}}\subseteq {\mathscr {J}}_n\) and \({\mathscr {J}}_n\in {\mathfrak {F}}_{{\mathscr {I}}}\), which is a contradiction. We conclude that \({\mathscr {J}}\notin {\mathfrak {F}}_{{\mathscr {I}}}\). \(\square \)
We now consider templates that are infinite descending chains. For this we consider the ordered infinite set \(I=\{1<2<\cdots \}\) and a collection of principal thick tensor ideals \({\mathscr {I}}_i\), \(i\geqslant 1\). We consider a template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) indexed by \(I^\mathrm{op}\), where each \({\mathfrak {F}}_i\) is given by

and \({\mathscr {A}}_i\) is any thick tensor ideal. From Proposition 5.6, we know that each \({\mathfrak {F}}_i\) is a monoidal semifilter and any non-empty increasing chain of ideals in the complement  of \({\mathfrak {F}}_{i}\) has an upper bound in
of \({\mathfrak {F}}_{i}\) has an upper bound in  . For any positive integers \(m\leqslant n\), we let \(T_n^m=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{n\geqslant i\geqslant m}\) be the template obtained by truncating T. Then, the truncated template \(T^m_n\) is indexed by the opposite of the finite ordered set \(\{m<m+1<\cdots <n\}\). We now set \({\mathscr {B}}_n^n={\mathscr {A}}_n\) and define \({\mathscr {B}}_n^m\) by inductively setting
. For any positive integers \(m\leqslant n\), we let \(T_n^m=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{n\geqslant i\geqslant m}\) be the template obtained by truncating T. Then, the truncated template \(T^m_n\) is indexed by the opposite of the finite ordered set \(\{m<m+1<\cdots <n\}\). We now set \({\mathscr {B}}_n^n={\mathscr {A}}_n\) and define \({\mathscr {B}}_n^m\) by inductively setting

For any given m, it is clear that we have an increasing chain \({\mathscr {B}}^m_m\subseteq {\mathscr {B}}^m_{m+1}\subseteq {\mathscr {B}}^m_{m+2} \subseteq \cdots \) and we set  . We now let
. We now let  be the infinite decreasing chain template indexed by the opposite \(I^\mathrm{op}\) of the ordered infinite set \(I=\{1<2<\cdots \}\).
be the infinite decreasing chain template indexed by the opposite \(I^\mathrm{op}\) of the ordered infinite set \(I=\{1<2<\cdots \}\).
Lemma 5.7
In the notation above, for any \(m\geqslant 1\), we have  .
.
Proof
By assumption, each  for the principal ideal \({\mathscr {I}}_i\). In particular, suppose that \({\mathscr {I}}_m\) is generated by \(x_m\) and consider some object
for the principal ideal \({\mathscr {I}}_i\). In particular, suppose that \({\mathscr {I}}_m\) is generated by \(x_m\) and consider some object  . Then, there exists an ideal \({\mathscr {J}}\in {\mathfrak {F}}_m\) such that
. Then, there exists an ideal \({\mathscr {J}}\in {\mathfrak {F}}_m\) such that  . Since \({\mathscr {J}}\supseteq {\mathscr {I}}_m\), it follows that
. Since \({\mathscr {J}}\supseteq {\mathscr {I}}_m\), it follows that  . Accordingly, there exists N large enough so that
. Accordingly, there exists N large enough so that  . In other words,
. In other words,  and we see that
and we see that  . Therefore, we have
. Therefore, we have  . On the other hand, it is clear that
. On the other hand, it is clear that  and hence
and hence  . Combining with (37), we have
. Combining with (37), we have

As before, we must have  and hence
and hence  . The result now follows from Proposition 4.8. \(\square \)
. The result now follows from Proposition 4.8. \(\square \)
Proposition 5.8
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category such that all thick tensor ideals are also radical. Let \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\) be a template as in (36) indexed by the opposite \(I^\mathrm{op}\) of the ordered infinite set \(I=\{1<2<\cdots \}\) and let  be as defined above. Then:
be as defined above. Then:
-
(a)
A chain \(\cdots \subseteq {\mathscr {P}}_2\subseteq {\mathscr {P}}_1\) of thick prime ideals is a realization of the template T if and only if it is also a realization of the template
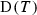 .
. -
(b)
The template T has a realization if and only if \({\mathscr {B}}^1_\infty \notin {\mathfrak {F}}_1\).
-
(c)
The template T is realizable if and only if each of the truncated templates \(T^m_n\) is realizable for \(1\leqslant m\leqslant n\).
Proof
(a) The “if part” is clear because each \({\mathscr {B}}^m_\infty \supseteq {\mathscr {A}}_m\). For the “only if” part, consider a realization \(\dots \subseteq {\mathscr {P}}_2\subseteq {\mathscr {P}}_1\) of the template \(T=\{({\mathscr {A}}_i,{\mathfrak {F}}_i)\}_{i\in I^\mathrm{op}}\). Then, for any \(1\leqslant m\leqslant n\),  must be a realization of the truncated template \(T^m_n\). Looking at the expression for \({\mathscr {B}}^m_n\) in (37), it follows from Proposition 4.9 that \({\mathscr {P}}_m\) realizes the pair \(({\mathscr {B}}_n^m,{\mathfrak {F}}_m)\). Hence, for each \(n\geqslant m\), we have \({\mathscr {P}}_m\supseteq {\mathscr {B}}_n^m\) and \({\mathscr {P}}_m\notin {\mathfrak {F}}_m\). It follows that
must be a realization of the truncated template \(T^m_n\). Looking at the expression for \({\mathscr {B}}^m_n\) in (37), it follows from Proposition 4.9 that \({\mathscr {P}}_m\) realizes the pair \(({\mathscr {B}}_n^m,{\mathfrak {F}}_m)\). Hence, for each \(n\geqslant m\), we have \({\mathscr {P}}_m\supseteq {\mathscr {B}}_n^m\) and \({\mathscr {P}}_m\notin {\mathfrak {F}}_m\). It follows that

whence \({\mathscr {P}}_m\) realizes the pair \(({\mathscr {B}}_\infty ^m,{\mathfrak {F}}_m)\).
(b) If T is realizable, it follows from part (a) that so is  and hence in particular \({\mathscr {B}}_\infty ^1\notin {\mathfrak {F}}_1\). Conversely, if \({\mathscr {B}}_\infty ^1\notin {\mathfrak {F}}_1\), we can choose a prime ideal \({\mathscr {P}}_1\) realizing \(({\mathscr {B}}_\infty ^1,{\mathfrak {F}}_1)\). From Lemma 5.7, we know that
and hence in particular \({\mathscr {B}}_\infty ^1\notin {\mathfrak {F}}_1\). Conversely, if \({\mathscr {B}}_\infty ^1\notin {\mathfrak {F}}_1\), we can choose a prime ideal \({\mathscr {P}}_1\) realizing \(({\mathscr {B}}_\infty ^1,{\mathfrak {F}}_1)\). From Lemma 5.7, we know that  for each \(m\geqslant 1\). It follows that we can choose a prime ideal \({\mathscr {P}}_2\subseteq {\mathscr {P}}_1\) realizing \(({\mathscr {B}}_\infty ^2,{\mathfrak {F}}_2)\) and so on to obtain a realization of
for each \(m\geqslant 1\). It follows that we can choose a prime ideal \({\mathscr {P}}_2\subseteq {\mathscr {P}}_1\) realizing \(({\mathscr {B}}_\infty ^2,{\mathfrak {F}}_2)\) and so on to obtain a realization of  . This gives a realization of T.
. This gives a realization of T.
(c) The “only if” part is obvious. For the “if part”, we suppose that each truncated template \(T^m_n\) is realizable for \(1\leqslant m\leqslant n\). In particular, the truncated template \(T^1_n\) is realizable for each \(n\geqslant 1\). Hence, \({\mathscr {B}}_n^1\notin {\mathfrak {F}}_1\) for each \(n\geqslant 1\). We know that  . From Proposition 5.6 (b), it follows that the increasing chain \({\mathscr {B}}_1^1\subseteq {\mathscr {B}}_2^1\subseteq {\mathscr {B}}_3^1\subseteq \cdots \) of ideals in
. From Proposition 5.6 (b), it follows that the increasing chain \({\mathscr {B}}_1^1\subseteq {\mathscr {B}}_2^1\subseteq {\mathscr {B}}_3^1\subseteq \cdots \) of ideals in  must have some upper bound in
must have some upper bound in  , say \({\mathscr {B}}\). But then, \({\mathscr {B}}\supseteq {\mathscr {B}}^1_\infty \). Since \({\mathfrak {F}}_1\) is a semifilter and \({\mathscr {B}}\notin {\mathfrak {F}}_1\), we must have \({\mathscr {B}}_\infty ^1\notin {\mathfrak {F}}_1\). From part (b), it now follows that the template T is realizable. \(\square \)
, say \({\mathscr {B}}\). But then, \({\mathscr {B}}\supseteq {\mathscr {B}}^1_\infty \). Since \({\mathfrak {F}}_1\) is a semifilter and \({\mathscr {B}}\notin {\mathfrak {F}}_1\), we must have \({\mathscr {B}}_\infty ^1\notin {\mathfrak {F}}_1\). From part (b), it now follows that the template T is realizable. \(\square \)
Finally, we will translate our reasoning in terms of irreducible closed subspaces of the inverse topology on  . We continue to assume that all thick tensor ideals in \({\mathscr {C}}\) are radical. As in Sect. 3, we denote by
. We continue to assume that all thick tensor ideals in \({\mathscr {C}}\) are radical. As in Sect. 3, we denote by  the spectral space
the spectral space  equipped with the inverse topology. As such, following [4, Theorem 14], for every thick tensor ideal
equipped with the inverse topology. As such, following [4, Theorem 14], for every thick tensor ideal  , there is a closed subspace
, there is a closed subspace

in inverse topology giving a one-to-one order reversing correspondence between thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) and closed subspaces of  . From (38), it is clear that for ideals \({\mathscr {I}}\),
. From (38), it is clear that for ideals \({\mathscr {I}}\),  , we must have
, we must have  and
and  for any family \(\{{\mathscr {I}}_i\}_{i\in I}\) of thick tensor ideals.
for any family \(\{{\mathscr {I}}_i\}_{i\in I}\) of thick tensor ideals.
Proposition 5.9
Let \(({\mathscr {C}},\otimes ,1)\) be a tensor triangulated category such that all thick tensor ideals are radical and let  be a basis of closed subspaces for
be a basis of closed subspaces for  . Let \({\mathfrak {F}}^*\) be a family of closed subspaces of
. Let \({\mathfrak {F}}^*\) be a family of closed subspaces of  having the following properties:
having the following properties:
-
(a)
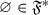 .
. -
(b)
For any closed
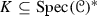 and any \(i,j\in I\) such that
and any \(i,j\in I\) such that 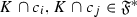 , we must have
, we must have 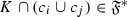 .
.
Then, if  is a closed subspace that is minimal with respect to not being in
is a closed subspace that is minimal with respect to not being in  , \(K_0\) is an irreducible closed subspace of
, \(K_0\) is an irreducible closed subspace of  .
.
Proof
Using the correspondence stated above, we must have ideals  , \(i\in I\), such that
, \(i\in I\), such that  . We now consider the family
. We now consider the family  of thick tensor ideals. Since
of thick tensor ideals. Since  , we have \({\mathscr {C}}\in {\mathfrak {F}}\). Further, condition (b) above corresponds to the following condition on \({\mathfrak {F}}\): given
, we have \({\mathscr {C}}\in {\mathfrak {F}}\). Further, condition (b) above corresponds to the following condition on \({\mathfrak {F}}\): given  and \(i,j\in I\)
and \(i,j\in I\)

Then, a closed subspace  that is minimal with respect to not being in \({\mathfrak {F}}^*\) corresponds to a thick tensor ideal \({\mathscr {I}}_0\) that is maximal with respect to not being in \({\mathfrak {F}}\). Now, suppose that there exist \({\mathscr {J}}\),
that is minimal with respect to not being in \({\mathfrak {F}}^*\) corresponds to a thick tensor ideal \({\mathscr {I}}_0\) that is maximal with respect to not being in \({\mathfrak {F}}\). Now, suppose that there exist \({\mathscr {J}}\),  such that
such that  but \( {\mathscr {I}}_0\not \supseteq {\mathscr {J}}\) and \({\mathscr {I}}_0\not \supseteq {\mathscr {K}}\). Since
but \( {\mathscr {I}}_0\not \supseteq {\mathscr {J}}\) and \({\mathscr {I}}_0\not \supseteq {\mathscr {K}}\). Since  is a basis for closed subspaces of
is a basis for closed subspaces of  , there exist \(G_{{\mathscr {J}}},G_{{\mathscr {K}}}\subseteq I\) such that
, there exist \(G_{{\mathscr {J}}},G_{{\mathscr {K}}}\subseteq I\) such that  and
and  . Then, we can choose
. Then, we can choose  and
and  such that
such that  and \({\mathscr {I}}_0\not \supseteq {\mathscr {I}}_{k'}\). Since \({\mathscr {I}}_0\) is maximal with respect to not being in \({\mathfrak {F}}\), we have
and \({\mathscr {I}}_0\not \supseteq {\mathscr {I}}_{k'}\). Since \({\mathscr {I}}_0\) is maximal with respect to not being in \({\mathfrak {F}}\), we have  and
and  . From (39), it follows that
. From (39), it follows that  . As in (17), we now have
. As in (17), we now have  . On the other hand, we have
. On the other hand, we have  and hence
and hence  , which is a contradiction. Hence, \({\mathscr {I}}_0\) is prime and
, which is a contradiction. Hence, \({\mathscr {I}}_0\) is prime and  is an irreducible closed subspace of
is an irreducible closed subspace of  . \(\square \)
. \(\square \)
Clearly, any family \({\mathfrak {F}}^*\) of closed subspaces of  containing \(\varnothing \) and closed under finite unions satisfies the conditions in Proposition 5.9. In that case, the corresponding family
containing \(\varnothing \) and closed under finite unions satisfies the conditions in Proposition 5.9. In that case, the corresponding family  of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) is simply a monoidal family. We will conclude by showing how to construct a family \({\mathfrak {F}}^*\) that is not closed under finite unions but still satisfies the conditions in Proposition 5.9. This will be done with the help of Ako families of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\).
of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\) is simply a monoidal family. We will conclude by showing how to construct a family \({\mathfrak {F}}^*\) that is not closed under finite unions but still satisfies the conditions in Proposition 5.9. This will be done with the help of Ako families of thick tensor ideals in \(({\mathscr {C}},\otimes ,1)\).
We consider the basis  of closed sets for
of closed sets for  . Then, any closed subspace
. Then, any closed subspace  can be expressed as the intersection
can be expressed as the intersection  . Suppose that \(0\ne x\in {\mathscr {C}}\) is a zero-divisor, i.e.,
. Suppose that \(0\ne x\in {\mathscr {C}}\) is a zero-divisor, i.e.,  . Further, suppose that we can choose a non-principal thick tensor ideal
. Further, suppose that we can choose a non-principal thick tensor ideal  . Hence,
. Hence,  . We now set
. We now set

and consider the corresponding family  of closed subspaces of
of closed subspaces of  . Clearly, since
. Clearly, since  , the family \({\mathfrak {F}}\) is not monoidal and hence the family \({\mathfrak {F}}^*\) of closed subspaces of
, the family \({\mathfrak {F}}\) is not monoidal and hence the family \({\mathfrak {F}}^*\) of closed subspaces of  is not closed under finite unions. Since \({\mathscr {C}}\in {\mathfrak {F}}\), we know that
is not closed under finite unions. Since \({\mathscr {C}}\in {\mathfrak {F}}\), we know that  . We claim that \({\mathfrak {F}}^*\) also satisfies condition (b) in Proposition 5.9. Otherwise, there exist basis elements c(a), c(b) with \(a,b\in {\mathscr {C}}\) and some closed subspace
. We claim that \({\mathfrak {F}}^*\) also satisfies condition (b) in Proposition 5.9. Otherwise, there exist basis elements c(a), c(b) with \(a,b\in {\mathscr {C}}\) and some closed subspace  such that \(K\cap c(a) \in {\mathfrak {F}}^*\) and \(K\cap c(b)\in {\mathfrak {F}}^*\) but
such that \(K\cap c(a) \in {\mathfrak {F}}^*\) and \(K\cap c(b)\in {\mathfrak {F}}^*\) but  . Since K is closed in
. Since K is closed in  , we can find a thick tensor ideal \({\mathscr {L}}\) such that \(K=c({\mathscr {L}})\). Then, we see that \(({\mathscr {L}},a)\in {\mathfrak {F}}\) and \(({\mathscr {L}},b)\in {\mathfrak {F}}\), but
, we can find a thick tensor ideal \({\mathscr {L}}\) such that \(K=c({\mathscr {L}})\). Then, we see that \(({\mathscr {L}},a)\in {\mathfrak {F}}\) and \(({\mathscr {L}},b)\in {\mathfrak {F}}\), but  . From the expression for \({\mathfrak {F}}\) in (40), this is possible only if one of the two ideals \(({\mathscr {L}},a)\) and \(({\mathscr {L}},b)\) is equal to (x) and the other is equal to \({\mathscr {J}}\). Accordingly, we have
. From the expression for \({\mathfrak {F}}\) in (40), this is possible only if one of the two ideals \(({\mathscr {L}},a)\) and \(({\mathscr {L}},b)\) is equal to (x) and the other is equal to \({\mathscr {J}}\). Accordingly, we have

and hence \({\mathscr {L}}=0\). But then, either \( {\mathscr {J}}=({\mathscr {L}}, a)=(a)\) or \({\mathscr {J}}=({\mathscr {L}},b)=(b)\) and \({\mathscr {J}}\) is principal, which is a contradiction.
References
Balmer, P.: The spectrum of prime ideals in tensor triangulated categories. J. Reine Angew. Math. 588, 149–168 (2005)
Balmer, P.: Supports and filtrations in algebraic geometry and modular representation theory. Amer. J. Math. 129(5), 1227–1250 (2007)
Balmer, P.: Spectra, spectra, spectra—tensor triangular spectra versus Zariski spectra of endomorphism rings. Algebr. Geom. Topol. 10(3), 1521–1563 (2010)
Balmer, P.: Tensor triangular geometry. In: Bhatia, R. (ed.) Proceedings of the International Congress of Mathematicians. Vol. II, pp. 85–112, Hindustan Book Agency, New Delhi (2010)
Balmer, P.: Separability and triangulated categories. Adv. Math. 226(5), 4352–4372 (2011)
Balmer, P.: Tensor triangular Chow groups. J. Geom. Phys. 72, 3–6 (2013)
Balmer, P.: Splitting tower and degree of tt-rings. Algebra Number Theory 8(3), 767–779 (2014)
Balmer, P.: Separable extensions in tensor-triangular geometry and generalized Quillen stratification, Ann. Sci. École Norm. Supér. (4) (to appear)
Balmer, P., Favi, G.: Gluing techniques in triangular geometry. Q. J. Math. 58(4), 415–441 (2007)
Balmer, P., Favi, G.: Generalized tensor idempotents and the telescope conjecture. Proc. London Math. Soc. (3) 102(6), 1161–1185 (2011)
Benson, D.J., Carlson, J.F., Rickard, J.: Thick subcategories of the stable module category. Fund. Math. 153, 59–80 (1997)
Benson, D.J., Iyengar, S.B., Krause, H.: Local cohomology and support for triangulated categories. Ann. Sci. École. Norm. Supér. (4) 41(4), 573–619 (2008)
Benson, D.J., Iyengar, S.B., Krause, H.: Stratifying triangulated categories. J. Topology 4(3), 641–666 (2011)
Benson, D., Iyengar, S.B., Krause, H.: Colocalizing subcategories and cosupport. J. Reine Angew. Math. 673, 161–207 (2012)
Bergman, G.M.: Arrays of prime ideals in commutative rings. J. Algebra 261(2), 389–410 (2003)
Dell’Ambrogio, I., Stevenson, G.: Even more spectra: tensor triangular comparison maps via graded commutative 2-rings. Appl. Categ. Structures 22(1), 169–210 (2014)
Devinatz, E.S., Hopkins, M.J., Smith, J.H.: Nilpotence and stable homotopy theory I. Ann. Math. (2) 128(2), 207–241 (1988)
Finocchiaro, C.A., Fontana, M., Loper, K.A.: Some closure operations in Zariski–Riemann spaces of valuation domains: a survey. In: Fontana, M., Frisch, S., Glaz, S. (eds.) Commutative Algebra, pp. 153–173. Springer, New York (2014)
Friedlander, E.M., Pevtsova, J.: \(\Pi \)-supports for modules for finite group schemes. Duke Math. J. 139(2), 317–368 (2007)
Goodearl, K.R., Warfield Jr., R.B.: An Introduction to Noncommutative Noetherian Rings. London Mathematical Society Student Texts, vol. 61, 2nd edn. Cambridge University Press, Cambridge (2004)
Hochster, M.: Prime ideal structure in commutative rings. Trans. Amer. Math. Soc. 142, 43–60 (1969)
Hovey, M., Palmieri, J.H., Strickland, N.P.: Axiomatic Stable Homotopy Theory. Memoirs of the American Mathematical Society, vol. 128(610). American Mathematical Society, Providence (1997)
Klein, S.: Chow groups of tensor triangulated categories. J. Pure Appl. Algebra 220(4), 1343–1381 (2016)
Klein, S.: Intersection products for tensor triangular Chow groups. J. Algebra 449, 497–538 (2016)
Lam, T.Y., Reyes, M.: A prime ideal principle in commutative algebra. J. Algebra 319(7), 3006–3027 (2008)
Lam, T.Y., Reyes, M.: Oka and Ako ideal families in commutative rings. In: Dung, N.V., Guerriero, F., Hammoudi, L., Kanwar, P. (eds.) Rings, Modules and Representations. Contemporary Mathematics, vol. 480, pp. 263–288, American Mathematical Society, Providence, RI (2009)
May, J.P.: The additivity of traces in triangulated categories. Adv. Math. 163, 34–73 (2001)
Peter, T.J.: Prime ideals of mixed Artin–Tate motives. J. \(K\)-Theory 11(2), 331–349 (2013)
Reyes, M.L.: A one-sided prime ideal principle for noncommutative rings. J. Algebra Appl. 9(6), 877–919 (2010)
Reyes, M.L.: Noncommutative generalizations of theorems of Cohen and Kaplansky. Algebr. Represent. Theory 15(5), 933–975 (2012)
Sanders, B.: Higher comparison maps for the spectrum of a tensor triangulated category. Adv. Math. 247, 71–102 (2013)
Schwartz, N., Tressl, M.: Elementary properties of minimal and maximal points in Zariski spectra. J. Algebra 323, 698–728 (2010)
Sharma, P.K.: A note on lifting of chains of prime ideals. J. Pure Appl. Algebra 192(1–3), 287–291 (2004)
Stevenson, G.: Support theory via actions of tensor triangulated categories. J. Reine Angew. Math. 681, 219–254 (2013)
Stevenson, G.: Subcategories of singularity categories via tensor actions. Compositio Math. 150(2), 229–272 (2014)
Thomason, R.W.: The classification of triangulated subcategories. Compositio Math. 105, 1–27 (1997)
Verdier, J.-L. Des Catégories Dérivées des Catégories Abéliennes. Astérisque 239 (1996)
Xu, F.: Spectra of tensor triangulated categories over category algebras. Arch. Math. (Basel) 103(3), 235–253 (2014)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Banerjee, A. Realizations of pairs and Oka families in tensor triangulated categories. European Journal of Mathematics 2, 760–797 (2016). https://doi.org/10.1007/s40879-016-0108-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-016-0108-2



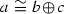 , both direct summands b and c lie in
, both direct summands b and c lie in 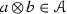 .
.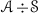 if and only if it contains a prime ideal realizing
if and only if it contains a prime ideal realizing 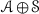 .
.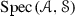 is finite. Then, a prime ideal
is finite. Then, a prime ideal 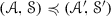 , i.e., any prime ideal realizing
, i.e., any prime ideal realizing 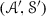 contains a prime ideal realizing
contains a prime ideal realizing 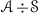 is contained in the radical of
is contained in the radical of 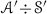 , i.e.,
, i.e.,  .
.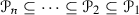 is a realization of the template
is a realization of the template 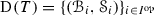 .
.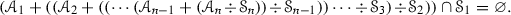
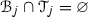 .
.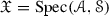 for some thick tensor ideal
for some thick tensor ideal 
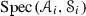 is a finite set.
is a finite set.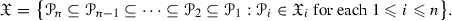
 is a constructible subset of
is a constructible subset of  .
. is pro-constructible, i.e., it may be expressed as an intersection of a family of constructible subsets of
is pro-constructible, i.e., it may be expressed as an intersection of a family of constructible subsets of  .
.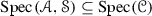 is a spectral space, i.e.,
is a spectral space, i.e., 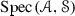 is quasi-compact, quasi-separated, has a basis of quasi-compact open subsets and every non-empty irreducible closed subset has a unique generic point.
is quasi-compact, quasi-separated, has a basis of quasi-compact open subsets and every non-empty irreducible closed subset has a unique generic point.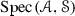 is a constructible subset of
is a constructible subset of 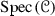 . Further, such subsets form a basis for the constructible topology on
. Further, such subsets form a basis for the constructible topology on 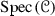 .
.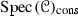 may be expressed as a union
may be expressed as a union 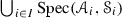 with each
with each 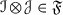 .
. for some object
for some object 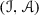 ,
, 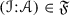 for some ideal
for some ideal 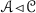 ) implies that
) implies that 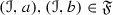 for objects
for objects 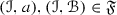 for some object
for some object 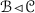 ) implies that
) implies that 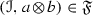 (resp.
(resp. 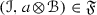 ).
). , we must have
, we must have  , we must have
, we must have 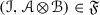 .
.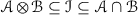 , we must have
, we must have 

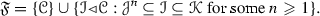
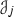 is prime.
is prime.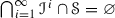 is also prime.
is also prime.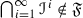 is also prime.
is also prime.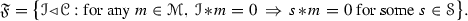
 denote the collection of all thick tensor ideals of
denote the collection of all thick tensor ideals of  has an upper bound in
has an upper bound in 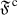 .
.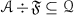 .
. is finite. Then, a prime ideal
is finite. Then, a prime ideal 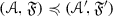 , i.e., any prime ideal that realizes
, i.e., any prime ideal that realizes 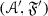 contains a prime ideal that realizes
contains a prime ideal that realizes 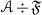 is contained in the radical of
is contained in the radical of 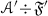 , i.e.,
, i.e.,  .
. is a realization of the template
is a realization of the template 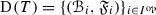 .
.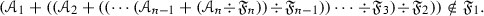
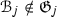 .
.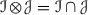 .
.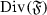 defined by
defined by 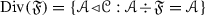
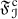 of
of 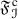 .
.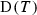 .
.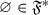 .
.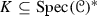 and any
and any 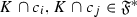 , we must have
, we must have 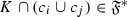 .
.