Abstract
In this paper we provide a general tool to prove the consistency of  with various combinatorial properties at \(\lambda \) typical at settings with \(2^\lambda >\lambda ^+\), that does not need a profound knowledge of the forcing notions involved. Examples of such properties are the first failure of GCH, a very good scale and the negation of the approachability property, or the tree property at \(\lambda ^+\) and \(\lambda ^{++}\).
with various combinatorial properties at \(\lambda \) typical at settings with \(2^\lambda >\lambda ^+\), that does not need a profound knowledge of the forcing notions involved. Examples of such properties are the first failure of GCH, a very good scale and the negation of the approachability property, or the tree property at \(\lambda ^+\) and \(\lambda ^{++}\).
Similar content being viewed by others
1 Introduction
While Cantor gave us the means to conceive infinite cardinals, it is clear that to use them in a fruitful way a thorough study of their structure is needed, and this is the aim of the field usually called “infinite combinatorics”. The key turning point for this study, as old as Set Theory, was the introduction of forcing [1]: it was clear then that much of the structural properties are independent from ZFC, therefore shifting the focus of the study from what is the structure of infinite cardinals to what it could be. In the few years after Cohen’s seminal results, the analysis of regular cardinals was pretty much complete, with the definition of many forcing notions that can change effortlessly the combinatorial properties not only of a single cardinal, but, using a method introduced by Easton [6], of all regular cardinals at once.
Changing combinatorial properties of singular cardinals, especially those of cofinality \(\omega \), proved to be much harder than in the regular cardinal case. As a result, the research on such properties is rich and varied, it provided and still provides many challenges. Some situations are even impossible: Silver [20] proved that SCH cannot fail first at a singular cardinal of uncountable cofinality, and Solovay [21] proved that above a strongly compact cardinal SCH must hold. The typical way to make SCH fail at a singular cardinal (i.e. blowing up the cardinality of its powerset) is to start with \(\kappa \) measurable, blowing up its power and then adding an \(\omega \)-sequence cofinal to \(\kappa \) with the Prikry forcing, to make it of cofinality \(\omega \). But \(2^\kappa >\kappa ^+\) permits a multitude of properties to hold, and it is an ongoing research to find more and more sophisticated variations of the Prikry forcing that permit different combinations of specific combinatorics on a singular cardinal.
While this research heavily involves large cardinals, their role has almost always been giving consistency strength to a certain scenery, but they rarely appear directly with the desired combinatorial property, for the simple reason that the great majority of large cardinals are regular cardinals, therefore unrelated to the problem. Moreover some large cardinals simply do not accept a lot of variety on the structure of singular cardinals, as noted above. Going up the hierarchy, however, one can find an exception. The strongest large cardinal axioms, called rank-into-rank axioms, do involve a singular cardinal of countable cofinality, and it is very natural to question the position of them in this field: as they imply all known large cardinal hypotheses, knowing their structure is crucial in the large cardinal field, as it trickles down to all the hierarchy.
Woodin [22] introduced what he called “Generic Absoluteness for I0”, and this proved to be key for this study: starting with I0, adding a Prikry sequence to its critical point \(\kappa \), an action that we noted typical for proving consistency results for singular cardinals, adds in fact I1. In [4] this was exploited to prove that it was possible to have  and \(2^\lambda >\lambda ^+\) at the same time, in the same way it was proved just with a measurable.
and \(2^\lambda >\lambda ^+\) at the same time, in the same way it was proved just with a measurable.
If the proof of \(2^\lambda >\lambda ^+\) uses the Prikry forcing, could we use the sophisticated variations of the Prikry forcing that appear in literature to prove the consistency of different combinations of specific combinatorics on a singular cardinal with I1? In this paper, we extend such theorem, describing a general procedure to be applied to many of the refined Prikry forcing notions, therefore automatically transferring the already known results about the combinatorics of singular cardinal of countable cofinality to cardinals that moreover satisfy very large cardinal properties, providing thus a number of new results and a tool that any researcher can use without going into the original details of the forcing notions involved.
In Sect. 2, all the preliminary facts are collected. In Sect. 3, the general procedure is described: the notion of \(\kappa \)-geometric forcing is introduced, and this is the key notion that will permit the proof to work; the procedure is tested with the Prikry forcing and tree Prikry forcing. In Sect. 4, the procedure is applied to the extender-based Prikry forcing, to provide  and the first failure of GCH at \(\lambda \) (this answers a question in [4]). In Sect. 5, the procedure is applied to two different flavors of the diagonal supercompact Prikry forcing, to achieve results on pcf combinatorics and the tree property. In Sect. 6, we see another application to the tree property. In Sect. 7, we note some possible directions for future research on the subject.
and the first failure of GCH at \(\lambda \) (this answers a question in [4]). In Sect. 5, the procedure is applied to two different flavors of the diagonal supercompact Prikry forcing, to achieve results on pcf combinatorics and the tree property. In Sect. 6, we see another application to the tree property. In Sect. 7, we note some possible directions for future research on the subject.
2 Preliminaries
To avoid confusion or misunderstandings, all notation and standard basic results are collected here.
Elementary embeddings have a key role in the definitions of all large cardinals from measurable to above. If M and N are sets or classes,  denotes that j is an elementary embedding from M to N. We write the case in which the elementary embedding is the identity, i.e., M is an elementary submodel of N, simply as
denotes that j is an elementary embedding from M to N. We write the case in which the elementary embedding is the identity, i.e., M is an elementary submodel of N, simply as  , while when j is indicated we always suppose that it is not the identity.
, while when j is indicated we always suppose that it is not the identity.
If  and either
and either  or \(N\subseteq M\) then it moves at least one ordinal. The critical point,
or \(N\subseteq M\) then it moves at least one ordinal. The critical point,  , is the least ordinal moved by j. If
, is the least ordinal moved by j. If  and \(N\subseteq M\), we define \(j^n\) as the composition of n copies of j, i.e., \(j^1=j\) and
and \(N\subseteq M\), we define \(j^n\) as the composition of n copies of j, i.e., \(j^1=j\) and  . Let j be an elementary embedding and
. Let j be an elementary embedding and  . Define \(\kappa _0=\kappa \) and \(\kappa _{n+1}=j(\kappa _n)\). Then
. Define \(\kappa _0=\kappa \) and \(\kappa _{n+1}=j(\kappa _n)\). Then  is the critical sequence of j.
is the critical sequence of j.
Kunen [11] proved under AC that if \(M=N=V_\eta \) for some ordinal \(\eta \leqslant \mathrm{Ord}\), and \(\lambda \) is the supremum of the critical sequence, then \(\eta \) cannot be bigger than \(\lambda +1\) (and of course cannot be smaller than \(\lambda \)). This at the time was considered as a stop to the large cardinal study, since an embedding  would have been the largest possible cardinal, but Kunen’s result leaves room for a new breed of large cardinal hypotheses, sometimes referred to in the literature as rank-into-rank hypotheses:
would have been the largest possible cardinal, but Kunen’s result leaves room for a new breed of large cardinal hypotheses, sometimes referred to in the literature as rank-into-rank hypotheses:
-
(I3)
For some \(\lambda \) there exists
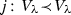 .
. -
(I2)
For some \(\lambda \) such that \(V_\lambda \subseteq M\) and \(\lambda \) is the supremum of the critical sequence there exists
 .
. -
(I1)
For some \(\lambda \) there exists
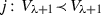 .
.
The consistency order of the above hypotheses is reversed with respect to their numbering: I1 is strictly stronger than I2, which in turn is strictly stronger than I3 (see [13]). All of these hypotheses are strictly stronger than all of the large cardinal hypotheses outside the rank-into-rank umbrella (see [10, 24.9] for n-huge cardinals, or [2] for the Wholeness Axiom). I3 enjoyed a particularly rich literature, as it has an interesting algebraic content [3].
Note that if j witnesses a rank-into-rank hypothesis, then \(\lambda \) is uniquely determined by j, so in the following \(\lambda \) always denotes the first nontrivial fixed point of the embedding j under consideration. We write  for
for  .
.
Given  with the critical sequence
with the critical sequence  , let \(A\subseteq V_\lambda \). Then we can define \(j^+(A)=\bigcup _{n\in \omega }j(A\cap V_{\kappa _n})\). Such \(j^+:V_{\lambda +1}\rightarrow V_{\lambda +1}\) is a \(\Sigma _0\) elementary embedding (see for example [12, Lemma 1]). The key point is that \(j^+\) is, in \(V_{\lambda +1}\), a definable class (definable with
, let \(A\subseteq V_\lambda \). Then we can define \(j^+(A)=\bigcup _{n\in \omega }j(A\cap V_{\kappa _n})\). Such \(j^+:V_{\lambda +1}\rightarrow V_{\lambda +1}\) is a \(\Sigma _0\) elementary embedding (see for example [12, Lemma 1]). The key point is that \(j^+\) is, in \(V_{\lambda +1}\), a definable class (definable with  as a parameter). Then one can ask whether \(j^+\) is stronger, i.e., a \(\Sigma _n\) elementary embedding, with \(n>0\). Laver proved in [13] that this is strictly stronger than
as a parameter). Then one can ask whether \(j^+\) is stronger, i.e., a \(\Sigma _n\) elementary embedding, with \(n>0\). Laver proved in [13] that this is strictly stronger than  , and yet still expressible in \(V_{\lambda +1}\). Now, \(j^+\) is a full elementary embedding (i.e., it witnesses
, and yet still expressible in \(V_{\lambda +1}\). Now, \(j^+\) is a full elementary embedding (i.e., it witnesses  if and only if it is \(\Sigma _n\) for every n). Therefore, suppose that
if and only if it is \(\Sigma _n\) for every n). Therefore, suppose that  . Then
. Then  and \(V_{\lambda +1}\) “knows” that j, as a class defined with parameter
and \(V_{\lambda +1}\) “knows” that j, as a class defined with parameter  , is an elementary embedding.
, is an elementary embedding.
Remark 2.1
Suppose that \(j:V_{\lambda +1}\rightarrow V_{\lambda +1}\). Then there are \(\varphi _n(x)\) formulas such that for any \(n\in \omega \),  iff j is an elementary embedding.
iff j is an elementary embedding.
This implies that if  , then
, then  . Note that this is peculiar to I1, as \(V_{\lambda +1}\) is not a model for ZFC. \(V_\lambda \) cannot satisfy
. Note that this is peculiar to I1, as \(V_{\lambda +1}\) is not a model for ZFC. \(V_\lambda \) cannot satisfy  , as \(V_\lambda \) is a model for ZFC and that goes against Kunen’s Theorem.
, as \(V_\lambda \) is a model for ZFC and that goes against Kunen’s Theorem.
In the early 1980’s Woodin proposed an axiom even stronger than all the previous ones:
-
(I0)
For some \(\lambda \) there exists
 with
with  .
.
Again,  expresses what is expected.
expresses what is expected.
Note that if \(\lambda \) witnesses I0, then  , because otherwise
, because otherwise  , and we would contradict the proof of Kunen’s Theorem [11], which shows that one cannot have
, and we would contradict the proof of Kunen’s Theorem [11], which shows that one cannot have  with critical point less than \(\lambda \) and a well-order of \(V_{\lambda +1}\) in V. The fact that I0 is strictly stronger than I1 was proved by Laver [13].
with critical point less than \(\lambda \) and a well-order of \(V_{\lambda +1}\) in V. The fact that I0 is strictly stronger than I1 was proved by Laver [13].
I0 is probably the most interesting of the rank-into-rank axioms: it is the only very large cardinal that induces a structure on an inner model, therefore creating a new field of research and new tools, and moreover the structure is reminiscent of the one induced by the Axiom of Determinacy, for reasons that are still not completely understood [22].
An embedding that witnesses I0 has an ultrapower structure.
Lemma 2.2
Let  be such that
be such that  . Let
. Let

Then U is an \(L(V_{\lambda +1})\)-ultrafilter such that  is well-founded. By condensation, the collapse of
is well-founded. By condensation, the collapse of  is \(L(V_{\lambda +1})\), and
is \(L(V_{\lambda +1})\), and  , the inverse of the collapse, is an elementary embedding. Moreover, there is an elementary embedding
, the inverse of the collapse, is an elementary embedding. Moreover, there is an elementary embedding  with
with  such that
such that  .
.
We can use the ultrapower structure to define iterability for j.
Definition 2.3
Let  with
with  be an elementary embedding, and suppose j is generated by \(U=U_j\). Define
be an elementary embedding, and suppose j is generated by \(U=U_j\). Define

and then define \(j_2\) as the map associated to j(U). Define the successive iterates in the usual way: let \(\alpha \) be an ordinal. Then
-
if \(\alpha =\beta +1\), \(M_\beta \) is well-founded and
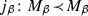 is the ultrapower via W, then
is the ultrapower via W, then 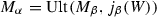 and \(j_\alpha =j_\beta (j_\beta )\);
and \(j_\alpha =j_\beta (j_\beta )\); -
if \(\alpha \) is a limit, let \((M_\alpha , j_\alpha )\) be the direct limit of \((M_\beta , j_\beta )\) with \(\beta <\alpha \).
We say that j is iterable, if for every \(\alpha \in {{\mathrm{Ord}}}\), \(M_\alpha \) is well-founded and  . In this case, we call \(j_{\alpha ,\beta }\) the natural embeddings between \(M_\alpha \) and \(M_\beta \).
. In this case, we call \(j_{\alpha ,\beta }\) the natural embeddings between \(M_\alpha \) and \(M_\beta \).
The following is a conjunction of [22, Lemmas 16 and 21].
Theorem 2.4
Let  with
with  be a proper elementary embedding. Then j is iterable. Moreover, for any \(n\in \omega \),
be a proper elementary embedding. Then j is iterable. Moreover, for any \(n\in \omega \),  .
.
Theorem 2.4 states that \(M_n=L(V_{\lambda +1})\) for \(n<\omega \), but \(M_\omega \) is definitively different. The key point is that  , so many characteristics of the critical point of j are transferred by elementarity to \(\lambda \) in \(M_\omega \). For example, in \(L(V_{\lambda +1})\),
, so many characteristics of the critical point of j are transferred by elementarity to \(\lambda \) in \(M_\omega \). For example, in \(L(V_{\lambda +1})\),  is measurable and there is a well-ordering of \(V_\lambda \), therefore \(\lambda \) is measurable in \(M_\omega \) and there is a well-ordering of
is measurable and there is a well-ordering of \(V_\lambda \), therefore \(\lambda \) is measurable in \(M_\omega \) and there is a well-ordering of  in \(M_\omega \).
in \(M_\omega \).
Trees are a typical structure that is investigated in combinatorics. Let \(\alpha \) be an ordinal. For any  ,
,  . A tree on \(\alpha \) is a subset of
. A tree on \(\alpha \) is a subset of  closed under initial segments. If T is a tree, for any \(s\in T\), denote
closed under initial segments. If T is a tree, for any \(s\in T\), denote  ,
,  and finally for any \(n\in \omega \),
and finally for any \(n\in \omega \),  .
.
3 General procedure
In [22], Woodin introduced Generic Absoluteness for I0, while in [4] Dimonte and Friedman used it to prove a single result about the power function and rank-into-rank embeddings. Here we introduce a general procedure that extends the scope of [4] to many more kinds of forcing, and in the next sections we will give some important examples.
One of the most important forcing notions in dealing with the combinatorics of singular cardinals of cofinality \(\omega \) is the Prikry forcing. It adds a cofinal sequence to a measurable cardinal.
Definition 3.1
A cardinal \(\kappa \) is called measurable if there exists a \(\kappa \)-complete ultrafilter on \(\kappa \).
Definition 3.2
Let \(\kappa \) be a measurable cardinal. Fix U, a normal measure on \(\kappa \). Define \(p\in {\mathbb {P}}\) if \(p=(s,A)\), where  , \(A\in U\) and \(\bigcup s<\bigcap A\). For \(p=(s,A)\), \(q=(t,B)\in {\mathbb {P}}\), we say \(q\leqslant p\) if \(s\subseteq t\), \(B\subseteq A\) and
, \(A\in U\) and \(\bigcup s<\bigcap A\). For \(p=(s,A)\), \(q=(t,B)\in {\mathbb {P}}\), we say \(q\leqslant p\) if \(s\subseteq t\), \(B\subseteq A\) and  .
.
The Prikry forcing is useful because it is a very “delicate” forcing [8]: it does not add bounded subsets of \(\kappa \), and is \(\kappa ^+\)-cc, so it does not change the cardinal structure above \(\kappa \). In other words, it makes \(\kappa \) singular while changing the universe as least as possible.
Definition 3.3
Let \(\kappa \) be a measurable cardinal. Fix U, an ultrafilter on \(\kappa \). The tree Prikry forcing
\({\mathbb {P}}\) is the set of conditions  , where
, where  is a finite sequence of ordinals in \(\kappa \), and
is a finite sequence of ordinals in \(\kappa \), and  is a tree of increasing sequences in \(\kappa \) with stem
is a tree of increasing sequences in \(\kappa \) with stem  , such that for any
, such that for any  ,
,  . We say that \(p\leqslant q\) if
. We say that \(p\leqslant q\) if  and
and  . We say that
. We say that  if \(p\leqslant q\) and
if \(p\leqslant q\) and  . For any \(p\in {\mathbb {P}}\) and
. For any \(p\in {\mathbb {P}}\) and  , we write
, we write  for
for  .
.
The difference between these two notions is minimal: the only difference is that the standard Prikry forcing uses a normal ultrafilter, while for the tree Prikry forcing normality is not needed. As for the majority of times the ultrafilters are normal, these two notions are interchangeable, and using one or the other is a matter of better clarity of the proof.
The general technique, in short, will be to start with  , and then Theorem 3.10 expresses the fact that if one forces with an “Easton-like” forcing and then with a “Prikry-like” forcing at \(\kappa \), by Generic Absoluteness one can have
, and then Theorem 3.10 expresses the fact that if one forces with an “Easton-like” forcing and then with a “Prikry-like” forcing at \(\kappa \), by Generic Absoluteness one can have  . While we have already a formal definition for “Easton-like” (reverse Easton iteration), we need a definition of “Prikry-like” suitable to our wants.
. While we have already a formal definition for “Easton-like” (reverse Easton iteration), we need a definition of “Prikry-like” suitable to our wants.
Definition 3.4
Let \({\mathbb {P}}\) be a forcing notion and \(\kappa \) a cardinal. We say that \({\mathbb {P}}\) is \(\kappa \)-geometric if
-
there exists a length measure of the conditions of \({\mathbb {P}}\), i.e. \(l:{\mathbb {P}}\rightarrow \omega \) such that \(l(1_{\mathbb {P}})=0\) and for any \(p,q\in {\mathbb {P}}\), if \(p\leqslant q\) then \(l(p)\geqslant l(q)\);
-
for any \(\alpha <\kappa \), if
 is a collection of open dense sets, then for every \(p\in {\mathbb {P}}\) there is a condition \(q\leqslant p\) such that whenever a filter contains q and meets all dense open sets \(E_n=\{p:l(p)>n\}\), it also meets all \(D_\beta \).
is a collection of open dense sets, then for every \(p\in {\mathbb {P}}\) there is a condition \(q\leqslant p\) such that whenever a filter contains q and meets all dense open sets \(E_n=\{p:l(p)>n\}\), it also meets all \(D_\beta \).
This notion implies the notion of \(\kappa \)-goodness that was first introduced by Woodin [22], and then perfectioned by Shi [19]. The change is due to the fact that \(\kappa \)-geometric is more natural in working with tree Prikry-like forcing, even if it works in general.
Lemma 3.5
The Prikry forcing on \(\kappa \) is \(\kappa \)-geometric.
Proof
It is a well-known fact that for any dense set D and any \(p\in {\mathbb {P}}\), there exists  and \(n\in \omega \) such that for any \(t\in [A]^n\),
and \(n\in \omega \) such that for any \(t\in [A]^n\),  , see for example [8, Lemma 1.13]. Now, suppose \(\alpha <\kappa \) and
, see for example [8, Lemma 1.13]. Now, suppose \(\alpha <\kappa \) and  is a collection of open dense sets. Let
is a collection of open dense sets. Let  be the sequence built with an iteration of the first sentence, i.e., for any \(\beta \leqslant \alpha \),
be the sequence built with an iteration of the first sentence, i.e., for any \(\beta \leqslant \alpha \),  is such that there exists \(n_{\beta +1}\) such that for any t of length n,
is such that there exists \(n_{\beta +1}\) such that for any t of length n,  , and if \(\beta \leqslant \alpha \) is limit, then by \(\kappa \)-closeness of U let \(q_\beta \) be just
, and if \(\beta \leqslant \alpha \) is limit, then by \(\kappa \)-closeness of U let \(q_\beta \) be just  .
.
Therefore \(q_\alpha \) is as wanted: let \(q'\leqslant q_\alpha =(s_{q_\alpha },A_{q_\alpha })\) be such that \(q'\in E_{n_\beta }\). Then

for some t with length bigger than \(n_\beta \). \(\square \)
The key point of the lemma, and in fact of any proof of \(\kappa \)-geometricness, is the variation of the Prikry conditionFootnote 1 that is presented in the first line of the proof. We isolate it in the following definition.
Definition 3.6
Let \(({\mathbb {P}},\leqslant ,\leqslant ^*)\) be a forcing notion with a length measure (as in Definition 3.4) such that  iff \(l(p)=l(q)\). Then \({\mathbb {P}}\) satisfies the *-Prikry condition if for every \(p\in {\mathbb {P}}\) and for every dense \(D\subseteq {\mathbb {P}}\), there are \(n\in \omega \) and
iff \(l(p)=l(q)\). Then \({\mathbb {P}}\) satisfies the *-Prikry condition if for every \(p\in {\mathbb {P}}\) and for every dense \(D\subseteq {\mathbb {P}}\), there are \(n\in \omega \) and  such that for any \(r\leqslant q\) with \(l(r)=l(q)+n\), \(r\in D\).
such that for any \(r\leqslant q\) with \(l(r)=l(q)+n\), \(r\in D\).
Such variation is pretty common in literature, even if it is often not explicitly stated, as the proof basically repeats the proof of the Prikry condition. It goes back to Prikry [17] and Mathias [14]. For completeness, we will sketch the proof for the tree Prikry forcing, so it will be clear to the reader how the proof goes for other kinds of forcing that satisfy the Prikry condition.
Lemma 3.7
Let \(\kappa \) be a measurable cardinal. Then the tree Prikry forcing \({\mathbb {P}}\) on \(\kappa \) satisfies the *-Prikry condition.
Sketch of the proof Fix a dense set D and a condition \(p\in {\mathbb {P}}\) with the tree  ; we should find a way to shrink
; we should find a way to shrink  to \(T^q\) so that
to \(T^q\) so that  is such that any n-extension of q is in D.
is such that any n-extension of q is in D.
The first step is to find  such that for any
such that for any  if there exists
if there exists  with \(q\in D\), then \((s,T'_s)\in D\), that is, such that the tree-part has no role in establishing whether extensions of p are in D or not. This can be done by induction on levels, choosing for any s, T such that \((s,T)\in D\), when it exists, and intersecting everything. The final \(T'\) will be such that
with \(q\in D\), then \((s,T'_s)\in D\), that is, such that the tree-part has no role in establishing whether extensions of p are in D or not. This can be done by induction on levels, choosing for any s, T such that \((s,T)\in D\), when it exists, and intersecting everything. The final \(T'\) will be such that  by completeness of the measure.
by completeness of the measure.
The second step is to reduce the tree again to \(T^q\) such that if  and
and  , then all extensions of p of the same length are in D. This exploits the fact that the successor of any element of \(T'\) is of measure one, therefore, as an example, consider
, then all extensions of p of the same length are in D. This exploits the fact that the successor of any element of \(T'\) is of measure one, therefore, as an example, consider  . Then either the elements of S that are “in D” (remember that by the first construction “being in D” does not depend on the tree-part) form a measure one set, or those that are not form a measure one set, and we cut the branches that are not in such set. By induction, we do this on all levels, also extending to double successors (i.e. we consider the elements such that all their successors have all their successors either in D or not), triple successors, etc. Again by completeness the resulting \(T^q\) is such that
. Then either the elements of S that are “in D” (remember that by the first construction “being in D” does not depend on the tree-part) form a measure one set, or those that are not form a measure one set, and we cut the branches that are not in such set. By induction, we do this on all levels, also extending to double successors (i.e. we consider the elements such that all their successors have all their successors either in D or not), triple successors, etc. Again by completeness the resulting \(T^q\) is such that  .
.
Then we have  such that all its successors of length n, for every n, are either in D or not. If there exists n such that all n-successors are in D, then we are done. But there must be one, because D is dense. \(\square \)
such that all its successors of length n, for every n, are either in D or not. If there exists n such that all n-successors are in D, then we are done. But there must be one, because D is dense. \(\square \)
Corollary 3.8
Let \(\kappa \) be a measurable cardinal. Then the tree Prikry forcing \({\mathbb {P}}\) on \(\kappa \) is \(\kappa \)-geometric.
Definition 3.9
Let \({\mathbb {P}}_\lambda \) be a forcing iteration of length \(\lambda \), where \(\lambda \) is either a strong limit cardinal or is equal to \(\infty \), the class of all ordinals. We say that \({\mathbb {P}}_\lambda \) is
-
reverse Easton if nontrivial forcing is done only at infinite cardinal stages, direct limits are taken at all inaccessible cardinal limit stages, and inverse limits are taken at all other limit stages; moreover, \({\mathbb {P}}_\lambda \) is the direct limit of
 if \(\lambda \) is regular or \(\infty \), the inverse limit of the
if \(\lambda \) is regular or \(\infty \), the inverse limit of the  , otherwise;
, otherwise; -
directed closed if for all \(\delta <\lambda \), \({\mathbb {Q}}_\delta \) is \(<\delta \)-directed closed, i.e., for any \(D\subseteq {\mathbb {Q}}_\delta \), \(|D|<\delta \) such that for any \(d_1,d_2\in D\) there is \(e\in D\) with \(e\leqslant d_1, e\leqslant d_2\), there exists \(p\in {\mathbb {Q}}_\delta \) such that \(p\leqslant d\) for any \(d\in D\);
-
\(\lambda \)-bounded if for all \(\delta <\lambda \), \({\mathbb {Q}}_\delta \) has size \(<\lambda \). Note that in the case \(\lambda =\infty \), this just means that each \({\mathbb {Q}}_\delta \) is a set-forcing.
Moreover, if j is any elementary embedding such that \(j``\lambda \subset \lambda \) and  , we say that \({\mathbb {P}}_\lambda \) is j-coherent if for any \(\delta <\lambda \),
, we say that \({\mathbb {P}}_\lambda \) is j-coherent if for any \(\delta <\lambda \),  .
.
The following theorem summarizes the general procedure.
Theorem 3.10
Let  with
with  . Let \({\mathbb {P}}\) be a directed closed, \(\lambda \)-bounded, j-coherent reverse Easton iteration. Let \({\mathbb {Q}}\) be a \(\kappa \)-geometric forcing in \((V_\lambda )^{V^{{\mathbb {P}}}}\) that adds a Prikry sequence to \(\kappa \). Then there exist G generic for \({\mathbb {P}}\) and H
V[G]-generic for \({\mathbb {Q}}\) such that
. Let \({\mathbb {P}}\) be a directed closed, \(\lambda \)-bounded, j-coherent reverse Easton iteration. Let \({\mathbb {Q}}\) be a \(\kappa \)-geometric forcing in \((V_\lambda )^{V^{{\mathbb {P}}}}\) that adds a Prikry sequence to \(\kappa \). Then there exist G generic for \({\mathbb {P}}\) and H
V[G]-generic for \({\mathbb {Q}}\) such that  .
.
The relevant point of the proof is the forcing \({\mathbb {Q}}\), as by [4, Lemmas 3.6 and 3.7] combined, for any G generic for \({\mathbb {P}}\),  ,
,  . So, for better readability, from now on we call the generic extension of \({\mathbb {P}}\) just V.
. So, for better readability, from now on we call the generic extension of \({\mathbb {P}}\) just V.
Let  be the \(\omega \)-th iterate of j. Then \(j_{0,\omega }({\mathbb {Q}})\) is a \(\lambda \)-geometric forcing that adds a Prikry sequence to \(\lambda \) in \(M_\omega \).
be the \(\omega \)-th iterate of j. Then \(j_{0,\omega }({\mathbb {Q}})\) is a \(\lambda \)-geometric forcing that adds a Prikry sequence to \(\lambda \) in \(M_\omega \).
Lemma 3.11
In V there are only \(\lambda \) open dense sets of \(j_{0,\omega }({\mathbb {Q}})\).
Proof
Since \({\mathbb {Q}}\in V_\lambda \), there exists \(n\in \omega \) such that \({\mathbb {Q}}\in V_{\kappa _n}\). In particular,  and its dense sets are in
and its dense sets are in  . But
. But  . \(\square \)
. \(\square \)
Proposition 3.12
There exists a generic ultrafilter \(H\in V\) of \(j_{0,\omega }({\mathbb {Q}})\).
Proof
Let  be an enumeration of dense sets of \(j_{0,\omega }({\mathbb {Q}})\) in V. For every \(n\in \omega \), fix \(q_n\) that witnesses \(\lambda \)-geometricness for
be an enumeration of dense sets of \(j_{0,\omega }({\mathbb {Q}})\) in V. For every \(n\in \omega \), fix \(q_n\) that witnesses \(\lambda \)-geometricness for  . Then for every m there exists \(q'_{n,m}<q_n\) such that \(q'_{n,m}\in E_m\). Let H be the filter \(\bigcup _{n,m\in \omega }{\mathscr {F}}_{q'_{n,m}}\), with \({\mathscr {F}}_q\) the filter generated by q. Then H is generic. \(\square \)
. Then for every m there exists \(q'_{n,m}<q_n\) such that \(q'_{n,m}\in E_m\). Let H be the filter \(\bigcup _{n,m\in \omega }{\mathscr {F}}_{q'_{n,m}}\), with \({\mathscr {F}}_q\) the filter generated by q. Then H is generic. \(\square \)
The following appeared in [22] as Theorem 136.
Theorem 3.13
(Generic Absoluteness) Let  with
with  be a proper elementary embedding. Let \((M_\omega ,j_\omega )\) be the \(\omega \)-th iterate of j and let
be a proper elementary embedding. Let \((M_\omega ,j_\omega )\) be the \(\omega \)-th iterate of j and let  be a sequence generic for the Prikry forcing on \(\lambda \) in \(M_\omega \). Then for all \(\alpha <\lambda \) there exists an elementary embedding
be a sequence generic for the Prikry forcing on \(\lambda \) in \(M_\omega \). Then for all \(\alpha <\lambda \) there exists an elementary embedding

such that  is the identity.
is the identity.
In particular, as  holds in \(L_1(V_{\lambda +1})\),
holds in \(L_1(V_{\lambda +1})\),  .
.
Proof of Theorem 3.10Let \(H\in V\) be \(j_{0,\omega }({\mathbb {P}})\)-generic. Fix g, one of the Prikry sequences added by \(j_{0,\omega }({\mathbb {Q}})\). Then \(M_\omega \subseteq M_\omega [g]\subseteq M_\omega [H]\subseteq V\). But \(M_\omega [g]\) satisfies Generic Absoluteness’ conditions, therefore  . But also
. But also  , therefore it must be
, therefore it must be  . As, by Theorem 3.13,
. As, by Theorem 3.13,  , it is immediate to see that for any formula \(\varphi \) and for any \(a\in M_\omega [g]\), \(M_\omega [g]\cap V_{\lambda +1}\vDash \varphi (a)\) iff \(M_\omega [H]\cap V_{\lambda +1}\vDash \varphi (a)\) iff
, it is immediate to see that for any formula \(\varphi \) and for any \(a\in M_\omega [g]\), \(M_\omega [g]\cap V_{\lambda +1}\vDash \varphi (a)\) iff \(M_\omega [H]\cap V_{\lambda +1}\vDash \varphi (a)\) iff  . But this is the situation of Remark 2.1, therefore
. But this is the situation of Remark 2.1, therefore  .
.
We have just proved that

Applying \(j^{-1}\), we have that

as we wanted to prove. \(\square \)
4 Extender-based Prikry forcing
The first application of \(\kappa \)-geometricness will be on the extender-based Prikry forcing. It was introduced by Gitik and Magidor, and the reader can find its exhaustive description in [8]. The aim of the forcing is to add many Prikry sequences to a strong enough cardinal, blowing up its power while not changing the power function below it. This is more difficult than just having \(\lambda \) singular and \(2^\lambda >\lambda ^+\): the proof for this is to take \(\lambda \) measurable, forcing \(2^\lambda >\lambda ^+\) and then adding a Prikry sequence to \(\lambda \). But Scott [18] proved that if \(\lambda \) is measurable and \(2^\lambda >\lambda ^+\), then for a measure one set below \(\lambda \), \(2^\kappa >\kappa ^+\), therefore this method would not give the first failure of GCH on \(\lambda \). The solution is to exploit the extender structure of the cardinal to add many Prikry sequences, at the same time blowing up the power and changing the cofinality.
Definition 4.1
Let \(\kappa \) and \(\gamma \) be cardinal. Then \(\kappa \) is \(\gamma \)-strong if there is  such that
such that  , \(\gamma <j(\kappa )\) and \(V_{\kappa +\gamma }\subseteq M\).
, \(\gamma <j(\kappa )\) and \(V_{\kappa +\gamma }\subseteq M\).
We write the definition as it is in [8]. Suppose GCH, and let \(\lambda \) be a 2-strong cardinal. For any \(\alpha <\lambda ^{++}\), define a \(\lambda \)-complete normal ultrafilter on \(\lambda \) as \(X\in U_\alpha \) if \(\alpha \in j(X)\). For any \(\alpha ,\beta <\lambda ^{++}\), define  if \(\alpha \leqslant \beta \) and for some
if \(\alpha \leqslant \beta \) and for some  , \(j(f)(\beta )=\alpha \). Then by a result in [8],
, \(j(f)(\beta )=\alpha \). Then by a result in [8],  is a \(\lambda ^{++}\)-directed order, and there exists
is a \(\lambda ^{++}\)-directed order, and there exists  such that
such that  is a nice system. There is no need to define a nice system here, the term is introduced only because the extender-based Prikry forcing is built on a nice system, the full definition can be found in [8].
is a nice system. There is no need to define a nice system here, the term is introduced only because the extender-based Prikry forcing is built on a nice system, the full definition can be found in [8].
Fix a nice system  . For any \(\nu <\lambda \) and \(\lambda <\alpha <\lambda ^{++}\), let us denote \(\pi _{\alpha ,0}(\nu )\) by \(\nu ^{\alpha ,0}\). We will write just \(\nu ^0\) when \(\alpha \) is obvious. By a °-increasing sequence of ordinals we mean a sequence
. For any \(\nu <\lambda \) and \(\lambda <\alpha <\lambda ^{++}\), let us denote \(\pi _{\alpha ,0}(\nu )\) by \(\nu ^{\alpha ,0}\). We will write just \(\nu ^0\) when \(\alpha \) is obvious. By a °-increasing sequence of ordinals we mean a sequence  of ordinals below \(\lambda \) such that \(\nu _0^0<\ldots <\nu _n^0\). We say that \(\mu \) is permitted for
of ordinals below \(\lambda \) such that \(\nu _0^0<\ldots <\nu _n^0\). We say that \(\mu \) is permitted for  if \(\mu ^0>\nu _i^0\) for all \(i=0,\ldots ,n\).
if \(\mu ^0>\nu _i^0\) for all \(i=0,\ldots ,n\).
Definition 4.2
The set of forcing conditions \({\mathbb {P}}\) consists of all elements p of the form

where
-
(i)
\(g\subseteq \lambda ^{++}\) of cardinality \(\leqslant \lambda \) which has a maximal element according to \(\leqslant _E\) and \(0\in g\).
-
(ii)
For \(\gamma \in g\), \(p^\gamma \) is a finite °-increasing sequence of ordinals \(<\lambda \).
-
(iii)
T is a tree, with a trunk
 , consisting of °-increasing sequences. All splittings in T are required to be on sets in
, consisting of °-increasing sequences. All splittings in T are required to be on sets in 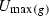 , i.e., for every \(\eta \in T\), if
, i.e., for every \(\eta \in T\), if  then the set
then the set 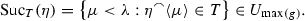
Also require that for
 , \({{\mathrm{Suc}}}_T(\eta _1)\subseteq {{\mathrm{Suc}}}_T(\eta _2)\).
, \({{\mathrm{Suc}}}_T(\eta _1)\subseteq {{\mathrm{Suc}}}_T(\eta _2)\). -
(iv)
For every
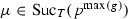 ,
,  .
. -
(v)
For every \(\gamma \in g\),
 is not permitted for \(p^\gamma \).
is not permitted for \(p^\gamma \). -
(vi)
 projects
projects 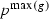 onto \(p^0\) (so
onto \(p^0\) (so 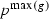 and \(p^0\) are of the same length).
and \(p^0\) are of the same length).
Let us denote g by  ,
,  by
by  , T by
, T by  ,
,  by \(p^{{{\mathrm{mc}}}}\) and
by \(p^{{{\mathrm{mc}}}}\) and  .
.
Definition 4.3
Let \(p,q\in {\mathbb {P}}\). We say that p extends q and denote this by \(p<q\) if
-
(i)
 .
. -
(ii)
For every
 , \(p^\gamma \) is an end-extension of \(q^\gamma \).
, \(p^\gamma \) is an end-extension of \(q^\gamma \). -
(iii)
\(p^{{{\mathrm{mc}}}(q)}\in T^q\).
-
(iv)
For every
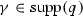 ,
, 
where
 is the largest such that
is the largest such that 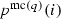 is not permitted for \(q^\gamma \).
is not permitted for \(q^\gamma \). -
(v)
 projects
projects  into \(T^q_{q^{{{\mathrm{mc}}}}}\).
into \(T^q_{q^{{{\mathrm{mc}}}}}\). -
(vi)
For every
 and
and 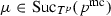 , if \(\mu \) is permitted for \(p^\gamma \), then
, if \(\mu \) is permitted for \(p^\gamma \), then  .
.
Definition 4.4
Let \(p,q\in {\mathbb {P}}\). We say that p is a direct extension of
q and denote this by  if
if
-
\(p<q\),
-
for every
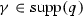 , \(p^\gamma =q^\gamma \).
, \(p^\gamma =q^\gamma \).
Lemma 4.5
([8]) \(\leqslant ^*\) is \(\lambda \)-complete.
We need to define what an n-extension is for this forcing.
Definition 4.6
Let \(p\in {\mathbb {P}}\) and  . Then
. Then  is defined as follows:
is defined as follows:
-
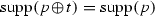 ;
; -
 ;
; -
 ;
; -
if
 ,
, 
where \(i_\gamma \) is the largest such that t(i) is not permitted by \(p^\gamma \).
A condition in \({\mathbb {P}}\) is therefore a set of finite sequences and T indicating the possible extensions not only of the last one, but, via projection, of all of them. Morally speaking,  is the largest extension of p that we can have choosing t (and its projections) as extension.
is the largest extension of p that we can have choosing t (and its projections) as extension.
Theorem 4.7
(Gitik, Magidor) Let \({\mathbb {P}}\) be as above. Then

In spirit, the Gitik–Magidor extender Prikry forcing is a tree Prikry forcing, therefore the proof for the *-Prikry condition is, in spirit, the same as of Lemma . In practice, it is much more complex, and the proof of that goes back to Merimovich [15]. In this case, it has this form: for every \(p\in {\mathbb {P}}\) and \(D\subseteq {\mathbb {P}}\) dense there exist  and \(n\in \omega \) such that for any \(t\in T^q\),
and \(n\in \omega \) such that for any \(t\in T^q\),  ,
,  .
.
It is tempting then to do as in Lemma 3.5, i.e., building a descending sequence of conditions that satisfy the *-Prikry condition. But there is a technical difference: in Lemma 3.5 (using the same notation), an \(n_\beta \)-extension of \(q_\alpha \) was also an \(n_\beta \)-extension of \(q_\beta \), and therefore in \(D_\beta \); in this case, an \(n_\beta \)-extension of \(q_\alpha \) can possibly not be an \(n_\beta \)-extension of \(q_\beta \), for example when  . Therefore we have to check that everything projects smoothly.
. Therefore we have to check that everything projects smoothly.
Proposition 4.8
Let \({\mathbb {P}}\) be as above. Then \({\mathbb {P}}\) is \(\lambda \)-geometric.
Proof
Let  be a sequence of open dense sets, with \(\alpha <\lambda \), \(p\in {\mathbb {P}}\), and let
be a sequence of open dense sets, with \(\alpha <\lambda \), \(p\in {\mathbb {P}}\), and let  , with \(q_0=p\), be the sequence built with an iteration of the *-Prikry condition, i.e., for any \(\beta \leqslant \alpha \),
, with \(q_0=p\), be the sequence built with an iteration of the *-Prikry condition, i.e., for any \(\beta \leqslant \alpha \),  is such that there exists \(n_{\beta +1}\) such that for any \(t\in T^{q_\beta }\) of length \(n_{\beta +1}\),
is such that there exists \(n_{\beta +1}\) such that for any \(t\in T^{q_\beta }\) of length \(n_{\beta +1}\),  , and if \(\beta \leqslant \alpha \) is limit, then by \(\lambda \)-closeness of \(\leqslant ^*\) let \(q_\beta \) be such that
, and if \(\beta \leqslant \alpha \) is limit, then by \(\lambda \)-closeness of \(\leqslant ^*\) let \(q_\beta \) be such that  for all \(\gamma <\beta \). We can assume
for all \(\gamma <\beta \). We can assume  , where TC is the complete tree of the increasing finite sequences in \(\lambda \).
, where TC is the complete tree of the increasing finite sequences in \(\lambda \).
Claim 4.9
For any \(\beta <\alpha \), for any \(t\in T^{q^\alpha }\),  .
.
Proof
Note that  Footnote 2. We prove it point by point.
Footnote 2. We prove it point by point.
-
 is well-defined, i.e.,
is well-defined, i.e.,  . This is true due to Definition 4.3 (v).
. This is true due to Definition 4.3 (v). -
 . This is true because
. This is true because  ,
, 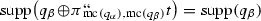
and by Definition 4.3 (i).
-
For any
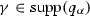 ,
,  . By definition, and since \((q_\alpha )^\gamma =(q_\beta )^\gamma \), this is true if and only if
. By definition, and since \((q_\alpha )^\gamma =(q_\beta )^\gamma \), this is true if and only if 
where \(i_\gamma \) is the largest such that \(t(i_\gamma )\) is not permitted by \((q_\alpha )^\gamma \) and \(j_\gamma \) is the largest such that
 is not permitted by \((q_\beta )^\gamma =(q_\alpha )^\gamma \). By Definition 4.2 (vi),
is not permitted by \((q_\beta )^\gamma =(q_\alpha )^\gamma \). By Definition 4.2 (vi),  , therefore by Definition 4.3 (vi),
, therefore by Definition 4.3 (vi), 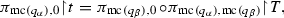
so \(i_\gamma =j_\gamma \). Therefore this point is true by Definition 4.3 (vi).
-
 is in
is in  . First of all,
. First of all, 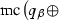
 . By definition,
. By definition, 
with
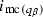 as above. By Definition 4.3 (ii)
as above. By Definition 4.3 (ii)  , and therefore
, and therefore 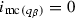 , so the point follows simply by definition of
, so the point follows simply by definition of  .
. -
 projects \(T_t^{q_\alpha \oplus t}\) into
projects \(T_t^{q_\alpha \oplus t}\) into  . By definition, \(T_t^{q_\alpha \oplus t}= T_t^{q_\alpha }\) and
. By definition, \(T_t^{q_\alpha \oplus t}= T_t^{q_\alpha }\) and  , so this is true by Definition 4.3 (v).
, so this is true by Definition 4.3 (v). -
For any
 and \(\mu \in {{\mathrm{Suc}}}_{T^{q\oplus t}}(t)\), if \(\mu \) is permitted for
and \(\mu \in {{\mathrm{Suc}}}_{T^{q\oplus t}}(t)\), if \(\mu \) is permitted for  then
then 
As \(T^{q_\alpha \oplus t}\) is a subtree of \(T^{q_\alpha }\), and \(\mu \) is permitted for
 means that it is also permitted for \((q_\alpha )^\gamma \), this is a direct consequence of Definition 4.3 (vi).\(\blacksquare \)
means that it is also permitted for \((q_\alpha )^\gamma \), this is a direct consequence of Definition 4.3 (vi).\(\blacksquare \)
Therefore \(q_\alpha \) is as wanted: let \(q'\leqslant q_\alpha \) be such that \(q'\in E_{n_\beta }\). Then  for some \(t\in T^{q_\alpha }\) with length \(n_\beta \). But, by Claim 4.9,
for some \(t\in T^{q_\alpha }\) with length \(n_\beta \). But, by Claim 4.9,  , and by definition
, and by definition  , so also \(q'\in D_\beta \). \(\square \)
, so also \(q'\in D_\beta \). \(\square \)
Corollary 4.10
Suppose  . Then there exists a generic extension in which
. Then there exists a generic extension in which  .
.
Proof
We want to apply Theorem 3.10. So first note that the forcing that forces GCH below \(\lambda \) is a directed closed, \(\lambda \)-bounded, j-coherent reverse Easton iteration, while the forcing that forces GCH above \(\lambda \) is \(\lambda \)-closed, and therefore does not touch I0. I0 clearly implies I2, and it is a well-known fact (see e.g. [10, Proposition 24.2]) that this is equivalent to the existence of  with \(V_\lambda \subseteq M\). We can construct k so that
with \(V_\lambda \subseteq M\). We can construct k so that  , so \(\kappa \) is 2-strong. Therefore we can apply the extender-based Pikry forcing to \(\kappa \). The elements of \({\mathbb {P}}\) on \(\kappa \) are \(\kappa \)-sequences of triples of elements of \(\kappa ^{++}\), finite sequences in \(\kappa \) and functions from \(\kappa ^\omega \) to \({\mathscr {P}}(\kappa )\), so we can say that the forcing is in \(V_{\kappa _1}\). The forcing adds a Prikry sequence to \(\kappa \) and it is \(\kappa \)-geometric, therefore the conditions of Theorem 3.10 are met. \(\square \)
, so \(\kappa \) is 2-strong. Therefore we can apply the extender-based Pikry forcing to \(\kappa \). The elements of \({\mathbb {P}}\) on \(\kappa \) are \(\kappa \)-sequences of triples of elements of \(\kappa ^{++}\), finite sequences in \(\kappa \) and functions from \(\kappa ^\omega \) to \({\mathscr {P}}(\kappa )\), so we can say that the forcing is in \(V_{\kappa _1}\). The forcing adds a Prikry sequence to \(\kappa \) and it is \(\kappa \)-geometric, therefore the conditions of Theorem 3.10 are met. \(\square \)
5 Diagonal supercompact Prikry forcings
There are many versions of the diagonal supercompact Prikry forcing, we are going to use the one in [9] (and later the one in [16]). First, there is a preparation forcing that forces \(2^\alpha =\alpha ^{+\omega +2}\) for all \(\alpha \) inaccessible. Then, the diagonal supercompact forcing exploits the fine normal ultrafilters that come from enough supercompactness of a cardinal to add Prikry sequences to it, while inducing an interesting pcf structure.
Definition 5.1
Let \(\kappa ,\gamma \) be cardinals. We say that \(\kappa \) is \(\gamma \)-supercompact if there exists a fine normal measure on \({\mathscr {P}}_\kappa (\gamma )\), i.e., a measure U such that for any \(f:{\mathscr {P}}_\kappa (\eta )\rightarrow \gamma \) with \(f(x)\in x\) for almost every x, f is constant on a set in U.
One interesting combinatorial principle is \(\Box _\kappa \), that states the existence of a coherent collection of clubs. While many combinatorial principles are consistent with the existence of large cardinals, \(\Box _\kappa \) fails above large enough cardinals (Solovay). It is of interest, therefore, investigating weakenings of such principle.
Definition 5.2
We say that a cardinal \(\kappa \) has the approachability property, \(\mathrm{AP}_\lambda \), if there exists a sequence  such that
such that
-
for \(\alpha \) limit, \(C_\alpha \) is a club in \(\alpha \) and
 ;
; -
there is a club \(D\subseteq \kappa ^+\) such that for any \(\alpha \in D\), for any \(\beta <\alpha \) there exists \(\gamma <\alpha \) such that \(C_\alpha \cap \beta =C_\gamma \).
It is not difficult to see that it is a weakening of \(\Box _\kappa \).
Another field of research in infinite combinatorics is the pcf theory: given a cardinal \(\kappa \) and  cofinal, it investigates the structure of the functions in \(\prod _{n\in \omega }\mu _n\), and it is a standard tool for the analysis of the combinatorics of a cardinal of cofinality \(\omega \).
cofinal, it investigates the structure of the functions in \(\prod _{n\in \omega }\mu _n\), and it is a standard tool for the analysis of the combinatorics of a cardinal of cofinality \(\omega \).
Definition 5.3
Let  be a sequence cofinal in \(\kappa \). A sequence
be a sequence cofinal in \(\kappa \). A sequence  is a very good scale if
is a very good scale if
-
 is a scale, i.e. such that for every \(\alpha <\beta <\kappa ^+\), \(f_\alpha (m)<f_\beta (m)\) for almost every m and for every \(f\in \prod _{n\in \omega }\mu _n\) there exists \(\beta <\kappa ^+\) and \(n\in \omega \) with \(f(m)<f_\beta (m)\) for every \(m>n\);
is a scale, i.e. such that for every \(\alpha <\beta <\kappa ^+\), \(f_\alpha (m)<f_\beta (m)\) for almost every m and for every \(f\in \prod _{n\in \omega }\mu _n\) there exists \(\beta <\kappa ^+\) and \(n\in \omega \) with \(f(m)<f_\beta (m)\) for every \(m>n\); -
for every \(\beta <\kappa ^+\) such that
 there exists a club C of \(\beta \) and \(n<\omega \) such that \(f_{\gamma _1}(m)<f_{\gamma _2}(m)\) for every \(\gamma _1<\gamma _2\in C\) and \(m>n\).
there exists a club C of \(\beta \) and \(n<\omega \) such that \(f_{\gamma _1}(m)<f_{\gamma _2}(m)\) for every \(\gamma _1<\gamma _2\in C\) and \(m>n\).
If \(\kappa \) is as above, we say that there exists a very good scale in \(\kappa \), \(\mathrm{VGS}_\kappa \).
Both these properties do not hold above a supercompact cardinal, and in [9] it is proven that having a very good scale does not imply the approachability property. We will prove that this holds also under rank-into-rank hypotheses.
Let \({\mathbb {E}}\) be the reverse Easton forcing of length \(\lambda \) that force \(2^\alpha =\alpha ^{+\omega +2}\) for all \(\alpha \) inaccessible. This forcing is:
-
directed closed: \({\mathbb {Q}}_\alpha \), the forcing that adds \(\alpha ^{+\omega +2}\) subsets of \(\alpha \), is \(<\alpha \)-directed closed;
-
\(\lambda \)-bounded: as \(\lambda \) is strong limit \(|{\mathbb {Q}}_\alpha |<\lambda \);
-
j-coherent: as \(j({\mathbb {Q}}_\alpha )\) is the poset consisting of the functions whose domain is a subset of \(j(\alpha )^{+\omega +2}\) of size less than \(j(\alpha )\), and whose range is a subset of the partial functions between \(j(\alpha )\) and \(j(\alpha )\), that is, \(j({\mathbb {Q}}_\alpha )={\mathbb {Q}}_{j(\alpha )}\).
Let \(\kappa \) be \(\kappa ^{+\omega +2}\)-supercompact, with \(U_\omega \) witnessing it and let \(U_n\) be the projection of \(U_\omega \) on \({\mathscr {P}}_\kappa (\kappa ^{+n})\), i.e.,

Clearly \(U_n\) is a normal ultrafilter on \({\mathscr {P}}_\kappa (\kappa ^{+n})\). Let \(a,b\in {\mathscr {P}}_\kappa (\kappa ^{+n})\) and \(b\cap \kappa \in \kappa \). Set

Definition 5.4
\(p\in {\mathbb {Q}}\) if  , where
, where
-
\(\forall l<n\; a_l^p\in {\mathscr {P}}_\kappa (\kappa ^{+n})\) and \(a_l^p\cap \kappa \) is an inaccessible cardinal;
-
\(\forall m\geqslant n\) \(X_m^p\in U_m\);
-
\(\forall m\geqslant n\, \forall b\in X_m^p\, \forall l<n\; a_l^p\underset{\sim }{\subset } b\);
-
\(\forall i<j<l\; a_i^p\underset{\sim }{\subset } a_j^p\).
For  , let us denote n as l(p). Moreover, for any collection of \(A_i\subseteq {\mathscr {P}}_\kappa (\kappa ^{+i})\), let
, let us denote n as l(p). Moreover, for any collection of \(A_i\subseteq {\mathscr {P}}_\kappa (\kappa ^{+i})\), let

For any collection \(A_a\), \(a\in {\mathscr {P}}_\kappa (\kappa ^{+n})\), let

It is a standard result that if each \(A_a\in U_n\), then \(\Delta A_a\in U_n\).
Definition 5.5
Let \(p,q\in {\mathbb {Q}}\). Then  if
if
-
\(l(p)=l(q)\);
-
\(\forall l<l(p)\; a_l^p=a_l^q\);
-
\(\forall m\geqslant l(p)\; X_m^p\subseteq X_m^q\).
Definition 5.6
Let \(p\in {\mathbb {Q}}\) and \(\mathbf {a}\in \widetilde{\prod }_{l(p)\leqslant n\leqslant m}X_n^p\). Then we denote by  the sequence
the sequence  , where
, where

Then \(p\leqslant q\) if there exists \(\mathbf {a}\) such that  .
.
Theorem 5.7
(Gitik, Sharon) Let G be generic for \({\mathbb {P}}\) and H be generic for \({\mathbb {Q}}\) as above. Then  .
.
Similarly to the proof of Lemma 3.5 we have
Proposition 5.8
\({\mathbb {Q}}\) as above is \(\kappa \)-geometric.
Corollary 5.9
Suppose  . Then there exists a generic extension in which there exists
. Then there exists a generic extension in which there exists  , \(2^{\kappa }>\kappa ^+\), there is a very good scale in \(\kappa \) but the approachability property does not hold in \(\kappa \).
, \(2^{\kappa }>\kappa ^+\), there is a very good scale in \(\kappa \) but the approachability property does not hold in \(\kappa \).
Proof
Let H be \({\mathbb {E}}\)-generic for V. By Theorem 3.10 (without the Prikry part),  still holds in V[H], say witnessed by k. Then
still holds in V[H], say witnessed by k. Then

defined in V[H], witnesses that  is \(\kappa ^{+\omega +2}\)-supercompact. Therefore we can force on \(\kappa \) with \({\mathbb {Q}}\). \({\mathbb {Q}}\subseteq \prod _{n\in \omega }{\mathscr {P}}_\kappa (\kappa ^{+n})\), so \({\mathbb {Q}}\subseteq V_{\kappa _1}\). The hypotheses of Theorem 3.10 are then satisfied, and Theorem 5.7 proves the corollary. \(\square \)
is \(\kappa ^{+\omega +2}\)-supercompact. Therefore we can force on \(\kappa \) with \({\mathbb {Q}}\). \({\mathbb {Q}}\subseteq \prod _{n\in \omega }{\mathscr {P}}_\kappa (\kappa ^{+n})\), so \({\mathbb {Q}}\subseteq V_{\kappa _1}\). The hypotheses of Theorem 3.10 are then satisfied, and Theorem 5.7 proves the corollary. \(\square \)
In [16], Neeman introduced a variation of the Gitik–Sharon forcing, that has a more structured preparation forcing and needs more large cardinal power. The result will involve the tree property.
Definition 5.10
Let \(\kappa \) be a cardinal. Then the tree property holds at \(\kappa \),  , if every tree of height \(\kappa \) and such that all levels have size \(<\kappa \) has a cofinal branch.
, if every tree of height \(\kappa \) and such that all levels have size \(<\kappa \) has a cofinal branch.
Suppose j witnesses  and let
and let  be the critical sequence of j.
be the critical sequence of j.
Lemma 5.11
 is limit of supercompact cardinals.
is limit of supercompact cardinals.
Proof
It is by reflection of rank-into-rank embeddings: for any \(\gamma <\kappa \), the sentence “ ” is true, witnessed by
” is true, witnessed by  (note that \(j(\gamma )=\gamma \)). Then, by elementarity, there exists
(note that \(j(\gamma )=\gamma \)). Then, by elementarity, there exists  with a critical point between \(\gamma \) and \(\kappa \). Such critical point is supercompact in \(V_\lambda \), and choosing different \(\gamma \) we have that the cardinals supercompact in \(V_\lambda \) form an unbounded subset of \(\kappa \). By elementarity, this is true also for \(\kappa _1\). \(\square \)
with a critical point between \(\gamma \) and \(\kappa \). Such critical point is supercompact in \(V_\lambda \), and choosing different \(\gamma \) we have that the cardinals supercompact in \(V_\lambda \) form an unbounded subset of \(\kappa \). By elementarity, this is true also for \(\kappa _1\). \(\square \)
Let \(\mu _0=\kappa \) and \(\mu _{i+1}\) be the smallest cardinal supercompact in \(V_\lambda \) larger than \(\mu _i\), and let \(\nu =\sup _{i\in \omega }\mu _i\). By the lemma above, \(\nu <\kappa _1\). Suppose GCH.
Proposition 5.12
(Shi [19]) There is a generic extension of V such that  holds and if \(\mu \) is a cardinal supercompact in \(V_\lambda \), \(\mu \) is indestructible by the \(\mu \)-directed closed forcing.
holds and if \(\mu \) is a cardinal supercompact in \(V_\lambda \), \(\mu \) is indestructible by the \(\mu \)-directed closed forcing.
So, we can suppose that all \(\mu _i\) are closed under \(\mu _i\)-directed closed forcing.
Let \({\mathbb {A}}_\lambda \) be the reverse Easton iteration that is not trivial only on \(V_\lambda \)-supercompact cardinals limits of \(V_\lambda \)-supercompact cardinals, and if \(\eta \) is such a cardinal, \({\mathbb {Q}}_\eta \) is the forcing that adds \(\nu (\eta )^{++}\) subsets to \(\eta \), with conditions of size \(<\eta \), where \(\nu (\eta )\) is the sup of the \(\omega \) \(V_\lambda \)-supercompact cardinals above \(\eta \). As noted before, if \(\eta <\lambda \) then \(\nu (\eta )<\lambda \).
-
\({\mathbb {A}}_\lambda \) is directed closed, because each \({\mathbb {Q}}_\eta \) is \(<\eta \)-directed closed;
-
\({\mathbb {A}}_\lambda \) is \(\lambda \)-bounded, because for each \(\eta \), \(|{\mathbb {Q}}_\eta |=\nu (\eta )^\eta <\lambda \), and \(\lambda \) is strong limit;
-
\({\mathbb {A}}_\lambda \) is j-coherent, because its definition depends only on \(\lambda \).
Let E be generic for \({\mathbb {A}}_\lambda \). Then in V[E]:
-
by Theorem 3.10,
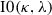 holds;
holds; -
by indestructibility, \(\kappa \) is \(V_\lambda \)-supercompact, and since the forcing is trivial from \(\kappa +1\) to \(\nu \), and closed enough, \(2^\kappa =\nu ^{++}\);
-
by Gitik–Sharon [9], there exists a \(\nu ^+\)-supercompactness measure on \(\kappa \).
We say that \(\pi \) is a \(\nu ^+\)-supercompactness measure on \(\kappa \) if  ,
,  and
and  .
.
Let U be the \(\nu ^+\)-supercompactness measure on \(\kappa \), and \(U_n\) the \(\mu _n\)-supercompactness measure on \(\kappa \) induced by U, i.e., \(X\in U_n\) iff \(\pi {``}\mu _n\in \pi (X)\).
Now the definition of the forcing is the same as Definition 5.4, with \(\mu _n\) instead of \(\kappa ^{+n}\): Let \(a,b\in {\mathscr {P}}_\kappa (\mu _n)\) and \(b\cap \kappa \in \kappa \). Set

Definition 5.13
\(p\in {\mathbb {Q}}\) if  , where
, where
-
\(\forall l<n\; a_l^p\in {\mathscr {P}}_\kappa (\mu _n)\) and \(a_l^p\cap \kappa \) is an inaccessible cardinal;
-
\(\forall m\geqslant n\), \(X_m^p\in U_m\);
-
\(\forall m\geqslant n\, \forall b\in X_m^p\, \forall l<n\; a_l^p\underset{\sim }{\subset } b\);
-
 .
.
For  , let us denote n as l(p). Moreover, for any collection of \(A_i\subseteq {\mathscr {P}}_\kappa (\mu _i)\), let \(\widetilde{\prod }_{n\in m}A_n\) be defined as in (1). For any collection of \(A_a\), \(a\in {\mathscr {P}}_\kappa (\mu _n)\), let
, let us denote n as l(p). Moreover, for any collection of \(A_i\subseteq {\mathscr {P}}_\kappa (\mu _i)\), let \(\widetilde{\prod }_{n\in m}A_n\) be defined as in (1). For any collection of \(A_a\), \(a\in {\mathscr {P}}_\kappa (\mu _n)\), let

It is a standard result that if each \(A_a\in U_n\), then \(\Delta A_a\in U_n\).
Definition 5.14
Let \(p,q\in {\mathbb {Q}}\). Then  if
if
-
\(l(p)=l(q)\);
-
\(\forall l<l(p)\; a_l^p=a_l^q\);
-
\(\forall m\geqslant l(p)\; X_m^p\subseteq X_m^q\).
Note that if G is generic for \({\mathbb {Q}}\) as above defined in V[E], \((2^{\kappa })^{V[E][G]}=(\nu ^{++})\). As \(\nu \) is collapsed to \(\kappa \), and no other cardinal is collapsed,  .
.
Theorem 5.15
(Neeman) If G is generic for \({\mathbb {Q}}\) as above defined in V[E], then  .
.
Similarly to the proof of Theorem 5.7 we have
Lemma 5.16
\({\mathbb {Q}}\) as above is \(\kappa \)-geometric.
Corollary 5.17
Suppose  . Then there exists a generic extension in which
. Then there exists a generic extension in which  holds.
holds.
Proof
The remarks above show that the hypotheses for Theorem 3.10 are satisfied: there are three preparation forcing notions (one for GCH, one for the indesctructibility of supercompactness, and one for blowing up the power of \(\kappa \)) and they are all reverse Easton iterations with the properties needed. The forcing \({\mathbb {Q}}\) is a subset of \(\prod _{n\in \omega }{\mathscr {P}}_\kappa (\mu _n)\), therefore in \(V[E]_{\kappa _1}\), by Lemma 5.11, and it is \(\kappa \)-geometric. So in V[E][H],  holds, but also (see above)
holds, but also (see above)  and
and  . \(\square \)
. \(\square \)
6 Tree property at the double successor
Some results can be achieved using the general procedure without much further effort. This is the case for the forcing introduced by Dobrinen and Friedman [5], to prove the tree property at a double successor of a singular cardinal.
Note that for  to hold, it must be that
to hold, it must be that  , so it is natural to ask whether
, so it is natural to ask whether  holds at the same time. This is another property that is implied by \(\Box _\kappa \).
holds at the same time. This is another property that is implied by \(\Box _\kappa \).
Definition 6.1
For any \(\kappa \) inaccessible, the forcing  is the set of subsets of \(2^{<\kappa }\) such that:
is the set of subsets of \(2^{<\kappa }\) such that:
-
\(s\in p\), \(t\subseteq s\rightarrow t\in p\);
-
each \(s\in p\) has a proper extension in p;
-
for any \(\alpha <\kappa \), if
 is a \(\subseteq \)-increasing sequence of elements of p, then \(\bigcup _{\beta <\alpha }s_\beta \in p\);
is a \(\subseteq \)-increasing sequence of elements of p, then \(\bigcup _{\beta <\alpha }s_\beta \in p\); -
there exists a club C(p) such that
 .
.
Extension is simply the inclusion.
Definition 6.2
For any \(\kappa \) inaccessible and \(\gamma (\kappa )\) the first weakly compact above it, \({{\mathrm{Sacks}}}^+(\kappa )\) is the \(\gamma (\kappa )\) iteration of  with supports of size \(\leqslant \kappa \).
with supports of size \(\leqslant \kappa \).
Let \({\mathbb {P}}\) be the reverse Easton forcing of length \(\lambda \) such that \({\mathbb {P}}_\alpha ={{\mathrm{Sacks}}}^+(\alpha )\). This forcing is clearly \(\lambda \)-bounded and j-coherent. [5, Fact 2.7] states that it is also closed. Moreover, [5, Theorem 3.2] shows that in the extension the tree property holds in the extension for \(\alpha ^{++}\), for any \(\alpha \) inaccessible.
Corollary 6.3
Suppose  . There exists a generic extension of V such that
. There exists a generic extension of V such that  holds.
holds.
Proof
Let \({\mathbb {P}}\) be  and \({\mathbb {Q}}\) be the Prikry forcing on \(\kappa \). Due to Theorem 3.10 and the remarks above, it suffices to show that \({\mathbb {Q}}\) is \(\kappa \)-geometric and it does not kill the tree property in \(\kappa ^{++}\). The first is Lemma 3.5, the second is [7, Theorem 2], and we are done. \(\square \)
and \({\mathbb {Q}}\) be the Prikry forcing on \(\kappa \). Due to Theorem 3.10 and the remarks above, it suffices to show that \({\mathbb {Q}}\) is \(\kappa \)-geometric and it does not kill the tree property in \(\kappa ^{++}\). The first is Lemma 3.5, the second is [7, Theorem 2], and we are done. \(\square \)
7 Open questions
The general procedure introduced in Theorem 3.10 has its own shortcomings. Among the many “Prikry-like” forcing notions, there are some that exploit the full supercompactness of one or many cardinals. A priori, this is not immediately useful: under  , \(\kappa \) is just \(\lambda \)-supercompact. Also, in [4] there is a proof that it is consistent to have \(\kappa \) less than the least supercompact, so it cannot be a consequence of I0. Thus, we can ask
, \(\kappa \) is just \(\lambda \)-supercompact. Also, in [4] there is a proof that it is consistent to have \(\kappa \) less than the least supercompact, so it cannot be a consequence of I0. Thus, we can ask
Question 7.1
Is \(\mathrm{I0} +L(V_{\lambda +1})\vDash (\kappa \text { is } \lambda ^+\text {-supercompact})\) consistent? If so, what is its consistency strength?
Note that we want \(\kappa \) to be supercompact in \(L(V_{\lambda +1})\) because the Prikry forcing in the general procedure must be in \(L(V_{\lambda +1})\), and as \(L(V_{\lambda +1})\) does not satisfy AC, but just \(\mathsf{DC}_\lambda \), asking for more than \(\lambda ^+\)-supercompactness can be improper.
It is also possible that there are ways to make the general procedure, always or just in some cases, obsolete. For now, there is no proof that I0 is needed for the consistency of I1 and the combinatorial properties above. The usual large cardinals analysis, in fact, many times has results that have the same large cardinal consistency: this case is different because, while usually one starts with a model with a large cardinal, forces the combinatorial property and proves that the large cardinal is intact, in this case the forcing “reflects” the large cardinal to a cardinal that had already the property desired. So we can ask
Question 7.2
Is it possible to have the results in Corollaries 4.10, 5.9, 5.17 and 6.3 with hypotheses weaker than I0? Or is it possible to have the consequences with hypotheses stronger than I1?
With generic absoluteness, it is already possible to raise I1 to  , with \(\alpha <\lambda \). An improvement of generic absolutness could improve also this, up to the so-called “internal I0”, i.e., the existence for any \(\alpha <\Theta \) of
, with \(\alpha <\lambda \). An improvement of generic absolutness could improve also this, up to the so-called “internal I0”, i.e., the existence for any \(\alpha <\Theta \) of  , but for I0 a different approach could be needed.
, but for I0 a different approach could be needed.
Notes
The Prikry condition is: for every \(p\in {\mathbb {P}}\) and for every \(\sigma \) statement in the forcing language, there exists
 such that
such that  or
or 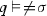 .
.The claim is in fact true in general, but in this case calculation is easier.
References
Cohen, P.J.: The independence of the Continuum Hypothesis. Proc. Nat. Acad. Sci. U.S.A. 50(6), 1143–1148 (1963)
Corazza, P.: The wholeness axiom and Laver sequences. Ann. Pure Appl. Logic 105(1–3), 157–260 (2000)
Dehornoy, P.: Elementary embeddings and algebra. In: Foreman, M., Kanamori, A. (eds.) Handbook of Set Theory, vol. 2, pp. 737–774. Springer, Dordrecht (2010)
Dimonte, V., Friedman, S.-D.: Rank-into-rank hypotheses and the failure of GCH. Arch. Math. Logic 53(3), 351–366 (2014)
Dobrinen, N., Friedman, S.-D.: The consistency strength of the tree property at the double successor of a measurable cardinal. Fund. Math. 208(2), 123–153 (2010)
Easton, W.B.: Powers of regular cardinals. Ann. Math. Logic 1(2), 139–178 (1970)
Friedman, S.-D., Halilović, A.: The tree property at \(\aleph _{\omega +2}\). J. Symbolic Logic 76(2), 477–490 (2011)
Gitik, M.: Prikry-type forcings. In: Foreman, M., Kanamori, A. (eds.) Handbook of Set Theory, vol. 2, pp. 1351–1447. Springer, Dordrecht (2010)
Gitik, M., Sharon, A.: On SCH and the approachability property. Proc. Amer. Math. Soc. 136(1), 311–320 (2008)
Kanamori, A.: The Higher Infinite. Perspectives in Mathematical Logic. Springer, Berlin (1994)
Kunen, K.: Elementary embeddings and infinitary combinatorics. J. Symbolic Logic 36(3), 407–413 (1971)
Laver, R.: On the algebra of elementary embeddings of a rank into itself. Adv. Math. 110(2), 334–346 (1995)
Laver, R.: Implications between strong large cardinal axioms. Ann. Pure Appl. Logic 90(1–3), 79–90 (1997)
Mathias, A.R.D.: On sequences generic in the sense of Prikry. J. Austral. Math. Soc. 15, 409–414 (1973)
Merimovich, C.: Extender-based Radin forcing. Trans. Amer. Math. Soc. 355(5), 1729–1772 (2003)
Neeman, I.: Aronszajn trees and failure of the singular cardinal hypothesis. J. Math. Log. 9(1), 139–157 (2009)
Prikry, K.L.: Changing Measurable into Accessible Cardinals. Dissertationes Mathematicae, vol. 68. PAN, Warsaw (1970)
Scott, D.: Measurable cardinals and constructible sets. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 9, 521–524 (1961)
Shi, X.: Axiom \(I_0\) and higher degree theory. J. Symbolic Logic 80(3), 970–1021 (2015)
Silver, J.: On the singular cardinals problem. In: James, R.D. (ed.) Proceedings of the International Congress of Mathematicians (Vancouver, 1974), vol. 1, pp. 265–268. Canadian Mathematical Congress, Montreal (1975)
Solovay, R.M.: Strongly compact cardinals and the GCH. In: Henkin, L., et al. (eds.) Proceedings of the Tarski Symposium. Proceedings of Symposia in Pure Mathematics, vol. 25, pp. 365–372. American Mathematical Society, Providence (1974)
Woodin, W.H.: Suitable extender models II: beyond \(\omega \)-huge. J. Math. Log. 11(2), 115–436 (2011)
Author information
Authors and Affiliations
Corresponding author
Additional information
Vincenzo Dimonte would like to thank the FWF (Austrian Science Fund) for its generous support through the project M 1514-N25, and the kind hospitality of the Kurt Gödel Research Center, Beijing Normal University and the Chinese Academy of Sciences. Liuzhen Wu would like to acknowledge the support through the funding Projects NSFC 11321101 and 11401567.
Rights and permissions
About this article
Cite this article
Dimonte, V., Wu, L. A general tool for consistency results related to I1. European Journal of Mathematics 2, 474–492 (2016). https://doi.org/10.1007/s40879-015-0092-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-015-0092-y



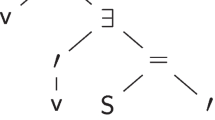

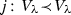 .
. .
.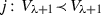 .
. with
with  .
.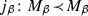 is the ultrapower via W, then
is the ultrapower via W, then 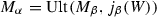 and
and  is a collection of open dense sets, then for every
is a collection of open dense sets, then for every  if
if  , otherwise;
, otherwise; , consisting of °-increasing sequences. All splittings in T are required to be on sets in
, consisting of °-increasing sequences. All splittings in T are required to be on sets in 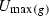 , i.e., for every
, i.e., for every  then the set
then the set 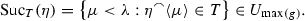
 ,
, 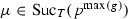 ,
,  .
. is not permitted for
is not permitted for  projects
projects 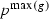 onto
onto 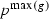 and
and  .
. ,
, 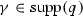 ,
, 
 is the largest such that
is the largest such that 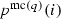 is not permitted for
is not permitted for  projects
projects  into
into  and
and 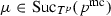 , if
, if  .
.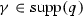 ,
, 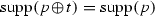 ;
; ;
; ;
; ,
, 
 is well-defined, i.e.,
is well-defined, i.e.,  . This is true due to Definition
. This is true due to Definition  . This is true because
. This is true because  ,
, 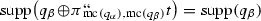
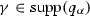 ,
,  . By definition, and since
. By definition, and since 
 is not permitted by
is not permitted by  , therefore by Definition
, therefore by Definition 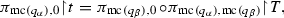
 is in
is in  . First of all,
. First of all, 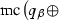
 . By definition,
. By definition, 
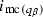 as above. By Definition
as above. By Definition  , and therefore
, and therefore 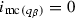 , so the point follows simply by definition of
, so the point follows simply by definition of  .
. projects
projects  . By definition,
. By definition,  , so this is true by Definition
, so this is true by Definition  and
and  then
then 
 means that it is also permitted for
means that it is also permitted for  ;
; is a scale, i.e. such that for every
is a scale, i.e. such that for every  there exists a club C of
there exists a club C of 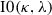 holds;
holds; .
. is a
is a  .
. such that
such that  or
or 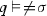 .
.