Abstract
The ring of constants of Lotka–Volterra derivations is determined in arbitrary dimension. It is always a polynomial ring.
Similar content being viewed by others
1 Introduction
Let \(n>2\) be an integer,  the n-variable polynomial ring over the field K of characteristic 0. A derivation of R is a K-linear map \(\delta :R\rightarrow R\) that satisfies the Leibniz rule
the n-variable polynomial ring over the field K of characteristic 0. A derivation of R is a K-linear map \(\delta :R\rightarrow R\) that satisfies the Leibniz rule  for every pair of polynomials. By this identity, the values at the generators \(\delta (x_i)=g_i\in R\), \(i=1,\ldots ,n\), determine \(\delta \). Another way of expressing this is
for every pair of polynomials. By this identity, the values at the generators \(\delta (x_i)=g_i\in R\), \(i=1,\ldots ,n\), determine \(\delta \). Another way of expressing this is

The polynomial \(f\in R\) is a constant of the derivation \(\delta \) if \(\delta (f)=0\). The set of constants of R is a subalgebra of R due to the Leibniz rule, we shall denote it \(R^\delta \). A central problem concerning derivations is to describe their rings of constants. There is no general procedure for determining \(R^\delta \) and it may be neither a polynomial ring nor a finitely generated ring (see [5] for more details).
Given parameters \(C_i\in K\), \(i=1,\ldots , n\), the Lotka–Volterra derivation d is defined on the generators as
where (and further on) the indexing is circular, that is \(n+e\) and e are identified for every integer e. The special case of the Volterra derivation, where all \(C_i=1\), was considered in [2]. In the present paper we shall observe a confirmation why the Volterra case is remarkable. The case \(n=3\) for arbitrary parameters \(C_i\) was considered in the paper [4]. Here we assume \(n>3\).
The Lotka–Volterra derivations are a type of factorizable derivations, that is, derivations defined by \(d(x_i)=x_if_i\), where \(f_i\) are polynomials of degree 1 for \(i=1,\ldots ,n\). We may associate the factorizable derivation with any given derivation of a polynomial ring, this helps to determine constants of arbitrary derivations (see, for example, [3]). Moreover, Lotka–Volterra systems play a significant role in population biology, laser physics and plasma physics (see for instance [1] and references therein).
Before stating the main theorem, we define the generating polynomials. Let  . Take any nonempty subset \({\mathcal {A}}\subseteq \mathbb {Z}_n\) of integers mod n closed under \(i\mapsto i+2\). If n is odd then \({\mathcal {A}}=\mathbb {Z}_n\); for n even we have two additional proper subsets
. Take any nonempty subset \({\mathcal {A}}\subseteq \mathbb {Z}_n\) of integers mod n closed under \(i\mapsto i+2\). If n is odd then \({\mathcal {A}}=\mathbb {Z}_n\); for n even we have two additional proper subsets  and
and  . Given \(\mathcal {A}\), let \(C_i\), \(i\in {\mathcal {A}}\), be positive rational numbers such that
. Given \(\mathcal {A}\), let \(C_i\), \(i\in {\mathcal {A}}\), be positive rational numbers such that  . Then there exist unique coprime positive integers \(\theta _i\), \(i\in {\mathcal {A}}\), such that \(\theta _{i+2}=C_i\theta _i\). (Indeed, the rational vectors \((\tau _i)_{i\in {\mathcal {A}}}\) form a 1-dimensional subspace because of fixed positive ratios. Hence if we take the given positive rational vectors, then multiplying by the smallest common denominator and dividing by the greatest common divisor of the numerators we obtain \((\theta _i)_{i\in {\mathcal {A}}}\).) Let us define \(g_{\mathcal {A}}=\prod _{i\in {\mathcal {A}}} x_i^{\theta _i}\). Let
. Then there exist unique coprime positive integers \(\theta _i\), \(i\in {\mathcal {A}}\), such that \(\theta _{i+2}=C_i\theta _i\). (Indeed, the rational vectors \((\tau _i)_{i\in {\mathcal {A}}}\) form a 1-dimensional subspace because of fixed positive ratios. Hence if we take the given positive rational vectors, then multiplying by the smallest common denominator and dividing by the greatest common divisor of the numerators we obtain \((\theta _i)_{i\in {\mathcal {A}}}\).) Let us define \(g_{\mathcal {A}}=\prod _{i\in {\mathcal {A}}} x_i^{\theta _i}\). Let  .
.
Our main results are the following two theorems.
Theorem 1.1
Let d be the Lotka–Volterra derivation with parameters \(C_1,\ldots ,C_n\). Then the ring of constants \(R^d\) is a polynomial algebra. Assume that not all parameters are equal to 1 and \(n>4\). Then the number of generators is equal to
-
0 if \(\prod C_i\ne 1\) and no \(g_{\mathcal {A}}\) is defined;
-
3 if n is even and both \(g_{\mathcal {E}}\) and \(g_{\mathcal {O}}\) are defined;
-
2 if n is odd and \(g_{\mathbb {Z}_n}\) is defined, or n is even and \(\prod C_i=1\) but only one of \(g_{\mathcal {E}}\) and \(g_{\mathcal {O}}\) is defined;
-
1 if \(\prod C_i=1\) but no \(g_{\mathcal {A}}\) is defined, or n is even and \(\prod C_i\ne 1\) but only one of \(g_{\mathcal {E}}\) and \(g_{\mathcal {O}}\) is defined.
Suppose now that \(n=4\). In this case there is a further quadratic invariant if  and there are two consecutive indices such that both corresponding parameters are equal to 1. Assume \(C_1=C_2=1\) and
and there are two consecutive indices such that both corresponding parameters are equal to 1. Assume \(C_1=C_2=1\) and  (for the other possibilities one has to rotate the indices appropriately), then
(for the other possibilities one has to rotate the indices appropriately), then

If \(C_1=C_2=C_3=1\) and  then this procedure would give two possibilities for \(f_4\), they differ by
then this procedure would give two possibilities for \(f_4\), they differ by  . As \(4x_1x_3=4g_{\mathcal {O}}\), which is defined in this case, one of the two possibilities for \(f_4\) is sufficient.
. As \(4x_1x_3=4g_{\mathcal {O}}\), which is defined in this case, one of the two possibilities for \(f_4\) is sufficient.
Theorem 1.2
Assume \(n=4\) and let d be the Lotka–Volterra derivation with parameters \(C_1,\ldots ,C_4\). Then the ring of constants \(R^d\) is a polynomial algebra. If not all parameters are equal to 1 then the number of generators is equal to
-
0 if \(\prod C_i\ne 1\) and none of \(g_{\mathcal {O}},g_{\mathcal {E}},f_4\) is defined;
-
3 if both \(g_{\mathcal {E}}\) and \(g_{\mathcal {O}}\) are defined;
-
2 if \(\prod C_i=1\) but only one of \(g_{\mathcal {E}}\) and \(g_{\mathcal {O}}\) is defined or one of parameters is equal to
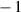 and the other three are equal to 1;
and the other three are equal to 1; -
1 if \(\prod C_i=1\) but \(g_{\mathcal {O}},g_{\mathcal {E}}\) are not defined, or
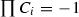 and only two consecutive parameters are equal to 1, or
and only two consecutive parameters are equal to 1, or 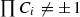 but one of \(g_{\mathcal {O}},g_{\mathcal {E}}\) is defined.
but one of \(g_{\mathcal {O}},g_{\mathcal {E}}\) is defined.
It is not stated explicitly in the theorems but the generators are always those polynomials \(g_{\mathcal {A}}\) that are defined together with f if \(\prod C_i=1\) (or together with \(f_4\) if \(n=4\),  and two consecutive parameters are equal to 1). Denote by \({\mathcal {H}}\) this set of generators. (If n is even and both \(g_{\mathcal {E}}\) and \(g_{\mathcal {O}}\) are defined, then of course \(g_{\mathbb {Z}_n}\) is also defined. But it is superfluous in the generating set because \(g_{\mathbb {Z}_n}=g_{\mathcal {E}}g_{\mathcal {O}}\).)
and two consecutive parameters are equal to 1). Denote by \({\mathcal {H}}\) this set of generators. (If n is even and both \(g_{\mathcal {E}}\) and \(g_{\mathcal {O}}\) are defined, then of course \(g_{\mathbb {Z}_n}\) is also defined. But it is superfluous in the generating set because \(g_{\mathbb {Z}_n}=g_{\mathcal {E}}g_{\mathcal {O}}\).)
It is routine to check, see Lemma 2.1, that f is a constant if and only if \(\prod C_i=1\), each \(g_{\mathcal {A}}\) is constant if defined and \(f_4\) is a constant if \(n=4\), \(C_1=C_2=1\), and  .
.
The statements of theorems are similar to [2, Theorem 1.1] where all parameters are equal to 1 and there are  free generators of the ring of constants. As it was noted there, the surprising feature is that the generators are independent. This phenomenon might deserve further study.
free generators of the ring of constants. As it was noted there, the surprising feature is that the generators are independent. This phenomenon might deserve further study.
The outline of proofs of theorems is also similar to the proof of [2, Theorem 1.1] subject to new complications related to arithmetic properties of parameters \(C_i\) which require different arguments in different cases.
The case \(n=4\) was also investigated in [6]. The problem is solved there for parameters such that \(C_1C_2C_3C_4\) is either 1 or not a root of unity. The last sentence of the statement in [6, Lemma 3.2] is not correct. The assumption should be \((C_1\cdots C_n)^m\ne 1\) instead of \(C_1\cdots C_n\ne 1\). In this paper we treat the more difficult case, when \(C_1C_2C_3C_4\ne 1\) is a root of unity. See Propositions 2.10 and 2.11.
2 Proofs
We prove Theorems 1.1 and 1.2 simultaneously, indicating the differences along the way. The proof splits into three parts. First, we show that the polynomials are indeed in the kernel of d. Second, that any polynomial in \(R^d\) can be expressed as a polynomial of elements of \(\mathcal {H}\). And finally, that they are algebraically independent. As the case \(n=4\) requires a special attention, Proposition 2.10 will be partly replaced by Proposition 2.11.
Before embarking on the proof we make a short observation. The polynomial ring has a grading \(R=\bigoplus _{a=0}^\infty R_a\), where \(R_a\) is the K-vectorspace of homogeneous polynomials of degree a. The derivation d admits this grading of R, more precisely, \(d(R_a)\subseteq R_{a+1}\). So the ring of constants has a grading  . In particular, if a polynomial is a constant of d, then so are all its homogeneous components. For a polynomial \(g\in R\) let M(g) denote the set of monomials occurring in g with a nonzero coefficient.
. In particular, if a polynomial is a constant of d, then so are all its homogeneous components. For a polynomial \(g\in R\) let M(g) denote the set of monomials occurring in g with a nonzero coefficient.
Let \(m=\prod _{i=1}^n x_i^{\alpha _i}\) be a monomial, then

That is, the coefficient of \(mx_i\) in d(m) is \(\alpha _{i+1}-C_{i-1}\alpha _{i-1}\). So
Looking at it from the back end, consider the monomial \(m'=\prod _{i=1}^n x_i^{\beta _i}\). Then

Now let us proceed with the first part of the proof.
Lemma 2.1
The elements of \(\mathcal {H}\) are in \(R^d\).
Proof
If \(\prod C_i=1\) then

If \(\prod _{i\in {\mathcal {A}}}C_i=1\) and each factor is positive and rational then \(g_{\mathcal {A}}\) is defined and

If \(n=4\), \(C_1=C_2=1\),  , then \(f_4\) is defined and
, then \(f_4\) is defined and

\(\square \)
The following proposition is technical in nature. Its function is to provide a tool for showing that if one monomial is in M(h), \(h\in R^d\), then many others are there as well. This to work we have to assume that for indices i (outside the examined area) either \(\beta _i=0\) or \(\beta _{i-1}=\beta _{i+1}=0\) so that by (2) the exponent of \(x_i\) might not decrease. It is not powerful enough in every case, so partial extensions are necessary in Propositions 2.10 and 2.11.
Proposition 2.2
Let \(m=\prod x_{\scriptscriptstyle i}^{\scriptscriptstyle \beta _i}\) be a monomial in M(h) for some \(h\in R^d\) and let \(1\leqslant j\leqslant n\) be an index such that \(C_j>0\). Assume that \(\beta _{j-1}=0=\beta _{j+3}\) and for every \(i<j-1\) or \(i>j+2\) one of \(\beta _i\) and \(\beta _{i+1}\) is zero. Further put \(r=\beta _{j+2}+\beta _{j+1}-C_j\beta _j\). Then there exists an integer \(t_0\geqslant r\) such that \(s_0=(r-t_0)/C_j\) is also an integer and

Conversely, if

then \(s_0\leqslant s\leqslant t\leqslant t_0\). If \(C_{j+1}\ne 0\), then

too. If \(C_{j+1}=0\) then \(r\leqslant \beta _{j+1}\).
Proof
Denote by \(e_{s,t}\) the coefficient of  in h. We have
in h. We have  and would like to conclude that \(e_{t,t}\ne 0\) for some \(t\geqslant r\).
and would like to conclude that \(e_{t,t}\ne 0\) for some \(t\geqslant r\).
We observe that the coefficient of  in d(h) is equal to
in d(h) is equal to

Note that no other monomial might contribute to  by our assumption on the exponents and by (2). See the comment preceding the proposition.
by our assumption on the exponents and by (2). See the comment preceding the proposition.
Pick the minimal \(s_0\) such that there exists some t for which \(e_{s_0,t}\ne 0\). (We have \(s_0\leqslant 0\), since \(e_{0,\beta _{j+1}}\ne 0\).) Consider the set  . Of course, \(\max T\leqslant \beta _{j+2}+\beta _{j+1}\) and \(\min T\geqslant s_0\). From (3) it follows that if \(t\in T\) then \(t+1\in T\) unless possibly for \(t=t_0=r-C_js_0\). If \(t_0\) is not an integer or if it happens that \(\max T>t_0\) then T is not bounded from above, a contradiction. So \(\max T=t_0\) must be an integer.
. Of course, \(\max T\leqslant \beta _{j+2}+\beta _{j+1}\) and \(\min T\geqslant s_0\). From (3) it follows that if \(t\in T\) then \(t+1\in T\) unless possibly for \(t=t_0=r-C_js_0\). If \(t_0\) is not an integer or if it happens that \(\max T>t_0\) then T is not bounded from above, a contradiction. So \(\max T=t_0\) must be an integer.
Pick the maximal \(t_1\) such that there exists some s for which \(e_{s,t_1}\ne 0\). (By the above, \(t_1\geqslant t_0\geqslant r\) and, by assumption, \(t_1\geqslant \beta _{j+1}\).) Let  . Again
. Again  and \(\max S\leqslant t_1\). From (3) it follows that if \(s-1\in S\) then \(s\in S\) unless possibly for \(s=s_1=(r-t_1)/C_j\) or \(s=t_1+1\). If \(s_1\) is not an integer or if it happens that \(\min S<s_1\) then S is not bounded from below, a contradiction. So \(s_1=\min S\) must be an integer and \(S=[s_1;t_1]\cap \mathbb {Z}\).
and \(\max S\leqslant t_1\). From (3) it follows that if \(s-1\in S\) then \(s\in S\) unless possibly for \(s=s_1=(r-t_1)/C_j\) or \(s=t_1+1\). If \(s_1\) is not an integer or if it happens that \(\min S<s_1\) then S is not bounded from below, a contradiction. So \(s_1=\min S\) must be an integer and \(S=[s_1;t_1]\cap \mathbb {Z}\).
By minimality, we have \(s_0\leqslant s_1\) so \(r-t_0=C_js_0\leqslant C_js_1=r-t_1\leqslant r-t_0\). Hence \(s_1=s_0\) and \(t_1=t_0\). Thus \(e_{s,t}\ne 0\) implies \(s_0\leqslant s\leqslant t\leqslant t_0\). The previous paragraph also implies that \(e_{s,t_0}\ne 0\) for \(s_0\leqslant s\leqslant t_0\), as claimed.
If \(C_{j+1}=0\) then by (3) we get \(0\ne e_{s-1,\beta _{j+1}}\Leftarrow 0\ne e_{s,\beta _{j+1}}\) unless possibly for \(s=(r-\beta _{j+1})/C_j\). As \(e_{0,\beta _{j+1}}\ne 0\) we must have \(s=(r-\beta _{j+1})/C_j\leqslant 0\) is an integer, as claimed.
If \(C_{j+1}\ne 0\) then by (3) we also have that \(t+1\in T\) implies \( t\in T\) unless possibly for \(t=s_0-1\). So \(T=[s_0;t_0]\cap \mathbb {Z}\), so \(0\ne e_{s_0,s_0}\). \(\square \)
In the following proposition the coefficients are determined. The monomial can be chosen to be  from the previous proposition.
from the previous proposition.
Proposition 2.3
Let \(h\in R^d\) and \(m=\prod x_{\scriptscriptstyle i}^{\scriptscriptstyle \beta _i}\) be a monomial in M(h) with the coefficient equal to A. Let \(1\leqslant j_0\leqslant n\) be an index such that  implies \(p,q\geqslant 0\). Assume that for every \(i<j_0\) or \(i>j_0+2\) one of \(\beta _i\) and \(\beta _{i+1}\) is zero and that \(\beta _{j_0+2}-\beta _{j_0}C_{j_0}=0\).
implies \(p,q\geqslant 0\). Assume that for every \(i<j_0\) or \(i>j_0+2\) one of \(\beta _i\) and \(\beta _{i+1}\) is zero and that \(\beta _{j_0+2}-\beta _{j_0}C_{j_0}=0\).
-
(i)
If \(C_{j_0}\ne 0\) then
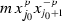 has the coefficient equal to
has the coefficient equal to 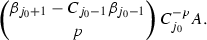
-
(ii)
If \(C_{j_0+1}=0=\beta _{j_0+3}\) then
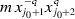 has the coefficient equal to 0. If \(C_{j_0+1}\ne 0\) then
has the coefficient equal to 0. If \(C_{j_0+1}\ne 0\) then 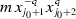 has the coefficient equal to $$\begin{aligned} {\beta _{j_0+1}-\beta _{j_0+3}/C_{j_0+1}\atopwithdelims ()q}\,C_{j_0+1}^{q}A. \end{aligned}$$
has the coefficient equal to $$\begin{aligned} {\beta _{j_0+1}-\beta _{j_0+3}/C_{j_0+1}\atopwithdelims ()q}\,C_{j_0+1}^{q}A. \end{aligned}$$ -
(iii)
Assume \(C_{j_0}\ne 0\) and \(\beta _{j_0-1}=0=\beta _{j_0+3}\). Suppose \(C_{j_0}\) is not positive rational or \(C_{j_0}=a/b\) with \((a,b)=1\) and \(p<a\) or \(q<b\). Then the coefficient of
 is equal to
is equal to 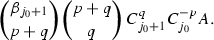
Proof
Let \(f_{p,q}\) denote the coefficient of  in M(h). By assumption, \(f_{p,q}=0\) if \(p<0\) or \(q<0\). As in the previous proof the coefficient of
in M(h). By assumption, \(f_{p,q}=0\) if \(p<0\) or \(q<0\). As in the previous proof the coefficient of  in d(h) is equal to
in d(h) is equal to
Let us first show (i). Put \(q=0\) and \(t=\beta _{j_0+1}-C_{j_0-1}\beta _{j_0-1}\). Then

By induction it implies  . Similarly, if \(C_{j_0+1}=0=\beta _{j_0+3}\) then \(qf_{0,q}=\beta _{j_0+3} f_{0,q-1}=0\). If \(C_{j_0+1}\ne 0\) then put \(t=\beta _{j_0+1}-\beta _{j_0+3}/C_{j_0+1}\) and
. Similarly, if \(C_{j_0+1}=0=\beta _{j_0+3}\) then \(qf_{0,q}=\beta _{j_0+3} f_{0,q-1}=0\). If \(C_{j_0+1}\ne 0\) then put \(t=\beta _{j_0+1}-\beta _{j_0+3}/C_{j_0+1}\) and

So  as claimed in (ii). To obtain (iii), let \(t=\beta _{j_0+1}\). Equality (4) simplifies to
as claimed in (ii). To obtain (iii), let \(t=\beta _{j_0+1}\). Equality (4) simplifies to

By (i) and (ii), the claim is true for \(p=0\) or \(q=0\) and we may apply induction on \(p+q\) as long as \(0<p,q\) but \(p<a\) or \(q<b\). These conditions imply \(0\ne q-pC_{j_0}\) so from the above and by the inductive assumption, we obtain

\(\square \)
The second and most difficult part of the proof of Theorems 1.1 and 1.2 is the following.
Lemma 2.4
If \(h\in R\) is such that \(d(h)=0\) then it is a polynomial in the elements of \({\mathcal {H}}\).
Proof
As the indexing of variables in the definition of the derivation is circular, we have freedom to choose the starting index. Not all of parameters are equal to 1 so without loss of generality we can assume that \(C_n\ne 1\). We would also choose \(C_n\ne 0\) if possible. That is impossible only if all parameters take values in the set \(\{0,1\}\). In this case either all parameters are equal to 0 or there is one parameter equal to 1 following another parameter equal to 0, then we let \(C_n=0\) and \(C_1=1\).
Clearly, it is enough to prove the lemma for homogeneous polynomials, so let \(h\in R_a\). We use the standard lexicographic ordering on monomials of \(R_a\). That is,  if \(\alpha _i<\beta _i\) at the first index that they are not equal. For a homogenous polynomial \(k\in R_a\) the leading monomial is the lexicographically largest monomial in M(k).
if \(\alpha _i<\beta _i\) at the first index that they are not equal. For a homogenous polynomial \(k\in R_a\) the leading monomial is the lexicographically largest monomial in M(k).
Assume by induction that h has lexicographically the smallest leading monomial among all homogenous polynomials that are counterexamples to the lemma. We prove that there is a polynomial expression F of the elements of \({\mathcal {H}}\) that has the same leading monomial (of course, it can have also the same coefficient, we may assume that the coefficient is equal to 1). So \(h-F\) has only lexicographically smaller monomials and hence can be expressed by induction. This will finish the proof of the lemma.
Let \(m_1=\prod _{i=1}^n x_{\scriptscriptstyle i}^{\scriptscriptstyle \alpha _i}\) be the leading monomial of h. The following two propositions describe the exponents of the leading monomial in detail. The first one implies that the even-indexed exponents of \(m_1\) are determined by \(\alpha _n=\alpha _0\), namely, for every \(n/2\geqslant i\geqslant 1\) we have  . Indeed, if it fails for some even indices then for the smallest such index
. Indeed, if it fails for some even indices then for the smallest such index  all assumptions of the proposition would hold. But the conclusion \(m_1\notin M(h)\) would contradict the original choice of \(m_1\in M(h)\). \(\square \)
all assumptions of the proposition would hold. But the conclusion \(m_1\notin M(h)\) would contradict the original choice of \(m_1\in M(h)\). \(\square \)
Proposition 2.5
Suppose \(m=\prod _{i=1}^n x_{\scriptscriptstyle i}^{\scriptscriptstyle \gamma _i}\) is a monomial and r is a positive integer with the following properties:
-
(i)
\(\gamma _n=\alpha _n\);
-
(ii)
\(\gamma _{2i-1}=\alpha _{2i-1}\) for \(1\leqslant i\leqslant r\);
-
(iii)
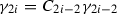 for \(1\leqslant i\leqslant r-1\);
for \(1\leqslant i\leqslant r-1\); -
(iv)
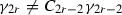 .
.
Then \(m\notin M(h)\).
Proof
Assume by contradiction that \(m\in M(h)\). The proof is by induction on r. Let \(r=1\). The coefficient of \(mx_1\) in d(m) is \(\gamma _2-C_n\alpha _n\ne 0\), see the line before (1). In turn, by (2), it may occur only in \(M(d(mx_1/x_i))\) for any index i. However, by the assumption, \(\gamma _1=\alpha _1\) so we have  for \(i>1\). By maximality of \(m_1\), these are not in M(h) so \(mx_1\) cannot be canceled. This contradiction establishes the proposition for \(r=1\) for every monomial.
for \(i>1\). By maximality of \(m_1\), these are not in M(h) so \(mx_1\) cannot be canceled. This contradiction establishes the proposition for \(r=1\) for every monomial.
Assume now \(r>1\) and that for \(r'<r\) the proposition holds for every monomial. Suppose the set  is nonempty. Let \(r'\) be its smallest element. As assumptions of the proposition hold for \(m=m_1\) and \(r=r'\) but the conclusion \(m_1\notin M(h)\) does not, we must have \({\mathcal {S}}=\varnothing \). In other words,
is nonempty. Let \(r'\) be its smallest element. As assumptions of the proposition hold for \(m=m_1\) and \(r=r'\) but the conclusion \(m_1\notin M(h)\) does not, we must have \({\mathcal {S}}=\varnothing \). In other words,

As in the first paragraph, \(mx_{2r-1}\) has the nonzero coefficient equal to \(\gamma _{2r}-C_{2r-2}\gamma _{2r-2}\) in d(m). Again, by (2), this may occur only in \(M(d(mx_{2r-1}/x_i))\) for some index i. If \(i>2r-1\) then, by virtue of (5),  so it cannot be in M(h). If \(i<2r-1\) is odd then, by assumption (iii), the coefficient of \(mx_{2r-1}\) is \(\gamma _{i+1}-C_{i-1}\gamma _{i-1}=0\) in \(d(mx_{2r-1}/x_i)\) so it cannot help in canceling the coefficient \(\gamma _{2r}-C_{2r-2}\gamma _{2r-2}\) of \(mx_{2r-1}\) in d(m).
so it cannot be in M(h). If \(i<2r-1\) is odd then, by assumption (iii), the coefficient of \(mx_{2r-1}\) is \(\gamma _{i+1}-C_{i-1}\gamma _{i-1}=0\) in \(d(mx_{2r-1}/x_i)\) so it cannot help in canceling the coefficient \(\gamma _{2r}-C_{2r-2}\gamma _{2r-2}\) of \(mx_{2r-1}\) in d(m).
If however \(i=2r'<2r-1\) is even then \(mx_{2r-1}/x_i\) satisfies assumptions of the proposition with \(r'\). So, by induction, \(mx_{2r-1}/x_i\notin M(h)\). This proves that if \(m\in M(h)\) then \(d(h)\ne 0\). This contradiction establishes the proposition. \(\blacksquare \)
Remark 2.6
In fact, in the proof we used (i’) \(C_n\gamma _n=C_n\alpha _n\), so the lemma holds if we assume \(C_n=0\) instead of (i). It implies \(\alpha _{2i}=0\) for all \(i\leqslant n/2\).
Proposition 2.7
Suppose \(m=\prod _{i=1}^n x_{\scriptscriptstyle i}^{\scriptscriptstyle \gamma _i}\in M(h)\) is a monomial and \(r<n/2\) is a positive integer with the following properties:
-
(i)
\(\gamma _n=\alpha _n\) (or \(C_n=0)\);
-
(ii)
\(\gamma _{2i-1}=\alpha _{2i-1}\) for \(1\leqslant i\leqslant r\);
-
(iii)
\(\gamma _{2i}=\alpha _{2i}\) for \(1\leqslant i\leqslant r\).
Then there exists a nonnegative integer \(\beta _{2r-1}\) such that \(C_{2r-1}(\gamma _{2r-1}-\beta _{2r-1})=\gamma _{2r+1}\) and \(m'=m(x_{2r}/x_{2r-1})^{\beta _{2r-1}}\in M(h)\). In particular, there exist nonnegative integers \(\beta '_{2i-1}\) such that \(C_{2i-1}(\alpha _{2i-1}-\beta '_{2i-1})=\alpha _{2i+1}\) for \(1\leqslant i<n/2\).
Proof
The proof is by contradiction. Assume that there exists the smallest positive integer r for which there is no such nonnegative integer \(\beta _{2r-1}\). Let \(m_2\in M(h)\). Suppose that
Denote by s the exponent of \(x_{2r-1}\) and by t the exponent of \(x_{2r}\) in \(m_2/m\). We claim that \(s+t\leqslant 0\), which we prove by (decreasing) induction on s.
As \(m_1\) is the leading monomial, \(s\leqslant 0\). If \(s=0\), then \(t\leqslant 0\), indeed. So let \(s<0\). If \(t\leqslant 0\), then we are done, so assume \(t>0\). Hence, by (1), the monomial \(m_2x_{2r-1}\in M(d(m_2))\) has the coefficient equal to  if \(r>1\), by Proposition 2.5, assumption (iii) and equation (6). If \(r=1\) and \(C_n>0\) then the coefficient of \(m_2x_1\) in \(d(m_2)\) is at least \(t+\gamma _2-C_n\gamma _n=t>0\), so \(m_2x_{2r-1}\in M(d(m_2))\). If \(r=1\) and \(C_n\ngtr 0\) then \(\gamma _2=\alpha _2=C_n\alpha _n=C_n\gamma _n=0\) and the coefficient of \(m_2x_1\) in \(d(m_2)\) is \(t>0\). So \(m_2x_{2r-1}\in M(d(m_2))\) also in this case.
if \(r>1\), by Proposition 2.5, assumption (iii) and equation (6). If \(r=1\) and \(C_n>0\) then the coefficient of \(m_2x_1\) in \(d(m_2)\) is at least \(t+\gamma _2-C_n\gamma _n=t>0\), so \(m_2x_{2r-1}\in M(d(m_2))\). If \(r=1\) and \(C_n\ngtr 0\) then \(\gamma _2=\alpha _2=C_n\alpha _n=C_n\gamma _n=0\) and the coefficient of \(m_2x_1\) in \(d(m_2)\) is \(t>0\). So \(m_2x_{2r-1}\in M(d(m_2))\) also in this case.
This monomial may also occur only in \(M(d(m_2x_{2r-1}/x_i))\) for some indices i. If \(i<2r-1\) is even then, by Proposition 2.5, it does not occur in M(h). (Note that here \(r>1\), so the exponent of \(x_n\) is \(\gamma _n\) in \(m_2x_{2r-1}/x_i\), so all assumptions of Proposition 2.5 are satisfied. If \(C_n=0\) then see Remark 2.6.) If \(i<2r-1\) is odd then \(\gamma _{i+1}-C_{i-1}\gamma _{i-1}=0\) is the coefficient of \(m_2x_{2r-1}\) in \(d(m_2x_{2r-1}/x_i)\). Otherwise \(i>2r-1\). Now we apply induction for \(m_2x_{2r-1}/x_r\) which still satisfies the conditions of (6), unless \(r>1\), \(i=n\) and \(C_n\ne 0\). If induction applies then the exponent of \(x_{2r-1}\) is equal to \(s+1\) and the exponent of \(x_{2r}\) is equal to t or \(t-1\), their sum is at least \(s+t\). But, by induction, their sum is at most 0, hence \(s+t\leqslant 0\).
If, however, induction does not apply then \(m_3=m_2x_{2r-1}/x_n\in M(h)\). Hence \(m_3x_1\in M(d(m_3))\) has the coefficient equal to \(\gamma _2-C_n(\gamma _n-1)=C_n\ne 0\). Now, for a monomial \(m_4=m_3x_1/x_l\in M(h)\) to cancel this the exponent of \(x_1\) is \(\gamma _1+1=\alpha _1+1\) in \(m_4\), so  , a contradiction. So in fact, induction must apply and we conclude \(s+t\leqslant 0\), as claimed.
, a contradiction. So in fact, induction must apply and we conclude \(s+t\leqslant 0\), as claimed.
We claim next that for every \(0\leqslant l\) the monomial \(m_1(x_{2r}/x_{2r-1})^{l}\in M(h)\). This is proved by induction on l. The case \(l=0\) is given, so let \(l>0\) and put \(m=m_1(x_{2r}/x_{2r-1})^{l-1}\in M(h)\). By the assumption on exponents, \(mx_{2r}\in M(d(m))\), the coefficient is \(\alpha _{2r+1}-C_{2r-1}(\alpha _{2r-1}-l+1)\ne 0\) as we argue by contradiction.
To cancel this from d(h) there must exist a monomial \(m_2=mx_{2r}/x_i\in M(h)\). If \(2<2r<i<n\) or \(2=2r<i\) then we contradict the above claim on \(s+t\). (In our situation \(s=1-l\), \(t=l\) and the conditions of (6) are satisfied.) If, however, \(r>1\) and \(i=n\) then \(mx_{2r}/x_n\in M(h)\) so \(mx_{2r}x_1/x_n\in M(d(mx_{2r}/x_n))\) has the coefficient \(\gamma _2-C_n(\gamma _n-1)=C_n\ne 0\). The exponent of \(x_1\) in any  is larger than \(\gamma _1=\alpha _1\), so
is larger than \(\gamma _1=\alpha _1\), so  which means that \(mx_{2r}x_1/x_n\) cannot be canceled, also a contradiction.
which means that \(mx_{2r}x_1/x_n\) cannot be canceled, also a contradiction.
If \(i<2r\) then, by Proposition 2.5, i cannot be even. So i must be odd, but if \(i<2r-1\) then (1) shows that the coefficient of \(mx_{2r}\) in \(d(m_2)\) is \(\gamma _{i+1}-C_{i-1}\gamma _{i-1}=0\). These imply that only \(m_2=mx_{2r}/x_{2r-1}=m_1(x_{2r}/x_{2r-1})^{l}\) can cancel it, so it must be in M(h). This proves our claim for every \(l\geqslant 0\).
However, \(m_1(x_{2r}/x_{2r-1})^{l}\in R\) only if \(l\leqslant \alpha _{2r-1}\) so the claim cannot be true for every l. This contradiction shows that indeed there must exist \(\beta _{2r-1}\geqslant 0\) satisfying the proposition. \(\blacksquare \)
Proposition 2.8
Suppose \(C_n\ne 0\) and \(m=\prod x_{\scriptscriptstyle i}^{\scriptscriptstyle \gamma _i}\in M(h)\) is such that \(\gamma _n=\alpha _n\), \(\gamma _1=\alpha _1\) and \(\gamma _2=\alpha _2=C_n\alpha _n\). If \(mx_n^k/m_2\in M(h)\), where  , then \(m_2=x_1^k\).
, then \(m_2=x_1^k\).
Proof
The proof is by induction on the exponent i of \(x_1\) in \(m_2\). Let \(m'=m x_n^k/m_2=\prod _j x_{\scriptscriptstyle j}^{\scriptscriptstyle \beta _j}\). Of course, \(\beta _j\leqslant \gamma _j\) for \(j<n\). We have \(\gamma _2=C_n\gamma _n\), so if \(\gamma _n>0\) then \(C_n=\gamma _2/\gamma _n>0\). If, on the other hand, \(\gamma _n=0\) then \(\gamma _2=\beta _2=0\).
Now \(x_1m'\in M(d(m'))\) has the coefficient \(\beta _2-C_n\beta _n=\gamma _2-C_n\gamma _n-(\gamma _2-\beta _2)-C_nk=0-\cdots \ne 0\). It could be canceled only by some  , where \(1<j\). All these are lexicographically larger than \(m_1\) if \(i=0\), a contradiction.
, where \(1<j\). All these are lexicographically larger than \(m_1\) if \(i=0\), a contradiction.
If \(i>0\), then the exponent of \(x_1\) is \(i-1\) in  . If \(j<n\) then
. If \(j<n\) then  satisfies the assumption of the proposition, so by induction
satisfies the assumption of the proposition, so by induction  , a contradiction. So we must have
, a contradiction. So we must have  and \(x_1m'/x_n=m x_n^{k-1}/(m_2/x_1)\) satisfies the assumption of the proposition. Here induction gives \(m_2/x_1=x_1^{k-1}\) and \(m_2=x_1^k\), as required. \(\blacksquare \)
and \(x_1m'/x_n=m x_n^{k-1}/(m_2/x_1)\) satisfies the assumption of the proposition. Here induction gives \(m_2/x_1=x_1^{k-1}\) and \(m_2=x_1^k\), as required. \(\blacksquare \)
Corollary 2.9
Suppose \(C_n\ne 0\) and \(m=\prod x_{\scriptscriptstyle i}^{\scriptscriptstyle \gamma _i}\in M(h)\) is such that \(\gamma _n=\alpha _n\), \(\gamma _1=\alpha _1\) and \(\gamma _2=\alpha _2=C_n\alpha _n\). Then \(l=\gamma _{1}-C_{n-1}\gamma _{n-1}\) is a nonnegative integer and  . In particular, \(\alpha _{1}-C_{n-1}\alpha _{n-1}\) is a nonnegative integer.
. In particular, \(\alpha _{1}-C_{n-1}\alpha _{n-1}\) is a nonnegative integer.
Proof
We show that otherwise \(m(x_n/x_1)^l\in M(h)\) for every \(l\geqslant 0\), an obvious contradiction.
For \(l=0\) this holds vacuously. Let \(l>0\) and suppose it holds for l, that is \(m'=m x_n^{l}/x_1^{l}\in M(h)\). The coefficient of \(m' x_n\in M(d(m'))\) is \(\gamma _1-l-C_{n-1}\gamma _{n-1}\). If it is 0 then \(\gamma _1-C_{n-1}\gamma _{n-1}=l\) a nonnegative integer as we claimed. Otherwise, it must be canceled by some  . By Proposition 2.8, \(j=1\) and we get the required monomial for \(l+1\), too. \(\blacksquare \)
. By Proposition 2.8, \(j=1\) and we get the required monomial for \(l+1\), too. \(\blacksquare \)
Proposition 2.10
Let \(h,g\in R^d\), where g is a monomial. If the leading monomial of h is \(m_1=x_1^k g\) with \(k>0\) then \(C_1C_2\cdots C_n\) is a k-th root of unity, in particular, all \(C_i\ne 0\). If further \(n>4\) then \(C_1C_2\cdots C_n=1\).
Proof
If \(1\ne g=\prod _i x_{\scriptscriptstyle i}^{\scriptscriptstyle \gamma _i}\) (with \(\gamma _i=\alpha _i\) for \(i\ne 1\)) is the monomial constant then

Hence \(\gamma _{i+2}=C_i\gamma _i\) for every i. If n is odd then \(C_1C_2\cdots C_n=1\) so the proposition is proved. Exactly the same works if n is even and \(\gamma _1\ne 0\ne \gamma _2\).
So we have to consider two cases. Either \(g=1\) or \(g=g_{\mathcal {A}}^l\) with \(l>0\) and \({\mathcal {A}}\in \{{\mathcal {E}},{\mathcal {O}}\}\). If \(l>0\) then we will use \(C_{i}\ne 0\) for \(i\in \mathcal {A}\) to prove that in certain monomials the exponent of \(x_i\) is not smaller than in g. For \(l=0\) this is obvious. The rest of the proof works equally for arbitrary l.
The proof is almost the same for \({\mathcal {E}}\) and for \({\mathcal {O}}\). First we assume \({\mathcal {A}}={\mathcal {O}}\) and \(l>0\), so \(C_{2i-1}>0\) for every \(1\leqslant i\leqslant n/2\). We apply Proposition 2.2 for \(j=n-1, n-3,\ldots , 1\) consecutively. In the first step \(r=k\) and \(m=m_1\). By Proposition 2.2, we obtain \(m_{n-1}=m_1(x_{n-1}/x_{1})^{k_{n-1}}\in M(h)\) with \(k_{n-1}\geqslant k\). If \(C_n=0\) then we get \(k\leqslant 0\), contrary to our assumption. So \(C_{n}\ne 0\) and we also get  . As \(m_1\) is the leading monomial \(k=k_{n-1}\).
. As \(m_1\) is the leading monomial \(k=k_{n-1}\).
By induction, we obtain monomials \(m_{2i-1}=m_{2i+1}(x_{2i-1}/x_{2i+1})^{k_{2i-1}}\in M(h)\) with \(k_{2i-1}\geqslant k_{2i+1}\). Finally we reach \(i=1\) and obtain a monomial \(m=m_3(x_1/x_3)^{k_{1}}\) in M(h) such that the exponent of \(x_1\) is \(\alpha _1-k_{n-1}+k_{1}\geqslant \alpha _1\). As \(m_1\) is the leading monomial we must have \(k_1=k_3=\cdots =k_{n-1}=k\). So in each of the applications of Proposition 2.2 we have \(r=t_0=k_{n-1}=k\), hence if  then \(0\leqslant s\leqslant t\leqslant k\).
then \(0\leqslant s\leqslant t\leqslant k\).
Let now \({\mathcal {A}}={\mathcal {E}}\) and \(l>0\), so \(C_{2i}>0\) for every \(1\leqslant i\leqslant n/2\). First we apply Proposition 2.2 for \(j=n\), \(m=m_1\). Then \(r=k\) and we get for \(s=0\), \(k_n=t_0\geqslant k\) that  . Now we proceed as in the odd case and consecutively we obtain monomials
. Now we proceed as in the odd case and consecutively we obtain monomials  with \(k_{2i}\geqslant k_{2i+2}\). Thus we find that in \(m_2\) the exponent of \(x_n\) is \(\alpha _n+k_n-k_{n-2}\leqslant \alpha _n\) and the exponent of \(x_2\) is \(\alpha _2+k-k_n+k_{2}\geqslant \alpha _2+k\). Now apply Proposition 2.2 for \(j=n\), \(m=m_3\). Then \(r\geqslant k\), so \(t_0\geqslant k\) and \(s=s_0\leqslant 0\) gives
with \(k_{2i}\geqslant k_{2i+2}\). Thus we find that in \(m_2\) the exponent of \(x_n\) is \(\alpha _n+k_n-k_{n-2}\leqslant \alpha _n\) and the exponent of \(x_2\) is \(\alpha _2+k-k_n+k_{2}\geqslant \alpha _2+k\). Now apply Proposition 2.2 for \(j=n\), \(m=m_3\). Then \(r\geqslant k\), so \(t_0\geqslant k\) and \(s=s_0\leqslant 0\) gives  . By \(m_1\) being the leading term, at every application of Proposition 2.2 we have \(r=t_0=k\) and \(s_0=0\) and all \(k_{2i}=k\).
. By \(m_1\) being the leading term, at every application of Proposition 2.2 we have \(r=t_0=k\) and \(s_0=0\) and all \(k_{2i}=k\).
From now on there is no loss of generality in assuming \({\mathcal {A}}={\mathcal {O}}\) or \(g=1\), that is, \(\alpha _{2i}=0\) for every i.
We now determine the coefficients in question. We will apply Proposition 2.3 repeatedly, but first we have to establish that all \(C_i\) are nonzero. Without loss of generality we assume that \(m_1\) has a coefficient equal to 1. We prove by induction on i that the coefficient of \(gx_i^{k}\) is \(\prod _{j<i} C_j^k\). We would like to apply Proposition 2.3 for \(j_0=i-1\). If i is even then the coefficient of \(gx_{i+1}^{k}\) is \(\prod _{j<i+1} C_j^k\) by considering \(q=k\) in Proposition 2.3 (ii). (By Proposition 2.2,  implies \(p,q\geqslant 0\).) If i is odd, then \(\beta _{j_0+3}>0\) implies \(C_{j_0+1}>0\) and \(k=\beta _{j_0+1}-\beta _{j_0+3}/C_{j_0+1}\). So we can apply Proposition 2.3 (ii) again. Finally, for \(i=n+1\) we get \(1=C_1^k\cdots C_{n}^k\) so \(z=C_1 C_2\cdots C_{n}\) is a k-th root of unity, in particular, all \(C_i\ne 0\). Let us abbreviate \(d_i=\prod _{j<i}C_j^k\). We see from our applications of Proposition 2.3 that for every i, s the coefficient of \(gx_i^{k-s}x_{i+1}^s\) is
implies \(p,q\geqslant 0\).) If i is odd, then \(\beta _{j_0+3}>0\) implies \(C_{j_0+1}>0\) and \(k=\beta _{j_0+1}-\beta _{j_0+3}/C_{j_0+1}\). So we can apply Proposition 2.3 (ii) again. Finally, for \(i=n+1\) we get \(1=C_1^k\cdots C_{n}^k\) so \(z=C_1 C_2\cdots C_{n}\) is a k-th root of unity, in particular, all \(C_i\ne 0\). Let us abbreviate \(d_i=\prod _{j<i}C_j^k\). We see from our applications of Proposition 2.3 that for every i, s the coefficient of \(gx_i^{k-s}x_{i+1}^s\) is  .
.
Now let \(n>4\). If \(z\ne 1\) then there must be an index j such that \(C_j\) is not positive rational. For otherwise every \(0<C_j\) and hence \(0<\prod C_j=z\) implies \(z=1\) as the only such root of unity. Fix this index j.
Case (
\(\star \)
):
j is odd. We use Proposition 2.3 with \(j_0=j\) and  . All assumptions are satisfied, so the coefficient of
. All assumptions are satisfied, so the coefficient of  is equal to
is equal to  . Also, the coefficient of
. Also, the coefficient of  is equal to
is equal to  .
.
Case (
\(\star \star \)
):
\(C_i\) is positive rational for every odd index i, so j is even. Proposition 2.2 is not sufficient in this case, we have to treat five consecutive indices. This is the point where it is crucial that \(n\ne 4\), so \(n\geqslant 6\). Let \(e_{a,b,c,d}\) denote the coefficient of  . Here we rely on the following equation expressing the coefficient of
. Here we rely on the following equation expressing the coefficient of  in \(d(h)=0\):
in \(d(h)=0\):
As j is even, we have \(e_{0,0,0,0}=d_{j+3}\ne 0\). We claim that if \(a<0\) or \(c<0\) or \(k-a-b-c-d<0\) then \(e_{a,b,c,d}=0\). Its proof is similar to the proof of Proposition 2.2.
Let \(a_0\leqslant 0\) be the smallest possible such that there exist \(b_0,c_0,d_0\) with \(e_{a_0,b_0,c_0,d_0}\ne 0\). Without loss of generality also assume that \(c_0\) is as small as possible for this \(a_0\). Suppose here  . Then by (7) for \(a_0,b_0+1,c_0,d_0\) we have \(e_{a_0,b_0+1,c_0,d_0-1}\ne 0\) or \(e_{a_0,b_0+1,c_0,d_0}\ne 0\). In either case we can increase b again. But clearly b is bounded, so we conclude that
. Then by (7) for \(a_0,b_0+1,c_0,d_0\) we have \(e_{a_0,b_0+1,c_0,d_0-1}\ne 0\) or \(e_{a_0,b_0+1,c_0,d_0}\ne 0\). In either case we can increase b again. But clearly b is bounded, so we conclude that  . Mutatis mutandis we get that if \(c_1\leqslant c_0\) is the smallest possible and \(a_1\) is the smallest possible for such \(c_1\) then
. Mutatis mutandis we get that if \(c_1\leqslant c_0\) is the smallest possible and \(a_1\) is the smallest possible for such \(c_1\) then  . As \(C_{j-1}>0\) we have \(c_1=c_0\) and \(a_1=a_0\). The same proof shows that \(k-a-b-c-d\) is the smallest for
. As \(C_{j-1}>0\) we have \(c_1=c_0\) and \(a_1=a_0\). The same proof shows that \(k-a-b-c-d\) is the smallest for  .
.
Consider now \(e_{a_0,b_0,c_0,d_0}\ne 0\) where  and
and  . By assumption, \(C_j\) is not positive rational (and nonzero), in particular, for nonnegative integers b, d the expression \(d-C_jb=0\) only if \(b=d=0\). Hence in (7) for \(a_0,b_0,c_0+1,d_0\) we have \(e_{a_0,b_0,c_0+1,d_0-1}\ne 0\) or \(e_{a_0,b_0-1,c_0+1,d_0}\ne 0\). We repeat this step \(b_0+d_0\) times to obtain \(e_{a_0,0,c_0+b_0+d_0,0}\ne 0\). Suppose \(a_0<0\) and hence
. By assumption, \(C_j\) is not positive rational (and nonzero), in particular, for nonnegative integers b, d the expression \(d-C_jb=0\) only if \(b=d=0\). Hence in (7) for \(a_0,b_0,c_0+1,d_0\) we have \(e_{a_0,b_0,c_0+1,d_0-1}\ne 0\) or \(e_{a_0,b_0-1,c_0+1,d_0}\ne 0\). We repeat this step \(b_0+d_0\) times to obtain \(e_{a_0,0,c_0+b_0+d_0,0}\ne 0\). Suppose \(a_0<0\) and hence  . We now apply Proposition 2.2 for the first three indices, that is for \(j-1,j,j+1\). We get
. We now apply Proposition 2.2 for the first three indices, that is for \(j-1,j,j+1\). We get  resulting in
resulting in  . That is
. That is  the exponent of
the exponent of  is at least \(\alpha _{j-1}+k+1\). By induction for \(i=j-3,j-5,\ldots ,3\) we obtain that the exponent of \(x_i\) in \(m_i\in M(h)\) is at least \(\alpha _i+k+1\). Thus we reach \(i=1\) and a monomial in M(h) where the exponent of \(x_1\) is at least \(\alpha _1+1\), contradicting that \(m_1\) is the leading monomial. So \(a_0=c_0=k-b_0-d_0=0\).
is at least \(\alpha _{j-1}+k+1\). By induction for \(i=j-3,j-5,\ldots ,3\) we obtain that the exponent of \(x_i\) in \(m_i\in M(h)\) is at least \(\alpha _i+k+1\). Thus we reach \(i=1\) and a monomial in M(h) where the exponent of \(x_1\) is at least \(\alpha _1+1\), contradicting that \(m_1\) is the leading monomial. So \(a_0=c_0=k-b_0-d_0=0\).
Now determine \(e_{0,s,k-1-s,1}\) using Proposition 2.3 for \(j_0=j\) and  . The above discussion confirms that the assumptions are satisfied. So
. The above discussion confirms that the assumptions are satisfied. So

As j is even, the assumptions of Proposition 2.3 (i) are satisfied for \(j_0=j-1\),  and
and  . So
. So  . We can now apply it again to \(j_0=j+1\),
. We can now apply it again to \(j_0=j+1\),  and
and  to get
to get  . Exactly the same way we obtain
. Exactly the same way we obtain  .
.
So in both cases \((\star )\) and \((\star \star )\) we find an odd index j such that the coefficient of  is
is  , while the coefficient of
, while the coefficient of  is
is  . We shift the indices by 2 in the second monomial using Proposition 2.3 again first for \(j_0=j+2\) and then for \(j_0=j\). The coefficient of
. We shift the indices by 2 in the second monomial using Proposition 2.3 again first for \(j_0=j+2\) and then for \(j_0=j\). The coefficient of  is
is  . Then the coefficient of
. Then the coefficient of  is
is  .
.
If \(n=5\) then we cannot do this as \(j+4\) and j are adjacent. But \(n=5\) is odd, so \(g=1\) and there is no worry that the exponent of \(x_i\) becomes smaller than in g (see the remark at the beginning of the proof). So we use Proposition 2.3 to compute the coefficients in a different way, we increase the indices one-by-one. Now the coefficient of  is
is  and using Proposition 2.3 for \(j_0=j-1\) the coefficient of
and using Proposition 2.3 for \(j_0=j-1\) the coefficient of  is
is  . Doing this again, the coefficient of
. Doing this again, the coefficient of  is equal to
is equal to  and the coefficient of
and the coefficient of  is equal to
is equal to  , the same as above.
, the same as above.
By a final induction we prove that the coefficient of  is equal to \(kd_{j+2}\prod _{i=2}^{s-1}C_{j+i}\). The details are omitted. The case \(s=n-2\) implies that the coefficient of
is equal to \(kd_{j+2}\prod _{i=2}^{s-1}C_{j+i}\). The details are omitted. The case \(s=n-2\) implies that the coefficient of  is
is  . However, we have already determined that to be
. However, we have already determined that to be  . So
. So

Hence \(z=1\) as required. \(\blacksquare \)
Proposition 2.11
Let \(n=4\) and \(h,g\in R^d\), where g is a monomial. Assume either every \(C_i\) is positive rational, or \(C_4\) is not. If the leading monomial of h is  with \(k>0\) then
with \(k>0\) then  . If
. If  then \(C_2=1\) and at least one of \(C_1=1\) and \(C_3=1\) also holds.
then \(C_2=1\) and at least one of \(C_1=1\) and \(C_3=1\) also holds.
Proof
By Proposition 2.10, we have  is a k-th root of 1. If all parameters are positive rational numbers then the product must be 1. From now on assume \(C_4\) is not positive rational. First we prove that if \(z\ne 1\) then
is a k-th root of 1. If all parameters are positive rational numbers then the product must be 1. From now on assume \(C_4\) is not positive rational. First we prove that if \(z\ne 1\) then  . In the next step we verify that
. In the next step we verify that  so k is even. Then we suppose by contradiction that \(C_1\ne 1\ne C_3\) from which we derive
so k is even. Then we suppose by contradiction that \(C_1\ne 1\ne C_3\) from which we derive  and subsequently we reach a contradiction.
and subsequently we reach a contradiction.
As \(C_4\) is not positive rational, \(g_{\mathcal {E}}\) is not defined, so \(g=g_{\mathcal {O}}^l\) or \(g=1\). Let \(f_{a,b,c}\) denote the coefficient of  in h. By assumption, without loss of generality \(f_{0,0,0}=1\). We observe that the coefficient of
in h. By assumption, without loss of generality \(f_{0,0,0}=1\). We observe that the coefficient of  in d(h) is equal to
in d(h) is equal to

We have to prove again that exponents cannot become negative, so \(a,b,c,k-(a+b+c)\geqslant 0\) if \(f_{a,b,c}\ne 0\). Of course, this holds if \(g=1\).
Suppose \(b_0\) is the smallest such that there exist \(a_0,c_0\) such that \(f_{a_0,b_0,c_0}\ne 0\). If \(a_0,c_0\) are not both 0 then by (8) one of them might be decreased by 1. (Using here that  ). Repeating this until both \(a_0,c_0\) become 0 we conclude \(f_{0,b_0,0}\ne 0\). This is the coefficient of \(gx_1^{k-b_0}x_3^{b_0}\), so by \(m_1\) being the leading monomial, \(b_0\geqslant 0\). By a similar argument, if \(a_1+b_1+c_1\) is the maximal possible such that \(f_{a_1,b_1,c_1}\ne 0\), then we conclude that \(f_{0,a_1+b_1+c_1,0}\ne 0\). If \(a_1+b_1+c_1>k\) then apply Proposition 2.2 for \(j=1\). We have \(t\geqslant r\geqslant a_1+b_1+c_1-C_1(k-a_1-b_1-c_1)>a_1+b_1+c_1\) (as \(C_1=1\) if \(g\ne 1\)). By Proposition 2.2, \(f_{0,a_1+b_1+c_1-t,0}\ne 0\) contradicting \(b_0\geqslant 0\). Thus indeed \(k-(a+b+c)\geqslant 0\), if \(f_{a,b,c}\ne 0\).
). Repeating this until both \(a_0,c_0\) become 0 we conclude \(f_{0,b_0,0}\ne 0\). This is the coefficient of \(gx_1^{k-b_0}x_3^{b_0}\), so by \(m_1\) being the leading monomial, \(b_0\geqslant 0\). By a similar argument, if \(a_1+b_1+c_1\) is the maximal possible such that \(f_{a_1,b_1,c_1}\ne 0\), then we conclude that \(f_{0,a_1+b_1+c_1,0}\ne 0\). If \(a_1+b_1+c_1>k\) then apply Proposition 2.2 for \(j=1\). We have \(t\geqslant r\geqslant a_1+b_1+c_1-C_1(k-a_1-b_1-c_1)>a_1+b_1+c_1\) (as \(C_1=1\) if \(g\ne 1\)). By Proposition 2.2, \(f_{0,a_1+b_1+c_1-t,0}\ne 0\) contradicting \(b_0\geqslant 0\). Thus indeed \(k-(a+b+c)\geqslant 0\), if \(f_{a,b,c}\ne 0\).
We have from the proof of Proposition 2.10 that

We apply Proposition 2.3 for \(j_0=1\), \(m=m_1\) to obtain

as \(C_4\) is not positive rational.
Next we claim that

The proof is by induction on s, for \(s=0\) we know it from (9). By (8) for \((k-s,1,s)\) we get
proving the claim for s.
We compare it for \(s=k-1\) to (9):

The sum is equal to  so in the parentheses above we have
so in the parentheses above we have

Dividing both sides of (11) by \(kC_1C_2\) and multiplying by \(zC_4^{k-1}\) we get

If \(z\ne 1\) then  , as claimed. From now on we assume
, as claimed. From now on we assume  . In particular, \(C_2=1\) implies
. In particular, \(C_2=1\) implies  and \(k\geqslant 2\) is even. Otherwise, \(C_2\) is not rational.
and \(k\geqslant 2\) is even. Otherwise, \(C_2\) is not rational.
If \(C_2\) is not rational then, using Proposition 2.3 (ii) for \(j_0=2\), we get

Comparing the case \(s=k-1\), \(t=1\) to (10) for \(t=k-1\), \(s=1\), we have

implying \(z=1\), as claimed.
From now on we assume that k is even, \(C_2=1\),  and we also suppose \(C_1\ne 1\ne C_3\) to derive contradiction. Next we claim
and we also suppose \(C_1\ne 1\ne C_3\) to derive contradiction. Next we claim

It is true for \(s=0\) and for \(t=0\) so we use induction for \(t+s\) assuming \(s,t>0\). From (8) for \((k+1-t-s,t,s)\) we obtain

We use the inductive assumption on the right hand side. We find identical factors  at both terms. Now we have
at both terms. Now we have

If we multiply by F, using \({k\atopwithdelims ()s+t}=(k+1-s-t)/(s+t)\cdot {k\atopwithdelims ()s+t-1}\), then we get that (13) implies (12).
Now we go on to prove that \(C_1C_3=1\). We use (8) for \((k-s-1,1,s)\):

Let us multiply this equation by \((1-C_3)^{-s}(1-C_1)^{s}(-1)^s\) and sum them up through \(s=0,\ldots , k-1\). In the resulting sum

because each term appears with opposite signs. For the rest we apply (10) and (12) to get

We divide by the nonzero \(kC_1^{k-1}\). We first split

where

Now we determine sums of the three distinct series. For this we abbreviate \(y=C_3(1-C_1)/(1-C_3)\), so \(y+1=(1-C_1C_3)/(1-C_3)\), \(C_1C_3(1+C_4)=C_1C_3-1\) and \(yC_1(1+C_4)=(y+1)(C_1-1)\). We have

(Note that the third conclusion is correct even for \(k=2\).)
Summing them up we get

Hence \(y+1=0\), that is  .
.
Now we derive the final contradiction. Use (8) for \((1,k-1,0)\) and for \((0,k-1,1)\) to get

The last terms in each of these equations can be obtained from (9)
We multiply the first equation by \(C_3\) and add to the second, thus canceling the coefficient of \(f_{0,k-1,0}\)

On the other hand, using (8) for \((1,k-2,1)\), we get

This implies \(C_1=1\) contradicting our assumptions. This finishes the proof of the proposition. \(\blacksquare \)
We are now ready to finish the proof of Lemma 2.4. We have \(h\in R^d\) of positive degree and \(m_1\in M(h)\), the leading monomial of h with respect to the lexicographic ordering of monomials. Recall that we assumed \(C_n\ne 1\). We also assumed that if \(C_n=0\) then every \(C_i\in \{0,1\}\) and either all \(C_i=0\) or \(C_1=1\). Of course, by Proposition 2.5, every exponent with even index \(\alpha _{2i}=0\) in this case.
If all \(C_i=0\) then, by Propositions 2.5 and 2.7, all \(\alpha _{i}=0\) save possibly \(\alpha _1>0\). But then Proposition 2.10 implies that all \(C_i\ne 0\). This contradiction shows that \(\alpha _1=0\) and \(R^d=K\) in this case.
If \(C_{n}=0\) but \(C_1=1\) then \(\alpha _1\geqslant \alpha _3\geqslant \cdots \), by Proposition 2.7. If all \(\alpha _i\) are equal and n is even then all coefficients with odd indices \(C_{2i+1}=1\) and \(m=g_{\mathcal {O}}^{\alpha _1}\) as we wanted. Otherwise, \(\alpha _{n-1}<\alpha _1\) (this clearly holds if n is odd, because then \(\alpha _{n-1}=0\)) so \(x_nm_1\in M(d(m))\). But this can be canceled only by \(x_nm_1/x_{n-1}\) and this can be repeated \(\alpha _{n-1}\) steps until no division by \(x_{n-1}\) is possible. (No other decrease is ever possible.) This contradiction shows that \(R^d=K\) also in this case.
So from now on we assume \(C_n\ne 0\). If \(C_1=0\) then all \(\alpha _{2i+1}=0\) for \(i>0\). If n is odd then it implies \(\alpha _{n}=0\) and hence all \(\alpha _i=0\) save possibly \(\alpha _1>0\). But then Proposition 2.10 is a contradiction and \(R^d=K\) again. If n is even then \(g_{\mathcal {E}}\) is defined and  . If \(\alpha _1>0\) then Proposition 2.10 implies that \(C_1\ne 0\), a contradiction. So \(\alpha _1=0\) and \(m_1=g_{\mathcal {E}}^l\) is a constant and the proof is done by induction for \(h-m_1\).
. If \(\alpha _1>0\) then Proposition 2.10 implies that \(C_1\ne 0\), a contradiction. So \(\alpha _1=0\) and \(m_1=g_{\mathcal {E}}^l\) is a constant and the proof is done by induction for \(h-m_1\).
From now on we assume \(C_1\ne 0\). For \(n=4\) also assume that either every parameter is positive rational, or that \(C_4\) is not.
We are going to derive a contradiction, so \(R^d=K\) unless the following two conditions hold:
-
(A)
In Proposition 2.7 we have \(C_{2i-1}\alpha _{2i-1}=\alpha _{2i+1}\) for every \(1<i<n/2\).
-
(B)
In Proposition 2.7 and Corollary 2.9 the two integers coincide: \(C_1(\alpha _{1}-\beta _1)=\alpha _{3}\) and \(\alpha _1'=\alpha _{1}-\beta _{1}=C_{n-1}\alpha _{n-1}\). In other words, \(C_{n-1}\alpha _{n-1}\) is a nonnegative integer and \(C_{1}C_{n-1}\alpha _{n-1}=\alpha _3\).
Claim 2.12
If (A) and (B) hold then h is a polynomial in the elements of \(\mathcal {H}\).
Proof
Let \(\alpha _i'=\alpha _i\) for \(i>1\). The equalities in (A) and (B) together with Proposition 2.5 imply that \(g=\prod _{i=1}^nx_{\scriptscriptstyle i}^{\scriptscriptstyle \alpha _i'}\) is a constant of d. If \(\alpha _i'\ne 0\) then \(\alpha _{i-2}' C_{i-2}\ne 0\) so by backward induction we get that all \(C_{i-2l}\) are positive rational. Take \({\mathcal {A}}\subseteq \mathbb {Z}_n\) minimal closed under \(j\mapsto j+2\) such that \(i\in \mathcal {A}\). Then by the above, \(\alpha _i'=\alpha _i'\prod _{j\in {\mathcal {A}}}C_{j}\) so \(\prod _{j\in {\mathcal {A}}} C_j=1\), hence \(g_{\mathcal {A}}\) is defined and  for every \(j\in \mathcal {A}\) with
for every \(j\in \mathcal {A}\) with  . So g can be expressed using the defined ones of \(g_{\mathbb {Z}_n},g_{\mathcal {E}},g_{\mathcal {O}}\). If \(\alpha '_1=\alpha _1\) then g is the leading monomial of h so \(h-g\) is lexicographically smaller so the proof is done by induction.
. So g can be expressed using the defined ones of \(g_{\mathbb {Z}_n},g_{\mathcal {E}},g_{\mathcal {O}}\). If \(\alpha '_1=\alpha _1\) then g is the leading monomial of h so \(h-g\) is lexicographically smaller so the proof is done by induction.
Suppose that \(\alpha _1'<\alpha _1\) and first assume \(n>4\). Then Proposition 2.10 applies and it follows that f is defined. Hence \(f^{\scriptscriptstyle \alpha _1-\alpha '_1}g\) has the same lexicographically largest monomial as h, we may cancel it and the proof is done by induction.
Finally, if \(n=4\) then Proposition 2.11 applies and it follows that f is defined or \(\alpha _1-\alpha '_1\) is even and \(f_4\) is defined. So either f is defined and \(f^{\alpha _1-\alpha '_1}g\) has the same lexicographically largest monomial as h, or \(f_4\) is defined and \(f_4^{\scriptscriptstyle (\alpha _1-\alpha '_1)/2}g\) has the same lexicographically largest monomial as h. In both cases we may cancel it and the proof is done by induction. \(\blacksquare \)
For the rest we assume that at least one of (A) and (B) does not hold. We first construct a monomial \(m=\prod x_{\scriptscriptstyle i}^{\scriptscriptstyle \gamma _i}\in M(h)\) such that
If (B) does not hold, then \(m=m_1\) suffices. If (B) holds and \(C_{n-1}=0\) or \(\alpha _{n-1}=0\) then (A) also holds with \(\alpha _{2i+1}=0\) for \(i>0\).
Suppose (B) holds but (A) does not, and let i be the smallest index such that \(C_{2i-1}\alpha _{2i-1}\ne \alpha _{2i+1}\). We apply Proposition 2.7 for decreasing indices \(r=i,i-1,\ldots , 2\). Suppose we have reached the step r, that is, given \(m=\prod x_{\scriptscriptstyle i}^{\scriptscriptstyle \gamma _i}\in M(h)\) with \(\gamma _i=\alpha _i\) if \(i<2r+1\) and for \(i=n\). By Proposition 2.7, there exists a nonnegative integer \(\beta _{2r-1}\) such that \(C_{2r-1}(\gamma _{2r-1}-\beta _{2r-1})=\gamma _{2r+1}\) and \(m'=m(x_{2r}/x_{2r-1})^{\beta _{2r-1}}\in M(h)\). We replace m for this \(m'\). In the step r the exponent of \(\gamma _{2r-1}\) decreases, so finally \(\gamma _3<\alpha _3=C_1C_{n-1}\alpha _{n-1}\). In every step \(\gamma _{n-1}\) is constant, only in step \(r=(n-1)/2\) may it grow. As \(C_1C_{n-1}\ne 0\) and \(0<\alpha _{n-1}\leqslant \gamma _{n-1}\) so  implies that \(C_1C_{n-1}>0\) is rational. But for \(C_1C_{n-1}>0\) we have \(\gamma _3<\alpha _3=C_1C_{n-1}\alpha _{n-1}\leqslant C_1C_{n-1}\gamma _{n-1}\). So in any case \(C_1C_{n-1}\gamma _{n-1}\ne \gamma _3\). And we have constructed \(m\in M(h)\) with properties (15).
implies that \(C_1C_{n-1}>0\) is rational. But for \(C_1C_{n-1}>0\) we have \(\gamma _3<\alpha _3=C_1C_{n-1}\alpha _{n-1}\leqslant C_1C_{n-1}\gamma _{n-1}\). So in any case \(C_1C_{n-1}\gamma _{n-1}\ne \gamma _3\). And we have constructed \(m\in M(h)\) with properties (15).
Claim 2.13
There is a monomial  such that
such that
We may choose to further assume one of \(\beta _2\leqslant 1\) and \(\beta _n\leqslant 1\).
Proof
We use Corollary 2.9 to obtain \(m=m_1(x_n/x_1)^l\) so  and \(C_{n-1}\gamma _{n-1}=\gamma _1+\beta _1=\alpha _1-l\). By (15), \(C_1(\gamma _1-l)\ne \gamma _3\) so \(mx_2\in M(d(m))\), hence it should be canceled by some \(mx_2/x_i\in M(h)\). By the previous equality, \(i\ne n\) so either \(i>2\) and we have the desired \(\beta _n+\beta _1+\beta _2=l-l+1>0\) with \(\beta _2=1\), or \(i=1\). If \(i=1\) then \(C_{n-1}\gamma _{n-1}\ne \gamma _1-l-1\) so \(mx_2x_n/x_1\in M(d(mx_2/x_1))\). Again, it has to be canceled by \(mx_2x_n/x_1^2\) or \(mx_n/x_1\), for otherwise we would get the desired \(\beta _n,\beta _1,\beta _2\) with \(\beta _2\leqslant 1\). This is repeated a number of times, each time increasing \(\beta _n\) by 1 and decreasing one of \(\beta _1\) and \(\beta _2\) by 1. We cannot go on infinitely because \(\beta _1\geqslant -\gamma _1\) and
and \(C_{n-1}\gamma _{n-1}=\gamma _1+\beta _1=\alpha _1-l\). By (15), \(C_1(\gamma _1-l)\ne \gamma _3\) so \(mx_2\in M(d(m))\), hence it should be canceled by some \(mx_2/x_i\in M(h)\). By the previous equality, \(i\ne n\) so either \(i>2\) and we have the desired \(\beta _n+\beta _1+\beta _2=l-l+1>0\) with \(\beta _2=1\), or \(i=1\). If \(i=1\) then \(C_{n-1}\gamma _{n-1}\ne \gamma _1-l-1\) so \(mx_2x_n/x_1\in M(d(mx_2/x_1))\). Again, it has to be canceled by \(mx_2x_n/x_1^2\) or \(mx_n/x_1\), for otherwise we would get the desired \(\beta _n,\beta _1,\beta _2\) with \(\beta _2\leqslant 1\). This is repeated a number of times, each time increasing \(\beta _n\) by 1 and decreasing one of \(\beta _1\) and \(\beta _2\) by 1. We cannot go on infinitely because \(\beta _1\geqslant -\gamma _1\) and  .
.
Similarly, if we desire \(\beta _n\leqslant 1\), we use Proposition 2.7 to obtain \(m=m_1(x_2/x_1)^l\) so  and \(C_1(\gamma _1-l)=\gamma _3\). By (15), \(C_{n-1}\gamma _{n-1}\ne \gamma _1-l\) so \(mx_n\in M(d(m))\), hence it should be canceled by some \(mx_n/x_i\in M(h)\). By the previous equality, \(i\ne 2\) so either \(i>2\) and we have the desired \(\beta _n+\beta _1+\beta _2=1-l+l>0\) with \(\beta _n=1\), or \(i=1\). If \(i=1\) then \(C_1(\gamma _1-l-1)=\gamma _3-C_1\ne \gamma _3\) so
and \(C_1(\gamma _1-l)=\gamma _3\). By (15), \(C_{n-1}\gamma _{n-1}\ne \gamma _1-l\) so \(mx_n\in M(d(m))\), hence it should be canceled by some \(mx_n/x_i\in M(h)\). By the previous equality, \(i\ne 2\) so either \(i>2\) and we have the desired \(\beta _n+\beta _1+\beta _2=1-l+l>0\) with \(\beta _n=1\), or \(i=1\). If \(i=1\) then \(C_1(\gamma _1-l-1)=\gamma _3-C_1\ne \gamma _3\) so  . Again, it has to be canceled by
. Again, it has to be canceled by  or \(mx_2/x_1\), for otherwise we would get the desired \(\beta _n,\beta _1,\beta _2\) with \(\beta _n\leqslant 1\). This is repeated a number of times but at most until we reach
or \(mx_2/x_1\), for otherwise we would get the desired \(\beta _n,\beta _1,\beta _2\) with \(\beta _n\leqslant 1\). This is repeated a number of times but at most until we reach  ,
,  , it cannot be continued further.\(\blacksquare \)
, it cannot be continued further.\(\blacksquare \)
We use this claim in the following way: If
then  so \(m_2x_1\in M(d(m_2))\) and it must be canceled by \(d(m_3)\) for some
so \(m_2x_1\in M(d(m_2))\) and it must be canceled by \(d(m_3)\) for some  . For this \(m_3/m_2=x_1/x_i\) so \(\beta _1'=\beta _1+1\) and \(\beta _n'+\beta _1'+\beta _2'\geqslant \beta _n+\beta _1+\beta _2>0\). We may replace \(m_2\) by this \(m_3\) and (16) still holds with larger \(\beta _1\). We can continue as long as (17) holds. Reaching some \(m_2\) for which \(\beta _1>0\) or \(\beta _1=0<\beta _2\) would imply that \(m_2\) is lexicographically larger than \(m_1\). This is our aim.
. For this \(m_3/m_2=x_1/x_i\) so \(\beta _1'=\beta _1+1\) and \(\beta _n'+\beta _1'+\beta _2'\geqslant \beta _n+\beta _1+\beta _2>0\). We may replace \(m_2\) by this \(m_3\) and (16) still holds with larger \(\beta _1\). We can continue as long as (17) holds. Reaching some \(m_2\) for which \(\beta _1>0\) or \(\beta _1=0<\beta _2\) would imply that \(m_2\) is lexicographically larger than \(m_1\). This is our aim.
If \(|C_n|>1\) then we use \(m_2\) from Claim 2.13 such that \(\beta _n+\beta _1+\beta _2>0\) and \(\beta _2\leqslant 1\), consequently, \(\beta _n\) is not negative. Now \(\beta _n=\beta _1=0\) and \(\beta _2=1\) mean that \(m_2\) is larger than \(m_1\), a contradiction. If \(\beta _n\geqslant |\beta _2|\) then \(|C_n\beta _n|>\beta _n\geqslant |\beta _2|\) implying \(C_n\beta _n-\beta _2\ne 0\). So (17) is satisfied and we obtain a monomial that is larger than \(m_2\). If, however, \(\beta _n<|\beta _2|\), then \(\beta _2=1\) and \(\beta _n=0\) and still \(C_n\beta _n-\beta _2\ne 0\) and we obtain a monomial that is larger than \(m_2\). We can continue and finally we get a monomial that is larger than \(m_1\), a contradiction.
If \(0<|C_n|<1\) then we use \(m_2\) from Claim 2.13 such that \(\beta _n+\beta _1+\beta _2>0\) and \(\beta _n\leqslant 1\). Proceeding exactly as in the previous case (but using \(\beta _2\geqslant |\beta _n|\) or \(\beta _2=0, \beta _n=1\)), we obtain a contradiction.
If \(C_n\) is not real then we use \(m_2\) from Claim 2.13 such that \(\beta _n+\beta _1+\beta _2>0\). We can proceed the same way as \(C_n\beta _n=\beta _2\) would imply \(\beta _n=\beta _2=0\) so \(\beta _1>0\), which is a contradiction.
Finally, if  then we use \(m_2\) from Claim 2.13 such that \(\beta _n+\beta _1+\beta _2>0\). We can proceed the same way as \(C_n\beta _n=\beta _2\) would imply \(\beta _n+\beta _2=0\) so \(\beta _1>0\) which is a contradiction.
then we use \(m_2\) from Claim 2.13 such that \(\beta _n+\beta _1+\beta _2>0\). We can proceed the same way as \(C_n\beta _n=\beta _2\) would imply \(\beta _n+\beta _2=0\) so \(\beta _1>0\) which is a contradiction.
This finishes the proof of Lemma 2.4. \(\square \)
For the third part we use the following Jacobi criterion for the algebraic independence of polynomials: Let
\(F_1,\ldots ,\,F_k\)
be polynomials in R. Let
\(J(F_1,\ldots ,F_k)\)
denote the
 matrix, whose (i, j)-entry is
matrix, whose (i, j)-entry is
 . Then
\(F_1,\ldots ,F_k\)
are algebraically independent if and only if
\(J(F_1,\ldots ,F_k)\)
has rank k.
. Then
\(F_1,\ldots ,F_k\)
are algebraically independent if and only if
\(J(F_1,\ldots ,F_k)\)
has rank k.
Lemma 2.14
The polynomials in \({\mathcal {H}}\) are algebraically independent.
Proof
Clearly, no two of the polynomials can be dependent, as they involve different variables. So assume all three are defined, that is n is even and \(\prod _{i\in {\mathcal {O}}} C_i=1=\prod _{i\in {\mathcal {E}}} C_i\). The Jacobi matrix \(J(f,g_{\mathcal {O}},g_{\mathcal {E}})\) truncated after the first three columns is
Its rows are independent as \(x_1^{-1}g_{\mathcal {O}}\) and \(x_3^{-1}g_{\mathcal {O}}\) are not constant multiples of each other. In the irregular case for \(n=4\), only at most one of \(g_{\mathcal {O}}\) and \(g_{\mathcal {E}}\) might be defined so this case does not need more attention. This finishes the proof of the lemma and of Theorems 1.1 and 1.2. \(\square \)
References
Bogoyavlenskiĭ, O.I.: Algebraic constructions of integrable dynamical systems—extension of the Volterra system. Russian Math. Surveys 46(3), 1–64 (1991)
Hegedűs, P.: The constants of the Volterra derivation. Cent. Eur. J. Math. 10(3), 969–973 (2012)
Maciejewski, A.J., Nowicki, A., Moulin Ollagnier, J., Strelcyn, J.-M.: Around Jouanolou non-integrability theorem. Indag. Math. (N.S.) 11(2), 239–254 (2000)
Moulin Ollagnier, J.M., Nowicki, A.: Polynomial algebra of constants of the Lotka–Volterra system. Colloq. Math. 81(2), 263–270 (1999)
Nowicki, A.: Polynomial Derivations and their Rings of Constants. Uniwersytet Mikołaja Kopernika, Toruń (1994)
Zieliński, J.: Rings of constants of four-variable Lotka–Volterra systems. Cent. Eur. J. Math. 11(11), 1923–1931 (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
The research was partly supported by OTKA (K 84233).
Rights and permissions
About this article
Cite this article
Hegedűs, P., Zieliński, J. The constants of Lotka–Volterra derivations. European Journal of Mathematics 2, 544–564 (2016). https://doi.org/10.1007/s40879-015-0091-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-015-0091-z



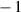 and the other three are equal to 1;
and the other three are equal to 1;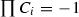 and only two consecutive parameters are equal to 1, or
and only two consecutive parameters are equal to 1, or 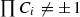 but one of
but one of 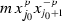 has the coefficient equal to
has the coefficient equal to 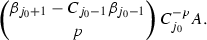
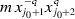 has the coefficient equal to 0. If
has the coefficient equal to 0. If 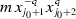 has the coefficient equal to
has the coefficient equal to  is equal to
is equal to 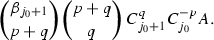
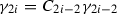 for
for 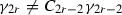 .
.