Abstract
We present a series of del Pezzo fibrations of degree 2 admitting an action of the Klein simple group and prove their nonrationality by the reduction modulo p method of Kollár. This is relevant to the embedding of the Klein simple group into the Cremona group of rank 3.
Similar content being viewed by others
1 Introduction
The Klein simple group \(G_\mathrm{K}\) is a finite simple group \(G_\mathrm{K} \cong \mathrm {PSL}_2 (\mathbb {F}_7)\) of order 168. It is well known that \(G_\mathrm{K}\) is the automorphism group of the Klein quartic curve which is defined in \(\mathbb {P}^2\) by the equation  . Let \(S_\mathrm{K}\) be the double cover of \(\mathbb {P}^2\) ramified along the Klein quartic curve. Then \(S_\mathrm{K}\) is a nonsingular del Pezzo surface of degree 2 admitting a faithful action of \(G_\mathrm{K}\). Belousov [3] proved that \(\mathbb {P}^2\) and \(S_\mathrm{K}\) are the only del Pezzo surfaces admitting a faithful action of \(G_\mathrm{K}\). In [1], Ahmadinezhad presented a series of \(G_\mathrm{K}\)-Mori fiber spaces
. Let \(S_\mathrm{K}\) be the double cover of \(\mathbb {P}^2\) ramified along the Klein quartic curve. Then \(S_\mathrm{K}\) is a nonsingular del Pezzo surface of degree 2 admitting a faithful action of \(G_\mathrm{K}\). Belousov [3] proved that \(\mathbb {P}^2\) and \(S_\mathrm{K}\) are the only del Pezzo surfaces admitting a faithful action of \(G_\mathrm{K}\). In [1], Ahmadinezhad presented a series of \(G_\mathrm{K}\)-Mori fiber spaces  over \(\mathbb {P}^1\) whose general fibers are isomorphic to \(S_\mathrm{K}\) for \(n \geqslant 0\). A G-Mori fiber space, where G is a group, is a G-equivariant version of Mori fiber space (see Definition 2.9). Among the above series of varieties,
over \(\mathbb {P}^1\) whose general fibers are isomorphic to \(S_\mathrm{K}\) for \(n \geqslant 0\). A G-Mori fiber space, where G is a group, is a G-equivariant version of Mori fiber space (see Definition 2.9). Among the above series of varieties,  is a del Pezzo fibration for \(n \geqslant 1\) while
is a del Pezzo fibration for \(n \geqslant 1\) while  is not (see Sect. 2 for details). We have the following conjectures concerning these varieties.
is not (see Sect. 2 for details). We have the following conjectures concerning these varieties.
Conjecture 1.1
(Cheltsov–Shramov [3, Conjecture 1.4]) The fibrations  and
and  , for \(n \geqslant 0\), are the only \(G_\mathrm{K}\)-Mori fiber spaces over \(\mathbb {P}^1\) in dimension 3.
, for \(n \geqslant 0\), are the only \(G_\mathrm{K}\)-Mori fiber spaces over \(\mathbb {P}^1\) in dimension 3.
Conjecture 1.2
(Ahmadinezhad [1, Conjecture 3.5]) The varieties \(X_n\) are non-rational for \(n \geqslant 2\).
Note that \(X_0\) and \(X_1\) are both rational. The main result of this paper is the following theorem which supports Conjecture 1.2.
Theorem 1.3
For \(n \geqslant 5\), a very general \(X_n\) is not rational.
We refer the reader to Sect. 3 for the meaning of very generality. Note that  is a del Pezzo fibration of degree 2 and it satisfies the so-called K-condition (or \(K^2\)-condition) for \(n \geqslant 2\). Thus, by the results of Pukhlikov [12] and Grinenko [5–7] on nonsingular del Pezzo fibrations of degree 2, if \(X_n\) were nonsingular, then it would be birationally rigid for \(n \geqslant 2\), which would imply nonrationality in a strong sense. Unfortunately, \(X_n\) is singular and we cannot apply the above results directly. Instead, we apply the Kollár’s reduction modulo p method introduced in [8] (see also [9]) to prove nonrationality of \(X_n\).
is a del Pezzo fibration of degree 2 and it satisfies the so-called K-condition (or \(K^2\)-condition) for \(n \geqslant 2\). Thus, by the results of Pukhlikov [12] and Grinenko [5–7] on nonsingular del Pezzo fibrations of degree 2, if \(X_n\) were nonsingular, then it would be birationally rigid for \(n \geqslant 2\), which would imply nonrationality in a strong sense. Unfortunately, \(X_n\) is singular and we cannot apply the above results directly. Instead, we apply the Kollár’s reduction modulo p method introduced in [8] (see also [9]) to prove nonrationality of \(X_n\).
This is relevant to the study of embeddings of the Klein simple group \(G_\mathrm{K} = \mathrm {PSL}_2 (\mathbb {F}_7)\) into the Cremona group \({\text {Cr}}_3 (\mathbb {C})\) of rank 3. If we are given a finite simple subgroup G of \({\text {Cr}}_3 (\mathbb {C}^3)\), then there is a rational G-Mori fiber space X / S such that the embedding \(G \subset {\text {Cr}}_3 (\mathbb {C})\) is given by \(G \subset \mathrm{Aut}(X) \subset \mathrm{Bir}(X) \cong {\text {Cr}}_3 (\mathbb {C})\) (see [11, Section 4.2]). Such a G-Mori fiber space X / S is called a Mori regularization of \(G \subset {\text {Cr}}_3 (\mathbb {C})\). Moreover, two embeddings \(G_1\) and \(G_2\) into \({\text {Cr}}_3 (\mathbb {C})\) of a finite simple subgroup G are conjugate if and only if there is a G-equivariant birational map between Mori regularizations \(X_1/S_1\) and \(X_2/S_2\) of \(G_1 \subset {\text {Cr}}_3 (\mathbb {C})\) and \(G_2 \subset {\text {Cr}}_3 (\mathbb {C})\), respectively. In [4], Cheltsov and Shramov proved that there are at least three non-conjugate embeddings of \(\mathrm {PSL}_2 (\mathbb {F}_7)\) into \({\text {Cr}}_3 (\mathbb {C})\) and each of them comes from rational (\(G_\mathrm{K}\)-) Fano threefolds. Theorem 1.3 implies that, for \(n \geqslant 5\), a very general  cannot be a Mori regularization of any subgroup of \({\text {Cr}}_3 (\mathbb {C})\) isomorphic to \(G_\mathrm{K}\). If Conjectures 1.1 and 1.2 are both true, then it follows that there is no embedding of \(\mathrm {PSL}_2 (\mathbb {F}_7)\) into \({\text {Cr}}_3 (\mathbb {C})\) coming from a \(G_\mathrm{K}\)-Mori fiber space over \(\mathbb {P}^1\) other than
cannot be a Mori regularization of any subgroup of \({\text {Cr}}_3 (\mathbb {C})\) isomorphic to \(G_\mathrm{K}\). If Conjectures 1.1 and 1.2 are both true, then it follows that there is no embedding of \(\mathrm {PSL}_2 (\mathbb {F}_7)\) into \({\text {Cr}}_3 (\mathbb {C})\) coming from a \(G_\mathrm{K}\)-Mori fiber space over \(\mathbb {P}^1\) other than  ,
,  and
and  . Note that, by [1, Theorem 3.4], there is a \(G_\mathrm{K}\)-equivariant birational map between \(X_1\) and
. Note that, by [1, Theorem 3.4], there is a \(G_\mathrm{K}\)-equivariant birational map between \(X_1\) and  .
.
The paper is organized as follows. In Sect. 2, we give an explicit construction of varieties \(X_n\). They are constructed as hypersurfaces of suitable weighted projective space bundle over \(\mathbb {P}^1\). Then we show that  is indeed a del Pezzo fibration for \(n \geqslant 1\). In Sect. 3, we prove the main theorem. The proof will be done by the Kollár’s reduction modulo p method, which we briefly recall in Sect. 3.2. The very first reduction step is done in Sect. 3.1. In Sect. 3.3, we work over a field of characteristic 2 and construct a specific big line bundle on some nonsingular model of \(X_n\) by making use of the purely inseparable double covering structure. This will complete the proof in view of the non-ruledness criterion given in Lemma 3.2.
is indeed a del Pezzo fibration for \(n \geqslant 1\). In Sect. 3, we prove the main theorem. The proof will be done by the Kollár’s reduction modulo p method, which we briefly recall in Sect. 3.2. The very first reduction step is done in Sect. 3.1. In Sect. 3.3, we work over a field of characteristic 2 and construct a specific big line bundle on some nonsingular model of \(X_n\) by making use of the purely inseparable double covering structure. This will complete the proof in view of the non-ruledness criterion given in Lemma 3.2.
2 Construction of del Pezzo fibrations
We construct del Pezzo fibrations  as hypersurfaces in suitable weighted projective space bundles over \(\mathbb {P}^1\). We refer the reader to [2] for Cox rings (which are also known as homogeneous coordinate rings) of toric varieties. In this section we work over \(\mathbb {C}\).
as hypersurfaces in suitable weighted projective space bundles over \(\mathbb {P}^1\). We refer the reader to [2] for Cox rings (which are also known as homogeneous coordinate rings) of toric varieties. In this section we work over \(\mathbb {C}\).
Throughout this paper, we define  . We see that f is the defining polynomial of the Klein quartic curve whose automorphism group is the Klein simple group. Let \(P_n\) be the projective simplicial toric variety with the Cox ring
. We see that f is the defining polynomial of the Klein quartic curve whose automorphism group is the Klein simple group. Let \(P_n\) be the projective simplicial toric variety with the Cox ring

which is \(\mathbb {Z}^2\)-graded as

and with the irrelevant ideal \(I = (w_0,w_1) \cap (x_0,x_1,x_2,y)\), that is, \(P_n\) is the geometric quotient

where the action of \((\mathbb {C}^*)^2\) on \(\mathbb {A}^6 = {\text {Spec}}\mathrm{Cox}(P_n)\) is given by the above matrix. Note that the Weil divisor class group \(\mathrm{Cl}(P_n)\) is isomorphic to \(\mathbb {Z}^2\). There is a natural morphism \(\mathrm{\Pi } :P \rightarrow \mathbb {P}^1\) defined as the projection to coordinates \(w_0,w_1\), and this realizes P as a weighted projective space bundle over \(\mathbb {P}^1\) whose fibers are  . For a nonnegative integer n and homogeneous polynomials
. For a nonnegative integer n and homogeneous polynomials  and
and  of degree respectively
of degree respectively  and 4, define
and 4, define

and let  . Throughout this paper, we assume that a does not have a multiple component.
. Throughout this paper, we assume that a does not have a multiple component.
Remark 2.1
Let us note that  constructed as above coincides with the one given in [1, Section 3]. Indeed, choose and fix any pair
constructed as above coincides with the one given in [1, Section 3]. Indeed, choose and fix any pair  of homogeneous polynomials of degree n such that
of homogeneous polynomials of degree n such that  and define
and define

Let \(\pi ' :\mathscr {X}'_n \rightarrow \mathbb {P}^1\) be the projection to the coordinates \(w_0,w_1\). Then, \((c = t = f = 0) \subset \mathscr {X}'_n\) is a disjoint union of n-curves \(C'_1,\ldots ,C'_n\) and \(\mathscr {X}'_n\) has a singularity of type  along each \(C'_i\). Blowing up \(\mathscr {X}'_n\) along these curves and then contracting the strict transforms of the \(\pi '\)-fibers containing \(C'_i\), we obtain a birational map \(\mathscr {X}'_n \dashrightarrow \mathscr {X}_n\) to the del Pezzo fibration \(\mathscr {X}_n \rightarrow \mathbb {P}^1\) constructed in [1].
along each \(C'_i\). Blowing up \(\mathscr {X}'_n\) along these curves and then contracting the strict transforms of the \(\pi '\)-fibers containing \(C'_i\), we obtain a birational map \(\mathscr {X}'_n \dashrightarrow \mathscr {X}_n\) to the del Pezzo fibration \(\mathscr {X}_n \rightarrow \mathbb {P}^1\) constructed in [1].
Now we have a birational map  defined by the correspondence
defined by the correspondence  . It is easy to see that \(\mathrm{\Psi }\) restricts to a birational map \(\psi :X_n \dashrightarrow \mathscr {X}'_n\). Moreover, it is straightforward to see that \(\psi ^{-1} :\mathscr {X}'_n \dashrightarrow X_n\) is obtained by blowing up \(\mathscr {X}'_n\) along \(C'_1,\ldots ,C'_n\) and then contracting the strict transforms of the fibers containing \(C'_i\). This shows
. It is easy to see that \(\mathrm{\Psi }\) restricts to a birational map \(\psi :X_n \dashrightarrow \mathscr {X}'_n\). Moreover, it is straightforward to see that \(\psi ^{-1} :\mathscr {X}'_n \dashrightarrow X_n\) is obtained by blowing up \(\mathscr {X}'_n\) along \(C'_1,\ldots ,C'_n\) and then contracting the strict transforms of the fibers containing \(C'_i\). This shows  .
.
Remark 2.2
Let us explain that both \(X_0\) and \(X_1\) are rational. If \(n = 0\), then we have  , where
, where  is a (nonsingular) del Pezzo surface of degree 2, and thus \(X_0\) is clearly rational. Suppose \(n = 1\). Then, as explained in Remark 2.1, \(X_1\) is birational to
is a (nonsingular) del Pezzo surface of degree 2, and thus \(X_0\) is clearly rational. Suppose \(n = 1\). Then, as explained in Remark 2.1, \(X_1\) is birational to  , where
, where  are homogeneous polynomials of degree 1 such that
are homogeneous polynomials of degree 1 such that  . It is clear that the projection
. It is clear that the projection  is birational. Hence \(\mathscr {X}'_1\) and \(X_1\) are rational.
is birational. Hence \(\mathscr {X}'_1\) and \(X_1\) are rational.
In the rest of this section, we show that \(\pi :X_n \rightarrow \mathbb {P}^1\) is indeed a del Pezzo fibration for \(n \geqslant 1\).
Definition 2.3
Let \(\pi :X \rightarrow \mathbb {P}^1\) be a surjective morphism with connected fibers from a normal projective 3-fold X. We say that \(\pi :X \rightarrow \mathbb {P}^1\) is a del Pezzo fibration over \(\mathbb {P}^1\) if the following conditions are satisfied:
-
X is \(\mathbb {Q}\)-factorial and has only terminal singularities.
-
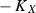 is \(\pi \)-ample.
is \(\pi \)-ample. -
\(\rho (X) = 2\).
Remark 2.4
We explain the natural affine open subsets of \(P_n\) and \(X_n\). We refer the reader to [13] for details. Since we will work over an algebraically closed field of characteristic 2 in the next section, we assume in this remark that the ground field of \(P_n\) and \(X_n\) is an algebraically closed field \(\Bbbk \) of arbitrary characteristic.
Denote by \(U_{w_i,x_j}\) the open subset \((w_i \ne 0) \cap (x_j \ne 0) \subset P_n\) and by \(U_{w_i,y}\) the open subset \((w_i \ne 0) \cap (y \ne 0) \subset P_n\). Then \(P_n\) is covered by \(U_{w_i,x_j}\) and \(U_{w_i,y}\) for \(i = 0,1\) and \(j = 0,1,2\); and \(U_{w_0,x_0}\) is the affine 4-space \(\mathbb {A}^4\). The restrictions of \(w_1, x_1,x_2,y\) on \(U_{w_0,x_0}\) form affine coordinates of \(U_{w_0,x_0}\). Indeed, if we denote by \(\widetilde{w}_1 = w_1/w_0\), \(\widetilde{x}_i = x_i/x_0\) for \(i = 1,2\) and  , then \(U_{w_0,x_0}\) is an affine 4-space with affine coordinates \(\widetilde{w}_0,\widetilde{x}_1,\widetilde{x}_2,\widetilde{y}\). The affine scheme \(X_n \cap U_{w_0,x_0}\) is defined by the equation
, then \(U_{w_0,x_0}\) is an affine 4-space with affine coordinates \(\widetilde{w}_0,\widetilde{x}_1,\widetilde{x}_2,\widetilde{y}\). The affine scheme \(X_n \cap U_{w_0,x_0}\) is defined by the equation  . The same description applies for the other \(U_{w_i,x_j}\).
. The same description applies for the other \(U_{w_i,x_j}\).
We see that \(U_{w_0,y}\) is the quotient  of \(\mathbb {A}^4\) by the action of
of \(\mathbb {A}^4\) by the action of  . Indeed, if we denote by \(\widetilde{w}_1 = w_1/w_0\),
. Indeed, if we denote by \(\widetilde{w}_1 = w_1/w_0\),  for \(i = 0,1,2\), then \(U_{w_0,y}\) is the quotient of \(\mathbb {A}^4\) with coordinates \(\widetilde{w}_1, \widetilde{x}_0,\widetilde{x}_1,\widetilde{x}_2\) under the \(\varvec{\mu }_2\)-action given by
for \(i = 0,1,2\), then \(U_{w_0,y}\) is the quotient of \(\mathbb {A}^4\) with coordinates \(\widetilde{w}_1, \widetilde{x}_0,\widetilde{x}_1,\widetilde{x}_2\) under the \(\varvec{\mu }_2\)-action given by

where  . Here, the above operation defines a ring homomorphism
. Here, the above operation defines a ring homomorphism  , where
, where  , and
, and  . When \(\Bbbk = \mathbb {C}\), we can replace \(\varvec{\mu }_2\) with
. When \(\Bbbk = \mathbb {C}\), we can replace \(\varvec{\mu }_2\) with  and the action is given simply by \(\widetilde{w}_0 \mapsto \widetilde{w}_0\) and
and the action is given simply by \(\widetilde{w}_0 \mapsto \widetilde{w}_0\) and  . The affine scheme \(X_n \cap U_{w_0,y}\) is the quotient of the affine scheme
. The affine scheme \(X_n \cap U_{w_0,y}\) is the quotient of the affine scheme  defined by the \(\varvec{\mu }_2\)-action. The same description applies for \(U_{w_1,y}\).
defined by the \(\varvec{\mu }_2\)-action. The same description applies for \(U_{w_1,y}\).
Sometimes we will abuse the notation and say that \(U_{w_0,x_0}\) is the affine 4-space \(\mathbb {A}^4\) with coordinates \(w_1,x_1,x_2,y\) and \(X_n \cap U_{w_0,x_0}\) is defined by  .
.
Lemma 2.5
The variety \(X_n\) is nonsingular outside \((x_0 = x_1 = x_2 = 0) \cap X_n\) and it has a singular point of type  at each point of \((x_0 = x_1 = x_2 = 0) \cap X_n\).
at each point of \((x_0 = x_1 = x_2 = 0) \cap X_n\).
Proof
Set \(U = U_{w_0,x_0}\) which is an affine 4-space with affine coordinates \(w_1,x_1,x_2,y\), then \(X_n \cap U\) is defined by  , where
, where  and \(f_0 = f (1,x_1,x_2)\). It is straightforward to see that
and \(f_0 = f (1,x_1,x_2)\). It is straightforward to see that

where the last equality holds since \(f_0 = f (1,x_1,x_2)\) defines a nonsingular curve in \(\mathbb {A}^2\). By symmetry, we conclude that \(X \cap U_{w_i,x_j}\) is nonsingular for \(i = 0,1\) and \(j = 0,1,2\). Since the open subsets \(U_{w_i,x_j}\) for \(i = 0,1\) and \(j = 0,1,2\) cover  , we see that \(X_n\) is nonsingular outside \((x_0 = x_1 = x_2 = 0) \cap X_n\).
, we see that \(X_n\) is nonsingular outside \((x_0 = x_1 = x_2 = 0) \cap X_n\).
Let \(P \in (x_0 = x_1 = x_2 = 0) \cap X_n\). Then \(a (P) = 0\) and we may assume that \(w_1\) vanishes at P after replacing \(w_0,w_1\). We work on  . We see that \(X_n \cap U\) is the quotient of
. We see that \(X_n \cap U\) is the quotient of  by the \(\varvec{\mu }_2\)-action and P corresponds to the origin. Since a vanishes at P and it does not have a multiple component, we have
by the \(\varvec{\mu }_2\)-action and P corresponds to the origin. Since a vanishes at P and it does not have a multiple component, we have  , so that \(x_0,x_1,x_2\) form local coordinates of V at the origin. Thus the point P is of type
, so that \(x_0,x_1,x_2\) form local coordinates of V at the origin. Thus the point P is of type  . \(\square \)
. \(\square \)
For \(n \geqslant 1\), we construct a birational morphism \(\theta :X_n \rightarrow V_n\) as follows. Set \(\xi _0 = w_0^n\), \(, \ldots , \xi _n = w_1^n\) and let

be the toric morphism defined by the correspondence  . Then the image of \(\mathrm{\Theta }\), which we denote by \(T_n\), is defined by \(h_1 = \cdots = h_N = 0\), where \(h_1, \ldots , h_N\) are the homogeneous polynomials in \(y_0,\ldots ,y_n\) defining the image of the n-ple Veronese embedding \(\mathbb {P}^1 \hookrightarrow \mathbb {P}^n_{y_0,\ldots ,y_n}\). We see that \(\mathrm{\Theta } :P_n \rightarrow T_n\) is a birational morphism contracting the divisor
. Then the image of \(\mathrm{\Theta }\), which we denote by \(T_n\), is defined by \(h_1 = \cdots = h_N = 0\), where \(h_1, \ldots , h_N\) are the homogeneous polynomials in \(y_0,\ldots ,y_n\) defining the image of the n-ple Veronese embedding \(\mathbb {P}^1 \hookrightarrow \mathbb {P}^n_{y_0,\ldots ,y_n}\). We see that \(\mathrm{\Theta } :P_n \rightarrow T_n\) is a birational morphism contracting the divisor  to the plane \(\mathrm{\Delta } = (y_0 = \cdots = y_n = 0) \subset T_n\). It follows that \(T_n\) is a projective simplicial toric variety with Picard number 1. The image of \(X_n\) under \(\mathrm{\Theta }\) is a hypersurface \(V_n\) in \(T_n\) defined by \(q + f = 0\), where \(q = q (y_0,\ldots ,y_n)\) is a quadratic polynomial such that
to the plane \(\mathrm{\Delta } = (y_0 = \cdots = y_n = 0) \subset T_n\). It follows that \(T_n\) is a projective simplicial toric variety with Picard number 1. The image of \(X_n\) under \(\mathrm{\Theta }\) is a hypersurface \(V_n\) in \(T_n\) defined by \(q + f = 0\), where \(q = q (y_0,\ldots ,y_n)\) is a quadratic polynomial such that  . The morphism
. The morphism  is a birational morphism contracting the divisor
is a birational morphism contracting the divisor  to the curve \(\mathrm{\Delta } \cap V_n \cong C\), where C is the plane curve defined by \(f = 0\).
to the curve \(\mathrm{\Delta } \cap V_n \cong C\), where C is the plane curve defined by \(f = 0\).
Lemma 2.6
If \(n \geqslant 1\), then \(V_n\) is a normal projective \(\mathbb {Q}\)-factorial 3-fold with Picard number 1.
Proof
Note that \(X_n\) is \(\mathbb {Q}\)-factorial since it has only quotient singularities. It follows that \(V_n\) is \(\mathbb {Q}\)-factorial since \(\theta \) is an extremal contraction (which is not necessarily \(K_{X_n}\)-negative). We see that the singularity of \(T_n\) along the plane \(\mathrm{\Delta }\) is of type  and \(V_n\) intersects \(\mathrm{\Delta }\) transversally. Moreover, outside the curve \(\mathrm{\Delta } \cap V_n\), singular points of \(V_n\) are of type
and \(V_n\) intersects \(\mathrm{\Delta }\) transversally. Moreover, outside the curve \(\mathrm{\Delta } \cap V_n\), singular points of \(V_n\) are of type  . This implies that \(V_n\) is a V-submanifold of \(T_n\) and thus, by [2, Proposition 3.5], \(V_n\) is quasi-smooth in \(T_n\). Here, we refer the reader to [2, Section 3] for the definitions of V-submanifold and quasi-smoothness. It then follows, from [14, Proposition 4], that \(\rho (V_n) = \rho (T_n) = 1\) since \(V_n\) is quasi-smooth hypersurface defined by a global section of an ample divisor on \(T_n\). \(\square \)
. This implies that \(V_n\) is a V-submanifold of \(T_n\) and thus, by [2, Proposition 3.5], \(V_n\) is quasi-smooth in \(T_n\). Here, we refer the reader to [2, Section 3] for the definitions of V-submanifold and quasi-smoothness. It then follows, from [14, Proposition 4], that \(\rho (V_n) = \rho (T_n) = 1\) since \(V_n\) is quasi-smooth hypersurface defined by a global section of an ample divisor on \(T_n\). \(\square \)
Lemma 2.7
For \(n \geqslant 1\), the fibration \(\pi :X_n \rightarrow \mathbb {P}^1\) is a del Pezzo fibration.
Proof
Assume that \(n \geqslant 1\). We see that X has only terminal singularities of type  and it is \(\mathbb {Q}\)-factorial. By Lemma 2.6, we have \(\rho (X_n) = \rho (V_n) + 1 = 2\) since \(\theta :X_n \rightarrow V_n\) is a birational morphism contracting a prime divisor. This shows that \(\pi \) is an extremal contraction and thus
and it is \(\mathbb {Q}\)-factorial. By Lemma 2.6, we have \(\rho (X_n) = \rho (V_n) + 1 = 2\) since \(\theta :X_n \rightarrow V_n\) is a birational morphism contracting a prime divisor. This shows that \(\pi \) is an extremal contraction and thus  is indeed a del Pezzo fibration. \(\square \)
is indeed a del Pezzo fibration. \(\square \)
Remark 2.8
The above arguments apply to more general cases without any change. Let  be a homogeneous polynomial of degree 4 such that the plane curve in \(\mathbb {P}^2\) defined by g is nonsingular. Then the hypersurface
be a homogeneous polynomial of degree 4 such that the plane curve in \(\mathbb {P}^2\) defined by g is nonsingular. Then the hypersurface  , where
, where  is a homogeneous polynomial of degree
is a homogeneous polynomial of degree  which does not have a multiple component, together with the projection \(\pi :X_n \rightarrow \mathbb {P}^1\) is a del Pezzo fibration provided that \(n \geqslant 1\).
which does not have a multiple component, together with the projection \(\pi :X_n \rightarrow \mathbb {P}^1\) is a del Pezzo fibration provided that \(n \geqslant 1\).
The variety \(V_n\) and the birational map \(\theta :X_n \dashrightarrow V_n\) are constructed in order to prove Lemma 2.7 and we will not use them in what follows. We give a definition of G-Mori fiber space.
Definition 2.9
Let G be a group. A G-Mori fiber space is a normal projective variety X, where G acts faithfully on X, together with a G-equivariant morphism \(\pi :X \rightarrow S\) onto a normal projective variety S with the following properties:
-
X is \(G \mathbb {Q}\)-factorial, that is, every G-invariant Weil divisor on X is \(\mathbb {Q}\)-Cartier, and X has only terminal singularities.
-
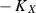 is \(\pi \)-ample.
is \(\pi \)-ample. -
\(\dim S < \dim X\) and \(\pi \) has connected fibers.
-
\({\text {rank}}\, {\text {Pic}}^G (X) - {\text {rank}}\, {\text {Pic}}^G (S) = 1\).
Note that the Klein simple group \(G = \mathrm {PSL}_2 (\mathbb {F}_7)\) acts on  along the fibers, so that
along the fibers, so that  is a G-Mori fiber space for \(n \geqslant 1\). For \(n = 0\),
is a G-Mori fiber space for \(n \geqslant 1\). For \(n = 0\),  is not a del Pezzo fibration. Nevertheless, we have \(\rho ^G (X_0) = 1\), so that
is not a del Pezzo fibration. Nevertheless, we have \(\rho ^G (X_0) = 1\), so that  is a G-Mori fiber space as well.
is a G-Mori fiber space as well.
3 Proof of Theorem 1.3
3.1 Reduction modulo 2
In the following, we drop the subscript n and write \(P = P_n\), \(X = X_n\). In the previous section, the toric variety P was defined over \(\mathbb {C}\). We can define P over an arbitrary field or more generally an arbitrary ring. For a field or a ring K, we denote by \(P_K\) the toric variety over \({\text {Spec}}K\) defined by the same fan as that of P. Then, since  is defined over \(\mathbb {Z}\), we can define the subscheme
is defined over \(\mathbb {Z}\), we can define the subscheme  for a homogeneous polynomial
for a homogeneous polynomial  of degree
of degree  .
.
Let  , \(\alpha _i \in \mathbb {C}\). Assume that \(\alpha _0,\dots ,\alpha _{2 n}\) are very general so that they are algebraically independent over \(\mathbb {Z}\). Then, the ring
, \(\alpha _i \in \mathbb {C}\). Assume that \(\alpha _0,\dots ,\alpha _{2 n}\) are very general so that they are algebraically independent over \(\mathbb {Z}\). Then, the ring  is isomorphic to a polynomial ring of
is isomorphic to a polynomial ring of  variables over \(\mathbb {Z}\) and the ideal (2) is a prime ideal. Define
variables over \(\mathbb {Z}\) and the ideal (2) is a prime ideal. Define

which is a DVR whose residue field is of characteristic 2. Then we can define  , which is a scheme over \({\text {Spec}}R\) and whose geometric generic fiber is isomorphic to \(X_{\mathbb {C}}\).
, which is a scheme over \({\text {Spec}}R\) and whose geometric generic fiber is isomorphic to \(X_{\mathbb {C}}\).
Lemma 3.1
Let \(\Bbbk \) be an algebraically closed field which is uncountable. If  is not ruled for a very general
is not ruled for a very general  , then
, then  is not ruled for a very general
is not ruled for a very general  .
.
Proof
Let \(X'\) be the geometric special fiber of \(X_R \rightarrow {\text {Spec}}R\) defined over \(\Bbbk \). We can write \(X' = (a' y^2 + f = 0) \subset P_{\Bbbk }\) for some  and \(a'\) corresponds to a very general element. By the Matsusaka theorem [9, V.1.6 Theorem], if \(X'\) is not ruled, then X is not ruled. This completes the proof. \(\square \)
and \(a'\) corresponds to a very general element. By the Matsusaka theorem [9, V.1.6 Theorem], if \(X'\) is not ruled, then X is not ruled. This completes the proof. \(\square \)
3.2 Kollár’s technique
In this subsection, we briefly recall Kollár’s argument of proving non-ruledness of suitable covering spaces in positive characteristic. We apply the following non-ruledness criterion which is a slight generalization of [9, V.5.1 Lemma].
Lemma 3.2
Let Y be a smooth proper variety defined over an algebraically closed field and \(\mathscr {M}\) a big line bundle on Y. If there is an injection \(\mathscr {M}\hookrightarrow (\mathrm{\Omega }_Y^i)^{\otimes m}\) for some \(i > 0\) and \(m > 0\), then Y is not separably uniruled.
Proof
Suppose that Y is separably uniruled. Then, there exists a separable dominant map  , where V is a normal projective variety. After shrinking V, we may assume that \(\varphi \) is a morphism and V is smooth. The homomorphism
, where V is a normal projective variety. After shrinking V, we may assume that \(\varphi \) is a morphism and V is smooth. The homomorphism  is an isomorphism on a non-empty open subset since \(\varphi \) is separable. This induces an injection
is an isomorphism on a non-empty open subset since \(\varphi \) is separable. This induces an injection  for any \(k \geqslant 1\). The invertible sheaf \(\mathscr {M}\) is big so that the global sections of
for any \(k \geqslant 1\). The invertible sheaf \(\mathscr {M}\) is big so that the global sections of  separate points on a nonempty open subset of
separate points on a nonempty open subset of  for a sufficiently large k. This is a contradiction since the global sections of \((\mathrm{\Omega }^i_{V \times \mathbb {P}^1})^{\otimes m k}\) do not separate points in a fiber. \(\square \)
for a sufficiently large k. This is a contradiction since the global sections of \((\mathrm{\Omega }^i_{V \times \mathbb {P}^1})^{\otimes m k}\) do not separate points in a fiber. \(\square \)
Remark 3.3
Our aim is to prove that the variety \(X_n\) defined over an algebraically closed field of characteristic 2 is not ruled. In view of Lemma 3.2, it is enough to construct a resolution \(r :Y \rightarrow X_n\) and a big line bundle \(\mathscr {M}\) which is a subsheaf of \((\mathrm{\Omega }^i_Y)^{\otimes m}\) for some \(m > 0\). As we will see in Sect. 3.3, there is a purely inseparable cover \(X_n \rightarrow Z_n\) of degree 2 for some normal projective variety \(Z_n\). In the following we explain the Kollár’s construction of a big line bundle on a nonsingular model of a suitable cyclic covering space in a general setting.
Let Z be a variety of dimension n defined over an algebraically closed field \(\Bbbk \) of characteristic \(p > 0\), \(\mathscr {L}\) a line bundle on Z and \(s \in H^0 (Z, \mathscr {L}^{\otimes m})\) a global section of \(\mathscr {L}^m\) for some \(m > 0\). Let \(U = {\text {Spec}}\bigoplus _{i \geqslant 0} \mathscr {L}^{- i}\) be the total space of the line bundle \(\mathscr {L}\) and let \(\rho _U :U \rightarrow Z\) be the natural morphism. We denote by  the zero section and define
the zero section and define

We say that  is the cyclic covering of Z obtained by taking mth roots of s. Set
is the cyclic covering of Z obtained by taking mth roots of s. Set  and let \(\rho = \rho _U{|}_X :X \rightarrow Z\) be the cyclic covering.
and let \(\rho = \rho _U{|}_X :X \rightarrow Z\) be the cyclic covering.
From now on we assume that Z is nonsingular and m is divisible by p. We have a natural differential  whose construction is given below. Let \(\tau \) be a local generator of \(\mathscr {L}\) and
whose construction is given below. Let \(\tau \) be a local generator of \(\mathscr {L}\) and  a local section. Let \(x_1,\ldots ,x_n\) be local coordinates of of Z. Then define
a local section. Let \(x_1,\ldots ,x_n\) be local coordinates of of Z. Then define

This is independent of the choices of local coordinates and the local generator \(\tau \), and thus defines d. For the section \(s \in H^0 (Z, \mathscr {L}^m)\), we can view d (s) as a sheaf homomorphism  . By taking the tensor product with \(\mathscr {L}^{-m}\), we obtain \(d s :\mathscr {L}^{- m} \rightarrow \mathrm{\Omega }^1_Z\).
. By taking the tensor product with \(\mathscr {L}^{-m}\), we obtain \(d s :\mathscr {L}^{- m} \rightarrow \mathrm{\Omega }^1_Z\).
Definition 3.4
([9, V.5.8 Definition]) We define \(\mathscr {Q}(\mathscr {L}, s) = ( \det \mathrm {Coker} (d s) )^{\vee \vee }\).
We have  .
.
Lemma 3.5
([9, 5.5 Lemma]) There is an injection  .
.
Remark 3.6
Let \(x_1,\ldots ,x_n\) be local coordinates of Z at a point P and  as before. Then,
as before. Then,  is generated by the form
is generated by the form

See [9, V.5.9 Lemma] for details.
Let us show that if the singularity of X is mild, then we can lift  to an invertible subsheaf of \(\mathrm{\Omega }^{n-1}_Y\), where Y is a suitable nonsingular model of X. For simplicity of description, we assume that \(p = 2\) and \(n = \dim Z = 3\).
to an invertible subsheaf of \(\mathrm{\Omega }^{n-1}_Y\), where Y is a suitable nonsingular model of X. For simplicity of description, we assume that \(p = 2\) and \(n = \dim Z = 3\).
Definition 3.7
([9, V.5.6 Definition], see also [9, V.5.7 Exercise]) We say that \(s \in H^0 (Z, \mathscr {L}^m)\) has a critical point at \(P \in Z\) if  vanishes at P. Denote by \(\mathrm{Crit}(s) \subset Z\) the set of critical points of s. We say that s has an almost nondegenerate critical point at P if in suitable choice of local coordinates \(x_1,x_2,x_3\) we can write
vanishes at P. Denote by \(\mathrm{Crit}(s) \subset Z\) the set of critical points of s. We say that s has an almost nondegenerate critical point at P if in suitable choice of local coordinates \(x_1,x_2,x_3\) we can write

where \(\alpha \in \Bbbk \),  for a local generator \(\tau \) of \(\mathscr {L}\) at P, \(h = h (x_1,x_2,x_3)\) consists of monomials of degree at least 3 and it does not involve \(x_1^3\).
for a local generator \(\tau \) of \(\mathscr {L}\) at P, \(h = h (x_1,x_2,x_3)\) consists of monomials of degree at least 3 and it does not involve \(x_1^3\).
Lemma 3.8
([9, V.5.10 Proposition]) Suppose that s has only almost nondegenerate critical points. Then the singularities of X are isolated singularities and they can be resolved by blowing up each singular point of X. Moreover, if we denote by \(r :Y \rightarrow X\) the blowup of each singular point of X, then \({r^*\rho ^* \mathscr {Q}(\mathscr {L},s) \hookrightarrow \mathrm{\Omega }^2_Y}\).
3.3 Construction of a big line bundle
Throughout this subsection, we work over an algebraically closed field \(\Bbbk \) of characteristic 2 which is uncountable. We write \(P = P_{\Bbbk }\) and \(X = X_{\Bbbk }\). We do not assume \(n \geqslant 5\) for the moment. Let  and \(X^{\circ }\! = X \cap P^{\circ }\). Note that \(P^{\circ }\) is the nonsingular locus of P. Define
and \(X^{\circ }\! = X \cap P^{\circ }\). Note that \(P^{\circ }\) is the nonsingular locus of P. Define

and set Z to be the hypersurface in Q defined by  . Let \(\rho :X \rightarrow Z\) be the morphism which is defined by the correspondence \(z = y^2\), which is a purely inseparable finite morphism of degree 2.
. Let \(\rho :X \rightarrow Z\) be the morphism which is defined by the correspondence \(z = y^2\), which is a purely inseparable finite morphism of degree 2.
Lemma 3.9
Let  be a general homogeneous polynomial of degree
be a general homogeneous polynomial of degree  . Then the set
. Then the set

consists of finitely many points and \(\mathrm{Crit}(a) \cap (a = 0) = \varnothing \). Moreover, for each \(P \in \mathrm{Crit}(a)\), we can choose a local coordinate w of \(\mathbb {P}^1\) at P such that

for some \(\alpha ,\beta \in \Bbbk \) with \(\alpha \ne 0\).
Proof
The set \(\mathrm{Crit}(a)\) is clearly a finite set of points. As a generality of a, we in particular require that a does not have a multiple component. It is then clear that \(\mathrm{Crit}(a) \cap (a = 0) = \varnothing \). The last assertion follows by counting dimension. Let \(P \in \mathbb {P}^1\) be a point and w a local coordinate of \(\mathbb {P}^1\) at P. We can write  , \(\alpha _i \in \Bbbk \). We say that a has a bad critical point at P if \(\alpha _1 = \alpha _3 = 0\). Two conditions \(\alpha _1 = \alpha _3 = 0\) are imposed for a to have a bad critical point at a given \(P \in \mathbb {P}^1\). Since P runs through \(\mathbb {P}^1\), we see that homogeneous polynomials a which have a bad critical point at some point \(P \in \mathbb {P}^1\) form at most \(2 - 1 = 1\) codimensional subfamily in the space of all
, \(\alpha _i \in \Bbbk \). We say that a has a bad critical point at P if \(\alpha _1 = \alpha _3 = 0\). Two conditions \(\alpha _1 = \alpha _3 = 0\) are imposed for a to have a bad critical point at a given \(P \in \mathbb {P}^1\). Since P runs through \(\mathbb {P}^1\), we see that homogeneous polynomials a which have a bad critical point at some point \(P \in \mathbb {P}^1\) form at most \(2 - 1 = 1\) codimensional subfamily in the space of all  . Thus, a general a does not have a bad critical point at all and the proof is completed. \(\square \)
. Thus, a general a does not have a bad critical point at all and the proof is completed. \(\square \)
Lemma 3.10
The set

consists of finitely many closed points and \(\mathrm{Crit}(f) \cap (f = 0) = \varnothing \). Moreover, for each \(P \in \mathrm{Crit}(f)\), we can choose local coordinates \(t_1, t_2\) of \(\mathbb {P}^2\) at P such that
for some \(\gamma \ne 0\).
Proof
We have

By a straightforward computation, we have

where \(\zeta \in \Bbbk \) is a primitive 7th root of unity. It is also straightforward to see that \(f (P) \ne 0\) for \(P \in \mathrm{Crit}(f)\). For the last assertion, we work on the affine open subset \(U = (x_0 \ne 0) \subset \mathbb {P}^2\). Note that \(\mathrm{Crit}(f) \subset U\). By setting \(x_0 = 1\), we think of \(x_1,x_2\) as affine coordinates of \(U \cong \mathbb {A}^2\). We have  on U. For the verification of the last assertion, it is enough to show that the Hessian of f at \(P = (1\!:\!\zeta ^{3 i}\!:\!\zeta ^i) \in \mathrm{Crit}(f)\) is nonzero. We have \(\partial ^2 f/\partial x_1^2 = 1\), \(\partial ^2 f/\partial x_1 \partial x_2 = x_1^2\) and \(\partial ^2 /\partial x_2^2 = 0\), so that we can compute the Hessian as
on U. For the verification of the last assertion, it is enough to show that the Hessian of f at \(P = (1\!:\!\zeta ^{3 i}\!:\!\zeta ^i) \in \mathrm{Crit}(f)\) is nonzero. We have \(\partial ^2 f/\partial x_1^2 = 1\), \(\partial ^2 f/\partial x_1 \partial x_2 = x_1^2\) and \(\partial ^2 /\partial x_2^2 = 0\), so that we can compute the Hessian as
Therefore, the last assertion is proved. \(\square \)
Set  and \(Z^{\circ }\! = Z \cap Q^{\circ }\).
and \(Z^{\circ }\! = Z \cap Q^{\circ }\).
Lemma 3.11
The quasi projective variety \(Z^{\circ }\) is nonsingular.
Proof
We work on the open subset \(U = U_{w_0,x_0} \subset Q\) which is an affine 4-space with coordinates \(w_1,x_1,x_2,z\). We see that \(Z \cap U\) is defined by  , where
, where  and \(f_0 = f (1,x_1,x_2)\). We have
and \(f_0 = f (1,x_1,x_2)\). We have
where the last equality follows since the curve \(f_0 = 0\) in \(\mathbb {A}^2\) is nonsingular. By symmetry, \(Z \cap U_{w_i,x_j}\) is nonsingular for \(i = 0,1\) and \(j = 0,1,2\). Since \(Z^{\circ }\) is covered by \(U_{w_i,x_j}\) for \(i = 0,1\) and \(j = 0,1,2\), the proof is completed. \(\square \)
Let \(H_Q\) and \(F_Q\) be divisor classes on Q which correspond to the weight \({}^t (0 \ 1)\) and \({}^t (1 \ 0)\), respectively, that is, \(F_Q\) is the fiber class of the projection \(Q \rightarrow \mathbb {P}^1\) and \(H_Q{|}_{F_Q} \in |\mathscr {O}_{\mathbb {P}(1,1,1,4)} (1)|\). We set \(H_Z = H_Q{|}_Z\) and \(F_Z = F_Q{|}_Z\). Define \(\mathscr {L}\) to be the sheaf  whose restriction on \(Z^{\circ }\) is an invertible sheaf. Note that we have \(z \in H^0 (Z,\mathscr {L}^2)\). It is clear that
whose restriction on \(Z^{\circ }\) is an invertible sheaf. Note that we have \(z \in H^0 (Z,\mathscr {L}^2)\). It is clear that  . In the following we choose and fix a general
. In the following we choose and fix a general  so that the assertions of Lemma 3.9 hold.
so that the assertions of Lemma 3.9 hold.
Lemma 3.12
The section \(z \in H^0 (Z^{\circ }\!, \mathscr {L}^2)\) has only almost nondegenerate critical points on \(Z^{\circ }\).
Proof
Let \(\mathrm{Crit}(z) \subset Z^{\circ }\) be the set of critical points of z. Since

z can be chosen as a part of local coordinates at every point \(P \in Z^{\circ }\) such that \(a (P) = 0\). It follows that z does not have a critical point at any point \(P \in X \cap (a = 0)\). We work on an open set \(U \subset Z^{\circ }\) on which \(a \ne 0\) and prove that  has only almost nondegenerate critical points on U. Since
has only almost nondegenerate critical points on U. Since  on U and a is a unit on U, it is enough to show that
on U and a is a unit on U, it is enough to show that  has only almost nondegenerate critical points on U. Let \(P \in U\) be a critical point of z. We have
has only almost nondegenerate critical points on U. Let \(P \in U\) be a critical point of z. We have

for \(i = 0,1\) and \(j = 0,1,2\). Since \(a (P) \ne 0\), we have \((\partial f/\partial x_j) (P) = 0\) for \(j = 0,1,2\). By Lemma 3.10, we have \(f (P) \ne 0\), which implies \((\partial a/\partial w_i) (P) = 0\) for \(i = 0,1\). By Lemmas 3.9 and 3.10, we can choose local coordinates \(w, t_1, t_2\) of Z at P such that

where \(\alpha , \beta , \gamma \in \Bbbk \) with \(\alpha ,\gamma \ne 0\), \(h = h (w,t_1,t_2)\) consists of monomials of degree at least 3 and it does not involve \(w^3\). This shows that z has only almost nondegenerate critical points on \(Z^{\circ }\). \(\square \)
Define  which is an invertible sheaf on \(Z^{\circ }\). By Lemma 3.5, we have
which is an invertible sheaf on \(Z^{\circ }\). By Lemma 3.5, we have  , where
, where  . By adjunction, we have
. By adjunction, we have  , hence
, hence  . Let \(H_P\) and \(F_P\) be the divisors on P which correspond to \({}^t (0 \ 1)\) and \({}^t (1 \ 0)\), respectively, so that \(F_P\) is the fiber class of \(\mathrm{\Pi } :P \rightarrow \mathbb {P}^1\) and
. Let \(H_P\) and \(F_P\) be the divisors on P which correspond to \({}^t (0 \ 1)\) and \({}^t (1 \ 0)\), respectively, so that \(F_P\) is the fiber class of \(\mathrm{\Pi } :P \rightarrow \mathbb {P}^1\) and  . We set \(H = H_P{|}_X\) and \(F = F_P{|}_X\). We have \(H = \rho ^*H_Z\) and \(F = \rho ^*F_Z\), hence
. We set \(H = H_P{|}_X\) and \(F = F_P{|}_X\). We have \(H = \rho ^*H_Z\) and \(F = \rho ^*F_Z\), hence  . Let \(\iota :X^{\circ } \hookrightarrow X\) be the open immersion. The sheaf
. Let \(\iota :X^{\circ } \hookrightarrow X\) be the open immersion. The sheaf  is a reflexive sheaf of rank 1 but is not invertible at each singular point of type
is a reflexive sheaf of rank 1 but is not invertible at each singular point of type  . We define
. We define  which is an invertible sheaf on X and we have an injection \(\mathscr {M}\hookrightarrow ((\mathrm{\Omega }_X^2)^{\otimes 2})^{\vee \vee }\).
which is an invertible sheaf on X and we have an injection \(\mathscr {M}\hookrightarrow ((\mathrm{\Omega }_X^2)^{\otimes 2})^{\vee \vee }\).
Note that X has two kinds of singularities both of which are isolated: one of them are the singular points on \(X^{\circ }\) corresponding to the critical points of z and the other ones are singular points of type  . Let \(r :Y \rightarrow X\) be the blowup of X at each singular point. By Lemmas 3.8 and 3.12, Y is nonsingular and we have an injection
. Let \(r :Y \rightarrow X\) be the blowup of X at each singular point. By Lemmas 3.8 and 3.12, Y is nonsingular and we have an injection  on the open subset \(Y^{\circ }\! = r^{-1} (X^{\circ })\). We will show that there is an injection
on the open subset \(Y^{\circ }\! = r^{-1} (X^{\circ })\). We will show that there is an injection  .
.
Lemma 3.13
There is an injection  .
.
Proof
Let P be a singular point of type  . Since we know that
. Since we know that  on the open subset \(Y^{\circ } = r^{-1} (X^{\circ })\), it is enough to show that
on the open subset \(Y^{\circ } = r^{-1} (X^{\circ })\), it is enough to show that  locally around the exceptional divisor of \(r :Y \rightarrow X\) over P. We can write
locally around the exceptional divisor of \(r :Y \rightarrow X\) over P. We can write  for some local section \(\eta \) of \(((\mathrm{\Omega }_{X}^2)^{\otimes 2})^{\vee \vee }\) since \(\mathscr {M}\subset ((\mathrm{\Omega }_{X}^2)^{\otimes 2})^{\vee \vee }\) is an invertible sheaf. We will show that
for some local section \(\eta \) of \(((\mathrm{\Omega }_{X}^2)^{\otimes 2})^{\vee \vee }\) since \(\mathscr {M}\subset ((\mathrm{\Omega }_{X}^2)^{\otimes 2})^{\vee \vee }\) is an invertible sheaf. We will show that

for some \(g, h_1,h_2 \in \mathscr {O}_{X,P}\), and then we will show that \(r^*\eta \) does not have a pole along the exceptional divisor over P.
After replacing \(w_0,w_1\), we assume that \(w_1\) vanishes at P (so that \(w_0\) does not vanish at P). We work on an open subset U of \(U_{w_0,x_0} \subset P\). Shrinking U, we assume \(a \ne 0\) on U. Then  . Let \(\widetilde{w}_1 = w_1/w_0\), \(\widetilde{x}_1 = x_1/x_0\), \(\widetilde{x}_2 = x_2/x_0\) be the restrictions of \(w_1,x_1,x_2\) to \(U_{w_0,x_0}\). Then, in view of Remark 3.6, after further shrinking U, we see that
. Let \(\widetilde{w}_1 = w_1/w_0\), \(\widetilde{x}_1 = x_1/x_0\), \(\widetilde{x}_2 = x_2/x_0\) be the restrictions of \(w_1,x_1,x_2\) to \(U_{w_0,x_0}\). Then, in view of Remark 3.6, after further shrinking U, we see that  is generated by
is generated by

In particular,

where K(X) is the function field of X.
Set \(\xi _i = x_i/y^{1/2}\) for \(i = 0,1,2\). Then \(\xi _0,\xi _1,\xi _2\) can be chosen as local coordinates of the orbifold chart of (X, P). Now we have \(\widetilde{x}_i = \xi _1/\xi _0\) for \(i = 1,2\), hence

Here, since the ground field is of characteristic 2 and \(\xi _0^2 \in \mathscr {O}_{X,P}\), we have the equality

for \(i = 1,2\). Thus  , where
, where  . It follows that
. It follows that

for some rational function g. By [10, Lemma 5.3], we see that  for some \(h \in \mathscr {O}_{X,P}\).
for some \(h \in \mathscr {O}_{X,P}\).
Now, by shrinking X, we assume that \(r :Y \rightarrow X\) is the blowup (more precisely, the weighted blowup with weight  ) at P. Then the order of the pole of the rational 2-form
) at P. Then the order of the pole of the rational 2-form

along the exceptional divisor E is at most 2 (in fact, an explicit computation shows that the above form does not have a pole along E but we do not need this strong estimate). It is clear that \(r^*\xi _i^2\) vanishes along E to order 1 so that \(r^* g\) vanishes along E to order at least 3. Therefore, \(r^*\eta \) does not have a pole along E and we have an injection  . \(\square \)
. \(\square \)
Lemma 3.14
If \(n \geqslant 5\), then the invertible sheaf \(\mathscr {M}\) is big.
Proof
Let m be a positive integer such that \(m > n/(n-4)\). We show that the complete linear system of  defines a birational map. Set
defines a birational map. Set  and
and  which are positive integers. Then
which are positive integers. Then

is a set of sections of \(\mathscr {M}^m\) and they define a generically finite map. Indeed, the restriction of sections  and
and  for \(0 \leqslant j_1, j_2 \leqslant 2\) on \(X \cap U_{w_0,y}\) are \(1, w_1\) and \(x_i^2\) for \(0 \leqslant j_1,j_2 \leqslant 2\) and they clearly define a generically finite map (in fact an isomorphism). It follows that the complete linear system of \(\mathscr {M}^m\) defines a generically finite map and thus \(\mathscr {M}\) is big. \(\square \)
for \(0 \leqslant j_1, j_2 \leqslant 2\) on \(X \cap U_{w_0,y}\) are \(1, w_1\) and \(x_i^2\) for \(0 \leqslant j_1,j_2 \leqslant 2\) and they clearly define a generically finite map (in fact an isomorphism). It follows that the complete linear system of \(\mathscr {M}^m\) defines a generically finite map and thus \(\mathscr {M}\) is big. \(\square \)
Proof of Theorem 1.3
Assume that \(n \geqslant 5\). By Lemmas 3.13, 3.14 and 3.2, a very general \(X_n\) defined over \(\Bbbk \) is not separably uniruled. In particular, it is not ruled. Then a very general \(X_n\) defined over \(\mathbb {C}\) is not ruled, by Lemma 3.1, and the proof is completed. \(\square \)
References
Ahmadinezhad, H.: On conjugacy classes of the Klein simple group in Cremona group (2013). arXiv:1310.5548 (to appear in Glasg. Math. J.)
Batyrev, V.V., Cox, D.A.: On the Hodge structure of projective hypersurfaces in toric varieties. Duke Math. J. 75(2), 293–338 (1994)
Belousov, G.: Log del Pezzo surfaces with simple automorphism groups. Proc. Edinb. Math. Soc. 58(1), 33–52 (2015)
Cheltsov, I., Shramov, C.: Three embeddings of the Klein simple group into the Cremona group of rank three. Transform. Groups 17(2), 303–350 (2012)
Grinenko, M.M.: Birational properties of pencils of del Pezzo surfaces of degrees 1 and 2. Sb. Math. 191(5), 633–653 (2000)
Grinenko, M.M.: Birational properties of pencils of del Pezzo surfaces of degrees 1 and 2. II. Sb. Math. 194(5), 669–696 (2003)
Grinenko, M.M.: Fibrations into del Pezzo surfaces. Russian Math. Surveys 61(2), 255–300 (2006)
Kollár, J.: Nonrational hypersurfaces. J. Amer. Math. Soc. 8(1), 241–249 (1995)
Kollár, J.: Rational Curves on Algebraic Varieties. Ergebnisse der Mathematik und ihrer Grenzgebiete, 3. Folge, vol. 32. Springer, Berlin (1996)
Okada, T.: Nonrational weighted hypersurfaces. Nagoya Math. J. 194, 1–32 (2009)
Prokhorov, Yu.: Simple finite subgroups of the Cremona group of rank 3. J. Algebraic Geom. 21(3), 563–600 (2012)
Pukhlikov, A.V.: Birational automorphisms of algebraic threefolds with a pencil of Del Pezzo surfaces. Izv. Math. 62(1), 115–155 (1998)
Reid, M.: Chapters on algebraic surfaces. Complex Algebraic Geometry. IAS/Park City Mathematics Series, vol. 3. American Mathematical Society, Providence (1997)
Roan, S.: Picard groups of hypersurfaces in toric varieties. Publ. Res. Inst. Math. Sci. 32(5), 797–834 (1996)
Acknowledgments
The author would like to thank Dr. Hamid Ahmadinezhad for useful conversations. He also would like to thank Professor Ivan Cheltsov for showing his interest to this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
The author is partially supported by JSPS KAKENHI Grant Number 26800019.
Rights and permissions
About this article
Cite this article
Okada, T. Nonrational del Pezzo fibrations admitting an action of the Klein simple group. European Journal of Mathematics 2, 319–332 (2016). https://doi.org/10.1007/s40879-015-0080-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-015-0080-2



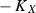 is
is 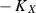 is
is