Abstract
We exhibit a series of new examples of rigid plane curves, that is, curves, whose collection of singularities determines them almost uniquely up to a projective transformation of the plane.
Similar content being viewed by others
1 Introduction
1.1 Background and motivation
We work over the complex field, though most of results can be stated over any algebraically closed field of characteristic zero.
The space \({\mathscr {C}}_d\) of plane curves of degree d can be identified with  . It has a natural equisingular stratification with the strata determined by the collection of degrees and multiplicities of irreducible components and by the collection of topological singularity types of the considered curves (see [10, 11]; below, the strata will be called the families of equisingular curves). Properties of this stratification have been studied by algebraic geometers since 19th century, attracting attention of leading experts like Zeuthen, Severi, Segre, Zariski and others (see, for example, [2] for a modern survey in this area).
. It has a natural equisingular stratification with the strata determined by the collection of degrees and multiplicities of irreducible components and by the collection of topological singularity types of the considered curves (see [10, 11]; below, the strata will be called the families of equisingular curves). Properties of this stratification have been studied by algebraic geometers since 19th century, attracting attention of leading experts like Zeuthen, Severi, Segre, Zariski and others (see, for example, [2] for a modern survey in this area).
In this paper we focus on the minimal equisingular families, that is, those which are formed by reduced curves and contain only finitely many orbits of the action of the group of projective transformations of the plane  . The curves belonging to these families are called rigid curves; the corresponding families we also call rigid (see Definition 1.2 below). The study of rigid curves is motivated by their appearance in several important problems. First of all, finite coverings of the projective plane branched along rigid curves are used to obtain examples of rigid, so called, Miyaoka–Yau surfaces (see, for example, [3, 5]). Next (cf. [6]), celebrated Belyi’s Theorem [1] says that each projective curve defined over \(\overline{\mathbb {Q}}\) can be represented as a finite covering of \(\mathbb {P}^1\) branched at three points. Note that any three points in \(\mathbb {P}^1\) are rigid in the sense of definition given below. Therefore we can hope that for any field F of transcendence degree two over \(\overline{\mathbb {Q}}\) there are a projective model X defined over \(\overline{\mathbb {Q}}\) with the field of rational functions \(\overline{\mathbb {Q}}(X)\simeq F\) and a finite morphism
. The curves belonging to these families are called rigid curves; the corresponding families we also call rigid (see Definition 1.2 below). The study of rigid curves is motivated by their appearance in several important problems. First of all, finite coverings of the projective plane branched along rigid curves are used to obtain examples of rigid, so called, Miyaoka–Yau surfaces (see, for example, [3, 5]). Next (cf. [6]), celebrated Belyi’s Theorem [1] says that each projective curve defined over \(\overline{\mathbb {Q}}\) can be represented as a finite covering of \(\mathbb {P}^1\) branched at three points. Note that any three points in \(\mathbb {P}^1\) are rigid in the sense of definition given below. Therefore we can hope that for any field F of transcendence degree two over \(\overline{\mathbb {Q}}\) there are a projective model X defined over \(\overline{\mathbb {Q}}\) with the field of rational functions \(\overline{\mathbb {Q}}(X)\simeq F\) and a finite morphism  branched along a rigid plane curve. There are interesting relations to the geometry of line arrangements (see [3]) and to rational cuspidal curves (see [9]).
branched along a rigid plane curve. There are interesting relations to the geometry of line arrangements (see [3]) and to rational cuspidal curves (see [9]).
The goal of our note is to exhibit examples of rigid curves of any degree and any genus, and rigid families covered by arbitrarily many orbits of the  -action.
-action.
1.2 Definitions and main results
Throughout the paper we consider isolated plane curve singular points up to topological equivalence, briefly calling any class of topologically equivalent singular points a singularity type. Given a singularity type S, the number of irreducible components of singular curve germs of type S is an invariant, which we denote \(m_S\). Cardinality of a finite set F will be denoted by |F|.
1.2.1 Irreducible rigid curves
Let \(S_1,\dots ,S_r\) be a sequence of distinct singularity types, \(n_1,\dots ,n_r\) a sequence of positive integers, \(r\ge 1\). Introduce the formal sum \({\mathbf S}=\sum _{i=1}^rn_iS_i\). Given a positive integer d, denote by \(V(d;g;{\mathbf S})\) the (equisingular) family of reduced, irreducible plane curves of degree d having precisely \(\sum _{i=1}^rn_i\) singular points and such that \(n_i\) singular points are of type \(S_i\), \(i=1,\dots ,r\). Here
is the geometric genus of the considered curves.
Such a family is a locally closed union of quasiprojective subvarieties of \({\mathscr {C}}_d\) (cf. [2]). It is, of course, invariant with respect to the action of  , and hence consists of entire orbits of the
, and hence consists of entire orbits of the  -action.
-action.
Definition 1.1
We say that a non-empty equisingular family \(V(d;g;{\mathbf S})\) is k
-rigid if it is the union of k distinct orbits of the  -action in \({\mathscr {C}}_d\) for some \(k\in {\mathbb {N}}\). If \(k=1\) then we say that V is strictly rigid. The curves belonging to a k-rigid family of plane curves are called rigid.
-action in \({\mathscr {C}}_d\) for some \(k\in {\mathbb {N}}\). If \(k=1\) then we say that V is strictly rigid. The curves belonging to a k-rigid family of plane curves are called rigid.
1.2.2 Reducible rigid curves
Considering reduced, irreducible curves, we, first, introduce families of reducible curves with numbered components, then identify families obtained from each other by permutation of components.
Let \(\mathbf{d}=(d_1,\dots , d_N)\) and \(\mathbf{g}=(g_1,\dots , g_N)\) be two collections of integers, \(d_i\ge 1\) and \(g_i\ge 0\) for \(i=1,\dots , N\). To encode the distribution of singularity types among components and the distribution of local branches centered at singular points that are intersection points of components, we do the following. For a fixed singularity type S and fixed N denote by \(\mathbf{J}_S=\{ J_{S,k}\}\) the set of all non-empty subsets \(J_{S,k}\) of \(\{1,2,\dots ,N\}\), \(1\le k\le \sum _{j=1}^{m_S} \left( {\begin{array}{c}N\\ j\end{array}}\right) \), such that \(|J_{S,k}|\le m_{S}\). Let \(V\bigl (\mathbf{d};\mathbf{g}; \sum _{\{ S_j\}}\sum _{\{ J_{S_j,k}\}}n_{J_{S_j,k}}S_j\bigr )\) be the family of plane reduced curves \(\overline{C}=C_1\cup \dots \cup C_N\subset {\mathbb {P}}^2\) such that \(C_i\) are irreducible curves of degree \(\deg C_i=d_i\) and genus \(g_i\), and for each type \(S_j\) of plane singularities the intersection \(\bigcap _{i\in J_{S_j,k}}C_i\) contains exactly \(n_{J_{S_j,k}}\) singular points of \(\overline{C}\) of the type \(S_j\) which do not lie in \(C_l\) for \(l\not \in J_{S_j,k}\). This is a locally closed union of quasiprojective subvarieties of \({\mathscr {C}}_d\) (cf. [2]).
The sum \(\mathbf{S}=\sum _{\{ S_j\}}\sum _{\{ J_{S_j,k}\}}n_{J_{S_j,k}}S_j\) is called the singularity type of the curves \(\overline{C}\in V(\mathbf{d};\mathbf{g};\mathbf{S})\). We identify the families \(V(\mathbf{d};\mathbf{g};\mathbf{S})\) obtained by permutations of the curves \(C_1,\dots ,C_N\) and compatible permutations of \(\mathbf{S}\).
A singularity type \(\mathbf{S}\) splits into two parts, \(\mathbf{S}=\mathbf{S}^\mathrm{ess}+\mathbf{S}^\mathrm{non\text {-}ess}\), as follows. For fixed \(\mathbf{d}\) and \(\mathbf{g}\), we say that \(\mathbf{S}^\mathrm{ess}\) is an essential part of the singularity type \(\mathbf{S}\) (and resp. \(\mathbf{S}^\mathrm{non\text {-}ess}\) is a non-essential part of the singularity type \(\mathbf{S}\)) if the family \(V(\mathbf{d;\mathbf g; \mathbf S})\) is determined uniquely by \(\mathbf{d},\mathbf{g}\), and the property that the curves \(\overline{C}\) have the singularities \(\mathbf{S}^\mathrm{ess}\) among all singularities of \(\overline{C}\). If \(\mathbf{S}^\mathrm{ess}\) is an essential part of a singularity type \(\mathbf{S}\), then we will use notation \(V(\mathbf{d;\mathbf g;\mathbf S}^\mathrm{ess}+\cdots )\) to denote the family \(V(\mathbf{d;\mathbf g;\mathbf S})\).
Definition 1.2
We say that a family \(V=V(\mathbf{d;\mathbf g; \mathbf S})\) is k
-rigid if it is the union of k distinct orbits of the  -action in \({\mathscr {C}}_d\) for some \(k\in {\mathbb {N}}\). If \(k=1\) then we say that V is strictly rigid. The curves belonging to a k-rigid family of plane curves are called rigid.
-action in \({\mathscr {C}}_d\) for some \(k\in {\mathbb {N}}\). If \(k=1\) then we say that V is strictly rigid. The curves belonging to a k-rigid family of plane curves are called rigid.
Note that the number of irreducible components of a k-rigid family \(V(\mathbf{d;\mathbf g;\mathbf S})\) is less than or equal to k (since it can (and does) happen that some orbits can lie in the closure of another) and, in particular, \(V(\mathbf{d;\mathbf g;\mathbf S})\) is irreducible if it is strictly rigid. Note also that if a family \(V(\mathbf{d};\mathbf{g};\mathbf{S})\) is rigid, then

1.2.3 Main results
Our results are as follows:
-
in Theorem 2.1, the complete list of rigid curves of degree \(\le 4\) is given;
-
in Theorem 3.1, we give an infinite series of examples of strictly rigid families of irreducible rational curves \(V(d;0;\mathbf{S})\);
-
in Theorem 4.1, for each \(g\ge 1\), we prove the existence of strictly rigid irreducible plane curves of genus g;
-
examples of irreducible 2-rigid families of irreducible curves are given in Theorems 5.1 and 5.2, and Theorem 5.3 provides examples of k-rigid families \(V(\mathbf{d};\mathbf{g};\mathbf{S})\) consisting of k irreducible components for each \(k\in {\mathbb {N}}\).
We do not know answers to the following questions, which seem to be interesting.
Question 1.3
Do there exist irreducible k-rigid families \(V(\mathbf{d};\mathbf{g};\mathbf{S})\) with \(k> 2\)?
Question 1.4
Do there exist irreducible 2-rigid families \(V(d;g;\mathbf{S})\) with \(g\ge 1\)?
Throughout the paper, we use the following notations for singularity types of plane curves:
-
\(T_{m,n}\), \(2\le m\le n\), is the type of singularity given by the equation \(x^m+y^{n}=0\); but if \(m=2\) then a singularity of type \(T_{2,n}\), as usual, will be denoted by \(A_{n-1}\) and the singularities of types \(T_{m,m}\) will be called simple.
-
\(T^m_{m,n}\), \(2\le m< n\), is the type of singularity given by the equation
 .
. -
\(T^n_{m,n}\), \(2\le m< n\), is the type of singularity given by the equation
 .
. -
\(T^{m,n}_{m,n}\), \(1\le m< n\), is the type of singularity given by the equation
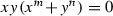 .
.
2 Rigid curves of small degree
In the following theorem, we provide the complete list of rigid reduced curves of degree \(\le 4\).
Theorem 2.1
Let \(\overline{C}\) be a rigid reduced curve of degree \(\le 4\). Then \(\overline{C}\) belongs to one of the following families:
-
(I)
strongly rigid families:
- (I\(_1)\) :
-
\(V(1;0;\varnothing )\);
- (I\(_2)\) :
-
\(V\bigl ((1,1);(0,0);A_1\bigr )\);
- (I\(_3)\) :
-
\(V(2;0;\varnothing )\);
- (I\(_4)\) :
-
\(V\bigl ((1,1,1);(0,0,0);3A_1\bigr )\);
- (I\(_5)\) :
-
\(V\bigl ((1,1,1);(0,0,0);T_{3,3}\bigr )\);
- (I\(_6)\) :
-
\(V\bigl ((2,1);(0,0);2A_1\bigr )\);
- (I\(_7)\) :
-
\(V\bigl ((2,1);(0,0);A_3\bigr )\);
- (I\(_8)\) :
-
\(V(3;0;A_1)\);
- (I\(_9)\) :
-
\(V(3;0;A_2)\);
- (I\(_{10})\) :
-
\(V\bigl ((1,1,1,1);(0,0,0,0);6A_1\bigr )\);
- (I\(_{11})\) :
-
 ;
; - (I\(_{12})\) :
-
 ;
; - (I\(_{13})\) :
-
 ;
; - (I\(_{14})\) :
-
 ;
; - (I\(_{15})\) :
-
 ;
; - (I\(_{16})\) :
-
 ;
; - (I\(_{17})\) :
-
 ;
; - (I\(_{18})\) :
-
\(V\bigl ((3,1);(0,0);T_{2,4}^2\bigr )\);
- (I\(_{19})\) :
-
\(V\bigl ((3,1);(0,0);T_{2,3}^3\bigr )\);
- (I\(_{20})\) :
-
 ;
; - (I\(_{21})\) :
-
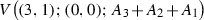 ;
; - (I\(_{22})\) :
-
\(V(4;0;3A_2)\);
- (I\(_{23})\) :
-
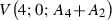 ;
; - (I\(_{24})\) :
-
\(V(4;0;A_{6})\);
-
(II)
irreducible 2-rigid families:
- (II\(_1)\) :
-
 ;
; - (II\(_2)\) :
-
\(V(4;0;T_{3,4})\).
Proof
It is well known that if \(\deg \overline{C}\le 3\) then only smooth cubics are not rigid. All other families \(V(\mathbf{d};\mathbf{g}; \mathbf{S})\) of curves of degree \(\le 3\) are listed in \((\mathrm{I}_1)\)–\((\mathrm{I}_9)\). Therefore we assume below that \(\deg \overline{C}=4\).
Again, it is well known that if \(\overline{C}\) consists of four lines or two lines and a quadric, then \(\overline{C}\) is not rigid if and only if \(\overline{C}\) consists of four lines having a common point or \(\overline{C}\) consists of a quadric Q and two lines in general position with respect to Q. The rigid families in the case when \(\overline{C}\) consists of four lines or two lines and a quadric is listed in \((\mathrm{I}_{10})\)–\((\mathrm{I}_{14})\).
Consider the case when \(\overline{C}\) consists of two irreducible components: either \(\overline{C}=Q_0\cup Q_1\), where \(Q_0\) and \(Q_1\) are smooth quadrics, or \(\overline{C}=C\cup L\), where C is a cubic and L is a line.
Consider the case when \(\overline{C}_1=Q_0\cup Q_1\in V((2,2);(0,0);\mathbf{S})\). We have \(\mathbf{S}=m_1A_1+m_3A_3+m_5A_5+m_7A_7\), where \(m_1+2m_3+3m_5+4m_7=4\). The singularity type \(\mathbf{S}\) consists of \(k=m_1+m_3+m_5+m_7\), \(1\le k\le 4\), singular points and if \(m_1=4\), that is, \(\mathbf{S}=4A_1\), then \(V((2,2);(0,0);4A_1)\) is not rigid by (1), since \(\dim V((2,2);(0,0);4A_1)=10\). Similarly, if \(m_1=2\), that is, \(\mathbf{S}=A_3+2A_1\), then  is not rigid, since
is not rigid, since  . So, we can assume that \(m_1\le 1\).
. So, we can assume that \(m_1\le 1\).
Consider the pencil of quadrics \(Q_{\lambda }\) defined by quadrics \(Q_0\) and \(Q_1\). It is easy to see that in the cases \(m_1=m_5=1\) or \(m_7=1\) it contains the unique degenerate element \(Q_{\infty }\) consisting of two (coinciding if \(m_7=1\)) lines \(L_1\cup L_2\) and in the case \(m_3=2\) it contains two degenerate elements one of which, \(Q_{\infty }\), consists of two coinciding lines \(L_1=L_2\) and the other one consists of two different lines. Let \(f(z_1,z_2,z_3)=0\) be an equation of the quadric \(Q_0\) and \(l_i(z_1,z_2,z_3)=0\), \(i=1,2\), be an equation of the line \(L_i\). Then, without less of generality, we can assume that

is the equation of \(Q_{\lambda }\). Moreover, applying a projective transformation, we can assume that \(f(z_1,z_2,z_3)=z_1^2-z_2z_3\) and \(l_1(z_1,z_2,z_3)=z_3\), \(l_1(z_1,z_2,z_3)= z_1\) in the case \(m_1=m_5=1\); \(l_1(z_1,z_2,z_3)=l_2(z_1,z_2,z_3)=z_1\) in the case \(m_3=2\); and \(l_1(z_1,z_2,z_3)=l_2(z_1, z_2,z_3)=z_3\) in the case \(m_7=1\). Therefore we can assume that
in the case \(m_1=m_5=1\),
in the case \(m_7=1\), and
in the case \(m_3=2\).
Note that if \(m_3=2\), then the degenerate element \(Q_{-1}\) of the pencil \(Q_{\lambda }\) consists of two lines \(z_2=0\) and \(z_3=0\) [see (4)].
In the case \(m_1=m_5=1\) (case \((\mathrm{I}_{15}))\) the strong rigidity of the curve \(\overline{C}_1\) follows from the equality \(\overline{C}_{\lambda }=Q_0\cup Q_{\lambda }=h_{\lambda }(\overline{C}_1)\) for each \(\lambda \in \mathbb {C}^*\), where the automorphism \(h_{\lambda }\) acts as follows: \(h_{\lambda }(z_1\!:\!z_2\!:\!z_3)=(\lambda z_1\!:\! \lambda ^2 z_2\!:\!z_3)\); and in the case \(m_7=1\) (case \((\mathrm{I}_{16}))\) the strong rigidity of the curve \(\overline{C}_1\) follows from equality \(\overline{C}_{\lambda ^2}=Q_0 \cup Q_{\lambda ^2}=h_{\lambda }(\overline{C}_1)\) for each \(\lambda \in \mathbb {C}^*\).
Let us show that \(\overline{C}_1\) is not rigid if \(m_3=2\). Indeed, assume that \(\overline{C}_1\) is rigid. Then for any two elements  , \(\lambda _{1}\ne \lambda _{2}\), there is a projective transformation
, \(\lambda _{1}\ne \lambda _{2}\), there is a projective transformation  such that \(h_{{\lambda }_1, {\lambda }_2}(\overline{C}_{{\lambda }_1})=\overline{C}_{{\lambda }_2}\), where \(\overline{C}_{\lambda }=Q_{0}\cup Q_{\lambda }\). The automorphism \(h_{{\lambda }_1,{\lambda }_2}\) leaves invariant the pencil \(Q_{\lambda }\). In particular, it leaves invariant the singular elements \(Q_{\infty }\) and \(Q_{-1}\) of the pencil \(Q_{\lambda }\),
such that \(h_{{\lambda }_1, {\lambda }_2}(\overline{C}_{{\lambda }_1})=\overline{C}_{{\lambda }_2}\), where \(\overline{C}_{\lambda }=Q_{0}\cup Q_{\lambda }\). The automorphism \(h_{{\lambda }_1,{\lambda }_2}\) leaves invariant the pencil \(Q_{\lambda }\). In particular, it leaves invariant the singular elements \(Q_{\infty }\) and \(Q_{-1}\) of the pencil \(Q_{\lambda }\),
Let us show that \(h_{\lambda _1,\lambda _2}(Q_0)\ne Q_0\) for \(\lambda _1\ne \lambda _2\). Indeed, if \(h_{\lambda _1,\lambda _2}(Q_0)= Q_0\), then in the case \(m_3=2\) we have either \(h^*_{\lambda _1,\lambda _2}(z_1) = az_1\), \(h^*_{\lambda _1,\lambda _2}(z_2)= bz_2\), and \(h^*_{\lambda _1,\lambda _2}(z_3)= cz_3\) or \(h^*_{\lambda _1, \lambda _2}(z_1)= az_1\), \(h^*_{\lambda _1,\lambda _2}(z_2)= bz_3\), and \(h^*_{\lambda _1,\lambda _2}(z_3)= cz_2\) for some a, b, c such that \(a^2=bc\), since \(h_{\lambda _1,\lambda _2}(Q_{\infty })= Q_{\infty }\) and \(h_{\lambda _1,\lambda _2} (Q_{-1})= Q_{-1}\). Therefore \(h_{\lambda _1,\lambda _2}(Q_{\lambda })= Q_{\lambda }\) for all \(\lambda \in \mathbb {C}\) that is possible only if \(\lambda _1=\lambda _2\). Therefore we must have \(h_{\lambda _1,\lambda _2}(Q_{0})= Q_{\lambda _2}\) and \(h_{\lambda _1,\lambda _2}(Q_{\lambda _1})= Q_{0}\). But, for three pairwise different  we obtain that
we obtain that  and hence \(\lambda _1=\lambda _3\). Contradiction.
and hence \(\lambda _1=\lambda _3\). Contradiction.
Consider the case when \(\overline{C}=C\cup L\), where C is a cubic and L is a line. It is easy to see that \(\overline{C}\) is rigid only if C is a rational curve. Therefore we have two cases: C is a nodal cubic or C is a cuspidal cubic.
Let C be a nodal cubic. Then (case \((\mathrm{I}_8)\)) \(V(3;0;A_1)\) is strongly rigid and \(\dim V(3;0;A_1)=8\). Therefore, L must be a “very special line” with respect to C, that is, L is either the tangent line of one of two branches of the node of C or L is the tangent line of C at a flex point of C. In both two cases it is easy to see that \(\overline{C}\) is strictly rigid and we have two cases: \((\mathrm{I}_{17})\)–\((\mathrm{I}_{18})\).
If C is a cuspidal cubic, then L is a tangent line to C or it passes through the cusp of C, since \(V(3;0;A_2)\) is strongly rigid and \(\dim V(3;0;A_2)=7\). If L is a tangent line to C at its cusp, then we have case (\(\mathrm{I}_{19}\)) and if L is the tangent line at the flex point of C, then we have case \((\mathrm{I}_{20})\). It is easy to see that in both cases \(\overline{C}\) is strongly rigid.
If L is a tangent line to C and it does not pass through the cusp of C, let us choose homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) such that \(z_3=0\) is an equation of L, \(z_1=0\) is an equation of the line tangent to C at its cusp, and the line given by the equation \(z_2=0\) passes through the cusp of C and the tangent point of L and C. Then there is a parametrization of C in \(\mathbb {P}^2\) of the following form:
where \(a\ne 0\). Denote by \(C_a\) a curve in \(\mathbb {P}^2\) given by parametrization (5). Now, the strong rigidity of  (case \((\mathrm{I}_{21})\)) follows from equality \(h(C_a\cup L)=C_1\cup L\), where the linear transformation
(case \((\mathrm{I}_{21})\)) follows from equality \(h(C_a\cup L)=C_1\cup L\), where the linear transformation  acts as follows, \(h(z_1\!:\!z_2\!:\!z_3)=(z_1\!:\!a^{-1}z_2\!:\!a^{-3}z_3)\).
acts as follows, \(h(z_1\!:\!z_2\!:\!z_3)=(z_1\!:\!a^{-1}z_2\!:\!a^{-3}z_3)\).
Let L be not the tangent line at the cusp of C and it pass through the cusp of C. Then if \(z_2=0\) is an equation of L, \(z_1=0\) is the line tangent to C at its cusp, and the line given by the equation \(z_3=0\) is tangent to C at its non-singular point p of the intersection \(C\cap L\), then again we can assume that C is given by parametrization (5) and there are two possibilities: either \(a=0\) or \(a\ne 0\). Denote by \(C_a\) a curve given by parametrization (5). It is easy to see that \(p\in C_0\cap L\) is the flex point of \(C_0\) if \(a=0\) and \(p\in C_a\cap L\) is not the flex point of \(C_a\) if \(a\ne 0\). Therefore there is not a linear transformation  such that \(h(C_0\cup L)=C_a\cup L\). On the other hand, the linear transformation \(h:(z_1\!:\!z_2\!:\!z_3)\rightsquigarrow (z_1\!:\!a^{-1}z_2\!:\!a^{-3}z_3)\) sends \(C_a\cup L\) to \(C_1\cup L\). Therefore \(V((3,1);(0,0), T_{2,3}^2)\) (case \((\mathrm{II}_1)\)) is an irreducible 2-rigid family.
such that \(h(C_0\cup L)=C_a\cup L\). On the other hand, the linear transformation \(h:(z_1\!:\!z_2\!:\!z_3)\rightsquigarrow (z_1\!:\!a^{-1}z_2\!:\!a^{-3}z_3)\) sends \(C_a\cup L\) to \(C_1\cup L\). Therefore \(V((3,1);(0,0), T_{2,3}^2)\) (case \((\mathrm{II}_1)\)) is an irreducible 2-rigid family.
Now, consider the case when \(\overline{C}\) is an irreducible curve of degree four. All possible types of singularities \(\mathbf{S}\) of irreducible curves of degree four are given in [8]:

where \(m_i\), \(1\le i\le 9\), are non-negative integers satisfying the following inequality:

By [7, Theorem 2], we have

Inequality (1) applied to (7) gives rise to the inequality

It is easy to see that inequalities (6) and (8) have only the following non-negative integer solutions:
-
\(m_2=3\) and \(m_i=0\) for \(i\ne 2\),
-
\(m_2=m_4=1\) and \(m_i=0\) for \(i\ne 2,4\),
-
\(m_6=1\) and \(m_i=0\) for \(i\ne 6\),
-
\(m_9=1\) and \(m_i=0\) for \(i\le 8\).
Therefore only the following irreducible curves \(\overline{C}\) of degree four can be rigid: either \(\overline{C}\in V(4;0;3A_2)\), or  , or \(\overline{C}\in V(4;0;A_6)\), or \(\overline{C}\in V(4;0;T_{3,4})\).
, or \(\overline{C}\in V(4;0;A_6)\), or \(\overline{C}\in V(4;0;T_{3,4})\).
The strict rigidity of a curve \(\overline{C}\in V(4;0;3A_2)\) (case \((\mathrm{I}_{22})\)) is well known.
To show that a curve  (case \((\mathrm{I}_{23})\)) is strictly rigid, let us choose a non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=0)=(0\!:\!0\!:\!1)\) is the singular point of \(\overline{C}\) of type \(A_4\) and the line \(z_1=0\) is tangent to \(\overline{C}\) at this point, the image \(f(t=\infty )=(1\!:\!0\!:\!0)\) is the singular point of \(\overline{C}\), and the line \(z_3=0\) is tangent to C at this point. Then (after a suitable linear change of the coordinate t) the morphism f is given by
(case \((\mathrm{I}_{23})\)) is strictly rigid, let us choose a non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=0)=(0\!:\!0\!:\!1)\) is the singular point of \(\overline{C}\) of type \(A_4\) and the line \(z_1=0\) is tangent to \(\overline{C}\) at this point, the image \(f(t=\infty )=(1\!:\!0\!:\!0)\) is the singular point of \(\overline{C}\), and the line \(z_3=0\) is tangent to C at this point. Then (after a suitable linear change of the coordinate t) the morphism f is given by
that is, \(\overline{C}\) is strictly rigid.
To show that a curve \(\overline{C}\in V(4;0;A_6)\) (case \((\mathrm{I}_{24})\)) is strictly rigid, note that, by Plücker formulas, \(\overline{C}\) must have a flex point. As above, let \(f:{\mathbb {P}}^1\rightarrow {\mathbb {P}}^2\) be a morphism such that \(\overline{C}=f({\mathbb {P}}^1)\). We can choose a non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=0)=(0\!:\!0\!:\!1)\) is the singular point of C, the line \(z_1=0\) is the tangent line to C at its singular point, the image \(f(t=\infty )=(1\!:\!0\!:\!0)\) is a flex point of C, and, moreover, the line \(z_3=0\) is the tangent line to C at this point. Then (after a suitable linear change of the coordinate t) the morphism f is given by
where \(a_2\ne 0\). It is easy to see that the polynomial \(F(t)-a_2(t-1)^2\) must be divisible by \(t^2\), since C has a singularity of type \(A_6\) at \((0\!:\!0\!:\!1)\). Therefore we have \(a_1=-2a_2\) and we can put \(a_2=1\), that is, \(V(4;0;A_6)\) is strictly rigid.
Let us show that the family \(V(4;0;T_{3,4})\) (case \((\mathrm{II}_{2})\)) is irreducible and 2-rigid. Indeed, let \(\overline{C}\in V(4;0;T_{3,4})\), then, by Plücker formulas, \(\overline{C}\) must have a flex point. Let \(f:{\mathbb {P}}^1\rightarrow {\mathbb {P}}^2\) be a morphism such that \(\overline{C}=f({\mathbb {P}}^1)\). We can choose non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=0)=(0\!:\!0\!:\!1)\) is the singular point of \(\overline{C}\), the line \(z_1=0\) is the tangent line to \(\overline{C}\) at its singular point, the image \(f(t=\infty )=(1\!:\!0\!:\!0)\) is a flex point of \(\overline{C}\), and, moreover, the line \(z_3=0\) is the tangent line to \(\overline{C}\) at this point. Then (maybe, after change of the coordinate t) the morphism f is given by
Therefore \(V(4;0;T_{3,4})\) is an irreducible family.
As in case \((\mathrm{II}_1)\), there are two possibilities: either \(a=0\) or \(a\ne 0\).
Denote by \(\overline{C}_a\in V(4;0;T_{3,4})\) a curve given by (11). It is easy to see that \(\overline{C}_0\) has the unique flex point, namely, \(p_1=(1\!:\!0\!:\!0)\), and one can check that the curve \(\overline{C}_1\) has two flex points, \(p_1\) and  . Hence there is no projective transformation
. Hence there is no projective transformation  such that \(\overline{C}_0=h(\overline{C}_1)\).
such that \(\overline{C}_0=h(\overline{C}_1)\).
If we perform the change \(t_1=at\), where \(a\ne 0\), then we get \(h(\overline{C}_1)=\overline{C}_a\), where
that is, \(V(4;0;T_{3,4})\) is 2-rigid. \(\square \)
Remark 2.2
According to Theorem 2.1, the families \(V((1,1,1,1);(0,0,0,0);T_{4,4})\) and \(V((2,2);(0,0); 2A_3)\) are not rigid and it is easy to see that
that is, (1) is not sufficient for \(V(\mathbf{d};\mathbf{g};\mathbf{S})\) to be a rigid family.
3 Strictly rigid rational curves of degree \(\ge \) 5
Theorem 3.1
For each \(n\ge 2\) the family \(V_n=V(2n; 0;3T_{n,n+1}+\cdots )\) is strictly rigid. The non-essential part of singularities of \(C\in V_n\) consists of simple singularities.
To prove Theorem 3.1 we need in the following result.
Theorem 3.2
Let \(\mathbf{d}_n=(n,1,1,1)\), \(\mathbf{g}=(0,0,0,0)\), and \(n_{(1,2)}=n_{(1,3)}=n_{(1,4)}=1\). Then the family

is strictly rigid for each \(n\ge 2\). The non-essential part of singularities of  consists of simple singularities.
consists of simple singularities.
We prove Theorems 3.1 and 3.2 simultaneously.
Proof of Theorems 3.1 and 3.2
Theorem 3.1 in the case \(n=2\) and Theorem 3.2 in the case \(n\le 3\) are well known, and we prove the general case by induction on n.
Assume that for \(n\le n_0\) Theorem 3.1 is true. Then the number of virtual cusps of \(C\in V_n\), \(n \le n_0\), is equal to  and the number of its virtual nodes is equal to
and the number of its virtual nodes is equal to  (see the definition of the numbers of virtual cusps and virtual nodes, for example, in [4]). Let \(\widehat{C}\) be the dual curve to C. By Plücker formulas, we have \(\deg \widehat{C}=n+1\) and the number of virtual cusps of the curve \(\widehat{C}\) is zero. Therefore the irreducible branches of the singular points of \(\widehat{C}\) are smooth and hence \(\widehat{C}\) has only simple singularities, since C has the only simple singularities and three singularities of type \(T_{n,n+1}\). Note also that \(\widehat{C}\) has three flex points, say \(p_1, p_2\), and \(p_3\). Let \(L_i\), \(i=1,2,3\), be the tangent line to \(\widehat{C}\) at the point \(p_i\). It is easy to see that
(see the definition of the numbers of virtual cusps and virtual nodes, for example, in [4]). Let \(\widehat{C}\) be the dual curve to C. By Plücker formulas, we have \(\deg \widehat{C}=n+1\) and the number of virtual cusps of the curve \(\widehat{C}\) is zero. Therefore the irreducible branches of the singular points of \(\widehat{C}\) are smooth and hence \(\widehat{C}\) has only simple singularities, since C has the only simple singularities and three singularities of type \(T_{n,n+1}\). Note also that \(\widehat{C}\) has three flex points, say \(p_1, p_2\), and \(p_3\). Let \(L_i\), \(i=1,2,3\), be the tangent line to \(\widehat{C}\) at the point \(p_i\). It is easy to see that

Moreover, if \(n\le n_0\) and the curve \(\overline{C}_1=C_1\cup L'_1\cup L'_2\cup L'_3\) belongs to  , then the curve \(C_1\) must have only simple singularities, since the dual curve \(\widehat{C}_1\) belongs to \(V_{n}\). Therefore the assumption that Theorem 3.1 is true for \(n\le n_0\) implies the statement of Theorem 3.2 for \(n\le n_0+1\).
, then the curve \(C_1\) must have only simple singularities, since the dual curve \(\widehat{C}_1\) belongs to \(V_{n}\). Therefore the assumption that Theorem 3.1 is true for \(n\le n_0\) implies the statement of Theorem 3.2 for \(n\le n_0+1\).
Remark 3.3
For \(n\le n_0+1\), it follows from strong rigidity that if  , \(i=1,2\), are two curves such that \(C_1\) and \(C_2\) have two common flex points, say \(p_1\) and \(p_2\), then their third flex points \(p_3=C_1\cap L_3\) and \(q_3=C_2\cap L_3\) should coincide, \(p_3=q_3\), and consequently \(C_1=C_2\).
, \(i=1,2\), are two curves such that \(C_1\) and \(C_2\) have two common flex points, say \(p_1\) and \(p_2\), then their third flex points \(p_3=C_1\cap L_3\) and \(q_3=C_2\cap L_3\) should coincide, \(p_3=q_3\), and consequently \(C_1=C_2\).
To complete the proof of theorems, note that if \(\overline{C}=C \cup L_1\cup L_2\cup L_3\) belongs to  for \(n\le n_0+1\), then \(\sigma (C)\in V_{n+1}\), where \(\sigma \) is a quadratic transformation of the plane with centers at vertices of the triangle \(L_1\cup L_2\cup L_3\). Therefore Theorem 3.1 in the case \(n=n_0+1\) follows from Theorem 3.2 and Remark 3.3. \(\square \)
for \(n\le n_0+1\), then \(\sigma (C)\in V_{n+1}\), where \(\sigma \) is a quadratic transformation of the plane with centers at vertices of the triangle \(L_1\cup L_2\cup L_3\). Therefore Theorem 3.1 in the case \(n=n_0+1\) follows from Theorem 3.2 and Remark 3.3. \(\square \)
The following theorem provides an infinite series of strictly rigid families parameterizing the unions of two rational curves.
Theorem 3.4
The families  , where \(n_{(1,2)}=n_{(1)}=1\), are strictly rigid for \(n\ge 2\).
, where \(n_{(1,2)}=n_{(1)}=1\), are strictly rigid for \(n\ge 2\).
Proof
Let

Then  and L is the line tangent to C at its singular point \(p_1\) of type \(T_{2n-1,2n}\). Let \(f:{\mathbb {P}}^1\rightarrow {\mathbb {P}}^2\) be a morphism such that \(C=f({\mathbb {P}}^1)\). We can choose non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=\infty )=p_1=(1\!:\!0\!:\!0)\) is the singular point of C of type \(T_{2n-1,2n}\) and the line L is given by the equation \(z_3=0\), \(f(t=0)=p_2=(0\!:\!0\!:\!1)\) is the singular point of C of type \(A_{4n-2}\) and the line \(z_1=0\) is the tangent line to C at \(p_2\). Then (maybe, after change of the coordinates in \({\mathbb {P}}^2\) and \({\mathbb {P}}^1\)) the morphism f is given by
and L is the line tangent to C at its singular point \(p_1\) of type \(T_{2n-1,2n}\). Let \(f:{\mathbb {P}}^1\rightarrow {\mathbb {P}}^2\) be a morphism such that \(C=f({\mathbb {P}}^1)\). We can choose non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=\infty )=p_1=(1\!:\!0\!:\!0)\) is the singular point of C of type \(T_{2n-1,2n}\) and the line L is given by the equation \(z_3=0\), \(f(t=0)=p_2=(0\!:\!0\!:\!1)\) is the singular point of C of type \(A_{4n-2}\) and the line \(z_1=0\) is the tangent line to C at \(p_2\). Then (maybe, after change of the coordinates in \({\mathbb {P}}^2\) and \({\mathbb {P}}^1\)) the morphism f is given by
where \(P_{2n-3}(t)=t^{2n-3}\!+\sum _{i=0}^{2n-4}a_it^{i}\).
To prove Theorem 3.4, it suffices to show that the polynomial \(P_{2n-3}(t)\) is defined uniquely by the property that the point \(p_2\) is a singular point of C of type \(A_{2(2n-1)}\). For this put \(x=z_2/z_3\), \(y=z_1/z_3\) and \(x_2=x\), \(y_2=y/x^2\). Then the germ of singularity \((C,0)\subset ({\mathbb {C}}^2,o)\), given by the parametrization (at \(t=0\)):

has singularity type \(A_{2(2n-3)}\) at the point  .
.
Consider a sequence of polynomials \(A_k(t)=t^k\!+\sum _{i=0}^{k-1}a_{i,k}t^i\), \(k\in {\mathbb {N}}\), where \(A_1(t) = t+1\) and

Now, Theorem 3.4 follows from
Lemma 3.5
Let a germ of singularity \((C,0)\subset ({\mathbb {C}}^2,o)\) of type \(A_{2k}\), \(k\ge 1\), be given by the parametrization (at \(t=0)\):

where \(P_{k}(t)=t^k\!+\sum _{i=0}^{k-1}a_it^i\) and  . Then the polynomial \(P_{k}(t)\) is defined uniquely and, moreover, \(P_k(t)=A_k(t)\).
. Then the polynomial \(P_{k}(t)\) is defined uniquely and, moreover, \(P_k(t)=A_k(t)\).
Proof
If \(k=1\) then it is easy to see that \(P_1(t)=t+1\). Assume that for \(k<k_0\) lemma is true and prove it in the case \(k=k_0\).
If \((C,0)\subset ({\mathbb {C}}^2,o)\) is a germ of singularity of type \(A_{2k_0}\), then the polynomial  is divisible by \(t^2\). Therefore
is divisible by \(t^2\). Therefore  , where \(Q_{k_0}(t)=t^{k_0-1}+\sum _{i=0}^{k_0-2}b_it^i\) is a polynomial of degree \(k_0-1\ge 1\) and the singularity given by
, where \(Q_{k_0}(t)=t^{k_0-1}+\sum _{i=0}^{k_0-2}b_it^i\) is a polynomial of degree \(k_0-1\ge 1\) and the singularity given by

is of type \(A_{2(k_0-1)}\). Then, by assumption, \(Q_{k_0-1}(t)=A_{k_0-1}(t)\) and hence
In particular, \(a_0=A_{k_0-1}(1)\), that is,

\(\square \)
4 Strictly rigid curves of positive genera
The following theorem states that the strongly rigid family \(V(4;0;3A_2)\) [see case \((\mathrm{I}_{22})\) in Theorem 2.1] is the first member in an infinite sequence of strictly rigid families.
Theorem 4.1
For any \(n\ge 2\), the family  is non-empty and strictly rigid.
is non-empty and strictly rigid.
Proof
Let C be a plane curve of degree 2n with singularities \(A_n+2T_{n,2n-1}\). Choose projective coordinates \((z_1\!:\!z_2\!:\!z_3)\) so that the singular points of type \(T_{n,2n-1}\) are located at \((0\!:\!1\!:\!0)\) and \((0\!:\!0\!:\!1)\) with tangent lines \(z_3=0\) and \(z_2=0\), respectively, and the remaining intersection points of C with these lines are \((1\!:\!-1\!:\!0)\) and \((1\!:\!0\!:\!-1)\), respectively. Then, in the affine coordinates \(x=z_2/z_1\), \(y=z_3/z_1\), the curve C is given by an equation
the following lemma completes the proof of theorem
Lemma 4.2
There exists a unique curve in \({\mathbb {C}}^2\), given by (14) and having a singularity of type \(A_n\) in \(({\mathbb {C}}^*)^2\). It is irreducible and has genus \([n/2]-1\).
Proof
Note that a singularity of type \(T_{n,2n-1}\) is analytically irreducible, \(\delta (T_{n,2n-1})=(n-1)^2\), and if a plane curve \(C'\) has a singular point of type \(T_{n,2n-1}\) then \(\deg C'\ge 2n-1\). Therefore the curve C in question is irreducible, since if a curve \(C'\) of degree \(2n-1\) has two singular points of type \(T_{n,2n-1}\), then

a contradiction.
Under assumption that C has no other singularities in \({\mathbb {C}}^2\), the genus value follows from the fact that \(\delta (T_{n,2n-1})=(n-1)^2\) and \(\delta (A_n)=[(n+1)/2]\).
To find a curve given by (14) and having a singularity of type \(A_n\), substitute (x, y) for (x / y, y) in (14) and multiply by y:
This is a quadratic equation in y with the discriminant

The existence of a singularity of type \(A_n\) on the considered curve in \(({\mathbb {C}}^*)^2\) is equivalent to the condition that \({\Delta }(x)\) has a root of multiplicity \(n+1\). We shall show that this condition has a unique solution \((a_1,\dots ,a_n)\) such that \(a_n\ne 0\), and that for this solution the other roots of \({\Delta }\) are simple. So, into the relation

we substitute \(x=z^2\),  , and then get an equivalent condition
, and then get an equivalent condition
Since the difference 4z of the factors in the former product in (16) is not divisible neither by \(1+\tau z\), nor by \(1-\tau z\) for any \(\tau \ne 0\), we reduce (16) (possibly replacing \(\tau \) by \(-\tau \)) to the conditions: for \(k=1,2\),
which are equivalent to the following combinations:
The latter relations in (17) yield that

which results in

whereas the former relations in (17) lead to the system

Observe that

where \(I_1>0\), and

where \(0<I_2<I_1\). Hence system (19) has a unique solution, which in view of (18) implies the uniqueness of the sought curve C.
The last step in the proof of Theorem 4.1 is to show that C has no other singularity in \({\mathbb {C}}^2\), or, equivalently, that the polynomial \({\Delta }(x)\) has no multiple root other than \(1/\tau ^2\) if \((a_1,\dots , a_n)\) is the solution of equations (18) and (19). Indeed, let \(x=\theta ^2\), \(\theta ^2\ne 1/\tau ^2\), be a root of \({\Delta }(x)\) of multiplicity \(m\ge 2\). Then \(z=(-1)^k\theta \) is a root of polynomial \(F_k(z)\) of multiplicity m. Consider the curve \(C'\) given by the equation \(w-1-\sum _{i=1}^na_iz^{2i}=0\). The curve \(C'\) is rational and it has singularity of type \(T_{2n-1,2n}\) at infinity. In the pencil of lines \(\lambda w+\mu z=0\), there are at least three lines which intersect \(C'\) in the number of points less than \(2n=\deg C'\): by assumption, each of the lines given by \(w=2z\) and \(w=-2z\) is tangent to \(C'\) at least at two points with multiplicities \(n+1\) and m, respectively, and the line given by \(z=0\) intersects \(C'\) at its singular point with multiplicity \(2n-1\). Let  be the normalization of \(C'\). By the Hurwitz formula, applied to morphism
be the normalization of \(C'\). By the Hurwitz formula, applied to morphism  of degree 2n defined by the pencil of lines \(\lambda w+\mu z=0\), we get the following inequality:
of degree 2n defined by the pencil of lines \(\lambda w+\mu z=0\), we get the following inequality:

which breaks down for \(m\ge 2\). \(\square \)
Consider the Fermat curve \(C_n\subset {\mathbb {P}}^2\) of degree \(n\ge 3\) given by the equation \(z_1^n+z_2^n+z_3^n=0\). By Plücker formulas, the dual curve \(\widehat{C}\) to C has degree \(n(n-1)\) and the following type of singularities:

where \(\mathbf{S}_{F_n}\) is a sum of singularity types of the simple singularities of the curve dual to the Fermat curve \(C_n\).
The following theorem will be used in the proof of Theorem 5.3 (see Sect. 5.2).
Theorem 4.3
Let  ,
,  , and \(n_{(1,2)}=n_{(1,3)}=n_{(1,4)}=n\), \(n_{(1)}=n_{(2,3)}=n_{(2,4)}=n_{(3,4)}=1\). Then the family
, and \(n_{(1,2)}=n_{(1,3)}=n_{(1,4)}=n\), \(n_{(1)}=n_{(2,3)}=n_{(2,4)}=n_{(3,4)}=1\). Then the family

is strictly rigid for each \(n\ge 3\).
Proof
Consider a curve \(\overline{C}=C_1\cup C_2\cup C_3\cup C_4\in V_n\) and denote the components \(C_i\) of \(\overline{C}\) as follows: \(C_1=C\) and \(C_i=L_{i-1}\) for \(i\ge 2\). The curves \(L_1, L_2, L_3\) are lines and C is a curve of degree \(n(n-1)\). The curve C has 3n singular points of the singularity type \(T_{n-1,n}\), since \(n_{(1,2)}=n_{(1,3)}=n_{(1,4)}=n\), and the set of all other singularities of C is \(\mathbf{S}_{F_n}\), that is, the singularity type of C is the same as the singularity type of the dual curve to the Fermat curve of degree n. Therefore, the dual curve \(\widehat{C}\) to C is non-singular and \(\deg \widehat{C}=n\), and to prove theorem, it suffices to show that there are homogeneous coordinates in \({\mathbb {P}}^2\) such that in this coordinate system the curve \(\widehat{C}\) is the Fermat curve.
Let \((z_1\!:\!z_2\!:\!z_3)\) be homogeneous coordinates in  such that \(p_1=(1\!:\!0\!:\!0)\), \(p_2=(0\!:\!1\!:\!0)\), and \(p_3=(0\!:\!0\!:\!1)\) are the points in
such that \(p_1=(1\!:\!0\!:\!0)\), \(p_2=(0\!:\!1\!:\!0)\), and \(p_3=(0\!:\!0\!:\!1)\) are the points in  dual, respectively, to the lines \(L_1, L_2\), and \(L_3\), and let
dual, respectively, to the lines \(L_1, L_2\), and \(L_3\), and let

be an equation of the curve \(\widehat{C}\), where \(\overline{i}=(i_1,i_2,i_3)\) and \(z^{\overline{i}}=z_1^{i_1}z_2^{i_2}z_3^{i_3}\). Without loss of generality, we can assume that \(a_{n,0,0}=a_{0,n,0}=a_{0,0,n}=1\) since the points \(p_1, p_2\), and \(p_3\) do not belong to the curve \(\widehat{C}\).
The curve \(\widehat{C}\) has 3n flex points given in local coordinates by the equation \(y=x^n\) and for \(i=1,2,3\) there are n lines \(L_{i,1},\dots , L_{i,n}\) from the pencil of lines passing through \(p_i\) such that they are tangent to \(\widehat{C}\) at its flex points.
Let \(q_j=L_{1,j}\cap \widehat{C}=(q_{1,j}\!:\!q_{2,j}\!:\!q_{3,j})\), \(1\le j\le n\), and let us rewrite the equation of the curve \(\widehat{C}\) in the form

where \(H_i(z_2,z_3)\) are homogeneous polynomials in \(z_2, z_3\) of degree i. Then for \(i=1,\dots ,n-1\) the homogeneous polynomial \(H_1^i(z_2,z_3)-H_i(z_2,z_3)\) of degree i has \(n>i\) different roots, namely, \((q_{2,1}\!:\!q_{3,1}),\dots , (q_{2,n}\!:\!q_{3,n})\). Therefore \(H_i(z_2,z_3)=H_1^i(z_2,z_3)\) and hence the polynomial \(F(z_1,z_2,z_3)\) has the form

where  is a homogeneous polynomial of degree n,
is a homogeneous polynomial of degree n,

with some \(\alpha \in \mathbb {C}\).
By the same arguments, we have

and

where \(G_1(z_1,z_3), P_1(z_1,z_2)\) and  are homogeneous polynomials of degree one and n respectively.
are homogeneous polynomials of degree one and n respectively.
It follows from (22) that  . Therefore
. Therefore

for some \(a,b,c\in {\mathbb {C}}\) (remind that, by assumption, \(a_{n,0,0}=a_{0,n,0}=a_{0,0,n}=1\)).
It follows from (22) and (24) that for \(1\le k\le n-1\),

In particular, \(G_1(z_1,z_3)=a^{n-1}z_1+cz_3\) and hence

It follows from (26) that
for \(1\le k\le n-1\) and \(1\le j\le k\). In particular, if we put \(j=k\) in (27), then we obtain that \(a^n=1\) if \(a\ne 0\).
Similarly, it follows from (23) and (24) that for \(1\le k\le n-1\),

In particular, \(P_1(z_1,z_3)=b^{n-1}z_1+cz_2\) and hence

It follows from (29) that
for \(1\le k\le n-1\) and \(1\le j\le k\). In particular, if \(c\ne 0\) then we obtain that \(c^2=c^n=1\), that is,  and n is an even number if
and n is an even number if  . If we put \(j=k\) in (30), then we obtain that \(b^n=1\) if \(b\ne 0\).
. If we put \(j=k\) in (30), then we obtain that \(b^n=1\) if \(b\ne 0\).
Let us show that the case when \(abc\ne 0\) is impossible. Indeed, if \(abc\ne 0\), then \(a^n=b^n=1\),  , and
, and  only if n is even. If we apply again (27) and (30) we obtain that \(c^{k-j}=(a/b)^{k-j}=(b/a)^{k-j}\) for \(1\le k\le n-1\) and \(1\le j\le k\). Therefore, \(c=a/b=b/a\) and hence
only if n is even. If we apply again (27) and (30) we obtain that \(c^{k-j}=(a/b)^{k-j}=(b/a)^{k-j}\) for \(1\le k\le n-1\) and \(1\le j\le k\). Therefore, \(c=a/b=b/a\) and hence
since \(a^n=c^n=1\). This contradicts the assumption that C is an irreducible reduced curve.
It easily follows from (27) and (30) that the case, when the only one number either a or b, or c is equal to zero, is also impossible.
In the case when \(a=b=0\) and \(c\ne 0\) we have \(F(z_1,z_2,z_3)=z_1^n+(z_2\pm z_3)^n\). But, it is impossible since C is an irreducible curve.
The cases \(a=c=0\), \(b\ne 0\) and \(b=c=0\), \(a\ne 0\) are also impossible since in these cases we have, respectively, that \(F(z_1,z_2,z_3)=(z_1+bz_3)^n+ z_2^n\) since \(b^n=1\) or \(F(z_1,z_2,z_3)=(z_1+az_2)^n+ z_3^n\) since \(a^n=1\). As a result, we obtain that \(a=b=c=0\), that is \(F(z_1,z_2,z_3)=z_1^n+ z_2^n+z_3^n\). \(\square \)
5 k-rigid curves with \(k\ge 2\)
5.1 2-rigid irreducible families of equisingular plane curves of degree \(\ge \) 5
An infinite series of irreducible 2-rigid families is given in the following two theorems.
Theorem 5.1
The families  are 2-rigid and irreducible for \(n\ge 2\).
are 2-rigid and irreducible for \(n\ge 2\).
Proof
Let  and let \(f:{\mathbb {P}}^1\rightarrow {\mathbb {P}}^2\) be a morphism such that \(C=f({\mathbb {P}}^1)\). We can choose non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=0)=p_1=(0\!:\!0\!:\!1)\) is the singular point of C of type \(T_{n+1,2n+1}\), the line \(z_1=0\) is the tangent line to C at \(p_1\), \(f(t=\infty )=p_2=(1\!:\!0\!:\!0)\) is the singular point of C of type \(T_{n,2n+1}\), the line \(L_3\) given by \(z_3=0\) is the tangent line to C at \(p_2\). Then (maybe, after change of coordinates in \({\mathbb {P}}^2\)) the morphism f is given by
and let \(f:{\mathbb {P}}^1\rightarrow {\mathbb {P}}^2\) be a morphism such that \(C=f({\mathbb {P}}^1)\). We can choose non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=0)=p_1=(0\!:\!0\!:\!1)\) is the singular point of C of type \(T_{n+1,2n+1}\), the line \(z_1=0\) is the tangent line to C at \(p_1\), \(f(t=\infty )=p_2=(1\!:\!0\!:\!0)\) is the singular point of C of type \(T_{n,2n+1}\), the line \(L_3\) given by \(z_3=0\) is the tangent line to C at \(p_2\). Then (maybe, after change of coordinates in \({\mathbb {P}}^2\)) the morphism f is given by
for some \(a\in {\mathbb {C}}\). Let \(C_a\) have parametrization (31). The intersection number of \(C_a\) and \(L_3\) at the point \(p_2\) is
Hence there is no projective transformation  such that \(h(C_0)=C_1\). On the other hand, if \(a\ne 0\), we make change \(t_1=at\), and then the projective transformation \(h((z_1\!:\!z_2\!:\!z_3))=(a^{2n+1}z_1\!:\!a^{n+1}z_2\!:\!z_3)\) sends \(C_1\) to \(C_a\). \(\square \)
such that \(h(C_0)=C_1\). On the other hand, if \(a\ne 0\), we make change \(t_1=at\), and then the projective transformation \(h((z_1\!:\!z_2\!:\!z_3))=(a^{2n+1}z_1\!:\!a^{n+1}z_2\!:\!z_3)\) sends \(C_1\) to \(C_a\). \(\square \)
Theorem 5.2
The families  are 2-rigid and irreducible for \(n\ge 3\).
are 2-rigid and irreducible for \(n\ge 3\).
Proof
Let  and let \(f:{\mathbb {P}}^1\rightarrow {\mathbb {P}}^2\) be a morphism such that \(C=f({\mathbb {P}}^1)\). As in the proof of Theorem 5.1, it is easy to show that we can choose non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=0)=p_1=(0\!:\!0\!:\!1)\) is the singular point of C of type \(T_{2n-1,4n}\), the line \(z_1=0\) is the tangent line to C at \(p_1\), \(f(t=\infty )=p_2=(1\!:\!0\!:\!0)\) is the singular point of C of type \(T_{2n+1,4n}\), and the line \(z_3=0\) is the tangent line to C at \(p_2\). Then (maybe, after change of the coordinates in \({\mathbb {P}}^2\) and \({\mathbb {P}}^1\)) the morphism f is given by
and let \(f:{\mathbb {P}}^1\rightarrow {\mathbb {P}}^2\) be a morphism such that \(C=f({\mathbb {P}}^1)\). As in the proof of Theorem 5.1, it is easy to show that we can choose non-homogeneous coordinate t in \({\mathbb {P}}^1\) and homogeneous coordinates \((z_1\!:\!z_2\!:\!z_3)\) in \({\mathbb {P}}^2\) such that \(f(t=0)=p_1=(0\!:\!0\!:\!1)\) is the singular point of C of type \(T_{2n-1,4n}\), the line \(z_1=0\) is the tangent line to C at \(p_1\), \(f(t=\infty )=p_2=(1\!:\!0\!:\!0)\) is the singular point of C of type \(T_{2n+1,4n}\), and the line \(z_3=0\) is the tangent line to C at \(p_2\). Then (maybe, after change of the coordinates in \({\mathbb {P}}^2\) and \({\mathbb {P}}^1\)) the morphism f is given by

for some \(a\in {\mathbb {C}}\). Let \(C_a\) has parametrization (32). The intersection number of \(C_a\) and \(L_1\) at the point \(p_1\) is
Hence there is no projective transformation  such that \(h(C_0)=C_1\). On the other hand, if \(a\ne 0\), we make change \(t_1=a^{-1}t\), and then the projective transformation \(h((z_1\!:\!z_2\!:\!z_3))=(a^{-4n}z_1\!:\!a^{1-2n}z_2\!:\!z_3)\) sends \(C_a\) to \(C_1\). \(\square \)
such that \(h(C_0)=C_1\). On the other hand, if \(a\ne 0\), we make change \(t_1=a^{-1}t\), and then the projective transformation \(h((z_1\!:\!z_2\!:\!z_3))=(a^{-4n}z_1\!:\!a^{1-2n}z_2\!:\!z_3)\) sends \(C_a\) to \(C_1\). \(\square \)
5.2 k-rigid families parameterizing curves with k connected components
Theorem 5.3
For each \(k\in {\mathbb {N}}\) there is a k-rigid family of equisingular plane curves consisting of k irreducible components.
Proof
Let \(n=2k+1\) and let \(n_{(1,2)}=n-2\), \(n_{(1,3)}=n_{(1,4)}=n\), and \(n_{(1)}=n_{(2,4)}=n_{(3,4)}=n_{(1,2,5)}=n_{(1,2,6)}=n_{(3,4,5,6)}=1\). Consider the family  , where
, where

and

where \(\mathbf{S}_{F_n}\) is a sum of singularity types of the simple singularities of the curve dual to the Fermat curve given by the equation \(z_1^n+z_2^n+z_3^n=0\).
Consider a curve \(\widetilde{C}=\bigcup _{i=1}^6C_i\in \overline{V}_n\). Denote the curve \(C_1\) by C and the curve \(C_i\) by \(L_{i-1}\) for \(i\ge 2\). The curves \(L_1, \dots , L_5\) are lines and C is a curve of degree \(n(n-1)\) and it is easy to see that \(\overline{C}=C\cup L_1\cup L_2\cup L_3\in V_n\), where \(V_n\) is the family of plane curves from Theorem 4.3. By Theorem 4.3, we can assume that C is the curve dual to the Fermat curve of degree n and \(L_i\) is given by the equation \(z_i=0\) for \(i=1,2,3\). Then it follows from the singularity type of the curve \(\widetilde{C}\) that \(L_4\) and \(L_5\) have, respectively, equations \(z_2+\varepsilon ^{m_1}z_3=0\) and \(z_2+\varepsilon ^{m_2}z_3=0\), where \(m_1\not \equiv m_2(\mathrm{mod}\, n)\) and \(\varepsilon \) is a primitive root of the equation \(x^n+1=0\).
Consider two curves \(\widetilde{C}_i=\overline{C}\cup L_{4,i}\cup L_{5,i}\in \overline{V}_n\), \(i=1,2\), where \(L_{4,i}\) is given by the equation \(z_2+\varepsilon ^{m_{1,i}}z_3=0\) and \(L_{5,i}\) is given by the equation \(z_2+\varepsilon ^{m_{2,i}}z_3=0\). It is easy to see that a projective transformation  such that \(\widetilde{C}_2=h(\widetilde{C}_1)\) exists if and only if
such that \(\widetilde{C}_2=h(\widetilde{C}_1)\) exists if and only if  . Hence \(\overline{V}_n\) is a \((n-1)/2\)-rigid family of plane curves consisting of \((n-1)/2=k\) irreducible components. \(\square \)
. Hence \(\overline{V}_n\) is a \((n-1)/2\)-rigid family of plane curves consisting of \((n-1)/2=k\) irreducible components. \(\square \)
References
Belyĭ, G.V.: On Galois extensions of a maximal cyclotomic field. Math. USSR-Izv. 14(2), 247–256 (1980)
Greuel, G.-M., Lossen, C., Shustin, E.: Equisingular families of projective curves. In: Catanese, F., et al. (eds.) Global Aspects of Complex Geometry, pp. 171–209. Springer, Berlin (2006)
Hirzebruch, F.: Some examples of algebraic surfaces. Contemporary Mathematics, vol. 9, pp. 55–71. American Mathematical Society, Providence (1981)
Kulikov, Vik.S.: A remark on classical pluecker’s formulae (2011). arXiv:1101.5042
Kulikov, Vik.S., Kharlamov, V.M.: On real structures on rigid surfaces. Izv. Math. 66(1), 133–150 (2002)
Paranjape, K.H.: A geometric characterization of arithmetic varieties. Proc. Indian Acad. Sci. Math. Sci. 112(3), 383–391 (2002)
Shustin, E.I.: Versal deformations in the space of planar curves of fixed degree. Funct. Anal. Appl. 21(1), 82–84 (1987)
Wall, C.T.C.: Geometry of quartic curves. Math. Proc. Cambridge Philos. Soc. 117(3), 415–423 (1995)
Zaidenberg, M.G., Orevkov, SYu.: On rigid rational cuspidal plane curves. Russian Math. Surveys 51(1), 179–180 (1996)
Zariski, O.: Studies in equisingularity I. Equivalent singularities of plane algebroid curves. Amer. J. Math. 87(2), 507–536 (1965)
Zariski, O.: Studies in equisingularity II. Equisingularity in codimension 1 (and characteristic zero). Amer. J. Math. 87(4), 972–1006 (1965)
Author information
Authors and Affiliations
Corresponding author
Additional information
The first author has been supported by grants of RFBR 14-01-00160 and 15-01-02158, and by the Government of the Russian Federation within the framework of the implementation of the 5-100 Programme Roadmap of the National Research University Higher School of Economics, AG Laboratory. The second author has been supported by the Hermann–Minkowski–Minerva Center for Geometry at the Tel Aviv University and by the German–Israeli Foundation Grant No. 1174-197.6/2011. Main ideas behind this work have appeared during the visit of the second author to the Higher School of Economics (Moscow). We are grateful to these institutions for support and excellent working conditions.
Rights and permissions
About this article
Cite this article
Kulikov, V.S., Shustin, E. On rigid plane curves. European Journal of Mathematics 2, 208–226 (2016). https://doi.org/10.1007/s40879-015-0062-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-015-0062-4




 .
. .
.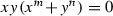 .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;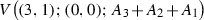 ;
;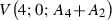 ;
; ;
;