On a space of entire functions rapidly decreasing on the real axis and its Fourier transform

Abstract

A weighted space of entire functions rapidly decreasing on the real axis is considered. The growth of these functions along the imaginary axis is controlled by some system of weight functions. The Fourier transforms of functions of this space are described as some space of infinitely differentiable functions on ${\mathbb {R}}$. An equivalent description of the considered space in terms of estimates on derivatives of functions on the real axis is obtained.

1 Introduction

1.1 On the problem

Let ${\Phi } =\{\varphi _m\}_{m=1}^{\infty }$ be a family of nondecreasing continuous functions $\varphi _m:[0, \infty ) \rightarrow {\mathbb {R}}$ such that for each $m \in {\mathbb {N}}$:

(i$_1$):

$\lim _{x \rightarrow + \infty } \varphi _m(x)/x= + \infty$;

(i$_2$):

for each $A > 0$ there exists a constant $C(m, A) > 0$ such that

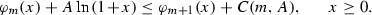
Moreover, in Theorems 1.2–1.4 the following additional conditions on ${\Phi }$ will be imposed (separately or together):

(i$_3$):

for each $k \in {\mathbb {N}}$ there exist constants $\sigma _k > 1$ and $\gamma _k > 0$ such that

$$\begin{aligned} \varphi _k(\sigma _k x) \le \varphi _{k+1}(x) + \gamma _k, \qquad x \ge 0; \end{aligned}$$

(i$_4$):

for each $k \in {\mathbb {N}}$ there exist numbers $\lambda _k > 1$, $h_k \in (1, \sigma _{k + 1})$ and $l_k > 0$ such that

$$\begin{aligned} \lambda _k \varphi _k(x) \le \varphi _{k + 1}(h_k x) + l_k, \qquad x \ge 0. \end{aligned}$$

Let $H({\mathbb {C}})$ be a space of entire functions on ${\mathbb {C}}$. For each $\nu \in {\mathbb {N}}$ and $k \in {\mathbb {Z}}_+$ define the space

Let $E(\varphi _{\nu })= \bigcap _{k=0}^{\infty } E_k(\varphi _{\nu })$, $E({\Phi })= \bigcup _{\nu =1}^{\infty } E(\varphi _{\nu })$. Since $p_{\nu , k}(f) \le p_{\nu , k+1}(f)$ for $f \in E_{k+1}(\varphi _{\nu })$, $E_{k+1}(\varphi _{\nu })$ is continuously embedded in $E_k(\varphi _{\nu })$. Endow $E(\varphi _{\nu })$ with a projective limit topology of spaces $E_k(\varphi _{\nu })$. Note that if $f \in E(\varphi _{\nu })$ then $p_{\nu +1, k}(f) \le e^{C(\nu , 1)} p_{\nu , k}(f)$ for each $k \in {\mathbb {Z}}_+$. This means that $E(\varphi _{\nu })$ is continuously embedded in $E(\varphi _{\nu + 1})$ for each $\nu \in {\mathbb {N}}$. Supply $E({\Phi })$ with a topology of an inductive limit of spaces $E(\varphi _{\nu })$.

Note that if ${\Omega }$ is a differentiable function on $[0, \infty )$ such that ${\Omega }(0) = {\Omega }'(0) = 0$ and its derivative is continuous, increasing and tending to infinity and functions $\varphi _m$ are defined on $[0, \infty )$ by the formula $\varphi _m(x) = {\Omega }(mx)$, $m \in {\mathbb {N}}$, then $E({\Phi })$ is the Gelfand–Shilov space of $W^{{\Omega }}$-type. Recall that $W^{{\Omega }}$-type (as other $W$-type) spaces have been introduced in 1950s by Gurevich [2, 3], and Gelfand and Shilov [1]. They described them by means of the Fourier transform and then applied this description to study the uniqueness of the Cauchy problem of partial differential equations.

In this paper we describe the space $E({\Phi })$ in terms of estimates on derivatives of functions on the real axis and study Fourier transform of functions of $E({\Phi })$ under additional conditions on ${\Phi }$. We would like to note the works of Sedletskii [8, 9] as closely related to the theme of our paper.

Results of the paper could be useful for theory of differential and pseudo-differential operators, mathematical physics, time-frequency analysis and some other fields of analysis.

1.2 Notation

Denote by ${\fancyscript{B}}$ the set of all functions $g \in C[0, \infty )$ such that $\lim _{x \rightarrow + \infty } g(x)/x= + \infty$. Let

For $g \in {\fancyscript{B}}$ let $g^*$ be the Young conjugate: $g^*(x) = \sup _{y \ge 0}(xy - g(y))$, $x \ge 0$. For a function $u:[0, \infty ) \rightarrow {\mathbb {R}}$ let $u[e](x)= u(e^x)$, $x \ge 0$. For brevity, functions $\varphi _m [e]$ are denoted by $\psi _m$.

The Fourier transform $\widehat{f}$ of $f \in E({\Phi })$ is defined by the formula

1.3 Main results

Let ${\Psi }^*=\{\psi _{\nu }^*\}_{\nu =1}^{\infty }$. For each $\nu \in {\mathbb {N}}$ and $m \in {\mathbb {Z}}_+$ let

Let ${\fancyscript{E}}(\psi _{\nu }^*) = \bigcap _{m=0}^{\infty }{\fancyscript{E}}_m(\psi _{\nu }^*)$, ${\fancyscript{E}}({\Psi }^*) = \bigcup _{\nu =1}^{\infty }{\fancyscript{E}}(\psi _{\nu }^*)$.

The first two theorems, proved in Sect. 3, are aimed to describe functions of the space $E({\Phi })$ in terms of estimates of their derivatives on ${\mathbb {R}}$.

Theorem 1.1

Let $f \in E({\Phi })$. Then $f_{|{\mathbb {R}}} \in {\fancyscript{E}}({\Psi }^*)$.

Theorem 1.2

Let the family ${\Phi }$ satisfy condition $(\mathrm{i}_3)$. Then each function $f \in {\fancyscript{E}}({\Psi }^*)$ admits $($a unique$)$ extension to an entire function belonging to $E({\Phi })$.

The proofs of these theorems follow the known schemes from [1]. Also they allow to obtain an additional information on the structure of the space $E({\Phi })$. Namely, let

$\nu \in {\mathbb {N}}$, $k \in {\mathbb {Z}}_+$, ${\fancyscript{H}}(\varphi _{\nu })$ be a projective limit of spaces ${\fancyscript{H}}_k(\varphi _{\nu })$, ${\fancyscript{H}}({\Phi })$ be an inductive limit of spaces ${\fancyscript{H}}(\varphi _{\nu })$. In Sect. 3 we show that if the family ${\Phi }$ satisfies condition $(\mathrm{i}_3)$ then $E({\Phi }) = {\fancyscript{H}}({\Phi })$, see Proposition 3.1.

Section 4 is devoted to characterization of the space $E({\Phi })$ by means of the Fourier transform under additional conditions on ${\Phi }$. For each $\nu \in {\mathbb {N}}$ and $m \in {\mathbb {Z}}_+$ we define the normed space

Let $G({\psi _{\nu }^*})= \bigcap _{m = 0}^{\infty } G_m({\psi _{\nu }^*})$, $G({{\Psi }^*})= \bigcup _{\nu = 1}^{\infty } G({\psi _{\nu }^*})$. Since for each $\nu \in {\mathbb {N}}$ and $m \in {\mathbb {Z}}_+$,

$$\begin{aligned} \Vert f \Vert _{m, \psi _{\nu }^*} \le \Vert f \Vert _{m+1, \psi _{\nu }^*}, \qquad f \in G_{m+1}\big ({\psi _{\nu }^*}\big ), \end{aligned}$$

$G_{m+1}({\psi _{\nu }^*})$ is continuously embedded in $G_m({\psi _{\nu }^*})$. Endow $G({\psi _{\nu }^*})$ with a topology defined by the family of norms , $m \in {\mathbb {Z}}_+$. Also note that for each $\nu \in {\mathbb {N}}$ and $m \in {\mathbb {Z}}_+$,

$$\begin{aligned} \Vert f \Vert _{m, \psi _{\nu + 1}^*} \le e^{C(\nu , 1)} \Vert f \Vert _{m, \psi _{\nu }^*}, \qquad f \in G_m\big ({\psi _{\nu }^*}\big ). \end{aligned}$$

Hence, $G({\psi _{\nu }^*})$ is continuously embedded in $G({\psi _{\nu + 1}^*})$. Supply $G({{\Psi }^*})$ with an inductive limit topology of spaces $G({\psi _{\nu }^*})$.

Theorem 1.3

Let ${\Phi }$ satisfy conditions $(\mathrm{i}_3)$ and $(\mathrm{i}_4)$. Then the Fourier transform ${\fancyscript{F}}:E({\Phi })\ni f \rightarrow \widehat{f}$ establishes an isomorphism of spaces $E({\Phi })$ and $G({{\Psi }^*})$.

Further, let ${{\Phi }^*}=\{{\varphi _{\nu }^*}\}_{\nu =1}^{\infty }$. For each $\nu \in {\mathbb {N}}$ and $m \in {\mathbb {Z}}_+$ define the normed space

For each $\nu \in {\mathbb {N}}$ let $GS({\varphi _{\nu }^*}) = \bigcap _{m \in {\mathbb {Z}_+}}GS_m({\varphi _{\nu }^*})$. Let $GS({{\Phi }^*})= \bigcup _{\nu \in {\mathbb {N}}}GS({\varphi _{\nu }^*})$. Note that for each $\nu \in {\mathbb {N}}$ and $m \in {\mathbb {Z}}_+$,

$$\begin{aligned} q_{m, \nu }(f) \le q_{m + 1, \nu }(f), \qquad f \in GS_{m+1}\big (\varphi _{\nu }^*\big ). \end{aligned}$$

Hence, $GS_{m+1}(\varphi _{\nu }^*)$ is continuously embedded in $GS_m(\varphi _{\nu }^*)$. Endow $GS({\varphi _{\nu }^*})$ with a topology defined by the family of norms $q_{\nu , m}$, $m \in {\mathbb {Z}}_+$. Also for each $\nu \in {\mathbb {N}}$ and $m \in {\mathbb {Z}}_+$,

$$\begin{aligned} q_{m, \nu + 1}(f) \le e^{C(\nu , 1)} q_{m, \nu }(f) , \qquad f \in GS_m\big (\varphi _{\nu }^*\big ). \end{aligned}$$

Hence, $GS({\varphi _{\nu }^*})$ is continuously embedded in $GS({\varphi _{\nu + 1}^*})$. Supply $GS({{\Phi }^*})$ with an inductive limit topology of spaces $GS({\varphi _{\nu }^*})$.

The main result of Sect. 5 is the following theorem.

Theorem 1.4

Let functions of the family ${\Phi }$ be convex on $[0, \infty )$ and ${\Phi }$ satisfy condition $(\mathrm{i}_3)$. Then $G({{\Psi }^*}) = GS({{\Phi }^*})$.

Note that if functions $\varphi _m$ are defined on $[0, \infty )$ by the formula $\varphi _m(x) = {\Omega }(\alpha _m x)$, where ${\Omega }$ is a differentiable function on $[0, \infty )$ such that ${\Omega }(0) = {\Omega }'(0) = 0$ and its derivative is continuous, increasing and tending to infinity and numbers $\alpha _m$ are positive and $\alpha _m < \alpha _{m+1}$, $m \in {\mathbb {N}}$, then the family ${\Phi }$ satisfies assumptions of Theorem 1.4.

2 Auxiliary results

The following two lemmas are essentially used in the next sections.

Lemma 2.1

Let $g \in {\fancyscript{B}}$, then for each $M>0$ there exists a constant $A>0$ such that

$$\begin{aligned} (g[e])^*(x) \le x \ln \frac{x}{M} - x + A, \qquad x > 0. \end{aligned}$$

Proof

By assumption, for each $M>0$ we can find a number $A > 0$ such that $g[e](y) \ge M e^y - A$ for all $y \ge 0$. Hence, for $x > 0$,

$\square$

Corollary 2.1

Let $g \in {\fancyscript{B}}$, then for each $b>0$ the series converges.

Lemma 2.2

Let $u, v \in {\fancyscript{B}}$ and for some $\rho > 0$, $\mu \ge 0$ and $C > 0$,

$$\begin{aligned} \rho u(x) \le v(x+\mu ) + C, \qquad x \ge 0. \end{aligned}$$

Then for all nonnegative numbers $\alpha$ and $\beta$ satisfying the equality $\alpha + \beta = \rho$ we have

where $A = \max {\bigl (C, \rho \min _{\xi \ge 0} u(\xi )- \min _{\xi \ge 0} v(\xi )\bigr )}$.

Proof

For all $x, y, t \in [0, \infty )$ and nonnegative numbers $\alpha$ and $\beta$ satisfying the equality $\alpha + \beta = \rho$ we have

Hence,

(1)

Note that for all $x, y \in [0, \infty )$,

From this and inequality (1) we obtain that for all $x, y \ge 0$,

where $A = \max {\bigl (C, \rho \min _{\xi \ge 0} u(\xi )- \min _{\xi \ge 0} v(\xi )\bigr )}$. $\square$

3 Alternative approach to description of $E({\Phi })$

3.1 3.1 Proof of Theorem 1.1

Let $f \in E({\Phi })$, then $f \in E(\varphi _{\nu })$ for some $\nu \in {\mathbb {N}}$. Fix $m \in {\mathbb {Z}_+}$. For all $x \in {\mathbb {R}}$, $n \in {\mathbb {Z}}_+$ and $R>0$ we have

where . From this we have

Using condition $(\mathrm{i}_2)$ on ${\Phi }$, we get

Further,

This means that

$$\begin{aligned} {\fancyscript{R}}_{m, \nu + 1}\big (f_{|{\mathbb {R}}}\big ) \le e^{C(\nu , m)} p_{\nu , m}(f). \end{aligned}$$

(2)

Therefore, $f_{|{\mathbb {R}}} \in {\fancyscript{E}}(\psi _{\nu + 1}^*)$. Thus, $f_{|{\mathbb {R}}} \in {\fancyscript{E}}({\Psi }^*)$.$\square$

Proof of Theorem 1.2

First note that due to condition $(\mathrm{i}_3)$ on ${\Phi }$ we have that for each $k \in {\mathbb {N}}$,

$$\begin{aligned} \psi _k \big (t+\delta _k\big ) \le \psi _{k + 1}(t) + \gamma _k, \qquad t \ge 0, \end{aligned}$$

where $\delta _k = \ln \sigma _k$. From this it easily follows that

$$\begin{aligned} \psi _k^*(x) - \psi _{k + 1}^*(x) \ge \delta _k x - \gamma _k, \qquad x \ge 0. \end{aligned}$$

(3)

Now let $f \in {\fancyscript{E}}({\Psi }^*)$. Then $f \in {\fancyscript{E}}(\psi _{\nu }^*)$ for some $\nu \in {\mathbb {N}}$. Hence, for each $m \in {\mathbb {Z}}_+$ we have

(4)

From this (taking into account that $\lim _{x \rightarrow + \infty }\psi _{\nu }^*(x)/x= + \infty )$ we get that for each $\varepsilon > 0$ there exists a constant $A_{\varepsilon } > 0$ such that for all $x \in {\mathbb {R}}$ and $n \in {\mathbb {Z}}_+$. So it is clear that the sequence converges to $f$ uniformly on compacts of the real axis and the series converges uniformly on compacts of ${\mathbb {C}}$ and, hence, its sum $F_f(z)$ is an entire function. Obviously, $F_f(x) = f(x)$, $x \in {\mathbb {R}}$. The uniqueness of holomorphic continuation is obvious.

Now we prove that $F_f \in E({\Phi })$. Let $m \in {\mathbb {Z}}_+$ be arbitrary. Using the equality

$$\begin{aligned} F_f(z) = \sum _{n=0}^{\infty } \frac{f^{(n)}(x)}{n!}\, (iy)^n, \qquad z = x+iy, \quad x,y \in {\mathbb {R}}, \end{aligned}$$

and inequality (4), we have

Now using inequality (3) and denoting $e^{\gamma _{\nu } + \delta _{\nu }}/\bigl (e^{\delta _{\nu }} - 1\bigr )$ by $B_{\nu }$, we have

Thus,

(5)

Recall that by condition $(\mathrm{i}_2)$ on ${\Phi }$ for each $k \in {\mathbb {N}}$ and $A > 0$ there exists a constant $C(k, A) > 0$ such that

Hence,

$$\begin{aligned} \psi _k(x) + A x \le \psi _{k+1}(x) + C(k, A), \qquad x \ge 0. \end{aligned}$$

From this we have that for all $\xi \ge 0$,

Then for all $x \ge 0$,

Thus, for each $k \in {\mathbb {N}}$ and $A > 0$ we have

(6)

Now with help of inequality (6) we obtain from estimate (5),

(7)

It is clear that

Hence,

As functions of the family ${\Phi }$ are nondecreasing and satisfy condition $(\mathrm{i}_3)$, it is possible to find a constant $K_{\nu , m} > 0$ such that for all $z \in {\mathbb {C}}$,

(8)

Thus, for each $m \in {\mathbb {Z}}_+$, . Hence, $F_f \in E(\varphi _{\nu + 3})$. Thus, $F_f \in E({\Phi })$.$\square$

3.2 Additional information on a structure of the space $E(\varPhi )$

In Sect. 1.3 for each $\nu \in {\mathbb {N}}$ we introduced the space ${\fancyscript{H}}(\varphi _{\nu })$ as a projective limit of spaces

and then defined the space ${\fancyscript{H}}({\Phi })$ as an inductive limit of spaces ${\fancyscript{H}}(\varphi _{\nu })$. Note that in view of inequality (6) the space ${\fancyscript{H}}(\varphi _{\nu })$ is continuously embedded in ${\fancyscript{H}}(\varphi _{\nu + 1})$ for each $\nu \in {\mathbb {N}}$.

Remark that if the family ${\Phi }$ satisfies condition $(\mathrm{i}_3)$ and functions $\psi _m$ are convex $[0, \infty )$, then ${\fancyscript{H}}({\Phi }) = E({\Phi })$. Indeed, for each $\nu \in {\mathbb {N}}$,

On the other hand, for each $\nu \in {\mathbb {N}}$ there exists a constant $d_{\nu } > 0$ such that $\varphi _{\nu }(1 + t) \le \varphi _{\nu }(\sigma _{\nu } t) + d_{\nu }$ for all $t \ge 0$. Using this inequality and condition $(\mathrm{i}_3)$, we have

From these inequalities our assertion easily follows. Using Theorems 1.1 and 1.2 we can prove a more strong assertion.

Proposition 3.1

Let the family ${\Phi }$ satisfy condition $(\mathrm{i}_3)$. Then $E({\Phi }) = {\fancyscript{H}}({\Phi })$.

Proof

Let $\nu \in {\mathbb {N}}$ and $f \in {\fancyscript{H}}(\varphi _{\nu })$. Using nondecreasity of $\varphi _{\nu }$ and condition $(\mathrm{i}_3)$ on ${\Phi }$ we can find a constant $K_{\nu } > 0$ such that for each $k \in {\mathbb {Z}}_+$,

$$\begin{aligned} p_{\nu + 1, k}(f) \le K_{\nu } {\fancyscript{N}}_{\nu , k}(f), \qquad f \in {\fancyscript{H}}(\varphi _{\nu }). \end{aligned}$$

From this it follows that the embedding $I:{\fancyscript{H}}({\Phi }) \rightarrow E({\Phi })$ is continuous.

The mapping $I$ is surjective too. Indeed, if $f \in E({\Phi })$ then $f \in E(\varphi _{\nu })$ for some $\nu \in {\mathbb {N}}$. Recall that by inequality (2) for each $k \in {\mathbb {Z}}_+$ we have ${\fancyscript{R}}_{k, \nu + 1}(f_{|{\mathbb {R}}}) \le e^{C_{\nu , k}} p_{\nu , k}(f)$. From this and inequality (7) (with $\nu$ replaced by $\nu + 1$) we obtain

$$\begin{aligned} {\fancyscript{N}}_{\nu + 3, k}(f) \le A_{\nu , k} p_{\nu , k}(f), \end{aligned}$$

where $A_{k, \nu }$ is some positive number. Hence, $f \in {\fancyscript{H}}(\varphi _{\nu + 3})$. Thus, $f \in {\fancyscript{H}}({\Phi })$. Moreover, the last estimate shows that the inverse mapping $I^{-1}$ is continuous. Hence, the equality $E({\Phi }) = {\fancyscript{H}}({\Phi })$ is topological as well.$\square$

Remark 3.1

Let the family ${\Phi }$ satisfy conditions $(\mathrm{i}_1)$–$(\mathrm{i}_3)$. Consider the family $\widetilde{\Phi }$ consisting of functions . Obviously, for each $\nu \in {\mathbb {N}}$ functions are continuous and nondecreasing on $[0, \infty )$. By inequality (6), for each $A > 0$ we have

Since for each $\nu \in {\mathbb {N}}$, $\lim _{x \rightarrow + \infty }(\psi _{\nu }^*)^*(x)/e^x= + \infty$ (it follows from Lemma 2.1) then

Thus, the family $\widetilde{\Phi }$ satisfies conditions of the form $(\mathrm{i}_1)$ and $(\mathrm{i}_2)$. Since ${\Phi }$ satisfies condition $(\mathrm{i}_3)$, using inequality (3), it is easy to get

$$\begin{aligned} (\psi _{\nu }^*)^* (t + \delta _{\nu }) \le (\psi _{\nu + 1}^*)^*(t) + \gamma _k, \qquad t \ge 0. \end{aligned}$$

Further, for all $x \ge 0$,

Hence, the family $\widetilde{\Phi }$ satisfies a condition of the form $(\mathrm{i}_3)$. Also note that functions are convex on $[0, \infty )$. Hence, ${\fancyscript{H}}(\widetilde{\Phi }) = E(\widetilde{\Phi })$. By Proposition 3.1, we have that $E({\Phi })= {\fancyscript{H}}({\Phi })$. Since $E(\widetilde{\Phi }) \equiv {\fancyscript{H}}({\Phi })$, we finally obtain $E({\Phi })= {\fancyscript{H}}({\Phi })={\fancyscript{H}}(\widetilde{\Phi })$.

4 Fourier transform of $E({\Phi })$

First we will prove that under condition $(\mathrm{i}_3)$ on ${\Phi }$ the space $G({\Psi }^*)$ admits a more simple description. For $\nu \in {\mathbb {N}}$ and $m \in {\mathbb {Z}}_+$ let

Let $Q(\psi _{\nu }^*)= \bigcap _{m \in {\mathbb {Z}_+}} Q_m(\psi _{\nu }^*)$, $Q({\Psi }^*)= \bigcup _{\nu =1}^{\infty } Q(\psi _{\nu }^*)$. With usual operations of addition and multiplication by complex numbers $Q(\psi _{\nu }^*)$ and $Q({\Psi }^*)$ are linear spaces. The family of norms $N_{\psi _{m, \nu }^*}$, $m \in {\mathbb {Z}}_+$, defines a locally convex topology in $Q(\psi _{\nu }^*)$. Endow $Q({\Psi }^*)$ with an inductive limit topology of spaces $Q(\psi _{\nu }^*)$.

Lemma 4.1

Let the family ${\Phi }$ satisfy condition $(\mathrm{i}_3)$. Then the spaces $Q({\Psi }^*)$ and $G({\Psi }^*)$ coincide.

Proof

Let $\nu \in {\mathbb {N}}$ and $f \in Q(\psi _{\nu }^*)$. Then for each $m \in {\mathbb {Z}}_+$, $N_{m, \psi _{\nu }^*}(f) < \infty$. Since $\Vert f \Vert _{m, \psi _{\nu }^*} \le N_{m, \psi _{\nu }^*}(f)$ for each $m \in {\mathbb {Z}}_+$, $f \in G_m(\psi _{\nu }^*)$. Thus, if $f \in Q({\Psi }^*)$ then $f \in G({\Psi }^*)$ and, obviously, the embedding mapping $J:Q({\Psi }^*) \rightarrow G({\Psi }^*)$ is continuous.

Now let $\nu \in {\mathbb {N}}$ and $f \in G(\psi _{\nu }^*)$. Let $m \in {\mathbb {Z}}_+$ be arbitrary and $n \in {\mathbb {Z}_+}$ be such that $0 \le n \le m$. Then

(9)

Obviously,

Now take into account that for each $b>0$, see Lemma 2.1. So we can find a constant $C_{\nu } >1$ such that

Using (9), we get

(10)

Further,

Using inequality (3), we have

From this and (10) we get for each $m \in {\mathbb {Z}}_+$,

(11)

where . Hence, $f \in Q(\psi _{\nu + 1}^*)$. From (11) it follows that the inverse mapping $J^{-1}$ acts from $G({\Psi }^*)$ to $Q({\Psi }^*)$ and is continuous. Thus, the topological equality $Q(\psi ^*)=G(\psi ^*)$ is established.$\square$

Proof of Theorem 1.3

Let $\nu \in {\mathbb {N}}$ and $f \in E(\varphi _{\nu })$. Then for all $n \in {\mathbb {Z}_+}$ and $x \in {\mathbb {R}}$ we have

(12)

Let $m \in {\mathbb {N}}$, $n \in {\mathbb {Z}}_+$ and $x \in {\mathbb {R}}$. For arbitrary $\eta \in {\mathbb {R}}$,

From this we get

If $x \ne 0$ then putting in the last inequality $\eta = -xt/\vert x \vert$ with $t > 0$, we have

Since

then from this and the previous estimate we obtain

(13)

If $x=0$ then $x^m \widehat{f}^{\,(n)}(x) =0$. From this and inequalities (12) and (13) (taking into account that $\psi _{\nu }^*(0)=-\inf _{t \ge 0} \psi _{\nu }(t) = -\varphi _{\nu }(1) \le -\varphi _{\nu }(0)$) we have for all $m \in {\mathbb {N}}$ and $n \in {\mathbb {Z}}_+$,

Thus, for all $k \in {\mathbb {Z}}_+$ we get

In other words, $\Vert \widehat{f} \Vert _{k, \psi _{\nu }^*} \le \pi p_{\nu , k + 2}(f)$, $f \in E(\varphi _{\nu }).$ From this inequality it follows that the linear mapping ${\fancyscript{F}}:f \in E({\Phi }) \rightarrow \widehat{f}$ acts from $E({\Phi })$ to $G({\Psi }^*)$ and is continuous.

Let us show that ${\fancyscript{F}}$ is surjective. Let $g \in G({\Psi }^*)$, then $g \in G(\psi _{\nu }^*)$ for some $\nu \in {\mathbb {N}}$. By the proof of Lemma 4.1, $g \in Q(\psi _{\nu + 1}^*)$. Hence, for all $m, k \in {\mathbb {Z}}_+$,

Put

and show that $f$ satisfies assumptions of Theorem 1.2. Let $m, n \in {\mathbb {Z}_+}$ be arbitrary, and $\xi \in {\mathbb {R}}$. Then

From this we have

Continuing the estimate, we get

(14)

Recall now that by assumption of theorem, for each $s \in {\mathbb {N}}$ there exist numbers $\lambda _s > 1$, $h_s \in (1, \sigma _{s + 1})$ and $l_s > 0$ such that

From this it follows that

where $\tau _s = \ln h_s$. Then, by Lemma 2.2, there exists a constant $K_s >0$ such that for all nonnegative numbers $\alpha$ and $\beta$ satisfying the equality $\alpha + \beta = \lambda _s$ we have

(15)

Using (15), we have from (14)

where $b_{\nu , 1}= e^{K_{\nu + 1}}/2$. Obviously, there exists a constant $b_{\nu , 2} > 0$ such that for all $m, n \in {\mathbb {Z}_+}$,

Note that the series converges, see Corollary 2.1. Now using inequality (3), we get

where . From this we have that for each $m \in {\mathbb {Z}_+}$ and all $n \in {\mathbb {Z}_+}$, $\xi \in {\mathbb {R}}$,

By Theorem 1.2, $f$ can be holomorphically continued (uniquely) to an entire function $F_f$ belonging to $E({\Phi })$. Obviously, $g = {\fancyscript{F}}(F_f)$. The proof of Theorem 1.2 (in particular, inequalities (4) and (8)) indicates that there is a constant $K(\nu , m) > 0$ such that for $z \in {\mathbb {C}}$, $z = x + i y$,

Thus, for each $m \in {\mathbb {Z}_+}$,

Taking into account inequality (11), we get

From this estimate it follows that the inverse mapping ${\fancyscript{F}}^{-1}$ is continuous.

Thus, it is proved that Fourier transform establishes a topological isomorphism between spaces $E({\Phi })$ and $G({\Psi }^*)$.$\square$

5 Special case of a family ${\Phi }$

In the proof of Theorem 1.4 the following three lemmas will be used.

Lemma 5.1

Let $g$ be a real-valued continuous function on $[0, \infty )$ such that $\lim _{x \rightarrow + \infty }g(x)/x= + \infty$. Then for each $\delta > 0$,

Proof

Let $\delta > 0$ be arbitrary. For each $x>0$ denote by $\xi (x)$ a point where the supremum of the function $u_x(\xi )= x \xi - g(\xi )$ over $[0, \infty )$ is attained. Note that $\xi (x) \rightarrow +\infty$ as $x \rightarrow +\infty$. Otherwise there are a number $M>0$ and a sequence $(x_j)_{j=1}^{\infty }$ of positive numbers $x_j$ converging to $+\infty$ such that $\xi (x_j) \le M$. Then $g^*(x_j)= x_j \xi (x_j) - g(\xi (x_j))$. But it contradicts to the fact that $\lim _{x \rightarrow + \infty } g^*(x)/x= + \infty .$ Thus, $\lim _{x \rightarrow + \infty } \xi (x)= + \infty .$ From this and the inequality

for all $x>0$, the assertion of lemma follows.$\square$

The proof of the following lemma essentially rests on ideas of Napalkov and Popenov from [7, Lemma 4].

Lemma 5.2

Let $u \in V$, then there exists a constant $K > 0$ depending on $u$ such that

Proof

It is known [4] that there exists a function $v \in V_u$ such that

$$\begin{aligned} \lim _{t \rightarrow +\infty }\! \frac{v(t)}{t} = \lim _{t \rightarrow 0+} \frac{t}{v(t)} = + \infty . \end{aligned}$$

Since $\vert v(t) - u(t) \vert \le A$, $t \ge 0$, for some $A>0$ then

$$\begin{aligned} \begin{aligned} \bigl \vert (v[e])^*(x) - (u[e])^*(x) \bigr \vert&\le A, \qquad x\ge 0, \\ \bigl \vert (v^*[e])^*(x) - (u^*[e])^*(x)\bigr \vert&\le A, \qquad x \ge 0. \end{aligned} \end{aligned}$$

(16)

Let $t > 0$ be arbitrary. Note that

Hence, for each $\xi , \mu \in {\mathbb {R}}$,

(17)

Using simple geometrical ideas, it is not difficult to see (firstly it was noticed by Popenov) that there exists a unique point $x_0>0$ such that

$$\begin{aligned} u_{-}'(x_0) \le \frac{t}{x_0} \le u_{+}'(x_0) \end{aligned}$$

(here $u_{-}'(x_0)$ is the left derivative at $x_0$ and $u_{+}'(x_0)$ is the right derivative at $x_0$) and if $x_0^* = t/x_0$ then the following equality holds:

$$\begin{aligned} u(x_0) + u^*(x_0^*)=t. \end{aligned}$$

Putting in (17), $\xi =\ln x_0$, $\mu =\ln x_0^*$, we get

(18)

Using inequalities (16), we get from (18)

It remains to put $K = v(1) + v^*(1) + 2A$.$\square$

The following lemma was proved in [5, 6].

Lemma 5.3

Let a lower semi-continuous function $u:[0, \infty ) \rightarrow {\mathbb {R}}$ be such that $\lim _{x \rightarrow + \infty }u(x)/x= + \infty$. Then

Proof of Theorem 1.4

First note that using convexity of functions of the family ${\Phi }$ and condition $(\mathrm{i}_3)$ on ${\Phi }$ we easily obtain that for each $k \in {\mathbb {N}}$,

In particular, this means that condition $(\mathrm{i}_4)$ holds in our case trivially with $\lambda _k = \sigma _k$ and . Also from the last inequality it follows that for each $k \in {\mathbb {N}}$ we have

Hence, by Lemma 2.2, for each $k \in {\mathbb {N}}$ there exists a number $A_k > 0$ such that for all nonnegative numbers $\alpha$ and $\beta$ satisfying the equality $\alpha + \beta = \sigma _k$ we have

(19)

Now let $\nu \in {\mathbb {N}}$ and $f \in G(\psi _{\nu }^*)$. Fix $m \in {\mathbb {Z}}_+$. Since $f \in Q(\psi _{\nu + 1}^*)$ (see the proof of Lemma 4.1), for all $k \in {\mathbb {Z}}_+$ and $n \in {\mathbb {Z}}_+$ such that $0 \le n \le m$,

(20)

Using inequality (19), nondecreasity of $\psi _{\nu + 1}^*$ and taking into account that $j! < 3j^{j+1}/e^j$ for all $j \in {\mathbb {N}}$, we have that for all $k \in {\mathbb {N}}$, $t \in [k, k+1)$ and $\mu \ge 1$,

From this using inequality (3), we obtain

where . Using Lemma 5.2, we get for some $C_{\nu , 2} > 0$ (not depending on $k$ and $t$),

We can choose a constant $C_{\nu , 3} > 0$ (not depending on $k$ and $t$) so that

From this it follows that

(21)

Obviously,

$$\begin{aligned} \inf _{t \ge 1} \,\bigl ((\varphi _{\nu + 3}^*[e])^*(t) - t \ln \mu \bigr )&\le -\ln \mu + \big (\varphi _{\nu + 3}^*[e]\big )^*(1),\\ \inf _{0 < t \le 1}\, \bigl ((\varphi _{\nu + 3}^*[e])^*(t) - t \ln \mu \bigr )&\ge -\ln \mu + \big (\varphi _{\nu + 3}^*[e]\big )^*(0). \end{aligned}$$

Consequently,

Denoting $(\varphi _{\nu + 3}^*[e])^*(1) - (\varphi _{\nu + 3}^*[e])^*(0)$ by $m_{\nu }$, we have

$$\begin{aligned} \inf _{t \ge 1}\, \bigl ((\varphi _{\nu + 3}^*[e])^*(t) - t \ln \mu \bigr ) \le \inf _{t > 0}\, \bigl ((\varphi _{\nu + 3}^*[e])^*(t) - t \ln \mu \bigr ) + m_{\nu }. \end{aligned}$$

With help of this inequality we have from (21)

(22)

For each $j \in {\mathbb {N}}$ choose $\theta _j \in V_{\varphi _j^*[e]}$. Then

$$\begin{aligned} \bigl \vert \theta _{j}(\xi ) - \varphi _j^*[e](\xi ) \bigr \vert&\le r_j, \qquad \xi \ge 0,\end{aligned}$$

(23)

$$\begin{aligned} \bigl \vert \theta _j^*(\xi ) - (\varphi _j^*[e])^*(\xi ) \bigr \vert&\le r_j, \qquad \xi \ge 0, \end{aligned}$$

(24)

where $r_j$ is some positive number depending on $\varphi _j^*[e]$ and $\theta _j$. From (22) using inequality (24), we have

where . Using the Young inversion formula, we obtain

From this, using inequality (23), we have

where . In other words,

Using this inequality and nondecreasity of $\varphi _{\nu + 3}^*$, we have

(25)

Note that using condition $(\mathrm{i}_3)$ on ${\Phi }$, it is easy to obtain that for each $j \in {\mathbb {N}}$,

$$\begin{aligned} \varphi _{j+1}^*(\xi ) \le \varphi _j^*\biggl (\frac{\xi }{\sigma _j}\biggr ) + \gamma _j, \qquad \xi \ge 0. \end{aligned}$$

(26)

Hence,

From this and Lemma 5.1 we get

$$\begin{aligned} \lim _{\xi \rightarrow + \infty } \!\frac{\varphi _j^*(\xi ) - \varphi _{j+1}^*(\xi )}{\xi }= + \infty . \end{aligned}$$

(27)

Going back to (25), we obtain with help of (27)

where $C_{\nu , 6}$ is some positive number. From this and inequality (20), we obtain that for $n \in {\mathbb {Z}_+}$ such that $0 \le n \le m$,

This means that

Taking into account inequality (11), we have

where $C_{\nu , 7}$ is some positive constant depending on $\nu$. From this it follows that the identity mapping $T$ acts from $G({\Psi }^*)$ to $GS({\Phi }^*)$ continuously.

Show that $T$ is surjective. Let $f \in GS({\Phi }^*)$. Then $f \in GS(\varphi _{\nu }^*)$ for some $\nu \in {\mathbb {N}}$. Let $m \in {\mathbb {Z}}_+$ be fixed, $x$ be arbitrary. For all $n \in {\mathbb {Z}_+}$ such that $0 \le n \le m$ we have

(28)

Using inequality (26), we have from (28)

Obviously, there exists a constant $\alpha _{\nu } > 1$ (not depending on $x$ and $n$) such that

In other words,

From this we have

Now using Lemma 5.3, we get

Consequently, for all $k \in {\mathbb {N}}$,

From this and (28) it follows that

This means that

(29)

Since $m \in {\mathbb {Z}}_+$ was arbitrary, $f \in G(\psi _{\nu + 1}^*)$. Hence, $f \in G({\Psi }^*)$.

From (29) it follows that the mapping $T^{-1}$ is continuous. Thus, the spaces $G({{\Psi }^*})$ and $GS({{\Phi }^*})$ coincide.$\square$