Abstract
In the paper (Kulikov in Sb Math 204(2):237–263, 2013), the ambiguity index \(a_{(G,O)}\) was introduced for each equipped finite group \((G,O)\). It is equal to the number of connected components of a Hurwitz space parametrizing coverings of a projective line with Galois group \(G\) assuming that all local monodromies belong to conjugacy classes \(O\) in \(G\) and the number of branch points is greater than some constant. We prove in this article that the ambiguity index can be identified with the size of a generalization of so called Bogomolov multiplier (Kunyavskiĭ in Cohomological and Geometric Approaches to Rationality Problems. Progress in Mathematics, vol 282, pp 209–217, 2010), see also (Bogomolov in Math USSR-Izv 30(3):455–485, 1988) and hence can be easily computed for many pairs \((G,O)\). In particular, the ambiguity indices are completely counted in the cases when \(G\) are the symmetric or alternating groups.
Similar content being viewed by others
1 Introduction
Let \(G\) be a finite group and \(O\) be a subset of \(G\) consisting of conjugacy classes \(C_i\) of \(G\), \(O= C_1\cup \dots \cup C_m\), which together generate \(G\). The pair \((G,O)\) is called an equipped group and \(O\) is called an equipment of \(G\). We fix the numbering of conjugacy classes contained in \(O\). One can associate a \(C\)-group \((\widetilde{G}, \widetilde{O})\) to each equipped group \((G,O)\). The \(C\)-group \(\widetilde{G}\) is generated by the letters of the alphabet \(Y=Y_O=\{ y_g : g\in O\}\) subject to relations

We assume \(\widetilde{O}=Y_O\) in the definition of \(\widetilde{G}\). There is an obvious natural homomorphism \(\beta :\widetilde{G}\rightarrow G\) given by \(\beta (y_g)=g\). It was shown in [11], that the commutator subgroup  is finite. The order \(a_{(G,O)}\) of the group
is finite. The order \(a_{(G,O)}\) of the group  was called the ambiguity index of the equipped finite group \((G,O)\).
was called the ambiguity index of the equipped finite group \((G,O)\).
The notion of equipped groups is related to the description of Hurwitz spaces parametrizing maps between projective curves with \(G\) as the monodromy group and the ambiguity index \(a_{(G,O)}\) is equal to the properly defined “asymptotic” number of connected components of Hurwitz space parametrizing covering of curves with fixed ramification data. More precisely, let \(f:E\rightarrow F\) be a morphism of a non-singular complex irreducible projective curve \(E\) onto a non-singular projective curve \(F\). Let us choose a point \(z_0\in F\) such that \(z_0\) is not a branch point of \(f\) hence the points \(f^{-1}(z_0)=\{ w_1,\ldots ,w_d\}\), where \(d=\deg f\), are simple. If we fix the numbering of points in \(f^{-1}(z_0)\) then we call \(f\) a marked covering.
Let \(B=\{ z_1, \dots , z_n\}\subset F\) be the set of branch points of \(f\). The numbering of the points of \(f^{-1}(z_0)\) defines a homomorphism  of the fundamental group
of the fundamental group  to the symmetric group \({\Sigma }_d\). Define \(G\subset {\Sigma }_d\) as \({\text {im}}\, f_* =G\). It acts transitively on \(f^{-1}(z_0)\). Let \(\gamma _1,\ldots ,\gamma _n\) be simple loops around, respectively, the points \(z_1,\ldots , z_n\) starting at \(z_0\). The image \(g_j=f_*(\gamma _j)\in G\) is called a local monodromy of \(f\) at the point \(z_j\). Each local monodromy \(g_j\) depends on the choice of \(\gamma _j\), therefore, it is defined uniquely up to conjugation in \(G\).
to the symmetric group \({\Sigma }_d\). Define \(G\subset {\Sigma }_d\) as \({\text {im}}\, f_* =G\). It acts transitively on \(f^{-1}(z_0)\). Let \(\gamma _1,\ldots ,\gamma _n\) be simple loops around, respectively, the points \(z_1,\ldots , z_n\) starting at \(z_0\). The image \(g_j=f_*(\gamma _j)\in G\) is called a local monodromy of \(f\) at the point \(z_j\). Each local monodromy \(g_j\) depends on the choice of \(\gamma _j\), therefore, it is defined uniquely up to conjugation in \(G\).
Denote by \(O=C_1\cup \cdots \cup C_m\subset G\) the union of conjugacy classes of all local monodromies and by \(\tau _i\) the number of local monodromies of \(f\) belonging to the conjugacy class \(C_i\). The collection \(\tau =(\tau _1C_1,\ldots ,\tau _mC_m)\) is called the monodromy type of \(f\). Assume that the elements of \(O\) generate the group \(G\). Then the pair \((G,O)\) is an equipped group. Let \({\text {HUR}}_{d,G,O,\tau }^m(F,z_0)\) be the Hurwitz space (see the definition of Hurwitz spaces in [4] or in [12]) of marked degree \(d\) coverings of \(F\) with Galois group \(G\subset {\Sigma }_d\), local monodromies in \(O\), and monodromy type \(\tau \).
The number of irreducible components of \({\text {HUR}}^m_{d,G,O,\tau }(F,z_0)\) for fixed \(d, G\), \(O, F\) is a function of an integer vector \(\tau = (\tau _1,\ldots ,\tau _m)\). It was proved in [12] that this number is constant for big \(\tau \). More precisely, for each equipped finite group \((G,O)\) there is \(T\) such that if for all \(i=1,\ldots ,m\) we have \(\tau _i\geqslant T\), \(i=1,\ldots ,m\), then the number of irreducible components of the Hurwitz space \({\text {HUR}}^m_{d,G,O,\tau }(F,z_0)\) is equal to \(a_{(G,O)}\). The (minimal) number \(T\) does not depend on the base curve \(F\) and the degree \(d\) of the covering.
The subgroup \(B_0(G)\subset H^2(G,{\mathbb {Q}}/{\mathbb {Z}})\) was defined and studied in [1]. It consists of elements of \(H^2(G,{\mathbb {Q}}/{\mathbb {Z}})\) which restrict trivially onto abelian subgroups of \(G\). It was conjectured in [2] that \(B_0(G)\) is trivial for simple groups. This conjecture was partially solved already in [2] and it was completely solved by Kunyavskiĭ in [13],Footnote 1 and by Kunyavskiĭ–Kang in [8] for a wider class of almost simple groups. The latter consists of groups \(G\) which contain some simple group \(L\) and in turn are contained in the automorphism group \(\mathrm{Aut}\,L\). Kunyavskiĭ in [13] called \(B_0(G)\) as Bogomolov multiplier and we are going to use his terminology here. Denote by \(b_0(G)\) the order of the group \(B_0(G)\) and denote by \(h_2(G)\) the order of the Schur multiplier of the group \(G\), that is, the order of the group \(H_2(G,{\mathbb {Z}})\).
The aim of this article is to prove
Theorem 1.1
For an equipped finite group \((G,O)\) we have the following inequalities:
In particular, \(a_{(G,G\setminus \{1\})}=b_0(G)\).
Since, by [13], \(b_0(G)=1\) for a finite almost simple group \(G\), we conclude
Corollary 1.2
Let \(G\) be a finite almost simple group. Then there is a constant \(T\) such that for any projective irreducible non-singular curve \(F\) each non-empty Hurwitz space \(\mathrm{HUR}^m_{d,G,G\setminus \{ 1\}, \tau }(F, z_0)\) is irreducible if all \(\tau _i\geqslant T\).
It was shown in [11] that if \(O_1\subset O_2\) are two equipments of a finite group \(G\), then \(a_{(G,O_2)}\leqslant a_{(G,O_1)}\).
For a symmetric group \({\Sigma }_d\), the famous Clebsch–Hurwitz theorem [3, 6] implies that the ambiguity index \(a_{({\Sigma }_d,T)}=1\), where \(T\) is the set of transpositions in \({\Sigma }_d\), and it was shown in [10] that the ambiguity index \(a_{({\Sigma }_d,O)}=1\) if the equipment \(O\) contains an odd permutation \(\sigma \in {\Sigma }_d\) such that \(\sigma \) leaves fixed at least two elements. Theorem 4.14 (see Sect. 4.4) gives the complete answer on the value of \(a_{({\Sigma }_d,O)}\) for each equipment \(O\) of \({\Sigma }_d\). Also in Sect. 4.4, we give the complete answer on the value of \(a_{({\mathbb {A}}_d,O)}\) for each \(d\) and for each equipment \(O\) of the alternating group \({\mathbb {A}}_d\).
In Sect. 2, we remind some properties of \(C\)-groups and prove one of the inequalities claimed in Theorem 1.1. In Sect. 3, we complete the proof of this theorem.
In Sect. 4, we investigate the properties of ambiguity indices of a quasi-cover of an equipped finite group \((G,O)\), and in Sect. 5, we give a cohomological description of the ambiguity indices.
In Sect. 6, we give examples of finite groups \(G\) with Bogomolov multiplier \(b_0(G)>1\). Therefore, for such \(G\) each non-empty space \({\text {HUR}}^m_{d,G,O, \tau }(F, z_0)\) consists of at least \(b_0(G)>1\) irreducible components for any \(\tau =(\tau _1,\ldots ,\tau _m)\) with big enough \(\tau _i\).
In this article, if \({\mathbb {F}}\) is a free group freely generated by an alphabet \(X\), \(N\) is a normal subgroup of \({\mathbb {F}}\), and a group \(G={\mathbb {F}}/N\), then a word \(w=w(x_{i_1},\ldots , x_{i_n})\) in letters \(x_{i_j}\in X\) and their inverses will be considered as an element of \(G\) in case if it does not lead to misunderstanding.
2 \(C\)-groups and their properties
Let us remind the definition of a \(C\)-group (see, for example, [9]).
Definition 2.1
A group \(G\) is a \(C\)-group if there is a set of generators \(x\in X\) in \(G\) such that a basis of relations between \(x\in X\) consists of the following relations:

where \(M\) is a subset of \(X^3\).
Thus the \(C\)-structure of \(G\) is defined by \(X\subset G\) and \(M\subset X^3\).
Let \({\mathbb {F}}\) be a free group freely generated by an alphabet \(X\). Denote by \(N\) the subgroup of \({\mathbb {F}}\) normally generated by the elements  , \((x_i,x_j,x_k)\in M\). The group \(N\) is a normal subgroup of \({\mathbb {F}}\). Let \(f:{\mathbb {F}}\rightarrow G={\mathbb {F}}/N\) be the natural epimorphism given by presentation (1). In the sequel, we consider each \(C\)-group \(G\) as an equipped group \((G,O)\) with the equipment \(O=f(X^{{\mathbb {F}}})\) (where \(X^{{\mathbb {F}}}\) is the orbit of \(X\) under the action of the group of inner automorphisms of \({\mathbb {F}}\)). The elements of \(O\) are called \(C\)-generators of the \(C\)-group \(G\). In particular, the equipped group \(({\mathbb {F}},X^{{\mathbb {F}}})\) is a \(C\)-group.
, \((x_i,x_j,x_k)\in M\). The group \(N\) is a normal subgroup of \({\mathbb {F}}\). Let \(f:{\mathbb {F}}\rightarrow G={\mathbb {F}}/N\) be the natural epimorphism given by presentation (1). In the sequel, we consider each \(C\)-group \(G\) as an equipped group \((G,O)\) with the equipment \(O=f(X^{{\mathbb {F}}})\) (where \(X^{{\mathbb {F}}}\) is the orbit of \(X\) under the action of the group of inner automorphisms of \({\mathbb {F}}\)). The elements of \(O\) are called \(C\)-generators of the \(C\)-group \(G\). In particular, the equipped group \(({\mathbb {F}},X^{{\mathbb {F}}})\) is a \(C\)-group.
A homomorphism \(f:G_1\rightarrow G_2\) of a \(C\)-group \((G_1,O_1)\) to a \(C\)-group \((G_2,O_2)\) is called a \(C\)-homomorphism if it is a homomorphism of equipped groups, that is, \(f(O_1)\subset O_2\). In particular, two \(C\)-groups \((G_1,O_1)\) and \((G_2,O_2)\) are \(C\) -isomorphic if they are isomorphic as equipped groups.
Claim 2.2
([9, Lemma 3.6]) Let \(N\) be a normal subgroup of \({\mathbb {F}}\) normally generated by a set of elements of the form  , where \(w_i\) and \(w_l\) are elements of \({\mathbb {F}}\) and \(x_j,x_k\in X\). Let \(f:{\mathbb {F}}\rightarrow G\simeq {\mathbb {F}}/N\) be the natural epimorphism. Then \((G,f(X^{{\mathbb {F}}}))\) is a \(C\)-group and \(f\) is a \(C\)-homomorphism.
, where \(w_i\) and \(w_l\) are elements of \({\mathbb {F}}\) and \(x_j,x_k\in X\). Let \(f:{\mathbb {F}}\rightarrow G\simeq {\mathbb {F}}/N\) be the natural epimorphism. Then \((G,f(X^{{\mathbb {F}}}))\) is a \(C\)-group and \(f\) is a \(C\)-homomorphism.
To each \(C\)-group \((G,O)\), one can associate a \(C\)-graph. By definition, the \(C\)-graph
\({\Gamma }={\Gamma }_{(G,O)}\)
of a \(C\)
-group
\((G,O)\) is a directed labeled graph whose set of vertices \(V=\{ v_{g_i}: g_i\in O\}\) is in one-to-one correspondence with the set \(O\). Two vertices \(v_{g_1}\) and \(v_{g_2}\), \(g_1, g_2\in O\), are connected by a labeled edge \(e_{v_{g_1}v_{g_2}v_g}\) (here \(v_{g_1}\) is the tail of \(e_{v_{g_1}v_{g_2}v_g}\), \(v_{g_2}\) is the head of \(e_{v_{g_1}v_{g_2}v_g}\), and \(v_{g}\) is the label of \(e_{v_{g_1}v_{g_2}v_g}\)) if and only if in \(G\) we have the relation  with some \(g\in O\).
with some \(g\in O\).
A \(C\)-homomorphism \(f:(G_1,O_1)\rightarrow (G_2,O_2)\) of \(C\)-groups induces a map \(f_*:{\Gamma }_{(G_1,O_1)}\rightarrow {\Gamma }_{(G_2,O_2)}\) from the \(C\)-graph \({\Gamma }_{(G_1,O_1)}\) in the \(C\)-graph \({\Gamma }_{(G_2,O_2)}\), where by definition, \(f_*(v_g)=v_{f(g)}\) for each vertex \(v_g\) of \(\Gamma _{(G_1,O_1)}\) and
for each edge \(e_{v_{g_1}v_{g_2}v_g}\) of \({\Gamma }_{(G_1,O_1)}\). The following claim is obvious.
Claim 2.3
A \(C\)-homomorphism \(f:(G_1,O_1)\rightarrow (G_2,O_2)\) is a \(C\)-isomorphism if \(f_*\) is one-to-one between the sets of vertices of \({\Gamma }_{(G_1,O_1)}\) and \({\Gamma }_{(G_2,O_2)}\).
In the sequel, we will consider only finitely presented \(C\)-groups (as groups without equipment) and \(C\)-graphs consisting of finitely many connected components. Denote by \(m\) the number of connected components of a \(C\)-graph \({\Gamma }_{(G,O)}\).
Then it is easy to see that  and any two \(C\)-generators \(g_1\) and \(g_2\) are conjugated in the \(C\)-group \(G\) if and only if \(v_{g_1}\) and \(v_{g_2}\) belong to the same connected component of \({\Gamma }_{(G,O)}\). Thus the set \(O\) of \(C\)-generators of the \(C\)-group \((G,O)\) is the union of \(m\) conjugacy classes of \(G\) and there is a one-to-one correspondence between the conjugacy classes of \(G\) contained in \(O\) and the set of connected components of \({\Gamma }_{(G,O)}\).
and any two \(C\)-generators \(g_1\) and \(g_2\) are conjugated in the \(C\)-group \(G\) if and only if \(v_{g_1}\) and \(v_{g_2}\) belong to the same connected component of \({\Gamma }_{(G,O)}\). Thus the set \(O\) of \(C\)-generators of the \(C\)-group \((G,O)\) is the union of \(m\) conjugacy classes of \(G\) and there is a one-to-one correspondence between the conjugacy classes of \(G\) contained in \(O\) and the set of connected components of \({\Gamma }_{(G,O)}\).
Denote by  the natural epimorphism. In the sequel, we fix some numbering of the connected components of \({\Gamma }_{(G,O)}\). Then the group \(H_1(G,{\mathbb {Z}})\simeq {\mathbb {Z}}^m\) obtains a natural base consisting of vectors \(\tau (g)=(0,\ldots ,0,1,0,\ldots ,0)\), where \(1\) stands on the \(i\)th place if \(g\) is a \(C\)-generator of \(G\) and \(v_g\) belongs to the \(i\)th connected component of \({\Gamma }_{(G,O)}\). For \(g\in G\) the image \(\tau (g)\) is called the type of \(g\).
the natural epimorphism. In the sequel, we fix some numbering of the connected components of \({\Gamma }_{(G,O)}\). Then the group \(H_1(G,{\mathbb {Z}})\simeq {\mathbb {Z}}^m\) obtains a natural base consisting of vectors \(\tau (g)=(0,\ldots ,0,1,0,\ldots ,0)\), where \(1\) stands on the \(i\)th place if \(g\) is a \(C\)-generator of \(G\) and \(v_g\) belongs to the \(i\)th connected component of \({\Gamma }_{(G,O)}\). For \(g\in G\) the image \(\tau (g)\) is called the type of \(g\).
Lemma 2.4
Let \(g_1, g_2\) be two \(C\)-generators of a \(C\)-group \((G,O)\), \(N\) the normal closure of \(g_1g_2^{-1}\) in \(G\), and \(f:G\rightarrow G_1=G/N\) the natural epimorphism. Then
- (i):
-
\((G_1,O_1)\) is a \(C\)-group, where \(O_1=f(O)\), and \(f\) is a \(C\)-homomorphism;
- (ii):
-
the map \(f_*:{\Gamma }_{(G,O)}\rightarrow {\Gamma }_{(G_1,O_1)}\) is a surjection;
- (iii):
-
if
 belongs to the center \(Z(G)\) of the group \(G\) and \(v_{g_1}\) and \(v_{g_2}\) belong to different components of \({\Gamma }_{(G,O)}\), then
belongs to the center \(Z(G)\) of the group \(G\) and \(v_{g_1}\) and \(v_{g_2}\) belong to different components of \({\Gamma }_{(G,O)}\), then
- (iii\(_1\)):
-
the number of connected components of the \(C\)-graph \({\Gamma }_{(G_1,O_1)}\) is less than the number of connected components of the \(C\)-graph \({\Gamma }_{(G,O)}\),
- (iii\(_2\)):
-
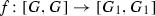 is an isomorphism.
is an isomorphism.
Proof
Claims (i), (ii), and (iii\(_1\)) are obvious. To prove (iii\(_2\)), note that \(N\) is a cyclic group generated by \(g_1g_2^{-1}\), since \(g_1g_2^{-1}\) belongs to the center \(Z(G)\). The type \(\tau \bigl ((g_1g_2^{-1})^n\bigr )\) is non-zero for \(n\ne 0\), since \(v_{g_1}\) and \(v_{g_2}\) belong to different connected components of \({\Gamma }_{(G,O)}\). Therefore, to complete the proof, it suffices to note that the groups \(N\) and  have trivial intersection, since \(\tau (g)=0\) for all
have trivial intersection, since \(\tau (g)=0\) for all  . \(\square \)
. \(\square \)
A \(C\)-group \((G,O)\) is called a \(C\)-finite group if the set of vertices of \(C\)-graph \({\Gamma }_{(G,O)}\) is finite or, the same, if the equipment \(O\) of \(G\) is a finite set.
Proposition 2.5
([11]) Let \((G,O)\) be a \(C\)-finite group. Then the commutator  is a finite group.
is a finite group.
As it was mentioned in Sect. 1, to each finite equipped group \((G,O)\), one can associate a \(C\)-group \((\widetilde{G}, \widetilde{O})\) defined as follows. The group \(\widetilde{G}\) is generated by the letters of the alphabet \(Y=Y_O=\{ y_g : g\in O\}\) subject to relations

Here \(\widetilde{O}=Y_O\) and there is a natural epimorphism \(\beta _O :\widetilde{G}\rightarrow G\) given by \(\beta _O (y_g)=g\).
Note also that a homomorphism of equipped groups \(f:(G_1,O_1)\rightarrow (G,O)\) induces a \(C\)-homomorphism \(\widetilde{f}:(\widetilde{G}_1,\widetilde{O}_1)\rightarrow (\widetilde{G},\widetilde{O})\) such that  .
.
Let the elements of a subset \(S\) of an equipment \(O\) of a group \(G\) generate the group \(G\) and \(O=S^G\), where \(S^G\) is the orbit of \(S\) under the action  . Denote by \({\mathbb {F}}_S\) a free group freely generated by the alphabet \(Y_S=\{ y_g : g\in S\}\) and by \(R_S\) the normal subgroup of \({\mathbb {F}}_S\) such that the natural epimorphism \(h_S:{\mathbb {F}}_S\rightarrow {\mathbb {F}}_S/R_S\simeq G\) gives a presentation of the group \(G\).
. Denote by \({\mathbb {F}}_S\) a free group freely generated by the alphabet \(Y_S=\{ y_g : g\in S\}\) and by \(R_S\) the normal subgroup of \({\mathbb {F}}_S\) such that the natural epimorphism \(h_S:{\mathbb {F}}_S\rightarrow {\mathbb {F}}_S/R_S\simeq G\) gives a presentation of the group \(G\).
Claim 2.6
Let \(\widetilde{R}_S\subset R_S\) be the normal subgroup normally generated by the elements of \(R_S\) of the form  , where \(w_{ij}\in {\mathbb {F}}_S\) and \(y_{g_i},y_{g_j}\in Y_S\). Then the \(C\)-group \((\widetilde{G},\widetilde{O})\) has the presentation \(\widetilde{G}\simeq {\mathbb {F}}_S/\widetilde{R}_S\) and the images of the elements of \(Y_S\) are \(C\)-generators of \(\widetilde{G}\).
, where \(w_{ij}\in {\mathbb {F}}_S\) and \(y_{g_i},y_{g_j}\in Y_S\). Then the \(C\)-group \((\widetilde{G},\widetilde{O})\) has the presentation \(\widetilde{G}\simeq {\mathbb {F}}_S/\widetilde{R}_S\) and the images of the elements of \(Y_S\) are \(C\)-generators of \(\widetilde{G}\).
Proof
Denote by \(G_1={\mathbb {F}}_S/\widetilde{R}_S\). By Claim 2.2, \(G_1\) is a \(C\)-group with \(C\)-equipment \(O_1=Y_S^{G_1}\) and there is a natural epimorphism \(\beta _S :(G_1,O_1)\rightarrow (G,O)\) given by \(\beta _S(y_g)=g\) for \(g\in S\).
Assume that \(S\) consists of elements \(g_1,\ldots ,g_n\in O\). If \(S\ne O\) then choose an element  . It is conjugated to some \(g_i\in S\). Denote by \(R_{g_{n+1}}\) the set of all presentations of \(g_{n+1}\) in the form
. It is conjugated to some \(g_i\in S\). Denote by \(R_{g_{n+1}}\) the set of all presentations of \(g_{n+1}\) in the form

Note that if

then  , that is,
, that is,

Similarly, if \(g_{n+1}=w_i(g_1,\ldots ,g_n)\) and  for some \(g_i,g_j\in S\), then
for some \(g_i,g_j\in S\), then

Therefore, if \(S_1=S\cup \{ g_{n+1}\}\), \({\mathbb {F}}_{S_1}\) is a free group freely generated by the alphabet \(Y_{S_1}=\{ y_g : g\in S_1\}\), \(R_{g_{n+1}}\) is the set of words of the form

defined by all relations (2), and \(\widetilde{R}_{S_1}\) is the normal closure in \({\mathbb {F}}_{S_1}\) of the set \(\widetilde{R}_S\cup R{g_{n+1}}\), then \(G_1\simeq {\mathbb {F}}_{S_1}/\widetilde{R}_{S_1}\) in view of relations (3) and (4).
Note that if we have a relation  for some \(g_i,g_j,g_k\in S_1\) then
for some \(g_i,g_j,g_k\in S_1\) then

If \(S_1\ne O\), then we can repeat the construction described above and obtain a presentation \(G_1\simeq {\mathbb {F}}_{S_2}/\widetilde{R}_{S_2}\), and so on. After several steps we obtain a presentation \(G_1\simeq {\mathbb {F}}_{O}/\widetilde{R}_{O}\). Note that, by induction, we deduce that for any relation in \(G\) of the form  for some \(g_i,g_j,g_k\in O\) we have
for some \(g_i,g_j,g_k\in O\) we have  . Therefore, there is a natural \(C\)-homomorphism \(f:(\widetilde{G},\widetilde{O})\rightarrow (G_1,O_1)\). By Claim 2.3, \(f\) is a \(C\)-isomorphism.\(\square \)
. Therefore, there is a natural \(C\)-homomorphism \(f:(\widetilde{G},\widetilde{O})\rightarrow (G_1,O_1)\). By Claim 2.3, \(f\) is a \(C\)-isomorphism.\(\square \)
For an equipped finite group \((G,O)\), consider a presentation of \(G\) of the following form. Let us take a free group \({\mathbb {F}}={\mathbb {F}}_O\) freely generated by the alphabet \(X_O=\{ x_g : g\in O\}\). Consider a normal subgroup \(R_O\subset {\mathbb {F}} \) such that \({\mathbb {F}}/R_O\simeq G\). Let \(h_O:{\mathbb {F}}\rightarrow {\mathbb {F}}/R_O\simeq G\) be the natural epimorphism.
We can associate to \((G,O)\) a group  . Denote by \(\alpha _O :\overline{G} \rightarrow G\) the natural epimorphism. By Claim 2.2, \((\overline{G}, \overline{O})\) is a \(C\)-group, where \(\overline{O}= h_O(X_O^{{\mathbb {F}}})\). Evidently, there is a natural epimorphism of \(C\)-groups \(\kappa _O:(\overline{G},\overline{O})\rightarrow (\widetilde{G},\widetilde{O})\) sending \(\kappa _O(x_g)=y_g\) for all \(g\in O\) and such that
. Denote by \(\alpha _O :\overline{G} \rightarrow G\) the natural epimorphism. By Claim 2.2, \((\overline{G}, \overline{O})\) is a \(C\)-group, where \(\overline{O}= h_O(X_O^{{\mathbb {F}}})\). Evidently, there is a natural epimorphism of \(C\)-groups \(\kappa _O:(\overline{G},\overline{O})\rightarrow (\widetilde{G},\widetilde{O})\) sending \(\kappa _O(x_g)=y_g\) for all \(g\in O\) and such that  . The \(C\)-group \((\overline{G},\overline{O})\) is called the universal central \(C\)
-extension of the equipped finite group \((G,O)\). It is easy to see that \(\alpha _O :\overline{G}\rightarrow G\) is a central extension of groups, that is, \(\ker \alpha _O\) is a subgroup of the center \(Z(\overline{G})\).
. The \(C\)-group \((\overline{G},\overline{O})\) is called the universal central \(C\)
-extension of the equipped finite group \((G,O)\). It is easy to see that \(\alpha _O :\overline{G}\rightarrow G\) is a central extension of groups, that is, \(\ker \alpha _O\) is a subgroup of the center \(Z(\overline{G})\).
We have

By Hopf’s integral homology formula, we have

Denote by \(h_2(G)\) the order of the group \(H_2(G,{\mathbb {Z}})\) and denote by \(K_{(G,O)}\) the subgroup of  generated by the elements of \(R_O\) of the form
generated by the elements of \(R_O\) of the form  , where \(g\in O\) and \(w\in {\mathbb {F}}\), and let \(k_{(G,O)}\) be its order.
, where \(g\in O\) and \(w\in {\mathbb {F}}\), and let \(k_{(G,O)}\) be its order.
Theorem 2.7
For an equipped finite group \((G,O)\) we have
Proof
We have \(\ker \kappa _O\subset \ker \alpha _O\). Therefore, \(\ker \kappa _O\subset Z(\overline{G})\). Let us show that for some \(n\geqslant 0\) there exist a sequence of \(C\)-groups \(\overline{G}_0={\mathbb {F}}/R_0,\ldots ,\overline{G}_n={\mathbb {F}}/R_n\), a sequence of \(C\)-homomorphisms

where  , and a \(C\)-homomorphism
, and a \(C\)-homomorphism  such that
such that
-
(i)
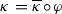 , where \(\varphi =\varphi _{n-1}\circ \cdots \circ \varphi _0\);
, where \(\varphi =\varphi _{n-1}\circ \cdots \circ \varphi _0\); -
(ii)
for each \(i\) the homomorphism
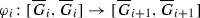 is an isomorphism;
is an isomorphism; -
(iii)
\(\overline{\kappa }_{*}\) induces a one-to-one correspondence between the connected components of the \(C\)-graphs \({\Gamma }_{(\overline{G}_n,\overline{O}_n)}\) and \({\Gamma }_{(\widetilde{G},\widetilde{O})}\).
Indeed, let us put \(R_0=R_O\) and consider the map \(\kappa _*\). If it induces a one-to-one correspondence between the connected components of the \(C\)-graphs \({\Gamma }_{(\overline{G},\overline{O})}\) and \({\Gamma }_{(\widetilde{G},\widetilde{O})}\), then \(n=0\) and it is nothing to prove.
Otherwise, for some \(g\in O\) there is a vertex \(v_{y_g}\) of \({\Gamma }_{(\widetilde{G},\widetilde{O})}\) whose preimage \(\kappa _*^{-1}(v_{y_g})\) contains at least two vertices, say \(v_{x_g}\) and \(v_{\,\overline{g}}\) (here \(\overline{g}\) is an element of \(X^{{\mathbb {F}}}\)), of \({\Gamma }_{(\overline{G},\overline{O})}\) belonging to different connected components of \({\Gamma }_{(\overline{G},\overline{O})}\).
Denote by \(R_1\) the normal closure of \(R_O\cup \{ x_g\overline{g}^{\,-1}\}\) in \({\mathbb {F}}\) and consider the natural homomorphism \(\varphi _0:\overline{G}\rightarrow \overline{G}_1={\mathbb {F}}/R_1\). The element \(x_g\overline{g}^{\,-1}\), considered as an element of \(\overline{G}\), belongs to \(\ker \kappa \). Therefore, \(x_g\overline{g}^{\,-1}\in Z(\overline{G})\).
Denote by \(\kappa _1:\overline{G}_1\rightarrow \widetilde{G}\) the homomorphism induced by \(\kappa \). By Lemma 2.4, the homomorphism \(\varphi _1\) is a \(C\)-homomorphism of \(C\)-groups. It is easy to see that  is an isomorphism and the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G}_1,\overline{O}_1)}\) is less than the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G},\overline{O})}\).
is an isomorphism and the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G}_1,\overline{O}_1)}\) is less than the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G},\overline{O})}\).
Assume now that \(\kappa _{1*}\) is not a one-to-one correspondence between the connected components of the \(C\)-graphs \({\Gamma }_{(\overline{G}_1,\overline{O}_1)}\) and \({\Gamma }_{(\widetilde{G},\widetilde{O})}\). Then for some \(g_1\in O\) there is a vertex \(v_{y_{g_1}}\) of \({\Gamma }_{(\widetilde{G},\widetilde{O})}\) which preimage \(\kappa _{1*}^{-1}(v_{y_{g_1}})\) contains at least two vertices \(v_{x_{g_1}}\) and \(v_{\,\overline{g}_1}\) of \({\Gamma }_{(\overline{G}_1,\overline{O}_1)}\) belonging to different connected components of \({\Gamma }_{(\overline{G}_1,\overline{O}_1)}\).
Hence we can repeat the construction described above and obtain a \(C\)-group  and \(C\)-homomorphisms \(\varphi _1:\overline{G}_1\rightarrow \overline{G}_2={\mathbb {F}}/R_2\), \(\kappa _2:\overline{G}_2\rightarrow \widetilde{G}\) such that
and \(C\)-homomorphisms \(\varphi _1:\overline{G}_1\rightarrow \overline{G}_2={\mathbb {F}}/R_2\), \(\kappa _2:\overline{G}_2\rightarrow \widetilde{G}\) such that  is an isomorphism and the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G}_2,\overline{O}_2)}\) is less than the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G}_1,\overline{O}_1)}\). Since the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G},\overline{O})}\) is finite, after several (\(n\)) steps of our construction we obtain the desired sequences of \(C\)-groups and \(C\)-homomorphisms.
is an isomorphism and the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G}_2,\overline{O}_2)}\) is less than the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G}_1,\overline{O}_1)}\). Since the number of connected components of the \(C\)-graph \({\Gamma }_{(\overline{G},\overline{O})}\) is finite, after several (\(n\)) steps of our construction we obtain the desired sequences of \(C\)-groups and \(C\)-homomorphisms.
Now, consider the \(C\)-homomorphism \(\overline{\kappa } :\overline{G}_n\rightarrow \widetilde{G}\). The \(C\)-graph \({\Gamma }_{(\widetilde{G},\widetilde{O})}\) consists of connected components \({\Gamma }_1,\ldots ,{\Gamma }_m\). Let \(\bigl \{v_{g_{i1}},\ldots , v_{g_{il_i}}\bigr \}\) be the set of the vertices of \({\Gamma }_i\). We have \(O=\{g_{ij}\}_{1\leqslant i\leqslant m, 1\leqslant j \leqslant l_i}\). Then \(\overline{{\Gamma }}_i=\overline{\kappa }_*^{\,-1}({\Gamma }_i)\) are the connected components of \({\Gamma }_{(\overline{G}_n,\overline{O}_n)}\). Let
Since the graph \(\overline{{\Gamma }}_i\) is connected, there are words \(w_{ijk}\) in letters of \(X_O\) and their inverses such that

Obviously, the elements  belong to
belong to  . Therefore, \(u_{ijk}\) as elements of \({\mathbb {F}}\) belong to
. Therefore, \(u_{ijk}\) as elements of \({\mathbb {F}}\) belong to  .
.
Consider the group \(\overline{G}_{n+1}={\mathbb {F}}/R_{n+1}\), where the group \(R_{n+1}\) is the normal closure of \(R_n\cup \{u_{ijk}\}_{1\leqslant i\leqslant m, 1\leqslant j\leqslant l_i, 1\leqslant k\leqslant r_{ij}}\) in \({\mathbb {F}}\). Then, by Claim 2.2, \(\overline{G}_{n+1}={\mathbb {F}}/R_{n+1}\) is a \(C\)-group and the natural map \(\overline{\kappa }_{1}:\overline{G}_{n+1}\rightarrow \widetilde{G}\), induced by \(\overline{\kappa }\), is a \(C\)-homomorphism. Moreover, \(\ker \varphi _{n}\) of the natural epimorphism \(\varphi _{n}:\overline{G}_n\rightarrow \overline{G}_{n+1}\) is a subgroup of  generated by the elements
generated by the elements  , where \(1\leqslant i\leqslant m\), \(1\leqslant j\leqslant l_i\), and \(1\leqslant k\leqslant r_{ij}\).
, where \(1\leqslant i\leqslant m\), \(1\leqslant j\leqslant l_i\), and \(1\leqslant k\leqslant r_{ij}\).
To complete the proof, it suffices to note that \(\overline{\kappa }_{1*}\) induces a one-to-one correspondence between the sets of vertices of the \(C\)-graphs \({\Gamma }_{(\overline{G}_{n+1},\overline{O}_{n+1})}\) and \({\Gamma }_{(\widetilde{G},\widetilde{O})}\), since all  belong to \(\ker \varphi _n\). Therefore, \(\overline{\kappa }_1\) is an isomorphism. \(\square \)
belong to \(\ker \varphi _n\). Therefore, \(\overline{\kappa }_1\) is an isomorphism. \(\square \)
Lemma 2.8
Let the order of \(g\in O\) be \(n\) and let  . Then the order of the element
. Then the order of the element  is a divisor of \(n\).
is a divisor of \(n\).
Proof
The elements \(x_g^n\) and  belong to the center of the group
belong to the center of the group  . Therefore,
. Therefore,

is the unity of  . \(\square \)
. \(\square \)
From Lemma 2.8 and Theorem 2.7 we have
Proposition 2.9
Let the equipment \(O\) of an equipped finite group \((G,O)\) consist of conjugacy classes of elements of orders coprime with \(h_2(G)\). Then \(a_{(G,O)}=h_2(G)\).
3 Proof of Theorem 1.1
By definition, the Bogomolov multiplier \(b_0(G)\) of a finite group \(G\) is the order of the group

where \(A\) runs over all abelian subgroups of \(G\).
Remark 3.1
Note that it suffices to consider only restrictions to abelian groups with two generators in order to determine that the element \(w\in H^2(G,{\mathbb {Q}}/{\mathbb {Z}}) \) is contained in \(B_0(G)\).
There is a natural duality between \(H^2(G,{\mathbb {Q}}/{\mathbb {Z}})\) and \(H_2(G,{\mathbb {Z}})\) since the groups \(Q/{\mathbb {Z}}\) and \(Z\) are Pontryagin dual (see, for example, [15]). Both groups are finite for finite groups \(G\) and hence the duality implies an isomorphism of \(H^2(G,{\mathbb {Q}}/{\mathbb {Z}})\) and  as abstract groups.
as abstract groups.
By Theorem 2.7, we have the inequality \(h_2(G)\geqslant a_{(G,O)}\) for any equipped finite group \((G,O)\). By [11, Corollary 2], we have \(a_{(G,O)}\geqslant a_{(G,G\setminus \{ 1\})}\) for each equipment \(O\) of \(G\). Therefore, to prove Theorem 1.1 it suffices to show that for the equipped finite group  its ambiguity index \(a_{(G,G\setminus \{ 1\})}\) is equal to \(b_0(G)\).
its ambiguity index \(a_{(G,G\setminus \{ 1\})}\) is equal to \(b_0(G)\).
In notation used in Sect. 2 and by Theorem 2.7, we have
where \(k_{(G,G\setminus \{ 1\})}\) is the order of the subgroup \(K_{G\setminus \{ 1\}}\) of the group

generated by the elements of \(R_{G\setminus \{ 1\}}\) of the form  , where
, where  and \(w\in {\mathbb {F}}_{G\setminus \{ 1\}}\).
and \(w\in {\mathbb {F}}_{G\setminus \{ 1\}}\).
Lemma 3.2
Let for some \(w_1,w_2\in {\mathbb {F}}_{G\setminus \{ 1\}}\) the commutator  belong to \(R_{G\setminus \{ 1\}}\). Then
belong to \(R_{G\setminus \{ 1\}}\). Then  , considered as an element of
, considered as an element of  , belongs to \(K_{G\setminus \{ 1\}}\).
, belongs to \(K_{G\setminus \{ 1\}}\).
Proof
First of all, note that if  , then
, then  in \(K_{G\setminus \{ 1\}}\), since \(K_{G\setminus \{ 1\}}\) is a subgroup of the center of the \(C\)-group
in \(K_{G\setminus \{ 1\}}\), since \(K_{G\setminus \{ 1\}}\) is a subgroup of the center of the \(C\)-group  and these four commutators are conjugated to each other in \({\mathbb {F}}_{G\setminus \{ 1\}}\). Similarly,
and these four commutators are conjugated to each other in \({\mathbb {F}}_{G\setminus \{ 1\}}\). Similarly,  , since
, since  is the inverse element to the element
is the inverse element to the element  . Note also that for any \(w_1\) the element
. Note also that for any \(w_1\) the element  belongs to \(K_{G\setminus \{ 1\}}\) if
belongs to \(K_{G\setminus \{ 1\}}\) if  .
.
Next, the elements \(w_1^{-1}\) and \(w_2^{-1}\), considered as elements of \(G\), are equal to some elements \(g_1\) and \(g_2\) of \(G\). Therefore, if  then
then

In addition, we have  and
and

Therefore,  (as an element of \(K_{G\setminus \{ 1\}}\)) is the inverse element to the element
(as an element of \(K_{G\setminus \{ 1\}}\)) is the inverse element to the element  and hence
and hence  . \(\square \)
. \(\square \)
To complete the proof of Theorem 1.1, note that, by Lemma 3.2, for each imbedding \(i:H\rightarrow G\) of an abelian group \(H\) generated by two elements the image of \(i_*:H_2(H,{\mathbb {Z}})\rightarrow H_2(G,{\mathbb {Z}})\) is a subgroup of \(K_{G\setminus \{ 1\}}\) and the group \(K_{G\setminus \{ 1\}}\) is generated by the images of such elements. Therefore, the group

coincides with the group \(B_0(G)\) and \(a_{(G,G\setminus \{ 1\})}=h_2(G)/k_{(G,G\setminus \{ 1\})}\). \(\square \)
4 Quasi-covers of equipped finite groups
In this section we use notation introduced in Sect. 2.
4.1 Definitions
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be a homomorphism of equipped groups. We say that \(f\) is a cover of equipped groups (or, equivalently, \((G_1,O_1)\) is a cover of \((G,O)\)) if
-
(i)
\(f\) is an epimorphism such that \(f(O_1)=O\);
-
(ii)
\(\ker f\) is a subgroup of the center \(ZG_1\) of \(G_1\);
-
(iii)
\(f_*:H_1(G_1,{\mathbb {Z}})\rightarrow H_1(G,{\mathbb {Z}})\) is an isomorphism.
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be a homomorphism of equipped finite groups. We say that \(S\subset O_1\) is a section of \(f\) if \(f_{|S}:S\rightarrow O\) is a one-to-one correspondence. Denote by \(O_S\subset O_1\) the orbit of \(S\) under the action of the group of the inner automorphisms of \(G_1\).
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be an epimorphism of equipped groups such that \(\ker f\subset ZG_1\). We say that \(f\) is a quasi-cover of equipped groups (or, equivalently, \((G_1,O_1)\) is a quasi-cover of \((G,O)\)) if there is a section \(S\) of \(f\) such that \(O_S=O_1\).
Below, we will assume that for a quasi-cover \(f\) of equipped groups a section \(S\) is chosen and fixed.
4.2 Properties of quasi-covers
Lemma 4.1
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be a cover of equipped finite groups and \(S\subset O_1\) a section. Then \(G_1\) is generated by the elements of \(S\).
Proof
Denote by \(G_{S}\) the subgroup of \(G_1\) generated by the elements of \(S\). Obviously, \(\varphi =f_{|G_{S}}:G_{S}\rightarrow G\) is an epimorphism and \(\ker \varphi \subset \ker f\subset ZG_1\). Therefore, to prove lemma it suffices to show that \(\ker f\subset G_{S}\). To show this, let us consider the natural epimorphism \(f_1:G_1\rightarrow G_2=G_1/\mathrm{ker}\, \varphi \) and the natural epimorphism \(\psi :G_2\rightarrow G\) induced by the cover \(f\). Obviously, \(\psi :(G_2,f_1(O_1))\rightarrow (G,O)\) is a cover of equipped finite groups and \(\psi _{|H}:H\rightarrow G\) is an isomorphism, where \(H=f_1(G_{S})\). Therefore, \(G_2\simeq \ker \psi \times G\). Consequently, \(\ker \psi =0\), since \(\psi _*:H_1(G_2,{\mathbb {Z}})\rightarrow H_1(G,{\mathbb {Z}})\) is an isomorphism and \(\ker \psi \) is an abelian group. \(\square \)
If \(S\) is a section of a cover \(f:(G_1,O_1)\rightarrow (G,O)\), then Lemma 4.1 implies that \(O_S=S^{G_1}\) is an equipment of \(G_1\) and \(f:(G_1,O_S)\rightarrow (G,O)\) is also a cover of equipped groups.
Below, we fix a section \(S\) of a cover \(f:(G_1,O_1)\rightarrow (G,O)\). Then the cover \(f\) can be considered as a quasi-cover.
In notation used in Sect. 2, consider the universal central \(C\)-extension  \({\rightarrow (G,O)}\) of an equipped finite group \((G,O)\). We have two natural epimorphisms \(h_O:{\mathbb {F}}_O\rightarrow G={\mathbb {F}}_O/R_O\) and
\({\rightarrow (G,O)}\) of an equipped finite group \((G,O)\). We have two natural epimorphisms \(h_O:{\mathbb {F}}_O\rightarrow G={\mathbb {F}}_O/R_O\) and  such that
such that  .
.
Lemma 4.2
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be a quasi-cover of equipped finite groups. Then there is an epimorphism  of equipped groups such that
of equipped groups such that  .
.
Proof
By Lemma 4.1, there is an epimorphism \(h_{S}:{\mathbb {F}}_O\rightarrow G_1\) defined by \(h_{S}(x_g)=\widehat{g}\in S\) for all \(g\in G\), where \(\widehat{g}= f_{|S}^{-1}(g)\). Denote by \(R_{S}=\ker h_{S}\). Obviously, we have  . Therefore, \(R_{S}\subset R_O\).
. Therefore, \(R_{S}\subset R_O\).
Let us show that the group  is a subgroup of \(R_{S}\). Indeed, consider any \(w\in R_O\). Then, as an element of \(G_1\), the element \(w\in \ker f\) and, consequently, \(w\) belongs to the center of \(G_1\). In particular, it commutes with any generator \(\widehat{g}\in S\) of \(G_1\) and hence
is a subgroup of \(R_{S}\). Indeed, consider any \(w\in R_O\). Then, as an element of \(G_1\), the element \(w\in \ker f\) and, consequently, \(w\) belongs to the center of \(G_1\). In particular, it commutes with any generator \(\widehat{g}\in S\) of \(G_1\) and hence  , that is,
, that is,  . The inclusion
. The inclusion  implies the desired epimorphism \(\alpha _{S}\). \(\square \)
implies the desired epimorphism \(\alpha _{S}\). \(\square \)
We say that a cover (respectively, a quasi-cover) of equipped finite groups \(f:(G_1,O_1)\rightarrow (G,O)\) is maximal if for any cover of equipped finite groups \(f_1:(G_2,O_2)\rightarrow (G_1,O_1)\) such that  is also a cover (respectively, quasi-cover) of equipped finite groups, the epimorphism \(f_1\) is an isomorphism.
is also a cover (respectively, quasi-cover) of equipped finite groups, the epimorphism \(f_1\) is an isomorphism.
Theorem 4.3
For any cover (respectively, quasi-cover) of equipped finite groups \(f:(G_1,O_1)\rightarrow (G,O)\), there is a maximal cover (respectively, quasi-cover) \(f_2:(G_2,O_2)\rightarrow (G,O)\) for which there is a cover \(f_1:(G_2,O_2)\rightarrow (G_1,O_S)\) such that
-
(i)
 ;
; -
(ii)
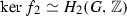 (respectively,
(respectively, 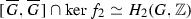 ).
).
Proof
Consider the epimorphism  defined in the proof of Lemma 4.2. The group \(\ker \alpha _{S}\) is a subgroup of the center of \(\overline{G}\).
defined in the proof of Lemma 4.2. The group \(\ker \alpha _{S}\) is a subgroup of the center of \(\overline{G}\).
Since  is a \(C\)-group and \(\overline{O}\) consists of \(M\) conjugacy classes, where \(M\leqslant |O|={\text {rk}}\, {\mathbb {F}}_O\), then
is a \(C\)-group and \(\overline{O}\) consists of \(M\) conjugacy classes, where \(M\leqslant |O|={\text {rk}}\, {\mathbb {F}}_O\), then  . Let \(\tau :\overline{G}\rightarrow {\mathbb {Z}}^M\) be the natural homomorphism (that is, \(\tau \) is the type homomorphism
. Let \(\tau :\overline{G}\rightarrow {\mathbb {Z}}^M\) be the natural homomorphism (that is, \(\tau \) is the type homomorphism  , see Sect. 1). The image \(\tau (\ker \alpha _{S})\) is a sublattice of maximal rank in \({\mathbb {Z}}^M\). Let us choose a \({\mathbb {Z}}\)-free basis \(a_1,\ldots , a_M\) in \(\tau (\ker \alpha _{S})\) and choose elements \(\overline{g}_i\in \ker \alpha _{S}\), \(1\leqslant i\leqslant M\), such that \(\tau (\overline{g}_i)=a_i\).
, see Sect. 1). The image \(\tau (\ker \alpha _{S})\) is a sublattice of maximal rank in \({\mathbb {Z}}^M\). Let us choose a \({\mathbb {Z}}\)-free basis \(a_1,\ldots , a_M\) in \(\tau (\ker \alpha _{S})\) and choose elements \(\overline{g}_i\in \ker \alpha _{S}\), \(1\leqslant i\leqslant M\), such that \(\tau (\overline{g}_i)=a_i\).
Denote by \(H_{S}\) a group generated by the elements \(\overline{g}_i\), \(1\leqslant i\leqslant M\), and denote by  . Then it is easy to see that \(H_S\simeq {\mathbb {Z}}^M\) is a subgroup of the center of \(\overline{G}\), the intersection
. Then it is easy to see that \(H_S\simeq {\mathbb {Z}}^M\) is a subgroup of the center of \(\overline{G}\), the intersection  is trivial, and
is trivial, and  .
.
Denote by \(G_2=\overline{G}/H_S\) the quotient group and by \(\alpha _{H_S}:\overline{G}\rightarrow G_2\) and \(f_1:G_2\rightarrow G_1\) the natural epimorphisms. We have  . Denote also by \(O_2=\alpha _{H_S}(\overline{O})\). Then it is easy to see that
. Denote also by \(O_2=\alpha _{H_S}(\overline{O})\). Then it is easy to see that  and \(f_1:(G_2,O_2)\rightarrow (G_1,O_S)\) are central extensions of equipped groups.
and \(f_1:(G_2,O_2)\rightarrow (G_1,O_S)\) are central extensions of equipped groups.
By construction, it is easy to see that  is trivial and \(\ker f_1\subset [G_1,G_1]\) is a subgroup of the center of \(G_1\). Therefore, the epimorphism \(f_1\) is a cover of equipped groups. In addition, it is easy to see that
is trivial and \(\ker f_1\subset [G_1,G_1]\) is a subgroup of the center of \(G_1\). Therefore, the epimorphism \(f_1\) is a cover of equipped groups. In addition, it is easy to see that  and
and  is a cover (respectively, quasi-cover) of equipped groups. We have
is a cover (respectively, quasi-cover) of equipped groups. We have

Therefore, if \(k_{f_i}=|{\ker }\, f_i|\), \(i=1,2\), is the order of the group \(\ker f_i\) and \(k_f\) is the order of \(\ker f\), then
Since we can repeat the construction described above to the cover (respectively, quasi-cover) \(f_2\) and applying again equality (5), where the new \(f\) is our \(f_2\) and the new \(f_1\) is a cover existence of which follows from assumption that the old \(f_2\) is not maximal, we obtain that the new \(f_1\) is an isomorphism, that is, the covering \(f_2\) is maximal. \(\square \)
In the case when  is an isomorphism of equipped finite groups, the maximal cover
is an isomorphism of equipped finite groups, the maximal cover  , constructed in the proof of Theorem 4.3, will be called a universal maximal cover.
, constructed in the proof of Theorem 4.3, will be called a universal maximal cover.
Corollary 4.4
For any equipped finite group \((G,O)\) there is a maximal cover of equipped groups. For any cover (respectively, quasi-cover) \(f:(G_1,O_1)\rightarrow (G,O)\) of equipped finite groups, \(k_f=|{\ker }\,f|\leqslant h_2(G)\) \((\)respectively, \(k_f=|{\ker }\,f\cap [G_1,G_1]|\leqslant h_2(G))\) and \(f\) is maximal if and only if \(k_f= h_2(G)\).
4.3 The ambiguity index of a quasi-cover of an equipped group
Let \((\widetilde{G}, \widetilde{O})\) be the \(C\)-group associated with an equipped group \((G,O)\) and \(\beta _O:(\widetilde{G}, \widetilde{O})\rightarrow (G,O)\) the natural epimorphism of equipped groups (see definitions in Sect. 2).
Theorem 4.5
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be a quasi-cover of equipped finite groups. Then there is a natural \(C\)-epimorphism  such that
such that  and
and  , where the \(C\)-epimorphism
, where the \(C\)-epimorphism  is defined in Sect. 2 and the \(C\)-epimorphism \(\widetilde{f}:(\widetilde{G}_1,\widetilde{O}_S)\rightarrow (\widetilde{G}, \widetilde{O})\) is associated with \(f\).
is defined in Sect. 2 and the \(C\)-epimorphism \(\widetilde{f}:(\widetilde{G}_1,\widetilde{O}_S)\rightarrow (\widetilde{G}, \widetilde{O})\) is associated with \(f\).
Proof
In notation used in the proof of Lemma 4.2, we have an inclusion \(R_S\subset R_O\) of normal subgroups of \({\mathbb {F}}_O\) which induces \(f:G_1={\mathbb {F}}_O/R_S\rightarrow G={\mathbb {F}}_O/R_O\).
Let \(\widetilde{R}_S\subset R_S\) be the normal subgroup normally generated by the elements of \(R_S\) of the form  , where \(w_{ij}\in {\mathbb {F}}_O\) and \(x_{g_i},x_{g_j}\in X_O\). For any \(w\in R_O\) and any generator \(x_g\), \(g\in O\), the commutator
, where \(w_{ij}\in {\mathbb {F}}_O\) and \(x_{g_i},x_{g_j}\in X_O\). For any \(w\in R_O\) and any generator \(x_g\), \(g\in O\), the commutator  , since \(f\) is a central extension of groups. Therefore,
, since \(f\) is a central extension of groups. Therefore,

By Claim 2.6, \(\widetilde{G}_1\simeq {\mathbb {F}}_S/\widetilde{R}_S\). Therefore, (6) induces an epimorphism  . Obviously, the \(C\)-epimorphism
. Obviously, the \(C\)-epimorphism  satisfies all properties claimed in Theorem 4.5. \(\square \)
satisfies all properties claimed in Theorem 4.5. \(\square \)
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be a cover (respectively, quasi-cover) of equipped finite groups and \(\widetilde{f}_S:(\widetilde{G}_1,\widetilde{O}_S)\rightarrow (\widetilde{G},\widetilde{O})\) a \(C\)-epimorphism associated with \(f:(G_1,O_S)\rightarrow (G,O)\). Denote by \(k_f\) the order of the group \(\ker f\cap [G_1,G_1]\) and by \(k_{\widetilde{f}_S}\) the order of the group \(\ker \widetilde{f}_S\cap [\widetilde{G}_1,\widetilde{G}_1]\).
Corollary 4.6
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be a quasi-cover of equipped finite groups, \(S\) a section of \(f\). Then

where \(k_S\) is the order of the group  .
.
Corollary 4.7
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be a cover (respectively, quasi-cover) of equipped finite groups, \(S\) a section of \(f\). Then for any equipment \(\widehat{O}\) of \(G_1\) (respectively, such that \(O_1\subset \widehat{O}\)) we have an inequality \(a_{(G_1,\widehat{O})}\leqslant h_2(G)\). If \(f\) is maximal, then \(a_{(G_1,\widehat{O})}=1\).
Proof
If \(f\) is a cover, then \(f:(G_1,\widehat{O})\rightarrow \bigl (G,f(\widehat{O})\bigr )\) is also a cover of equipped groups and \(a_{(G_1,\widehat{O})}\leqslant h_2(G)\) by Corollary 4.6.
As it was mentioned in Sect. 1, we have \(a_{(G_1,\widehat{O})}\leqslant a_{(G_1,O_1)}\) if \(O_1\subset \widehat{O}\) and if \(f\) is a quasi-cover, then \(a_{(G_1,O_1)}\leqslant h_2(G)\) by Corollary 4.6.
If \(f\) is maximal, then \(k_f=h_2(G)\) by Corollary 4.4 and, therefore, if \(f\) is a cover then \(f:(G_1,\widehat{O})\rightarrow \bigl (G,f(\widehat{O})\bigr )\) is also maximal. It follows from Corollary 4.6 that \(a_{(G_1,\widehat{O})}=1\) in the case of maximal covers, and \(a_{(G_1,\widehat{O})}\leqslant a_{(G_1,O_1)}=1\) in the case of maximal quasi-covers \(f\). \(\square \)
Let \(f:(G_1,O_1)\rightarrow (G,O)\) be a cover of equipped finite groups such that \(f^{-1}(O)=O_1\). We say that \(f\) splits over a conjugacy class \(C\subset O\) if \(f^{-1}(C)\) consists of at least two conjugacy classes of \(G_1\). The number \(s_{f}(C)\) of the conjugacy classes contained in \(f^{-1}(C)\) is called the splitting number of the conjugacy class \(C\) for \(f\). We say that \(f\) splits completely over \(C\) if \(s_f(C)=k_{f}\), where \(k_f=|{\ker }\,f|\).
Let \(C\) be a conjugacy class in \(G\). Consider the subgroups \(K_C\subset K_{G\setminus \{ 1\}}\) of the group

where \(K_C\) is generated by the elements of \(R_{G\setminus \{ 1\}}\) of the form  ,
,  . Let \(k_C\) be the order of the group \(K_C\).
. Let \(k_C\) be the order of the group \(K_C\).
Proposition 4.8
Let  be a universal maximal cover of equipped finite groups and let \(C\) be a conjugacy class in \(G\). Then
be a universal maximal cover of equipped finite groups and let \(C\) be a conjugacy class in \(G\). Then  .
.
Proof
For \(g\in C\) the preimage \(f^{-1}(C)\) consists of the conjugacy classes of the elements \(zx_g\), where

Note that \(\ker f\subset ZG_1\) and \(\ker f\) acts transitively on the set of the conjugacy classes \(C_1,\ldots , C_{k_f(C)}\) involving in \(f^{-1}(C)\), \(z(C_i)=C_j\) if \(z\overline{g}\in C_j\) for \(\overline{g}\in C_i\).
Let \(x_g\in C_1\), where \(g\in C\). Then \(z(C_1)=C_1\) if and only if for some \(w\in G_1\) we have \(wx_gw^{-1}=zx_g\), that is,  .
.
If \(f(w)=h\) then \(w=z_1x_{h}\) for some \(z_1\in \ker f\) and, therefore,  , that is, \(z\in K_C\). The converse statement that each element \(z\in K_C\) leaves fixed the conjugacy class \(C_1\) is obvious. \(\square \)
, that is, \(z\in K_C\). The converse statement that each element \(z\in K_C\) leaves fixed the conjugacy class \(C_1\) is obvious. \(\square \)
Proposition 4.9
Let  be a universal maximal cover of equipped finite groups. Then \(a_{(G,O)}=h_2(G)\) if and only if \(f\) splits completely over each conjugacy class \(C\subset O\). If \(s_f(C)=1\) for some conjugacy class \(C\subset O\) then \(a_{(G,O)}=1\).
be a universal maximal cover of equipped finite groups. Then \(a_{(G,O)}=h_2(G)\) if and only if \(f\) splits completely over each conjugacy class \(C\subset O\). If \(s_f(C)=1\) for some conjugacy class \(C\subset O\) then \(a_{(G,O)}=1\).
Proof
We have \(k_f=h_2(G)\). The map \(g \mapsto x_g\) is a section in \(O_1\). Denote by \(\overline{O}\) the equipment of \(G_1\) consisting of the elements conjugated to \(x_g\), \(g\in O\). Therefore,  is a maximal cover of equipped groups and Proposition 4.9 follows from Corollary 4.6. \(\square \)
is a maximal cover of equipped groups and Proposition 4.9 follows from Corollary 4.6. \(\square \)
Proposition 4.10
Let  be a universal maximal cover of equipped finite groups and let \(C_1\subset O\) and \(C_2\subset O\) be two conjugacy classes contained in an equipment of \(G\). Then \(a_{(G,O)}=1\) if \(s_f(C_1)\) and \(s_f(C_2)\) are coprime.
be a universal maximal cover of equipped finite groups and let \(C_1\subset O\) and \(C_2\subset O\) be two conjugacy classes contained in an equipment of \(G\). Then \(a_{(G,O)}=1\) if \(s_f(C_1)\) and \(s_f(C_2)\) are coprime.
Proof
The group \(\ker \widetilde{f}_S\cap [\widetilde{G}_1,\widetilde{G}_1]\subset H_2(G,\mathbb Z)\) contains two subgroups \(K_{C_1}\) and \(K_{C_2}\) whose indices in \(H_2(G,\mathbb Z)\) are coprime. This fact and Corollary 4.6 imply the statement. \(\square \)
Proposition 4.11
Let  be a universal maximal cover of equipped finite groups and let \(h_2(G)=pq\), where \(p\) and \(q\) are coprime integers. Let \(C_1\subset O\) be a conjugacy class such that \(s_f(C_1)=q\) and let \(s_f(C)\) be coprime with \(p\) for each conjugacy class \(C\subset O\). Then the ambiguity index \(a_{(G,O)}=p\).
be a universal maximal cover of equipped finite groups and let \(h_2(G)=pq\), where \(p\) and \(q\) are coprime integers. Let \(C_1\subset O\) be a conjugacy class such that \(s_f(C_1)=q\) and let \(s_f(C)\) be coprime with \(p\) for each conjugacy class \(C\subset O\). Then the ambiguity index \(a_{(G,O)}=p\).
Proof
Similarly, the statement follows from Corollary 4.6, since the group \(\ker \widetilde{f}_S\cap [\widetilde{G}_1, \widetilde{G}_1]\subset H_2(G,{\mathbb {Z}})\) is generated by subgroups \(K_{C_1}\) of index \(p\) in \(\ker f\) and subgroups of indices coprime to \(p\). \(\square \)
4.4 The ambiguity indices of symmetric groups and alternating groups
In [5], the following theorems were proved.
Theorem 4.12
([5, Theorem 3.8]) Let \(\widetilde{{\Sigma }}_d\) be a maximal cover of the symmetric group \({\Sigma }_d\). The conjugacy classes of \({\Sigma }_d\) which split in \(\widetilde{{\Sigma }}_d\) are: \((a)\) the classes of even permutations which can be written as a product of disjoint cycles with no cycles of even length; and \((b)\) the classes of odd permutations which can be written as a product of disjoint cycles with no two cycles of the same length (including \(1\)).
Theorem 4.13
([5, Theorem 3.9]) Let \(\widetilde{{\mathbb {A}}}_d\) be the maximal cover of the alternating group \({\mathbb {A}}_d\). The conjugacy classes of \({\mathbb {A}}_d\) which split in \(\widetilde{{\fancyscript{A}}_d}\) are: \((a)\) the classes of permutations whose decompositions into disjoint cycles have no cycles of even length; and \((b)\) the classes of permutations which can be expressed as a product of disjoint cycles with at least one cycle of even length and with no two cycles of the same length (including \(1\)).
Remind that, by definition, an equipment \(O\) of \({\Sigma }_d\) must contain a conjugacy class of odd permutation since the elements of the equipment must generate the group.
It is well known that for the symmetric group \({\Sigma }_d\), \(d\geqslant 4\), and for the alternating group \({\mathbb {A}}_d\), \(d\ne 6,7\), \(d\geqslant 4\), the order of the Schur multiplier \(h_2({\Sigma }_d)=h_2({\mathbb {A}}_d)=2\). The following theorems are straightforward consequences of Proposition 4.8 and Theorems 4.9–4.13.
Theorem 4.14
Let \(O\) be an equipment of a symmetric group \({\Sigma }_d\). Then \(a_{({\Sigma }_d,O)}=2\) if and only if \(O\) consists of conjugacy classes of odd permutations such that they can be written as a product of disjoint cycles with no two cycles of the same length (including \(1\)) and conjugacy classes of even permutations such that they can be written as a product of disjoint cycles with no cycles of even length. Otherwise, \(a_{({\Sigma }_d,O)}=1\).
Theorem 4.15
Let \(O\) be an equipment of an alternating group \({\mathbb {A}}_d\), \(d\ne 6,7\). Then \(a_{({\mathbb {A}}_d,O)}=2\) if and only if \(O\) consists of conjugacy classes of permutations whose decompositions into disjoint cycles have no cycles of even length and the classes of permutations which can be expressed as a product of disjoint cycles with at least one cycle of even length and with no two cycles of the same length (including \(1\)). Otherwise, \(a_{({\mathbb {A}}_d,O)}=1\).
It is well known that in the case when \(d= 6,7\), the order of the Schur multiplier \(h_2({\mathbb {A}}_d)=6\).
For \(\sigma \in {\mathbb {A}}_d\) denote by \(c(\sigma )=(l_1,\ldots , l_m)\) the cycle type of permutation \(\sigma \), that is, the collection of lengths \(l_i\) of non-trivial (that is \(l_i\geqslant 2\)) cycles entering into the factorization of \(\sigma \) as a product of disjoint cycles. For a conjugacy class \(C\) in \({\mathbb {A}}_d\) the collection \(c(C)=c(\sigma )\) is called the cycle type of \(C\) if \(\sigma \in C\). It is well known that the cycle type \(c(C)\) does not depend on the choice of \(\sigma \in C\) and there are at most two conjugacy classes in \({\mathbb {A}}_d\) of a given cycle type \(c\).
The group \({\mathbb {A}}_d\), \(d=6,7\), has the following non-trivial conjugacy classes:
-
(I)
two conjugacy classes of each cycle type \((5)\), \((2,4)\), and (if \(d=7\)) \((7)\);
-
(II)
two conjugacy classes of cycle type \((3)\) and one conjugacy class of cycle type \((3,3)\);
-
(III)
one conjugacy class of cycle type \((2,2)\) and one conjugacy class of cycle type \((2,2,3)\) if \(d=7\).
Proposition 4.16
The ambiguity index \(a_{({\mathbb {A}}_d,O)}\), \(d=6,7\), takes the following values:
- (I):
-
\(a_{({\mathbb {A}}_d,O)}=6\) if \(O\) contains only the elements of conjugacy classes of type (I);
- (II):
-
\(a_{({\mathbb {A}}_d,O)}=2\) if \(O\) contains only the elements of conjugacy classes of type (I) and the elements of at least one conjugacy class of type (II);
- (III):
-
\(a_{({\mathbb {A}}_d,O)}=3\) if \(O\) contains only the elements of conjugacy classes of type (I) and the elements of at least one conjugacy class of type (III);
- (II+III):
-
\(a_{({\mathbb {A}}_d,O)}=1\) if \(O\) contains the elements of at least one conjugacy class of type (II) and the elements of at least one conjugacy class of type (III).
Proof
Let  be the universal maximal cover. Note that, by [13], \(a_{({\mathbb {A}}_d,{\mathbb {A}}_d\setminus \{ 1\})}=1\). Therefore, there exist elements \(\sigma _1,\ldots ,\sigma _4\) in \({\mathbb {A}}_d\) such that
be the universal maximal cover. Note that, by [13], \(a_{({\mathbb {A}}_d,{\mathbb {A}}_d\setminus \{ 1\})}=1\). Therefore, there exist elements \(\sigma _1,\ldots ,\sigma _4\) in \({\mathbb {A}}_d\) such that  and
and  in
in  have, respectively, order two and three.
have, respectively, order two and three.
It is easy to see that for an element \(\sigma \) belonging to a conjugacy class \(C\) of type (I) the centralizer \(Z(\sigma )\subset {\mathbb {A}}_d\) of the element \(\sigma \) is a cyclic group generated by \(\sigma \). Therefore, \(K_C\) is the trivial group and hence \(s_f(C)=h_2({\mathbb {A}}_d)\). Therefore, by Proposition 4.9, \(a_{({\mathbb {A}}_d,O)}=6\) if \(O\) contains only the elements of conjugacy classes of type (I).
Let \(\sigma \) be of cycle type \((2,2,3)\). Without loss of generality, we can assume that \(\sigma =\sigma _1\sigma _2\), where \(\sigma _1=(1,2)(3,4)\) and \(\sigma _2=(5,6,7)\). Then the centralizer \(Z(\sigma )\subset {\mathbb {A}}_d\) of \(\sigma \) is  , where
, where  and \(\sigma _3=(1,3)(2,4)\). We have
and \(\sigma _3=(1,3)(2,4)\). We have  in the group
in the group  . Therefore \(K_C\), where \(C\) has type \((2,2,3)\), is a group of order at most two since the order of \(\sigma _1\) is two (see Lemma 2.8) and it is of order two if and only if
. Therefore \(K_C\), where \(C\) has type \((2,2,3)\), is a group of order at most two since the order of \(\sigma _1\) is two (see Lemma 2.8) and it is of order two if and only if  is not the unity in
is not the unity in  . But, the embeddings \(\langle \sigma _1,\sigma _3\rangle \subset {\mathbb {A}}_d\subset {\Sigma }_d\) define a sequence of homomorphisms
. But, the embeddings \(\langle \sigma _1,\sigma _3\rangle \subset {\mathbb {A}}_d\subset {\Sigma }_d\) define a sequence of homomorphisms
such that the image of the non-trivial element  in \(H_2(\langle \sigma _1,\sigma _3\rangle ,{\mathbb {Z}})\) is non-trivial in \(H_2({\Sigma }_d,{\mathbb {Z}})\). Therefore, \(s_f(C)=3\) for the conjugacy class \(C\) of cyclic type \((2,2,3)\) and, similarly, \(s_f(C)=3\) for the conjugacy class \(C\) of cyclic type \((2,2)\), since \(K_C\) is a subgroup of \(H_2({\mathbb {A}}_d,{\mathbb {Z}})\simeq {\mathbb {Z}}/6{\mathbb {Z}}\) generated by the elements of the second order (see Proposition 4.8) and only the elements of \(K_{C_1}\) and \(K_{C_2}\) can generate the subgroup of order two in \(H_2({\mathbb {A}}_d,{\mathbb {Z}})\).
in \(H_2(\langle \sigma _1,\sigma _3\rangle ,{\mathbb {Z}})\) is non-trivial in \(H_2({\Sigma }_d,{\mathbb {Z}})\). Therefore, \(s_f(C)=3\) for the conjugacy class \(C\) of cyclic type \((2,2,3)\) and, similarly, \(s_f(C)=3\) for the conjugacy class \(C\) of cyclic type \((2,2)\), since \(K_C\) is a subgroup of \(H_2({\mathbb {A}}_d,{\mathbb {Z}})\simeq {\mathbb {Z}}/6{\mathbb {Z}}\) generated by the elements of the second order (see Proposition 4.8) and only the elements of \(K_{C_1}\) and \(K_{C_2}\) can generate the subgroup of order two in \(H_2({\mathbb {A}}_d,{\mathbb {Z}})\).
Let \(\sigma \) be of cycle type \((3,3)\). Without loss of generality, we can assume that \(\sigma =\sigma _1\sigma _2\), where \(\sigma _1=(1,2,3)\) and \(\sigma _2=(4,5,6)\). Then the centralizer \(Z(\sigma )\subset {\mathbb {A}}_d\) of \(\sigma \) is  . Therefore,
. Therefore,  is not the unity in
is not the unity in  only if \(\overline{\sigma }=\sigma _1^{\pm 1}\), either \(\overline{\sigma }=\sigma _2^{\pm 1}\), or \(\overline{\sigma }= \sigma _1\sigma _2^{-1}\), or \(\overline{\sigma }= \sigma _1^{-1}\sigma _2\). We have
only if \(\overline{\sigma }=\sigma _1^{\pm 1}\), either \(\overline{\sigma }=\sigma _2^{\pm 1}\), or \(\overline{\sigma }= \sigma _1\sigma _2^{-1}\), or \(\overline{\sigma }= \sigma _1^{-1}\sigma _2\). We have

in  and, similarly,
and, similarly,  , since the elements
, since the elements  and
and  belong to the center of the group
belong to the center of the group  . Therefore, the group \(K_{C_1}\) is a non-trivial group of order three if and only if \(K_{C_2}\) is a non-trivial group of order three, where \(C_1\) is a conjugacy class of the cycle type \((3)\) and \(C_2\) is the conjugacy class of the cycle type \((3,3)\), and hence \(s_f(C_1)=s_f(C_2)=2\). Now Proposition 4.16 follows from Propositions 4.9–4.11. \(\square \)
. Therefore, the group \(K_{C_1}\) is a non-trivial group of order three if and only if \(K_{C_2}\) is a non-trivial group of order three, where \(C_1\) is a conjugacy class of the cycle type \((3)\) and \(C_2\) is the conjugacy class of the cycle type \((3,3)\), and hence \(s_f(C_1)=s_f(C_2)=2\). Now Proposition 4.16 follows from Propositions 4.9–4.11. \(\square \)
5 Cohomological description of the ambiguity indices
In notation used in Sect. 2, for an equipped finite group \((G,O)\) a subgroup \(K_{(G,O)}\) of \(H_2(G,{\mathbb {Z}})\) was defined as follows: \(K_{(G,O)}\) is the subgroup of  generated by the elements of \(R_O\) of the form
generated by the elements of \(R_O\) of the form  , where \(g\in O\) and \(w\in {\mathbb {F}}_O\), and \(k_{(G,O)}\) is its order.
, where \(g\in O\) and \(w\in {\mathbb {F}}_O\), and \(k_{(G,O)}\) is its order.
Denote

a subgroup of \(H^2(G,{\mathbb {Q}}/{\mathbb {Z}})\) dual to \(K_{(G,O)}\). As in the proof of Theorem 1.1, it is easy to show that

where \(A\) runs over all abelian subgroups of \(G\) generated by two elements \(g\in O\) and \(h\in G\). Let \(b_{(G,O)}\) be the order of the group \(B_{(G,O)}\). In particular, \(b_{(G,G\setminus \{ 1\})}=b_0(G)\).
The next theorem immediately follows from Theorem 2.7.
Theorem 5.1
For an equipped finite group \((G,O)\) we have \(a_{(G,O)}=b_{(G,O)}\).
The group \(H^2(G,{\mathbb {Q}}/{\mathbb {Z}})\) is a direct sum of primary components, \(H^2(G,{\mathbb {Q}}/{\mathbb {Z}}) = {\Sigma }_p H^2(G,{\mathbb {Q}}/{\mathbb {Z}})_{p}\), where primes \(p\) run through a subset of primes dividing the order of of \(H^2(G,{\mathbb {Q}}/{\mathbb {Z}})\) and hence \(G\). Therefore, we have the following
Proposition 5.2
If the set of conjugacy classes \(O\) consists of all classes of the elements of prime orders then \(a_{(G,O)}=b_0(G)\). Moreover, it is sufficient to consider such classes only for primes dividing \(h_2(G)\).
Note that \(H^2(G,{\mathbb {Q}}/{\mathbb {Z}})_{p}\) embeds into \(H^2(\mathrm{Syl}_p(G),{\mathbb {Q}}/{\mathbb {Z}})_{p}\) where \(\mathrm{Syl}_p(G)\) is a Sylow \(p\)-subgroup of \(G\). Similarly, the \(p\)-primary component \(B_0(G)_{p}\) is a subgroup of \(B_0(\mathrm{Syl}_p(G))\).
More explicit versions of Proposition 5.2 for different groups provide with simple methods to compute \(B_0(G)\).
6 An example of a finite group \(G\) with \(b_0(G)>1\)
The following groups were constructed in the article of Saltman [14]. Consider a finite \(p\)-group \(G_p\) of order \(p^9\) which is a central extension of \(A_p={\mathbb {Z}}_p^4\), where \({\mathbb {Z}}_p\) is a cyclic group of order \(p\). Denote the generators of \(A_p\) by \(x_i,i=1,\ldots ,4\). The center of \(G_p\) is generated by pairwise commutators  with one relation
with one relation  . Thus there is a natural exact sequence
. Thus there is a natural exact sequence
The following lemma first appeared in different notation in [14] and then in [1] in the current form.
Lemma 6.1
\(B_0(G_p)= {\mathbb {Z}}_p\).
Proof
It is shown in [1] that for a central extension \(G\) of an abelian group \(A\) the group \(B_0(G)\) is contained in the image of \(H^2(A,{\mathbb {Q}}/{\mathbb {Z}})\) in \(H^2(G,{\mathbb {Q}}/{\mathbb {Z}})\) under the cohomology map induced by projection \(\pi _A:G\rightarrow A\).
The proof is based on analysis of the standard spectral sequence with \(E_2^{pq}= H^p(A,H^q(K,{\mathbb {Q}}/{\mathbb {Z}}))\) converging to \(H^{p+q}(G,{\mathbb {Q}}/{\mathbb {Z}})\) for \(p+q=2\), where \(K\) is a kernel of \(\pi _A\).
The group \(H^2(A_p,{\mathbb {Q}}/{\mathbb {Z}}) = {\mathbb {Z}}_p^6\) and it is generated by elements  . The kernel of the map \(H^2(A_p,{\mathbb {Q}}/{\mathbb {Z}})\rightarrow H^2(G_p,{\mathbb {Q}}/{\mathbb {Z}})\) is Pontryagin dual to the center \({\mathbb {Z}}_p^5\) of \(G_p\). Thus the image of \(H^2(A_p,{\mathbb {Q}}/{\mathbb {Z}})\) in \(H^2(G_p,{\mathbb {Q}}/{\mathbb {Z}})\) is a cyclic \(p\)-group generated by one element \(w\).
. The kernel of the map \(H^2(A_p,{\mathbb {Q}}/{\mathbb {Z}})\rightarrow H^2(G_p,{\mathbb {Q}}/{\mathbb {Z}})\) is Pontryagin dual to the center \({\mathbb {Z}}_p^5\) of \(G_p\). Thus the image of \(H^2(A_p,{\mathbb {Q}}/{\mathbb {Z}})\) in \(H^2(G_p,{\mathbb {Q}}/{\mathbb {Z}})\) is a cyclic \(p\)-group generated by one element \(w\).
Let us show that \(w\) is in \(B_0(G_p)\). The element \(w\) defines an element in \(H^2(B,{\mathbb {Q}}/{\mathbb {Z}}) = {\mathbb {Z}}_p\) for any abelian subgroup \(B\subset G_p\) of rank \(2\). The fact that the element \(w\) is in \(B_0(G_p)\) is equivalent to the triviality of the restriction of \(w\) on any abelian subgroup \(B\subset G_p\) of rank \(2\) [1].
Since \(w\) is induced from \(A_p\) its restriction is automatically trivial on any such \(B\) with a projection \(\pi _A(B)\) contained in cyclic subgroup of \(A_p\). Thus it is enough to check that \(w\) is trivial on any abelian subgroup in \(G_p\) which surjects onto rank \(2\) subgroup \({\mathbb {Z}}_p^2\subset {\mathbb {Z}}_p^4= A_p\).
However, \(G_p\) does not contain such subgroups. Indeed, assume \(x_1,y_1\in G_p\) generate an abelian subgroup \(B\) of rank \(2\) in \(G_p\) which projects into the abelian rank \(2\) subgroup of \( A_p\) with generators \(x,y\). Then the commutator  is contained in the space of non-trivial relations for \(G_p\).
is contained in the space of non-trivial relations for \(G_p\).
We know, however, that the only non-trivial relation in \(G_p\) between commutators of elements in \(A_p\) is  . The element
. The element  in \({\mathbb {Z}}_p^6\) cannot be represented as
in \({\mathbb {Z}}_p^6\) cannot be represented as  for a pair \(x,y\in A_p\). Hence such a group \(B\) cannot exist and any abelian subgroup of \(G_p\) projects into a cyclic subgroup of \(A_p\). Therefore, \(w\) restricts trivially onto any abelian subgroup with two generators in \(G_p\) and \(w\) is contained \(B_0(G_p)\). Since \(w\) is non-trivial the group \(B_0(G_p)\) is non-trivial and equal to \({\mathbb {Z}}_p\).\(\square \)
for a pair \(x,y\in A_p\). Hence such a group \(B\) cannot exist and any abelian subgroup of \(G_p\) projects into a cyclic subgroup of \(A_p\). Therefore, \(w\) restricts trivially onto any abelian subgroup with two generators in \(G_p\) and \(w\) is contained \(B_0(G_p)\). Since \(w\) is non-trivial the group \(B_0(G_p)\) is non-trivial and equal to \({\mathbb {Z}}_p\).\(\square \)
References
Bogomolov, F.A.: The Brauer group of quotient spaces of linear representations. Math. USSR-Izv. 30(3), 455–485 (1988)
Bogomolov, F., Maciel, J., Petrov, T.: Unramified Brauer groups of finite simple groups of Lie type \(A_\ell \). Am. J. Math. 126(4), 935–949 (2004)
Clebsch, A.: Zur Theorie der Riemann’schen Fläche. Math. Ann. 6(2), 216–230 (1873)
Fulton, W.: Hurwitz schemes and irreducibility of moduli of algebraic curves. Ann. Math. 90(3), 542–575 (1969)
Hoffman, P.N., Humphreys, J.F.: Projective Representations of the Symmetric Groups. In: Oxford Mathematical Monographs. Clarendon Press/Oxford University Press, New York (1992)
Hurwitz, A.: Ueber Riemann’sche Flächen mit gegebenen Verzweigungspunkten. Math. Ann. 39(1), 1–60 (1891)
Jezernik, U., Moravec, P.: Universal commutator relations, Bogomolov multipliers, and commuting probability. arXiv:1307.6533 (2013)
Kang, M., Kunyavskiĭ, B.: The Bogomolov multiplier of rigid finite groups. Arch. Math. (Basel) 102(3), 209–218 (2014)
Kulikov, Vik.S.: Hurwitz curves. Rus. Math. Surv. 62(6), 1043–1119 (2007)
Kulikov, Vik.S.: Factorization semigroups and irreducible components of the Hurwitz space. II. Izv. Math. 76(2), 356–364 (2012)
Kulikov, Vik.S.: Factorizations in finite groups. Sb. Math. 204(2), 237–263 (2013)
Kulikov, Vik.S., Kharlamov, V.M.: Covering semigroups. Izv. Math. 77(3), 594–626 (2013)
Kunyavskiĭ, B.: The Bogomolov multiplier of finite simple groups. In: Cohomological and Geometric Approaches to Rationality Problems. Progress in Mathematics, vol. 282, pp. 209–217. Birkhäuser, Boston (2010)
Saltman, D.J.: Noether’s problem over an algebraically closed field. Invent. Math. 77(1), 71–84 (1984)
Spanier, E.H.: Algebraic Topology. Springer, New York (1981)
Author information
Authors and Affiliations
Corresponding author
Additional information
The financial support from the Government of the Russian Federation within the framework of the implementation of the 5-100 Programme Roadmap of the National Research University, Higher School of Economics, AG Laboratory is acknowledged by both authors. The first author was also supported by Simons Travel Grant. The second author was partially supported by NSh-2998.2014, RFBR 14-01-00160.
Rights and permissions
About this article
Cite this article
Bogomolov, F.A., Kulikov, V.S. The ambiguity index of an equipped finite group. European Journal of Mathematics 1, 260–278 (2015). https://doi.org/10.1007/s40879-014-0015-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-014-0015-3




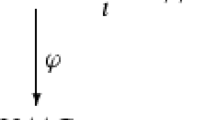
 belongs to the center
belongs to the center 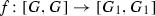 is an isomorphism.
is an isomorphism.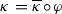 , where
, where 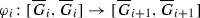 is an isomorphism;
is an isomorphism; ;
;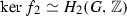 (respectively,
(respectively, 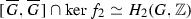 ).
).