Introduction

Spherical cavity-expansion (SCE) and cylindrical cavity expansion (CCE) approximations have been developed and successfully employed for deep penetration and ductile hole growth perforation problems respectively (see Johnsen et al. [1]). Bishop et al. [2] developed equations for the quasi-static SCE and CCE problems, where they assumed the plastic region of the solid materials to have linear hardening with no volume change (incompressible), and the elastic region to follow Hooke’s law with Young’s modulus E, and Poisson’s ratio \(\nu\). These solutions were used to estimate the forces acting on conical-nose punches pushed quasi-statically into metal targets. When linear strain hardening was employed, the plastic region must be considered incompressible for both the SCE and CCE problems. The reason for this was because if elastic compressibility is considered in the plastic region with strain hardening, hydrostatic stress terms appear explicitly in the strain hardening term. Therefore, closed-form analytical solutions were not possible with an elastically compressible linear hardening plastic region, and numerical formulations are required to obtain solutions.

In Crozier and Hunter [3], a similarity transformation method (this method requires the problem to be self-similar with no length scales) was employed with analytical expressions for the coupled nonlinear conservation of mass and momentum equations. In that study, a plane strain solution for the radial stress \(\sigma_{r}\) acting at the cavity surface for the dynamic CCE problem was obtained, where the solid material was assumed to be elastically compressible and perfectly plastic. Comparable similarity transformation methods have previously been employed with elastically compressible perfectly plastic SCE problems in [4] and [5]; however, the CCE problem is significantly more complex, and must be solved in cylindrical and not spherical coordinates. For the CCE similarity transformation solutions, it is assumed that a cylindrical cavity is expanded from a zero initial radius at a constant expansion velocity V in a homogeneous isotropic plane strain material of infinite extent such that no length scales are associated with the problem. Additionally, it has been shown in [3] that a fully incompressible CCE solution is generally not attainable due to the logarithmic singularity associated with the integration of the conservation of linear momentum inertia term in the elastic region at infinity.

Using the similarity transformation method similar to that proposed in [3], Forrestal et al. [6] obtained a closed form dynamic plane strain CCE solution for the radial stress \(\sigma_{r}\) acting at the cavity surface along with the elastic–plastic interface velocity for homogeneous and isotropic power-law strain hardening materials. This CCE solution was then employed with Newton’s second law giving the CCE approximation used to obtain ballistic limit and residual velocities for ductile hole growth perforation of aluminum plates by conical-nose projectiles. However, due to the logarithmic singularity at infinity associated with the incompressible elastic region solution, the elastic region had to be assumed compressible [3]. Additionally, the power-law strain hardening material requires the plastic region to be modeled as incompressible due to the hydrostatic stress term required in the strain hardening constitutive model. The problems associated with fully elastically compressible quasi-static strain hardening SCE and CCE solutions are discussed by Hill [7], and for the dynamic SCE solution by Hopkins [8]. In both of these studies, elastically compressible strain hardening solutions were never obtained. Eventually though, the dynamic elastically compressible strain hardening SCE probem was solved by Luk et al. [9] using a small arc process with a predictor corrector ordinary differential equation (ODE) solver. An additional problem that is also associated with the CCE solution obtained in [6] is that it eventually reaches a critical expansion velocity, at which point the solution becomes complex and physically unrealistic.

In Warren [10], both power-law strain hardening and power-law strain rate effects were included in the total strain constitutive model for the incompressible plastic region. However, since strain rate effects introduce a length scale, a similarity transformation solution for the incompressible plastic region was not possible. However, because the plastic region was assumed incompressible, the conservation of mass equation is uncoupled from the conservation of linear momentum equation, and is directly integrated. Results from the conservation of mass integration were then used to directly integrate the conservation of linear momentum equation giving the radial stress at the cavity surface \(\sigma_{r} \left( a \right)\) along with the elastic–plastic interface velocity c. For the compressible elastic region, material density was assumed constant, and the convective acceleration and velocity terms were assumed negligible along with strain rate effects. Results from [10] illustrate that strain rate effects increase the magnitude of the radial stress at the cavity surface, and if neglected, the solution reduces to that obtained in [6].

Numerous studies published in open literature [1, 11,12,13,14] have utilized the dynamic homogeneous and isotropic plane strain CCE solution with strain hardening as derived in [6] using the required assumptions for the plastic and elastic regions. The CCE solution obtained in [6] is employed with Newton’s second law in the cylindrical radial direction giving the CCE approximation for ductile hole growth perforation of ductile targets by assorted projectiles. The goal of the CCE approximation is to estimate values for the ballistic limit, and residual velocities for ductile targets struck by projectiles with various geometries and material properties. In [1], the associated target penetration and/or perforation was modeled using rigid projectiles, and strain hardening or perfectly plastic constitutive models for the target materials. In Børvik et al. [11] and [12], the CCE approximation was employed to study the perforation of AA5083-H116 aluminum alloy plates struck by conical and ogive-nose long steel rods and APM2 bullets. The same strain hardening model in the present study was also used with the CCE approximation ductile hole growth perforation in [11] and [12]. Similar studies using 7075-T651 and 6082-T651 aluminum alloy plates struck by APM2 bullets were also modeled using the CCE approximation in [11], and results are given in references [13, 14].

In [15], SCE simulations using a two-dimensional axisymmetric explicit transient dynamic FEM was employed using an incremental geomaterial constitutive model that could not be used with analytical formulations. These simulations required using a very small initial spherical cavity expanded over a wide range of expansion velocities V applied to the surface nodes of the initial spherical cavity. Warren et al. [15] observed that the radial stress at the cavity surface was initially less than that which would be obtained from a similarity transformation analytical formulation with a zero initial radius. However, with the FEM formulation in [15] the radial stress at the cavity surface quickly converges approximately to the desired self-similar result that would be obtained from a elastically compressible similarity transformation formulation (which is not possible with the proposed incremental geomaterial constitutive model) for all expansion velocities considered.

The main objective of the present study is to ascertain the effect of assuming an incompressible strain hardening plastic region, and a compressible elastic region for analytical solutions for dynamic CCE problems. The quantification of these assumptions is achieved by comparing similarity transformation analytical results and FE simulations for the radial stress \(\sigma_{r} (a)\) at the cavity surface of cylindrical cavities being opened from a zero or an extremely small cylindrical cavity radius at constant expansion velocities V. It is shown that the FE simulations that start with an extremely small cylindrical cavity radius converge to values for the radial stress \(\sigma_{r} (a)\) independent of the cavity radius a as with the analytical results obtained using a similarity transformation. Furthermore, since the bulk wave speed is independent of strain hardening, the elastic–plastic interface velocity c is also independent of the cavity radius a and of strain hardening; thus it is shown that the elastic–plastic wave speed c from the strain hardening FE simulations and perfectly plastic FE simulations asymptote the bulk wave speed obtained from the elastically compressible perfectly plastic material numerical solution based on an analytical formulation using a similarity transformation as done in [16].

Results from this study illustrate the effect of assuming an incompressible power-law hardening plastic region, and a compressible linear elastic region on the closed form analytical dynamic CCE solutions. These solutions are commonly employed with the CCE approximation to determine the ballistic limit and residual velocities for ductile hole growth perforation problems. In addition, these results also provide a quantitative measure of the error introduced by assuming an incompressible plastic region for strain hardening target materials.

Analytical Power-Law Strain Hardening CCE Solution

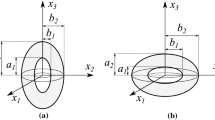
For the solution of this problem, a homogeneous, isotropic, strain hardening, and cylindrically symmetric cavity is expanded from a zero initial radius to a radius a at a constant expansion velocity V in a medium of infinite extent as illustrated in Fig. 1. This expansion produces both plastic and elastic response regions. The assumed incompressible plastic region is bounded by the radii r = a and r = b, where r is the radial Eulerian coordinate, b = ct is the elastic–plastic interface position, t is time, and c is the elastic–plastic interface velocity. Additionally, the linear elastic region is assumed to be compressible, and is bounded by r = b and r = d, where \(d = c_{d} t\) with \(c_{d}\) being the elastic dilatational wave speed. From [6], the equations for momentum and mass conservation in Eulerian coordinates with cylindrical symmetry for both response regions are given as

$$\frac{{\partial \sigma_{r} }}{\partial r} + \frac{{\left( {\sigma_{r} - \sigma_{\theta } } \right)}}{r} = - \rho \left( {\frac{\partial \upsilon }{{\partial t}} + \upsilon \frac{\partial \upsilon }{{\partial r}}} \right)$$
(1a)
$$\rho_{o} \frac{\partial }{\partial r}\left[ {\left( {r - u} \right)^{2} } \right] = 2r\rho ,$$
(1b)
Fig. 1
figure 1

Response regions for the cylindrical cavity-expansion problem

Full size image

where \(\sigma_{r}\) and \(\sigma_{\theta }\) are the radial and circumferential components of the true Cauchy stress measured positive in compression, \(\rho_{o}\) and \(\rho\) are material densities in the undeformed and deformed configurations, u and \(\upsilon\) are particle displacement and velocity in the radial direction with outward motion measured positive, and are related by the material time derivative of the radial particle displacement which can be expressed as

$$\frac{\partial u}{{\partial t}} = \upsilon \left( {1 - \frac{\partial u}{{\partial r}}} \right).$$
(2)

Furthermore, due to proportional (radial) loading conditions with the proposed CCE problem, total strains are employed which eliminates the need for an incremental stress–strain formulation.

Incompressible Plastic Region

In the incompressible plastic region \(a \le r \le b\), the true logarithmic strain–displacement relations for radial and circumferential strains are given by

$$\varepsilon_{r} = \ln \left( {1 - \frac{\partial u}{{\partial r}}} \right)$$
(3a)
$$\varepsilon_{\theta } = \ln \left( {1 - \frac{u}{r}} \right),$$
(3b)

respectively. For an incompressible material, \(\rho\) = \(\rho_{o}\), and in cylindrical coordinates under plane strain conditions, \(\varepsilon_{z} = 0\) giving \(\varepsilon_{r} = - \varepsilon_{\theta }\).

We fit the homogeneous isotropic linear elastic (using Hooke’s law) and power-law strain hardening equations to a universal experimental uniaxial stress–strain curve given by

$$\sigma = \left\{ {\begin{array}{ll} {E\varepsilon ,} & {\sigma \le Y} \\ {Y\left( {\frac{{E\varepsilon }}{Y}} \right)^{n} ,} & {\sigma > Y} \\ \end{array} } \right.,$$
(4a,b)

where \(\sigma\) and \(\varepsilon\) are the uniaxial true Cauchy stress and true strain respectively, E is Young’s modulus, Y is the quasi-static yield strength, and n is the strain hardening exponent.

For an incompressible material under plane strain conditions, we assume \(\sigma_{z} = {{\left( {\sigma_{r} + \sigma_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{r} + \sigma_{\theta } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\) as discussed in [6]. From this assumption, the equivalent strain \(\overline{\varepsilon }\) and the von Mises stress \(\overline{\sigma }\) are related to the true principal radial strain and true principal Cauchy stress difference by

$$\overline{\varepsilon } = \frac{2}{\sqrt 3 }\varepsilon_{r}$$
(5a)
$$\overline{\sigma } = \frac{\sqrt 3 }{2}\left( {\sigma_{r} - \sigma_{\theta } } \right).$$
(5b)

Substuting Eqs. (5a, 5b) into (4b) gives the principal stress difference

$$\sigma_{r} - \sigma_{\theta } = \left( {\frac{2}{\sqrt 3 }} \right)^{1 + n} Y\left[ {\frac{{E\varepsilon_{r} }}{Y}} \right]^{n} ,$$
(6)

and at the elastic–plastic interface, there is no strain hardening; therefore, \(\sigma_{r} - \sigma_{\theta } = {{2Y} \mathord{\left/ {\vphantom {{2Y} {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}\). Due to the self-similarity of the problem, we implement a similarity transformation in the plastic region as done in [6] with the dimensionless similarity transformation variable

$$\xi = \frac{r}{ct},$$
(7a)

along with the additional dimensionless variables

$$S = \frac{{\sigma_{r} }}{Y},\,\,\,\,U = \frac{\upsilon }{c},\,\,\,\,\overline{u} = \frac{u}{ct},\,\,\,\gamma = \frac{V}{c},$$
(7b–e)

where c is the elastic–plastic interface velocity, S is the dimensionless radial stress, U is the dimensionless particle velocity, \(\overline{u}\) is the dimensionless particle displacement, and γ is the dimensionless cavity-expansion velocity. Eliminating \(\sigma_{\theta }\) from Eq. (1a) with Eqs. (3a) and (6), and using Eq. (7a–e) transforms the partial differential equation (PDE) for conservation of linear momentum in Eq. (1a) to the ODE

$$\frac{\mathrm{d}S}{{\mathrm{d}\xi }} = - \left( {\frac{2}{\sqrt 3 }} \right)^{1 + n} \left( \frac{E}{Y} \right)\frac{1}{\xi }\left[ {\ln \left( {1 - \frac{{\mathrm{d}\overline{u}}}{\mathrm{d}\xi }} \right)} \right]^{n} + \frac{{\rho_{o} c^{2} }}{Y}\left( {\xi - U} \right)\frac{\mathrm{d}U}{{\mathrm{d}\xi }},$$
(8)

where \(\gamma \le \xi \le 1\). Next, Eqs. (7a–e) transforms conservation of mass in Eq. (1b), and the material time derivative in Eq. (2) to

$$\frac{\mathrm{d}}{\mathrm{d}\xi }\left[ {\left( {\xi - \overline{u}} \right)^{2} } \right] = 2\xi$$
(9a)
$$U\left( {1 - \frac{{\mathrm{d}\overline{u}}}{\mathrm{d}\xi }} \right) = \overline{u} - \xi \frac{{\mathrm{d}\overline{u}}}{\mathrm{d}\xi }.$$
(9b)

At the cavity surface, the boundary condition is

$$\overline{u}\left( {\xi = \gamma } \right) = \gamma .$$
(10)

Solving Eq. (9a) subject to the boundary condition in Eq. (10) gives the solution

$$\overline{u} = \xi - \left( {\xi^{2} - \gamma^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} .$$
(11)

Substituting Eqs. (11) into (9b) gives

$$U = \frac{{\gamma^{2} }}{\xi }.$$
(12)

Next, substituting Eqs. (11) and (12) into Eq. (8) gives the dimensionless radial stress as

$$\begin{gathered} S\left( \xi \right) = S\left( 1 \right) + \frac{2}{\sqrt 3 }\left[ {\frac{E}{\sqrt 3 Y}} \right]^{n} \int_{\xi }^{1} {\frac{1}{\xi }} \left[ {\ln \left( {\frac{{\xi^{2} }}{{\xi^{2} - \gamma^{2} }}} \right)} \right]^{n} \mathrm{d}\xi \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{\rho_{o} V^{2} }}{2Y}\left[ {\gamma^{2} - 2\ln \xi - \frac{{\gamma^{2} }}{{\xi^{2} }}} \right], \hfill \\ \end{gathered}$$
(13)

where \(S\left( 1 \right)\), and \(c\) are obtained from the solution of Eq. (1a) in the compressible linear elastic region.

Compressible Linear Elastic Region

In the compressible linear elastic region \(b \le r \le d\), the solution for the dimensionless radial stress is obtained using the method in [6]. For this problem, the material is assumed to obey Hooke’s law. Additionally, plane strain and small strains are assumed where \(\varepsilon_{z}\) = 0 and

$$\varepsilon_{r} = - \frac{\partial u}{{\partial r}}$$
(14a)
$$\varepsilon_{\theta } = - \frac{u}{r}.$$
(14b)

Using Hooke’s law, stress–strain relations are obtained as

$$\sigma_{r} = \overline{\lambda }(\varepsilon_{r} + \varepsilon_{\theta } ) + 2\overline{\mu }\varepsilon_{r}$$
(15a)
$$\sigma_{\theta } = \overline{\lambda }(\varepsilon_{r} + \varepsilon_{\theta } ) + 2\overline{\mu }\varepsilon_{\theta }$$
(15b)
$$\sigma_{z} = \overline{\lambda }(\varepsilon_{r} + \varepsilon_{\theta } ),$$
(15c)

where \(\overline{\lambda }\) and \(\overline{\mu }\) are the Lamé elastic constants, and are defined in terms of Young’s modulus E and Poisson’s ratio \(\nu\) by

$$\overline{\lambda } = \frac{\nu E}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}$$
(16a)
$$\overline{\mu } = \frac{E}{{2\left( {1 + \nu } \right)}}.$$
(16b)

Substituting Eqs. (15a, 15b, 15c) and (16a, 16b) into (1a), and neglecting the convective acceleration and velocity terms, along with assuming the material has a negligible change in material density \((\rho \approx \rho_{o} )\) gives

$$- \left( {\overline{\lambda } + 2\overline{\mu }} \right)\frac{{\partial^{2} u}}{{\partial r^{2} }} - \left( {\overline{\lambda } + 2\overline{\mu }} \right)\left[ {\frac{1}{r}\frac{\partial u}{{\partial r}} - \frac{u}{{r^{2} }}} \right] = - \rho_{o} \frac{{\partial^{2} u}}{{\partial t^{2} }}.$$
(17)

Using the dilatational wave speed given by \(c_{d}^{2} = {{\left( {\overline{\lambda } + 2\overline{\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {\overline{\lambda } + 2\overline{\mu }} \right)} {\rho_{o} }}} \right. \kern-\nulldelimiterspace} {\rho_{o} }}\) in Eq. (17) gives the PDE for conservation of linear momentum in terms of the displacement u, radial coordinate r, and time t as

$$\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{{\partial r}} - \frac{u}{{r^{2} }} = \frac{1}{{c_{d}^{2} }}\frac{{\partial^{2} u}}{{\partial t^{2} }}.$$
(18)

From self-similarity, the PDE given by Eq. (18) is also solved using a similarity transformation with the transformation variable in Eq. (7a), the dimensionless variables in Eqs. (7b–e), and also the ratio

$$\alpha = \frac{c}{{c_{d} }}.$$
(19)

Using Eqs. (7a–e) and (19) in Eq. (18) transforms the PDE equation for linear momentum to the second order ODE

$$\left( {1 - \alpha^{2} \xi^{2} } \right)\frac{{\mathrm{d}^{2} \overline{u}}}{{\mathrm{d}\xi^{2} }} + \frac{1}{\xi }\frac{{\mathrm{d}\overline{u}}}{\mathrm{d}\xi } - \frac{{\overline{u}}}{{\xi^{2} }} = 0.$$
(20)

Applying reduction of order as done in [1], with boundary conditions

$$\overline{u}\left( {{1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha }} \right) = 0$$
(21a,b)
$$\sigma_{r} \left( {\xi = 1} \right) - \sigma_{\theta } \left( {\xi = 1} \right) = \frac{2Y}{{\sqrt 3 }}$$

gives the dimensionless radial stress S, particle velocity U, and displacement \(\overline{u}\) in the linear elastic region \(1 \le \xi \le {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha }\) as

$$S\left( \xi \right) = \frac{{\alpha^{2} }}{{\sqrt 3 \left( {1 - 2\nu } \right)\sqrt {1 - \alpha^{2} } }}\left[ {\ln \left( {\frac{{1 + \sqrt {1 - \alpha^{2} \xi^{2} } }}{\alpha \xi }} \right) + \frac{{\left( {1 - 2\nu } \right)\sqrt {1 - \alpha^{2} \xi^{2} } }}{{\alpha^{2} \xi^{2} }}} \right]$$
$$U\left( \xi \right) = \frac{{2Y\left( {1 + \nu } \right)\sqrt {1 - \alpha^{2} \xi^{2} } }}{{\sqrt 3 E\sqrt {1 - \alpha^{2} } }}$$
(22a–c)
$$\overline{u}\left( \xi \right) = \frac{{Y\left( {1 + \nu } \right)}}{{\sqrt 3 \left( {1 - 2\nu } \right)\sqrt {1 - \alpha^{2} } }}\left[ {\frac{{\sqrt {1 - \alpha^{2} \xi^{2} } }}{\xi } - \xi \alpha^{2} \ln \left( {\frac{{1 + \sqrt {1 - \alpha^{2} \xi^{2} } }}{\alpha \xi }} \right)} \right],$$

and at the elastic–plastic interface \(\xi = 1,\)

$$S\left( 1 \right) = \frac{{\alpha^{2} }}{{\sqrt 3 \left( {1 - 2\nu } \right)\sqrt {1 - \alpha^{2} } }}\left[ {\ln \left( {\frac{{1 + \sqrt {1 - \alpha^{2} } }}{\alpha }} \right) + \frac{{\left( {1 - 2\nu } \right)\sqrt {1 - \alpha^{2} } }}{{\alpha^{2} }}} \right]$$
$$U\left( 1 \right) = \frac{{2Y\left( {1 + \nu } \right)}}{\sqrt 3 E}$$
(23a–c)
$$\overline{u}\left( 1 \right) = \frac{{Y\left( {1 + \nu } \right)}}{{\sqrt 3 \left( {1 - 2\nu } \right)\sqrt {1 - \alpha^{2} } }}\left[ {\sqrt {1 - \alpha^{2} } - \alpha^{2} \ln \left( {\frac{{1 + \sqrt {1 - \alpha^{2} } }}{\alpha }} \right)} \right].$$

Response Equations

With the assumption of a constant material density \(\rho_{o}\) in both the plastic and elastic regions, the radial stress, particle velocity, and particle displacement are continuous across the elastic–plastic interface through the Rankine-Hugoniot jump conditions for mass and momentum conservation as discussed in [3].

The elastic-plastic interface velocity c is obtained using Eqs. (12) and (23b) at \(\xi = 1\) in terms of the cavity-expansion velocity V from

$$\gamma = \frac{V}{c} = \left[ {\frac{\sqrt 3 E}{{2\left( {1 + \nu } \right)Y}}} \right]^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}} .$$
(24)

Substituting Eqs. (23a) in (13) gives the dimensionless radial stress in the plastic region as

$$\begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,S\left( \xi \right) = \frac{1}{\sqrt 3 }\left\{ {1 + \left[ {\frac{E}{\sqrt 3 Y}} \right]^{n} \int_{{1 - \left( {{\gamma \mathord{\left/ {\vphantom {\gamma \xi }} \right. \kern-\nulldelimiterspace} \xi }} \right)^{2} }}^{{1 - \gamma^{2} }} {\frac{{\left( { - \ln x} \right)^{n} }}{{\left( {1 - x} \right)}}} \mathrm{d}x} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{\rho_{o} V^{2} }}{2Y}\left\{ {\frac{1}{{\left( {1 - \nu } \right)\sqrt {1 - \alpha^{2} } }}\ln \left[ {\frac{{1 + \sqrt {1 - \alpha^{2} } }}{\alpha }} \right]} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { + \gamma^{2} - 2\ln \xi - \frac{{\gamma^{2} }}{{\xi^{2} }}} \right\}. \hfill \\ \end{gathered}$$
(25)

As discussed in [10], the second term \(\gamma^{2}\) in the inertial component of Eq. (25) accounts for the error in neglecting the convective acceleration and velocity terms in Eq. (18) for the elastic region, and is therefore neglected. The value of ∝ as a function of expansion velocity V is obtained from Eqs. (19) and (24) as

$$\alpha = \left[ {\frac{{\sqrt 3 \left( {1 - 2\nu } \right)\rho_{o} }}{{2\left( {1 - \nu } \right)Y}}} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} V.$$
(26)

At the cavity surface \(\xi = \gamma\), and the dimensionless radial stress is

$$\begin{gathered} \,\,\,\,S\left( \gamma \right) = \frac{1}{\sqrt 3 }\left\{ {1 + \left[ {\frac{E}{\sqrt 3 Y}} \right]^{n} \int_{0}^{{1 - \gamma^{2} }} {\frac{{\left( { - \ln x} \right)^{n} }}{{\left( {1 - x} \right)}}} \mathrm{d}x} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{\rho_{o} V^{2} }}{2Y}\left\{ {\frac{1}{{\left( {1 - \nu } \right)\sqrt {1 - \alpha^{2} } }}\ln \left[ {\frac{{1 + \sqrt {1 - \alpha^{2} } }}{\alpha }} \right] - \ln \left( {\gamma^{2} } \right) - 1} \right\}. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered}$$
(27)

In Eq. (27), the integral in the quasi-static strength term of the solution is improper due to the weak logarithmic singularity in the integrand at x = 0; however, it is an integrable singularity, and can be easily evaluated using an open integration algorithm as discussed in Press et al. [17].

Analytical Elastically Compressible Perfectly Plastic CCE Solution

In this section, we consider the same problem as in Sect. “Analytical Power-Law Strain Hardening CCE Solution”; however, now we consider the plastic region to be elastically compressible perfectly plastic. By assuming the plastic region to be elastically compressible perfectly plastic, the elastic–plastic interface velocity c is the same as that obtained from the FEM simulations of the elastically compressible power-law hardening problem described Section “FEM CCE Problem Formulations”. Additionally, using Hooke’s law in the elastic region causes the elastic–plastic interface velocity to saturate, and asymptotes along the value of the bulk wave speed \(c_{p} = \sqrt {{K \mathord{\left/ {\vphantom {K {\rho_{o} }}} \right. \kern-\nulldelimiterspace} {\rho_{o} }}}\), where the bulk modulus \(K = {E \mathord{\left/ {\vphantom {E {\left[ {3\left( {1 - 2\nu } \right)} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {3\left( {1 - 2\nu } \right)} \right]}}\).

For this CCE problem, we employ Eq. (1a) for conservation of linear momentum. However, with elastic compressibility, \(\rho \ne \rho_{o}\) in the plastic region, and the analysis is simplified using mass conservation as a function of time as done in [16] with the elastically compressible perfectly plastic SCE problem. Therefore, in Eulerian coordinates for the CCE problem, mass conservation is given by

$$\rho \left( {\frac{\partial \upsilon }{{\partial r}} + \frac{\upsilon }{r}} \right) = - \left( {\frac{\partial \rho }{{\partial t}} + \upsilon \frac{\partial \rho }{{\partial r}}} \right).$$
(28)

Additionally, for the elastically compressible perfectly plastic region

$$\begin{gathered} p = K\eta = K\varepsilon_{ii} = K\left( {1 - \frac{{\rho_{o} }}{\rho }} \right) \hfill \\ p = \frac{1}{3}\left( {\sigma_{r} + \sigma_{\theta } + \sigma_{z} } \right), \hfill \\ \sigma_{r} - \sigma_{\theta } = \frac{2}{\sqrt 3 }Y \hfill \\ \end{gathered}$$
(29a–c)

where p is the pressure, and \(\eta\) is the elastic volumetric strain. Furthermore, following Hill [7], we assume plane strain conditions such that \(\varepsilon_{z} = 0\). The axial stress is also reasonably assumed in the plastic region to be equal to the average of the radial and circumferential stresses \(\sigma_{z} = {{\left( {\sigma_{r} + \sigma_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{r} + \sigma_{\theta } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\), but equal to zero in the elastic region as discussed in [7]. For the plastic region, Eqs. (1a), (28), and (29a–c) are combined to eliminate \(\sigma_{\theta }\) and ρ giving

$$\begin{gathered} \frac{{\partial \sigma_{r} }}{\partial r} + \frac{2Y}{{\sqrt 3 r}} = \frac{{ - \rho_{o} }}{{\left( {1 - \eta } \right)}}\left( {\frac{\partial \upsilon }{{\partial t}} + \upsilon \frac{\partial \upsilon }{{\partial r}}} \right) \hfill \\ \frac{\partial \upsilon }{{\partial r}} + \frac{\upsilon }{r} = \frac{ - 1}{{K\left( {1 - \eta } \right)}}\left( {\frac{{\partial \sigma_{r} }}{\partial t} + \upsilon \frac{{\partial \sigma_{r} }}{\partial r}} \right). \hfill \\ \eta = \frac{{\sigma_{r} }}{K} - \frac{Y}{\sqrt 3 K} \hfill \\ \end{gathered}$$
(30a–c)

To obtain a solution, a similarity transformation is employed in both the elastically compressible perfectly plastic and elastic regions. This provides a coupled set of nonlinear ODEs for the plastic region that uses boundary conditions obtained from the linear elastic region in Sect. “Analytical Power-Law Strain Hardening CCE Solution” at the elastic plastic interface (\(\xi = 1\)). In the plastic region, the similarity transformation variable from Eq. (7a) is employed along with the dimensionless variables given by Eqs. (7c–e) with the additional dimensionless variables

$$S = \frac{{\sqrt 3 \sigma_{r} }}{2Y},\;\;T = \frac{2Y}{{\sqrt 3 K}},\;\;\lambda = \frac{c}{{c_{p} }},\;\;\gamma = \frac{V}{c},$$
(31a–d)

where \(c_{p} = \sqrt {{K \mathord{\left/ {\vphantom {K {\rho_{o} }}} \right. \kern-\nulldelimiterspace} {\rho_{o} }}}\) is the bulk wave speed giving the coupled set of first order non-linear ODE’s

$$\begin{gathered} \frac{\mathrm{d}S}{{\mathrm{d}\xi }} + \frac{1}{\xi } = \frac{{\lambda^{2} }}{{T\left( {1 - \eta } \right)}}\left( {\xi - U} \right)\frac{\mathrm{d}U}{{\mathrm{d}\xi }} \hfill \\ \frac{\mathrm{d}U}{{\mathrm{d}\xi }} + \frac{U}{\xi } = \frac{T}{{\left( {1 - \eta } \right)}}\left( {\xi - U} \right)\frac{\mathrm{d}S}{{\mathrm{d}\xi }}, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\eta = T\left( {S - \frac{1}{2}} \right) \hfill \\ \end{gathered}$$
(32a–c)

For numerical evaluation, we put Eqs. (32a,b) in a form suitable for using the Runge–Kutta ODEINT routine from [17], and the equations are given by

$$\begin{gathered} \frac{\mathrm{d}U}{{\mathrm{d}\xi }} = \frac{{\frac{T}{\xi }\left( {\frac{\xi - U}{{1 - \eta }}} \right) + \frac{U}{\xi }}}{{\lambda^{2} \left( {\frac{\xi - U}{{1 - \eta }}} \right)^{2} - 1}} \hfill \\ \frac{\mathrm{d}S}{{\mathrm{d}\xi }} = \frac{{\frac{{\lambda^{2} }}{T}\left( {\frac{\xi - U}{{1 - \eta }}} \right)\frac{U}{\xi } + \frac{1}{\xi }}}{{\lambda^{2} \left( {\frac{\xi - U}{{1 - \eta }}} \right)^{2} - 1}}. \hfill \\ \end{gathered}$$
(33a,b)

with this numerical integration procedure, a value of \(\lambda = {c \mathord{\left/ {\vphantom {c {c_{p} }}} \right. \kern-\nulldelimiterspace} {c_{p} }}\) is selected, where \(0 \le \lambda \le 1\). The integration proceeds through the plastic region \(\gamma \le \xi \le 1\) using the boundary conditions from Eqs. (23a,b) at \(\xi = 1\). When \(\xi = \gamma\), the value of the cavity-expansion velocity is \(V = \gamma c\) is obtained corresponding to the initially specified value of \(\lambda = {c \mathord{\left/ {\vphantom {c {c_{p} }}} \right. \kern-\nulldelimiterspace} {c_{p} }}\).

FEM CCE Problem Formulations

In this section, we obtain results using the explicit transient dynamic FE computer program ABAQUS/Explicit [18]. Dynamic plane strain CCE simulations were obtained over a range of cavity-expansion velocities for elastically compressible strain hardening and perfectly plastic infinitely extended response regions. For plane strain problems, the thickness of the body is eliminated making the problem two-dimensional. Therefore, 4-node isoparametric quadrilateral uniform strain reduced integration elements (CPE4R elements in [18]) with a lumped mass matrix were used in this study to construct the discrete explicit Lagrangian FE CCE problem formulations that is solved using the commercial ABAQUS/Explicit [18] software. With these explicit FE simulations, an explicit central difference time integration scheme as described in [18] is employed to integrate the equations of motion through time. This time integration algorithm is only conditionally stable; therefore, a time increment \(\Delta t\) less than the Courant stability limit of the problem must be used. A conservative estimate is obtained from the approximation

$$\Delta t = \zeta \min \left( {\frac{{L_{e,i} }}{{\tilde{c}_{d,i} }}} \right),$$
(34)

where \(L_{e,i}\) and \(\tilde{c}_{d,i}\) are the characteristic element dimension of element i, and its effective dilatational wave speed of which both are calculated internally. The parameter \(\zeta\) is a user defined scale factor, and in this study, it was taken to be 0.01 to maintain numerical stability during the simulations.

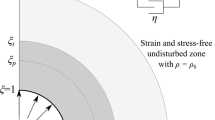
This FE formulation requires a small pre-existing cylindrical cavity to be expanded at a constant expansion velocity V in a material medium of infinite extent to eliminate any possible wave reflections. Therefore, to satisfy the infinite medium requirement, 32 infinite 4-node plane strain elements (CIPE4 elements in [18]), shown in Fig. 2, were used to represent the outer boundary of the cylindrical cavity mesh. Furthermore, from symmetry, only a quarter of the CCE problems were required for the simulations. As with the SCE simulations in [15], the numerical solutions of this CCE problem converge to accurate approximate self-similar radial stress values at the cavity surface. Therefore, these weak formulation results are approximately equivalent to the corresponding strong formulation results obtained from the exact same problems using an elastically compressible analytic formulation (if it were attainable). From these numerical simulations, radial stress values at the cavity surface \(\sigma_{r} \left( a \right)\) along with elastic–plastic interface velocities c are obtained as functions of expansion velocities V for dynamic elastically compressible strain hardening and perfectly plastic CCE problems in a plane strain medium of infinite extent.

Fig. 2
figure 2

Two-dimensional plane strain finite element mesh of an expanding cylindrical cavity (where R is in mm)

Full size image

Constitutive Model

The constitutive equation for the plastic region assumes von Mises (J2) plasticity with an associated flow rule as described in [18]. Therefore, there is no volumetric plastic strain, and in addition, the material considered in this study has a large bulk modulus K, so the total volume strain is small. The linear elasticity associated with the simulations is defined with the volumetric (dilatational) and shear (deviatoric) components of stress and strain through Hooke’s law, and the pressure-volumetric strain relation is given by

$$p = - \frac{1}{3}\sigma_{ii} = - K\varepsilon_{ii} ,$$
(35)

where \(\sigma_{ii}\) and \(\varepsilon_{ii}\) are the first invariants of the true Cauchy stress and true strain tensors, respectively. The true deviatoric strain and stress tensors are given by

$$\begin{gathered} e_{ij} = \varepsilon_{ij} - \frac{1}{3}\varepsilon_{kk} \delta_{ij} \hfill \\ s_{ij} = \sigma_{ij} - \frac{1}{3}\sigma_{kk} \delta_{ij} , \hfill \\ \end{gathered}$$
(36a,b)

where \(\delta_{ij}\) is the Kronecker delta, and \(\varepsilon_{ij}\) and \(\sigma_{ij}\) are the true strain and Cauchy stress tensors respectively. The incremental strain rate additive decomposition of the total strain rate and its integrated form using the standard definition of corotational measures are given by

$$\eqalign{ & \mathrm{d}{\varepsilon _{ij}} = \mathrm{d}\varepsilon _{ij}^\mathrm{el} + d\varepsilon _{ij}^\mathrm{pl} \cr & {\varepsilon _{ij}} = \varepsilon _{ij}^\mathrm{el} + \varepsilon _{ij}^\mathrm{pl} \cr}$$
(37a,b)

respectively, where \(\varepsilon_{ij}^\mathrm{el}\) and \(\varepsilon_{ij}^\mathrm{pl}\) are the elastic and plastic components of the true strain tensor \(\varepsilon_{ij}\). For elastic–plastic constitutive models, the objective corotational Jaumann stress rate is used with the Kirchhoff stress \(\tau_{ij} = J\sigma_{ij}\), where J = det \(\left| {F_{kK} } \right|\) is the determinant of the deformation gradient \(F_{kK}\). The Kirchhoff stress \(\tau_{ij}\) is work conjugate to the strain measure whose rate is the rate of deformation tensor \(D_{ij}\), and is widely used with numerical algorithms for metal plasticity constitutive models. The objective corotational Jaumann stress rate in terms of the Kirchhoff stress tensor is

$$\frac{{\mathrm{d}^{\nabla J} \tau_{ij} }}{\mathrm{d}t} = \frac{{\mathrm\tau_{ij} }}{\mathrm{d}t} - W_{ik} \tau_{kj} + \tau_{ik} W_{kj} ,$$
(38)

where \(W_{ij}\) is the spin tensor obtained by decomposing the velocity gradient tensor \(L_{ij}\) into its symmetric and skew-symmetric parts such that \(L_{ij} = D_{ij} + W_{ij}\).

Plastic flow is introduced through a J2 von Mises plastic power-law isotropic hardening plasticity constitutive model, and a perfectly plastic constitutive model. For the power-law hardening, the functional form given by Eq. (4b) is not available in ABAQUS/Explicit [18]; therefore, we utilize the J2 plasticity tabulated data constitutive model where the yield surface is defined as

$$f = \overline{\sigma } - H\left( {e_{p} } \right) = 0,$$
(39)

where \(f\) is the plastic potential, \(\overline{\sigma }\) is the von Mises equivalent stress, and \(H\left( {e_{p} } \right)\) is the strain hardening as a function of the equivalent true deviatoric plastic strain \(e_{p}\) (or as a constant in the case of a perfectly plastic material). The tabulated data is used to define the plastic potential in Eq. (39) which provides the associated flow rule for the incremental plastic strain as

$$\mathrm{d}e_{ij}^\mathrm{pl} = \frac{3}{2}\frac{{s_{ij} }}{{\overline{\sigma }}}\mathrm{d}e_{p} .$$
(40)

Finite Element Formulations

The axisymmetric geometry for the CCE simulations is discretized using the finite element mesh illustrated in Fig. 2. The mesh consists of 16,928 four node two-dimensional isoparametric elements with a total of 17,490 nodes. The horizontal and vertical axes shown in Fig. 2 are lines of symmetry, and infinite elements are employed on the outer boundary. As done with the SCE simulations in [15], a constant radial velocity boundary condition is applied to the nodes of a small preexisting cylindrical cavity surface with an initial radius of R = 0.1 mm as shown in Fig. 2. The cavity surface is accelerated from rest to V during the first 2 µs using a fifth order polynomial ramp function to smoothen the increase in velocity. Inertia effects arising from the acceleration cause a small local peak stress when the acceleration ceases. Using for instance a linear ramp function would increase the local peak, but the solution will always converge to the same steady state stress level. Additionally, for all simulations the outer boundary of infinite elements had an initial radius of R = 100 mm, and default values of hourglass control and artificial bulk viscosity were used as described in [18]. A series of CCE simulations were done over a range of expansion velocities V giving the radial stress at the cavity surface \(\sigma_{r} \left( a \right)\) as a function of time. The simulations were terminated when the radial stress at the cavity surface attained a constant value which provides the approximate self-similar solution that would be obtained from an analytic formulation of the dynamic elastically compressible strain hardening CCE solution.

Comparison of Analytical Model Predictions with FE Results

As previously discussed, the objective of this study is to compare values of radial stress at the cavity surface \(\sigma_{r} \left( a \right)\) and elastic–plastic interface velocities c as functions of the radial expansion velocity V obtained analytically (strong formulations) and from FE simulations (weak formulations). Therefore, results developed in Sects. “Analytical Power-Law Strain Hardening CCE Solution” and “Analytical Elastically Compressible Perfectly Plastic CCE Solution” for incompressible power-law strain hardening and elastically compressible perfectly plastic CCE problems are compared with the FE elastically compressible strain hardening and perfectly plastic simulated results as described in Sect. FEM CCE Problem Formulations. A comparison of the analytic and FE cavity-expansion radial stress \(\sigma_{r} \left( a \right)\) values and elastic plastic interface velocity c results for the elastically compressible perfectly plastic CCE problem illustrates the accuracy of the ABAQUS/Explicit [18] simulations. Additionally, the results with comparisons including strain hardening provides an estimate of the error associated with neglecting elastic strains in the plastic region. As discussed in references [1, 3, 9,10,11,12], using CCE solutions with the CCE approximation has been extensively used for ductile hole growth perforation problems.

The material properties used for the comparisons in this study are for 6061-T6511 aluminum alloy obtained from large strain compression data given in [10]. For this aluminum alloy, the material properties E = 68.9 GPa, Y = 276 MPa, ρ0 = 2710.0 kg/m3, v = 1/3, and n = 0.072 are used for both analytical solutions and FEM simulations.

The radial stress at the cavity surface as a function of time for the elastically compressible power-law strain hardening aluminum alloy for cavity-expansion velocities V ranging from 25 to 1000 m/s were obtained from 17 FE simulations. The results from all velocities are shown in Fig. 3. For the 17 cavity-expansion velocities considered, all radial stresses from the FE simulations converge to the self-similar values in approximately 5 μs. The same approach was also utilized for the elastically compressible perfectly plastic simulations with similar results. The self-similar constant radial stress values are given in Table 1 for each of the 17 cavity-expansion velocities associated with both FE constitutive models. In Fig. 4, the radial stress at the cavity surface from FE simulations is given as a function of cavity-expansion velocity V for both elastically compressible power law strain hardening and perfectly plastic yield criteria along with the analytical elastically compressible perfectly plastic solution from Sect. “Analytical Elastically Compressible Perfectly Plastic CCE Solution”. In this figure, it is observed that the radial stress at the cavity surface for power-law strain hardening is approximately 1% greater than the perfectly plastic values at all cavity-expansion velocities considered. In addition, at the lower cavity-expansion velocities the elastically compressible analytical perfectly plastic solution correlates best with the elastically compressible perfectly plastic FE solution, while at higher cavity-expansion velocities it correlates better with the elastically compressible power-law hardening FE solution. It is hypothesized that the reason for this may be due to numerous possible numerical errors associated with the FE weak formulation. However, as observed for this 6061-T6511 aluminum alloy, the fully elastically compressible radial stress values at the cavity wall for all the cavity-expansion values considered are very close, and the power-law hardening does not appear to introduce a significant effect with the final solutions as observed with the simulated results with and without power-law hardening.

Fig. 3
figure 3

Simulated radial stress versus time for all 17 cavity expansion velocities V for the elastically compressible power-law strain hardening CCE simulations

Full size image
Table 1 Radial stress and elastic–plastic interface velocity as a function of expansion velocity from FE results
Full size table
Fig. 4
figure 4

Radial stress at the cavity surface as a function of cavity-expansion velocity for power-law strain hardening and perfectly plastic elastically compressible FEM simulations and the analytic perfectly plastic elastically compressible solution with v = 1/3

Full size image

In Fig. 5, the radial stress at the cavity surface \(\sigma_{r} \left( a \right)\) as a function of cavity-expansion velocity V using Eq. (27) is compared with the results from FE simulations using the elastically compressible power-law strain hardening yield criteria along with the corresponding non-linear least-squares fit to the 17 FE simulations as given by the quadratic equation

$$\sigma_{r} \left( a \right) = 1020.0 + 1.2156V + 0.0039V^{2} ,$$
(41)
Fig. 5
figure 5

Radial stress at the cavity surface as a function of cavity-expansion velocity using Eq. (27) with an incompressible plastic region, the FEM elastically compressible power-law hardening solution with v = 1/3, and the non-linear least-squares fit to the FEM elastically compressible power-law hardening data given by Eq. (41)

Full size image

where \(\sigma_{r} \left( a \right)\) is given in MPa, and \(V\) is in m/s. Here, it is observed that the radial stress from the FE simulations exhibits less resistance (lower radial stress values at the cavity surface) than the analytic solution in Eq. (27) for values of V below the critical cavity-expansion velocity associated with Eq. (27). In Eq. (26), the critical cavity-expansion velocity occurs at approximately 488.4 m/s, at which point the elastic–plastic interface velocity c becomes equal to the dilatational wave speed. At this cavity-expansion velocity, Eq. (27) becomes complex based on material properties and is unphysical. Furthermore, the elastically compressible FE simulations provide physically realistic radial stress values \(\sigma_{r} \left( a \right)\) for cavity-expansion velocities V beyond the critical velocity from Eq. (27) up to the point where Hooke’s law is not applicable due to the fact it is not an equation of state (EOS) as discussed in [19].

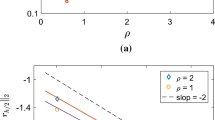
Another factor that appears to contribute to the over prediction of the radial stress by Eq. (27) is the increased extent of the plastic region due to its assumed incompressibility. From Eq. (24) with the incompressible plastic region, it is observed that the elastic–plastic interface velocity c increases linearly with the cavity expansion velocity up to the dilatational wave speed \(c_{d}\) where ∝ = 1.0 as illustrated in Fig. 6. This indicates that the analytical solution from Eq. (24) has a larger plastic zone than that of both the elastically compressible power-law strain hardening and perfectly plastic FE simulations along with the elastically compressible perfectly plastic analytic solution from Sect. “Analytical Elastically Compressible Perfectly Plastic CCE Solution”. Additionally, from the Rankine-Hugoniot jump conditions at the elastic–plastic interface \(\xi = 1\), the stresses and particle velocities are continuous and equal on both sides of the interface. Therefore, from Fig. 6 it is observed that all of the elastically compressible methods considered in this study have approximately the same elastic–plastic interface velocities, and are given in Table 1 for each of the 17 FE simulations associated with both constitutive models. Additionally, from the use of Hooke’s law with all of the models in this study as opposed to an EOS capable of modeling a shock front in the material prevents shock fronts from forming as discussed in [19]. Therefore, all of the elastically compressible CCE solutions asymptote along the bulk wave speed value given by \(c_{p}\) from Eq. (31c). This result also implies that the closed form analytical power-law hardening solution that assumes an incompressible plastic region causes a larger bulk of material to strain harden in the plastic region with increasing expansion velocities and increases the resistance at the cavity surface as observed in Fig. 5. For lower expansion velocities, it is observed that Eq. (27) exhibits resistance values at the cavity surface close to that from the fully elastically compressible FE simulations. However, above an expansion velocity of approximately V = 200 m/s the expansion resistance values start to diverge with Eq. (27) giving larger resistance values for the 6061-T6511 aluminum alloy material from [10] used in this study. Thus, the increasing difference in the elastic–plastic interface velocities c with increasing cavity-expansion velocities V by considering the plastic region to be elastically compressible provides some physical insight into the observed difference in the radial stress values at the cavity surface due to increasing cavity-expansion velocities. These results hold for other materials as well. For comparison, the same methodology as laid out in this work was applied to four additional materials using data given in Table 2 of reference [1], the materials being Weldox 700E, Weldox 500E, AA6070-T6 and AA6060. The main results in terms of radial stresses and elastic–plastic interface velocities are given in Fig. 7 along with comparisons with analytical solutions to the dynamic power-law strain hardening CCE problem.

Fig. 6
figure 6

Elastic–plastic interface velocity c versus cavity-expansion velocity V for the closed form analytic power-law hardening solution with an incompressible plastic region, elastically compressible power-law hardening and perfectly plastic FEM simulations, and the analytic elastically compressible perfectly plastic solution along with bulk and dilatational wave speeds

Full size image
Fig. 7
figure 7

Radial stresses vs. cavity expansion velocities up to 600 m/s (a), and elastic–plastic interface velocities (b) for four additional power-law strain hardening materials using material data given in Ref. [1]. The square markers in (a) indicate the FEM solutions, while the solid lines show the analytical solutions from Eq. (27). In (b), the solid lines are still the analytical solutions, this time as obtained by Eqs. (19) and (26) up to their respective bulk wave speeds, while the dashed lines show the FEM solutions

Full size image

Concluding Remarks

In this study, we analyzed the effect of an incompressible plastic region and a compressible elastic region on the analytical solutions of the dynamic homogenous isotropic power-law strain hardening CCE problem subjected to plane strain conditions with a cavity expanding from a zero initial radius in an infinite medium. To obtain a closed form analytical solution for this problem, the plastic region must be taken as elastic and plastically incompressible, otherwise hydrostatic stress terms must be explicitly included in the elastically compressible strain hardening term, thereby making the problem intractable. Furthermore, for a dynamic solution, the elastic region must be taken as compressible to avoid a logarithmic singularity associated with the conservation of linear momentum inertia term in a medium of infinite extent as discussed in [3].

However, as an alternative to the analytical formulation of the elastically compressible dynamic strain hardening CCE problem, an explicit FE formulation was employed in this study to obtain solutions for the radial stress at the cavity surface \(\sigma_{r} \left( a \right)\) along with the elastic–plastic interface velocity c. Additionally, with the proposed FE formulation, Hooke’s law was also employed as discussed in [18] to describe the linear elastic behavior in both the plastic and elastic regions of the material. Therefore, with the FE formulations considered, all of the elastic deformation is associated with the hydrostatic and deviatoric elastic strains, and are not required for defining the von Mises power-law strain hardening or perfectly plastic constitutive models. Thus, in this study, the FE formulation in ABAQUS Explicit [18] was employed to obtain solutions for the elastically compressible CCE problems that are either power-law strain hardening or perfectly plastic. Additionally, since solutions are obtainable for the analytical (strong form) elastically compressible perfectly plastic CCE problem, its results are used to provide an estimate for the accuracy of the FE simulations.

From Fig. 5, it is observed that the error in radial stress at the cavity surface associated with neglecting elastic compressibility in the plastic region in the analytical model increases with increasing expansion velocities. Furthermore, it also appears that this error in the radial stress at the cavity surface with the closed form analytical model would continue to increase for expansion velocities beyond its critical velocity limit if it were attainable. Therefore, considering the plastic region to be elastically compressible causes the radial stress at the cavity surface to decrease, and the elastic–plastic interface velocity c to saturate asymptotically to the bulk wave speed when Hooke’s law is used.

As observed in references [10,11,12,13], when target inertia is included with the analytic formulation, the ballistic limit velocity increases, and the residual velocities decrease. Additionally, in most cases using an analytical dynamic strain hardening model, the ballistic limit velocities are greater than the experimental values. Furthermore, the residual velocities are less than the experimental values; however, when target inertia is neglected in the analytical model, the ballistic limit velocities are less than both the experimental ballistic limit velocities, and the residual velocities. Therefore, results from this study imply that the target resistance is reduced by considering the plastic region to be elastically compressible as expected, and the target resistance decreases more with increasing cavity-expansion velocities. This result is also substantiated from the observation that the elastic–plastic interface velocity saturates and asymptotes along the material’s bulk wave speed \(c_{p}\) when Hooke’s law is employed to define the linear elastic response as illustrated by both the FE solutions, and also the elastically compressible perfectly plastic analytical CCE solution at increased cavity-expansion velocities. For these three CCE problems the elastic–plastic interface velocities are the same because they have the same yield stress at the elastic–plastic interface. Therefore, one of the most important results from this study indicates that the CCE approximation accounting for target inertia gives higher values for ballistic limit velocities compared to the results from the FE simulations. Thus, using the FE simulations for the CCE approximations in references [10,11,12,13] will give results that are in better agreement with existing experimental results. Furthermore, from this study, the most significant result is that the proposed FE formulation with strain hardening gives radial stress values at the cavity surface as a function of the cavity-expansion velocity V that do not have a physically unrealistic critical velocity value in which the closed form analytic solution becomes complex and physically unrealistic as illustrated in Fig. 5. In addition, a nonlinear least squares fit to the simulated FE radial stress values at the cavity surface as a function of cavity-expansion velocity provides a quadratic expression as given by Eq. (41) for the elastically compressible power-law hardening radial stress at the cavity surface that includes target inertia, and can be easily implemented with the CCE approximation for ductile hole growth perforation problems. This expression is expected to match experimental ductile hole growth perforation data better than the previous closed form analytical strain hardening formulation that requires the plastic region to be incompressible and the elastic region to be compressible. However, comparisons with experimental ballistic results are beyond the scope of the present study, but may be considered in the next phase of this research program.