1 Introduction

The characterization of the mechanical properties of biomedical materials and structures is a fundamental step towards numerical modelling, which can be exploited as a tool for evaluating the interaction between prostheses and biological tissues [1,2,3,4]. At this purpose, reliable inputs are needed for numerical analysis, such as structural geometrical conformation, boundary and loading conditions, and materials behavior [5]. A variety of methods have been developed to measure mechanical properties, including biaxial and uniaxial tensile tests, creep, stress relaxation, bending and compression tests. Among these methods, one of the most commonly used is uniaxial tensile to evaluate elastic properties and stiffness [6], that requires a precise measure of the specimen strain. This measurement can be performed by “clamp-to-clamp” elongation, even if a limited slippage of the sample could potentially occur, thus compromising its reliability. In addition, strain and stress fields are non-uniform within the specimen [7,8,9,10] and this heterogeneity reveals through the variation of lateral contraction and necking in different regions of the sample, that are not dependent on the intrinsic material behavior only, but also on the specimen geometry [11, 12]. These limitations of “clamp-to-clamp” analysis may be overcome through local strain measurement with contact or non-contact extensometers. Contact extensometers, such as electrical-resistance strain gauges [13] and mechanical [14], provide high-precision strain measurement in many applications, but suffer some practical problems if used for testing biomedical materials. Indeed, strain gauges need to be physically attached to the specimen and their weight and positioning may influence the mechanical response of the sample [15]. To overcome these disadvantages, non-contact extensometers using a digital video camera and various digital image processing algorithms able to track marker motions [16,17,18] have been widely adopted. Also non-contact techniques still present some limitations, since the accuracy of the markers-tracking and its post-processing can introduce errors. Besides, the kind of marker and its coupling to the tested sample can locally change the real mechanical response of the specimen. Concerning markers drawn on sample surface with an ink, the accuracy of the measurement could be also affected by marker deformation during sample elongation [19]. The selection of the marker is also conditioned by the sample itself, as in the case of specimens that do not present a uniform surface, e.g. in the case of synthetic meshes for surgical repair of hernias [20], or need to be tested in a wet environment, as biological tissues.

Literature studies regarding mechanical testing of biomedical materials report few details about the markers used and attachment method [21,22,23,24,25]. Marker points or lines are often drawn on sample surface, but specific information on ink properties is not usually provided. Similar issues related to marker selection and positioning can be highlighted even in the field of mechanical testing of biological tissues, including additional difficulties due to sample hydration. By way of example, enamel paint was successfully applied on tendons and placenta, even if drawn markers presented quite large dimensions [26, 27]. Together with a limited description of the typology of adopted markers and attaching methods, the effect of these aspects on the mechanical behavior of tested samples is not exhaustively addressed in the literature. Therefore, the aim of this work is evaluating the effects of different settings for the coupling markers-sample and assessment of their tracking during uniaxial tensile testing on different biomedical polymers.

2 Materials and Methods

2.1 Materials

Two materials for biomedical application were selected for this investigation, in particular an elastomer and a synthetic mesh. The elastomer 300 SIL 50-BL is a silicone film of 1.5 mm thickness and was provided by Comitec SNC (Como, Italy). The synthetic mesh is an industrial net (manufactured by Edilacilia, Rome, Italy) already characterized in the literature [18, 28].

2.2 Sample Preparation

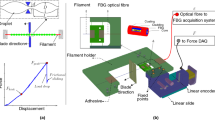
Rectangular samples with 1:3 width-to-free length ratio were cut for tensile testing. The samples of the synthetic material had a constant tested area (width 19 mm x free length 56 mm), with different thicknesses depending on the material itself. In the case of synthetic meshes, two orthogonal test directions (Fig. 1a) were considered, due to mesh anisotropy.

Fig. 1
figure 1

Test directions A and B indicated with reference to net textile pattern (a). Images of markers on the net and their rendering for tracking in the case of paint markers (b, c) or physical markers (d, e)

Full size image

For every tested material, samples without any marker were firstly tested, as a reference for following experiments. Afterwards, marked specimens were taken into account, with five markers having a diameter smaller than 1 mm located in the central area of every sample (in detail, four markers at the edges of a square with 5 mm sides and a marker in the center).

Different solutions were examined for the markers, that can be divided into two main categories: paint markers (Fig. 1b) and physical markers (Fig. 1d) attached with the use of an adhesive substance. In the first category, either a commercial lacquer (mainly based on nitrocellulose, ethyl acetate, butyl acetate, propyl acetate and isopropylalcohol) or an acrylic paint (generally used for 3D painting) were used for drawing the markers on the samples. Both paints can be partially absorbed (i.e. by the mesh) with limited control on the desired shape of the markers. To reduce this issue, physical markers were selected and attached to the sample either with cyanoacrylate or medical spray band.

2.3 Tensile Tests

Uniaxial tensile tests were performed on a Bose ElectroForce® Planar Biaxial Test Bench instrument (TA Instruments, New Castle, USA) with a load cell of 200 N. Tests were carried out up to 40% strain at a constant strain rate of 0.1% s−1. In the case of silicone only, preliminary tests up to 100% strain were performed at the same strain rate on samples with ink markers, for a comparison with technical data provided by the manufacturer. Five repetitions for each configuration were performed.

To accomplish contactless marker tracking, a high-FPS acquisition camera (Allied Vision Prosilica GE680, Edmund Optics Inc., Barrington, USA) was positioned perpendicularly to the sample. The image recorded by the camera was subject to a threshold procedure, thus obtaining monochromatic markers (Fig. 1c, e) and determining their center of mass through a pixel-weighted operation. The distance between the field of view of the camera and the area of the sample was the closest as possible allowing the tracking of the markers for the entire duration of the test. At the same time, the set-up enabled to enlarge markers as much as possible, thus obtaining a clear shape of the marker and a stable centroid of each marker in order to reduce the error introduced by the threshold procedure. Markers position was recorded by means of WinTest software (Version: 7.01), that automatically computed Green–Lagrange strains in test direction (ε11) and orthogonally to it (ε22).

In the case of surgical mesh only, contactless measurement of the local deformation was carried out without markers as well. A video of the mesh in the center of the specimen was recorded and frames corresponding to specific nominal strain values were analyzed with the image processing software ImageJ (NIH) [29] to calculate local strain from mesh knots positions during the test.

2.4 Data Analysis

Force versus displacement were acquired for each sample. Moreover, Green–Lagrange strain in the center of the sample was recorded by marker tracking in the test direction and orthogonally to it. During the acquisition, residual errors could affect the real position of the markers, thus, a post-processing elaboration was developed to clear the acquired signals. In particular, a user-dedicated script was developed in MATLAB R2017b (MathWorks, Natick, MA) to perform a non-parametric smoothing.

For each experimental test, nominal membrane force F/w0 was calculated as current force F divided by the initial width of the sample w0. Nominal strain ε was calculated as the ratio between the imposed elongation and the initial length of the sample. True value of membrane force F/w was computed as the ratio between current force and current width of the sample w (as product of w0 and local strain ε22 in the direction orthogonal to the loading direction) and displayed versus the local strain ε11 in the loading direction. Mean values of nominal membrane force, true membrane force, current width and local strains, with associated standard deviations (SD), were calculated for each group of tests. Statistical analysis was used to compare membrane force values at different strain levels, namely at 10% and 20% (when applicable). These strain levels were selected in a range which is compatible with physiological strain for biomedical materials in vivo. Data were analyzed using non-parametric Mann–Whitney U test.

3 Results

The nominal and true local values of stress versus strain of silicone measured from uniaxial tensile tests are reported in Fig. 2a up to a strain of 100%. Experimental data are shown with associated SDs, reported as a light-colored band. These data have been considered for verifying the reliability and accuracy of test procedure by comparing the tangent modulus of silicone calculated from experimental data with the one reported in technical data sheet provided by the manufacturer (Fig. 2b).

Fig. 2
figure 2

Nominal and true local values of stress versus strain of silicone in uniaxial tensile tests (a); Comparison of silicone tangent modulus between experimental data (± SD) and technical data provided by the manufacturer (b)

Full size image

Figure 3 shows the mechanical behavior of silicone samples tested with different markers, namely cyanoacrylate, lacquer and medical spray band. Acrylic paint was not used in this case, due to poor adhesion on silicone surface. Experimental data are shown with associated SDs, reported as a light-colored band in the positive range only. In Fig. 3c, no data are shown with reference to mechanical test without markers. Indeed, the silicone samples present a rather uniform surface that does not allow to measure local deformation without any marker, as in the case of synthetic meshes, discussed in the following. As a consequence, it is not possible to evaluate if the local mechanical behavior, measured with lacquer markers, is different from the true local response of the material without any surface modification. Vertical band in Fig. 3c refers to SD associated to F/w while horizontal band indicates SD associated to ε11. Even if SDs are included in the graph for all data, they are visible only for some curves due to their very low ranges. Results of statistical analysis are reported in Table 1.

Fig. 3
figure 3

Mechanical behavior of silicone samples with different markers: nominal membrane force F/w0 versus nominal strain ε (a); strain ε during test time (b); true local value of membrane force F/w vs. local strain ε11 along test direction (c)

Full size image
Table 1 Mann-Whitney U test for silicone, comparing nominal (F/w0) or true (F/w) membrane force at different strain levels (ε = 0.1; ε = 0.2) with different markers (NC no marker, C cyanoacrylate, L lacquer, MSB medical spray band)
Full size table

As concern the synthetic mesh, results in different test directions must be evaluated separately, due to a strong mesh anisotropy. In direction A (Fig. 4), an initial membrane force increase is followed by a long plateau and by a sharp rise at large strain, about above 25-30%. Differently, in direction B (Fig. 5), the mesh is stiffer and exhibits an almost linear response. Strain at break is more than 40% in direction A and 20–25% in direction B.

Fig. 4
figure 4

Mechanical behavior of synthetic mesh samples with different markers along direction A: nominal membrane force F/w0 versus nominal strain ε (a); strain ε during test time (b); true local value of membrane force F/w versus local strain ε11 along test direction (c)

Full size image
Fig. 5
figure 5

Mechanical behavior of synthetic mesh samples with different markers along direction B: nominal membrane force F/w0 versus nominal strain ε (a); strain ε during test time (b); true local value of membrane force F/w versus local strain ε11 along test direction (c)

Full size image

Results indicated as “no marker” refer to nominal values recorded by WinTest software in Figs. 4a and 5a, while they represent the results of video frame post-processing at five time instants or strain levels, respectively in Figs. 4b and 5b or Figs. 4c and 5c. SDs associated to experimental data are reported as a light-colored band in the positive range only, except in the case of video post-processing results, where SDs are displayed as error bands. As in the previous graph for silicone, in Figs. 4c and 5c, vertical band refers to SD associated to F/w and horizontal band indicates SD associated to ε11. Results of statistical analysis are reported in Tables 2 and 3 for directions A and B respectively.

Table 2 Mann-Whitney U test for synthetic mesh in direction A, comparing nominal (F/w0) or true (F/w) membrane force at different strain levels (ε = 0.1; ε = 0.2) with different markers (NC no marker, C cyanoacrylate, A acrylic paint, L lacquer, MSB medical spray band)
Full size table
Table 3 Mann-Whitney U test for synthetic mesh in direction B, comparing nominal (F/w0) or true (F/w) membrane force at different strain levels (ε = 0.1; ε = 0.2) with different markers (NC no marker, C cyanoacrylate, A acrylic paint, L lacquer, MSB medical spray band)
Full size table

In Figs. 3b, 4b and 5b, a time instant corresponds to the same elongation for each sample, since a constant strain rate is applied.

4 Discussion

In order to verify the reliability of the test procedure proposed in this work, nominal and true local values of stress versus strain can be compared in the case of silicone (Fig. 2a). For strain higher than 8%, an increasing difference is measured between nominal and true local values at increasing strain. These data provide an idea of the approximation induced by considering nominal values only. Indeed, local strain in the test direction is slightly higher than nominal strain, since the deformation of the sample is free in its central region, while it is about 5% smaller near its ends, due to the constraint provided by the grips. Local measurements allow also evaluating the progressive transverse contraction of the sample, producing a value of true stress higher than nominal stress, at the same strain level. In Fig. 2b, the tangent modulus of silicone calculated from experimental data of nominal and true local strain can be compared with the tangent modulus measured by the manufacturer in compliance with DIN 53504. According to this standard, “dog-bone” shaped specimens are tested to achieve a uniform stress distribution in the center of the sample and contact extensimeter is used to measure local deformation. It can be clearly noticed that local measurements in the configuration adopted in this work can be compared to technical data in compliance with test standards, thus supporting the reliability of this test procedure.

The effect of different markers on silicone has then been investigated (Fig. 3). The global mechanical response of this material, reported in terms of nominal membrane force versus nominal strain (Fig. 3a), does not show significant variations at 10% and 20% strain depending on the use of different markers (Table 1). However, considering the trend of strain versus test time (Fig. 3b), a smaller strain is always detected from markers with respect to the assigned strain, differently from what expected, as discussed above. This deviation of the mechanical behavior depends on the specific marker and suggests that sample deformation is reduced in its central region, due to a stiffness increase that raises when applying, in the order, lacquer, physical markers with medical spray band or physical markers with cyanoacrylate. This effect is enhanced by analyzing the true local value of membrane force versus local strain (Fig. 3c), where a significant stiffness increase is found with physical markers attached with medical spray band and cyanoacrylate. Both at 10% and 20% strain, the true local value of membrane force with lacquer markers is lower than with physical markers attached to the sample surface. In this case, the response with physical markers with the two different gluing methods does not provide any significant difference.

Considering the mechanical behavior of synthetic mesh in direction A (Fig. 4a), the nominal membrane force does not show significant difference at 10% strain depending on the use of different markers (Table 2). At 20% strain, both in the case of physical markers attached with medical spray band and cyanoacrylate, higher membrane force values are found with respect to the sample without markers. Moreover, results with cyanoacrylate show a significant difference form the ones without markers (p value < 0.01) and with acrylic paint or lacquer (p- alue < 0.05). This effect seems to be even more pronounced at higher strain levels, which were not analyzed in detail by statistical analysis because such strain level is not reached in vivo by surgical meshes [30] and therefore is less appropriate for this investigation. Figure 4b shows that a slightly higher strain is measured directly form mesh knot displacements with respect to the assigned strain. Contrarily, the strain detected from markers is always lower than assigned strain, suggesting that all kind of markers induce a stiffening of the central area of the sample, being stiffer, in the order, with cyanoacrylate, medical spray band, lacquer and acrylic paint. The same behavior is confirmed also in Fig. 4c, where the effect of cyanoacrylate is particularly evident. As highlighted also by statistical analysis, the mechanical response is significantly different when attaching physical markers with cyanoacrylate, both from the response without any marker and with other kinds of markers. Moreover, in this case, the comparison with local strain measurements from mesh knot displacements shows that all different kinds of markers induce a modification in the mechanical response of this samples. This can be correlated with mesh structure, since knot tightening mechanism can be strongly affected by the deposition of paints that solidify, such as acrylic paint and lacquer, or glues, like cyanoacrylate and spray band, able to limit the sliding of mesh fibers in knots during mesh traction. In conclusion, in this case, the solution which is expected to interfere less with the native mechanical behavior of surgical mesh is acrylic paint, which is probably slightly more compliant than lacquer after drying.

Concerning synthetic mesh in direction B (Fig. 5), the effect of different markers is similar, even if less pronounced than in direction A. The global mechanical response in terms of nominal membrane force versus nominal strain (Fig. 5a) does not present significant variations at 10% and 20% strain (Table 3). The strain measured with different markers in Fig. 5b are similar to assigned strain, except than in the case of cyanoacrylate. For any marker configuration, the local response in direction B (Fig. 5c) is comparable with local measurements from mesh knot displacements, while it appears significantly different when using cyanoacrylate to attach markers. These data highlight that the use of cyanoacrylate for markers attachment has a significant stiffening effect, which can have a strong impact on the mechanical response of biomedical materials tested with this technique, especially if presenting high anisotropy or inhomogeneity, such as in the case of surgical meshes. The stiffening effect of cyanoacrylate is more evident in case of softer materials, while it could have limited effects on more stiff samples. In this sense, the use of this glue could be particularly critical when testing soft materials, as specific biomedical polymers, whose mechanical response is altered by the attachment of markers. Probably, the same issues could be extended to soft biological tissues, where cyanoacrylate is often used as adhesive substance. In this regard, further tests should be carried out to study the effect of different markers on biological tissues, where local strain measurement may be complex due to the variability of sample surface properties and tissue hydration.

Another aspect to mention is related to the effect of the size of markers and their relative distance, despite the fact that a quantitative analysis is not developed in this work. Indeed, with the increase of marker size and the reduction of their relative distance, the local stiffness of the material is likely to become higher. This aspect can be critical when dealing with small samples, since the area of strain measurement is necessarily reduced and markers must be positioned closely one to the other. With bigger sample size, the area of local measurement can be extended, thus overcoming this issue.

5 Conclusions

This study is aimed at investigating the effects of different solutions for markers to determine the local mechanical behavior of biomedical polymers during tensile tests. By analyzing the results, different trends have been clearly highlighted. In general, the global mechanical response of tested materials is not affected by the type of markers and gluing technique, up to 20% strain, which can be assumed as a physiological strain range for biomedical materials in vivo. Nonetheless, when markers are joined to the sample with cyanoacrylate, softer materials show a stiffening even at about 20% strain. By observing the true local behavior of the analyzed materials, results show that the technique used to draw or apply the marker affects the local mechanical response of the material. This effect is more pronounced for cyanoacrylate, which can be considered the major cause of sample stiffening after markers attachment. Nonetheless, especially in the case of surgical mesh tested in its more compliant direction, all kinds of markers induce a modification in the local mechanical response, probably because both paints and glues limit the sliding of mesh fibers during knot tightening in tensile mode.

This study presents some limitations, as it was carried out for few materials and at a single strain rate. However, it is reasonable that the present findings can characterize also experimental results on other similar materials or for different strain rates. The results of this study can be useful in planning mechanical tests on biomedical materials and could avoid errors in the characterization of their mechanical behavior. Similarly, the feasibility of these techniques could be also throughout evaluated in the case of tensile testing of soft tissues.