1 Introduction

In PET tomography, a radioactive isotope containing emitting positrons is fed into the body to produce a body’s metabolism map. Due to annihilation between a positron and an electron, a pair of γ-rays is emitted in opposite directions along a line at each spatial coordinate. Emission follows a Poisson law [1]. Each pair of γ-rays is revealed by a detector unit, i.e. a coincidence detectors pair placed in an array of detector units surrounding the body. In the PET reconstruction, when using iterative-based algorithms, the goal is to obtain the maximum likelihood (ML) estimate of the emission density from the coincidence measurements at any line uniformly distributed in angle. Since the introduction of the ML expectation maximization (EM) approach to emission image reconstruction from projections, the statistical reconstruction of PET images based on the Poisson model has been studied extensively [2–4]. The assumption that the emission occurs according to Poisson statistics is widely accepted, but the formulation of ML reconstruction based on a Poisson model is supported only by an idealized PET scanner [5]. In routine use PET scanners, deviation from Poisson statistics occurs and has different causes. Such causes can compromise accuracy in determining the system matrix when not suitably accounted for. One cause of deviation from Poisson statistics is the correction of scatter and random coincidences on the projection data (sinograms) [4, 6]: once corrections are applied, the data are no longer Poisson distributed. It compromises the estimation of the emission density based on ML reconstruction [7, 8]. The introduction into the system matrix of physical effects, such as positron range, dead-time and pile-up, non-colinearity, variation in detection-pair sensitivity [9, 10], can cause changes in the Poisson-based models [11]. In literature, several statistical image reconstruction algorithms are proposed that take into account the non-exactly Poisson statistic of the emission data; the proposed models are approximations of the Poisson [19], shifted Poisson [8], or Gaussian models [5, 12, 13]. In such papers an improvement in the model accuracy and/or in the computation are demonstrated; however, no quantitative evaluation of deviation from Poisson statistics is defined.

Modern PET scanners and novel prototypes use EM-based algorithms that preserve the Poisson nature of the data taking into account the scatter and random estimates during the reconstruction process [14]. However, such statistical algorithms produce bias and higher variability in applications where images are reconstructed from a relatively small number of counts [15–17]. It is an important aspect to take into account, especially for cold regions and/or dynamic PET data reconstruction; in fact, bias and variability of reconstructed data can lead to an incorrect activity evaluation and to inexact kinetic parameters estimate. An accurate evaluation of the deviation of the measured data from Poisson statistics could lead to an appropriate correction, reducing bias and variability. In digital image acquisition, in addition to the stochastic nature of the photon-counting, the intrinsic thermal and electronic noise should be accounted for. Such sources of artefacts are usually described by a Poisson model corrupted with additive Gaussian noise [18, 19]. Statistical properties of PET measured data must be known when denoising operations are necessary. Usually denoising methods are based on the hypothesis of the presence of white Gaussian noise. In order to maintain such assumption, a variance stabilizing transformation (VST) is performed in non-Gaussian data that transforms non-Gaussian process in a Gaussian one [20]. Also in this case, the statistics of data must be accurately known, in fact the expression of VST varies according to the statistic of the data [21]. Therefore, a method that accurately defines the statistics of PET measured data, also in the conditions of deviations from Poisson statistics, has important implications in quantitative evaluation of PET data.

The Negative Binomial (NB) distribution model has been studied extensively in monitoring the over-dispersion (or variance that exceeds the mean) of the data [22–25]. Applications of the NB distribution model range from epidemiology and biology [26] to bioinformatics [27, 28] in low counting rate (λ < 20). Beyond such a range of values, to our knowledge, its use remains unexplored. The importance of the NB model to approximate the statistical behavior of PET measurements, pre-corrected for attenuation and accidental coincidences, was firstly proposed in [29]. In such paper the authors focused their simulation to test new estimators of activity using a fixed value for the NB parameters. Conversely, the goal of our paper was twofold: to exploit the accuracy of the NB dispersion parameter estimation and to test the NB model to assess the statistics of PET projections (collected into sinograms) in a wide range of emission rates and noise combinations. We focused on uncorrected and corrected (random and scatter coincidence correction) sinograms.

In the present work, two Monte Carlo simulations were carried out: the first one was performed for evaluating and characterizing the α parameter estimator; in this simulation NB-data are generated and the mean and dispersion parameter are estimated according to the maximum likelihood estimation method. The second Monte Carlo simulation was performed for generating measurement PET data from an emission phantom in the sinogram domain, for correcting them from scatter and accidental emissions, and for evaluating the statistical properties of the resulting data. Finally, in order to evaluate the potential of the NB model to improve image quality, the conventional expectation maximization–maximum likelihood (EM-ML) reconstruction algorithm was applied on the simulated sinograms and the quality of resulting images was compared.

2 Materials

2.1 Measurement Model

To assess deviation from Poisson statistics, we need to relate emitting points in the object plane to their projection in the sinogram. It allows relating the statistics in the sinogram to the activity fed into the body.

It is well-known that data acquired in the object plane along lines-of-responses (LORs) consist of a set of projections, covering the sinogram plane according to the following relationship:

$$\lambda (z,w) \to P(l,\theta )$$
(1)

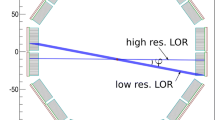
where \(P(l,\theta )\) is the one-dimensional projection of the two-dimensional object function \(\lambda (z,w)\) along LORs at an angle \(\theta\)(−π ≤ θ < π), when l varies from −L to L for a field of view (FOV) of diameter 2L. Each projection profile fills a column in the sinogram; columns are filled as the angle \(\theta\) varies. As an example (Fig. 1), a cylindrical phantom of radius r < L, placed in the center of the FOV, is related to a rectangular area in the sinogram, extending from −r to + r (row) and from \(- \pi\) to \(\pi\) (column). For a cylindrical phantom containing uniform activity, the amplitude of the sinogram will reach its maximum at l = 0 for any \(\theta\), that is the projection \(P(0,\theta )\) for (−π ≤ θ < π) corresponding to the LORs crossing the phantom at any angle along its diameter. At increasing l values (|l| > 0) the relevant projections assume lower amplitudes with respect to its maximum in the row at l = 0. In Fig. 1b a schematic representation of the sinogram is shown, it includes only the geometrical delimitations of the phantom projections and not the sinogram amplitudes. The line in the sinogram corresponding to the maximum value is schematically highlighted in Fig. 1b with a thick line. By choosing the row at l = 0 in the sinogram, a link with the object placed at the center of the scanner is established. Then, a cylindrical phantom in the center of the bore in the scanner works as a sort of ‘input function’ to characterize the overall projection system.

Fig. 1
figure 1

Schematic representation of the relationship between object plane and sinogram for a cylindrical phantom placed into the center of the FOV of a PET scanner. The emissions sum along the red line in a corresponds to the red point into the sinogram in b

Full size image

The measurement model we use in (1) includes the following noise terms:

$$P(l,\theta ) = P_{T} (l,\theta ) + RC(l,\theta ) + SC(l,\theta )$$
(2)

where \(P_{T} (l,\theta )\) represents the true emission counts and RC and SC are the accidental (random) and Compton (scatter) coincidences, respectively.

Usually, PET scanners detect coincidences during ‘prompt’ and ‘delayed’ windows. Prompt coincidences represent true coincidences corrupted by random plus scatter events, while delayed coincidences represent random events only. In conventional image reconstruction, random corrections are made by subtracting delayed coincidences from the total events [7]. Such an approach is expected to contribute to deviation from Poisson statistics. We recall that random events occur when two distinct annihilations produced at two distinct locations are detected by a detector pair within the same time window. These uncorrelated events raise the background on the images, growing with the square of the activity and with the increase in coincidence timing window.

Scatter corrections are performed after random corrections, by a post-processing technique. Scatter coincidences arise from annihilations for which photons deviate from their original directions and contribute to producing false counts. The scatter component increases with the activity and is not influenced by the time window width. These behaviours, similar to those encountered in true coincidence detection, make the scatter correction a big challenge. Correction for scatter events is supported by extensive literature [30]. Scatter correction can be performed by subtracting the modelled scatter events from the total sinogram during the post-processing phase. The simplest scatter correction method is based on the assumption that spatial distribution of scatter is modelled by fitting a Gaussian function to each projection profile in the sinogram. More accurate methods exist, such as the single-scatter simulation (SSS) [10, 31]: an estimate of scattered events distribution and the relevant contribution in the sinogram can be derived using information from data relevant to the total sinogram and the attenuation and from computer modelling of the photon interaction physics. Anyway, whatever the scatter model used, scatter correction contributes to deviation from Poisson statistics.

In this paper we focus on the effect produced by correction for random and scatter events in the sinogram domain, and quantitatively characterize such effects, due to their importance in quantitative analysis of PET data [6, 32]. Without loss of generality, let us consider the corrected two-dimensional radioactivity distribution discretized into a matrix of nb × na (number of bins per number of angles) points \(P_{C} (\Delta l,\Delta \theta )\). A single line in the sinogram can be modelled as a vector y such as: \({\mathbf{y}} = y_{1} ,y_{2} , \ldots y_{na}\) where na is the number of angles in the projection of the two-dimensional object.

2.2 Negative Binomial distribution

The importance of NB distribution is due to its peculiarity to model count data with different degrees of over-dispersion, i.e. deviation of the variance value respect to the mean value.

For a single line in the sinogram, we can express the NB distribution in terms of two parameters: the mean of the y vector, \(\bar{y}\), and the parameter k as follows [22]:

$$P(Y = y;\bar{y},k) = \frac{{\varGamma (\bar{y} + k)}}{\varGamma (k) \cdot y!}\left( {\frac{k}{{\bar{y} + k}}} \right)^{k} \left( {\frac{{\bar{y}}}{{\bar{y} + k}}} \right)^{y} ,\;\bar{y} > 0,k > 0,y = 0,1, \ldots$$
(3)

where Γ is the gamma function and y is a nonnegative integer value.

From the probability density function of the NB distribution, it appears that the k parameter is an essential part of the model. Estimation of k is important to estimate deviations from Poisson distribution.

For a more direct identification of the over-dispersion, it is useful to use the transformation: \(\alpha\) = 1/k, where \(\alpha\) > 0 is the over-dispersion parameter. The mean of the NB distribution is \(\bar{y}\) (like Poisson distribution) and, using the method of moments [33], the variance \(\sigma^{2}\) is:

$$\sigma^{2} = \bar{y}\left( {1 + \alpha \bar{y}} \right)$$
(4)

As \(\alpha\) gets small in respect to \(\bar{y}\), the NB distribution converges to a Poisson distribution, being \(\sigma^{2} = \bar{y}\) for \(\alpha\) = 0. This means that the NB distribution is more general than the Poisson distribution. We will use \(\bar{y}\) and \(\alpha\) parameters to quantitatively characterize measured PET data statistics.

2.3 ML Estimation of the Dispersion Parameter α

Several mathematical methods can be used for estimating the parameters of NB distribution [24, 25, 33]. The challenge of estimating the dispersion parameter α for the NB distribution is that the estimating equation has multi-roots. In [25], the maximum likelihood estimation (MLE) method is proposed which actually can always give a unique solution based on a fixed-point iteration algorithm. It is derived by using the log-likelihood \(l(\bar{y},\alpha )\) of the probability density function (3) over na samples:

$$l(\bar{y},\alpha ) = na^{ - 1} \sum\limits_{i = 1}^{na} {\left[ {y_{i} \log (\bar{y}) - \left( {y_{i} + \alpha^{ - 1} } \right)\log \left( {1 + \alpha \bar{y}} \right) + \sum\limits_{\nu = 0}^{{y_{i} - 1}} {\log \left( {1 + \alpha \nu } \right)} } \right]} ,\alpha > 0$$
(5)

The MLE solution of Eq. (5) yields the estimated mean \(\hat{\bar{y}}\) and sample dispersion \(\hat{\alpha }\). In this study, the estimation is obtained by using the MatlabFootnote 1 function “nbinfit” on Eq (5). The nbinfit function returns the MLEs for the parameters of the negative binomial distribution.

The bias (bias) and the standard deviation (std) of the dispersion parameter \(\hat{\alpha }\) are useful indices for characterizing the performance of the ML estimator.

The bias is defined as follows:

$$bias = \frac{1}{N}\sum\limits_{i = 1}^{N} {\hat{\alpha }_{i} - \alpha = \bar{\alpha } - \alpha }$$
(6)

where the average operation is performed over N repetitions of the same experiment, \(\hat{\alpha }_{i}\) is estimated at each repetition over a sample of size na, and \(\bar{\alpha }\) is the sample mean calculated over the \(\hat{\alpha }_{i}\) (i = 1,…,N) estimates.

The std is defined as follows:

$$std = \sqrt {\frac{1}{N - 1}\sum\limits_{i = 1}^{N} {(\hat{\alpha }_{i} - \bar{\alpha })^{2} } }$$
(7)

3 Methods

3.1 Dispersion Parameter α Evaluation and Characterization

To evaluate and to characterize the α parameter estimator, we used Monte Carlo simulation, in accordance with the procedure adopted in previous works on this topic [22, 24, 25]. In those reports the α parameter values were estimated in the low range of \(\bar{y}\) (\(\bar{y} < 20\)). In this paper, we extend the analysis of \(\bar{y}\) to much higher values to support interpretation of PET projections data.

The Monte Carlo simulation was produced according to the following steps:

  1. 1.

    Generation of repeated NB data, combining the following parameters: sample size, na, ranging from 200 to 1000; true mean, \(\bar{y}\), ranging from 1 to 2000; variance, \(\sigma^{2}\), ranging from 1 to 7 times the \(\bar{y}\) value. NB data are generated with the Matlab function “nbinrnd”.

  2. 2.

    For each combination of na, \(\bar{y}\) and \(\sigma^{2}\), the following estimations were performed:

    • \(\hat{\alpha }\) estimation over the sample size na, each estimation was repeated 300 times

    • evaluation of the mean \(\bar{\alpha }\) over the \(\hat{\alpha }_{i}\) values estimated at the previous step

    • bias evaluation using Eq. (6)

    • std evaluation over \(\hat{\alpha }_{i}\) estimates using Eq. (7).

3.2 Sinogram Data Generation and Statistical Analysis

Emission sinograms were generated by projection of two-dimensional radioactivity distribution functions into sinograms (true coincidences). On each sinogram, both random and scatter coincidences were added to account for theoretical and experimental evidence [34]. A simple model of attenuation was applied based on the knowledge of the attenuation coefficient \(\mu\) and the phantom dimensions.

As far as the measurement system, we simulated an ideal condition with: ideal detectors with equal sensitivity, efficiency, and detection cross section.

We used Monte Carlo simulation according to the model in (2).

In the simulation, the following properties and dimensions were used:

  • uniform cylindrical phantom with radius of 10 cm and length of 15 cm, in a circular FOV of 70 cm in diameter;

  • total number of pixels on the image plane: nz × nw = 128 × 128

  • number of points for each projection nb = 186; number of angles na = 360, from −π to π

  • pixel dimension on the image plane: 5.5 × 5.5 mm2

  • plane thickness: 3.2 mm

  • activity per voxel \(\lambda\): from 0.1 to 200 Bq/voxel

  • mSin index: defined as the maximum value evaluated on the sinogram data points

  • random coincidence events (RC): from 10 to 50% of mSin

  • scatter coincidence events (SC): from 10 to 50% of mSin

  • attenuation coefficient: \(\mu\) = 0.1 cm−1.

For any combination of \(\lambda\) and (RC + SC) values, two sinograms were generated: the total sinogram \(P(\Delta l,\Delta \theta )\)(discrete formulation of \(P(l,\theta )\) in Eq. (2)), and the corrected sinogram \(P_{C} (\Delta l,\Delta \theta )\) (discrete formulation of \(P_{C} (l,\theta )\)).

Note that, given an injected activity per voxel value \(\lambda\), data projection operation generates a sinogram corresponding to the count of coincidences detected by the ideal acquisition system. According to Eq. (1), in the coming text we will relate the parameters extracted from sinogram analysis to the injected activity per voxel \(\lambda\).

Total sinogram \(P(\Delta l,\Delta \theta )\) was obtained by projection of an object whose emission obeys Poisson distribution with a mean level of activity per voxel λ. On each sinogram, the attenuation effect is included. Then, a combination of random and scatter events (RC + SC) was added to obtain the total uncorrected sinogram.

Random coincidences were generated as Poisson events identically distributed in the sinogram, whose mean value is chosen as a percentage of mSin. Scatter spatial distribution in the sinogram was generated according to the single-scatter simulation (SSS) model, as described in [31].

The corrections for random and scatter coincidences were accomplished via noise subtraction from \(P(\Delta l,\Delta \theta )\) and the following corrected sinogram (\(P_{C} (\Delta l,\Delta \theta )\)) was obtained:

$$P_{C} (\Delta l,\Delta \theta ) = \left[ {P(\Delta l,\Delta \theta ) - RC(\Delta l,\Delta \theta )} \right] - SC(\Delta l,\Delta \theta )\;\Delta l = 1, \ldots nb\;\Delta \theta = - \pi , \ldots ,\pi$$
(8)

On the simulated \(P(\Delta l,\Delta \theta )\) and \(P_{C} (\Delta l,\Delta \theta )\) a Region-Of-Interest (ROI) was selected in the middle of the sinogram. In the simulation, the ROI coincides with the central line, organized in a vector y of na points. As previously pointed out, for a homogeneous circular object, the central line is relevant to the sum of the phantom contributions situated along its diameter, at each angle θ.

The procedure was repeated N = 50 times for each λ, RC and SC values, and the relevant ensemble statistic was evaluated. For the central line of the sinogram \(P_{C} (0,\Delta \theta )\) data, the ensemble statistic includes the evaluation of the ensemble average \(\bar{Y}_{c}\) of the estimated NB parameter \(\bar{y}\) and the ensemble average \(\bar{\alpha }\) of the NB parameter \(\hat{\alpha }\).

3.3 Data Reconstruction Analysis

In order to evaluate the potential of the NB model to improve image quality, the conventional expectation maximization–maximum likelihood (EM-ML) reconstruction algorithm was applied on all the simulated sinograms. The “eml_em” code, included into the irt (image reconstruction tool) software tool [35] was used for reconstructing images from the sinograms. The “eml_em” function in the tool includes the option for random and scatter correction during the reconstruction, subject to supplying maps of random and scattering events.

Comparisons among reconstructed data were made for all λ, RC % and SC % values, for the three classes of data: data not corrected (i.e. starting from \(P(\Delta l,\Delta \theta )\)), data corrected before reconstruction (i.e. starting from \(P_{C} (\Delta l,\Delta \theta )\)), data not corrected but using correction model inside the reconstruction \((P(\Delta l,\Delta \theta ) + CDR)\), where CDR means ‘correction during reconstruction’. As performance index, the mean square error (MSE) between the reconstructed images and the discrete phantom image \(\lambda (\Delta z,\Delta w)\) was evaluated. For each class of data, the MSE was normalized to the maximum among the three curves.

3.4 Phantom Sinograms Analysis

Phantom study was performed using sinograms available in the EM-MC database, generated with the PETEGS software package that includes realistic PET clinical studies [36].

The phantom consists of a NEMA uniform cylinder (10 cm radius, 18 cm length), filled with a homogeneous 18F water solution (100 MBq of total activity) and acquired with a GE-Advance PET tomograph. We considered the total (true coincidences + scatter events) and scattered simulated sinograms, with nb = 283 and na = 336, from −π to π. The total sinogram does not include random coincidences. The analysis on phantom data was performed in two steps.

First, the total sinogram \(PP(\Delta l,\Delta \theta )\) was analyzed within a ROI placed at the center of the sinogram. The ROI was constituted by one row from which a vector of na = 336 data points was constructed. Data analysis consisted in the same procedure applied to simulated sinogram data.

In a second step, we generated and analyzed the corrected sinogram \(PP_{C} (\Delta l,\Delta \theta )\). Corrected sinogram was generated according to Eq. (8), by subtracting the scatter sinogram SC(∆l, ∆θ), available in the database, to the total events sinogram.

The same statistical analysis performed on the simulated sinograms, was done on the phantom data \(PP(\Delta l,\Delta \theta )\) and \(PP_{C} (\Delta l,\Delta \theta )\).

4 Results

4.1 Dispersion Parameter Estimator Behaviour

In Fig. 2 the sample mean \(\bar{\alpha }\) of the estimated values \(\hat{\alpha }_{i}\) (i = 1,…,N), and the standard deviation (std) are shown, in logarithmic scale, as function of the true mean (\(\bar{y}\)) for three sample variance values (\(\sigma^{2}\) = 1* \(\bar{y}\), 4* \(\bar{y}\), 7* \(\bar{y}\)), and two sample sizes: na = 200 in Fig. 2a and na = 1000 in Fig. 2b. The std was evaluated according to Eq. (7). A blow-up of the plots for \(\bar{y} \le 100\) are shown in the top of the figures.

Fig. 2
figure 2

Lower row log of the estimated mean and std of the simulated dispersion parameter \(\alpha\), vs the true mean (\(\bar{y}\)), for three \(\sigma^{2}\) values; a sample size na = 200, b sample size na = 1000; upper row a blow-up of the plots for \(\bar{y} \le 100\)

Full size image

Figure 3 shows, in logarithmic scale, the bias of ML estimator of the dispersion parameter \(\alpha\) (bias), as function of the true mean (\(\bar{y}\)), for three variance values (\(\sigma^{2}\) = 1* \(\bar{y}\), 4* \(\bar{y}\), 7* \(\bar{y}\)) and two sample size values: na = 200 in Fig. 3a and na = 1000 in Fig. 3b). The bias was evaluated according to Eq. (6). A blow-up of he plots for \(\bar{y} \le 100\) are shown in the top of the figures.

Fig. 3
figure 3

Lower row log of the bias of the simulated dispersion parameter \(\alpha\), vs the true mean (\(\bar{y}\)), for three \(\sigma^{2}\) values; a sample size na = 200, b sample size na = 1000; upper row a blow-up of the plots for \(\bar{y} \le 100\)

Full size image

4.2 Simulated Sinogram Data Results

In Fig. 4 an example of \(P(\Delta l,\Delta \theta )\) and \(P_{C} (\Delta l,\Delta \theta )\) generation steps is shown, with average activity per voxel \(\lambda\) = 50, RC = 10% and SC = 30% of mSin. In particular the following steps are shown: in 4a the attenuated-true events projection, in 4b the \(RC(\Delta l,\Delta \theta )\) sinogram, in 4c the \(SC(\Delta l,\Delta \theta )\) sinogram, in 4d the resulting \(P(\Delta l,\Delta \theta )\), and in 4e the \(P_{C} (\Delta l,\Delta \theta )\) obtained according to Eq. (8).

Fig. 4
figure 4

An example of the procedure used to generate uncorrected and corrected sinograms. a Attenuated-true events projection P T (Δl,Δθ); b random coincidence events sinogram RC(Δl,Δθ); c scattering coincidence events sinogram SC(Δl,Δθ); d total events sinogram P(Δl,Δθ); e corrected sinogram P C (Δl,Δθ) obtained according to Eq. (8)

Full size image

In Fig. 5 estimated \(\bar{\alpha }\) values and std, in log scale, on \(P_{C} (\Delta l,\Delta \theta )\) data, for different values of average activity per voxel \(\lambda\) and  % of combinations of RC(Δl, Δ θ) and SC(Δl, Δθ) events are shown. In Fig. 5a–c the SC value was fixed at SC = 10, 30 and 50%, respectively, and the trends of estimated \(\bar{\alpha }\) is shown for three RC values (RC = 10, 30 and 50%). In Fig. 5d, the RC value was fixed at RC = 30% and the curves are relevant to three SC values (SC = 10, 30 and 50%). As previously pointed out, the estimated \(\bar{\alpha }\) was related to the injected activity per voxel \(\lambda\) in accordance with Eq. (1). Both axes are in log scale.

Fig. 5
figure 5

Estimated (\(\bar{\alpha }\)) values and std, in log scale, on \(P_{C} (\Delta l,\Delta \theta )\) data, for different values of \(\lambda\) and  % of combinations of RC and SC event. a Fixed SC = 10%, three values of RC (RC = 10, 30 and 50%); b fixed SC = 30%, three values of RC, as in a; c fixed SC = 50%, three values of RC, as in a; d fixed RC = 30%, three values of SC (SC = 10, 30 and 50%). Both axes are in log scale

Full size image

Figure 6 shows the trend of the estimated \(\bar{\alpha }\) values vs the mean counts \(\bar{Y}_{c}\) in the sinogram ROI. Both the axes are in log scale. The curves are relevant to percentages of noise (SC + RC) values ranging from 20 to 100% of mSin, obtained with different combination of RC and SC values. For instance the percentage of noise (RC + SC) = 40% comes from RC = 10% and SC = 30% or, vice versa, from RC = 30% and SC = 10%. Each curve in Fig. 6 is the average among the possible combinations of SC and RC used to reach one among the percentages of noise values.

Fig. 6
figure 6

Estimated \(\hat{\alpha }\) values vs \(\bar{Y}_{c}\) for different noise level values; both the axis are in log scale

Full size image

4.3 Data Reconstructed Analysis Results

Data reconstruction was performed according to the conventional EM-ML algorithm with the number of iterations equal to 25, that guarantees the algorithm convergence. In Fig. 7 reference and reconstructed images are shown for λ = 50, RC = 10% and SC = 30%: 7a reference image, 7b–d reconstructed images, respectively from \(P(\Delta l,\Delta \theta )\), \(P_{C} (\Delta l,\Delta \theta )\) and \((P(\Delta l,\Delta \theta ) + CDR)\). In Fig. 8 the normalized MSE between the reconstructed images and the discrete phantom image is shown as function of λ values (in log scale) and relevant to four representative RC % and SC % conditions. In particular, the plots are relevant to: a, RC = 10% and SC = 10%, b, RC = 10% and SC = 50%, c, RC = 50% and SC = 10% and d, RC = 50% and SC = 50%. In each figure, the MSE values obtained from \(P(\Delta l,\Delta \theta )\), \(P_{C} (\Delta l,\Delta \theta )\) and \((P(\Delta l,\Delta \theta ) + CDR)\) are shown.

Fig. 7
figure 7

Reference and reconstructed images according to the EM-ML algorithm, with \(\lambda\) = 50, SC = 10%, RC = 50%. a Reference image; b image reconstructed starting from \(P(\Delta l,\Delta \theta )\); c image reconstructed starting from \(P_{C} (\Delta l,\Delta \theta )\); d image reconstructed starting from \((P(\Delta l,\Delta \theta ) + CDR)\)

Full size image
Fig. 8
figure 8

Normalized MSE values (in a.u.) evaluated on reconstructed images with the EM-ML algorithm starting from \(P(\Delta l,\Delta \theta )\) and \(P_{C} (\Delta l,\Delta \theta )\) sinograms, for different values of: \(\lambda\),  % of combinations of RC and SC event, and reference sinograms. a SC = 10% and RC = 10%, b RC = 10% and SC = 50%, c RC = 50% and SC = 10%, d RC = 50% and SC = 50%. λ values are in log scale

Full size image

4.4 Phantom Sinogram Analysis Results

In Fig. 9, the \(PP(\Delta l,\Delta \theta )\) and the corrected \(PP_{C} (\Delta l,\Delta \theta )\) sinograms are shown.

Fig. 9
figure 9

Physical-phantom’s sinograms, a uncorrected \(PP(\Delta l,\Delta \theta )\), b corrected \(PP_{C} (\Delta l,\Delta \theta )\)

Full size image

Table 1 shows the statistical analysis results relevant to the phantom sinograms. The mean \(\bar{y}\) and the estimated \(\hat{\alpha }\) dispersion parameters where evaluated according to Eq. (5), the variance (\(\sigma_{{\bar{y}}}^{2}\)) was evaluated according to Eq. (4). The estimated \(\bar{y}\) and \(\sigma_{{\bar{y}}}^{2}\) were evaluated on both uncorrected \(PP(\Delta l,\Delta \theta )\) and corrected \(PP_{C} (\Delta l,\Delta \theta )\) sinograms; the \(\hat{\alpha }\) parameter was evaluated on \(PP_{C} (\Delta l,\Delta \theta )\).

Table 1 Phantom sinogram statistical analysis results
Full size table

5 Discussion

This paper documents an attempt to use the NB distribution model to describe the measured PET data for a wide range of emission rates and noise levels. To support such objective, firstly a series of NB distributions were simulated for different values of the mean and the dispersion parameter. The mean and the dispersion parameters were evaluated using the MLE method. According to simulations the dispersion parameter \(\alpha\) appears a good estimator that well characterizes the deviation of the data from Poisson statistics.

The \(\alpha\) estimator previously characterized was used to assess the deviation from Poisson distribution of corrected sinogram data for different noise compositions. A further result of the study was the possibility to link the results of the statistical analysis performed on sinogram data, directly to the activity distribution into the phantom, according to Eq. (1). This important issue was assessed using a simplified measurement model; however, such simplified measurement model needs to be further improved by accounting for a more realistic measurement system.

A first important outcome of the paper is reported in Figs. 2 and 3. The results shown in Fig. 2 confirm previous studies performed in a different field. In particular, comparing the Fig. 2a with b, the std becomes smaller as the sample size na increases, for all the combinations of \(\bar{y}\) and \(\sigma^{2}\) values. Such results are supported by the literature showing that a small sample size can seriously affect the estimation of the dispersion parameter [33]. As \(\bar{y}\) approaches \(\sigma^{2}\) (see the blue curves), the std is higher than in the green and red curves relevant to higher degrees of overdispersion. Such evidences are likely due to the difficulty of the NB model to operate as \(\alpha\) get close to zero. In such situation it would be preferable to use the Poisson model. Moreover, as described in Eq. (4), as \(\bar{y}\) increases the dispersion \(\bar{\alpha }\) decreases. This means that for high emission values the process tends toward a Poisson one. The results shown in Fig. 3 document that the ML estimator overestimates the dispersion parameter, for any \(\bar{y}\) and na values.

The bias is largely due to the size of the true dispersion parameter: it becomes larger as \(\alpha\) decreases, and becomes smaller as sample mean increases [24]. The bias can be compensated for, as described in [24, 37]; however, in applications that do not require the nominal value of the dispersion parameter, the ML estimate can be used without corrections. A second important finding is the demonstration of the accuracy of the NB model to fit sinogram corrected data in a wide range of noise. The Fig. 5, that is relevant to corrected sinogram \(P_{C} (\Delta l,\Delta \theta )\) simulation analysis, confirms the trend of Fig. 2: as \(\lambda\) value increases, the dispersion parameter \(\bar{\alpha }\) decreases. More interesting is that such trend happens at any RC and SC combinations values. Moreover, as the  % of RC + SC noise increases, the α-value increases; this means that as the noise increases, the statistics of the sinograms move away from the Poisson distribution. Further results concern the interpretation of the std in the RC = 10% and SC = 10% curves. It results larger with respect to the other noise combinations. In reality, deviation from Poisson on corrected data with RC = 10% and SC = 10% (see Fig. 5a) is very low, and consequently the \(\alpha\) coefficient is very low. As previously discussed (see Fig. 2), the ML estimate based on NB model does not seem the best choice when \(\alpha\) approximates zero. However, as the noise increases as in Fig. 5b, c, the NB model greatly improves its performance.

The graphs shown in Fig. 6 can be a useful instrument for evaluating the noise level in the experimental corrected sinograms \(P_{C} (\Delta l,\Delta \theta )\). In fact, taking a ROI in the sinogram the Y c and \(\hat{\alpha }\) values are estimated and reported in the abscissa and the ordinate of Fig. 6, respectively. The relevant crossing point in the graph is the noise percentage in the measured PET data. We highlight that in Fig. 6 the \(\bar{Y}_{c}\) values are used as x-axis, instead of \(\lambda\) values, for emphasizing the possibility of using such graphs directly on measured data. It does not precludes the possibility of relating \(\bar{Y}_{c}\) to \(\lambda\). The numerical relationship between λ and \(\bar{Y}_{c}\) is contextual to the phantom property and geometry used in the simulation. For instance, by changing phantom dimension, spatial resolution or FOV, the correspondence between λ and \(\bar{Y}_{c}\) has to be recalculated.

We recall that the λ value herein used is the average number of disintegrations/seconds/voxel. In our simulation, it corresponds to a range of injected doses, approximately from 100 KBq to 40 MBq; typical doses used in clinical examination are included in such simulated values.

The results shown in Figs. 7 and 8 document the influence of different correction approaches on the quality of the reconstructed images using conventional EM-ML. In Fig. 7b, the image from uncorrected sinogram, \(P(\Delta l,\Delta \theta )\), appears to be the worst one, due to the contribution of uncorrected noise. The images of Fig. 7c, d, from \(P_{C} (\Delta l,\Delta \theta )\) and \((P(\Delta l,\Delta \theta ) + CDR)\) respectively, appear comparable. Previous remarks are supported by the MSE trends shown in Fig. 8. Indeed, with reference to \(P(\Delta l,\Delta \theta )\) sinogram, the MSE trend (blue lines) is in favour of correction for AC and SC noise in all the plots. By comparing the results of the procedures applied to \(P_{C} (\Delta l,\Delta \theta )\) and \((P(\Delta l,\Delta \theta ) + CDR)\) (green and red curves respectively), it appears that the \((P(\Delta l,\Delta \theta ) + CDR)\) algorithm generates a lower MSE value especially for \(\lambda > 0.1\) (red curve) with respect to the green curve (relevant to \(P_{C} (\Delta l,\Delta \theta )\) data). A possible explanation is to enquire into the deviations from Poisson due to corrections prior to the application of the conventional algorithm. Such deviations make the conventional algorithm not optimized for such unexpected scenario. Previous concerns lead us to speculate on the chance of introducing a new algorithms accounting for the actual statistics of sinogram data.

The results reported in Table 1 primarily confirm the trend observed in simulated sinograms data and support the simulation results. The estimated \(\hat{\alpha }\) > 0 on \(P(\Delta l,\Delta \theta )\) should be due to the presence of physical effects, as previously described, that lead to deviation from Poisson and this is more evident in low count conditions, as it happened on the experimental phantom data.

It is worth to note that another way to evaluate data over-dispersion is to calculate the Fano factor [38], defined as the ratio of the variance of data to its mean. However, such index is not able to characterize the statistical model, i.e., Poisson vs NB, differently from the method herein proposed.

The statistical analysis was performed on a ROI constituted by one line in the sinogram. The choice of the best number of lines aimed to establish a compromise between the minimum sample number na requested for an effective statistical analysis, from one side, and the homogeneity of the ROI data, from the other side. From a number of trials performed using a different number of lines (from a single line placed at the centre of the sinogram, to five lines crossing the centre of the sinogram), the one line solution resulted the best choice, i.e., na = 360 data samples.

With regard to the attenuation properties of the simulated phantoms, we assumed a homogeneous phantom with a constant attenuation value of μ = 0.1 cm−1, which is a typical value for tissues in the photon energy range used in PET [39].

We did not perform and analyse attenuation-corrected data, since in current PET scanners, combined with computer tomography scanners (PET/CT scanners), the attenuation correction operation is usually performed during image reconstruction [40], or on reconstructed data [41] and not on the sinogram data.

In the present work we did not include the dead-time and the pile-up events, so we did not treat their influence in the statistical behaviour of the measured PET data, although it should be interesting to analyse, and it will be a promising topic for a future work.

The NB-based analysis has been performed on 2D PET data, mainly for maintaining computational simplicity without losing the possibility of using the proposed method on a 3D dataset. In fact, it is well-known that in 2D mode, the scanner only collects direct and cross planes organized into direct planes, while in fully 3D mode, the scanner collects all, or most, oblique planes [42]. In both acquisition methods, collected data can be considered as line-integral data, as described in the model herein proposed. The main differences between 3D and 2D data are the sensitivity and the statistical noise level associated with photon counting. In particular, in 3D measurements the sensitivity is higher but, in spite of this, the scatter fraction increases from 10–15% to 30–40% [43]. 3D PET data can be rebinned, i.e. sorted in a stack of 2D data set, each one organized as sinogram [42]; in clinical PET scanners the most used rebinning algorithm is FORE, where data sorting is performed on the Fourier plane, [44]. As a consequence of rebinning operation, the resulting statistical parameter values change properly [12]. The data analysis described for 2D data can be performed on 3D data considering a spherical homogeneous phantom, by selecting a ROI in the sinogram covering a central region that includes the projections, for each angle, of the whole phantom crossing its centre. Then, the proposed statistical analysis method can be easily exploited on 3D data sets, by considering the suitable λ and noise levels.

Currently, PET scanners include the collection of emission data in list mode [45]; this allows consideration of variable interval times in the reconstruction of data; also in these cases, in order to apply routinely-used reconstruction algorithms, the sinograms are built and the described NB distribution model analysis can be performed.

In the present work, we showed a new method for characterizing the statistic of measured PET data. Moreover, we used a basic expectation maximization ML-based algorithm to compare reconstructed images in the validity of the Poisson model. It is the objective of a future work to develop a new image reconstruction technique based on NB model, in order to compare the NB-based reconstructed images with the most conventional Poisson-based reconstructed images.

6 Conclusion

In PET data analysis, the importance of accurately modeling data is paramount for helping us to understand the statistical nature of the data in order to develop efficient reconstruction algorithms and processing methods that reduce noise.

The NB distribution seems suitable for assessing the statistical nature of the sinogram data, also when they deviate from Poisson, due to its capacity to measure over-dispersion in a wide range of \(\lambda\) values.

The novelty of the present work is that the statistical model herein used can accurately describe measured PET data statistic, in a wide range of emission λ values and noise (accidental and random coincidences), and after corrections; it is useful for accurate reconstruction of PET images and for pre-filter processing. Moreover, from the NB model it is possible to estimate the α-index that describes the deviation of the measured data from the Poisson statistics. A link exists among the dispersion parameter α-values and the level of noise present in the measured data; this allows to derive the level of noise from the estimated mean and α-value.