Skip to main content
SpringerLink
Log in

Wavelet-Based Multiscale Sample Entropy and Chaotic Features for Congestive Heart Failure Recognition Using Heart Rate Variability

  • Original Article
  • Published:
Journal of Medical and Biological Engineering Aims and scope Submit manuscript

Abstract

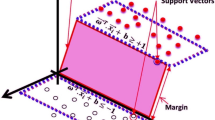
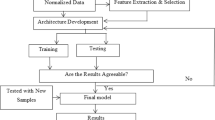
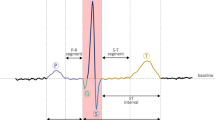
This study explores the discrimination power of a multiscale analysis method based on the discrete wavelet transform (DWT) in characterizing nonlinear features for congestive heart failure (CHF) recognition. Two DWT paradigms, namely standard DWT and DWT with reconstruction (RDWT), were employed to characterize two categories of nonlinear features, namely sample entropy (SE) and chaotic features, for CHF recognition based on heart rate variability (HRV). The performance of the wavelet-based analysis methods was compared to that of a traditional coarse grained average (CGA) method. The support vector machine was used as a classifier and the capability of the features was evaluated using the leave-one-out cross-validation method. The results show that when using solely SE features, all three multiscale analysis methods (CGA, DWT, and RDWT) with five dyadic scales outperform traditional CGA with twenty consecutive scales in characterizing HRV for CHF recognition. When using chaotic features calculated from the five dyadic scales, RDWT outperformed DWT and CGA with sensitivity, specificity, and accuracy rates of 95.45, 97.22, and 96.55 %, respectively. This performance was even superior to that obtained using both SE and chaotic features. The proposed multiscale analysis method using 5-scale RDWT and chaotic features outperforms three well-known CHF classifiers reported in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Malik, M. (1996). Heart rate variability: Standards of measurement, physiological interpretation and clinical use. Circulation, 93, 1043–1065.

    Article  Google Scholar 

  2. Asyali, M. H. (2003) Discrimination power of long-term heart rate variability measures. In Proceedings of the 25th Annual International Conference of the IEEE EMBS (pp. 200–203). Cancum, Mexico.

  3. Marwan, N., Wessel, N., Meyerfwld, U., Schirdewan, A., & Kurths, J. (2002). Recurrence-plot-based measures of complexity and their application to heart-rate-variability data. Physical Review E, 66, 026702.

    Article  Google Scholar 

  4. Sakki, M., Kalda, J., Vainu, M., & Laan, M. (2004). The distribution of low-variability periods in human heartbeat dynamics. Physica A, 338, 255–260.

    Article  Google Scholar 

  5. Skinner, J. E., Goldberger, A. L., Mayer-Kress, G., & Ideker, R. E. (1990). Chaos in the heart: Implications for clinical cardiology. Nature Biotechnology, 8, 1018–1024.

    Article  Google Scholar 

  6. Poon, C.-S., & Merrill, C. K. (1997). Decrease of cardiac chaos in congestive heart failure. Nature, 389, 492–495.

    Article  Google Scholar 

  7. Kantz, H., & Schreiber, T. (2004). Nonlinear time series analysis (2nd ed.). Cambridge: Cambridge University Press.

    MATH  Google Scholar 

  8. Costa, M., Goldberger, A. L., & Peng, C.-K. (2002). Multiscale entropy analysis of complex physiological time series. Physical Review Letters, 89, 068102.

    Article  Google Scholar 

  9. Thuraisingham, R. A., & Gottwald, G. A. (2006). On multiscale entropy analysis for physiological data. Physica A, 366, 323–332.

    Article  Google Scholar 

  10. Mallat, S. (2009). A wavelet tour of signal processing: The sparse way (3rd ed.). Burlington: Elsevier Inc.

    Google Scholar 

  11. Lee, M.-Y. and Yu, S.-N. (2012) Multiscale sample entropy based on discrete wavelet transform for clinical heart rate variability recognition. In Proceedings of the 34th Annual International Conference of the IEEE EMBS, San Diego, CA, USA (pp. 4299–4302).

  12. Richmann, J. S., & Moorman, J. R. (2000). Physiological time series analysis using approximate entropy and sample entropy. American Journal of Physiology-Heart and Circulatory Physiology, 278, H2039–H2049.

    Google Scholar 

  13. Isler, Y., & Kuntalp, M. (2007). Combining classical HRV indices with wavelet entropy measures to performance in diagnosing congestive heart failure. Computers in Biology and Medicine, 37, 1502–1510.

    Article  Google Scholar 

  14. Melillo, P., Fusco, R., Sansone, M., Bracale, M., & Pecchia, L. (2011). Discrimination power of long-term heart rate variability measures for chronic heart failure detection. Medical & Biological Engineering & Computing, 49, 67–74.

    Article  Google Scholar 

  15. Kheder, G., Taleb, R., Kachouri, A., Massoued, M. B. and Samet, M. (2009) Feature extraction by wavelet transforms to analyze the heart rate variability during two meditation technique, Chapter 32. In Advances in Numerical Methods, Lecture Notes in Electrical Engineering, New York: Springer.

  16. McClellan, J. H., Schafer, R. W., & Yoder, M. A. (2003). Signal processing first, Upper Saddle River. New Jersey: Pearson Prentice Hall.

    Google Scholar 

  17. Pincus, S. M. (1991). Approximate entropy as a measure of system complexity. Proceedings of the National Academy of Sciences USA, 88, 2297–2301.

    Article  MathSciNet  MATH  Google Scholar 

  18. Pincus, S. M. (1995). Approximate entropy (ApEn) as a complexity measure. Chaos, 5, 110–117.

    Article  Google Scholar 

  19. Pincus, S. M. (2001). Assessing serial irregularity and its implications for health. Annals of the New York Academy of Sciences, 954, 245–267.

    Article  Google Scholar 

  20. Goldberger, A. L., & West, B. J. (1987). Applications of nonlinear dynamics to clinical cardiology. Annals of the New York Academy of Sciences, 504, 195–213.

    Article  Google Scholar 

  21. Takens, F. (1981). Detecting strange attractors in turbulence in dynamical system and turbulence. Berlin: Springer.

    Google Scholar 

  22. Grassberger, P., & Procaccia, I. (1983). Characterization of strange attractors. Physical Review Letters, 50, 346–349.

    Article  MathSciNet  Google Scholar 

  23. Rosenstein, M. T., Collins, J. J., & De Luca, C. J. (1993). A practical method for calculating largest Lyapunov exponents from small data sets. Physica D: Nonlinear Phenomena, 65, 117–134.

    Article  MathSciNet  MATH  Google Scholar 

  24. Albano, A. M., Muench, J., & Schwartz, C. (1988). Singular-value decomposition and Grassberger-Procaccia algorithm. Physical Review A, 38, 3017–3026.

    Article  MathSciNet  Google Scholar 

  25. Fraser, A. M., & Swinney, H. L. (1986). Independent coordinates for strange attractors from mutual information. Physical Review A, 33, 1134–1140.

    Article  MathSciNet  MATH  Google Scholar 

  26. Kugiumtzis, D. (1996). State space reconstruction parameters in the analysis of chaotic time series—the role of the time window length. Physica D: Nonlinear Phenomena, 95, 13–28.

    Article  MATH  Google Scholar 

  27. Kim, H. S., Eykholt, R., & Salas, J. D. (1999). Nonlinear dynamics, delay times, and embedding windows. Physica D: Nonlinear Phenomena, 127, 48–60.

    Article  MATH  Google Scholar 

  28. Otani, M. and Jones,A. (2000) Automated embedding and the creep phenomenon in chaotic time series. http://users.cs.cf.ac.uk/Antonia.J.Jones/UnpublishedPapers/Creep.pdf.

  29. Cao, L. (1997). Practical method for determining the minimum embedding dimension of a scalar time series. Physica D: Nonlinear Phenomena, 110, 43–50.

    Article  MATH  Google Scholar 

  30. Wolf, A., Swift, J., Swinney, H., & Vastano, J. (1985). Determining Lyapunov exponents from a time series. Physica D: Nonlinear Phenomena, 16, 285–317.

    Article  MathSciNet  MATH  Google Scholar 

  31. Physiobank. Available: http://www.physionet.org/physiobank/database.

  32. Yeh, R.-G., Chen, G.-Y., Shieh, J.-S., & Kuo, C.-D. (2009). Parameter investigation of detrended fluctuation analysis for short-term human heart rate variability. Journal of Medical and Biological Engineering, 30, 277–282.

    Article  Google Scholar 

  33. Lee, M.-Y. and Yu,S.-N. (2010) Improving discriminality in heart rate variability analysis using simple artifact and trend removal preprocessors. In Proceedings of the 32nd Annual International Conference of the IEEE EMBS (pp. 4574–4577). Buenos Aires, Argentina.

  34. Vapnik, V. N. (1995). The nature of statistical learning theory. New York: Springer.

    Book  MATH  Google Scholar 

  35. Chou, C.-M. (2011). Wavelet-based multi-scale entropy analysis of complex rainfall time series. Entropy, 13, 241–253.

    Article  Google Scholar 

  36. Li, P., Liu, C. Y., Wang, X. P., Li, L. P., Yang, L., Chen, Y. C., & Liu, C. C. (2013). Testing pattern synchronization in coupled systems through different entropy-based measures. Medical and Biological Engineering and Computing, 51, 581–591.

    Article  Google Scholar 

  37. Kaffashi, F., Foglyano, R., Wilson, C. G., & Loparo, K. A. (2008). The effect of time delay on approximate & sample entropy calculations. Physica D: Nonlinear Phenomena, 237, 3069–3074.

    Article  MathSciNet  MATH  Google Scholar 

  38. Alcaraz, R., Abásolo, D., Hornero, R., & Rieta, J. J. (2010). Optimal parameters study for sample entropy-based atrial fibrillation organization analysis. Computer Methods and Programs in Biomedicine, 99, 124–132.

    Article  Google Scholar 

  39. Amoud, H., Snoussi, H., Hewson, D., Doussot, M., & Duchene, J. (2007). Intrinsic mode entropy for nonlinear discriminant analysis. IEEE Signal Processing Letters, 14, 297–300.

    Article  Google Scholar 

  40. Hu, M., & Liang, H. (2012). Adaptive multiscale entropy analysis of multivariate neural data. IEEE Transactions on Biomedical Engineering, 59, 12–15.

    Article  Google Scholar 

  41. Chou, Y., Zhang, A., Wang, P. & Gu, J. (2014). Pulse rate variability estimation method based on sliding window iterative DFT and Hilbert transform. Journal of Medical and Biological Engineering, 34, 347–355.

Download references

Acknowledgments

This study was supported in part by Grants NSC 100-2221-E-194-063 and NSC 101-2221-E-194-019 from the National Science Council, Taiwan.

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, National Chung Cheng University, 168 University Road, Ming-Hsiung, Chia-Yi County, 621, Taiwan

    Sung-Nien Yu & Ming-Yuan Lee

Authors
  1. Sung-Nien Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ming-Yuan Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sung-Nien Yu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, SN., Lee, MY. Wavelet-Based Multiscale Sample Entropy and Chaotic Features for Congestive Heart Failure Recognition Using Heart Rate Variability. J. Med. Biol. Eng. 35, 338–347 (2015). https://doi.org/10.1007/s40846-015-0035-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40846-015-0035-6

Keywords

Search

Navigation