Skip to main content
SpringerLink
Log in

Investigating Children’s Thinking About Suspended Balances

  • Article
  • Published:
New Zealand Journal of Educational Studies Aims and scope Submit manuscript

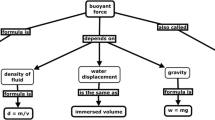
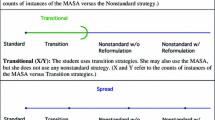
Abstract

With limited prior research on young children’s learning of the measurement of mass, the study reported in this paper provides insights that can usefully inform teaching. Close examination of the actions and conversations of 12 children of 5–7 years of age, as they experimented for the first time with suspended balance scales, led to the identification of themes presented in this paper through focused discussion of the explorations of five of the children. Stimulated by exploration and investigation of the tool, children were creative in figuring out how the tool worked, reasoned mathematically, and gave attention to some “big” ideas of mathematics. They were also able to transfer knowledge, express notions of equivalence, mathematise and generalise from their experiences. The study emphasises the importance of eliciting children’s mathematical reasoning, the value of attending to what children notice, and the need for careful and specific use of comparative terms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Australian Curriculum Assessment and Reporting Authority, ACARA. (2014). Australian curriculum: Mathematics. http://www.australiancurriculum.edu.au/mathematics/Curriculum/F-10?layout=1.

  • Barrett, J. E., Cullen, C., Sarama, J., Clements, D. H., Klanderman, D., Miller, A. L., et al. (2011). Children’s unit concepts in measurement: A teaching experiment spanning grades 2 through 5. ZDM, 43, 637–650. doi:10.1007/s11858-011-0368-8.

    Article  Google Scholar 

  • Brainerd, C. J. (1974). Training and transfer of transitivity, conservation, and class inclusion of length. Child Development, 45(2), 324–334.

    Article  Google Scholar 

  • Cheeseman, J. (2008). Young children’s accounts of their mathematical thinking. In O. Figueras, J. L. Cortina, S. Alatorre, T. Rojano, & A. Sepulveda (Eds.), Proceedings of the joint meeting of PME 32 and PME-NA (Vol. 2, pp. 289–296). Morelia: International Group for the Psychology of Mathematics Education.

    Google Scholar 

  • Cheeseman, J. (2009). Challenging mathematical conversations. In R. Hunter & B. Bicknell (Eds.), Crossing divides. Proceedings of the Mathematics Education Research Group of Australasia conference (Vol. 1, pp. 113–120). Sydney: MERGA.

    Google Scholar 

  • Cheeseman, J., & McDonough, A. (2016). Fostering mathematical curiosity. In S. Dockett & A. MacDonald (Eds.), Just do good research: Commentary on the work and influence of Bob Perry (pp. 142–151). Albury: Peridot Education.

    Google Scholar 

  • Cheeseman, J., McDonough, A., & Clarke, D. (2011). Investigating children’s understanding of the measurement of mass. In J. Clark, B. Kissane, J. Mousley, T. Spencer, & S. Thornton (Eds.), Mathematics: Traditions and [new] practices (Vol. 1, pp. 174–182). Adelaide: Australian Association of Mathematics Teachers and the Mathematics Education Research Group of Australasia.

    Google Scholar 

  • Cheeseman, J., McDonough, A., & Ferguson, S. (2014). Investigating young children’s learning of mass measurement. Mathematics Education Research Journal, 26(2), 131–150. doi:10.1007/s13394-013-0082-7.

    Article  Google Scholar 

  • Clark, A. (2007). A hundred ways of listening. Young Children, 62(3), 76–81.

    Google Scholar 

  • Clarke, D., Cheeseman, J., McDonough, A., & Clarke, B. (2003). Assessing and developing measurement with young children. In D. H. Clements (Ed.), Learning and teaching measurement: 2003 Yearbook (pp. 68–80). Reston, VA: National Council of Teachers of Mathematics.

    Google Scholar 

  • Clements, D. H. (1997). Constructing constructivism. Teaching Children Mathematics, 4(4), 198–200.

    Google Scholar 

  • Cobb, P. (1995). Mathematical learning and small-group interaction: Four case studies. In P. Cobb & H. Bauersfeld (Eds.), The emergence of mathematical meaning: Interaction in classroom cultures (pp. 25–129). Hillsdale, NJ: Lawrence Erlbaum.

    Google Scholar 

  • Common Core State Standards Initiative. (2014). Measurement and data. http://www.corestandards.org/Math/Content/MD/.

  • Davies, N., & Walker, K. (2007). Teaching as listening: Another aspect of teachers’ content knowledge in the numeracy classroom. In J. Watson & K. Beswick (Eds.), Mathematics: Essential research essential practice. Proceedings of the 30th annual conference of the Mathematics Education Research Group of Australasia (Vol. 1, pp. 217–255). Hobart: MERGA.

    Google Scholar 

  • Denmark, T., Barco, E., & Voran, J. (1976). Final report: A teaching experiment on equality (PMDC Technical Report No. 6). Tallahassee, FL: Florida State University.

  • Department for Education. (2014). National curriculum in England: Mathematics programmes of study. https://www.gov.uk/government/publications/national-curriculum-in-england-mathematics-programmes-of-study/national-curriculum-in-england-mathematics-programmes-of-study.

  • Dockett, S., & Perry, B. (2007). Trusting children’s accounts in research. Journal of Early Childhood Research, 5(1), 47–63. doi:10.1177/1476718x07072152.

    Article  Google Scholar 

  • Ernest, P. (1994). Mathematics, education and philosophy: An international perspective. London: Falmer Press.

    Google Scholar 

  • Formosinho, J., & Araujo, S. (2006). Listening to children in a way to reconstruct knowledge about children: Some methodological implications. European Early Childhood Education Research Journal, 15(2), 197–211.

    Google Scholar 

  • Hall, R. (2000). Video recording as theory. In A. E. Kelly & R. A. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 647–664). Mahwah, NJ: Lawrence Erlbaum Associates.

    Google Scholar 

  • Hipkins, K. (2009). Determining meaning for key competencies via assessment practices. Assessment Matters, 1, 4–19.

    Google Scholar 

  • Lampert, M. (1990). When the problem is not the question and the solution is not the answer: Mathematical knowing and teaching. American Educational Research Journal, 27, 29–63.

    Article  Google Scholar 

  • Lansdown, G. (2004). Participation and young children. Early Childhood Matters, 103, 4–14.

    Google Scholar 

  • Lee, S. (2012a). Thinking conversations: An open-ended and exploratory approach to assessing students’ thinking competence. New Zealand Journal of Educational Studies, 47(1), 5–17.

    Google Scholar 

  • Lee, S. (2012b). Toddlers as mathematicians? Australasian Journal of Early Childhood, 37(1), 30–37.

    Google Scholar 

  • MacDonald, A. (2010). Heavy thinking: Young children’s theorising about mass. Australian Primary Mathematics Classroom, 15(4), 4–8.

    Google Scholar 

  • Mason, J. (2010). Effective questioning and responding in the mathematics classroom. http://xtec.cat/centres/a8005072/articles/effective_questioning.pdf.

  • McDonough, A. (2002). Naive yet knowing: Young learners portray beliefs about mathematics and learning. Doctor of Philosophy PhD Dissertation, Australian Catholic University, Melbourne.

  • McDonough, A., Cheeseman, J., & Ferguson, S. (2012). Insights into children’s understandings of mass measurement. In T. Y. Tso (Ed.), Proceedings of the 36th conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 201–208). Taipei: PME.

    Google Scholar 

  • McDonough, A., Cheeseman, J., & Ferguson, S. (2013). Young children’s emerging understandings of the measurement of mass. Australasian Journal of Early Childhood, 38(4), 13–20.

    Google Scholar 

  • McDonough, A., & Sullivan, P. (2011). Learning to measure length in the first three years of school. Australasian Journal of Early Childhood, 36(3), 27.

    Google Scholar 

  • McDonough, A., & Sullivan, P. (2014). Seeking insights into young children’s beliefs about mathematics and learning. Educational Studies in Mathematics, 87(3), 279–296. doi:10.1007/s10649-014-9565-z.

    Article  Google Scholar 

  • Ministry of Education Singapore. (2014). 2013 Primary mathematics teaching and learning syllabus. https://www.moe.gov.sg/docs/default-source/document/education/syllabuses/sciences/files/mathematics-syllabus-%28primary-1-to-4%29.pdf.

  • Neumann, M. (2014). Mathematics teaching: Listening, probing, interpreting and responding to children’s thinking. Investigations in Mathematics Learning, 6(3), 1–28.

    Google Scholar 

  • New Zealand Ministry of Education. (2014). The New Zealand curriculum online. http://nzcurriculum.tki.org.nz/The-New-Zealand-Curriculum/Mathematics-and-statistics.

  • Outhred, L., & Mitchelmore, M. (2000). Young children’s intuitive understanding of rectangular area measurement. Journal for Research in Mathematics Education, 31(2), 144–167.

    Article  Google Scholar 

  • Peräkylä, A. (2005). Analysing talk and text. In N. Denzin & Y. Lincoln (Eds.), Handbook of qualitative research (3rd ed., pp. 869–886). Newbury Park, CA: Sage.

    Google Scholar 

  • Salgad, F., & Stacey, K. (2014). Item context factors affecting students’ performance on mathematics items. In J. Anderson, M. Cavanagh, & A. Prescott (Eds.), Curriculum in focus: Research guided practice (Proceedings of the 37th annual conference of the Mathematics Education Research Group of Australasia) (pp. 55–62). Sydney: MERGA.

    Google Scholar 

  • Sarama, J., & Clements, D. H. (2009). “Concrete” computer manipulatives in mathematics education. Child Development Perspectives, 3(3), 145–150.

    Article  Google Scholar 

  • Sarama, J., Clements, D. H., Barrett, J., Van Dine, D. W., & McDonel, S. (2011). Evaluation of a learning trajectory for length in the early years. ZDM, 43(5), 667–680.

    Article  Google Scholar 

  • Schiller, W., & Einarsdottir, J. (2009). Special issue: Listening to young children’s voices in research—Changing perspectives/changing relationships. Early Child Development and Care, 179(2), 125–130.

    Article  Google Scholar 

  • Sfard, A. (2001). There is more to discourse than meets the ears: Looking at thinking as communicating to learn more about mathematical learning. Educational Studies in Mathematics, 46(1/3), 13–57.

    Article  Google Scholar 

  • Sfard, A., Nescher, P., Streefland, L., Cobb, P., & Mason, J. (1998). Learning mathematics through conversation: Is it as good as they say? For the Learning of Mathematics, 18(1), 41–51.

    Google Scholar 

  • Skemp, R. (1986). Twice five plus the wings of a bird [video]. London: BBC.

    Google Scholar 

  • Smith, J., van den Heuvel-Panhuizen, M., & Teppo, A. (2011). Learning, teaching, and using measurement: Introduction to the issue. ZDM, 43(5), 617–620.

    Article  Google Scholar 

  • Spinillo, A. G., & Batista, R. F. (2009). A sense of measurement: What do children know about the invariant principles of different types of measurement? In M. Tzekaki, M. Kaldrimidou, & H. Sakonidis (Eds.), Proceedings of the 33rd conference of the International Group for the Psychology of Mathematics Education (Vol. 5, pp. 161–168). Thessaloniki: PME.

    Google Scholar 

  • Thornbury, S., & Slade, D. (2006). Conversation: From description to pedagogy. Cambridge: Cambridge University Press.

    Book  Google Scholar 

  • van Oers, B. (2014). The roots of mathematising in young children’s play. In U. Kortenkamp, B. Brandt, C. Benz, G. Krummheuer, S. Ladel, & R. Vogel (Eds.), Early mathematics learning (pp. 111–124). New York: Springer.

    Chapter  Google Scholar 

  • Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27(4), 458–477.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Monash University, Melbourne, Australia

    Jill Cheeseman & Dianne Golemac

  2. Australian Catholic University, Melbourne, Australia

    Andrea McDonough

Authors
  1. Jill Cheeseman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andrea McDonough
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dianne Golemac
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jill Cheeseman.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cheeseman, J., McDonough, A. & Golemac, D. Investigating Children’s Thinking About Suspended Balances. NZ J Educ Stud 52, 143–158 (2017). https://doi.org/10.1007/s40841-016-0073-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40841-016-0073-9

Keywords

Search

Navigation