On Total Domination and Hop Domination in Diamond-Free Graphs

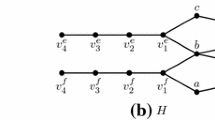
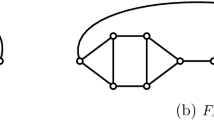
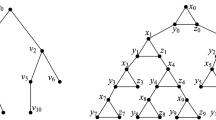
Abstract

Two vertices in a graph are said to 2-step dominate each other if they are at distance 2 apart. A set S of vertices in a graph G is a hop dominating set of G if every vertex outside S is 2-step dominated by some vertex of S. The hop domination number, $\gamma _{h}(G)$, of G is the minimum cardinality of a hop dominating set of G. A set S of vertices in a graph G is a total dominating set of G if every vertex in G is adjacent to at least one vertex of S. The total domination number, $\gamma _{t}(G)$, of G is the minimum cardinality of a total dominating set of G. It is known that if G is a triangle-free graph, then $\gamma _{h}(G)\le \gamma _{t}(G)$. But there are connected graphs G for which the difference $\gamma _{h}(G)-\gamma _{t}(G)$ can be made arbitrarily large. It would be interesting to find other classes of graphs G that satisfy $\gamma _{h}(G)\le \gamma _{t}(G)$. In this paper, we study the relationship between total domination number and hop domination number in diamond-free graph. We prove that if G is diamond-free graph of order n with the exception of two special graphs, then $\gamma _{h}(G)- \gamma _{t}(G)\le \frac{n}{6}$. Furthermore, we find two subclasses of diamond-free graphs G that satisfy $\gamma _{h}(G)\le \gamma _{t}(G)$ and generalize the known result.