Composition, Compatibility, and the Functional Performances of Ternary NiTiX High-Temperature Shape Memory Alloys

Abstract

A general procedure to optimize shape memory alloys (SMAs) for specific engineering performance metrics is outlined and demonstrated through a study of ternary, NiTiX high-temperature SMAs, where X = Pd, Hf, Zr. Transformation strains are calculated using the crystallographic theory of martensite and compared to the cofactor conditions, both requiring only lattice parameters as inputs. Measurements of transformation temperatures and hysteresis provide additional comparisons between microstructural-based and transformation properties. The relationships between microstructural-based properties and engineering performance metrics are then thoroughly explored. Use of this procedure demonstrates that SMAs can be tuned for specific applications using relatively simple, fast, and inexpensive measurements and theoretical calculations. The results also indicate an overall trade-off between compatibility and strains, suggesting that alloys may be optimized for either minimal hysteresis or large transformation strains and work output. However, further analysis of the effects of aging shows that better combinations of uncompromised properties are possible through solid solution strengthening.

Introduction

Shape memory alloys (SMAs) are a class of advanced materials that can exhibit desirable multifunctional properties such as combinations of large recoverable strains, high strengths, temperature sensing, actuation, and energy conversion. Currently, near equiatomic compositions of nickel-titanium (NiTi or Nitinol) dominate commercial SMA technologies [1]. However, many demonstrated technologies are limited in their ability to be commercialized by the properties and performance of binary NiTi. These limitations have motivated decades of research which focused on developing SMAs that outperform NiTi. These efforts have produced exciting results. Examples include NiTiHf alloys with transformation temperatures and strengths nearly twice those of NiTi [1–4], and NiTiCu alloys that can undergo 10⁷ fully reversed superelastic cycles and demonstrate the exact same functional performance in cycle 10⁷ as in cycle 1 [5, 6]. These successes demonstrate that by varying chemical compositions and thermomechanical treatments, SMA microstructures and in turn SMA properties can be successfully optimized and tuned for specific engineering applications.

Shape memory behaviors in alloys are enabled by a thermoelastic martensitic transformation between a high-temperature, high-symmetry austenite phase and a low-temperature, low-symmetry martensite phase [7]. Overall SMA performance is generally defined in terms of operating temperatures, mechanical work, life, and energy dissipation/efficiency. Operating temperatures for SMAs are defined with respect to the start (s) and finish (f) temperatures for transforming to austenite (A) and martensite (M) phases, A _s , A _f , M _s, and M _f. Mechanical work is the integrated area under the stress–strain curve; thus, higher transformation stresses and/or strains increase this performance metric. Life, for SMAs, can refer to cycles to material failure (structural fatigue) or cycles to operational failure (functional fatigue) [8]. Finally, energy dissipation/efficiency is dictated by the transformation hysteresis which is a direct measure of the energy dissipated during forward and reverse phase transformation [9, 10]. Hence, hysteresis and the life of SMAs are related, as small hysteresis is an indicator of highly reversible transformation and low amounts of damage or irreversible plastic deformation incurred during the phase transformation process. In the absence of mechanical load, hysteresis can be defined as the difference between the austenite-to-martensite transformation temperatures and the martensite-to-austenite transformation temperatures, after [11, 12]. In total, all of these performance metrics are dictated by microstructure and chemical composition.

While significant developments have been made in models of chemistry-microstructure–property relationships (e.g., [13–16]), predicting the performances of new SMAs solely through computations remains an open challenge. Thus, establishing an efficient procedure to analyze experimentally measured process-structure-property trends of SMA systems is a critical tool toward predicting and designing new SMAs. Toward this purpose, mathematical descriptions of the compatibility of microstructure interfaces in SMAs have been formulated (formulations given in Sect. 2) and used to guide combinatorial experimental searches for promising new alloys [9, 17–19]. Through these efforts, it has been shown that as compatibility between austenite and martensite phases across interfaces decreases, the size of the hysteresis increases [9, 18, 20–22]. It then follows that alloys with the most compatible interfaces should have the longest lives and most repeatable functional performances.

However, these approaches do not account for important microstructure “material genomes” that improve the performances of SMAs, such as dislocations structures and precipitates. Precipitates, in particular, have proved important to SMA actuator design. The cold work + aging treatments developed for binary NiTi by Miyazaki et al. [23] established the status-quo for processing biomedical NiTi alloys for use in isothermal environments (i.e., inside the human body). However, for actuation, this processing is not ideal. The dislocation structures created by cold work to impart strength to binary NiTi alloys are not stable in cycling temperatures by more than 50 °C hundreds to thousands of times. Thermal excitation of the dislocations (even by small amounts) encourages their mobility and reorganization. Thus, binary alloys processed with the same means used to stabilize their microstructures for biomedical applications experience functional fatigue (a.k.a. “walking,” “ratcheting,” “shakedown,” etc.) when used for actuator applications. Intermetallic precipitates enabled by ternary alloying, however, have shown to add great resistance to functional fatigue, such that an alloy may merely be cast and heat treated to achieve functional stability.

Furthermore, the SMA with the most theoretically compatible interfaces reported to date but no precipitates, Zn₄₅Au₃₀Cu₂₅ fractured after some 16,000+ cycles through phase transformation without any load [20]. NiTiCu alloys with precipitates yet worse compatibility, however, have demonstrated 10⁷ fully reversed transformation cycles under load [5]. Growth of precipitates has also been shown to dramatically reduce hysteresis [1]. Thus, it is clear that while theoretically rational, the established methodology of screening alloys solely based on compatibility of austenite–martensite interfaces is incomplete in its ability to evaluate all engineering aspects of SMAs. Still, the alternative program of decade-long alloy development programs is expensive and cumbersome.

Hence, the goal of this paper is to more completely map the interplay between chemistry, microstructure, and properties using simple, established measurements and calculations. In this article, we expand upon compatibility-based evaluation methodology to simultaneously consider precipitation, recoverable strains, and work output. Through this expanded lens, we compare nickel-titanium-(palladium, hafnium, zirconium) ternary high-temperature SMAs, some of which have been previously reported, others that are new to this work. Note that “high-temperature” SMAs means alloys with transformation temperatures greater than the maximum transformation temperature of binary NiTi compositions, which is 390 K. The result is a unified approach to evaluate SMAs using only lattice parameters and transformation temperatures, considering chemical composition, processing, and existing data. This procedure can be used to identify trends and trade-offs in engineering performances. Using this information, materials can be optimized specifically for unique applications.

Before proceeding to describe this work in more detail, definitions of a few terms are given. Strains that are recoverable through phase transformation are driven by the symmetry difference between the austenite and martensite phases, as well as martensite reorientation strains. In this work, we categorize these strains as follows:

Single variant transformation strain	The strain observed when a single austenite crystal fully transforms to a single martensite crystal
Reorientation strain	The strain observed when a single martensite crystal of fully twins to another single martensite crystal. The detwinning strain is simply the opposite strain, and is also a reorientation strain
Transformation twinning strain	The strain observed when a single austenite crystal fully transforms to martensite twins

Methods

Calculations

Here we summarize the collection of calculations used to map structure–property relations of SMAs in Sect. 3. The crystallographic theory of martensite (also called the Phenomenological Theory of Martensite) originated more than 50 years ago as a means to calculate the geometrically plausible austenite–martensite, twinned martensite, and austenite-twinned martensite interfaces knowing only the austenite and martensite lattice parameters [11, 24–28]. The calculations are made using the transformation stretch matrices, or Bain matrices, $\varvec{U}_{i}$, where i ranges from 1 to the number of martensite variants. The number of variants for a given transformation is equal to the number of symmetries in the austenite point group, ${\mathcal{L}}^{a}$, divided by the number of symmetries in the martensite point group, ${\mathcal{L}}^{m}$ [11]. There are different ways of calculating the transformation matrices, depending on the chosen lattice vector bases. In this work, cubic-to-orthorhombic transformation matrix convention is adopted from [21], and the cubic-to-monoclinic conventions from [24, 25], as summarized in [11]. It is important to note that the NiTiHf and NiTiZr cubic-to-monoclinic alloys in this paper have “face-diagonal” variants, and the ZrAuCu cubic-to-monoclinic alloys have “cube-edge” variants. For this reason, they have different transformation matrices and different twin modes. For more information on the distinction between “cube-edge” variant transformation matrices from “face-diagonal,” see [30].

Two variants, i and j, can form twinned microstructures when their transformation matrices satisfy the mathematical kinematic compatibility condition called the twinning equation:

$$\varvec{RU}_{j} - \varvec{U}_{i} = \varvec{a} \otimes \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} }$$

(1)

This condition stipulates that the two variants must be related by a rotation in ${\mathcal{L}}^{a}$ that is not also in ${\mathcal{L}}^{m}$. The resulting twin pair (i, j) can be related through a pure rotation $\varvec{R}$ and form a twin interface with a plane normal $\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} }$ and a twin shear $\varvec{a}$. For the case where two variants are related in this way, there are two distinct solutions. These solutions are conventionally classified as Type I/II twins or domains or Compound twins or domains. For the distinction between twins and domains, see Ref. [18]. Only twins are investigated in this paper. Solutions to Eq. (1) were found following the procedures in [11, 26, 28]. For convenience, twin pairs are commonly organized into twin modes, or twin sets, where each mode groups common twin solutions. For more details, see Refs. [11, 29]. The twin mode designations used in this work are given in Sect. 3.

Unless a martensite variant has near perfect compatibility with an austenite lattice (i.e., λ _II  = 1), the variant cannot form a kinematically compatible interface with the austenite by itself. Still, in this circumstance, a martensite twin structure may be able to form an austenite interface through the average gradient of the two variants, $f\varvec{RU}_{j} + \left( {1 - f} \right)\varvec{U}_{i}$, where f is the volume fraction of $\varvec{U}_{j}$ within the twinning microstructure. The mathematical condition for such kinematic compatibility is called the habit plane equation and is given as

$$\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R} }\left\{ {f\varvec{RU}_{j} + \left( {1 - f} \right)\varvec{U}_{i} } \right\} - \varvec{I} = \varvec{b} \otimes \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m} }$$

(2)

where I is the identity matrix. If a twin pair (i, j) can produce a solution to this equation and i ≠ j, then there will be four distinct solutions (or in special cases, only two solutions) for each Type I twin and each Type II twin (totaling eight solutions for each (i, j)). For each solution, the average gradient and the identity matrix are related through some rotation $\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R} }$, $\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m} }$ is the habit plane or austenite–martensite interface normal, and $\varvec{b}$ is the shape strain. The existence of a solution for the habit plane equation can be reduced to two simple conditions (assuming that λ _II  ≠ 1).

$$\delta^{*} = \varvec{a} \cdot \varvec{U}_{i} \left( {\varvec{U}_{i}^{2} - \varvec{I}} \right)^{ - 1} \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \le - 2$$

(3)

$$tr\varvec{U}_{i}^{2} - \det \varvec{U}_{i}^{2} - 2 + \frac{1}{{2\delta^{*} }}\left| \varvec{a} \right|^{2} \ge 0$$

(4)

If these inequalities are met exactly, then there are only two distinct solutions for each Type I and Type II twin [28].

The cofactor conditions are conditions of compatibility between the austenite and martensite phases and represent degeneracies of the crystallographic theory of martensite. There are three cofactor conditions.

$$CC1: \lambda_{II} = 1$$

(5)

$$CC2: \varvec{a} \cdot \varvec{U}_{i} cof\left( {\varvec{U}_{i}^{2} - \varvec{I}} \right)\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } = 0$$

(6)

$$CC3: tr\varvec{U}_{i}^{2} - \det \varvec{U}_{i}^{2} - \frac{1}{4}\left| \varvec{a} \right|^{2} - 2 > 0$$

(7)

An alloy that satisfies the cofactor conditions will have special microstructural compatibilities. An alloy that perfectly satisfies CC1 will be able to form a compatible, straight (zero curvature) interface between austenite and a single variant of martensite with no elastic transition layer or geometrically necessary defects. If the alloy additionally satisfies CC2 and CC3, then it will be able to form twins of any relative volume fraction, f, with zero elastic transition layer, where the twin pairs satisfy the relations in Eqs. 1 and 2 [17, 18] and the curvature of the interface can change using different values of f. It should be noted that CC3 is a relatively mild condition and is satisfied by all alloys considered for this paper.

According to elastic energy minimization, an austenite domain will transform to the martensite variant that provides the largest transformation strain in the direction of the applied load. Following [11], the maximum recoverable strain under a uniaxial tensile or compressive load is given by Eqs. 8, 9, where $\hat{\varvec{e}}$ is the direction of the applied load.

$$Maximum\,recoverable\,tensile\,strain= \mathop {\hbox{max} }\limits_{{U_{i = 1, \ldots k} }} \sqrt {\hat{\varvec{e}} \cdot \varvec{U}_{i} \hat{\varvec{e}}} - 1$$

(8)

$$Maximum\,recoverable\,compressive\,strain= \left| {\mathop {\hbox{min} }\limits_{{U_{i = 1, \ldots k} }} \sqrt {\hat{\varvec{e}} \cdot \varvec{U}_{i} \hat{\varvec{e}}} - 1} \right|$$

(9)

It can be shown that the tensile solution is a function of only the largest principal stretch, λ _III (i.e., the largest eigenvalue of the $\varvec{U}_{i}$), and the compressive solution is a function of only the smallest principal stretch, λ _I (i.e., the smallest eigenvalue of the $\varvec{U}_{i}$).

$$Maximum\,recoverable\,tensile\,strain = \lambda_{III} - 1$$

(10)

$$Maximum\,recoverable\,compressive\,strain = 1 - \lambda_{I}$$

(11)

Following [16], the maximum recoverable shear strain in a plane with the normal, $\hat{\varvec{n}}$, in the shear direction, $\varvec{s}$, is given by

$$Maximum\,recoverable\,shear\,strain = \mathop {\hbox{max} }\limits_{{U_{i = 1, \ldots k} }} \frac{1}{2}\hat{\varvec{s}} \cdot \left( {\varvec{U}_{i}^{T} \cdot \varvec{U}_{i} - \varvec{I}} \right)\hat{\varvec{n}}$$

(12)

The maximum possible shear strain is found by cycling through all variants over all possible planes and all possible directions. It can be shown that the solution is a function of only λ _I and λ _III , where

$$Maximum\,recoverable\,shear\,strain = \frac{1}{4}\left( {\lambda_{III}^{2} - \lambda_{I}^{2} } \right)$$

(13)

Reorientation strains can be calculated by finding the magnitude of the strains that result from variant i twinning into variant j for all martensite twin pairs (i, j) satisfying Eq. 1. For a given alloy, this strain will depend on the orientation and the twinning mode. Summarizing the derivation given in [31], knowing the twinning shear, s, we can calculate the deformation gradient $\varvec{F^{\prime}}$ of the twin formation with respect to an orthonormal twin plane coordinate system $\hat{\varvec{e}}_{i}^{'}$, where $\hat{\varvec{e}}_{i}^{'}$ is defined by the shear direction, $\varvec{\eta}_{1}$, and $\hat{\varvec{e}}_{2}^{'}$ is defined by the twin plane normal, $\varvec{K}_{1}$.

$$\varvec{F^{\prime}} = I + s\hat{\varvec{e}}_{1}^{'} \otimes \hat{\varvec{e}}_{2}^{'}$$

(14)

This deformation can be written with respect to an arbitrary orthonormal specimen coordinate system using the rotation, $\varvec{A}$, from the orthonormal twin plane coordinate system, $\hat{\varvec{e}}_{i}^{'}$, to the orthonormal specimen coordinate system, $\hat{\varvec{e}}_{i}^{{}}$.

$$A_{ij} = \hat{\varvec{e}}_{i} \cdot \hat{\varvec{e}}_{i}^{'} = \cos \left( {i,j^{\prime}} \right)$$

(15)

$$\varvec{F} = \varvec{A} \cdot \varvec{F^{\prime}} \cdot \varvec{A}^{T}$$

(16)

$\varvec{F}$ is the deformation gradient of the twin formation with respect to the orthonormal specimen coordinate system, $\hat{\varvec{e}}_{i}$. Having calculated the deformation gradient for each known twinning mode, the axial strain of a single crystal subjected to twinning, ɛ ^twinning, may be calculated for a load applied in the $\hat{\varvec{e}}_{{\left( {hkl} \right)}}$ direction, where $\hat{\varvec{e}}_{{\left( {hkl} \right)}}$ is the unit normal vector of (hkl) planes of the austenite lattice.

$$\varepsilon^{twinning} = \left( {\varvec{F} \cdot \hat{\varvec{e}}_{{\left( {hkl} \right)}} } \right) \cdot \hat{\varvec{e}}_{{\left( {hkl} \right)}} - 1$$

(17)

The maximum possible reorientation strain is the maximum magnitude of axial strain considering all possible orientations and all twinning modes.

The transformation twinning strain is the strain that results from an austenite domain transforming into a domain of the martensite twin pair i − j, where the twin pair satisfies Eqs. 1 and 2. The calculation for the maximum transformation twinning strain is identical to that of the maximum reorientation/detwinning strain, just using a different deformation gradient, $\varvec{F^{\prime}}$. Using the magnitude of the shape strain, $\left| \varvec{b} \right|$, one can calculate the deformation gradient $\varvec{F^{\prime}}$ of the transformation twin formation with respect to an orthonormal habit plane coordinate system, $\hat{\varvec{e}}_{i}^{'}$, where $\hat{\varvec{e}}_{1}^{'}$ is defined by the shape strain direction, $\varvec{b}$, and $\hat{\varvec{e}}_{2}^{'}$ is defined by the habit plane normal, $\hat{\varvec{m}}$.

The critical transformation temperature, θ _C , and the thermal hysteresis, H, reported in this work are calculated according to

$$\theta_{C} = \frac{1}{4}\left( {A_{s} + A_{f} + M_{s} + M_{f} } \right)$$

(18)

$$H = \frac{1}{2}\left( {A_{s} + A_{f} - M_{s} - M_{f} } \right)$$

(19)

Materials

The materials reported in this work are given in Table 1. In this article, we use a shorthand notation where ternary alloys are identified by the atomic percent of the ternary alloying element; e.g., Ni_50.3Ti_25.6Hf_24.1 is referred to as 24.1Hf. The 7Pd, 9Pd, 10Pd, 11Pd, 18Pd, 20Pd, and 25Pd alloys were previously reported in [21, 32], 15Pd and 46Pd in [33], NiTi in [34], 9.5Hf, 15Hf, and 20Hf_Ti in [35], 20Hf_Ni in [1, 2]. The 24.1Hf, 17.5Zr, and 20Zr are new alloys reported for the first time in this work. We also compare with Zn₄₅Au₃₀Cu₂₅ [20], as it is the alloy with the most compatible interfaces according to the cofactor conditions (5–7) ever reported, and also Ti₅₄Ni₃₄Cu₁₂ (12Cu) [5], the alloy with the best reported resistance to both functional and structural fatigue to-date, and Ti₅₁Ni₃₆Cu₁₃ (13Cu) [5], an alloy of the same family but without precipitates. The importance of these alloy qualities is further discussed in Sect. 4 (Tables 2, 3).

Table 1 Compositions, heat treatments, and literature references for all alloys used in the calculations and comparisons presented in this paper

Table 2 A comparison of some microstructural parameters between Ti₅₄Ni₃₄Cu₁₂ (12Cu) and Ti₅₄Ni₃₄Cu₁₃ (13Cu) [5]

Table 3 A comparison of some microstructural parameters between aged (20Hf_Nia) and unaged (20Hf_Ni u) Ni_50.3Ti_29.7Hf₂₀ [1]

These new alloys were processed as 0.5 kg ingots by vacuum induction melting of the elemental constituents using a graphite crucible and then casting into in copper chill mold. The ingots were homogenized in vacuum at 1050 °C for 72 h and subsequently extruded at 900 C. Samples for XRD and DSC were EDM cut from the extruded rods and samples for XRD were subsequently polished prior to analysis. Samples in the “aged condition” were heat treated at 550 °C for 3 h. in flowing argon and air cooled.

Lattice Parameter Measurements

For the new alloys, lattice parameters were measured using a Bruker D8 Discover X-ray diffractometer configured with an Anton Paar HTK 2000 hot stage. Experiments were performed on a Pt heating filament with a thin layer of thermally conductive carbon paste affixing the sample to the heating filament. Sample temperature was monitored via two thermocouples, one native to the Pt heating filament and a second thermal couple bonded to each sample via thermally conductive silver paste. In our measurements, the sample temperature did not differ from the instrument temperature by more than ±1 °C.

XRD data were collected using Cu radiation with a Ni filter. Scans were made from 10° to 100° − 2θ, in 0.04° steps, with a dwell time of 2 s. Lattice parameters were extracted using the Pawley fitting routine native to Topas X-ray diffraction analysis software. The high-temperature B2 phase was fit first, then the precipitates. The precipitate structures were then copied to the martensite patterns and fixed, then the martensite structure was fit, and finally the precipitate structure parameters were relaxed again to adjust for temperature differences. Measurements were made at three temperatures above A_f (~A_f + 20, 30, and 50 °C) and two below M_f (~M_f − 10 and at room temperature) for most alloys. The single-phase linear thermal expansion in these regions was used to extrapolate the lattice parameters to the critical temperature for each alloy system. Calculations were made for this temperature.

Results

The NiTiHf and NiTiZr alloys in this study undergo a cubic-to-monoclinic phase transformation with face-diagonal martensite variants, similar to binary NiTi. Using the calculations introduced in Sect. 2.1, there are 12 martensite variants, 84 possible martensite twin pairs that satisfy Eq. 1 (where the pairs (i, j) and (j, i) are counted as two pairs, following the convention used in [29]), and four possible twin modes, A–D (following [11, 29]). The twin pairs in Mode A are Compound, and the twin pairs in Modes B-D are Type I and II. According to the conditions in Eqs. (3) and (4), only the twin pairs in Modes B and C can form compatible habit planes for all of the cubic-to-monoclinic alloys, resulting in 48 possible transformation twin pairs (24 Type I and 24 Type II). For each twin pair that is capable of forming compatible habit planes, there are four distinct habit plane solutions, resulting in 192 possible habit planes. The only exception in this work is 24.1Hf, which was found to have no twin pairs capable of forming compatible habit planes according to Eqs. (3) and (4).

All of the NiTiPd and NiTiCu alloys undergo a cubic-to-orthorhombic phase transformation. Thus, they have 6 martensite variants, 30 possible twin pairs, and two possible twin modes, A and B (following [11, 21, 36]). The twin pairs in Mode A are Compound twins, and Mode B comprises Type I and II twins. As reported in [21], the twin pairs in Mode A cannot form compatible habit planes when λ _II  > 1, and twin pairs in Mode B cannot form compatible habit planes when λ _II  < 1. Thus, the cubic-to-orthorhombic alloys with λ _II  < 1 (7Pd, 9Pd, 10Pd, 12Cu, and 13Cu) have only 6 twin pairs capable of forming compatible habit planes and 24 possible habit plane solutions. The other cubic-to-orthorhombic alloys, which all have λ _II  > 1 have 24 twin pairs capable of forming compatible habit planes and 96 possible habit plane solutions.

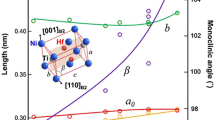
The relationship between the tertiary species composition and the middle eigenvalue, λ _II , is shown in Fig. 1. Both the cubic-to-orthorhombic and cubic-to-monoclinic SMAs show a general trend of λ _II deviating further from unity as the amount of the ternary alloying element is increased. For cubic-to-orthorhombic, λ _II deviates farther from one with increasing composition (above one for NiTiPd alloys and below one for NiTiCu alloys), and for cubic-to-monoclinic, λ _II decreases from unity with increasing composition. The 9Pd alloy has a λ _II just below one (0.9988) and the 11Pd alloy has a λ _II just above one, or perhaps approximately one considering experimental uncertainty (1.0001), indicating that a NiTiPd alloy with a tertiary composition of 11 or just below 11 will have λ _II  = 1. Aging the 15Pd alloy appears to have the effect of increasing λ _II outside of the general trend. However, the Ti-content of the 15Pd and 46Pd alloy is slightly higher than the other NiTiPd alloys, which could also influence this deviation. Comparing the unaged and aged 20Hf_Ni alloys, the aged 20Hf_Ni has λ _II closer to one, suggesting an improvement in compatibility, though it is still very far from one relative to the other alloy systems. Both the unaged 20Hf_Ni alloy and the unaged 20Hf_Ti alloy have comparable λ _II values, although the unaged 20Hf_Ti λ _II is slightly closer to one. Comparing the aged 20Hf_Ni and the aged 20Zr, the former has a λ _II closer to one.

Fig. 1

Tertiary species composition (at.%) versus λ_II for cubic-to-orthorhombic SMAs and cubic-to-monoclinic SMAs. Aged alloys are indicated by open triangular symbols. Approximate trend lines are shown for cubic-to-monoclinic unaged cubic-to-orthorhombic alloys. Note: these trends are only true for cubic-to-monoclinic alloys with “cube-edge” type variants

The results given in Figs. 2, 3, 4, 5, 6, 7, 8, 9, and 10, 11 are plotted as functions of both λ _II and composition to document relationships between λ _II and other properties while simultaneously comparing property–composition relationships. In this manner, the critical temperatures, θ _C , are examined in Fig. 2. The critical temperature decreases as the amount of ternary alloying addition decreases for each alloy system. Trends for critical temperature as a function of composition are nearly linear and very similar to data reported in [22]. As previously reported [1, 37], aging the 20Hf_Ni alloy increases θ _C , compared to the same material in the unaged condition, since the precipitates are Ni-rich, drawing the matrix closer to stoichiometry [38]. Critical temperatures do not trend with λ _II , which affirms that they have no definitive relationship with the geometry of the phases.

Fig. 2

Critical temperature (°C) versus a λ_II and b tertiary species composition (at.%) for cubic-to-orthorhombic SMAs and cubic-to-monoclinic SMAs. Binary NiTi is not included as this information was not reported in the original reference

Fig. 3

Hysteresis (°C) versus a λ _II and b tertiary species composition (at.%) for cubic to orthorhombic SMAs and cubic-to-monoclinic SMAs. Binary NiTi is not included as this information was not reported in the original reference. Approximate trend lines are shown for unaged cubic-to-orthorhombic alloys

Fig. 4

Monoclinic angle, β (°) versus a λ _II and b tertiary species composition (at.%) for cubic-to-monoclinic SMAs

Fig. 5

Maximum tensile single variant transformation strain (a, b), maximum compressive single variant transformation strain (c, d), and maximum shear transformation strain (e, f) versus λ _II and tertiary species composition (at.%) for cubic-to-orthorhombic SMAs and cubic-to-monoclinic SMAs. Although the Zr-Au-Cu alloys are not derivative NiTiX alloys, they are included in (a, c, e) to allow for comparison, given their remarkable properties

Fig. 6

Maximum tensile single variant transformation strain, maximum compressive single variant transformation strain, and maximum shear transformation strain versus monoclinic angle, β (°) (a–c), a/a ₀ (d–f), b/a ₀ (g–h), and c/a ₀ (i–l), for cubic-to-monoclinic SMAs

Fig. 7

Maximum axial reorientation strain versus λ _II and tertiary species composition (at.%) for cubic-to-orthorhombic SMAs, comparing twin pairs exhibiting Mode A-Compound twinning (a, b) and Mode B-Type I/II twinning (c, d)

Fig. 8

Maximum axial reorientation strain versus λ _II and tertiary species composition (at.%) for cubic-to-monoclinic SMAs, comparing twin pairs exhibiting Mode A-Compound twinning (a, b), Mode B-Type I/II twinning (c, d), Mode C-Type I/II twinning (e, f), and Mode D-Type I/II twinning (g and h). For comparison, Zn₄₅Au₃₀Cu₂₅ (λ _II  = 1.0006) has maximum axial reorientation strains of 1.4 and 5.4 % for its two compound modes and 11.6 and 6.4 % for its two Type I/II modes

Fig. 9

Maximum axial transformation twinning strain versus λ _II and tertiary species composition (at.%) for cubic-to-orthorhombic SMAs, comparing twin pairs exhibiting Mode A-Compound twinning (a, b) and Mode B-Type I/II twinning (c, d). Notice that all alloys either appear in Mode A (if λ _II  < 1) or Mode B (if λ _II  > 1) due to habit plane compatibility

Fig. 10

Maximum axial transformation twinning strain versus λ _II and tertiary species composition (at.%) for cubic-to-monoclinic SMAs, comparing twin pairs exhibiting Mode B-Type I/II twinning (a, b) and Mode C-Type I/II twinning (c, d). None of the Mode A or Mode D twin pairs can satisfy habit plane compatibility. Notice that the 24.1Hf does not appear since it cannot form any compatible habit planes. For comparison, Zn₄₅Au₃₀Cu₂₅ (λ _II  = 1.0006) has maximum transformation twinning strains of 5.8 % for its only habit plane-compatible Compound mode and 1.6 % for its only habit plane-compatible Type I/II mode

Fig. 11

Values of the second cofactor condition, CC2, versus λ _II and tertiary species composition (at.%) for cubic-to-orthorhombic SMAs, comparing twin pairs exhibiting Mode A-Compound twinning (a, b), Mode B-Type I twinning (c, d), and Mode B-Type II twinning (e and f)

Thermal hysteresis, H, is shown in Fig. 3 as a function of λ _II and tertiary species composition. As previously reported, for the unaged NiTiPd alloys, hysteresis is lowest near λ _II  = 1, and the hysteresis increases as λ _II deviates from 1 in either direction (e.g., [9, 18, 20, 21, 32]). The aged NiTiPd alloys, however, show that the growth of P-phase precipitates reduces hysteresis. In fact, aged 15Pd has the lowest hysteresis of any NiTiPd alloy considered here (10 °C), even though it has a λ _II of 1.011, relatively far from 1. The Ni–Ti–Cu alloys have relatively low hysteresis, although it is interesting that the 13Cu alloy has a lower hysteresis than the 12Cu alloy since the 12Cu alloy showed better resistance to functional fatigue. Similarly, unaged NiTiHf alloys show a clear, expected correlation between λ _II and hysteresis according to theory, while aging defies this trend. Comparing the aged versus unaged 20Hf_Ni alloys, the aged 20Hf_Ni alloy has a lower hysteresis than the unaged (36 °C for unaged versus 28.5 °C for aged), even though the values of λ _II are similar (0.9337 for unaged versus 0.9394 for aged). The unaged 20Hf_Ti alloy has a much higher hysteresis (70 °C) than aged or unaged 20Hf_Ni, even though they all have similar λ _II values. Comparing the aged 20Hf_Ni alloy and the aged 20Zr alloy, the aged 20Hf_Ni alloy has a lower hysteresis (42.25 °C for 20Zr vs. 28.5 °C for 20Hf), even though their values of λ _II are also similar (0.9380 for 20Zr vs. 0.9394 for 20Hf_Ni).

The non-orthogonal monoclinic angle, β, is shown as a function of λ _II and tertiary species composition in Fig. 4. Overall, β decreases as λ _II  → 1, and increases as the tertiary species composition increases. The significance of β as an optimization criterion is discussed later in this section.

The maximum theoretical tensile, compressive, and shear single variant transformation strains are shown in Fig. 5 as a function of λ _II and tertiary species composition. For cubic-to-orthorhombic alloys, the dominant trend shows that transformation strains are a maximum for λ _II  > 1, and they decrease as λ _II decreases, irrespective of λ _II  = 1 (Fig. 5a, c, e). They also decrease with decreasing tertiary species composition. Interestingly, examining the λ _II trends, aging does not seem to matter—the Cu and Pd alloys trend together in a linear fashion, with the exception of the 46Pd alloy (Fig. 5a, c, e). Compared compositionally, the Cu alloys have much lower strains than the Pd alloys, which show a very non-linear behavior with the aged 15Pd exhibiting slightly larger strains compared to the general trend for unaged Pd alloys (Fig. 5b, d, f).

Cubic-to-monoclinic alloys exhibit the opposite trend. Theoretical transformation strains are maximum for λ _II  < 1 and decrease as λ _II increases (Fig. 5a, c, e), except for the binary NiTi compression outlier (Fig. 5c). Comparing the aged versus unaged 20Hf_Ni alloys, aging increases the strains for all three loading modes. The unaged 20Hf_Ni and unaged 20Hf_Ti alloys have near identical strains, although the unaged 20Hf_Ti strains are slightly but consistently lower. Finally, the aged 20Zr alloy exhibits the largest strains of any of the ternary alloys. The spreads of recoverable tensile and shear strains (Fig. 5a, b, e, f) are larger for cubic-to-monoclinic than for cubic-to-orthorhombic transformations, even though they both span approximately the same range of λ _II values. However, compressive strain variations are similar (Fig. 5c, d).

The maximum theoretical tensile, compressive, and shear single variant transformation strains are shown in Fig. 6 as a function of the monoclinic angle β. All of the strains increase very linearly with β, regardless of processing or tertiary species. The trends between the strains and the monoclinic lattice parameters (normalized by the austenite lattice parameter) are slightly less clear. Overall, the strains increase as b/a ₀ decreases and c/a ₀ increases and have no correlation with a/a ₀. The tuning of the angle β, therefore, can have very predictable effects on the theoretical strains as opposed to the lattice parameter lengths. The relationship between single variant transformation strains and cubic-to-orthorhombic lattice parameters is not shown. This is because, in the absence of a non-orthogonal angle, the eigenvalues are equivalent to the orthorhombic lattice parameters normalized to the cubic lattice parameter. Following the discussion in Sect. 2.1, the single variant transformation strains are a direct function of the eigenvalues. As a result, whereas β is an optimal tuning parameter for cubic-to-monoclinic, the normalized lattice parameters are optimal tuning parameters for cubic-to-orthorhombic.

The maximum axial reorientation strains for orthorhombic structures are shown in Fig. 7, again as a function of λ _II and tertiary species composition. Mode A (Compound) twins do not exhibit a definitive trend with respect to λ _II or composition (Fig. 7a, b). Mode B (Type I/II) twins show a general increase in strain as λ _II increases and as ternary alloy composition increases (c, d), and they are much larger than that of Mode A. As was observed of single variant transformation strain trends, twinning strains for Mode B twins trend according to λ _II independent of the ternary alloying element (Fig. 7c), even though the Cu alloys have much lower Mode B strains than Pd alloys (Fig. 7d).

The maximum axial reorientation strains for monoclinic martensites are shown in Fig. 8. Modes A (Compound), B (Type I/II), and C (Type I/II) twins show a general increase in strain as λ _II decreases from unity and as composition increases (Fig. 8a–f), while Mode D (Type I/II) twins do not exhibit any clear trends (Fig. 8g, h). As with the tensile and shear single variant transformation strains, the monoclinic twinning strains are larger than those of orthorhombic martensite, with correlations to λ _II and composition that are more pronounced. Different from transformation strains, the twinning strains for all modes are largest for aged 24.1Hf, while the aged 20Zr alloy shows the second largest. Similar to transformation strains (Fig. 5), reorientation strains for all modes are slightly larger for aged 20Hf_Ni than for unaged 20Hf_Ni, and are slightly smaller for unaged 20Hf_Ti than for unaged 20Hf_Ni.

The maximum axial transformation twinning strains for cubic-to-orthorhombic alloys are shown in Fig. 9. Again, these are the strains incurred from transforming from a single austenite grain to a single martensite twin according to the Phenomenological Theory of Martensite [28, 39]. Notice that only 7Pd, 9Pd, 10Pd, 12Cu, and 13Cu strains are plotted for Mode A (Fig. 9a, b) and 11Pd, 15Pd, 20Pd, 25Pd, 18Pd 46Pd for Mode B. The omission of data points results from lack of solutions of compatible habit planes for all types of twins, as documented at the beginning of this section. An opposite trend develops relative to martensite twinning (Fig. 7)—the Mode A (Compound) transformation twinning strains increase as λ _II decreases from unity, while mode B (Type I/II) transformation twins do not exhibit a definitive trend with respect to λ _II or composition. However, similar to all previous cases, the Cu alloys exhibit lower Mode A strains according to composition, but follow the general trend according to λ _II .

The analogous transformation twinning strains for cubic-to-monoclinic alloys are shown in Fig. 10. Notice that only Modes B and C are shown and 24.1Hf does not appear at all, as these are the only habit plane solutions. Both modes show a general increase in strain as λ _II decreases from unity and as composition increases. As with the single variant strains and the reorientation strains, the transformation twinning strains are larger than cubic-to-orthorhombic transformations, with correlations to λ _II and composition that are more pronounced. Similar to single variant transformations (Fig. 5) and the reorientation strains (Fig. 8), aged 20Zr exhibits the largest strains and aged 20Hf_Ni strains are larger than unaged 20Hf_Ni. Converse to Figs. 5 and 8, the unaged 20Hf_Ti alloy has slightly larger strains than the unaged 20Hf_Ni alloy.

The values of the second cofactor condition, CC2, for cubic-to-orthorhombic alloys are shown in Fig. 11. The trend of the Mode B, Type I/II twins for the Pd alloys is an almost perfectly linear decrease in CC2 (toward the ideal value of 0) as λ _II decreases. The minimum CC2 of 4.7e−5 is not at λ _II  = 1, but instead is at the lowest Pd composition of 7. The CC2 of the Pd alloys decreases with decreasing composition. The 12Cu and 13Cu alloys, which have λ _II of 0.9906 and 0.9892, exhibit larger CC2 values of 2.3e−4 and 2.5e−4 and do not trend with the Pd alloys with respect to λ _II or composition. The Mode A CC2 trends (Fig. 11a, b) are not as definitive as for Mode B (Fig. 11c, d), and the values are much larger. Also, the 46Pd alloy shows the largest Mode B CC2 of 7.6e−3, yet the lowest Mode A CC2 of 1.4e−4.

The values of the second cofactor condition, CC2, for cubic-to-monoclinic alloys are shown in Fig. 12. For Modes A-C, CC2 decreases as λ _II approaches unity and as composition decreases. For Mode D (Fig. 12k–n), the trend is not as clear. However, the CC2 values for Mode D are 1–3 orders of magnitude lower than that of the other twin modes. With the exception of Mode D, the CC2 values for cubic-to-monoclinic alloys are larger than that of cubic-to-orthorhombic alloys. Comparing aged 20Hf_Ni and aged 20Zr, 20Hf_Ni has lower CC2 values for all twin modes. Comparing aged 20Hf_Ni and unaged 20Hf_Ni, aged 20Hf_Ni has lower CC2 values for all twin modes. Aged 20Hf_Ni has the lowest CC2 value of 2.4e−5 (Mode D, Type II) of any alloy, cubic-to-monoclinic or cubic-to-orthorhombic. This is much lower than Ti₅₄Ni₃₄Cu₁₂ CC2 values (all of the order 10⁻⁴ [5]), and this is even closer-to-ideal than Zn₄₅Au₃₀Cu₂₅, which has CC2 values of roughly 5.0e−5 and 8.1e−4 for its two Compound modes, 4.0e−5 and 9.9e−4 for its two Type I modes, and 3.6e−5 and 9.9e−4 for its two Type II modes [20]. The unaged 20Hf_Ni has the second lowest CC2 after aged 20Hf_Ni at 3.0e−5.

Fig. 12

Values of the second cofactor condition, CC2, versus λ _II and tertiary species composition (at.%) for cubic-to-monoclinic SMAs, comparing twin pairs exhibiting Mode A-Compound twinning (a, b), Mode B-Type I twinning (c, d), Mode B-Type II twinning (e, f), Mode C-Type I twinning (g, h), Mode C-Type II twinning (i, j), Mode D-Type I twinning (k, l), and Mode D-Type II twinning (g, h). For comparison, Zn₄₅Au₃₀Cu₂₅ has CC2 values of roughly 5.0e−5 and 8.1e−4 for its two Compound modes, 4.0e−5 and 9.9e−4 for its two Type I modes, and 3.6e−5 and 9.9e−4 for its two Type II modes

Finally, to further facilitate one point in the ensuing discussion, we report actuation responses of the 24.1Hf alloy in Fig. 13.

Fig. 13

Actuation responses of the 24.1 Hf alloy under different applied loads are shown

Discussion

As stated in the Introduction, the purpose of this study is to gain new insights into the design of NiTiX high-temperature SMAs. The optimization of λ _II  = 1 is now a fairly well known story in the SMA alloy development community, but the ramifications of the second cofactor condition and the relationships between compatibility and functional strains are relatively unexplored topics. Furthermore, recent results showing that precipitation used to stabilize the reversible nature of thermoelastic martensitic transformations in an alloy where λ _II is not near 1, but CC2 is very near zero [5] has raised two questions: (1) does λ _II  = 1 need to be satisfied? (2) is a near-zero CC2 more important than λ _II  = 1? Since it will probably take many years to fully understand the ramifications of cofactor conditions relative to λ _II  = 1, and also the role of precipitates in martensitic transformations, we will attempt to discuss the implications of the data presented in the previous section in the light of these new possibilities.

Number of Possible Reversible Deformations

As previously discussed, a defect-free alloy with λ _II  = 1, CC2 = 0, and CC3 > 0 theoretically has an infinite number of possible reversible deformations available at no interfacial energy cost. This is the attraction of an alloy that perfectly, or nearly perfectly satisfies all cofactor conditions, such as Zn₄₅Au₃₀Cu₂₅ [20]. One speculation we propose based on our results is that an alloy that does not satisfy λ _II  = 1 but does have ideal, or near-ideal CC2 may have an extended number of possible reversible deformations relative to those predicted by the phenomenological theory of martensite. Without λ _II  ≈ 1, any twin system will be restricted to the twinning equation (Eq. 1), the habit plane equation (Eq. 2), and the habit plane compatibility conditions (Eqs. 3, 4). A solution satisfying these geometric requirements will prescribe a specific, fixed phase fraction for the two martensite variants. The expected effect of CC2 ≈ 0 is to relax these phase fraction constraints, in turn allowing more possible low-dissipation reversible deformations.

This rationale would explain the reported excellent resistance to functional fatigue and remarkable strength of the aged 20Hf_Ni alloy [1], which has λ _II  = 0.9394 but the lowest CC2 reported to date (2.4e-5) (Fig. 12m,n), as well as the remarkable repeatability and life of the 12Cu alloy strengthened with precipitates [5]. Both of these alloys not only have relatively poor λ _II values, but also have relatively low hysteresis (Fig. 3a) and low CC2 (for certain twin modes). The aged 20Hf_Ni alloy not only has λ _II  = 0.9394 but also has the lowest CC2 reported to date (Fig. 12m, n). For these alloys, the presence of the precipitates is clearly critical. Because an alloy with λ _II  ≠ 1 cannot have zero elastic transition layers, there will be an energy cost to creating and moving interfaces. However, the coherent and semi-coherent precipitates create local stress fields that nucleate transformation and reverse transformation, limiting the need for growth and the movement of interfaces [1, 6]. Furthermore, the full or partial coherency of the precipitates may make it possible to form low-energy precipitate-martensite interfaces when combined with the flexible phase fractions resulting from the low CC2. This postulate is supported by both unaged 20Hf_Ni and aged 20Hf_Ni having similar λ _II values and exceptionally low CC2 values, but the aged 20Hf_Ni (with its semi-coherent precipitates) having the lowest hysteresis. The necessity of the precipitates is especially likely in the case of 12Cu, which has precipitates with dual epitaxy.

The 12Cu and aged 20Hf_Ni alloys are examples of a departure from the popular λ _II  → 1, low hysteresis trend due to the presence of precipitates, especially when combined with low CC2. All of the cubic-to-orthorhombic transforming alloys have CC2 values similar to 12Cu, but only 15Pd and 46Pd are also aged (Fig. 11). These two NiTiPd alloys have values of λ _II farther from ideal than any other NiTiPd alloy, and aged 15Pd has the lowest hysteresis of any of these alloys (Fig. 3a). The aged 24.1Hf unaged 20Hf_Ti, and aged 20Zr alloys have the lowest hystereses following the aged 20Hf alloy, despite the fact that there are two unaged cubic-to-monoclinic alloys with λ _II values closer to one (9.5Hf and 15Hf, Fig. 3a). Both aged 20Zr and aged 24.1Hf have relatively large CC2 values (Fig. 12), but it is possible that they are still low enough (especially mode D, Fig. 12k–n) to decrease the hysteresis when combined with precipitation. This idea is especially supported in considering the 24.1Hf alloy—according to λ _II and the habit plane Eqs. (2), this alloy should not have any compatible austenite–martensite interfaces. This result suggests that it should be a very poor shape memory alloy. Yet the actuation responses of a single sample suggested to incrementally increasing load (Fig. 13) clearly demonstrate that the alloy shows both high transformation temperatures and good recoverable strain. These results are consistent with Wang and Sehitoglu [3]. The coherency of the precipitates, which we think is an important factor, should also be investigated for all of these cases.

Strains vs. Compatibility

There is an overall trade-off between microstructural properties that lead to large work output (strains) versus microstructural features that lead to high stability and fatigue resistance (cofactor conditions). For unaged alloys, CC2 approaches its ideal value of 0 as λ _II  → 1 (Figs. 11, 12) and the hysteresis minimizes as λ _II  → 1 (Fig. 3a). However, the single variant transformation (Fig. 5), reorientation (Figs. 7, 8), and transformation twinning strains (Figs. 9, 10) generally decrease as λ _II  → 1. This trade-off between microstructural properties will lead to a trade-off between engineering performance metrics—i.e., between stability and work output. However, as discussed in Sect. 4.1, aged alloys can diverge from this trade-off. For example, aged 20Hf_Ni has a λ _II value far from one but still has low hysteresis.

Cubic-to-monoclinic alloys exhibit larger single variant transformation (Fig. 5), reorientation/detwinning (Fig. 8), and transformation twinning strains (Fig. 10) than cubic-to-orthorhombic SMAs (Figs. 5, 7, 9). These strains are more drastically influenced by composition and λ _II , suggesting that they will be more sensitive to tuning. On the other hand, cubic-to-orthorhombic alloys exhibit lower hysteresis (Fig. 3) and have lower CC2 values with the exception of monoclinic Mode D (Figs. 11, 12). The actual shape of the monoclinic crystal system versus that of the orthorhombic crystal system may contribute to these trade-offs. Specifically, the non-orthogonal monoclinic angle, β, resulting from the shearing aspect of transformation naturally gives rise to larger strains yet it also makes compatibility between phases more difficult. This is further demonstrated in Figs. 4 and 6, which show that as β increases λ _II gets farther from ideal, and as β increases, the maximum single variant transformation strains increase very predictably.

Unaged versus Aged

A comparison of the aged 20Hf_Ni and unaged 20Hf_Ni alloys is particularly enlightening, since they have identical tertiary species compositions. Using all of the microstructural trends presented in this paper, it appears that aging 20Hf_Ni improves both compatibility and strains. Aging 20Hf_Ni reduced hysteresis (Fig. 3), brought λ _II slightly closer to ideal (0.9394 for aged 20Hf_Ni versus 0.9337 for unaged 20Hf), and decreased CC2 for all possible twin systems (Fig. 12). Aging 20Hf_Ni also increased the single variant transformation strains (Fig. 5), the reorientation strains (Fig. 8), and the transformation twinning strains (Fig. 10) for all twin modes. Thus, even though aging SMAs will cause a fraction of the volume to be occupied with non-transforming precipitates, the work output may still be substantial because of the transformation strains and the strengthening from precipitation.

Aging puts the 15Pd λ _II value further from 1 relative to the unaged NiTiPd λ _II trend (Fig. 1). Despite this λ _II value, 15Pd also has the lowest hysteresis (~10 °C) of any alloy in this paper (Fig. 3), though a quaternary NiTiPdCu alloy with lower hysteresis and more ideal λ _II was reported in other work [19]. Also, the aged 12Cu and aged 13Cu λ _II values are not particularly close to one, even though 12Cu was predicted to have a λ _II closest to 1 for Ni–Ti–Cu alloys according to the combinatorial study in [9]. In spite of this, both 12Cu and 13Cu have low hysteresis (Fig. 3). These observations reaffirm the divergence from typical theoretical λ _II -hysteresis trends for aged alloys. The effect of aging 15Pd on strains (Figs. 5, 7, 9) and CC2 (Fig. 11) is quite subtle.

Comparing Tertiary Species

It is convenient to have an assessment of both aged 20Hf_Ni and aged 20Zr to compare the effect of different tertiary species. Aged 20Hf_Ni had a λ _II slightly closer to one (0.9394 for aged 20Hf versus 0.9380 for aged 20Zr), lower hysteresis (Fig. 3), and lower CC2 values for all possible twin systems (Fig. 12). On the other hand, aged 20Zr had larger single variant transformation strains (Fig. 5), reorientation strains (Fig. 8), and transformation twinning strains (Fig. 10) for all twin modes. This suggests that a tertiary species of Hf will improve compatibility and a tertiary species of Zr will improve strains.

One must be careful distinguishing between the effect of tertiary species and the effect of aging when comparing NiTiPd and NiTiCu, since both of the NiTiCu species are aged. Some observations can still be made. For example, Cu as a tertiary species seems to decrease λ _II from one, while similar compositions of Pd will increase λ _II from one (Fig. 1). This is very apparent comparing 13Cu and 15Pd, which are both aged. Because these are cubic-to-orthorhombic alloys, this means that aged 15Pd cannot form theoretically compatible habit planes for Mode A twins, and aged 13Cu cannot form theoretically compatible habit planes for Mode B twins. Because aging had some a negligible effect on strains and CC2 for 15Pd, it can be hypothesized that Cu as a tertiary species appears to decrease strains (Figs. 5, 7, 9) and decrease CC2 (Fig. 11).

Conclusion

The approach taken in this paper demonstrates a method by which engineers can analyze trends between composition and microstructural properties to predict and design better SMAs. By using these trends together with a basic understanding of how microstructural properties give rise to engineering performance measures, alloys can be designed by tuning compositions for specific engineering performance metrics without complicated micromechanical models or costly mechanical testing. The eigenvalue λ _II is an especially useful optimization parameter, as it can be used to predict many different kinds of microstructural properties once the symmetry change of a transformation is established. However, the CC2 cofactor condition seems to be equally, if not more important and when combined with the right precipitates may be used to circumvent the strict need for λ _II  → 1. Using these criteria, some trends and trade-offs were revealed.

• Hysteresis, which is commonly improved by creating alloys with λ _II  → 1, may also be improved by aging in alloys where CC2 approaches zero.

• Low CC2 values combined with precipitation may reduce hysteresis and increase stability, regardless of λ _II . This effect could be tied to precipitate coherencies, but further investigations are needed to test this hypothesis.

• Theoretical strains are generally larger and more sensitive to tuning for cubic-to-monoclinic alloys than for cubic-to-orthorhombic alloys.

• Aging can be used as a tool to tune realized transformation and twinning strains.

• There is often a trade-off between theoretical strains versus microstructural compatibility (λ _II , CC2).

• The tertiary species element can be used to control microstructural properties. For example, in comparing Hf vs. Zr ternary alloying elements, 20 at.% of both in alloys with 50.3 at.% Ni result in θ_c of ~ 160 °C. However, Hf has slightly better compatibility and lower hysteresis, while Zr exhibits larger strains, suggesting Hf would be a better choice if maximum fatigue life were desired, Zr for higher strains.